An On-Chip RBC Deformability Checker Significantly Improves Velocity-Deformation Correlation
Abstract
:1. Introduction
2. Related Works
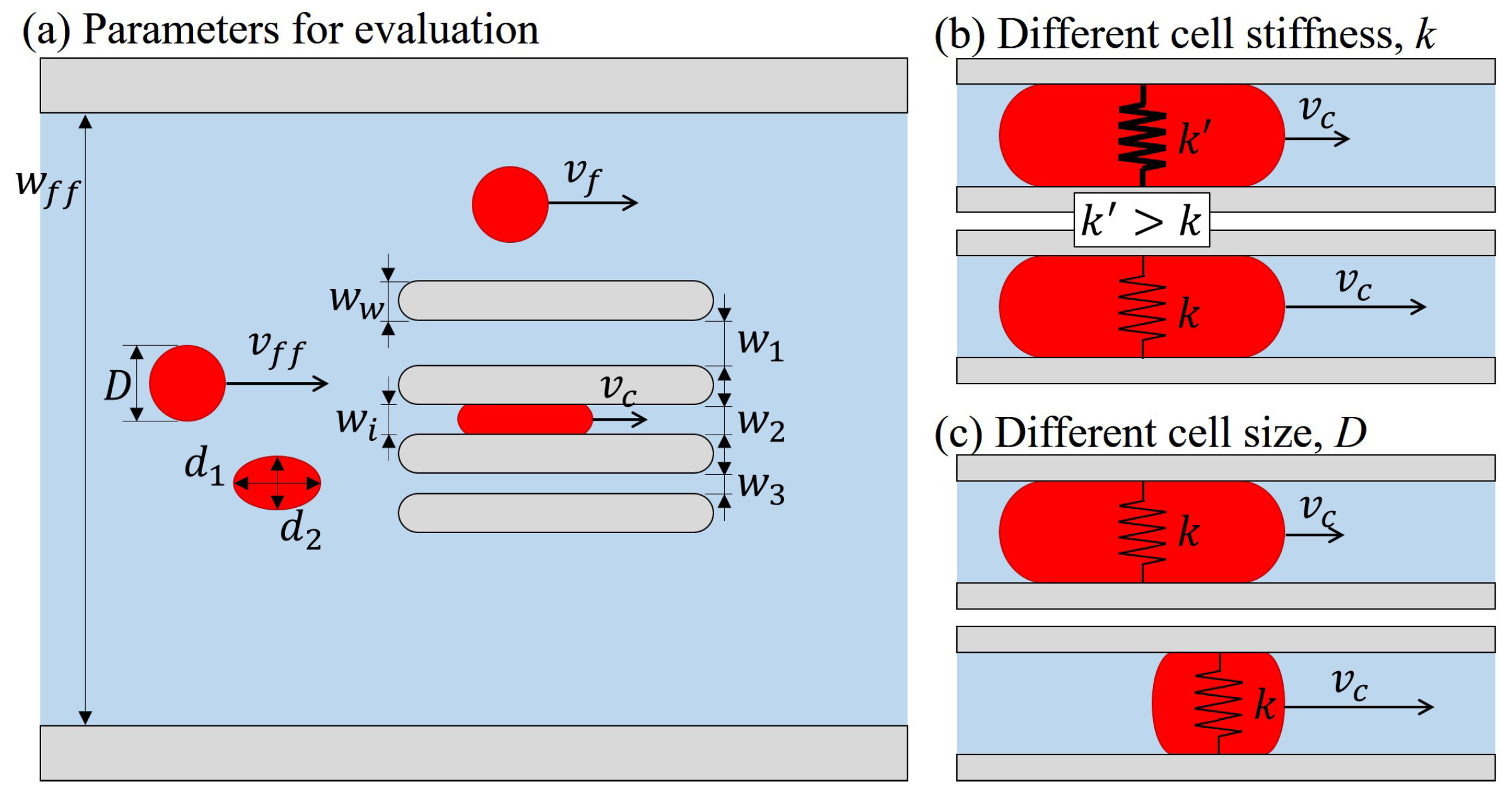
3. The Proposed Method
4. Experiments
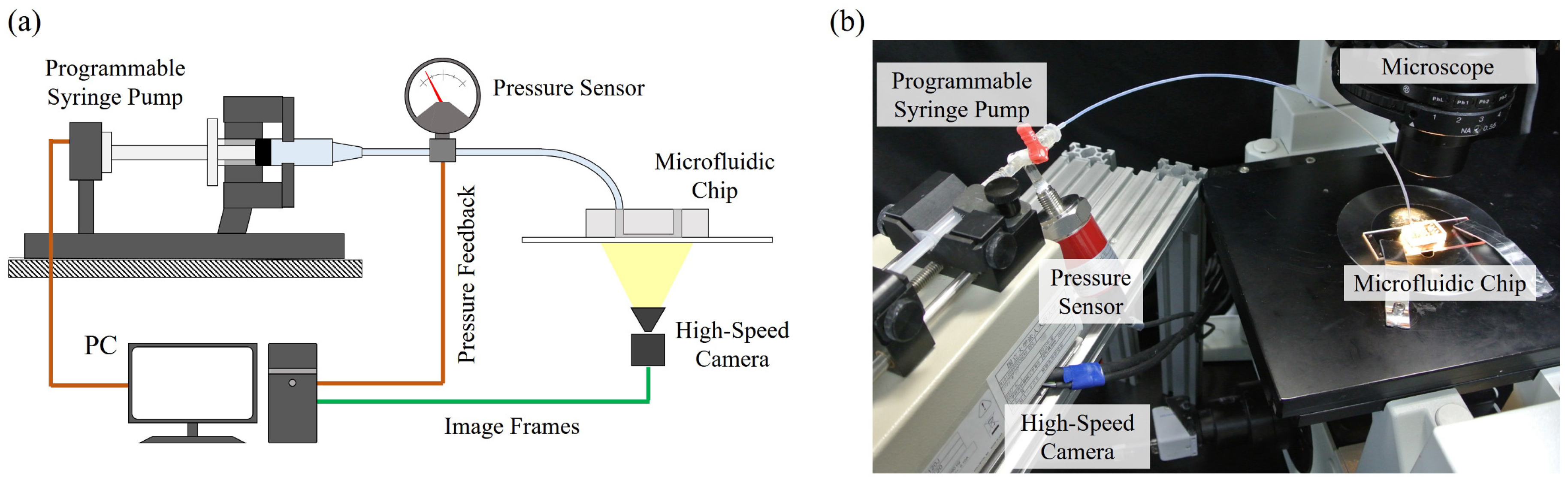
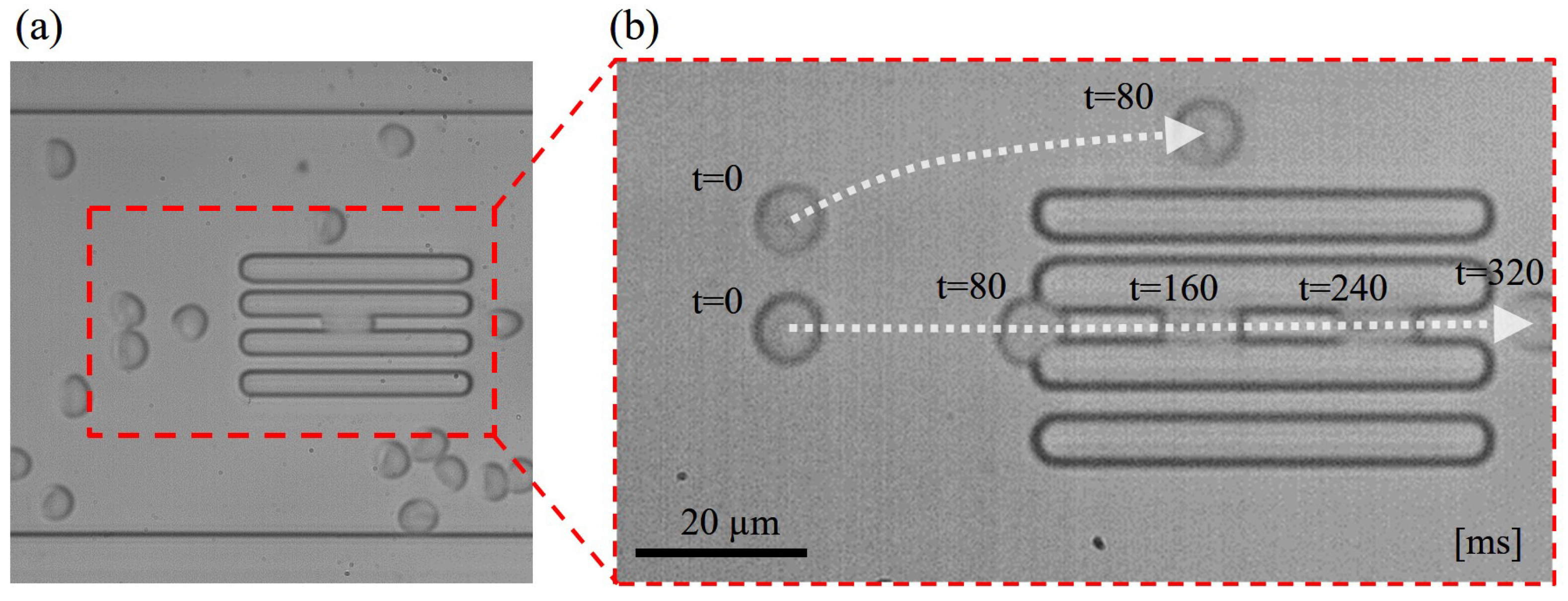
4.1. Experimental System
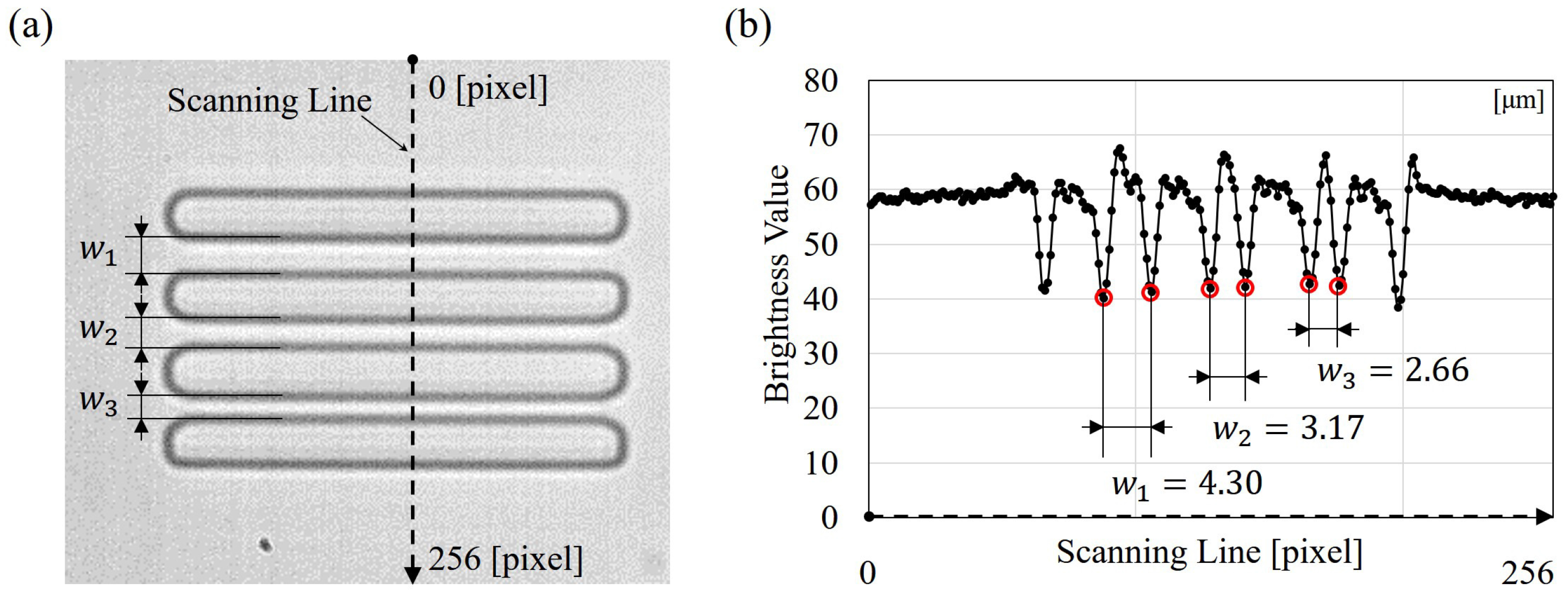
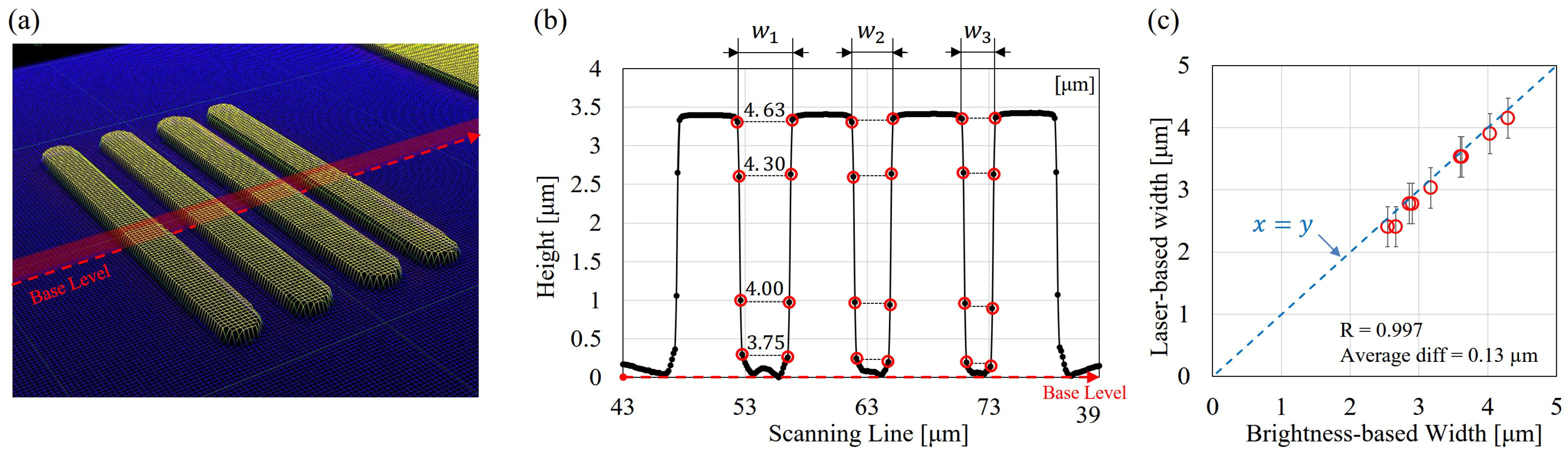
4.2. Microchip Fabrication and Width Calibration
4.3. Experimental Procedure
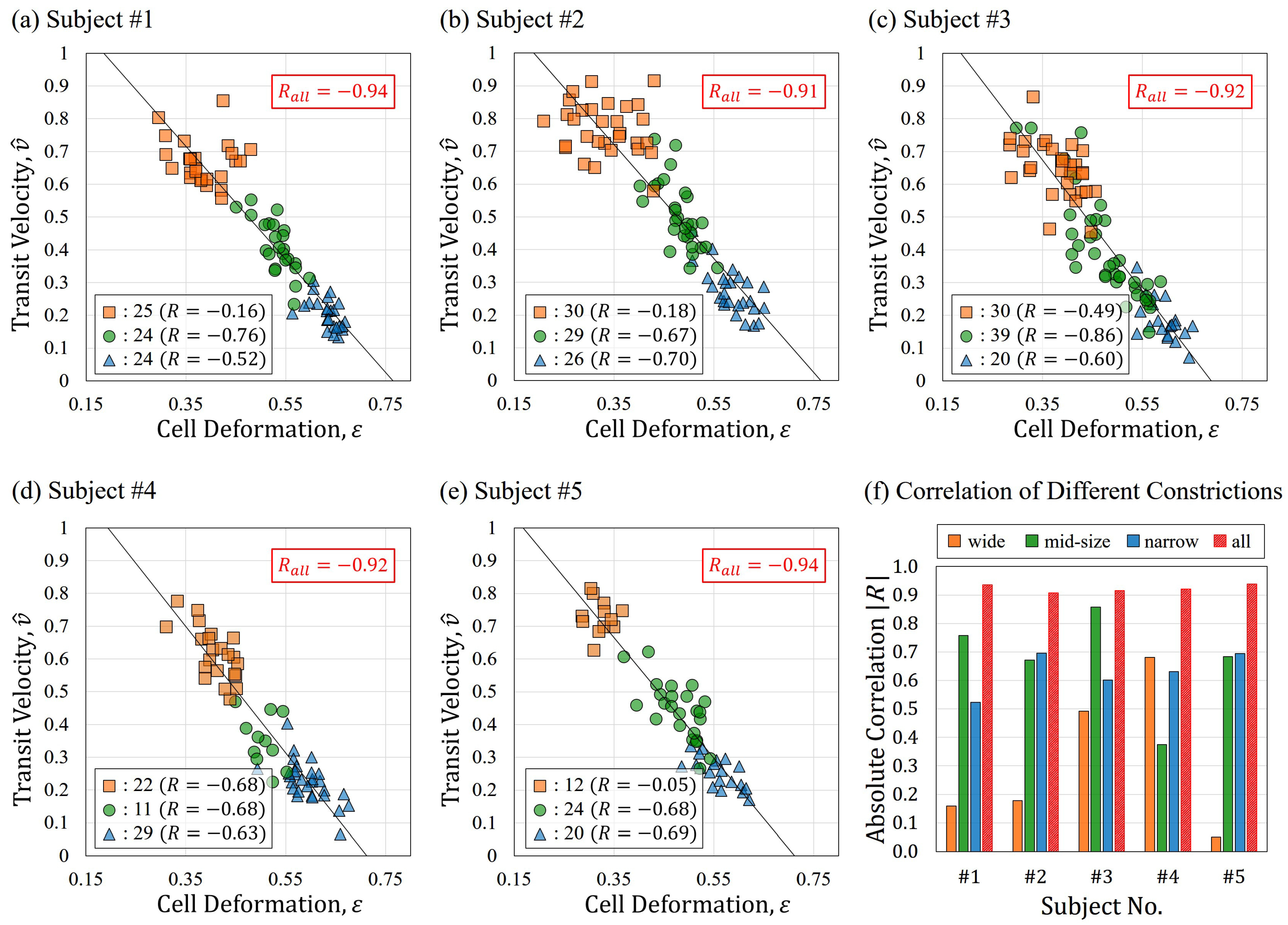
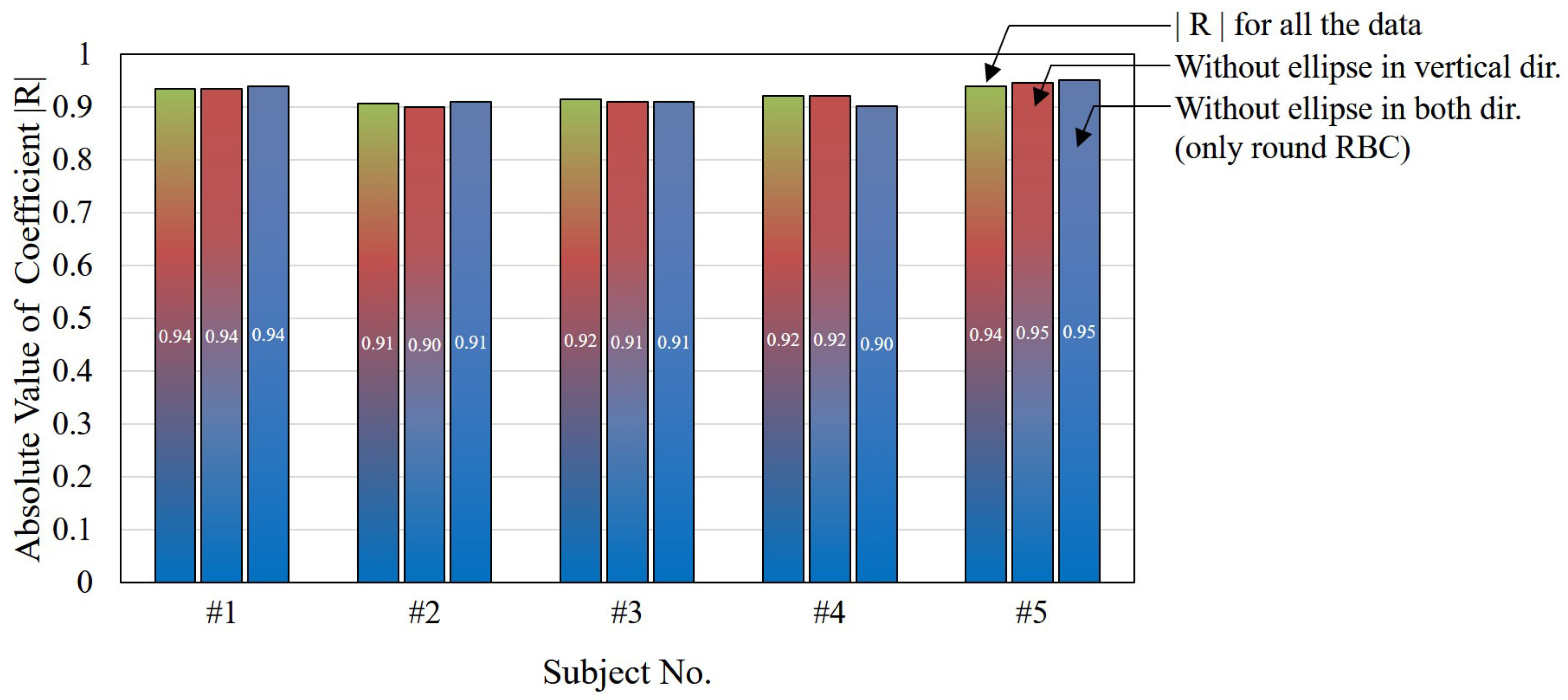
4.4. Experimental Results
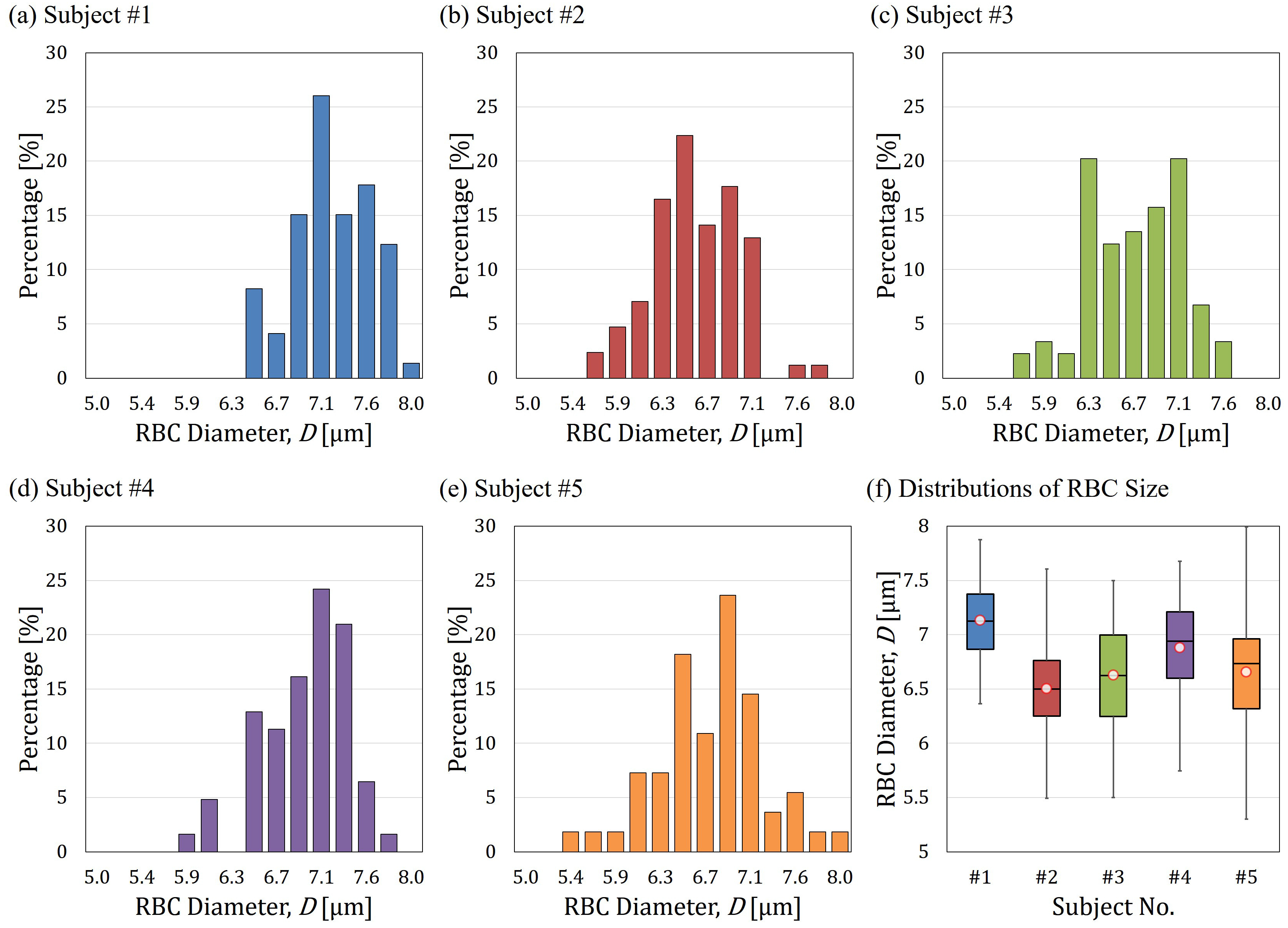
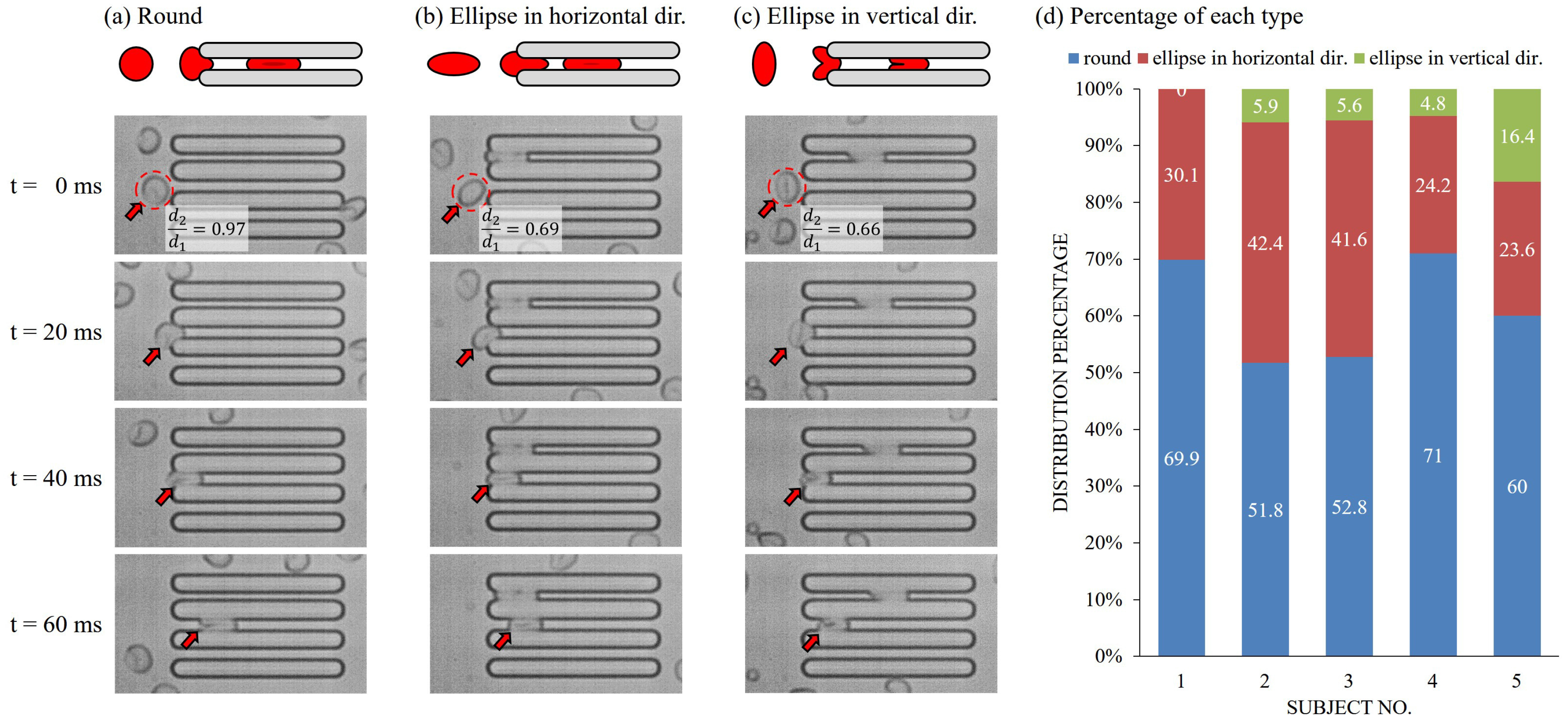
5. Discussion
5.1. The Effect of RBC Size Distribution
5.2. The Effect of RBC Shape and Orientation
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lim, C.; Zhou, E.; Quek, S. Mechanical models for living cells—A review. J. Biomech. 2006, 39, 195–216. [Google Scholar] [CrossRef] [PubMed]
- Glenister, F.K.; Coppel, R.L.; Cowman, A.F.; Mohandas, N.; Cooke, B.M. Contribution of parasite proteins to altered mechanical properties of malaria-infected red blood cells. Blood 2002, 99, 1060–1063. [Google Scholar] [CrossRef] [PubMed]
- Trickey, W.R.; Lee, G.M.; Guilak, F. Viscoelastic properties of chondrocytes from normal and osteoarthritic human cartilage. J. Orthop. Res. 2000, 18, 891–898. [Google Scholar] [CrossRef] [PubMed]
- Nash, G.B.; O’Brien, E.; Gordon-Smith, E.C.; Dormandy, J.A. Abnormalities in the mechanical properties of red blood cells caused by Plasmodium falciparum. Blood 1989, 74, 855–861. [Google Scholar] [PubMed]
- Reid, H.; Dormandy, J.; Barnes, A.; Lock, P.; Dormandy, T. Impaired red cell deformability in peripheral vascular disease. Lancet 1976, 307, 666–668. [Google Scholar] [CrossRef]
- Zheng, Y.; Shojaei-Baghini, E.; Azad, A.; Wang, C.; Sun, Y. High-throughput biophysical measurement of human red blood cells. Lab Chip 2012, 12, 2560–2567. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.D.; Sakuma, S.; Arai, F.; Kaneko, M. A new dimensionless index for evaluating cell stiffness-based deformability in microchannel. IEEE Trans. Biomed. Eng. 2014, 61, 1187–1195. [Google Scholar] [CrossRef] [PubMed]
- Hirose, Y.; Tadakuma, K.; Higashimori, M.; Arai, T.; Kaneko, M.; Iitsuka, R.; Yamanishi, Y.; Arai, F. A new stiffness evaluation toward high speed cell sorter. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 4113–4118.
- Xue, C.; Wang, J.; Zhao, Y.; Chen, D.; Yue, W.; Chen, J. Constriction channel based single-cell mechanical property characterization. Micromachines 2015, 6, 1794–1804. [Google Scholar] [CrossRef]
- Tsai, C.D.; Mizoue, K.; Kaneko, M.; Sakuma, S.; Arai, F. Novel microfluidic chip for extracting cell deformability. In Proceedings of the 2015 IEEE International Conference on Mechatronics and Automation, Beijing, China, 2–5 August 2015; pp. 2136–2144.
- Binnig, G.; Quate, C.F.; Gerber, C. Atomic force microscope. Phys. Rev. Lett. 1986, 56, 930–933. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.Y.H.; Lim, C.T. Biomechanics approaches to studying human diseases. Trends Biotechnol. 2007, 25, 111–118. [Google Scholar] [CrossRef] [PubMed]
- Tsukada, K.; Sekizuka, E.; Oshio, C.; Minamitani, H. Direct measurement of erythrocyte deformability in diabetes mellitus with a transparent microchannel capillary model and high-speed video camera system. Microvasc. Res. 2001, 61, 231–239. [Google Scholar] [CrossRef] [PubMed]
- Tan, Y.; Sun, D.; Wang, J.; Huang, W. Mechanical characterization of human red blood cells under different osmotic conditions by robotic manipulation with optical tweezers. IEEE Trans. Biomed. Eng. 2010, 57, 1816–1825. [Google Scholar] [CrossRef] [PubMed]
- Radmacher, M.; Fritz, M.; Kacher, C.M.; Cleveland, J.P.; Hansma, P.K. Measuring the viscoelastic properties of human platelets with the atomic force microscope. Biophys. J. 1996, 70, 556–567. [Google Scholar] [CrossRef]
- Brandao, M.; Fontes, A.; Barjas-Castro, M.; Barbosa, L.; Costa, F.; Cesar, C.; Saad, S. Optical tweezers for measuring red blood cell elasticity: Application to the study of drug response in sickle cell disease. Eur. J. Hematol. 2003, 70, 207–211. [Google Scholar] [CrossRef]
- Zheng, Y.; Nguyen, J.; Wei, Y.; Sun, Y. Recent advances in microfluidic techniques for single-cell biophysical characterization. Lab Chip 2013, 13, 2464–2483. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zheng, Y.; Tan, Q.; Shojaei-Baghini, E.; Zhang, Y.L.; Li, J.; Prasad, P.; You, L.; Wu, X.Y.; Sun, Y. Classification of cell types using a microfluidic device for mechanical and electrical measurement on single cells. Lab Chip 2011, 11, 3174–3181. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.D.; Sakuma, S.; Arai, F.; Taniguchi, T.; Ohtani, T.; Sakata, Y.; Kaneko, M. Geometrical alignment for improving cell evaluation in a microchannel with application on multiple myeloma red blood cells. RSC Adv. 2014, 4, 45050–45058. [Google Scholar] [CrossRef]
- Sakuma, S.; Kuroda, K.; Tsai, C.D.; Fukui, W.; Arai, F.; Kaneko, M. Red blood cell fatigue evaluation based on close-encountering point between extensibility and recoverability. Lab Chip 2014, 14, 1135–1141. [Google Scholar] [CrossRef] [PubMed]
- Henon, Y.; Sheard, G.J.; Fouras, A. Erythrocyte deformation in a microfluidic cross-slot channel. RSC Adv. 2014, 4, 36079–36088. [Google Scholar] [CrossRef]
- Kuo, F.; Ho, M.; Dai, J.; Fan, M. Atomic force microscopy for dynamic observation of human erythrocytes in a microfluidic system. RSC Adv. 2015, 5, 101319–101326. [Google Scholar] [CrossRef]
- Otto, O.; Rosendahl, P.; Mietke, A.; Golfier, S.; Herold, C.; Klaue, D.; Girardo, S.; Pagliara, S.; Ekpenyong, A.; Jacobi, A.; et al. Real-time deformability cytometry: On-the-fly cell mechanical phenotyping. Nat. Methods 2015, 12, 199–202. [Google Scholar] [CrossRef] [PubMed]
- Gossett, D.R.; Tse, H.T.K.; Lee, S.A.; Ying, Y.; Lindgren, A.G.; Yang, O.O.; Rao, J.; Clark, A.T.; Carlo, D.D. Hydrodynamic stretching of single cells for large population mechanical phenotyping. Proc. Natl. Acad. Sci. USA 2012, 109, 7630–7635. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yin, X. Parallel separation of multiple samples with negative pressure sample injection on a 3-D microfluidic array chip. Electrophoresis 2007, 28, 1281–1288. [Google Scholar] [CrossRef] [PubMed]
- Javanmard, M.; Babrzadeh, F.; Nyrén, P.; Davis, R.W. Improvement in cell capture throughput using parallel bioactivated microfluidic channels. Biomed. Microdevices 2012, 14, 625–629. [Google Scholar] [CrossRef] [PubMed]
- Gifford, S.C.; Frank, M.G.; Derganc, J.; Gabel, C.; Austin, R.H.; Yoshida, T.; Bitensky, M.W. Parallel microchannel-based measurements of individual erythrocyte areas and volumes. Biophys. J. 2003, 84, 623–633. [Google Scholar] [CrossRef]
- Young, E.W.K.; Wheeler, A.R.; Simmons, C.A. Matrix-dependent adhesion of vascular and valvular endothelial cells in microfluidic channels. Lab Chip 2007, 7, 1759–1766. [Google Scholar] [CrossRef] [PubMed]
- Myrand-Lapierre, M.E.; Deng, X.; Ang, R.R.; Matthews, K.; Santoso, A.T.; Ma, H. Multiplexed fluidic plunger mechanism for the measurement of red blood cell deformability. Lab Chip 2015, 15, 159–167. [Google Scholar] [CrossRef] [PubMed]
- Oh, K.W.; Lee, K.; Ahn, B.; Furlani, E.P. Design of pressure-driven microfluidic networks using electric circuit analogy. Lab Chip 2012, 12, 515–545. [Google Scholar] [CrossRef] [PubMed]
- Salehyar, S.; Zhu, Q. Deformation and internal stress in a red blood cell as it is driven through a slit by an incoming flow. Soft Matter 2016, 12, 3156–3164. [Google Scholar] [CrossRef] [PubMed]
- Yoshikawa, S.; Tsai, C.H.D.; Sakuma, S.; Arai, F.; Kaneko, M. Realtime cell tracking in a microchannel. In Proceedings of the 2013 10th International Conference on Ubiquitous Robots and Ambient Intelligence, Jeju, Korea, 30 October–2 November 2013; pp. 144–147.

© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, C.-H.D.; Tanaka, J.; Kaneko, M.; Horade, M.; Ito, H.; Taniguchi, T.; Ohtani, T.; Sakata, Y. An On-Chip RBC Deformability Checker Significantly Improves Velocity-Deformation Correlation. Micromachines 2016, 7, 176. https://doi.org/10.3390/mi7100176
Tsai C-HD, Tanaka J, Kaneko M, Horade M, Ito H, Taniguchi T, Ohtani T, Sakata Y. An On-Chip RBC Deformability Checker Significantly Improves Velocity-Deformation Correlation. Micromachines. 2016; 7(10):176. https://doi.org/10.3390/mi7100176
Chicago/Turabian StyleTsai, Chia-Hung Dylan, Junichi Tanaka, Makoto Kaneko, Mitsuhiro Horade, Hiroaki Ito, Tatsunori Taniguchi, Tomohito Ohtani, and Yasushi Sakata. 2016. "An On-Chip RBC Deformability Checker Significantly Improves Velocity-Deformation Correlation" Micromachines 7, no. 10: 176. https://doi.org/10.3390/mi7100176
APA StyleTsai, C.-H. D., Tanaka, J., Kaneko, M., Horade, M., Ito, H., Taniguchi, T., Ohtani, T., & Sakata, Y. (2016). An On-Chip RBC Deformability Checker Significantly Improves Velocity-Deformation Correlation. Micromachines, 7(10), 176. https://doi.org/10.3390/mi7100176






