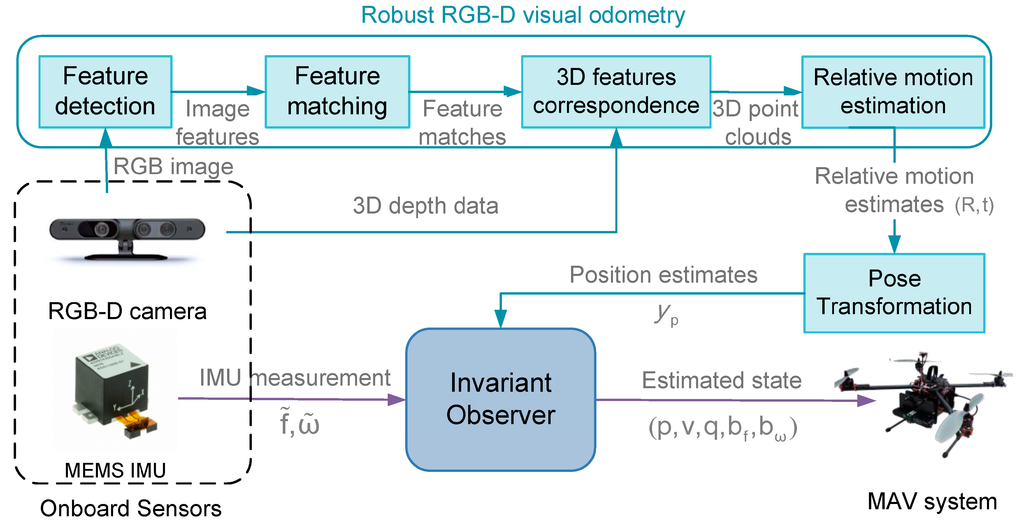
Abstract
This paper presents a non-linear state observer-based integrated navigation scheme for estimating the attitude, position and velocity of micro aerial vehicles (MAV) operating in GPS-denied indoor environments, using the measurements from low-cost MEMS (micro electro-mechanical systems) inertial sensors and an RGB-D camera. A robust RGB-D visual odometry (VO) approach was developed to estimate the MAV’s relative motion by extracting and matching features captured by the RGB-D camera from the environment. The state observer of the RGB-D visual-aided inertial navigation was then designed based on the invariant observer theory for systems possessing symmetries. The motion estimates from the RGB-D VO were fused with inertial and magnetic measurements from the onboard MEMS sensors via the state observer, providing the MAV with accurate estimates of its full six degree-of-freedom states. Implementations on a quadrotor MAV and indoor flight test results demonstrate that the resulting state observer is effective in estimating the MAV’s states without relying on external navigation aids such as GPS. The properties of computational efficiency and simplicity in gain tuning make the proposed invariant observer-based navigation scheme appealing for actual MAV applications in indoor environments.
1. Introduction
Micro aerial vehicles (MAV) are playing an increasingly important role in both civil and military applications. The recent development of MAV technologies has provide such vehicles with capabilities to accomplish a variety of tasks such as search and rescue, disaster relief, surveillance of hostile territory, as well as inspection of hazardous environments such as indoor fire monitoring, investigation of hazardous or hostile buildings, disaster inspection of enclosed infrastructures (collapsed buildings, underground mines and subway stations after earthquakes or terrorist attacks, etc.) [1,2,3,4]. MAVs with autonomous capabilities are ideal candidates for these tasks since such environments are highly risky for human beings and inaccessible by ground robots. In recent years, the development of MAV navigation technologies in indoor or enclosed environments has been an active area of research. However, the development of such autonomous MAVs poses a number of technical challenges in the field of navigation and control. One of the key problems is the state estimation of MAVs since the control and other decision-making functions rely on reliable and accurate knowledge of the MAV’s position, attitude and velocity. This requires the design and development of lightweight navigation systems to provide reliable state estimation of the vehicle. Due to onboard payload limitations, the navigation of MAVs generally relies on lightweight, low-cost MEMS (micro electro-mechanical systems) based IMU (inertial measurement unit) sensors which typically consist of rate gyroscopes, accelerometers and magnetometers. Although the angular velocity and attitude of the vehicle can be estimated using inertial measurements, the accurate translational velocity and position cannot be obtained by simply integrating inertial data due to the unbounded bias of low-cost MEMS sensors. For conventional outdoor robot applications, a GPS is commonly used as an aid to provide absolute position measurement for the vehicle. However, a GPS does not function effectively in urban canyons and it is even unavailable in indoor and enclosed environments. As a result, exteroceptive sensors such as laser rangefinders, cameras and RGB-D sensors are used as aids to inertial systems, and measurements of exteroceptive sensors can be fused with inertial measurements to bound the sensor bias and provide more accurate state estimates.
In recent years, there has been considerable research on the development of indoor MAV systems using exteroceptive aided inertial navigation approaches. Laser rangefinders have been successfully implemented in previous MAV systems for indoor exploration and mapping [5,6,7,8,9,10]. However, laser rangefinders can only provide distance measurements inside the 2D sensing plane of the sensor, thus their effectiveness is restricted to environments characterized with vertical structures. Moreover, they are unable to fully utilize the information in a 3D environment. In addition, both monocular [11,12,13] and stereo vision [14,15,16] technologies based on onboard cameras have also been employed to provide relative estimates for indoor navigation of MAVs. Although appealing in many applications, the monocular and stereo vision based approaches have several drawbacks in addressing indoor MAV navigation problems: Conventional RGB cameras do not directly provide distance information of environments, thus monocular/stereo vision based approaches must calculate the depth data using image features, which is a computationally intensive process.
The recent development of low-cost commercial RGB-D devices has led to increased capabilities for MAV applications. RGB-D devices are based on structured light technologies and can provide depth data even in poorly textured environments. Taking advantage of RGB-D devices, many researchers have achieved successful results in the field of indoor MAV navigation, such as state estimation, control and indoor mapping [17,18]. Despite these advances achieved in this domain, there is still significant progress to be made in developing more robust and computationally efficient visual odometry approaches for MAVs in complex environments, using lightweight and low-cost RGB-D devices and MEMS sensors.
The primary contributions in this paper are as follows: firstly, this paper presents a novel robust RGB-D based visual odometry (VO) approach that estimates the MAV’s relative motion by extracting and matching features of successive frames captured by the RGB-D camera. We made several extensions in the primary aspects of RGB-D visual odometry and proposed a robust featuring detection and matching strategy (termed OFC-ORB, optical flow-constrained ORB), as well as a robust inlier detection and relative motion estimation framework (termed Consistency-RANSAC, Consistency- random sample consensus). The properties of the proposed robust RGB-D VO ensure the algorithm’s computational efficiency and improve its robustness for complex environments with various texture conditions, as well as images blurs and partitions caused by the MAV’s maneuvers, making the approach particularly suitable for MAVs operating in complex environments. The second contribution is the design of a nonlinear observer-based state estimation framework that fuses the inertial data with aiding measurements from the RGB-D VO, which is built upon the invariant observer theory. The system dynamics and observation model for the RGB-D visual-aided inertial navigation problem is formulated, followed by the verification of system symmetries, and the invariant state observer is finally derived based on the system model. Using the resulting RGB-D aided-inertial navigation framework, the drift of inertial sensors can be corrected, yielding a more accurate estimate of the MAV’s states. Taking advantage of the invariant observer’s tuning and computational simplicity, the resulting state estimation approach is well-suited to implementations on MAVs with constrained payloads and computation capabilities. Finally, the paper presents the implementations of the proposed approaches and design on a quadrotor MAV platform, along with validations through indoor flight experiments. Experimental results demonstrate that the proposed RGB-D visual aided-inertial navigation framework can provide accurate and reliable state estimates for MAVs without relying on external navigation aids such as GPS.
The remaining contents of this paper are organized as follows. A brief review of related work is presented in Section 2. Section 3 provides an overview of the RGB-D visual/inertial navigation scheme. Details of the robust RGB-D relative motion estimation are described in Section 4, followed by the design of invariant observer-based state estimation method in Section 5. After the implementations and experimental validations of the resulting system design in Section 6, the paper is finally concluded in Section 7.
2. Related Work
Most types of MAV have non-linear dynamics and the aided inertial navigation systems are formulated as nonlinear models. Therefore, the state estimation of such systems is a typical non-linear state observer design problem, where the most widely used approach by far is the extended Kalman filter (EKF) and its variants. In recent research on MAVs, EKF-based methods have been applied in the vast majority of MAV state estimation applications and have demonstrated appealing performance. Rather than directly accounting for the nonlinearity, the EKFs linearize the system dynamics and observation model about the current best estimate, and apply the Kalman filter based on the linear approximation of the system. There are several variants and implementations of the EKFs, depending on the formulation of the system dynamics and observation model, as well as the representation of attitude and estimation errors. Typical examples of the conventional EKF-based state estimation scheme proposed by Bachrach et al. [5,6,7], Chowdhary et al. [8,9] and Sobers et al. [10] utilize laser scan-matching algorithms to provide position and heading measurements of the MAV, and fuse these measurements with inertial information via EKFs. The systems developed by Bachrach et al. [5,6,7] employ two groups of measurements, where the IMU readings are treated as measurements of the attitude and accelerations, and laser scan-matching outputs are incorporated as position and heading measurements. In contrast, the state estimation scheme in [8,9,10] utilizes the gyroscope and accelerometer measurements as noisy inputs of the state propagation model, while the attitude error is estimated as part of the MAV states and is used to correct the final altitude estimates. Similarly, EKF-based approaches have also been applied to visual-aided state estimation schemes of MAVs. In [11], a single camera is leveraged in an inertial-optical flow framework to obtain a metric velocity estimate, which is then treated as a measurement to a real-time EKF scheme. The proposed navigation scheme is capable of operating onboard a processor and enables real-time control of the MAV. A navigation and mapping system developed by Wu [12,13] consists of two EKF estimators, where the MAV’s position, velocity and attitude are estimated via a EKF scheme by fusing IMU measurements and observations of landmark features provided by monocular-vision. A separate mapping EKF estimator approximates the landmark feature positions when the MAV’s state estimates are available. Acgtelik et al. [14,15] use an EKF estimator to provide state estimates for the autonomous navigation and exploration of MAVs. The EKF sensor fusion filter combines relative motion estimates from the stereo visual odometry with IMU measurements, and periodically incorporates position corrections from a SLAM module to bound the drift. More recently, Voigt et al. [16] proposed an EKF-based visual-inertial ego-motion estimation method that combines stereo vision and IMU measurements in a tightly coupled manner. The resulting scheme utilizes IMU state and covariance propagation information to aid the feature matching of the stereo vision, leading to increased efficiency and robustness of MAV state estimation in complex industrial environments. In addition, EKF based methods have also proven useful for RGB-D vision-aided navigation of MAVs, and relevant examples can be found in [17,18]. Among the variants of the EKFs, multiplicative extended Kalman filters (MEKF) are especially useful for MAV attitude estimation applications. In order to employ a non-singular attitude representation in the estimator, MEKFs formulate the attitude as a multiplication of an estimated attitude quaternion and an error quaternion representing the deviation between the above estimates and true attitude. Due to the advantages of the non-singularity representation, the MEKF method has been applied to the design of micro attitude and heading reference system (AHRS) [19], as well as the MAV velocity and attitude estimation problem [20]. Although EKFs have been successfully applied in a number of applications, they have several disadvantages in addressing the navigation problem of MAVs. Since EKFs relies on the linearization of the system, the accuracy of state estimation may degrade significantly in cases that involve high degree of nonlinearities. In addition, the tuning and identification of EKFs’ parameters such as noise covariance and initial estimate parameters require extensive experiments, which may reduce the suitability for actual MAV applications.
The sigma-point unscented Kalman filter (UKF) is an effective alternative to the conventional EKFs when the system dynamics or observation model is highly non-linear, or the states are highly uncertain. To cope with high non-linearity and uncertainty, the UKF employs a high-order stochastic linear approximation of non-linear systems using weighted sigma-points. A UKF-based monocular vision-IMU system is proposed in [21] to perform state estimation, mapping, as well as self-calibration of the transform parameters between the camera and IMU. Moreover, Van der Merwe et al. [22] apply a UKF estimator to the design of a loosely-coupled GPS/INS (inertial navigation system) integration navigation system on an autonomous unmanned helicopter. However, the UKF also operates under the assumption of a Gaussian system, and it is therefore less effective for applications with non-Gaussian models. In contrast, the particle filter (PF) does not necessarily require the assumption that the process and measurement noise are Gaussian, and it operates by approximating the posterior distribution of the states using sampled, weighted particles. This property makes the PF more suitable for non-Gaussian estimation problems. A typical example of the PF-based state estimation method can be found in [23], where a Gaussian PF-based filter is employed to compute pseudo-measurements from laser data, and these laser measurements are integrated with IMU data to yield a full estimate. The resulting framework is implemented onboard a fixed wing MAV which is capable of performing aggressive flight in indoor environments. Due to the high computational cost, the PFs have not yet found wide use in actual MAV applications.
Alternatively to the aforementioned optimal estimators, several nonlinear observer approaches have been introduced into MAV state estimation applications in the past few years. Unlike optimal estimation approaches that propagate the posterior conditional probability distribution of the state using sequences of observations, nonlinear observer-based approaches are generally designed directly on the nonlinear geometry of the systems. Nonlinear observers are especially attractive since they are usually accompanied by global stability proofs of observer error dynamics, i.e., global convergence of the estimation error for all initial conditions and system trajectories [24]. In [25], a Luenberger observer-based fusion filter is designed and implemented onboard a quadrotor MAV. The proposed filter combines the IMU measurements and absolute position estimates provided by a monocular visual SLAM (simultaneous localization and mapping) module, featuring a high update rate of position and velocity estimates to enable fast position control. Similarly, Boutayeb et al. [26] propose a time-varying reduced-order Luenberger-like observer for the velocity estimation for a MAV using linear acceleration measurements. Recent work has also focused on applying sliding-mode observers and adaptive observers to the MAV state estimation problems. Benallegue et al. [27,28] utilize a sliding-mode observer to estimate the MAV’s velocity, as well as model uncertainties and disturbances such as winds. Taking advantage of this observer, a feedback linearization controller [27] and a back-stepping controller [28] are employed to achieve MAV position tracking control in the presence of external disturbances. Nonlinear adaptive observer techniques are employed in [29] for velocity estimation of a quadrotor MAV, using noisy acceleration and angular measurements from IMUs, and the resulting observer demonstrates robustness to measurement noise in simulations. However, the proposed adaptive observer may be computationally demanding for onboard implementations since the cascade observer contains high-order terms. It is also worth mentioning the recent work on the observer based simultaneous state estimation and sensor fault diagnosis for MAV. In [30], a group of reduced-order time varying observers are designed to diagnose and isolate accelerometers faults, and to simultaneously estimate the MAV velocity from acceleration measurements. Despite the aforementioned research on observer-based approaches, it remains to be seen whether the non-linear observer can be more generally useful for actual MAVs.
In particular, an important development that came from previous research on system symmetries theory is the symmetry-preserving observer. Bonnabel et al. [31,32] propose the invariant observer which is built on the invariant properties (symmetry geometry) of such systems. In [31,32], it is proved that when the system is invariant by a transformation Lie-group, one can design a nonlinear invariant observer that possesses the same symmetry properties as the original system. A relevant approach that is closely related to invariant observer is the complementary filter [33], which is designed directly on the matrix representation of the special orthogonal group SO(3). The invariant observer method is applied to the design of low-cost AHRS in [34,35,36], and is further used in the GPS-aided inertial navigation system for outdoor MAV applications in [37,38,39]. In addition, examples of complementary filter-based visual/inertial state estimation of a helicopter MAV can be found in [40].
The invariant observer provides a systematic approach of designing non-linear state observer for a class of systems symmetry properties. Instead of linearizing the system model as in the EKF based approach, the invariant observer takes advantage of the symmetry geometry of the system, yielding an invariant state estimation error dynamics, and therefore the calculation of observer gains can be simplified. Moreover, the gain matrices of the observer are constant on permanent trajectories sets rather than equilibrium points. Due to its properties of computational efficiency and simplicity in parameters tuning, the invariant observer is well suitable for the state estimation of actual MAV platforms with limited onboard computational resources. Motivated by previous research, we seek to adapt the invariant observer approach to the design of a RGB-D visual/inertial navigation scheme, in order to provide state estimates for indoor MAV systems without relying on external navigation aids.
4. Robust RGB-D Visual Odometry
As described previously, RGB-D visual odometry refers to the process of estimating the relative motion of the MAV between successive time steps, using environmental features from consecutive images captured by the RGB-D camera. The sequence of motion estimates can then be integrated as position observations into the data fusion algorithm. A contribution from this paper is the development of a robust RGB-D VO approach which extends existing algorithms in VO operations including feature detection and matching, as well as relative motion calculation. The overall process flow of the robust RGB-D VO is illustrated in Figure 2. Details on the proposed robust RGB-D VO steps will be specified in the following subsections.
4.1. Robust Feature Detection and Matching
The robust feature detection and matching strategy proposed in this paper is built on the ORB detector (oriented FAST (features from accelerated segment test) and rotated BRIEF; ORB is first proposed in [41]) as well as the optical flow method (Figure 2). The RGB image captured by the RGB-D camera is converted to grayscale first, and a scale pyramid scheme of the image is then established using Gaussian kernels with different scale factors, such that features can be extracted from each level to enhance robustness. The ORB detector is utilized in our system due to its computational efficiency and robustness in feature detection. The ORB algorithm utilizes the FAST (features from accelerated segment test) detector [42] to extract feature points from each level of the image scale pyramid. The basic idea of the FAST detector is to determine a feature point by comparing the intensity threshold to the grayscale gradient between a center pixel and pixels in its circular neighborhood [42]. Although FAST detector is computationally efficient in finding corner features, it generates large responses along edges that provide rare useful information. Therefore, the ORB algorithm employs a Harris response measure to filter features extracted by FAST. For each FAST feature, a Harris response is computed using its grayscale gradient and all the features are then sorted in a descending order of the Harris responses. The n features with the highest Harris responses are selected to eliminate edge points (where n is a pre-defined number). In addition, the ORB also incorporates an orientation component calculated using the intensity centroid method to improve the rotation invariance of feature detection. In the feature detection step of our approach, the corresponding depth data is also extracted from the depth image, and features without corresponding depth are pruned out to eliminate fault detections. After that, a bit string-based descriptor consisting of a fixed-length vector is computed for each feature to uniquely describe the feature. The descriptor employed in the ORB algorithm is based on an extension of the BRIEF (binary robust independent elementary features) [43], termed the rBRIEF, which calculates feature’s descriptor vector by performing a series of grayscale intensity binary tests in an image pixel patch around the feature. In order to enhance the BRIEF’s invariance to planar rotation, the rBRIEF computes the descriptor by steering the pixel patch according to the orientation of the feature. Through the above operations, the feature detection step generates a set of features from an image, each with a BRIEF descriptor represented by a vector of length n (n = 256 for the ORB).
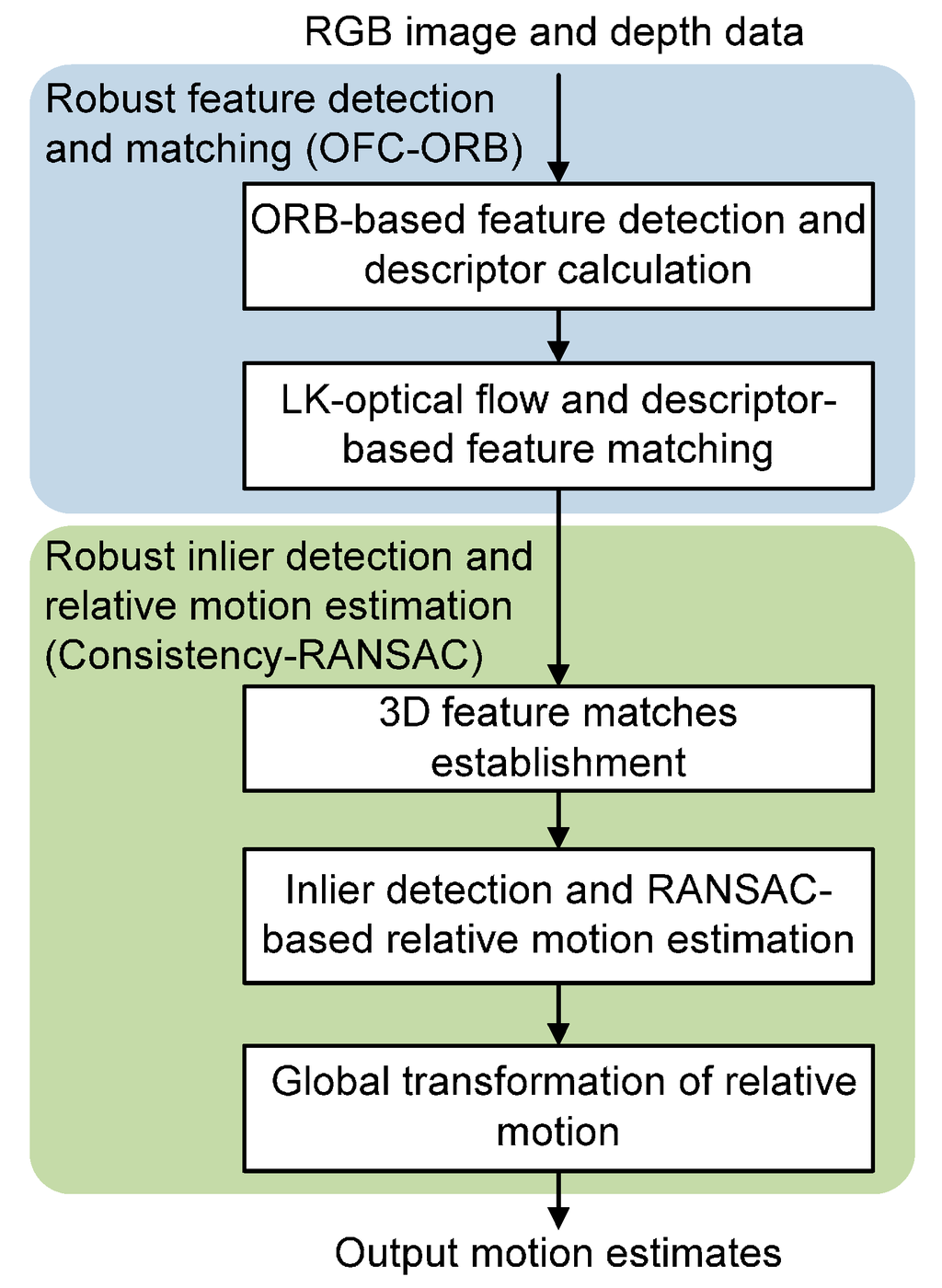
Figure 2.
Process flow of the robust RGB-D visual odometry. ORB, oriented FAST and rotated BRIEF algorithm; OFC-ORB, optical flow-constrained ORB; RANSAC, random sample consensus algorithm.
Once the features are extracted from consecutive images, the feature matching procedure is performed to generate feature correspondence. In order to increase the robustness of the feature matching procedure to complex task scenarios that involve varied feature quality, lighting conditions and motion blur, we propose a robust feature-matching strategy called OFC-ORB (optical flow-constrained ORB) that combines optical-flow tracking and ORB feature descriptor-based matching. The basic idea of the OFC-ORB strategy is to constrain the ORB descriptor-based feature matching using a confidence sub-window region predicted by the optical-flow tracking. An inverse-check procedure based on descriptor-based matching and optical flow estimation is also employed to remove false matching. This strategy significantly reduces outliers and increases robustness of the feature matching in complex environments.
The OFC-ORB algorithm proposed in this paper employs the LK-optical-flow approach [44] to compute the optical-flow disparities between successive images. Let Im and Im+1 be two consecutive grayscale images captured at time tm and tm+1 = tm + ∆t by the RGB-D camera. The functions Im(u) and Im+1(u) provide the respective grayscale intensity values of pixel u at the location u = [x, y]T in two images. Given a point p = [xp, yp]T in image Im, the objective of the optical flow-based tracking is to find the corresponding point q = [xq, yq]T in Im+1, with the optical-flow disparity d = [dx, dy]T that minimizes the following error function:
where wx, wv denote the size of the pixel window around p and q. The Lucas–Kanade (LK)-optical-flow approach employs the first-order linear approximation of the error function given by Equation (1), and solves the above problem using a Newton-Raphson iteration method. Let dk be the optical-flow calculated from the kth iteration step and d0 = 0. The k + 1th iteration calculates δk that minimizes the following error function:
Given δk, the optical-flow from the k + 1th iteration step can be obtained by:
The above calculations repeat until k exceeds the maximum iteration number, or δk < ∆δ (∆δ is a pre-defined threshold), and the estimates of dk converge to optimal d ideally.
In order to achieve a tradeoff between local accuracy and robustness, a pyramid representation [45] of the image is established in the OFC-ORB algorithm, and the optical-flow tracking is performed recursively through each level of the pyramid to obtain a more accurate optical flow estimate. Let I be the original image (i.e., the image intensity function) of size nx × ny, and it is considered as the zeroth level of the pyramid, i.e., I0 = I, the pyramid representation of the image I can be established as follows: Define l = 0, 1, 2, …, ln as levels of the pyramid, and let Il−1 be the image of the l − 1th level of size , , the lth level image Il is given by:
where x, y denotes the coordinates of pixels in the image, and the size of the l − 1th level image (, ) must satisfy the following constraint:
After the construction of the image pyramid, the optical-flow estimation is performed recursively at each level. The optical-flow estimation procedure starts from the top level (ln) of the pyramid, and the estimate results from the previous level are used as initial parameters of the computations in the next level to obtain a refined estimate. This procedure traverses the image pyramid until the original level image is reached (l0).
The pyramid optical-flow tracking procedure is illustrated in Figure 3. Define and as the original two consecutive images, and denote the corresponding point in the kth level of p as pk, pk = [, ]T. Following Equations (4) and (5), the relationship of pk and p is given by: pk = p/2k. Assume that gk = [, ]T is the optical-flow estimate calculated from level ln to level lk+1, and set the initial optical-flow estimate at level ln to zero (i.e., gk = [0 0]T). The level lk images can be centered-compensated using the initial estimate gk:
The disparity dk between the compensated images and can be estimated following the aforementioned LK-optical-flow method, which operates by minimizing the following error function:
The initial optical-flow estimate gk can then be corrected using dk:
gk−1 can be used as the initial estimate of the computation in level lk−1. The above procedure goes on through the pyramid to the original level l0, and the final estimate of the optical-flow d is given by:
The above pyramid implementation enables the estimation of optical-flow to handle large-scale motions, while maintaining local sub-pixel accuracy.
Taking advantage of the ORB detector and the optical-flow tracking strategy, the OFC-ORB proposed in this paper improves the descriptor-based feature matching by employing the optical-flow information for predicting confidence regions and checking false matching. The overall process flow of the OFC-ORB strategy is depicted in Figure 4, and the primary steps of the OFC-ORB strategy are presented in Algorithm 1. For consecutive images, the OFC-ORB employs the optical-flow tracking strategy to predict a confidence sub-window in the previous image of each feature in the current image (lines 5 and 6). Therefore, the descriptor-based search of feature matches can then be constrained to this sub-window around the expected feature point as predicted by the optical flow algorithm. After finding the best matches from the predicted region in the previous image (line 7), an inverse matching procedure is performed in the current image to check existing matches, and so that false matches can be removed (line 8). Finally, the optical-flow tracking is introduced again to compute the optical-flow disparities between the current feature matches (line 10). These disparities are compared to the optical-flow parameters obtained in the previous sub-window prediction step to further eliminate outliers (lines 11–13).
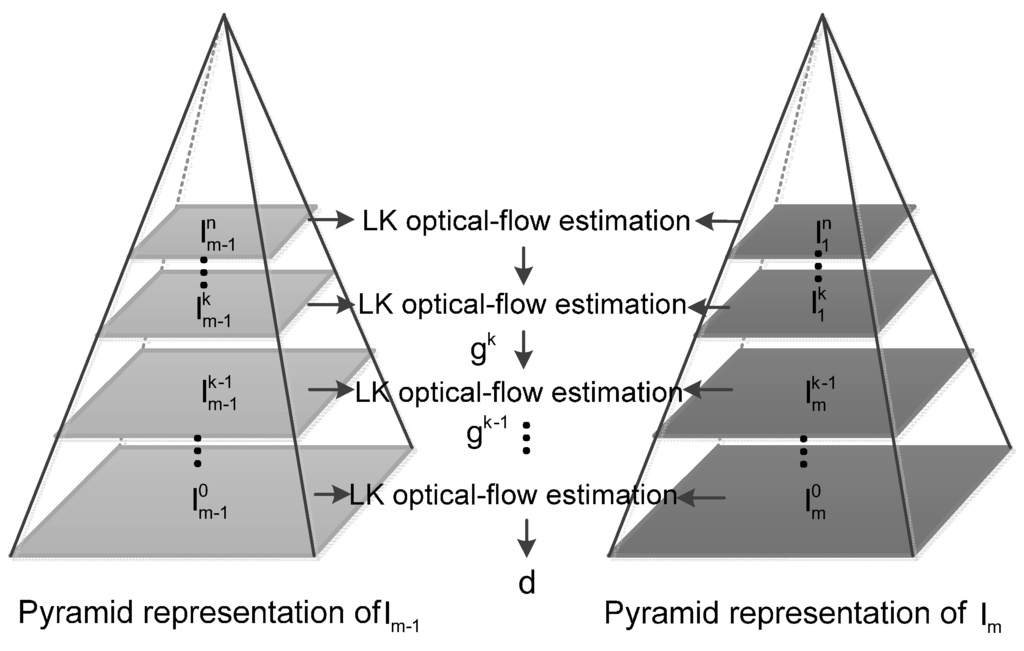
Figure 3.
Pyramid implementation of the optical-flow tracking operation. LK optical-flow: Lucas–Kanade optical-flow algorithm.
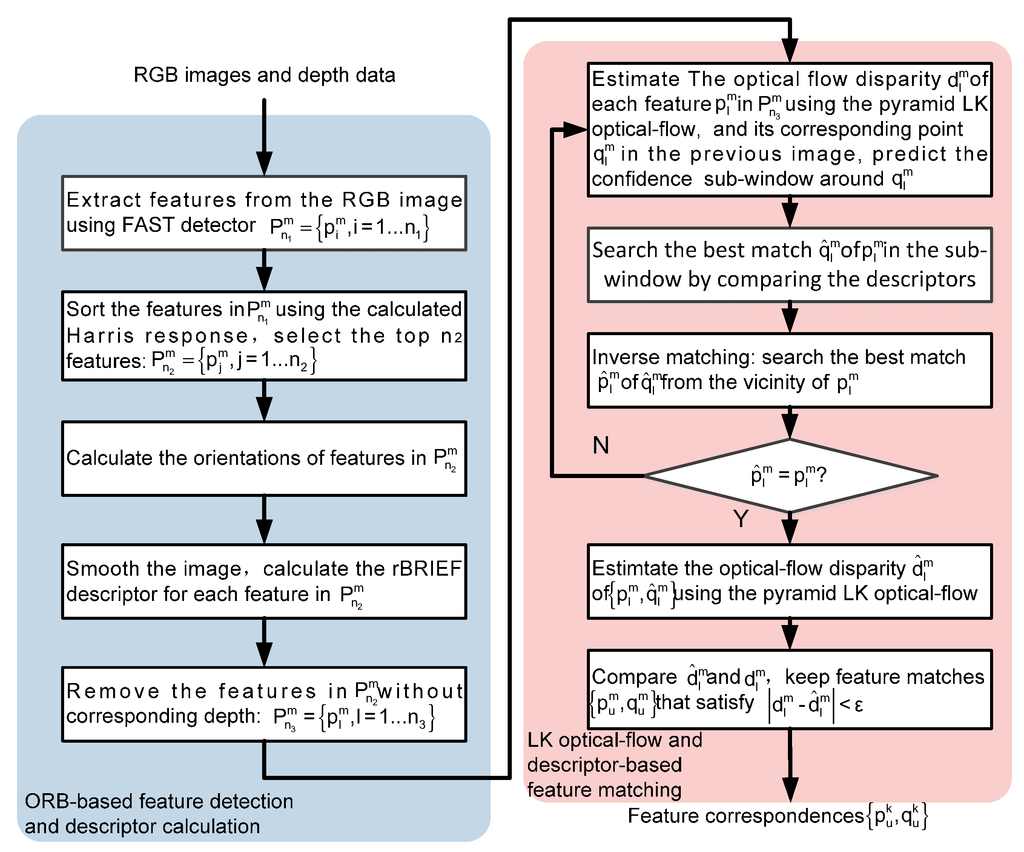
Figure 4.
Process flow of the OFC-ORB feature detection and matching strategy.
Algorithm 1. OFC-ORB feature detection and matching.
| Input | Two consecutive images captured by the RGB-D camera |
| Output | Feature correspondence set S of |
| 1 | Extract features from respectively, using the ORB detector, compute the descriptor for each feature of |
| 2 | Extract the depth data for each feature of , discard features that do not have corresponding depth, sort features in in an ascending order of the x-coordinates, obtain |
| 3 | Initialize the feature correspondence set |
| 4 | for each |
| 5 | Estimate the optical-flow vector of using the pyramid LK-optical-flow algorithm, calculate the corresponding point in : . |
| 6 | Build the confidence sub-window of size centered at |
| 7 | Find the best match of from , by searching for that satisfies: |
| 8 | Build a sub-window centered at in , find the best match of from |
| 9 | if |
| 10 | Estimate the optical-flow vector between |
| 11 | if |
| 12 | |
| 13 | end if |
| 14 | end if |
| 15 | end for |
| 16 | return S |
The primary advantage of the OFC-ORB feature detection and matching strategy is that it achieves a balance between robustness and computational efficiency. The prediction of the sub-window based on optical-flow tracking can restrict the search of feature correspondences to a small confidence region, which reduces false matches and increases the robustness to complex environments and the impacts caused by MAV motion. In addition, the overall computations can be reduced because of the constrained search region of feature matching, as well as the increased number of inliers for the relative motion estimation procedure.
4.2. Robust Inlier Detection and Relative Motion Estimation
Once the 2D image feature matches are extracted by the OFC-ORB procedure, these feature matches are corresponded to 3D-space using their corresponding depth data from the depth image, yielding two sets of 3D point clouds with known correspondences, denoted as Pm−1, Qm (Pm−1 = {pi}, Qm = {qi}, i = 1, …, n, ). Given these consecutive 3D feature correspondences captured at different time steps, the MAV’s relative motion from the prior to the subsequent time step can be estimated based on the transformation of the two 3D point clouds. The concept of relative motion estimation is illustrated in Figure 5.
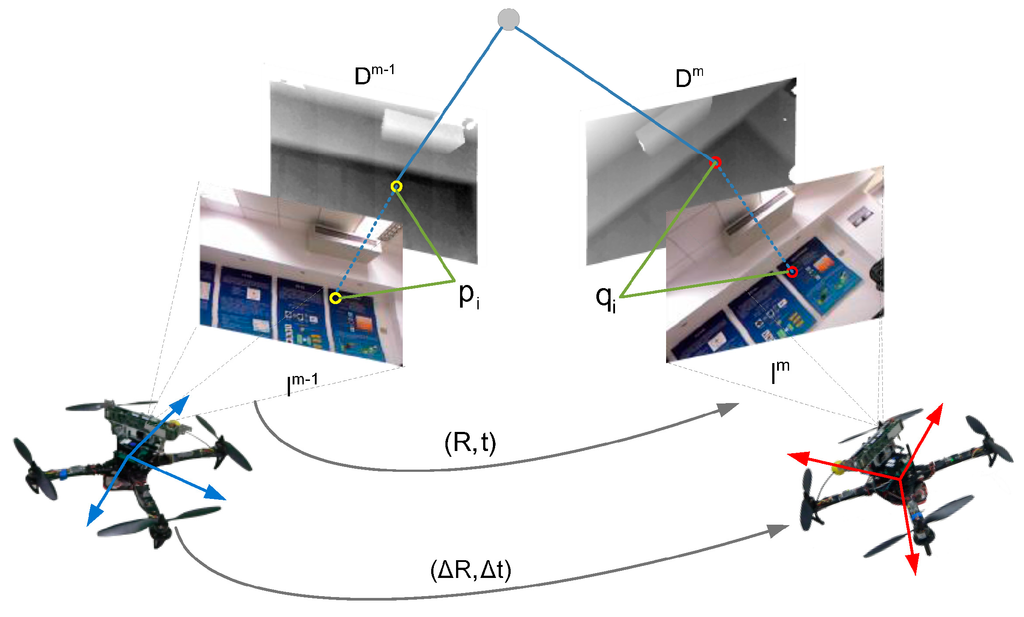
Figure 5.
Relative motion estimation of MAV based on the RGB-D visual odometry.
The transformation of two 3D point clouds consists of the rotation R and translation t, and the relationship of the 3D feature correspondences can then be given by:
where denotes the error vector. The optimal solution of R and t in a least-square sense can be obtained by minimizing the following error function:
In the system designed in this paper, the above problem is solved using the SVD (singular value decomposition) approach [46], where the basic idea is built on the property that rigid motion does not change the relative distances between points and their centroid of a rigid body. Assume to be the optimal solution that minimizes the error function in Equation (11), and let: P'm−1 = {p'i} be the 3D point cloud obtained by applying the optimal transformation to Qm
According to the distance-preserving property of rigid body motion, the centroid of the transformed 3D point cloud P'm−1 must coincide with that of the actual point cloud Pm−1:
where:
denotes the centroid of point cloud Qm. Following Equations (13) and (14), we have:
The relative distance between each point and the centroid can be given by:
Following Equations (15) and (16), the error function in Equation (11) can be rewritten as:
As can be seen from Equation (17), the transformed error function contains only the transformation component R. Therefore, the above simplified least-square problem can be solved through two primary steps: (1) Find the optimal that minimizes the error function in Equation (17); (2) Calculate according to Equation (15).
The detailed procedures of the SVD-based algorithm are as follows. The centroids () of two point clouds are computed first, and the relative distances (∆pi, ∆qi) are then calculated according to Equation (16). Given ∆pi, ∆qi, the algorithm computes the following matrix:
Apply SVD to matrix H:
The optimal estimate of and can then be obtained by:
A detailed mathematical proof of the SVD-based approach can be found in [46]. The above procedure yields the optimal estimate of the relative motions between consecutive time steps given two groups of 3D feature correspondences.
It can be concluded from the above calculation procedure that the performance of relative motion estimation relies heavily on the quality of extracted feature correspondences, and it is thus highly sensitive to outliers. Although the optical-flow-constrained feature matching strategy described in Section 4.1 can significantly reduce the ratio of false matches, a robust strategy is necessary to further eliminate outliers. In order to ensure robustness and computational efficiency, we propose the Consistency-RANSAC, a refinement of the conventional RANSAC, which employs feature consistency check in the inlier detection procedure. The distance-preserving constraint of rigid motion is used again in the design of the consistency check strategy: ideally, the relative Euclidean distance between two points belonging to a rigid body should be identical to thier distance after rigid motions. For the visual odometry problem, this property indicates that the distances between different 3D features do not change substantially from one time step to the subsequent time step (i.e., consistency). Recall the two 3D point clouds Pm−1, Qm, let pi, pj ϵ Pm−1 be two arbitrary 3D features from the 3D point clouds Pm−1 at time m − 1, and qi, qj ϵ Qm denote their corresponding matches in Qm at time m, respectively. The consistency constraints of {pi, pj} and {qi, qj} is then given as:
where δ represents the threshold, and pi, pj, qi, qj are expressed in the same global coordination. By performing the consistency check to the 3D feature correspondences, the algorithm can prune out incorrect matches that do not satisfy the consistency constraints in Equation (21) (i.e., The deviations of relative distances exceed the threshold δ). Using the consistency check results, finding the largest set of inliers can be transformed into the problem of determining the maximum clique on a graph. This problem can then be solved by iteratively adding feature matches with the greatest degree (i.e., feature matches with the largest number of consistent matches), which is consistent with all the feature matches in the existing consistent set. After finding the set of inliers, the final relative motion is estimated using an improved RANSAC procedure which operates by selecting consensus feature matches based on their similarity to a hypothesis, and progressively refining the relative motion hypothesis based on the selected inliers [47]. Since the consistency check-based inlier detection procedure has already increased the ratio of inliers, the RANSAC procedure can generate a good estimate through only a very limited number of iterations. This significantly reduces the overall computation cost of the algorithm.
The overall Consistency-RANSAC inlier detection and relative motion estimation procedure is illustrated in Algorithm 2. The algorithm starts by checking the consistency of the given 3D feature matches. Unlike the conventional consistency check strategy that directly utilizes the relative distances between different feature points, we first calculate the centroid of each 3D point cloud (, line 1), and then compute the relative distances ((∆pi, ∆qi) from each 3D feature point to its corresponding centroid (line 3). These relative distances-to-centroid are then used to check the consistency of each pair of feature matches: the algorithm computes the errors between the distances-to-centroid of feature points and those of their corresponding matches (line 4), and sort all the 3D feature points according to these consistency errors (line 6). The last ξ% (ξ = (n − n1)/n) feature match pairs with the largest consistency errors in the sorted feature point set are discarded (line 7). Using the distances-to-centroid information, the above refined strategy exempts the consistency check from the conventional time-consuming maximum-clique search procedure, and can ensure a high ratio of inliers.
Based on the detected inlier feature point set (Q), a refined RANSAC procedure is performed to further prune out outliers and compute the final motion estimate. In each iteration, λ pairs of feature matches are drawn randomly from the inlier set Q (line 11) to compute an initial hypothesis of the relative motion (R0, t0 line 13), using the SVD-based least-square approach described previously. The rest of the feature match pairs in Q are then checked for their compatibility with this initial hypothesis, by computing the transformation error using R0, t0, and comparing this error to the consensus error bound ε (line 15), and all compatible feature match pairs are added to a consensus set Sc (line 16). This operation serves to prune out outliers from Q. Once we get a sufficient number of feature match pairs in the consensus set (line 16), these data in Sc are used to compute a refined motion estimate (R1, t1). To adjust the consensus threshold, the average transformation error of feature matches in Sc is calculated using (R1, t1) (lines 21–24), and this error is used as the updated consensus error bound ε in the next iteration cycle if it is lower than the original ε (line 26). The above procedure continues until the probability of finding a better solution becomes sufficiently low (e.g., the difference between current average transformation error and prior consensus error is negligibly small), and the current solution is then accepted as the final motion estimate of (R, t) (line 28).
Algorithm 2. Consistency-RANSAC inlier detection and relative motion estimation.
| Input | Two 3D point clouds with correspondences: |
| Output | Relative motion of |
| 1 | Calculate the centroid of |
| 2 | for i = 1 to n |
| 3 | |
| 4 | |
| 5 | end for |
| 6 | Sort the point set in the ascending order of : |
| 7 | Select the top n1 pairs of feature matches: |
| 8 | RANSAC initialization: , , |
| 9 | while do |
| 10 | Initialize the sample set and the jth consensus set: , |
| 11 | Randomly select pairs of feature matches from Q: |
| 12 | |
| 13 | Estimate that minimizes the error function given in Equation (17) based on SVD approach, using features in |
| 14 | for each AND do |
| 15 | if |
| 16 | |
| 17 | end if |
| 18 | end for |
| 19 | if |
| 20 | Re-estimate that minimizes the error function based on SVD approach, using features in the consensus set |
| 21 | for each do |
| 22 | |
| 23 | end for |
| 24 | |
| 25 | if |
| 26 | , |
| 27 | end if |
| 28 | if |
| 29 | break |
| 30 | end if |
| 31 | end if |
| 32 | |
| 33 | end while |
| 34 | return |
Taking advantage of the reduced ratio of outliers generated by consistency check, the number of iterations in RANSAC can be constrained effectively. The maximum iteration number (MaxIteration in line 9) can be set to a small integer between 5 and 10. The consistency check strategy along with RANSAC framework can significantly reduce outliers and increase robustness in motion estimation, while ensuring computational efficiency for real-time implementations.
4.3. Global Transformation of Relative Motions
The motion estimation procedure described in Section 4.2 provides a sequence of estimated transformations (R, t) of consecutive 3D feature point clouds at different time steps. Note that in actual applications, the features are actually fixed in the environment while the MAV moves around the features. Therefore, given the estimated feature transformation T of feature points, the corresponding motion (∆T) of the MAV’s current body frame with respect to the prior frame can be obtained by:
where ∆R, ∆t denote the rotation and translation component, respectively. We can derive a global representation of the MAV’s pose with respect to an initial pose T0 using the following sequence of homogenous transformations:
where ∆T denotes the relative transformation of the MAV’s pose at different time steps. This global motion estimate can then be used as a measurement of the MAV’s state in the data fusion scheme.
5. Invariant Observer Based State Estimation
5.1. Review of Invariant Observer Theory
The state estimation based on aided-inertial navigation systems is a typical nonlinear state observer design problem, where few general approaches exist for such problem. However, when the system possesses the geometry with symmetries under a transformation group, its state observer can be designed using a systematic approach, namely the invariant observer, which is originally proposed by Bonnabel et al. [31,32]. The primary feature of the invariant observer is that it is built upon the system’s symmetry geometry and yields an invariant form of the state estimation error, which significantly simplifies the derivation of the observer gains and convergence analysis, making the observer particularly suitable for MAVs with computationally constrained onboard embedded systems. In this section, the theoretical foundations of the invariant observer are reviewed, which will be used to design the state observer of the RGB-D/inertial navigation system in following sections.
Definition 1.
(Transformation Lie roup) Define G as a Lie group with identity e, and let M be a manifold. The transformation group ϕgϵG acting on the manifold M can be defined as a smooth map and:
The inverse group action is also a smooth map, this makes a diffeomorphism.
Consider a system of the following form:
where both f, h are smooth maps, and (x, u, y) ϵ X × U × Y. For the state estimation problem of systems modeled as the above formulation, (x, u, y) represent the state, system input and output, respectively, where are all smooth manifolds (i.e., the state manifold, the input manifold and the output manifold, respectively). Assuming that B = X × U is the trivial fiber bundle over the state manifold X, let φg: G × X → X, ψg: G × U → U and ρg: G × Y → Y be the smooth Lie group actions on the system’s state, input and output manifold, respectively, where is G the system’s Lie group with the property described in Definition 1. The invariance of the system in Equation (25) by the transformation group G can be defined as:
Definition 2.
(G-invariance and G-equivariance) The system dynamics in Equation (25) is G-invariant if:
and for the output map , the system is G-equivariant if:
The property in Equations (26) and (27) can also be expressed as: X = f(X, U), Y = h(X, U), i.e., the system dynamics and outputs is invariant by the transformation group G. In coordinates, Equation (26) reads:
Similarly, Equation (27) can be rewritten as:
If the invariant system of Equation (25) verifies the properties described in Definition 2, the existence of its invariant observer can be verified by the following theorem [31]:
Theorem 1.
For a G-invariant and G-equivariant system , y = h(x, u), there exists an invariant observer that verifies the following properties:
where the terms in Equation (30) are as follows:
- (a)
- ;
- (b)
- , i.e., the observer is invariant by the transformation group.
- (1)
- wi is the invariant frame. A vector field w: TX → X is G-invariant if it verifies:The invariant frame is defined as the invariant vector fields that form a global frame for TX. Therefore, forms a basis for TxX. An invariant frame can be calculated by:where υi ϵ TeX is a basis of υi ϵ TeX, and γ(x) is the moving frame. Following the Cartan moving frame method, the moving frame γ(x) can be derived by solving φg(x) = c for g = γ(x), where c is a constant. In particular, one can choose c = e such that γ(x) = x−1.
- (2)
- denotes the invariant output error, which is defined as follows:Definition 3.(Invariant output error) The smooth map is an invariant error which verifies the following properties:
- (a)
- For any , is invertible;
- (b)
- For any , ;
- (c)
- For any , ;
According to the moving frame method, the invariant output error can be given by: - (3)
- is the invariant of G, which verifies:Following the moving frame method, the invariant is obtained by:where γ(x) is the moving frame.
- (4)
- Li is a 1 × r observer gain matrix that depends on I and ε, such that:
The observer gains can be obtained using the invariant state estimation error, which is defined as:
Definition 4.
(Invariant state estimation error) The smooth map is an invariant state estimation error if it satisfies the following properties:
- (a)
- is a diffeomorphism on X × X;
- (b)
- For any , ;
- (c)
- .
Theorem 2 [31]. For a G-invariant and G-equivariant system given by Equation (25), the state estimation error of its invariant state observer is given as:
with the following dynamics:
where are the invariants that take the form as in Equation (35).
As can be seen from Equation (38), in contrast to the state error dynamics of general nonlinear observer which depends on the trajectory of the system ((x(t), u(t))), the dynamics of the invariant state error depends only on the estimated invariants . This significantly simplifies the stability analysis and the selection of observer gains.
A comprehensive description of the mathematical foundation and proof of the invariant observer theory can be found in [31,32].
5.2. Sensor Measurement Models
As described previously, the onboard sensors equipped on the MAV consist of two primary parts: the MEMS IMU module and the RGB-D camera. The MEMS IMU module integrates three types of tri-axial sensors, generating tri-axial scalar measurements expressed in the MAV’s body-fixed coordinate: a tri-axial gyroscope module that provides measurements of the angular rate ωm, a tri-axial accelerometer module that provides measurements of the acceleration fm, as well as a tri-axial magnetometer module that measures the local magnetic field vector expressed in the body-fixed frame: ym, where the magnetic field vector can be considered as constant over a small-scale operating environment.
All measurements provided by the above inertial sensor are corrupted by sensor bias and measurement noises. It is a common practice to assume that the imperfections of sensor measurements include two components: a constant additive bias term and a Gaussian noise term with mean zero. Therefore, the gyroscope signals ωm can be modeled as:
where ω is the actual angular rate, bω denotes the constant gyroscope bias, and νω is Gaussian noise with zero mean. Similarly, signals of the accelerometer model can be modeled as:
where f is the actual acceleration, bf represents the constant accelerometer bias, and νf is also a Gaussian noise vector with zero mean.
The local magnetic field in the earth-fixed can be expressed frame as m = [mx, 0, mz]T. Since the magnetometer is fixed with the MAV body, the magnetic readings provided by the magnetometer are measured in the body-fixed frame, which also contain sensor noises. Denoting q as the quaternion that represents the orientation of the MAV’s body fixed frame with respect to the ground-fixed frame, the magnetometer model can be given as:
where ym is the readings of the magnetometer, and m denotes the Gaussian noise with zero mean.
The RGB-D visual odometry described in Section 4 can provide estimates of the MAV’s relative motion, which form observations of the MAV’s state and can be used as an aid to the inertial measurements (note that estimates of MAV’s rotations are not used as observations of the MAV’s attitude, since it is more desirable to utilize the inertial measurements for attitude estimation). In addition, an ultrasonic altimeter is employed in our system to measure the MAV’s altitude relative to the ground. For our system, the translation estimates of the RGB-D visual odometry are transformed into the MAV’s positions in the global frame, this yields the following output model of the RGB-D VO and altimeter:
where yp and ys are measurements of the RGB-D visual odometry and altimeter, respectively. px,y and pz denote the MAV’s planar positions and altitude in the global frame. Both yp and νs are the Gaussian white-noise of measurements.
5.3. RGB-D Visual/Inertial Navigation System Model
In our system, the MAV’s orientation is represented in the quaternion formulation since the quaternion parameterization is nonsingular and well-suited for implementation on computer systems. Using the aforementioned measurement model of gyroscope and accelerometer sensors, as well as the kinematics of a rigid body, the quaternion-based dynamics model of the MAV can be formulated as:
where q is the unit attitude quaternion representing the orientation of the body-fixed frame with respect to the global frame; and represent the MAV’s position and velocity in the global frame, respectively; g = [0 0 g]T is the local gravity vector in the ground-fixed frame. The state vector chosen for observer design is x = [q p v bω bf]T, along with the system input u = [ωm fm g]T.
The observations of the system consist of two parts: the magnetic measurements ym in the body-fixed frame and measurements of the MAV’s position yp ys provided by RGB-D VO and altimeter, both expressed in the global frame. Using the measurement model given in Equations (41) and (42), the system output is written as:
5.4. Observer Design of the RGB-D Visual/Inertial Navigation System
In order to verify the invariant properties of the RGB-D/inertial navigation system, the system dynamics model in Equation (43) is rewritten by ignoring the noise terms:
Similarly, the system output model in Equation (44) is now given as:
Following the definitions and theorems described in Section 5.1, we can verify the invariant properties of the system dynamics and output model, by defining the transformation Lie group G that acts on the state manifold X through the following actions:
where g = (q0, p0, bω,0, bf,0) denotes the group action of G with the following physical meaning: q0 and p0 represent the constant rotations and translations in the global frame, and bω,0, bf,0 ϵ R3 denote constant translations on the bias of gyroscopes and accelerometers, respectively.
Similarly, the group actions on the system input and output manifold (U, Y) can be defined as:
Following Equation (28), we have:
Therefore, the dynamics model in Equation (45) verifies . Following Definition 2, it can be concluded that the RGB-D visual/inertial navigation system is G-invariant.
Similarly, using the group actions ψg(u) and ρg(y), we can directly verify:
Following Definition 2, the system output model given in Equation (46) is G-equivariant under the group actions φg, ψg and ρg. As a result, the existence of the invariant observer for the system in Equations (45) and (46) can be guaranteed by Theorem 1. Using the verified invariant properties of the system dynamics and output, we can now design the invariant state observer for the RGB-D visual/inertial navigation system by following the systematic steps described in Section 5.1.
As mentioned previously in Section 5.1, the moving frame γ(x) of the invariant observer can be obtained by solving φg(x) = c. Let c be the unity (i.e., c = e), φg(x) can be given as:
Solving the above equations, the moving frame can be given by:
Therefore, the invariants of group G can be obtained by:
where is the complete set of invariants of G which depends on the system output y = h(x, u).
Using the invariants and , the invariant output error can be obtained by following Definition 3:
Denoting () as the basis vectors of the tangent space TeX over the state manifold , the invariant frame wi(x) is calculated by:
where according to Equation (53).
Following Theorem 1 and Equation (57), the invariant observer of system in Equations (45) and (46) can be given by:
where Li are 1 × 3 gain matrices of the observer. Notice that:
where Lq is a 3 × 6 matrix, and the rows of Lq are from row matrix . Other terms in Equation (58) that associated with the observer gains can also be transformed in the same manner, leading to:
Following Equation (37), the invariant state estimation error η of the observer can be obtained by:
Therefore, the dynamics of the state estimation error η can be directly obtained by calculating and bringing in the invariant terms :
As can be seen from Equation (62), the dynamics of the invariant state error depends on the estimated state only through the invariant terms rather than the trajectory of the system, which simplifies the calculation of the observer gains. Using the invariant state error in Equation (61), the invariant output error is rewritten as:
5.5. Calculation of Observer Gains Based on Invariant-EKF
In order to calculate the gain matrices (L) of the invariant observer in Equation (60), we adopted a systematic approach based on the invariant-EKF (IEKF) [37]. The basic idea of the IEKF is to linearize the dynamics of the invariant state estimation error η about the current estimated state, and implement a Kalman filter on the linearized error dynamics to obtain the optimal observer gains. Details of the IEKF-based observer gains calculation will be specified in the parts of this subsection.
To better illustrate the IEKF method, we first recall the standard EKF approach that operates by linearizing the system dynamics. Consider the following nonlinear system described by:
where w, v denote the mutually-independent process and measurement Guassian white-noise with covariances , , respectively. B, D are the input matrices of the noise vectors. The optimal state estimate that minimizes the estimation error can be obtained using the conventional continuous-time EKF procedure given by:
where K denotes the Kalman gain, and A, C are the Jacobian of the process model f and measurement model h with respect to the current estimated state (, ), respectively. According to the EKF method, we linearize the system dynamics and output model given by Equation (64) about the latest estimated state using Taylor expansion:
Equation (65) can be rewritten as:
Following Equations (66) and (67), the dynamics of the EKF state estimation error is given by:
As described in Section 5.1, the invariant observer of the RGB-D visual/inertial navigation system was initially designed without considering the process and measurement noises. Introducing the noise terms w, v, the system dynamics and the associated invariant observer are rewritten as:
Recall the invariant state estimation error given by Equation (37): . From Equation (69), we can find that the time derivative of the estimation error will also contain the noise terms w, v. According to the IEKF, we can now linearize about the latest estimated state. Denote as the actual state estimation error, and should be close to the group identity e (i.e., ) when . Let , it is proved in [48] that by linearizing about the dynamics of reads:
which takes the same form as in the conventional EKF case (Equation (68). Therefore, the observer gains L can be obtained from K, which is calculated following the procedure given by Equation (65).
As discussed in subsection 5.3, the RGB-D visual/inertial navigation system model with noise terms is given as in Equations (43) and (44) (Note that px,y, pz and vp, vs are now merged and denoted as p and vp):
The invariant observer with noise terms is now written as:
where the invariant output error is given as:
The derivation of the invariant state estimation error dynamics is the same as described in Subsection 5.4. Computing the time derivative of η, we have:
where , and .
Linearizing the output error given by Equation (73) about and omitting the high-order terms (, ), we can obtain:
Similarly, denoting , the linearized is given by:
Denoting and , Equation (76) takes the following form:
where:
As can be found from Equation (78), the matrix K is composed by the gains of the invariant observer in Equation (60). Therefore, observer gains L can be extracted from matrix K, which is updated via the procedure given by Equation (65) using matrices A, B, C, D.
6. Implementation and Experimental Results
6.1. Implementation Details and Experimental Scenarios
In order to validate the effectiveness of the proposed RGB-D visual/inertial navigation scheme via flight test, the robust RGB-D VO and invariant observer were implemented on a prototype quadrotor MAV system shown in Figure 6a. The quadrotor was equipped with an onboard low-cost MEMS IMU (ADIS16405, produced by Analog Devices Inc., Norwood, MA, USA, Figure 6b) and an RGB-D camera (PrimeSense Carmine 1.08, produced by PrimeSense Inc., Tel-Aviv, Israel, Figure 6c).
The ADIS16405 IMU consists of tri-axial gyroscope, accelerometer and magnetometer and provided inertial and magnetic measurement data at a rate of 100 Hz. The PrimeSense Carmine camera outputs RGB image and depth data with a resolution of 640 × 480 (pixels), at a rate of 30 Hz. The robust RGB-D VO algorithm described in Section 4 is implemented based on C++ and the OpenCV library [49], and runs at a same rate of 30 Hz. The overall invariant observer is implemented using an Euler numerical integration method and a complementary update scheme: the rough state estimate is propagated at 100 Hz, using the system dynamics and inertial measurements (u), while the full estimate is updated at a rate of 30 Hz, when the measurement from the RGB-D VO is available.
Using the prototype quadrotor MAV system, a series of flight tests were carried out in two typical indoor scenarios shown in Figure 7. Scenario 1 represents the indoor environment inside a laboratory, and the MAV is controlled to follow a smooth 3D rectangular trajectory in the laboratory. The environment of Scenario 2 was a corridor inside a building, and after taking off from one end, the MAV is guided to traverse the corridor to land at the other end. For all flight experiments, the environments are without access to GPS signal and the MAV must rely only on the RGB-D visual/inertial navigation scheme to obtain state estimates.

Figure 6.
Experiment system: a prototype quadrotor MAV equipped with a RGB-D camera and a low-cost MEMS IMU module. (a) Prototype quadrotor MAV system; (b) MEMS IMU: ADIS16405; (c) RGB-D Camera: PrimeSense Carmine 1.08.

Figure 7.
Indoor flight test scenarios. (a) Scenario 1: an actual laboratory; (b) Scenario 2: a corridor inside a building. Both environments are without access to GPS signal.
6.2. Indoor Flight Test Results
6.2.1. RGB-D Visual Odometry Test Results
We first conducted a number of experiments to evaluate the performance of the robust RGB-D VO described in Section 3, using the RGB image and depth data provided by the onboard PrimeSense Carmine RGB-D camera. Figure 8 shows the feature detection and matching results in Scenario 1. Figure 8a illustrates the features (drawn in green and blue) extracted by the ORB detector from two consecutive images. Examples of the feature correspondences found by the OFC-ORB strategy from the detected features are show in Figure 8b, and the lines connecting the pairs of points represent the correspondence relationships of features. Figure 8c shows the corresponding depth image and the optical-flow disparity (drawn in green) between consecutive images. The experimental results demonstrate the effectiveness of the OFC-ORB strategy, as well as its robustness to image noise and motion blur.

Figure 8.
Experimental results of feature detection and matching. (a) Features extracted from images captured at time step m − 1 (left) and m (right); (b) feature correspondences; (c) depth image captured by the RGB-D camera (left) and optical-flow between consecutive images (right).
To further evaluate the computational efficiency of the proposed strategy, the performance of OFC-ORB and various existing methods (Harris Corner, SIFT (Scale-invariant feature transform), SURF (speeded up robust features)) were compared in terms of time spent on finding feature correspondences. We applied different methods to the same pairs of 640 × 480 images captured by the RGB-D camera and recorded the overall computation time. For each method, the algorithm ran on the same computer platform (a single-board computer mounted on the MAV), the experiment was repeated 30 times and the average computation time was calculated over these experiments. The performance comparisons of various methods are shown in Table 1. As can be seen from Table 1, the OFC-ORB feature detection and matching strategy outperforms other existing in terms of computation efficiency. This feature makes it suitable for implementation on computationally constrained onboard platforms.

Table 1.
Performance comparisons of various algorithms.
| Algorithms | Average Time (ms) |
|---|---|
| Harris Corner | 16.6 |
| SIFT | 6290.1 |
| SURF | 320.5 |
| OFC-ORB | 13.2 |
6.2.2. State Estimation Results
The state estimation results from indoor flight tests are plotted in Figure 9. Figure 9a,c depicts examples of attitude and velocity estimates of Scenario 1 and Scenario 2 from the invariant observer, respectively. The estimated position of Scenario 1 and Scenario 2 are shown in Figure 9b,d. These results indicate that the drifts of the low-cost MEMS IMU sensor can be effectively bounded through data fusion of RGB-D VO estimates and inertial measurements using the proposed invariant observer.
For comparison purposes, an external motion capture camera is employed in the flight tests of Scenario 1 to record the actual flight data, which is used as the ground truth trajectory. Both the estimated position and the ground truth 3-D trajectory derived from the external motion capture camera are plotted in Figure 9b. The results indicate that the estimated position closely matches the ground truth trajectory, except for a slightly larger deviation in the x-direction (east) of approximately 7 cm in maximum, which is likely due to a decreased number of environmental features along that direction. Despite these occasional deviations, the flight test results prove that the overall performance and accuracy of state estimation are satisfactory, and the proposed navigation scheme can provide reliable and accurate state estimates for stabilization and control of the MAV. In addition, the overall RGB-D visual/inertial navigation scheme can operate effectively in indoor environments, without relying on external navigation aids such as GPS.
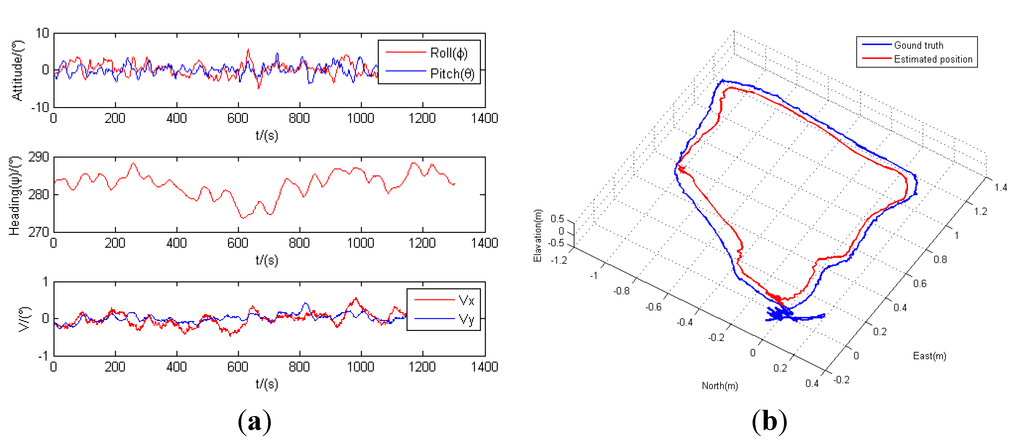
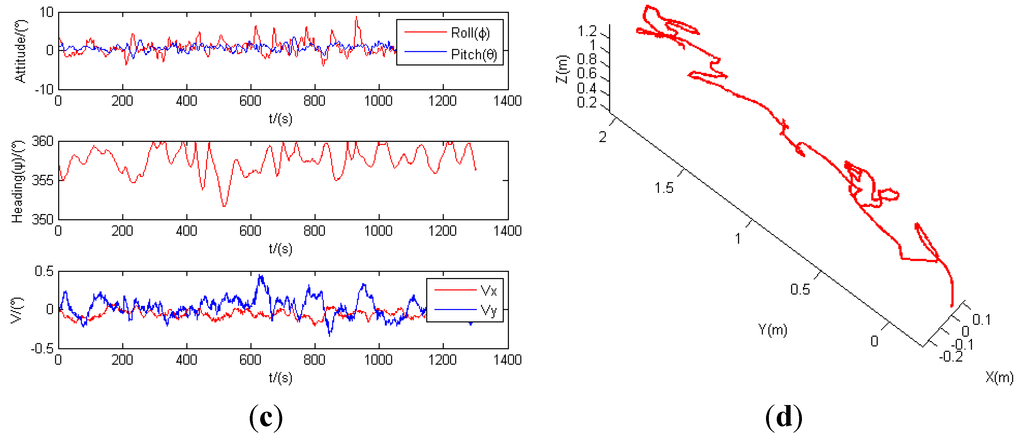
Figure 9.
State estimation results. (a) Attitude and velocity estimates of Scenario 1; (b) estimated position vs. ground truth trajectory of Scenario 1; (c) attitude and velocity estimates of Scenario 2; (d) estimated position of Scenario 2.
7. Conclusions and Future Work
This paper presents an integrated RGB-D visual/inertial navigation scheme for the state estimation of MAVs operating in GPS-denied indoor environments. A robust RGB-D visual odometry approach was developed to estimate the relative motions of the MAV using consecutive image and depth data provided by the RGB-D camera. The motion estimates from the RGB-D VO are fused with MEMS IMU measurements through the invariant observer, which is designed based on the symmetry-preserving observer theory. The proposed navigation scheme and corresponding algorithms were implemented on a quadrotor MAV, and experimental results from indoor flight test demonstrate the efficiency and robustness of the RGB-D VO, as well as the effectiveness of the invariant observer-based estimation approach. Future work will focus on evaluating the system in more challenging, actual indoor environments with disturbances, and comparing the invariant observer-based approach with other existing filters.
Acknowledgments
This work was supported in part by the China High-Tech 863 Program under Grants 2001AA415340 and 2007AA04Z1A6, and in part by the National Natural Science Foundation of China under Grant 61174168, as well as the Aviation Science Foundation of China under Grants 20100758002 and 20128058006. The authors appreciate the technical support in the experiments provided by Zhen Tian.
Author Contributions
Dachuan Li proposed the integrated RGB-D visual/inertial navigation scheme, designed and developed the invariant observer-based state estimation approach, and wrote the paper. Liangwen Tang developed the RGB-D visual odometry algorithm, and Sheng Yang developed the quadrotor MAV prototype system and conducted the flight experiments. Nong Cheng provided advices on the derivation of the navigation system model. Qing Li and Jingyan Song supervised the work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bouabdallah, S.; Bermes, C.; Grzonka, S.; Gimkiewicz, C.; Brenzikofer, A.; Hahn, R.; Schafroth, D.; Grisetti, G.; Burgard, W.; Siegwart, R. Towards palm-size autonomous helicopters. J. Intell. Robot. Syst. 2011, 61, 445–471. [Google Scholar] [CrossRef]
- Goodrich, M.A.; Cooper, J.L.; Adams, J.A.; Humphrey, C.; Zeeman, R.; Buss, B.G. Using a mini-UAV to support wilderness search and rescue: Practices for human–robot teaming. In Proceedings of 2007 IEEE International Workshop on Safety, Security and Rescue Robotics (SSRR 2007), Rome, Italy, 27–29 September 2007.
- Tomic, T.; Schmid, K.; Lutz, P.; Domel, A.; Kassecker, M.; Mair, E.; Grixa, I.L.; Ruess, F.; Suppa, M.; Burschka, D. Toward a fully autonomous UAV: Research platform for indoor and outdoor urban search and rescue. IEEE Robot. Autom. Mag. 2012, 19, 46–56. [Google Scholar] [CrossRef]
- Lin, L.; Roscheck, M.; Goodrich, M.; Morse, B. Supporting wilderness search and rescue with integrated intelligence: autonomy and information at the right time and the right place. In Proceedings of 24th AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010; pp. 1542–1547.
- Bachrach, A.; He, R.; Roy, N. Autonomous flight in unknown indoor environments. Int. J. Micro Air Veh. 2009, 4, 277–298. [Google Scholar]
- Bachrach, A.; He, R.; Roy, N. Autonomous flight in unstructured and unknown indoor environments. In Proceedings of European Conference on Micro Aerial Vehicles (EMAV 2009), Delft, The Netherlands, 14–17 September 2009.
- Bachrach, A.; Prentice, S.; He, R.; Roy, N. RANGE: Robust autonomous navigation in GPS-denied environments. J. Field Robot. 2011, 28, 644–666. [Google Scholar] [CrossRef]
- Chowdhary, G.; Sobers, D.M., Jr.; Pravitra, C.; Christmann, C.; Wu, A.; Hashimoto, H.; Ong, C.; Kalghatgi, R.; Johnson, E.N. Self-contained autonomous indoor flight with ranging sensor navigation. J. Guid. Control Dyn. 2012, 29, 1843–1854. [Google Scholar] [CrossRef]
- Chowdhary, G.; Sobers, D.M.; Pravitra, C.; Christmann, C.; Wu, A.; Hashimoto, H.; Ong, C.; Kalghatgi, R.; Johnson, E.N. Integrated guidance navigation and control for a fully autonomous indoor UAS. In Proceedings of AIAA Guidance Navigation and Control Conference, Portland, OR, USA, 8–11 August 2011.
- Sobers, D.M.; Yamaura, S.; Johnson, E.N. Laser-aided inertial navigation for self-contained autonomous indoor flight. In Proceedings of AIAA Guidance Navigation and Control Conference, Toronto, Canada, 2–5 August 2010.
- Weiss, S.; Achtelik, M.W.; Lynen, S.; Chli, M.; Siegwart, R. Real-time onboard visual-inertial state estimation and self-calibration of MAVs in unknown environments. In Proceedings of 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 957–964.
- Wu, A.D.; Johnson, E.N.; Kaess, M.; Dellaert, F.; Chowdhary, G. Autonomous flight in GPS-denied environments using monocular vision and inertial sensors. J. Aerosp. Comput. Inf. Commun. 2013, 10, 172–186. [Google Scholar]
- Wu, A.D.; Johnson, E.N. Methods for localization and mapping using vision and inertial sensors. In Proceedings of AIAA Guidance, Navigation, and Control Conference, Honolulu, HI, USA, 18–21 August 2008.
- Acgtelik, M.; Bachrach, A.; He, R.; Prentice, S.; Roy, N. Stereo vision and laser odometry for autonomous helicopters in GPS-denied indoor environments. Proc. SPIE 2009, 7332, 733219. [Google Scholar]
- Achtelik, M.; Roy, N.; Bachrach, A.; He, R.; Prentice, S.; Roy, N. Autonomous navigation and exploration of a quadrotor helicopter in GPS-denied indoor environments. In Proceedings of the 1st Symposium on Indoor Flight, International Aerial Robotics Competition, Mayagüez, Puerto Rico, 21 July 2009.
- Voigt, R.; Nikolic, J.; Hurzeler, C.; Weiss, S.; Kneip, L.; Siegwart, R. Robust embedded egomotion estimation. In Proceedings of 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), San Francisco, CA, USA, 25–30 September; pp. 2694–2699.
- Bachrach, A.; Prentice, S.; He, R.; Henry, P.; Huang, A.S.; Krainin, M.; Maturana, D.; Fox, D.; Roy, N. Estimation, planning, and mapping for autonomous flight using an RGB-D camera in GPS-denied environments. Int. J. Robot. Res. 2012, 31, 1320–1343. [Google Scholar] [CrossRef]
- Leishman, R.; Macdonald, J.; McLain, T.; Beard, R. Relative navigation and control of a hexacopter. In Proceedings of 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 4937–4942.
- Guerrero-Castellanos, J.F.; Madrigal-Sastre, H.; Durand, S.; Marchand, N.; Guerrero-Sanchez, W.F.; Salmeron, B.B. Design and implementation of an attitude and heading reference system (AHRS). In Proceedings of 2011 8th International Conference on Electrical Engineering Computing Science and Automatic Control (CCE), Merida, Mexico, 26–28 October 2011.
- Bonnabel, S.; Martin, P.; Salaün, E. Invariant extended Kalman filter: Theory and application to a velocity-aided attitude estimation problem. In Proceedings of Joint 48th IEEE Conference on Decision and Control and 2009 28th Chinese Control Conference (CDC/CCC 2009), Shanghai, China, 15–18 December 2009; pp. 1297–1304.
- Kelly, J.; Sukhatme, G.S. Visual-inertial sensor fusion: Localization, mapping and sensor-to-sensor self-calibration. Int. J. Robot. Res. 2011, 30, 56–79. [Google Scholar] [CrossRef]
- Van der Merwe, R.; Wan, E. Sigma-point Kalman filters for integrated navigation. In Proceedings of 60th Annual Meeting of the Institute of Navigation (ION), Dayton, OH, USA, 7–9 June 2004; pp. 641–654.
- Bry, A.; Bachrach, A.; Roy, N. State estimation for aggressive flight in GPS-denied environments using onboard sensing. In Proceedings of 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 1–8.
- Crassidis, J.L.; Markley, F.L.; Cheng, Y. Survey of nonlinear attitude estimation methods. J. Guid. Control Dyn. 2007, 30, 12–28. [Google Scholar] [CrossRef]
- Achtelik, M.; Achtelik, M.; Weiss, S.; Siegwart, R. Onboard IMU and monocular vision based control for MAVs in unknown in- and outdoor environments. In Proceedings of 2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 3056–3063.
- Boutayeb, M.; Richard, E.; Rafaralahy, H.; Souley Ali, H.; Zaloylo, G. A simple time-varying observer for speed estimation of UAV. In Proceedings of 17th IFAC World Congress, Seoul, Korea, 6–11 July 2008; pp. 1760–1765.
- Benallegue, A.; Mokhtari, A.; Fridman, L. High-order sliding-mode observer for a quadrotor UAV. Int. J. Robust Nonlinear Control 2008, 18, 427–440. [Google Scholar] [CrossRef]
- Madani, T.; Benallegue, A. Sliding mode observer and backstepping control for a quadrotor unmanned aerial vehicles. In Proceedings of 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 5887–5892.
- Benzemrane, K.; Santosuosso, G.L.; Damm, G. Unmanned aerial vehicle speed estimation via nonlinear adaptive observers. In Proceedings of 2007 American Control Conference, New York, NY, USA, 9–13 July 2007.
- Rafaralahy, H.; Richard, E.; Boutayeb, M.; Zasadzinski, M. Simultaneous observer based sensor diagnosis and speed estimation of unmanned aerial vehicle. In Proceedings of 47th IEEE Conference on Decision and Control (CDC 2008), Cancun, Mexico, 9–11 December 2008; pp. 2938–2943.
- Bonnabel, S.; Martin, P.; Rouchon, P. Symmetry-preserving observers. IEEE Trans. Autom. Control 2008, 53, 2514–2526. [Google Scholar] [CrossRef]
- Bonnabel, S.; Martin, P.; Rouchon, P. Non-linear symmetry-preserving observers on lie groups. IEEE Trans. Autom. Control 2009, 54, 709–1713. [Google Scholar]
- Mahony, R.; Hamel, T.; Pflimlin, J.-M. Nonlinear complementary filters on the special orthogonal group. IEEE Trans. Autom. Control 2008, 53, 1203–1218. [Google Scholar] [CrossRef]
- Martin, P.; Salaun, E. Invariant observers for attitude and heading estimation from low-cost inertial and magnetic sensors. In Proceedings of 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 1039–1045.
- Martin, P.; Salaun, E. Design and implementation of a low-cost attitude and heading nonlinear estimator. In Proceedings of Fifth International Conference on Informatics in Control, Automation and Robotics, Signal Processing, Systems Modeling and Control, Funchal, Portugal, 11–15 May 2008; pp. 53–61.
- Martin, P.; Salaün, E. Design and implementation of a low-cost observer-based attitude and heading reference system. Control Eng. Pract. 2010, 18, 712–722. [Google Scholar] [CrossRef]
- Bonnabel, S. Left-invariant extended Kalman filter and attitude estimation. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 1027–1032.
- Barczyk, M.; Lynch, A.F. Invariant extended Kalman filter design for a magnetometer-plus-GPS aided inertial navigation system. In Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC), Orlando, FL, USA, 12–15 December 2011; pp. 5389–5394.
- Barczyk, M.; Lynch, A.F. Invariant observer design for a helicopter UAV aided inertial navigation system. IEEE Trans. Control Syst. Technol. 2013, 21, 791–806. [Google Scholar] [CrossRef]
- Cheviron, T.; Hamel, T.; Mahony, R.; Baldwin, G. Robust nonlinear fusion of inertial and visual data for position, velocity and attitude estimation of UAV. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, Roma, Italy, 10–14 April 2007; pp. 2010–2016.
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 2564–2571.
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In Proceedings of Computer Vision–ECCV 2006, 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; Springer: Berlin, Germany, 2006; Volume 1, pp. 430–443. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. Brief: Binary robust independent elementary features. In Proceedings of Computer Vision–ECCV 2010, 11th European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; Springer: Berlin, Germany; pp. 778–792.
- Lucas, B.D.; Kanade, T. An iterative image registration technique with an application to stereo vision. Proc. IJCAI 1981, 81, 674–679. [Google Scholar]
- Bouguet, J.Y. Pyramidal Implementation of the Affine Lucas Kanade Feature Tracker Description of the Algorithm. Available online: http://robots.stanford.edu/cs223b04/algo_affine_tracking.pdf (accessed on 20 April 2015).
- Arun, K.S.; Huang, T.S.; Blostein, S.D. Least-squares fitting of two 3-D point sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 5, 698–700. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Nistér, D. Preemptive RANSAC for live structure and motion estimation. Mach. Vis. Appl. 2005, 16, 321–329. [Google Scholar] [CrossRef]
- OpenCV. Available online: http://opencv.org/ (accessed on 27 December 2014).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).