Mechanical Analysis of a Pneumatically Actuated Concentric Double-Shell Structure for Cell Stretching
Abstract
:1. Introduction
2. Methods
2.1. Experimental Characterisation of the Device
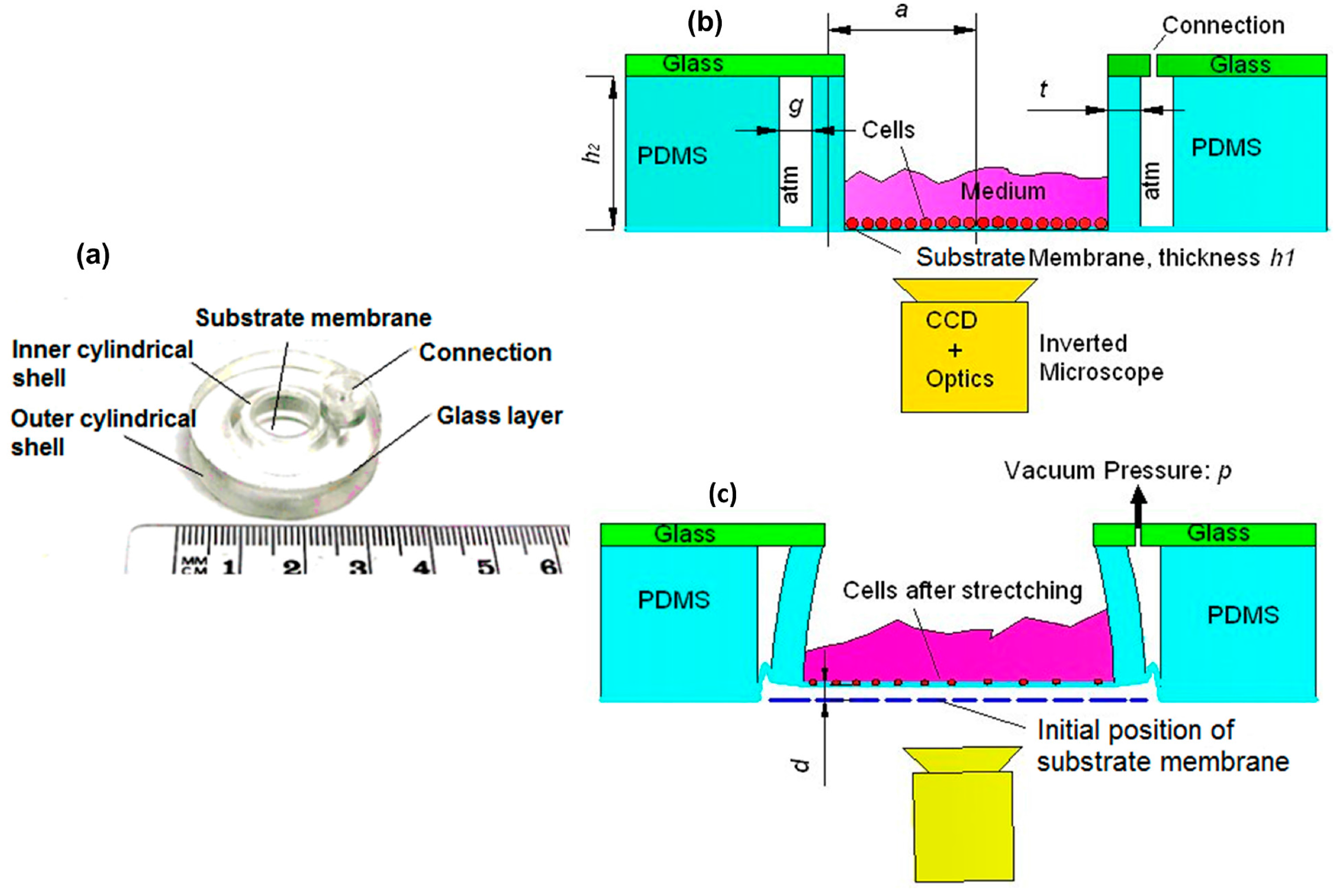
2.2. Deformation Analysis of the Structure
| Parameters | Values (mm) |
|---|---|
| Centreline radius of the inner cylindrical shell, a | 6.75 |
| Thickness of the inner cylindrical shell wall, t | 1.5 |
| Height of the cylindrical shells, h2 | 7 |
| Thickness of the substrate membrane, h1 | 0.12 |
| Width of the gap between the cylindrical shells, g | 2 |
2.2.1. Substrate Membrane
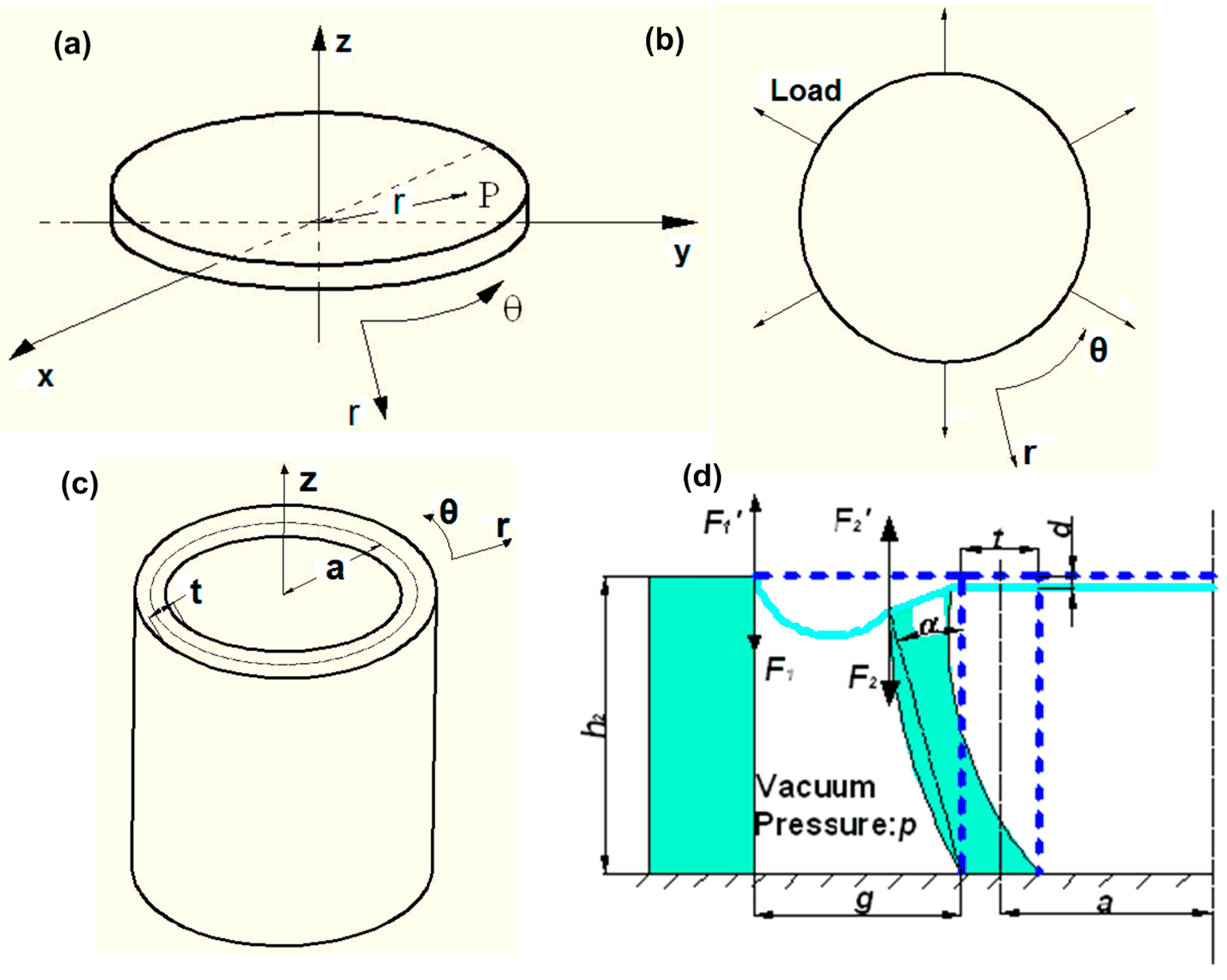
2.2.2. Cylindrical Shell
2.2.3. In-Plane Strain and Out-of-Plane Displacement of Substrate Membrane
2.3. Determination of the Elastic Modulus of PDMS
2.3.1. Constitutive Model
2.3.2. Boundary Conditions and Mesh
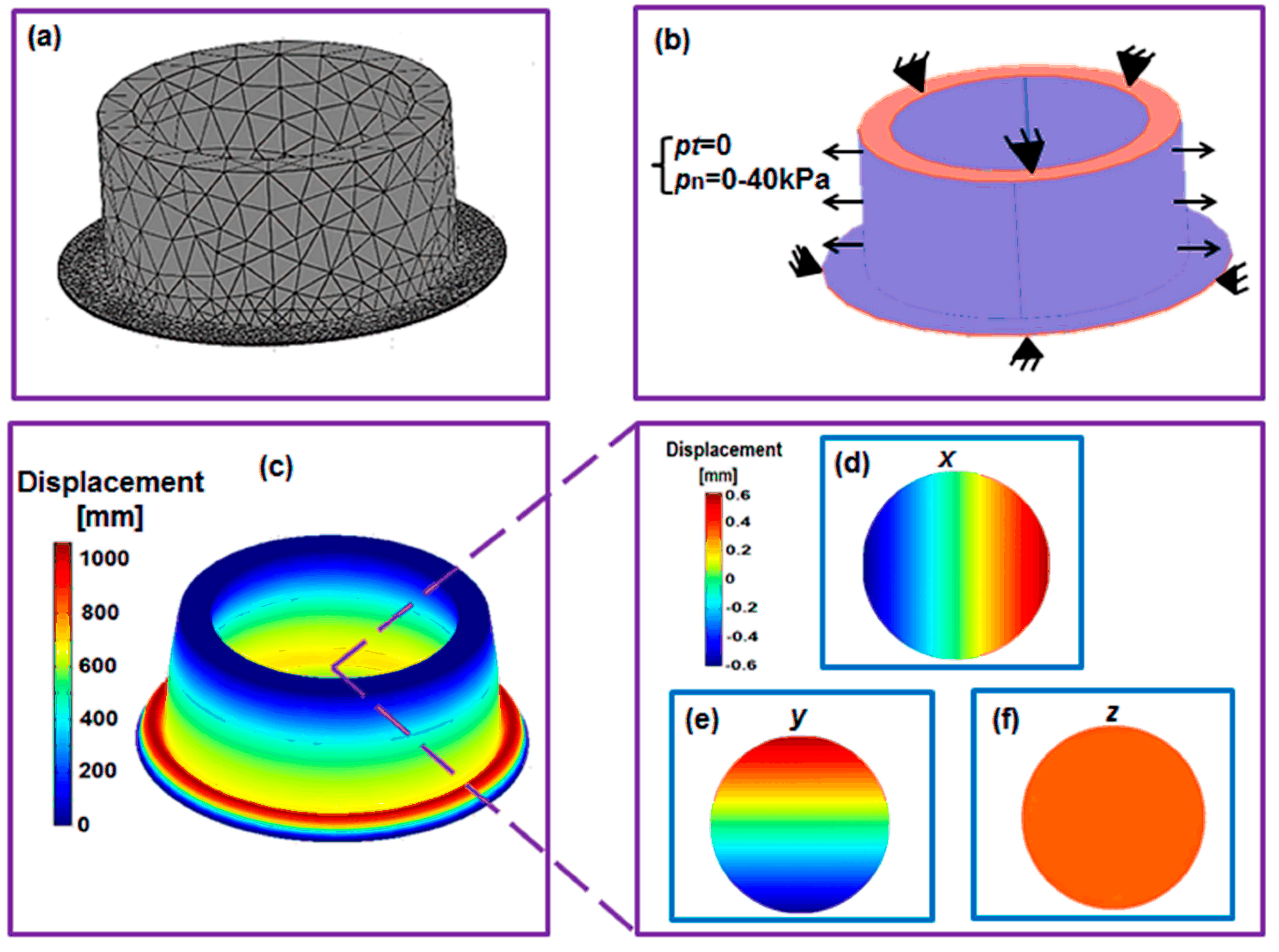
2.3.3. Estimation of the Elastic Modulus
3. Analytical Model Validation
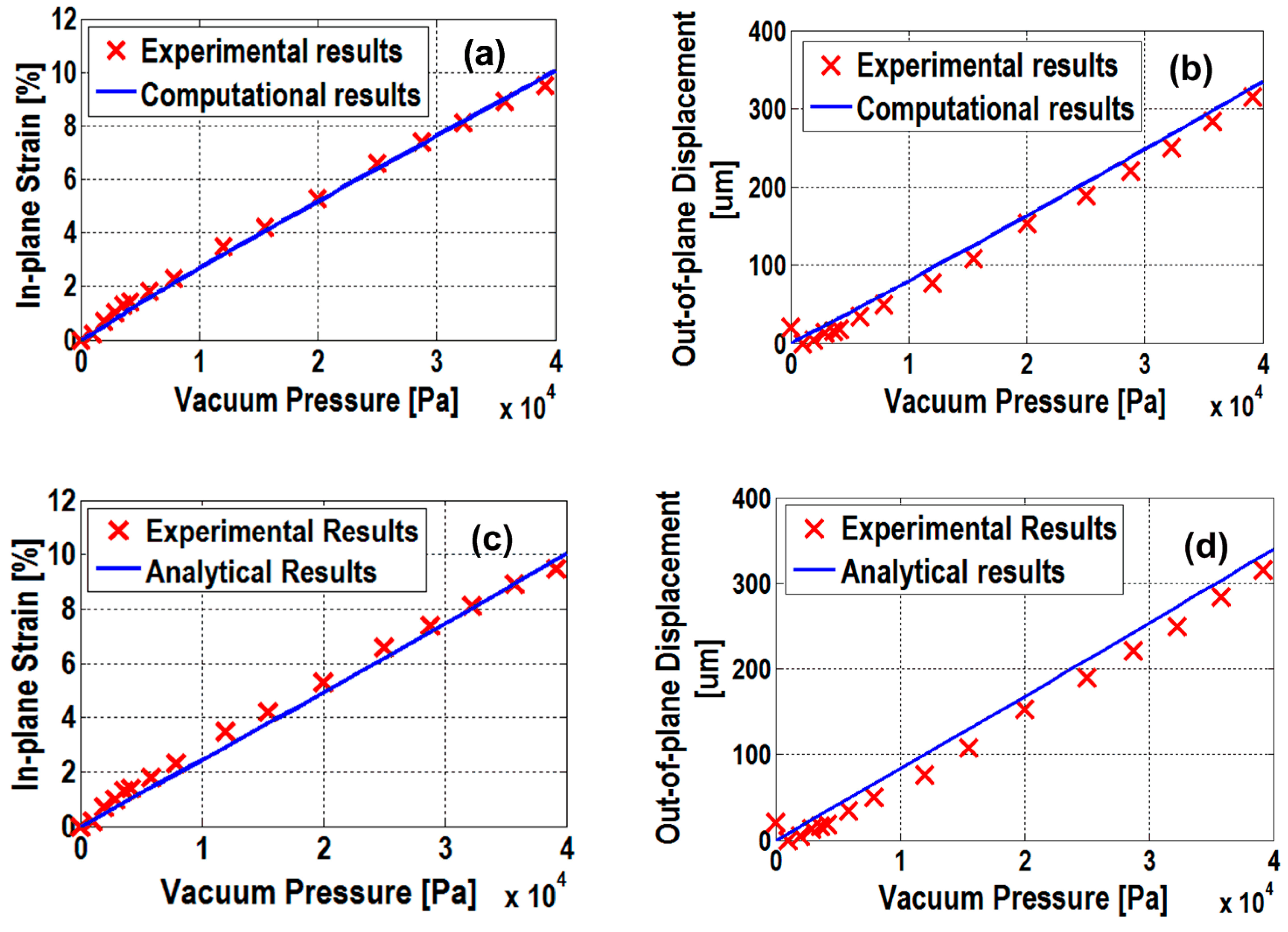
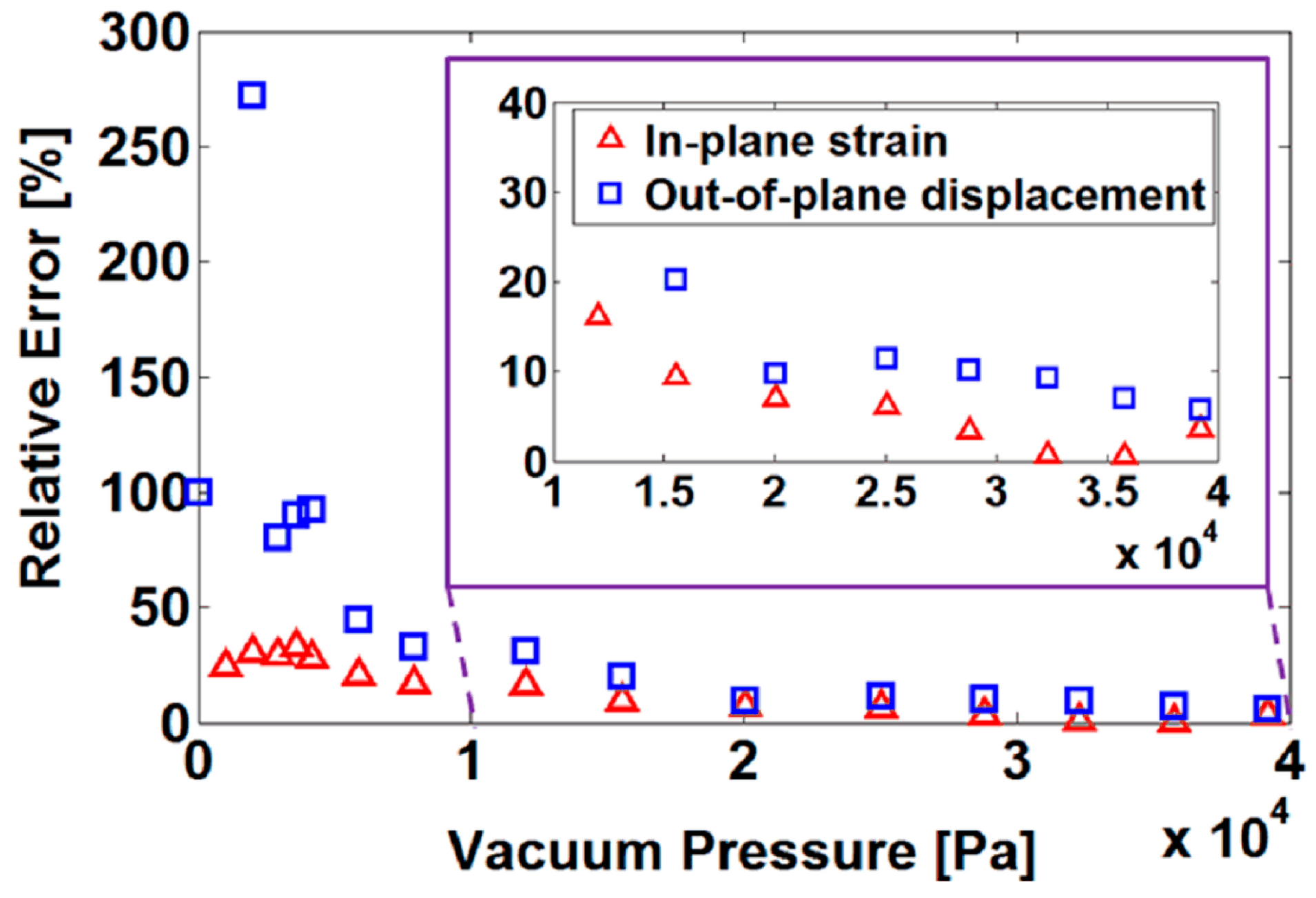
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Appendix A: Deformation Analysis of Circular Membrane
Appendix B: Deformation Analysis of Cylindrical Shell
Appendix C: Calculation of Total Potential Energy
Conflicts of Interest
References
- Boerboom, R.A.; Rubbens, M.P.; Driessen, N.J.B.; Bouten, C.V.C.; Baaijens, F.P.T. Effect of strain magnitude on the tissue properties of engineered cardiovascular constructs. Ann. Biomed. Eng. 2008, 36, 244–253. [Google Scholar] [CrossRef] [PubMed]
- Desmaele, D.; Boukallel, M.; Regnier, S. Actuation means for the mechanical stimulation of living cells via microelectromechanical systems: A critical review. J. Biomech. 2011, 44, 1433–1446. [Google Scholar] [CrossRef] [PubMed]
- Gwak, S.J.; Bhang, S.H.; Kim, I.K.; Kim, S.S.; Cho, S.W.; Jeon, O.; Yoo, K.J.; Putnam, A.J.; Kim, B.S. The effect of cyclic strain on embryonic stem cell-derived cardiomyocytes. Biomaterials 2008, 29, 844–856. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zheng, L.S.; Gong, X.H.; Jia, X.L.; Song, W.; Liu, M.L.; Fan, Y.B. Effect of Cyclic Strain on Cardiomyogenic Differentiation of Rat Bone Marrow Derived Mesenchymal Stem Cells. PloS One 2012, 7, e34960. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Miyagawa, S.; Miki, K.; Saito, A.; Fukushima, S.; Higuchi, T.; Kawamura, M.; Kawamura, T.; Ito, E.; Kawaguchi, N.; Sawa, Y.; Matsuura, N. In vivo differentiation of induced pluripotent stem cell-derived cardiomyocytes. Circ. J. Off. J. Jpn. Circ. Soc. 2013, 77, 1297–1306. [Google Scholar]
- Kreutzer, J.; Ikonen, L.; Hirvonen, J.; Pekkanen-Mattila, M.; Aalto-Setala, K.; Kallio, P. Pneumatic cell stretching system for cardiac differentiation and culture. Med. Eng. Phys. 2014, 36, 496–501. [Google Scholar] [CrossRef] [PubMed]
- Simmons, C.S.; Petzold, B.C.; Pruitt, B.L. Microsystems for biomimetic stimulation of cardiac cells. Lab Chip 2012, 12, 3235–3248. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Xie, Y.Y.; Yuan, B.; Xu, J.; Gong, P.Y.; Jiang, X.Y. A stretching device for imaging real-time molecular dynamics of live cells adhering to elastic membranes on inverted microscopes during the entire process of the stretch. Integr. Biol. 2010, 2, 288–293. [Google Scholar] [CrossRef]
- Brown, T.D. Techniques for mechanical stimulation of cells in vitro: A review. J. Biomech. 2000, 33, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.H.; Wong, P.K.; Park, J.; Levchenko, A.; Sun, Y. Microengineered platforms for cell mechanobiology. Ann. Rev. Biomed. Eng. 2009, 11, 203–233. [Google Scholar] [CrossRef]
- Bottlang, M.; Simnacher, M.; Schmitt, H.; Brand, R.A.; Claes, L. A cell strain system for small homogeneous strain applications. Biomed. Tech. 1997, 42, 305–309. [Google Scholar] [CrossRef]
- Colombo, A.; Cahill, P.A.; Lally, C. An analysis of the strain field in biaxial Flexcell membranes for different waveforms and frequencies. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2008, 222, 1235–1245. [Google Scholar] [CrossRef]
- Winston, F.K.; Macarak, E.J.; Gorfien, S.F.; Thibault, L.E. A system to reproduce and quantify the biomechanical environment of the cell. J. Appl. Physiol. 1989, 67, 397–405. [Google Scholar] [PubMed]
- Gopalan, S.M.; Flaim, C.; Bhatia, S.N.; Hoshijima, M.; Knoell, R.; Chien, K.R.; Omens, J.H.; McCulloch, A.D. Anisotropic stretch-induced hypertrophy in neonatal ventricular myocytes micropatterned on deformable elastomers. Biotechnol. Bioeng. 2003, 81, 578–587. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Niu, X.F.; Song, W.; Guan, C.D.; Feng, Q.L.; Fan, Y.B. Combined effects of mechanical strain and hydroxyapatite/collagen composite on osteogenic differentiation of rat bone marrow derived mesenchymal stem cells. J. Nanomater. 2013, 2013. [Google Scholar] [CrossRef]
- Jacobs, C.; Grimm, S.; Ziebart, T.; Walter, C.; Wehrbein, H. Osteogenic differentiation of periodontal fibroblasts is dependent on the strength of mechanical strain. Arch. Oral. Biol. 2013, 58, 896–904. [Google Scholar] [CrossRef] [PubMed]
- Thompson, M.S.; Abercrombie, S.R.; Ott, C.E.; Bieler, F.H.; Duda, G.N.; Ventikos, Y. Quantification and significance of fluid shear stress field in biaxial cell stretching device. Biomech. Model. Mechanobiol. 2011, 10, 559–564. [Google Scholar] [CrossRef] [PubMed]
- Yoon, S.H.; Reyes-Ortiz, V.; Kim, K.H.; Seo, Y.H.; Mofrad, M.R.K. Analysis of circular PDMS microballoons with ultralarge deflection for MEMS design. J. Microelectromech. Syst. 2010, 19, 854–864. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Zhou, J.H.; Dai, W.; Zheng, Y.Z.; Wu, H.K. A convenient platform of tunable microlens arrays for the study of cellular responses to mechanical strains. J. Micromech. Microeng. 2011, 21, 054017. [Google Scholar] [CrossRef]
- Vaughan, T.J.; Haugh, M.G.; McNamara, L.M. A fluid-structure interaction model to characterize bone cell stimulation in parallel-plate flow chamber systems. J. R. Soc. Interface 2013, 10, 20120900. [Google Scholar]
- Ventsel, E.; Krauthammer, T. Thin Plates and Shells: Theory, Analysis, and Applications; CRC Press: New York, NY, USA, 2001. [Google Scholar]
- Dow, J.A. A Unified Approach to the Finite Element Method and Error Analysis Procedures; Academic Press: Waltham, MA, USA, 1998. [Google Scholar]
- Carrillo, F.; Gupta, S.; Balooch, M.; Marshall, S.J.; Marshall, G.W.; Pruitt, L.; Puttlitz, C.M. Nanoindentation of polydimethylsiloxane elastomers: Effect of crosslinking, work of adhesion, and fluid environment on elastic modulus. J. Mater. Res. 2005, 20, 2820–2830. [Google Scholar] [CrossRef]
- Liu, M.; Chen, Q.F. Characterization study of bonded and unbonded polydimethylsiloxane aimed for bio-micro-electromechanical systems-related applications. J. Micro/Nanolithogr. MEMS MOEMS 2007, 6, 023008. [Google Scholar] [CrossRef]
- Wu, C.L.; Lin, H.C.; Hsu, J.S.; Yip, M.C.; Fang, W.L. Static and dynamic mechanical properties of polydimethylsiloxane/carbon nanotube nanocomposites. Thin Solid Films 2009, 517, 4895–4901. [Google Scholar] [CrossRef]
- Cotton, D.P.J.; Popel, A.; Graz, I.M.; Lacour, S.P. Photopatterning the mechanical properties of polydimethylsiloxane films. J. Appl. Phys. 2011, 109, 054905. [Google Scholar] [CrossRef]
- Fuard, D.; Tzvetkova-Chevolleau, T.; Decossas, S.; Tracqui, P.; Schiavone, P. Optimization of poly-di-methyl-siloxane (PDMS) substrates for studying cellular adhesion and motility. Microelectron. Eng. 2008, 85, 1289–1293. [Google Scholar] [CrossRef]
- Misra, S.; Ramesh, K.T.; Okamura, A.M. Modelling of non-linear elastic tissues for surgical simulation. Comput. Method Biomech. Biomed. Eng. 2010, 13, 811–818. [Google Scholar] [CrossRef]
- Shafa, M.; Krawetz, R.; Zhang, Y.; Rattner, J.B.; Godollei, A.; Duff, H.J.; Rancourt, D.E. Impact of stirred suspension bioreactor culture on the differentiation of murine embryonic stem cells into cardiomyocytes. BMC Cell Biol. 2011, 12. [Google Scholar] [CrossRef]
- Geuss, L.R.; Suggs, L.J. Making cardiomyocytes: How mechanical stimulation can influence differentiation of pluripotent stem cells. Biotechnol. Prog. 2013, 29, 1089–1096. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Jia, X.L.; Bai, K.; Gong, X.H.; Fan, Y.B. Effect of fluid shear stress on cardiomyogenic differentiation of rat bone marrow mesenchymal stem cells. Arch. Med. Res. 2010, 41, 497–505. [Google Scholar] [CrossRef] [PubMed]
- Das, R.H.J.; Jahr, H.; Verhaar, J.A.N.; van der Linden, J.C.; van Osch, G.J.V.M.; Weinans, H. In vitro expansion affects the response of chondrocytes to mechanical stimulation. Osteoarthr. Cartil. 2008, 16, 385–391. [Google Scholar] [CrossRef] [PubMed]
- Kikidis, M.L.; Papadopoulos, C.A. Slenderness ratio effect on cracked beam. J. Sound. Vib. 1992, 155, 1–11. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Kreutzer, J.; Pajunen, S.; Kallio, P. Mechanical Analysis of a Pneumatically Actuated Concentric Double-Shell Structure for Cell Stretching. Micromachines 2014, 5, 868-885. https://doi.org/10.3390/mi5040868
Zhao F, Kreutzer J, Pajunen S, Kallio P. Mechanical Analysis of a Pneumatically Actuated Concentric Double-Shell Structure for Cell Stretching. Micromachines. 2014; 5(4):868-885. https://doi.org/10.3390/mi5040868
Chicago/Turabian StyleZhao, Feihu, Joose Kreutzer, Sami Pajunen, and Pasi Kallio. 2014. "Mechanical Analysis of a Pneumatically Actuated Concentric Double-Shell Structure for Cell Stretching" Micromachines 5, no. 4: 868-885. https://doi.org/10.3390/mi5040868
APA StyleZhao, F., Kreutzer, J., Pajunen, S., & Kallio, P. (2014). Mechanical Analysis of a Pneumatically Actuated Concentric Double-Shell Structure for Cell Stretching. Micromachines, 5(4), 868-885. https://doi.org/10.3390/mi5040868




