Next Article in Journal
Active Continuous-Flow Micromixer Using an External Braille Pin Actuator Array
Next Article in Special Issue
Photomechanical Bending of Azobenzene-Based Photochromic Molecular Fibers
Previous Article in Journal
Enhanced Liquid Metal Micro Droplet Generation by Pneumatic Actuation Based on the StarJet Method
Previous Article in Special Issue
Micromanufacturing in Fused Silica via Femtosecond Laser Irradiation Followed by Gas-Phase Chemical Etching
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Micromachines
Volume 4
Issue 1
10.3390/mi4010067
micromachines-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effects of Micromachining Processes on Electro-Osmotic Flow Mobility of Glass Surfaces

by
Yosuke Koga
1,
Reiko Kuriyama
2,
Yohei Sato
2,
Koichi Hishida
2 and
Norihisa Miki
1,*
1
Department of Mechanical Engineering, Keio University, 3-14-1 Hiyoshi, Kohoku-ku, Yokohama, Kanagawa, 223-8522, Japan
2
Department of System Design Engineering, Keio University, 3-14-1 Hiyoshi, Kohoku-ku, Yokohama, Kanagawa, 223-8522, Japan
*
Author to whom correspondence should be addressed.
Micromachines 2013, 4(1), 67-79; https://doi.org/10.3390/mi4010067
Submission received: 4 January 2013 / Revised: 16 February 2013 / Accepted: 20 February 2013 / Published: 13 March 2013
(This article belongs to the Special Issue Glass Micromachining and Applications of Glass)
Browse Figures
Versions Notes

Abstract

:
Silica glass is frequently used as a device material for micro/nano fluidic devices due to its excellent properties, such as transparency and chemical resistance. Wet etching by hydrofluoric acid and dry etching by neutral loop discharge (NLD) plasma etching are currently used to micromachine glass to form micro/nano fluidic channels. Electro-osmotic flow (EOF) is one of the most effective methods to drive liquids into the channels. EOF mobility is affected by a property of the micromachined glass surfaces, which includes surface roughness that is determined by the manufacturing processes. In this paper, we investigate the effect of micromaching processes on the glass surface topography and the EOF mobility. We prepared glass surfaces by either wet etching or by NLD plasma etching, investigated the surface topography using atomic force microscopy, and attempted to correlate it with EOF generated in the micro-channels of the machined glass. Experiments revealed that the EOF mobility strongly depends on the surface roughness, and therefore upon the fabrication process used. A particularly strong dependency was observed when the surface roughness was on the order of the electric double layer thickness or below. We believe that the correlation described in this paper can be of great help in the design of micro/nano fluidic devices.

1. Introduction

Because there are many beneficial size effects at the micro and nano scales, such as short mixing times, high efficiency in chemical reactions, and minute amounts of reagents and effluent liquids, micro/nano fluidic devices have been extensively studied for use in biomedical applications [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. In particular, nano fluidic devices that contain nano channels can be used for separation and filtration [21], single-molecule detection [22,23,24,25,26], highly efficient PCR [27], chemical analysis [28,29] and nano-photonic sensors [30], with great help of development of nanofabrication technologies [31,32,33,34,35,36,37,38,39,40,41,42,43]. As the channels are reduced in size, the surface roughness and surface chemistry become dominant in determining the dynamics of flow. Electro-osmotic flow (EOF) is well-known to depend on the surface chemistry of the channel walls. An electric double-layer is formed near the channel wall, depending on the wall surface. When an external electric field is applied, the layer moves, generating EOF. Electro-osmotic pumping is considered to be more efficient in driving liquids in micro/nano channels than applying differential pressure by an external pump, given the high viscous drag. The wall surface charge can be quantified by the zeta potential. Therefore, the EOF can be predicted by the given zeta potential and vice versa. The relationship between the zeta potential and EOF can be described by the Smoluchowski equation when the surface roughness is smaller than the electric double layer [44,45,46].
The EOF can be measured by micro-particle image velocimetry (PIV) [47,48,49,50]. Fluorescent nano/micro beads are typically used as tracers, and a confocal microscope can be used to deduce the velocity distribution in three dimensions [51,52,53,54,55,56,57,58,59]. Evanescent waves generated by total index reflection of a laser can be used to derive the velocity near the liquid/wall interface, within approximately 50 nm, when they are used as the excitation light for the fluorescent tracer particles [60,61,62,63,64].
As we described above, the zeta potential can be calculated from a precisely measured EOF using the Smoluchowski equation, but this approach cannot be always applied to practical cases. The relation was modified for non-wetting charged surfaces by considering the fluid slip effect [65], which was experimentally validated [66]. Surface roughness is another factor that needs to be taken into consideration. Since surface roughness does affect EOF, this leads to errors in the zeta potential. On the other hand, even though the zeta potential of the channel wall material was known, it cannot accurately predict the resulting EOF in manufactured nano channels due to the surface roughness.
The surface roughness depends on the manufacturing process [67]. For example, glass, one of the most commonly used materials due to its superior chemical resistivity and transparency, can be patterned by wet etching using hydrofluoric acid (HF), dry etching, or mechanical machining. Wet etching is an isotropic technique but can be conducted at low cost. Dry etching can create anisotropic profiles with a high accuracy and a high aspect ratio. Mechanical machining can be used to fabricate three-dimensional structures. Each etching process culminates in a different surface geometry, depending on the etching conditions.
In this work, we attempted to experimentally obtain the EOF mobility, which is affected by both surface roughness and surface chemistry. The surface roughness is strongly affected by the manufacturing method and etching conditions. We prepared glass channels by wet etching and dry etching using various recipes, and formed micro-channels by attaching micropatterned polydimethyl siloxane (PDMS). We measured the EOF near the glass surface using microPIV, and the glass surface geometry was investigated by atomic force microscopy (AFM). We attempted to correlate the surface topography, and thus, the micromaching processes, with the EOF mobility. Since the Smoluchowski equation can be used to deduce the zeta potential only when the roughness is smaller than the electric double layer thickness, the EOF mobility obtained in the experiments cannot provide the true zeta potential that represents the chemical properties of the surface. Instead, we discuss the potential usage of an effective zeta potential, which is obtained by substituting the EOF mobility into the Smoluchowski equation and depends on both the chemical and topographical properties of the surface. When the effective zeta potential of micromachined glass surfaces is known, the EOF can be deduced using the Smoluchowski equation. The obtained data will be of great help in precisely designing high-performance nano/micro fluidic devices.

2. Material and Method

2.1. Micromachining of Glass Substrates

In our experiments, we used borosilicate glass (C030401, Matsunami Glass Ind., Ltd., Osaka, Japan) as the wall material. Hydrofluoric acid (HF) was purchased from Wako Pure Chemical Industries, Ltd., Osaka, Japan. Plasma etching of glass was conducted by NLD-570 (Ulvac, Inc., Kanagawa, Japan). The surface geometry after the machining process was investigated by atomic force microscopy (SPM-9700, Shimadzu, Kyoto, Japan).
The most frequently used glass manufacturing method is wet etching by HF. HF can pattern glass by the following reaction;
SiO2 + 6HF → H2SiF6 + 2H20
We conducted two experiments. First, we fixed the etching depth at 10 µm and used HF with concentrations of 1%, 3%, 5%, 7%, and 9%. The required etching periods were 5460, 1500, 580, 330, and 280 s, respectively. In the second experiment, glass substrates were immersed in 5% HF for 5, 10, 15, 20, or 25 min. The etching was conducted in a cleanroom environment at 25 °C and 40% Rh. We prepared five samples for each condition. Note that in these experiments, the whole surfaces were etched, i.e., no mask pattern was used.
While deep reactive ion etching of silicon has been extensively used in manufacturing MEMS for decades [68,69], the etching of glass using neutral loop discharge (NLD) is a promising technology for manufacturing glass micro/nano structures [70,71,72,73]. NLD employs plasma generated along a closed magnetic neutral line by a radio frequency (RF) electric field. NLD plasma has a high plasma density at a relatively low gas pressure, and can be applicable to high-aspect-ratio anisotropic etching.
In our experiments, borosilicate glass plates were etched by NLD-570 while they were attached to a 6-inch silicon carbide wafer with a silicone oil compound to dissipate heat during the etching. We varied the antenna power to be 250, 500, 1200, or 1800 W. The etching periods were controlled to achieve 5-μm-deep patterns, which led to 5880, 3840, 1800, or 1560 s etch times, respectively. Other representative etching parameters are: APC pressure of 0.4 Pa, trigger pressure of 1 Pa, PFC pressure of 400 Pa, both gas flow rates of C3F8 and CHF3 of 10 sccm, bias RF power of 300 W, currents for magnet top, middle, and bottom of 12.2 A, 17 A, 12.2 A, respectively. We prepared five samples for each condition. Note that in these experiments, the whole surfaces were etched, i.e., no mask pattern was used.
The surface geometry was investigated by atomic force microscopy SPM-9700after the machining process. 10 measurement areas 10 µm by 10 µm in size were randomly selected from each sample.

2.2. Measurement of EOF

The EOF velocity was measured by micro PIV. When charged tracing particles are used for the measurement, the measured velocity is the summation of EOF and electrophoretic flow velocities [56]. The electrophoretic velocity under the identical measurement conditions was obtained in advance and then, subtracted from the measured velocity by micro PIV to deduce the EOF velocity.
First, as described above, glass plates were micromachined by either wet etching with HF or dry etching using NLD plasma. Note that these etching processes created no patterns on the glass surfaces. A polydimethyl siloxane (PDMS, Silpot 184, Toray, Tokyo, Japan) structure with a channel 1 mm in width, 30 mm in length, and 100 µm in height and inlet/outlet holes molded from photolithography patterned SU-8 (SU-8 3000, Nippon Kayaku, Tokyo, Japan) was bonded onto the glass plates after oxygen plasma treatment, as shown in Figure 1. Fluorescent micro beads 0.2 µm in diameter (FluoSpheres carboxylate-modified microspheres 0.2 µm yellow-green fluorescent, Molecular Probes, Inc., Eugene, OR, USA) were used as the tracing particles. These beads were excited by a laser with a wavelength of 505 nm, and emitted fluorescence at 515 nm. 0.5 mL of carboxylate solution containing 2wt% of microbeads was mixed with 99.5 mL of deionized water. Then, this solution was mixed with a solution containing 1 Ml of 1 M HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid), 1 mL of 0.1 M KCl, and 98 mL of deionized water. We introduced this 0.005% fluorescent micro-bead solution into the channel. An electric field of 13.3 V/mm was applied and an EOF was generated. The experiments were conducted at 25 °C and 40% Rh. pH of the fluorescent solution was 7.15 and the produced electric double layer thickness was calculated to be 30.2 nm under these conditions. The velocity at the center of the channel in the horizontal plane and 5 µm above the glass surface was measured by micro-PIV. Though three channel walls were made of PDMS, the EOF generated near the glass surface was determined by the characteristics of the glass surface [56]. In order to prevent electrolysis, the measurement started 2 s after the electric field was applied and the measurement time was limited to be 2 s. Note that we experimentally confirmed that the EOF became steady 1 s after the field was applied. The micro PIV measurement was conducted one time for a sample since it was difficult to wash out all the tracing particles from the channel after each measurement, i.e., 5 EOF velocity data were obtained for one machining condition.
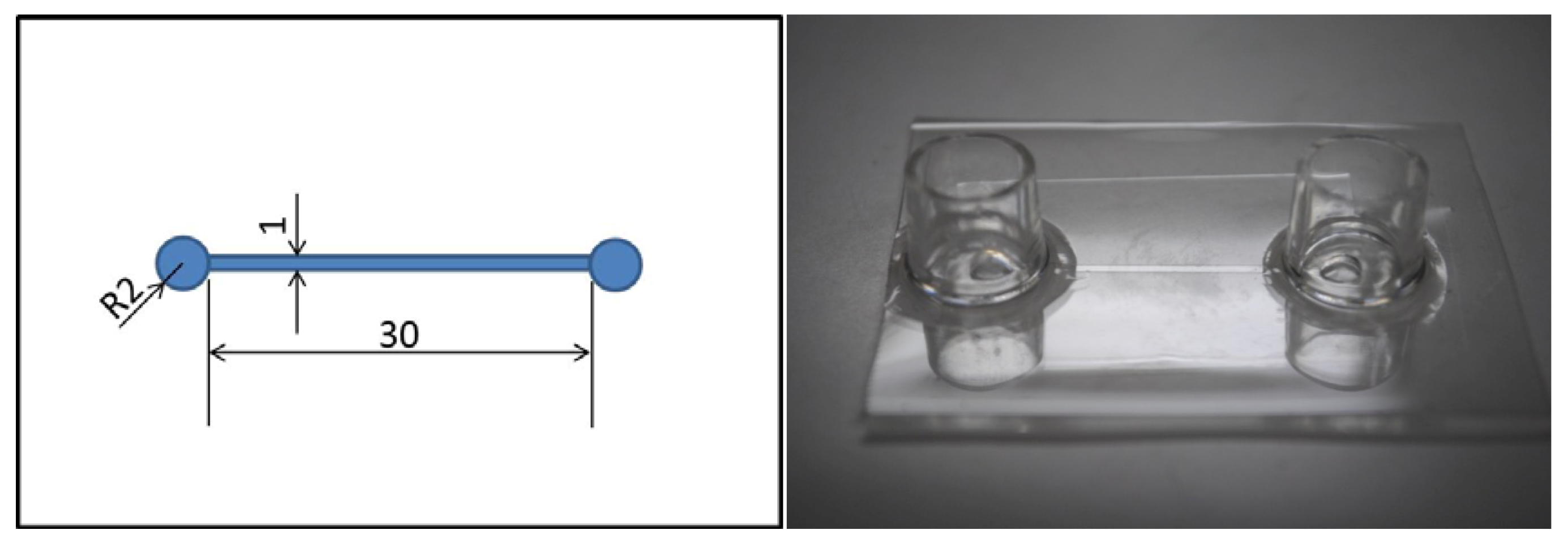
Micromachines 04 00067 g001 1024
Figure 1. A micro-channel used to evaluate the electro-osmotic flow (EOF).
Figure 1. A micro-channel used to evaluate the electro-osmotic flow (EOF).
Micromachines 04 00067 g001

3. Experiments

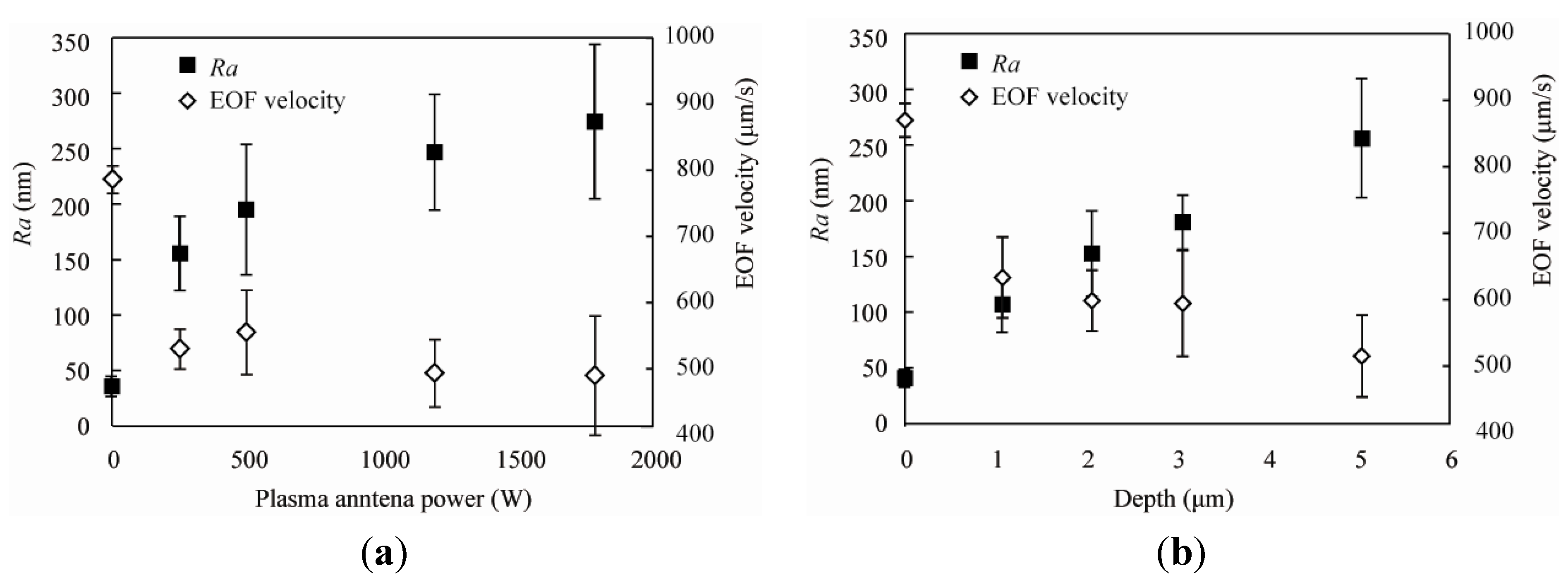
3.1. Surface Roughness after Glass Patterning

Figure 2 shows surface topography images of untreated glass, glass wet-etched by 5 µm, and glass dry-etched by 5 µm obtained by AFM. Dry etching using NLD plasma drastically increased the surface roughness, while wet etching did not. In wet etching using HF, the concentration of HF did not affect the surface roughness, as represented by the arithmetic mean value Ra except the case of 1% concentration, as shown in Figure 3a. Ra of the non-treated glass surface was 43 nm, while that of the glass treated by 1% HF was 61 nm. This was most likely caused by the long wet etching time required by 1% HF of 5460 s to achieve an etching depth of 10 µm. When 5% HF was used as the etchant, the surface roughness decreased in the first 15 min of etching, which was a nature of isotropic wet etching. The surface roughness increased slightly when the etching time was greater than 20 min as shown in Figure 3b.
On the contrary, Ra of the surface etched by NLD plasma strongly depended on the plasma power when we fixed the etching depth at 5 µm, as shown in Figure 4a. Ra increased from approximately 160 nm to 280 nm when the plasma power was increased from 250 W to 1800 W. For a plasma power of 1200 W, Ra increased from 40 nm to 210 nm as the etching progressed, as shown in Figure 4b.

3.2. EOF Measurement

The EOF velocity generated in channels with glass surfaces treated by wet etching is summarized in Figure 3. Figure 3a shows the surface roughness and EOF velocity for glass substrates etched by 10 µm using different concentrations of HF. The glass substrate treated by 1% HF generated an EOF velocity of 660 µm/s, while the non-treated glass substrate generated an EOF velocity of 870 µm/s. Figure 3b shows the relationship between the etching time by 5% HF and the EOF velocity. In both graphs, the EOF velocity decreased with increasing surface roughness, and there was a strong correlation between surface roughness and EOF velocity.
For dry-etched samples, as shown in Figure 4, the EOF velocity decreased as the roughness increased, although the trend was not as strong as with the wet-etched samples. Figure 4a shows EOF velocities for glass substrates etched by 5 µm with various antenna RF power values in NLD etching. The etching time was controlled to achieve a depth of 5 µm. 0 W corresponds to a non-treated glass substrate. The EOF velocity slightly decreased with increasing power, and was 500 µm/s at 1800 W. The EOF velocity as a function of etching depth at 1200 W is shown in Figure 4b. The EOF velocity decreased with increasing time, and reached 510 µm/s at a depth of 5 µm.
Micromachines 04 00067 g002 1024
Figure 2. Atomic force microscopy (AFM) images of (a) non-treated, (b) wet-etched, and (c) dry-etched glass surfaces.
Figure 2. Atomic force microscopy (AFM) images of (a) non-treated, (b) wet-etched, and (c) dry-etched glass surfaces.
Micromachines 04 00067 g002
Micromachines 04 00067 g003 1024
Figure 3. Surface roughness (Ra) and the EOF velocity of glass surfaces treated by hydrofluoric acid (HF) (a) with different HF concentrations and (b) for different etching times.
Figure 3. Surface roughness (Ra) and the EOF velocity of glass surfaces treated by hydrofluoric acid (HF) (a) with different HF concentrations and (b) for different etching times.
Micromachines 04 00067 g003
Figure 5 summarizes the relationship between the EOF velocity and the surface roughness Ra of the samples used in the experiments. The white diamonds represent the wet-etched samples and the black diamonds represent the dry-etched samples. The graph indicates that the EOF velocity decreased drastically until the surface roughness reached 60 nm. When the surface roughness exceeded 100 nm, the EOF velocity decreased, but the trend was weak. The EOF strongly depends on the electric double layer, which is 30.2 nm at the ionic concentrations used in our experiments. Therefore, when the roughness is on the same order as the electric double layer, the EOF velocity is very sensitive to the roughness. When the roughness is several times greater than the electric double layer, the EOF is only slightly affected by the roughness.
Micromachines 04 00067 g004 1024
Figure 4. Surface roughness (Ra) and the EOF velocity for the glass surfaces treated by neutral loop discharge (NLD) plasma etching (a) with different plasma antenna power values and (b) for different etching depths with a plasma power of 1200 W.
Figure 4. Surface roughness (Ra) and the EOF velocity for the glass surfaces treated by neutral loop discharge (NLD) plasma etching (a) with different plasma antenna power values and (b) for different etching depths with a plasma power of 1200 W.
Micromachines 04 00067 g004

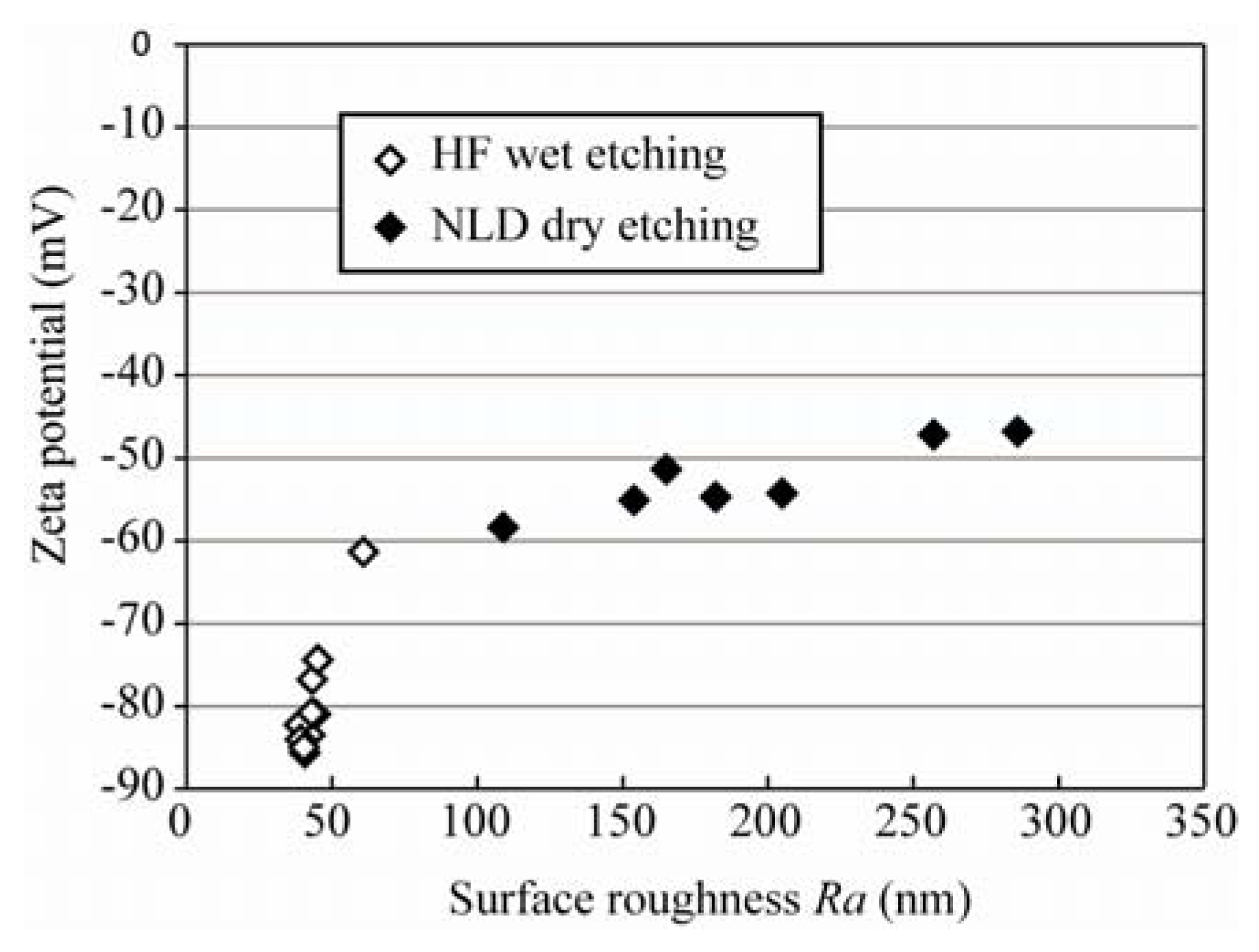
3.3. Effective Zeta Potential

The EOF velocity depends on the electric field, viscosity and permittivity of the liquid, and the surface properties of the channel. The surface properties include physical characteristics, surface roughness, and chemical properties. The zeta potential is used as a measure of the chemical properties, and can be deduced using the Smoluchowski equation if the roughness is smaller than the thickness of the electric double layer,
Micromachines 04 00067 i001
where U is the average velocity in the channel, μ and ε are the viscosity and permittivity, respectively, Micromachines 04 00067 i002 is the zeta potential, and E is the applied electric field strength [46].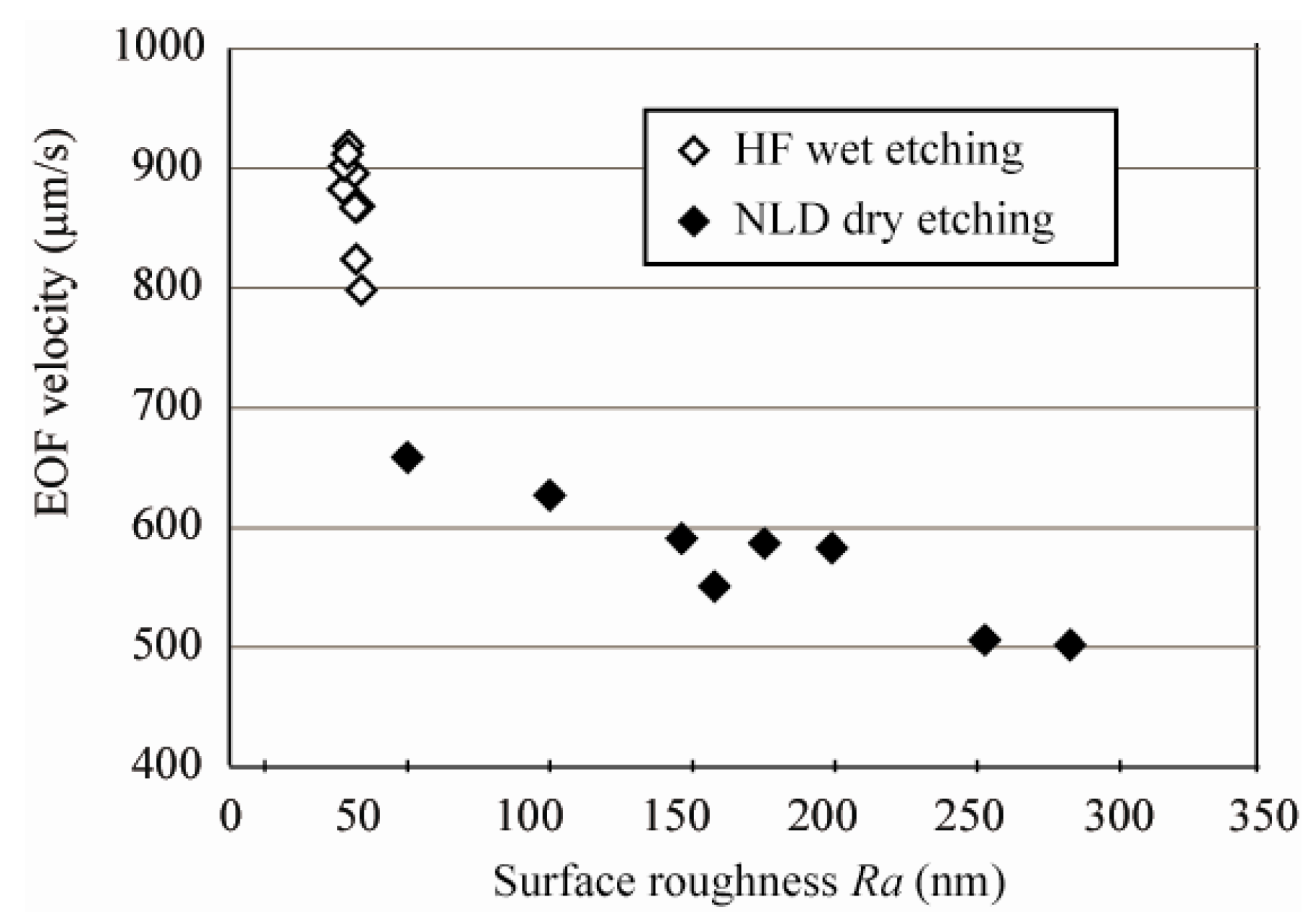
Micromachines 04 00067 g005 1024
Figure 5. EOF velocity as a function of surface roughness.
Figure 5. EOF velocity as a function of surface roughness.
Micromachines 04 00067 g005
Micromachines 04 00067 g006 1024
Figure 6. Effective zeta potential as a function of surface roughness.
Figure 6. Effective zeta potential as a function of surface roughness.
Micromachines 04 00067 g006
In our experiments, given the large surface roughness, Equation (2) cannot be used to deduce the true zeta potential that represents the chemical properties of the surface. However, Equation (2) will provide the effective zeta potential, which includes both the chemical properties and the topography of the surface. In designing nano/micro fluidic devices utilizing EOF, this effective zeta potential, which depends on the fabrication process and the surface roughness, should be used instead of the true zeta potential.
Figure 6 shows the effective zeta potential from Equation (2), substituting U by the experimentally deduced average velocity in the channel, μ and ε by 8.5 × 10−4 Pa·s and 6.87 × 10−10 F/m, respectively, and E by 13.3 V/mm. The zeta potential ranged from −86 mV to −47 mV when Ra varied from 43 nm to 290 nm. In particular, when the roughness was on the same order as the electric double layer, the zeta potential was found to be sensitive to the roughness.

4. Conclusions

The glass manufacturing processes determines the surface roughness. Wet etching by HF produces minimal surface roughness and therefore, the EOF velocities do not vary from the non-treated glass, but it is isotropic and may not to be suitable for precision nanoscale manufacturing. NLD plasma dry etching is a promising anisotropic manufacturing process for nano/micro glass channels, although it was found to increase the surface roughness, adversely affecting the EOF velocities.
The EOF velocity showed a strong correlation with the surface roughness, particularly when the arithmetic mean value of Ra was on the same order as the thickness of the electric double layer. Therefore, we proposed the use of an effective zeta potential that takes both chemical and physical properties of the surfaces into consideration. The relationship between the surface roughness or manufacturing processes, and EOF velocities or the effective zeta potential, obtained in this work can be readily applied to the precise design of nano/micro fluidic devices.

Acknowledgements

This work was supported by a Grant-in-Aid for Scientific Research (S) (21226006). We greatly appreciate the “Sensing center for nano/micro thermofluid & thermal properties, Keio University” of “Low-Carbon Research Network” funded by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan for the microPIV system.

References

  1. Manz, A.; Graver, N.; Widmer, H.M. Miniaturized total chemical-analysis systems—a novel concept for chemical sensing. Sens. Actuators B 1990, 1, 244–248. [Google Scholar] [CrossRef]
  2. Shoji, S. Fluids for sensor systems. Top. Curr. Chem. 1998, 194, 163–188. [Google Scholar] [CrossRef]
  3. Khandurina, J.; Guttman, A. Bioanalysis in microfluidic devices. J. Chromatogr. A 2002, 943, 159–183. [Google Scholar] [CrossRef]
  4. Chovan, T.; Guttman, A. Microfabricated devices in biotechnology and biochemical processing. Trends Biotechnol. 2002, 20, 116–122. [Google Scholar] [CrossRef]
  5. Huikko, K.; Kostiainen, R.; Kotiaho, T. Introduction to micro-analytical systems: Bioanalytical and pharmaceutical applications. Eur. J. Pharm. Sci. 2003, 20, 149–171. [Google Scholar]
  6. Sheehan, A.D.; Quinn, J.; Daly, S.; Dillon, P.; O’Kennedy, R. The development of novel miniaturized immuno-sensing devices: A review of a small technology with a large future. Anal. Lett. 2003, 36, 511–537. [Google Scholar]
  7. Sato, K.; Hibara, A.; Tokeshi, M.; Hisamoto, H.; Kitamori, T. Microchip-based chemical and biochemical analysis systems. Adv. Drug Deliv. Rev. 2003, 55, 379–391. [Google Scholar]
  8. Lee, S.J.; Lee, S.Y. Micro total analysis system (mu-TAS) in biotechnology. Appl. Microbiol. Biot. 2004, 64, 289–299. [Google Scholar]
  9. Sun, Y.; Kwok, Y.C. Polymeric microfluidic system for DNA analysis. Anal. Chim. Acta 2006, 556, 80–96. [Google Scholar]
  10. Gu, Y.; Miki, N. A microfilter utilizing a polyethersulfone porous membrane with nanopores. J. Micromech. Microeng. 2007, 17, 2308–2315. [Google Scholar] [CrossRef]
  11. Tanaka, Y.; Sato, K.; Shimizu, T.; Yamato, M.; Okano, T.; Kitamori, T. Biological cells on microchips: New technologies and applications. Biosens. Bioelectron. 2007, 23, 449–458. [Google Scholar] [CrossRef]
  12. Chen, Y.; Wang, X.H.; Hong, M.; Erramilli, S.; Mohanty, P. Surface-modified silicon nano-channel for urea sensing. Sens. Actuators 2008, 133, 593–598. [Google Scholar] [CrossRef]
  13. Suzuki, H.; Takeuchi, S. Microtechnologies for membrane protein studies. Anal. Bioanal. Chem. 2008, 391, 2695–2702. [Google Scholar] [CrossRef]
  14. Gu, Y.; Miki, N. Multilayered microfilter using a nanoporous PES membrane and applicable as the dialyzer of a wearable artificial kidney. J. Micromech. Microeng. 2009, 19. [Google Scholar] [CrossRef]
  15. Xu, X.; Zhang, S.; Chen, H.; Kong, J. Integration of electrochemistry in micro-total analysis systems for biochemical assays: Recent developments. Talanta 2009, 80, 8–18. [Google Scholar] [CrossRef]
  16. Ota, H.; Yamamoto, R.; Deguchi, K.; Tanaka, Y.; Kazoe, Y.; Sato, Y.; Miki, N. Three-dimensional spheroid-forming lab-on-a-chip using micro-rotational flow. Sens. Actuators B 2010, 147, 359–365. [Google Scholar] [CrossRef]
  17. Liu, K.K.; Wu, R.G.; Chuang, Y.J.; Khoo, H.S.; Huang, S.-H.; Tseng, F.-G. Microfluidic systems for biosensing. Sensors 2010, 10, 6623–6661. [Google Scholar] [CrossRef]
  18. Wlodkowic, D.; Cooper, J.M. Tumors on chips: Oncology meets microfluidics. Curr. Opin. Chem. Biol. 2010, 14, 556–567. [Google Scholar] [CrossRef]
  19. Ota, H.; Kodama, T.; Miki, N. Rapid formation of size-controlled three dimensional hetero-cell aggregates using micro-rotation flow for spheroid study. Biomicrofluidics 2011, 5. [Google Scholar] [CrossRef]
  20. Ota, H.; Miki, N. Microfluidic experimental platform for producing size-controlled three-dimensional spheroids. Sens. Actuators A 2011, 169, 266–273. [Google Scholar] [CrossRef]
  21. Shen, C.; Mokkapati, V.R.S.S.; Pham, H.T.M.; Sarro, P.M. Micromachined nanofiltration modules for lab-on-a-chip applications. J. Micromech. Microeng. 2012, 22. [Google Scholar] [CrossRef]
  22. Wang, K.; Yue, S.; Wang, L.; Jin, A.; Gu, C.; Wang, P.; Wang, H.; Xu, X.; Wang, Y.; Niu, H. Nanofluidic channels fabrication and manipulation of DNA molecules. IEEE Proc. Nanobiotechnol. 2006, 153, 11–15. [Google Scholar] [CrossRef]
  23. Das, S.K.; Austin, M.D.; Akana, M.C.; Deshpande, P.; Cao, H.; Xiao, M. Single molecule linear analysis of DNA in nano-channel labeled with sequence specific fluorescent probles. Nucleic Acids Res. 2010, 38. [Google Scholar] [CrossRef]
  24. Liu, C.; Qu, Y.Y.; Luo, Y.; Fang, N. Recent advances in single-molecule detection on micro- and nano-fluidic devices. Electrophoresis 2011, 32, 3308–3318. [Google Scholar] [CrossRef]
  25. Kish, L.L.; Kameoka, J.; Granqvist, C.G.; Kish, L.B. Log-normal distribution of single molecule fluorescence bursts in micro/nano-fluidic channels. Appl. Phys. Lett. 2011, 99. [Google Scholar] [CrossRef]
  26. Abad, E.; Juarros, A.; Retolaza, A.; Merino, S.; Marie, R.; Kristensen, A. DNA analysis by single molecule stretching in nanofluidic biochips. Microelectron. Eng. 2011, 88, 300–304. [Google Scholar]
  27. Eun, D.S.; Shin, J.K.; Lee, J.H. Enhanced micro-PCR chip using TiO2nanofluidic heat-sink. Sens. Lett. 2009, 9, 276–282. [Google Scholar]
  28. Chen, P.; Feng, X.; Du, W.; Liu, B-F. Microfluidic chips for cell sorting. Front. Biosci. 2008, 13, 2464–2483. [Google Scholar] [CrossRef]
  29. Mawatari, K.; Tsukahara, T.; Sugii, Y.; Kitamori, T. Extended-nano fluidic systems for analytical and chemical technologies. Nanoscale 2010, 2, 1588–1595. [Google Scholar]
  30. Huang, M.; Yanik, A.A.; Chang, T.Y.; Altug, H. Sub-wavelength nanofluidics in photonic crystal sensors. Opt. Express 2009, 17, 24224–24233. [Google Scholar]
  31. Cao, H.; Yu, Z.N.; Wang, J.; Tegenfeldt, J.O.; Austin, R.H.; Chen, E.; Wu, W.; Chou, S.Y. Fabrication of 10 nm enclosed nanofluidic channels. Appl. Phys. Lett. 2002, 81, 174–176. [Google Scholar] [CrossRef]
  32. Pepin, A.; Youninou, P.; Studer, V.; Lebib, A.; Chen, Y. Nanoimprint lithography for the fabrication of DNA electrophoresis chips. Microelectron. Eng. 2002, 61, 927–932. [Google Scholar]
  33. Zheng, H.J.; Wang, Z.L.; Feinerman, A.D. Fabrication of micro/nano fluidic channels with sacrificial galvanic coupled metals. Nanotechnology 2006, 17, 3183–3188. [Google Scholar]
  34. Shao, P.E.; van Kan, A.; Wang, L.P.; Ansari, K.; Bettiol, A.A.; Watt, F. Fabrication of enclosed nanochannels in poly(methylmethacrylate) using proton beam writing and thermal bonding. Appl. Phys. Lett. 2006, 88. [Google Scholar] [CrossRef]
  35. Kehagias, N.; Chansin, G.; Reboud, V.; Zelsmann, M.; Schuster, C.; Kubenz, M.; Reuther, F.; Gruetzner, G.; Sotomayer Torres, C.M. Embedded nano channels fabricated by non-selective reverse contact UV nanoimprint lithography technique. Microelectron. Eng. 2007, 84, 921–924. [Google Scholar]
  36. Wong, C.C.; Agarwal, A.; Balasubramanian, N.; Kwong, D.L. Fabrication of self-sealed circular nano/microfluidic channels in glass substrates. Nanotechnology 2007, 18. [Google Scholar] [CrossRef]
  37. Koller, D.M.; Galler, N.; Ditlbacher, H.; Hohenau, A.; Leitner, A.; Aussenegg, F.R.; Kren, J.R. Direct fabrication of micro/nano fluidic channels by electron beam lithography. Microelectron. Eng. 2009, 86, 1314–1316. [Google Scholar]
  38. Yang, R.; Lu, B.R.; Wang, J.; Xie, S-Q.; Chen, Y.; Hug, E.; Qu, X-P.; Liu, R. Fabrication of micro/nano fluidic channels by nanoimprint lithography and bonding using SU-8. Microelectron. Eng. 2009, 86, 1379–1381. [Google Scholar]
  39. Venkatakrishnan, K.; Jariwala, S.; Tan, B. Maskless fabrication of nano-fluidic channels by two-photon absorption (TPA) polymerization of SU-8 on glass substrate. Opt. Express 2009, 17, 2756–2762. [Google Scholar]
  40. Kim, S.K.; Cho, H.; Park, H.K.; Kim, J.H.; Chung, B.H. Fabrication of nanochannels by anisotropic wet etching on silicon-on-insulator wafers and their applications to DNA stretch. J. Nanosci. Nanotechnol. 2010, 10, 637–642. [Google Scholar]
  41. Fernandez-Cuesta, I.; Palmarelli, A.L.; Liang, X.G.; Zhang, J.; Dhuey, S.; Olynick, D.; Cabrini, S. Fabrication of fluidic devices with 30 nm nanochannels by direct imprinting. J. Vac. Sci. Technol. B 2011, 29. [Google Scholar] [CrossRef]
  42. Afanasiev, A.; Lahdesmaki, I.; Parviz, B.A. Fabrication and electrical characterization of integrated nano-scale fluidic channels. Microsyst. Technol. 2011, 17, 1511–1518. [Google Scholar]
  43. Hong, L.F.; Pan, T.R. Surface microfluidics fabricated by photopatternable superhydrophobic nanocomposite. Microfluid. Nanofluid. 2011, 10, 991–997. [Google Scholar]
  44. Hunter, R.J. Zeta potential in Colloid Science: Principles and Applications; Academic Press: New York, NY, US, 1981. [Google Scholar]
  45. Sze, A.; Erickson, D.; Ren, L. Zeta-potential measurement using the Smoluchowski equation and the slope of the current-time relationship in electrosmotic flow. J. Colloid Interf. Sci. 2003, 261, 402–410. [Google Scholar]
  46. Venditti, R.; Xuan, X.C.; Li, D.Q. Experimental characterization of the temperature dependence of zeta potential and its effect on electroosmotic flow velocity in microchannels. Microfluid. Nanofluid. 2006, 2, 493–499. [Google Scholar]
  47. Santiago, J.G.; Wereley, S.T.; Meinhart, C.D.; Beebe, D.J.; Adrian, R.J. A particle image velocimetry system for microfluidics. Exp. Fluids 1998, 25, 316–319. [Google Scholar]
  48. Sato, Y.; Hishida, K. Electrokinetic effects on motion of submicron particles in microchannel. Fluid Dyn. Res. 2006, 38, 787–802. [Google Scholar]
  49. Lindken, R.; Rossi, M.; Grosse, S.; Westerweel, J. Micro-Particle Image Velocimetry (mu PIV): Recent developments, applications, and guidelines. Lab Chip 2009, 9, 2551–2567. [Google Scholar] [CrossRef]
  50. Tatsumi, K.; Nishitani, K.; Fukuda, K.; Katsumoto, Y.; Nakabe, K. Measurement of electroosmotic flow velocity and electric field in microchannels by micro-particle image velocimetry. Meas. Sci. Technol. 2010, 21. [Google Scholar] [CrossRef]
  51. Park, J.S.; Choi, C.K.; Kihm, K.D. Optically sliced micro-PIV using confocal laser scanning microscopy (CLSM). Exp. Fluids 2004, 37, 105–119. [Google Scholar]
  52. Lima, R.; Wada, S.; Tsubota, K.; Yamaguchi, T. Confocal micro-PIV measurements of three-dimensional profiles of cell suspension flow in a square microchannel. Meas. Sci. Technol. 2006, 17, 797–808. [Google Scholar] [CrossRef]
  53. Park, J.S.; Kihm, K.D. Use of confocal laser scanning microscopy (CLSM) for depthwise resolved microscale-particle image velocimetry (µ-PIV). Opt. Lasers Eng. 2006, 44, 208–223. [Google Scholar]
  54. Ichiyanagi, M.; Sato, Y.; Hishida, K. Optically sliced measurement of velocity and pH distribution in microchannel. Exp. Fluids 2007, 43, 425–435. [Google Scholar]
  55. Kinoshita, H.; Kaneda, S.; Fujii, T.; Oshima, M. Three-dimensional measurement and visualization of internal flow of a moving droplet using confocal micro-PIV. Lab Chip 2007, 7, 338–346. [Google Scholar]
  56. Ichiyanagi, M.; Sasaki, S.; Sato, Y.; Hishida, K. Micro-PIV/LIF measurements on electrokinetically-driven flow in surface modified microchannels. J. Micromech. Microeng. 2009, 19. [Google Scholar] [CrossRef]
  57. Lee, S.J.; Kim, S. Advanced particle-based velocimetry techniques for microscale flows. Microfluid. Nanofluid. 2009, 6, 577–588. [Google Scholar]
  58. Oishi, M.; Kinoshita, H.; Fujii, T.; Oshima, M. Simultaneous measurement of internal and surrounding flows of a moving droplet using multicolour confocal micro-particle image velocimetry (micro-PIV). Meas. Sci. Technol. 2011, 22. [Google Scholar] [CrossRef]
  59. Williams, S.J.; Park, C.; Wereley, S.T. Advances and applications on microfluidic velocimetry techniques. Microfluid. Nanofluid. 2010, 8, 709–726. [Google Scholar]
  60. Zettner, C.M.; Yoda, M. Particle velocity field measurements in a near-wall flow using evanescent wave illumination. Exp. Fluids 2003, 34, 115–121. [Google Scholar]
  61. Banerjee, A.; Kihm, K.D. Three-dimensional tracking of nanoparticles using R-TIRFM technique. J. Heat Trans. 2004, 126. [Google Scholar] [CrossRef]
  62. Kazoe, Y.; Sato, Y. Effect of ion motion on zeta-potential distribution at microchannel wall obtained from nanoscale laser-induced fluorescence. Anal. Chem. 2007, 79, 6727–6733. [Google Scholar]
  63. Kazoe, Y.; Miyakawa, S.; Miki, N.; Sato, Y. Fluorescence imaging technique of surface electrostatic potential using evanescent wave illumination. Appl. Phys. Lett. 2009, 92. [Google Scholar] [CrossRef]
  64. Min, Y.U.; Kim, K.C. Hybrid micro-/nano-particle image velocimetry for 3D3C multi-scale velocity field measurement in microfluidics. Meas. Sci. Technol. 2011, 22. [Google Scholar] [CrossRef]
  65. Joly, L.; Ybert, C.; Trizac, E.; Bocquet, L. Liquid friction on charged surfaces: From hydrodynamic slippage to electrokinetics. J. Chem. Phys. 2006, 125. [Google Scholar] [CrossRef]
  66. Lim, J.M.; Chun, M.S. Curvature-induced secondary microflow motion in steady electro-osmotic transport with hydrodynamic slippage effect. Phys. Fluids 2011, 23. [Google Scholar] [CrossRef]
  67. Miki, N.; Spearing, S.M. Effect of nanoscale surface roughness on the bonding energy of direct-bonded silicon wafers. J. Appl. Phys. 2003, 94, 6800–6806. [Google Scholar]
  68. Ayón, A.A.; Braff, R.; Lin, C.C.; Sawin, H.H.; Schmidt, M.A. Characterization of a time multiplexed inductively coupled plasma etcher. J. Electrochem. Soc. 1999, 146, 339–349. [Google Scholar]
  69. Miki, N.; Teo, C.J.; Ho, L.C.; Zhang, X. Enhancement of rotordynamic performance of high-speed micro-rotors for power MEMS applications by precision deep reactive ion etching. Sens. Actuators A 2003, 104, 263–267. [Google Scholar]
  70. Chen, W.; Itoh, M.; Hayashi, T.; Uchida, T. Dry etch process in magnetic neutral loop discharge plasma. Jpn. J. Appl. Phys. 1998, 37, 332–336. [Google Scholar]
  71. Chen, W.; Morikawa, Y.; Itoh, M.; Hayashi, T.; Sugita, K.; Shindo, H.; Uchida, T. Very uniform and high aspect ratio anisotropy SiO2 etching process in magnetic neutral loop discharge plasma. J. Vac. Sci. Technol. A 1999, 17, 2546–2550. [Google Scholar]
  72. Chen, W.; Sugita, K.; Morikawa, Y.; Yasunami, S.; Hayashi, T.; Uchida, T. Application of magnetic neutral loop discharge plasma in deep silica etching. J. Vac. Sci. Technol. A 2001, 19, 2936–2940. [Google Scholar]
  73. Uchida, T.; Hamaguchi, S. Magnetic neutral loop discharge (NLD) plasmas for surface processing. J. Phys. D 2008, 41. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Koga, Y.; Kuriyama, R.; Sato, Y.; Hishida, K.; Miki, N. Effects of Micromachining Processes on Electro-Osmotic Flow Mobility of Glass Surfaces. Micromachines 2013, 4, 67-79. https://doi.org/10.3390/mi4010067

AMA Style

Koga Y, Kuriyama R, Sato Y, Hishida K, Miki N. Effects of Micromachining Processes on Electro-Osmotic Flow Mobility of Glass Surfaces. Micromachines. 2013; 4(1):67-79. https://doi.org/10.3390/mi4010067

Chicago/Turabian Style

Koga, Yosuke, Reiko Kuriyama, Yohei Sato, Koichi Hishida, and Norihisa Miki. 2013. "Effects of Micromachining Processes on Electro-Osmotic Flow Mobility of Glass Surfaces" Micromachines 4, no. 1: 67-79. https://doi.org/10.3390/mi4010067

Article Metrics

Back to TopTop