Modeling and Control of Electrowetting Induced Droplet Motion
Abstract
:| Nomenclature | ||
|---|---|---|
| Symbol | Description | Units |
| A | Area | m2 |
| c | Damping coefficient | Ns∙m−1 |
| D | Electric displacement | C∙m−2 |
| E | Electric field | V∙m−1 |
| E | Energy | J |
| F | Force | N |
| FCL | Contact line force | N |
| FD | Drag force | N |
| Fel | Electrostatic force | N |
| FW | Friction Force | N |
| f | Frequency | Hz |
| ge | Gap between control electrodes | m |
| H | Droplet height | m |
| k | Spring constant | N∙m−1 |
| M | Droplet mass | kg |
| R | Radius | m |
| Uav | Average droplet velocity | m∙s−1 |
| V | Voltage | V |
| v | Vertical droplet velocity | m∙s−1 |
| Vol | Droplet volume | m2 |
| W | Energy | J |
| Ẇ | Power | W |
| we | Width of an electrode | m |
| x | Droplet position | m |
| Greek Symbols | ||
| α | Tilt angle | rad |
| ζ | Coefficient of contact line friction | Pa∙s |
| θA | Advancing contact angle | rad |
| θR | Receding contact angle | rad |
| μ | Fluid dynamic viscosity | N∙s∙m−2 |
| μf | Dynamic viscosity filler medium | N∙s∙m−2 |
| ω0 | Natural angular frequency | rad/s |
1. Introduction
2. General Description of the Dynamic Droplet Model
2.1. Dynamic Model Formulation
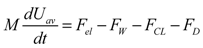 (1)
(1)- M: mass of the droplet;
- Uav: average velocity of the droplet;
- Fel: electrostatic driving force;
- Fw: shear force between the droplet and the channel;
- FCL: contact-line friction force;
- FD:drag force on filler liquid.
2.1.1. Formulation for the Forces Acting on the Droplet
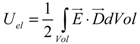 (2)
(2)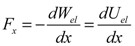 (3)
(3) and the electric displacement
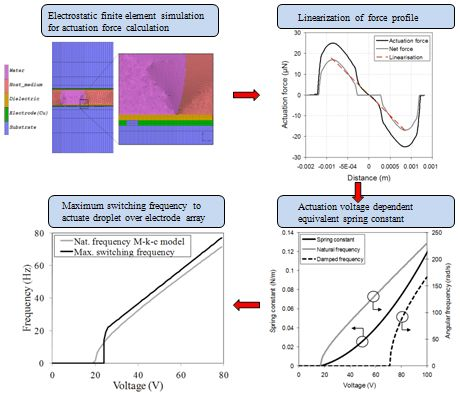
and the electric displacement 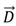 . The simulations are performed for conductive and dielectric liquids, using the applied voltages as boundary conditions: the voltage at the activated control electrode will be put at the applied voltage V. The voltages at the other control electrodes in the bottom layer and at the ground electrode are set to 0 V. In a quasi-static approach, the electrostatic actuation force is calculated from the computed electrostatic energy in Equation (2) at each droplet position. The electrostatic simulations are performed using 2D and 3D finite element models. For all simulations, a grid sensitivity analysis is performed to ensure a grid independent solution. The result of the grid sensitivity analysis indicates the number of cells and the required dimension of the cells. For the 2D case, the number of cells is typically in the order of 30,000 cells. In the case of a 3D simulation, the grid consists of around 250,000 elements. Figure 1 shows an example of a grid 2D electrostatic simulation.
. The simulations are performed for conductive and dielectric liquids, using the applied voltages as boundary conditions: the voltage at the activated control electrode will be put at the applied voltage V. The voltages at the other control electrodes in the bottom layer and at the ground electrode are set to 0 V. In a quasi-static approach, the electrostatic actuation force is calculated from the computed electrostatic energy in Equation (2) at each droplet position. The electrostatic simulations are performed using 2D and 3D finite element models. For all simulations, a grid sensitivity analysis is performed to ensure a grid independent solution. The result of the grid sensitivity analysis indicates the number of cells and the required dimension of the cells. For the 2D case, the number of cells is typically in the order of 30,000 cells. In the case of a 3D simulation, the grid consists of around 250,000 elements. Figure 1 shows an example of a grid 2D electrostatic simulation. 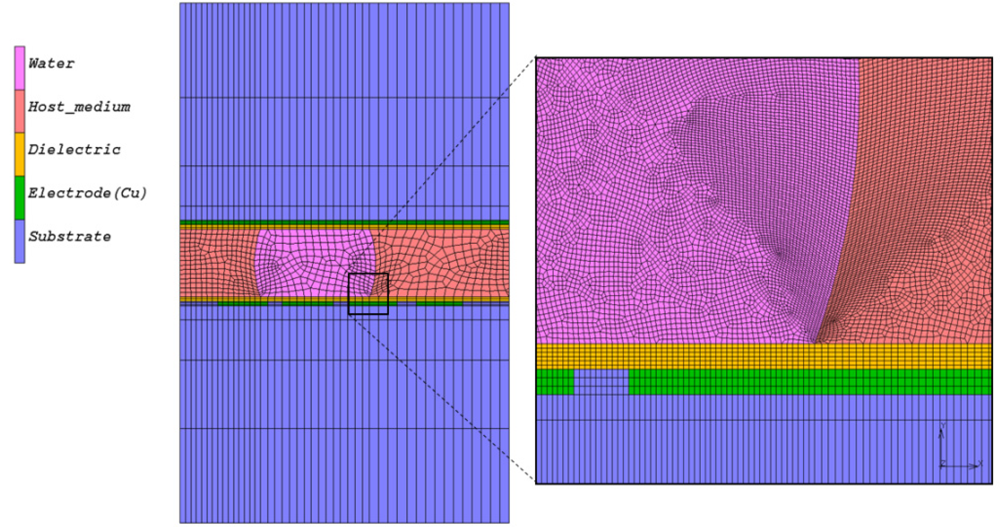
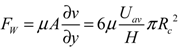 (4)
(4)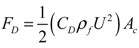 (5)
(5)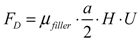 (6)
(6)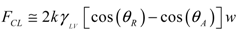 (7)
(7)
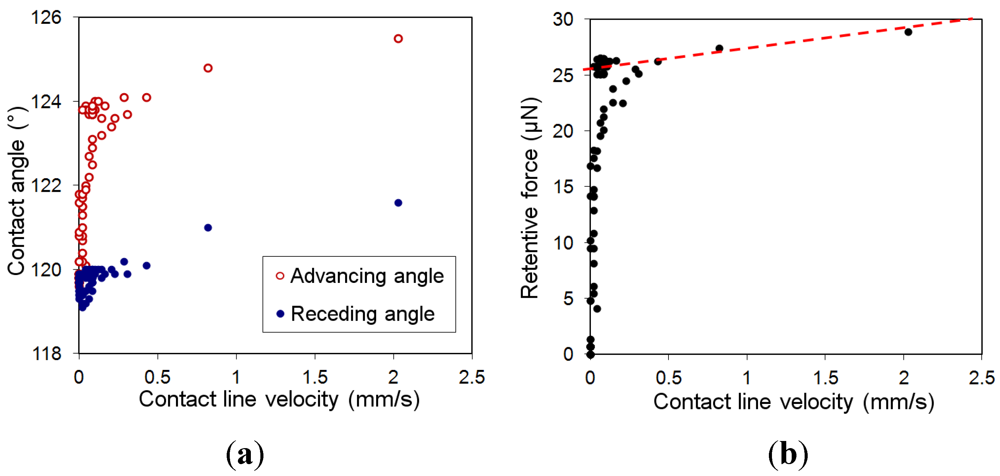
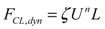 (8)
(8)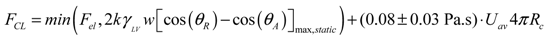 (9)
(9)2.1.2. Summary for the Model Formulation
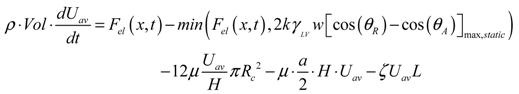 (10)
(10)| Category | Description | Symbol | Planar |
|---|---|---|---|
| Geometrical | Droplet volume | Vol | 2.7 μL |
| Channel height/diameter | H/D | 1 mm | |
| Electrode pitch | we + ge | 1 mm | |
| Electrode gap | ge | 100 μm | |
| Drag coefficient | Cd | 30 | |
| Insulation thickness | t | 1 μm | |
| Material properties | Droplet viscosity | μd | 1.005 Pa∙s |
| Droplet density | ρ | 1,000 kg/m3 | |
| Surface tension | γ | 72 Mn/m | |
| Contact line friction (static) | [cos( θR) - cos θA]max,st. | ~8 μN | |
| Contact line friction coeff. | ζ | 0.08 Ns/m2 | |
| Contact angle | θ | 110° | |
| Dielectric const. insulation | εr | 3 | |
| Application | Voltage | V | 45 V |
| Start position | x0 | −1 mm | |
| Switching frequency | f | 25 Hz |
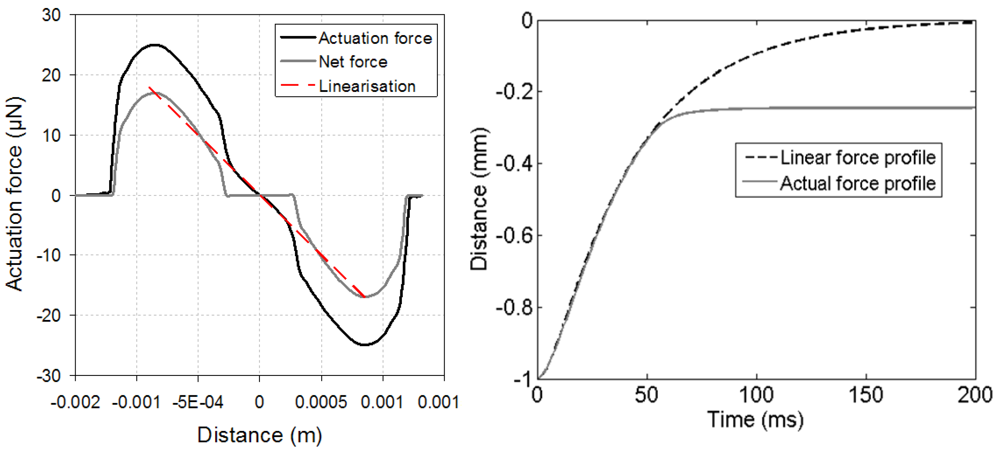
2.2. Model Linearization
 (11)
(11)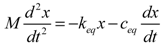 (12)
(12)
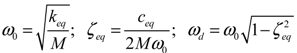 (13)
(13)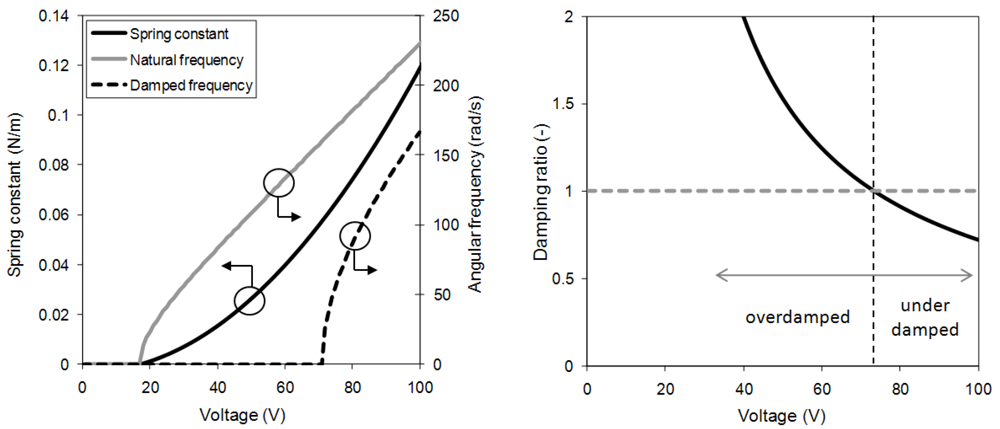
2.3. Model Limitations
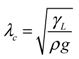 (14)
(14)3. Droplet Motion and Control
3.1. Model Solution Strategy
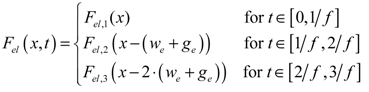 (15)
(15)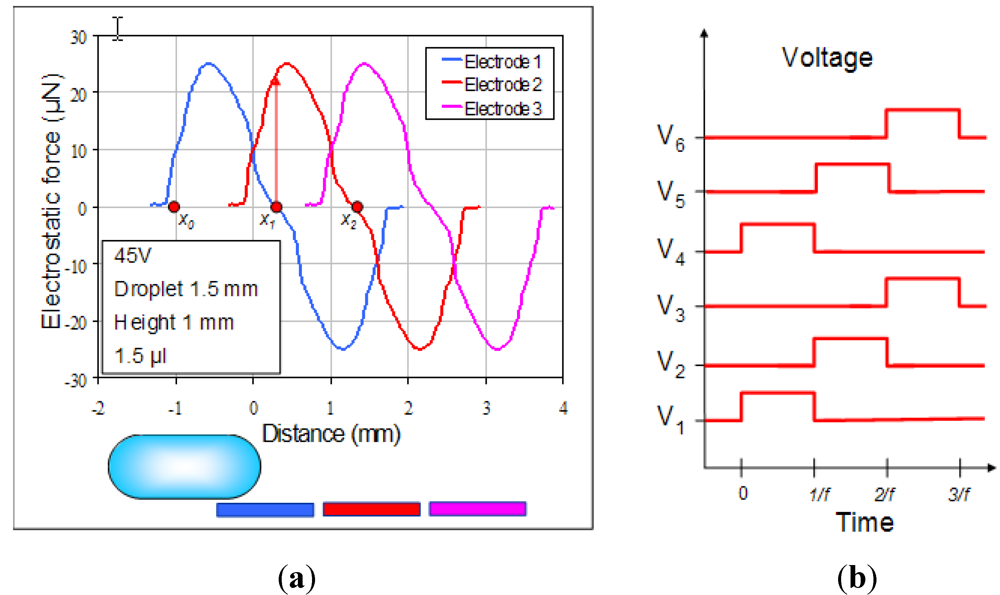
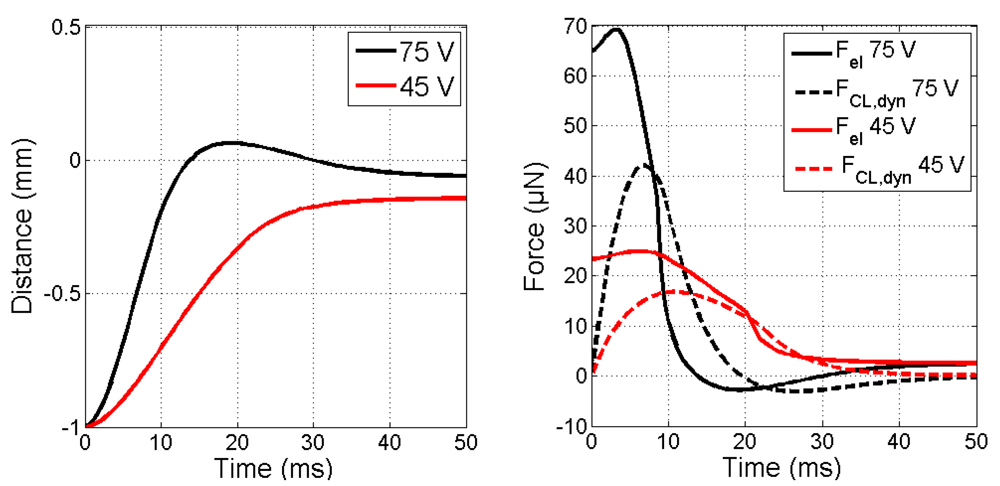
3.2. Single Electrode Response
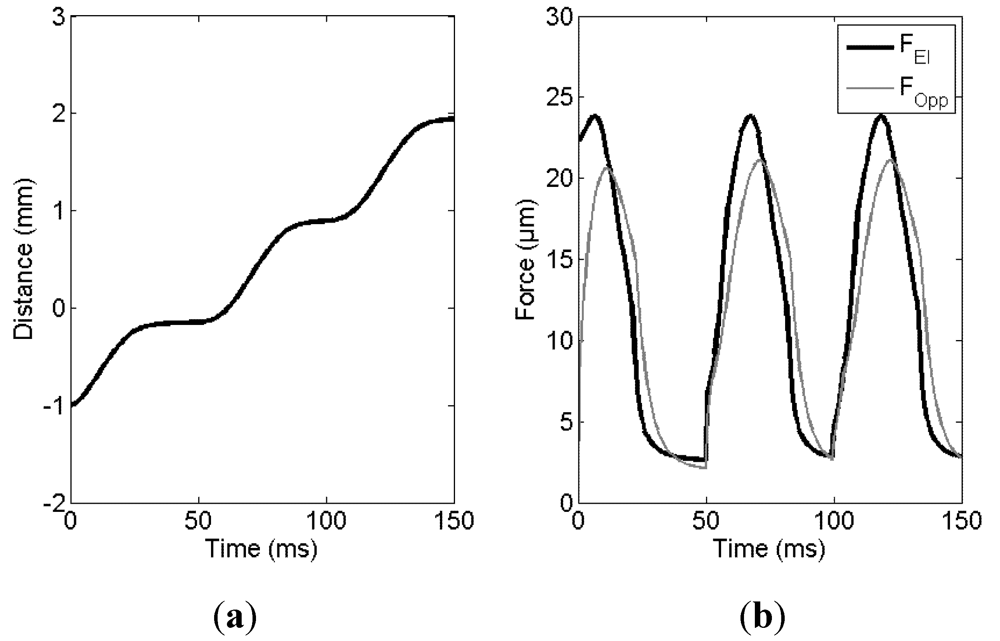
3.3. Droplet Trajectory over an Array of Electrodes
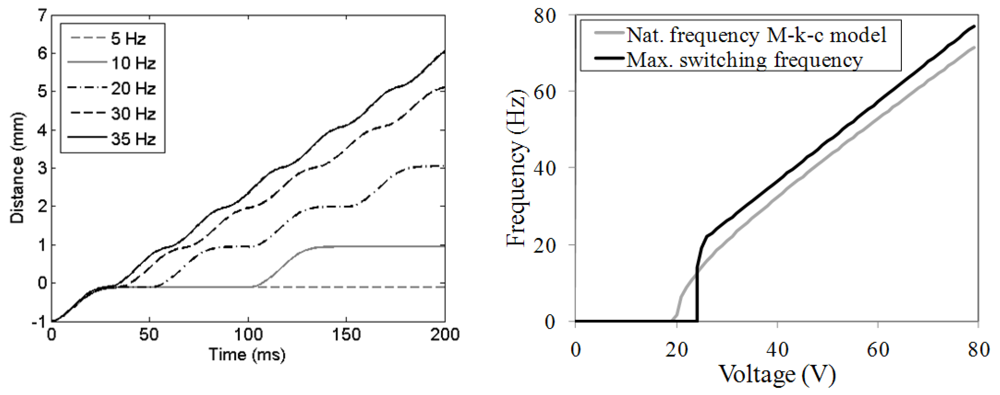
3.4. Influence of Switching Frequency
 (16)
(16)4. Conclusions
References
- Mugele, F.; Baret, J.-C. Electrowetting: From basics to applications. J. Phys. Condens. Matter. 2005, 17, R705–R774. [Google Scholar] [CrossRef]
- De Gennes, P.-G.; Brochard-Wyart, F.; Quere, D. Capillarity and Wetting Phenomena; Springer: New York, NY, USA, 2004. [Google Scholar]
- Fouillet, Y.; Jary, D.; Chabrol, C.; Claustre, P.; Peponnet, C. Digital microfluidic design and optimization of classic and new fluidic functions for lab on a chip systems. Microfluid. Nanofluid. 2007, 4, 159–165. [Google Scholar]
- Pollack, M.G.; Shenderov, A.; Fair, R.B. Electrowetting-based actuation of droplets for integrated microfluidics. Lab Chip 2002, 2, 96–101. [Google Scholar] [CrossRef]
- Cho, S.K.; Moon, H.; Kim, C.J. Creating, transporting, cutting, and merging liquid droplets by electrowetting-based actuation for digital microfluidic circuits. J. Microelectromechan. Syst. 2003, 12, 70–80. [Google Scholar] [CrossRef]
- Chakrabarty, K.; Su, F. Digital Microfluidic Biochips: Synthesis, Testing, and Reconfiguration Technique; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Berge, B.; Peseux, J. Variable focal lens controlled by an external voltage: An application of electrowetting. Eur. Phys. J. E 2000, 3, 159–163. [Google Scholar] [CrossRef]
- Yang, S.; Krupenkin, T.N.; Mach, P.; Chandross, E.A. Tunable and latchable liquid microlens with photopolymerizable components. Adv. Mater. 2003, 15, 940–943. [Google Scholar] [CrossRef]
- Kuiper, S.; Hendriks, B.H.W. Variable-focus liquid lens for miniature cameras. Appl. Phys. Lett. 2004, 85, 1128–1130. [Google Scholar]
- Hayes, R.A.; Feenstra, B.J. Video-speed electronic paper based on electrowetting. Nature 2003, 425, 383–385. [Google Scholar]
- Heikenfeld, J.; Steckl, A.J. High-transmission electrowetting light valves. Appl. Phys. Lett. 2005. [Google Scholar] [CrossRef]
- Washizu, M. Electrostatic actuation of liquid droplets for microreactor applications. IEEE Trans. Ind. Appl. 1998, 34, 732–737. [Google Scholar] [CrossRef]
- Lee, J.; Kim, C.-J. Surface-tension-driven microactuation based on continuous electrowetting. J. Microelectromech. Syst. 2000, 9, 171–180. [Google Scholar] [CrossRef]
- Yun, K.S.; Cho, I.J.; Bu, J.U.; Kim, C.-J.; Yoon, E. A surface-tension driven micropump for low-voltage and low-power operations. J. Microelectromech. Syst. 2002, 11, 454–461. [Google Scholar] [CrossRef]
- Quilliet, C.; Berge, B. Electrowetting: A recent outbreak. Curr. Opin. Colloid Interface Sci. 2001, 6, 34–39. [Google Scholar] [CrossRef]
- Pamula, V.K.; Chakrabarty, K. Cooling of integrated circuits using droplet-based microfluidics. In Proceedings of the 13th ACM Great Lakes Symposium on VLSI 2003, Washington, DC, USA, 28–29 April 2003; pp. 84–87.
- Paik, P.Y.; Pamula, V.K.; Chakrabarty, K. Thermal effects on droplets transport in digital microfluidics with application to chip cooling. In Proceedings of theInter Society Conference on Thermal Phenomena, Las Vegas, NV, USA, 1–4 June 2004; pp. 649–654.
- Paik, P.Y.; Pamula, V.K.; Chakrabarty, K. Droplet-based hot spot cooling using topless digital microfluidics on a printed circuit board. In Proceedings of the IEEE International Workshop on Thermal Investigations of ICs and Systems, Belgirate, Italy, 27–30 September 2005; pp. 278–283.
- Mohseni, K. Effective cooling of integrated circuits using liquid alloy electrowetting. In Proceedings of the 21st Semi-Therm Symposium, San Jose, CA, USA, 15–17 March 2005; pp. 20–25.
- Nicole, C.; Lasance, C.J.M.; Prins, M.W.J.; Baret, J.-C.; Decre, M.M.J. A Cooling System for Electronic Substrates. WIPO Patent WO 2006/016293 A1, 16 February 2005. [Google Scholar]
- Garimella, S.V.; Bahadur, V. Electrowetting Based Heat Spreader. U.S. Patent 11/752702, 23 May 2007. [Google Scholar]
- Oprins, H.; Danneels, J.; van Ham, B.; Vandevelde, B.; Baelmans, M. Convection heat transfer in electrostatic actuated liquid droplets for electronics cooling. Microelectron. J. 2008, 39, 966–974. [Google Scholar] [CrossRef]
- Oprins, H.; Vandevelde, B.; Fiorini, P.; Beyne, E.; de Vos, J.; Majeed, B. Device for cooling integrated circuits. U.S. Patent 20110304987 A1, 1 June 2011. [Google Scholar]
- Oprins, H.; Fiorini, P.; de Vos, J.; Majeed, B.; Vandevelde, B.; Beyne, E. Modeling, design and fabrication of a novel electrostatically actuated droplet based impingement cooler. In Proceedings of the 10th PowerMEMS, Leuven, Belgium, 30 November–3 December 2010; pp. 191–194.
- Majeed, B.; Jones, B.; Oprins, H.; Vandevelde, B.; Sabuncogolu, D.; Fiorini, P. Fabrication of an electrostatically actuated impingement cooling device. In Proceedings of the 44th International Symposium on Microelectronics, Long Beach, CA, USA, 9–13 October 2011.
- Ren, H.; Fair, R.B.; Pollack, M.G.; Schayghnessy, E.J. Dynamics of electrowetting droplet transport. Sens. Actuat. B 2002, 87, 201–206. [Google Scholar] [CrossRef]
- Bahadur, V.; Garimella, S.V. An energy-based model for electrowetting-induced droplet actuation. J. Micromech. Microeng. 2006, 16, 1494–1503. [Google Scholar] [CrossRef]
- Ren, H.; Fair, R.B.; Pollack, M.G. Automated on-chip droplet dispensing with volume control by electro-wetting actuation and capacitance metering. Sens. Actuat. B 2004, 98, 319–327. [Google Scholar] [CrossRef]
- Berthier, J.; Dubois, P.; Clementz, P.; Claustre, P.; Peponnet, C.; Fouillet, Y. Actuation potentials and capillary forces in electrowetting based microsystems. Sens. Actuat. A 2007, 134, 471–479. [Google Scholar] [CrossRef]
- Shapiro, B.; Moon, H.; Garrell, R.L.; Kim, C.-J. Equilibrium behaviour of sessile drops under surface tension, applied external fields, and material variations. J. Appl. Phys. 2003, 93, 5794–5811. [Google Scholar] [CrossRef]
- Mohseni, K.; Baird, E. Digitized heat transfer using electrowetting on dielectric. Nanoscale Microscale Thermophys. Eng. 2007, 11, 99–120. [Google Scholar] [CrossRef]
- Blake, T.D. The physics of moving wetting lines. J. Colloid Interface Sci. 2006, 299, 1–13. [Google Scholar] [CrossRef]
- Bonn, D.; Eggers, J.; Indekeu, J.; Meunier, J.; Rolley, E. Wetting and spreading. Rev. Mod. Phys. 2009, 81, 739–805. [Google Scholar] [CrossRef]
- Extrand, C.W.; Kumagai, Y. Liquid drops on an inclined plane: The relation between contact angles, drop shape and retentive force. J. Colloid Interface Sci. 1995, 170, 515–521. [Google Scholar] [CrossRef]
- Chen, J.H.; Hsieh, W.H. Electrowetting-induced capillary flow in a parallel-plate channel. J. Colloid Interface Sci. 2006, 296, 276–283. [Google Scholar] [CrossRef]
- Chen, N.; Kuhl, T.; Tadmor, R.; Lin, Q.; Israelachvili, J. Large deformations during the coalescence of fluid interfaces. Phys. Rev. Lett. 2004. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Oprins, H.; Vandevelde, B.; Baelmans, M. Modeling and Control of Electrowetting Induced Droplet Motion. Micromachines 2012, 3, 150-167. https://doi.org/10.3390/mi3010150
Oprins H, Vandevelde B, Baelmans M. Modeling and Control of Electrowetting Induced Droplet Motion. Micromachines. 2012; 3(1):150-167. https://doi.org/10.3390/mi3010150
Chicago/Turabian StyleOprins, Herman, Bart Vandevelde, and Martine Baelmans. 2012. "Modeling and Control of Electrowetting Induced Droplet Motion" Micromachines 3, no. 1: 150-167. https://doi.org/10.3390/mi3010150
APA StyleOprins, H., Vandevelde, B., & Baelmans, M. (2012). Modeling and Control of Electrowetting Induced Droplet Motion. Micromachines, 3(1), 150-167. https://doi.org/10.3390/mi3010150