Improved Operation of the Modified Non-Inverting Step-Down/Up (MNI-SDU) DC-DC Converter
Abstract
1. Introduction
- An asynchronous operation mode with a fixed time offset for the MNI-SDU converter, which reduces ripple, stress levels, and power losses.
- Design expressions of the MNI-SDU converter in this proposed operation.
- A methodology to select an appropriate value for the fixed time offset.
- The linearized model and transfer functions of the MNI-SDU converter under the proposed operation mode.
- A methodology to select adequate parameters of a current-mode controller.
- An efficiency analysis demonstrating enhanced efficiency.
- Experimental results validating the theoretical analysis.
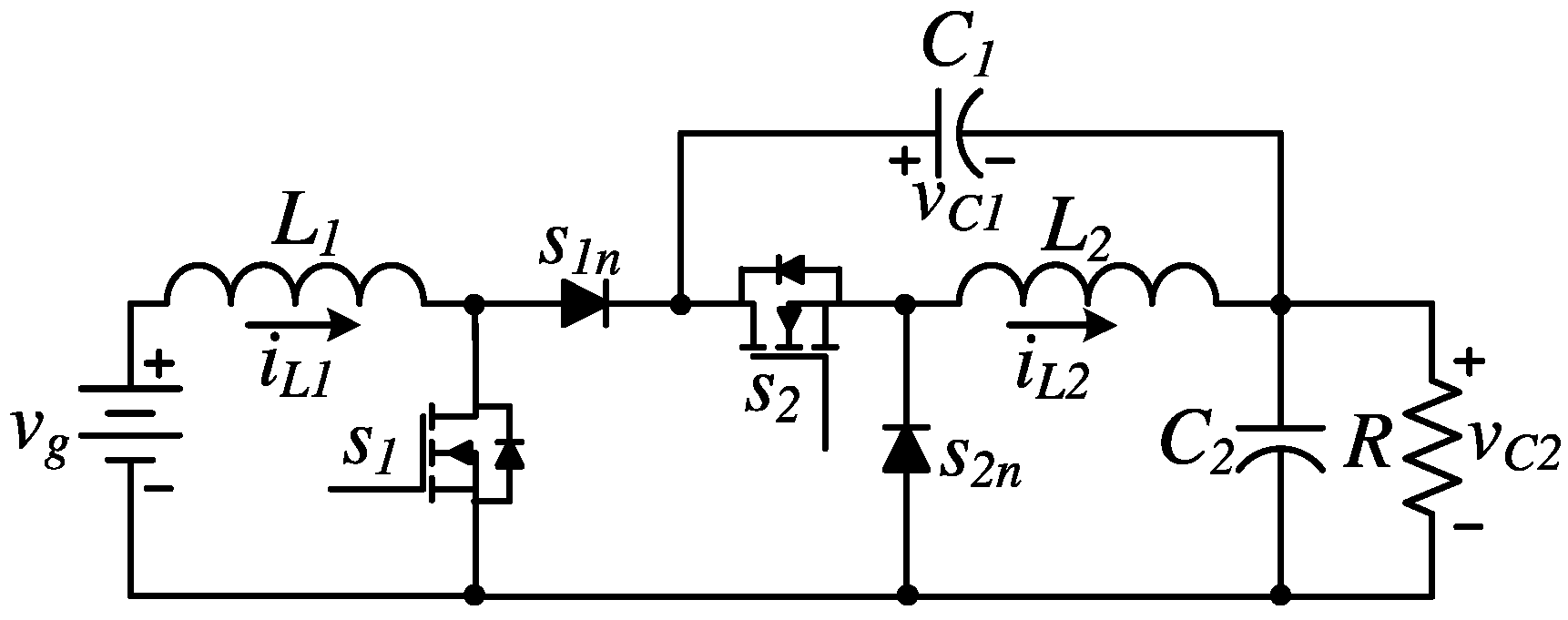
2. The MNI-SDU Converter in Its Original Operation
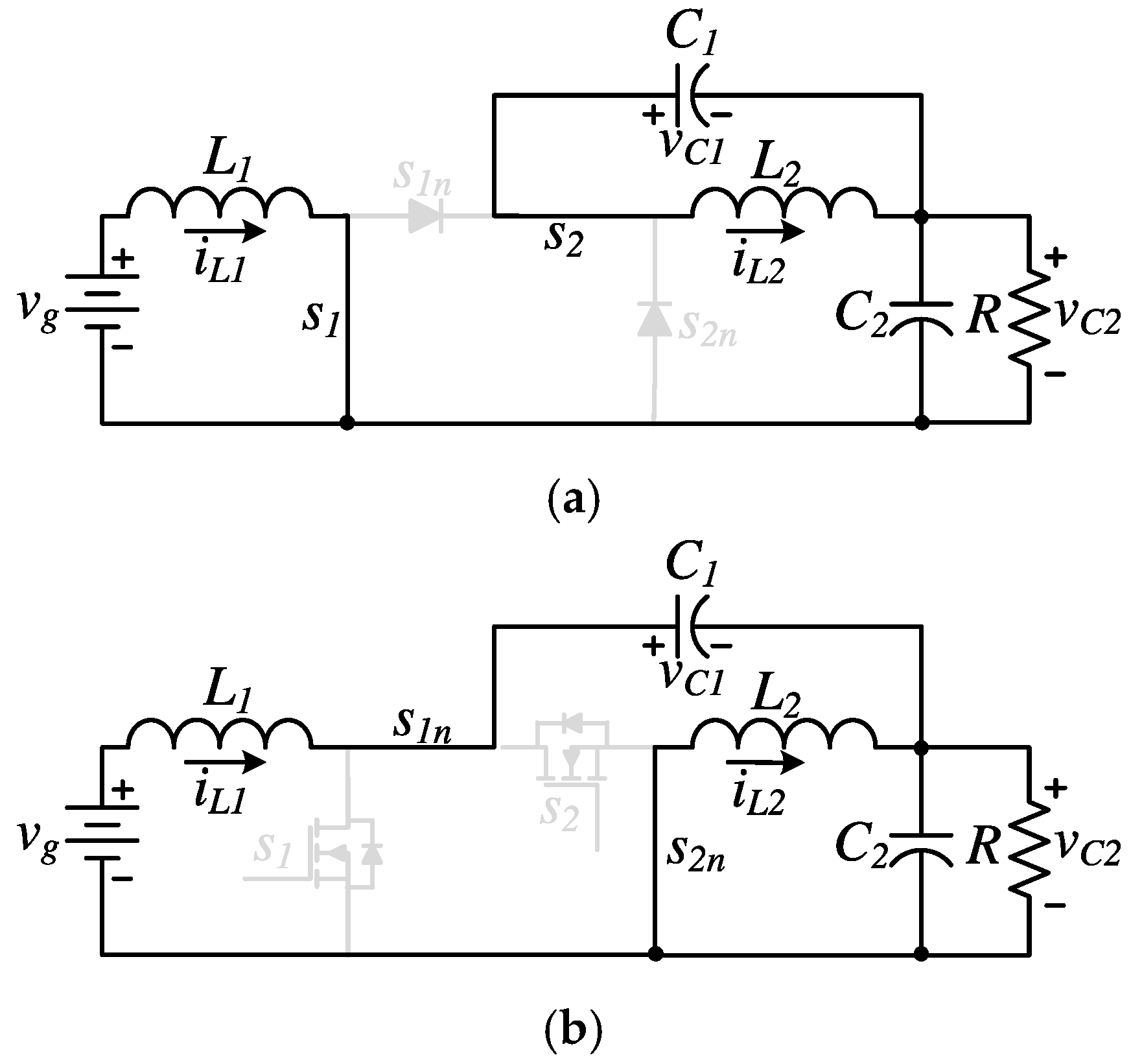
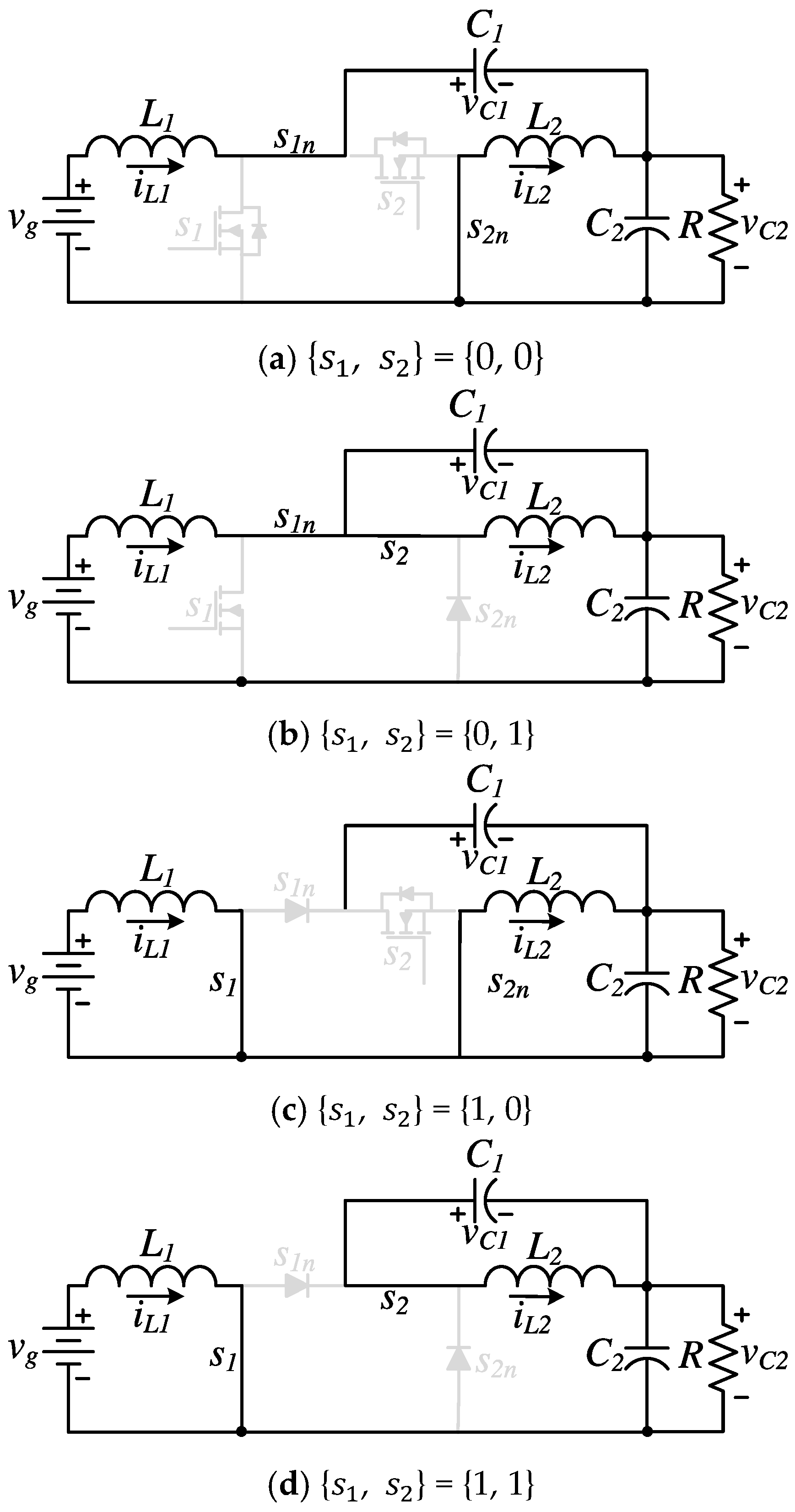
3. The Proposed Operation
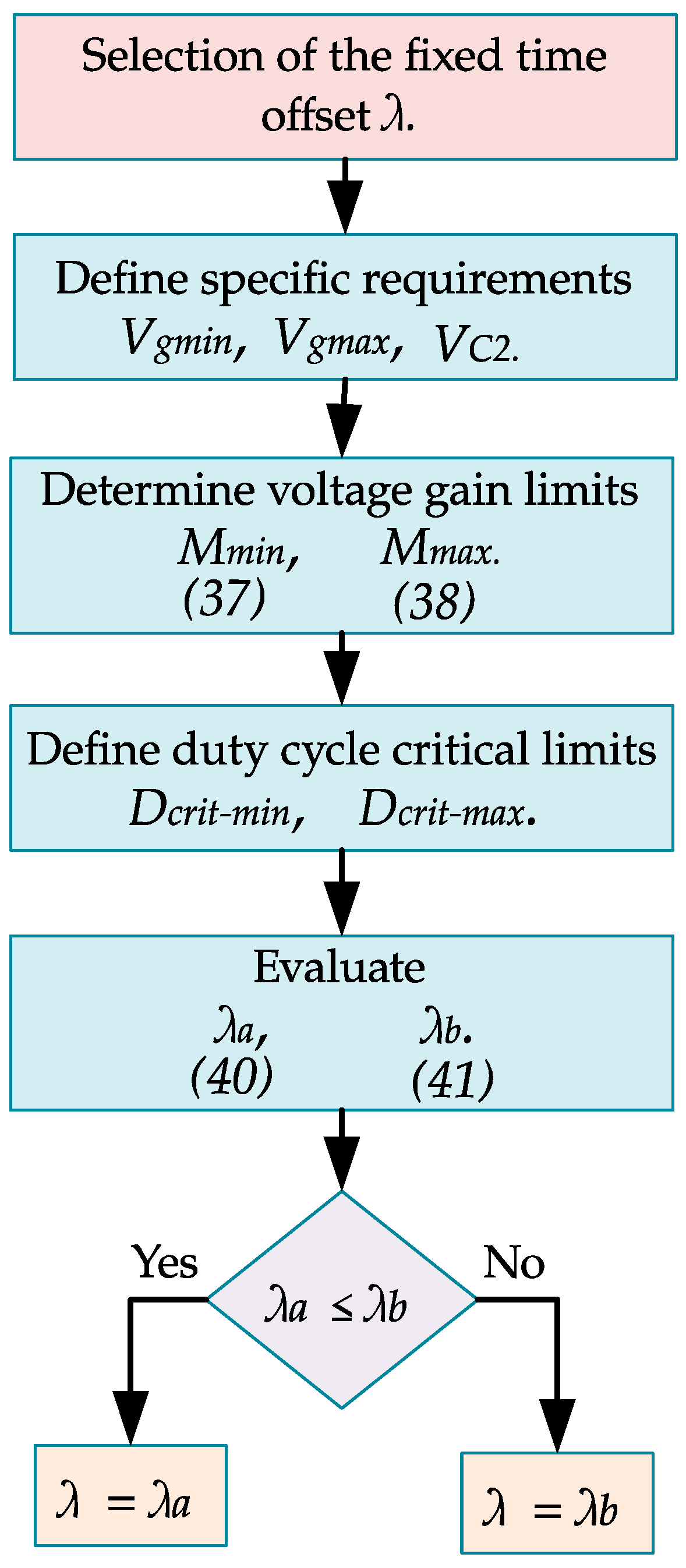
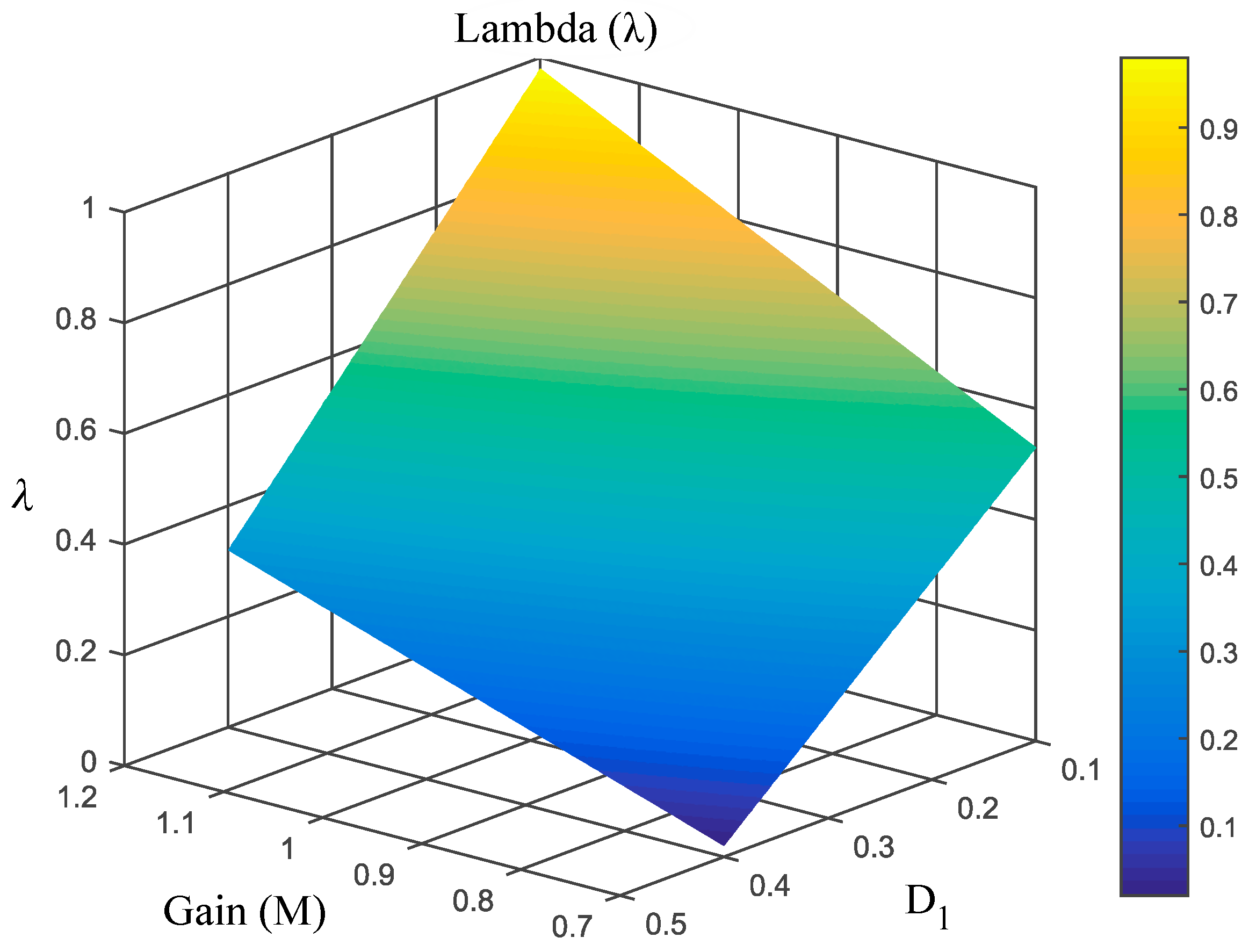
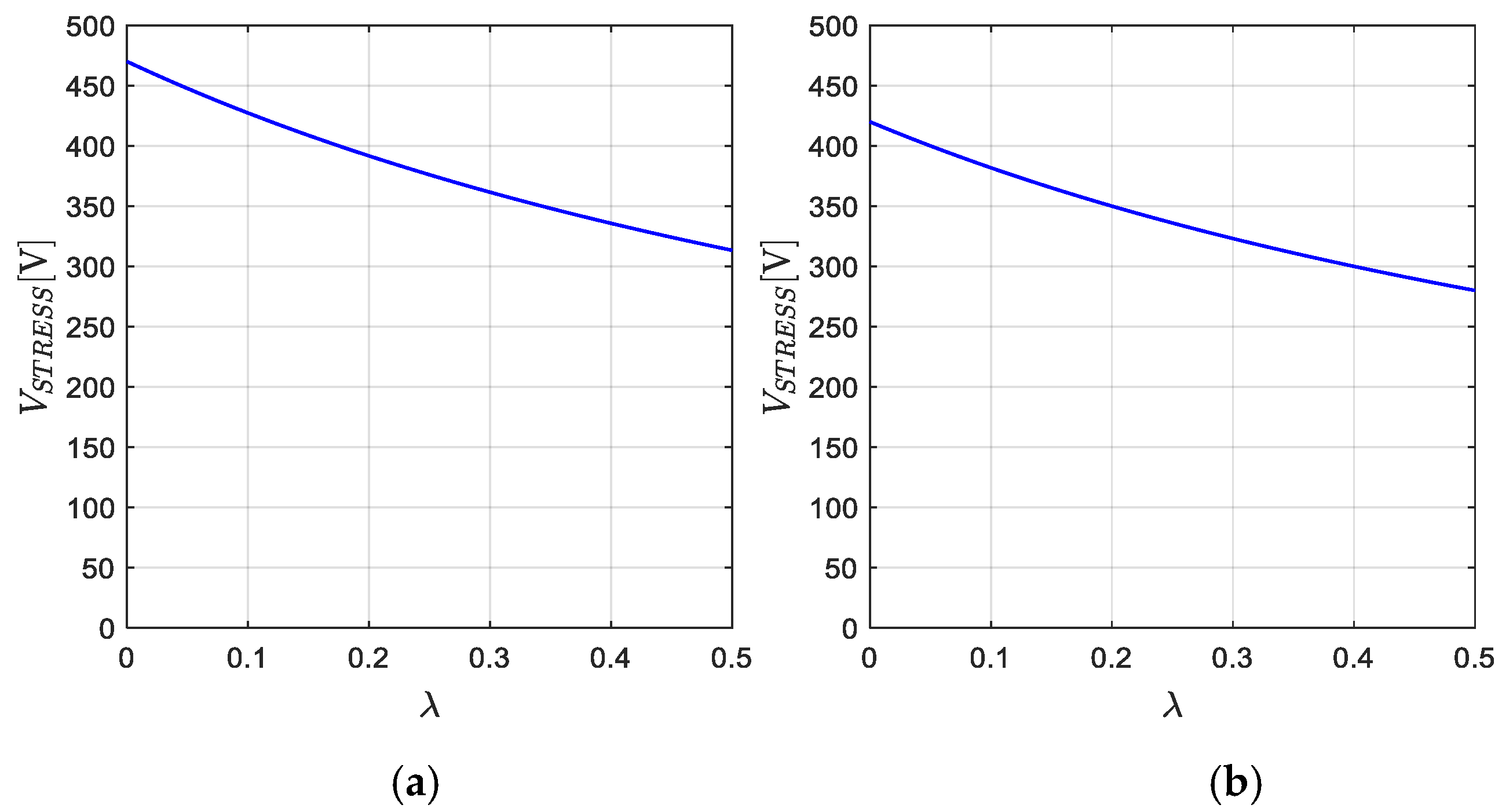
Selection of the Fixed Time Offset λ
- Define the specific voltage requirements according to the application: the minimum voltage of the source , the maximum voltage of the source , and the desired voltage reference . Remember that, in steady state .
- Obtain the maximum and minimum voltage gain according to,
- Determine the minimum and maximum critical duty cycles, denoted as and , at which the converter operates reliably. To ensure proper operation of the converter, the duty cycle must satisfy the following inequality,
- Obtain values that meet the maximum and minimum requirements. The nominal duty cycle for the active switch is and for the active switch is , where . Thus, the possible minimum value of is and the possible maximum value of is . According to (31), the voltage gain value . Thus, the value of λ to obtain the minimum voltage gain with the critical minimum duty cycle conditions is
- 5.
- Select the value of λ as the lowest between and , i.e.,
4. Control Design
4.1. Inner Current Loop
4.2. Outer Voltage Loop
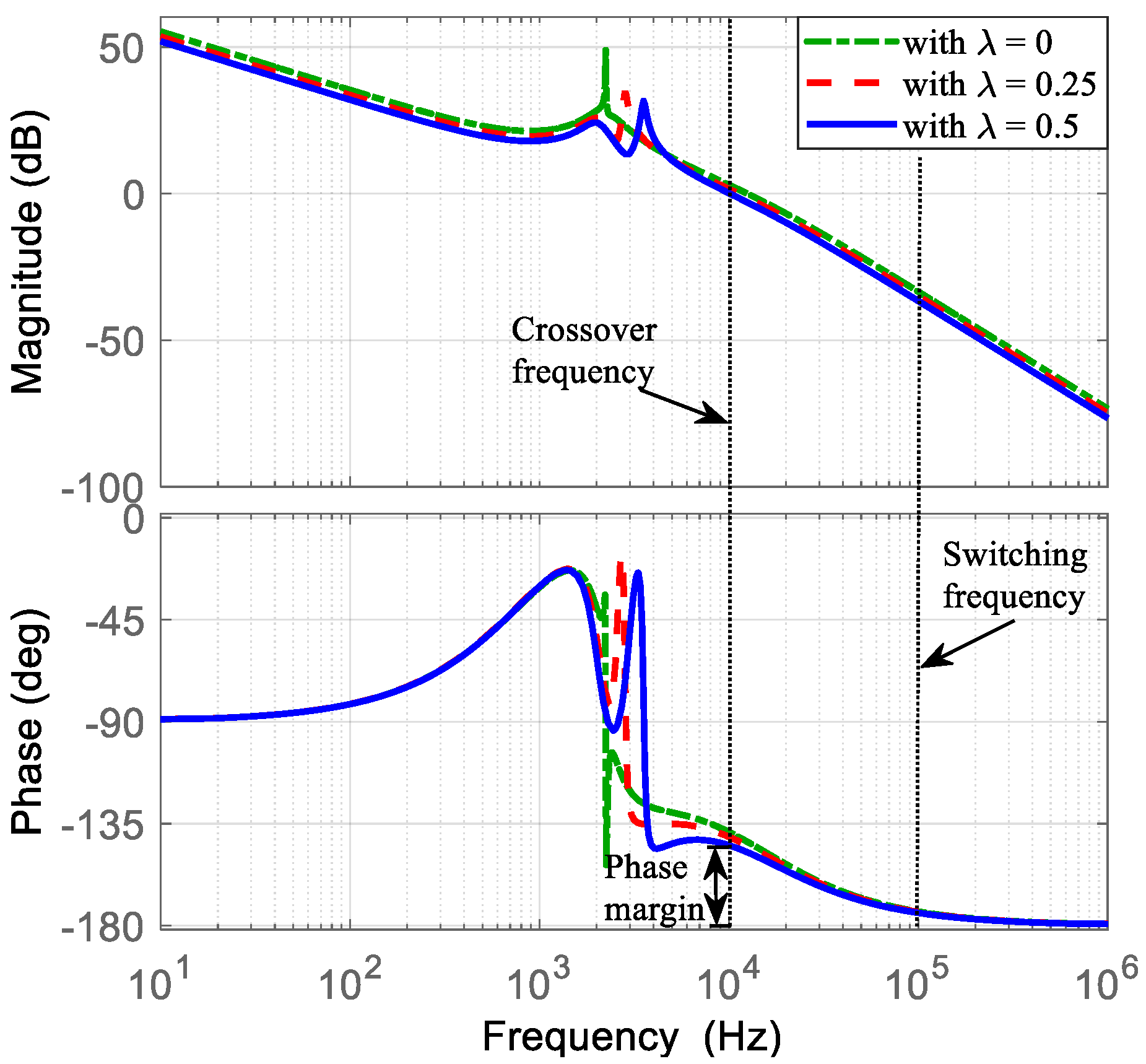
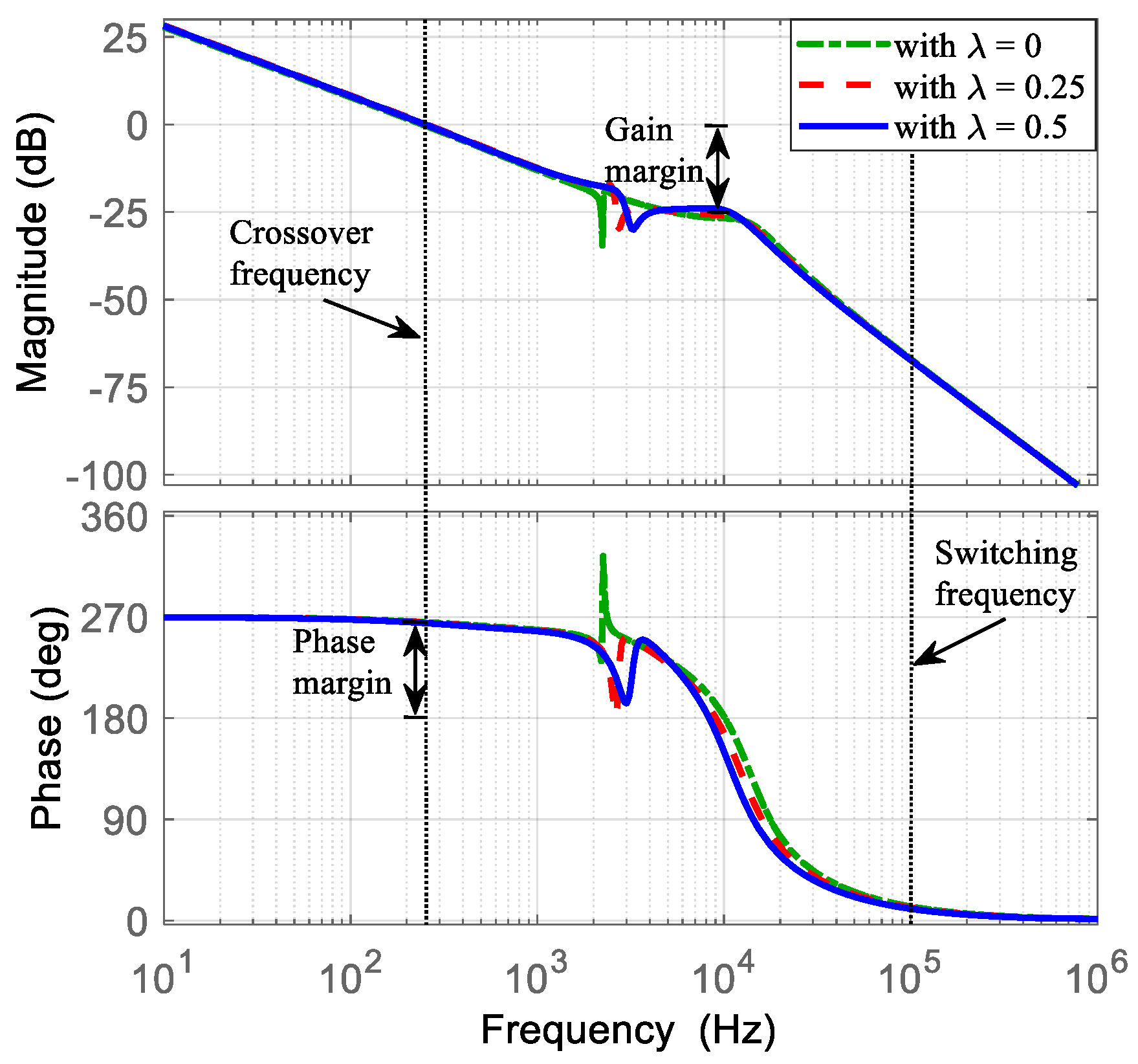
- For relative stability, the slope at the crossover frequency must be approximately −20 dB/dec.
- To improve steady-state accuracy, the gain at low frequencies should be high.
- For robust stability, ensure a gain margin greater than 10 dB and a phase margin greater than 60 degrees.
5. Results and Comments
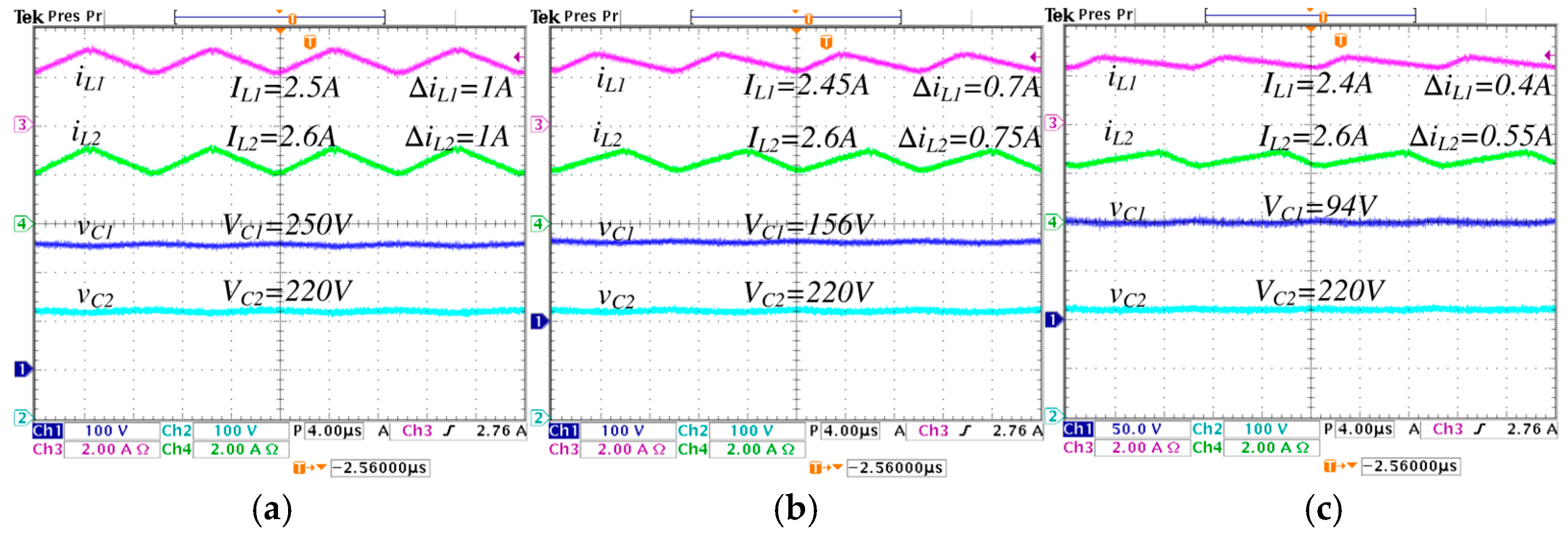
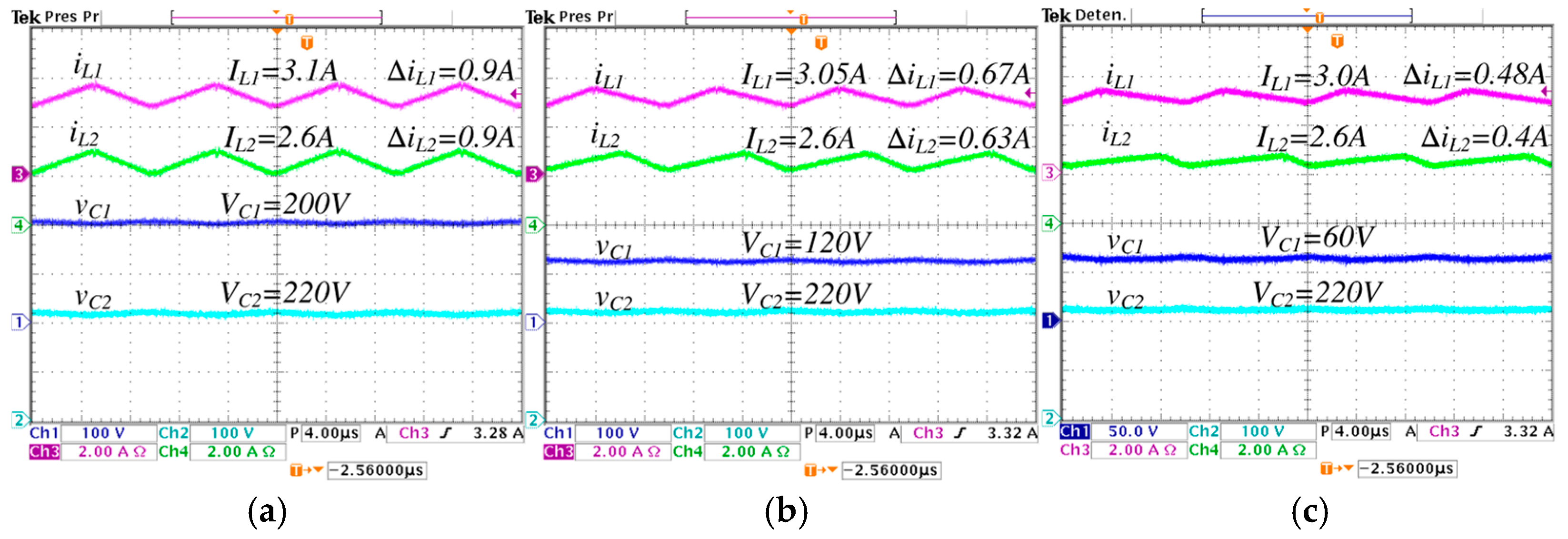
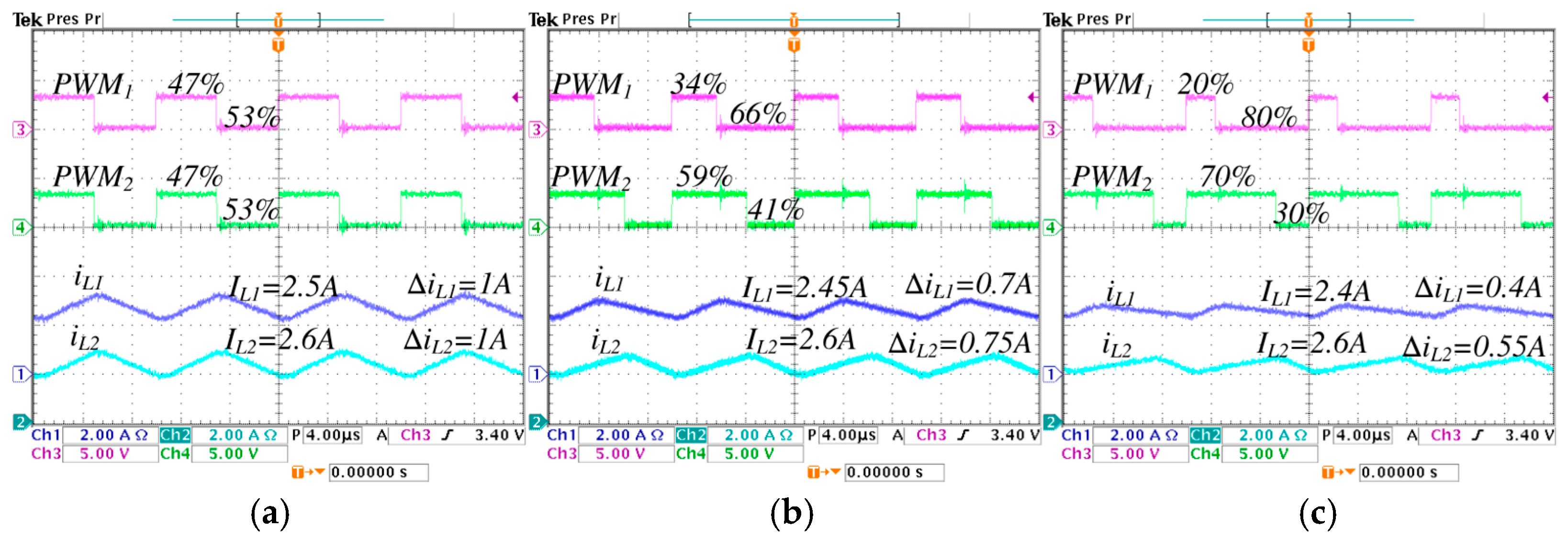
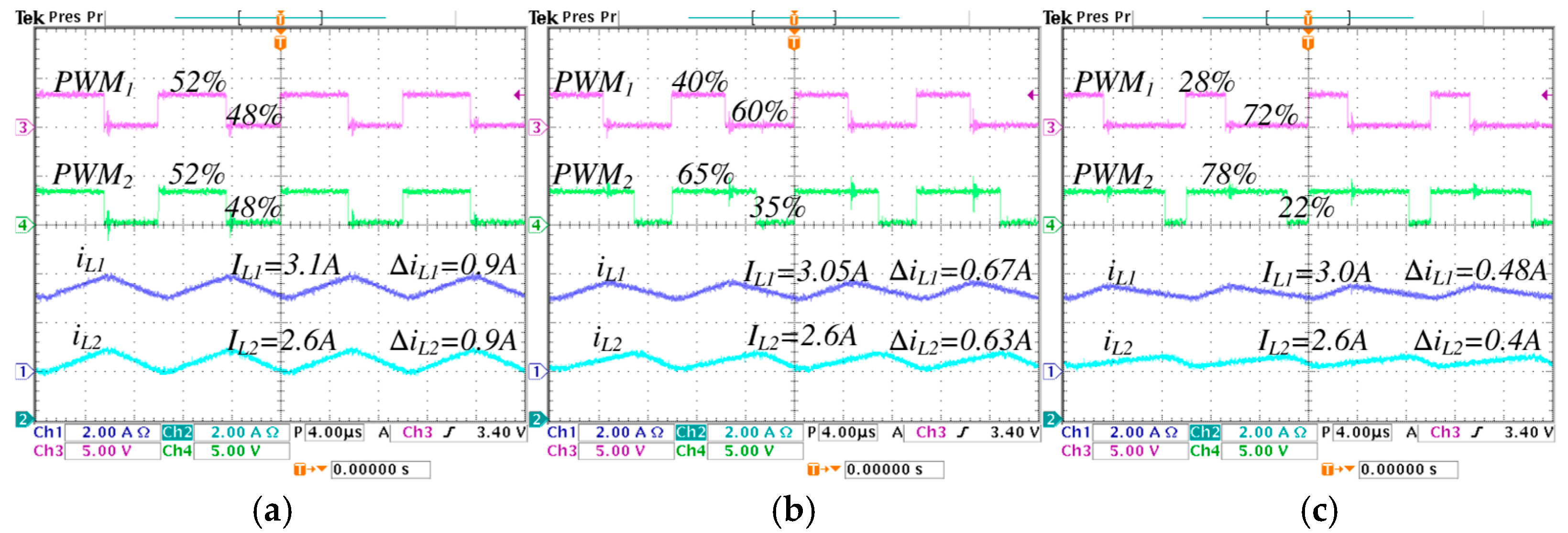
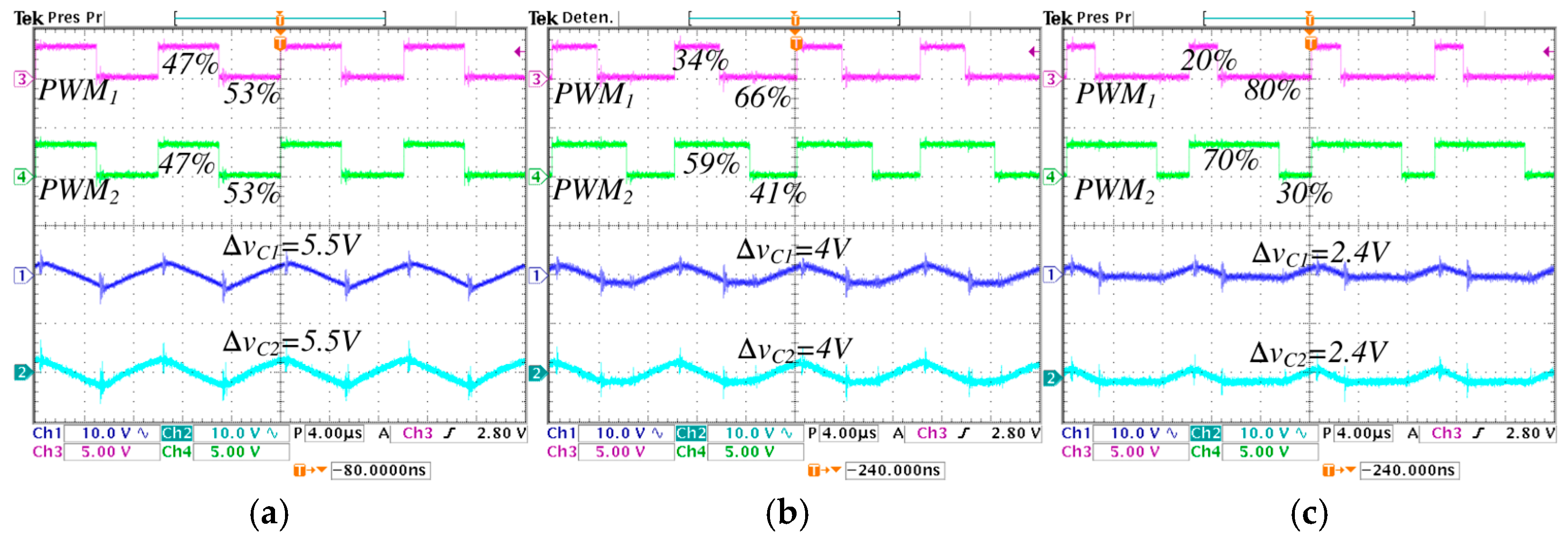
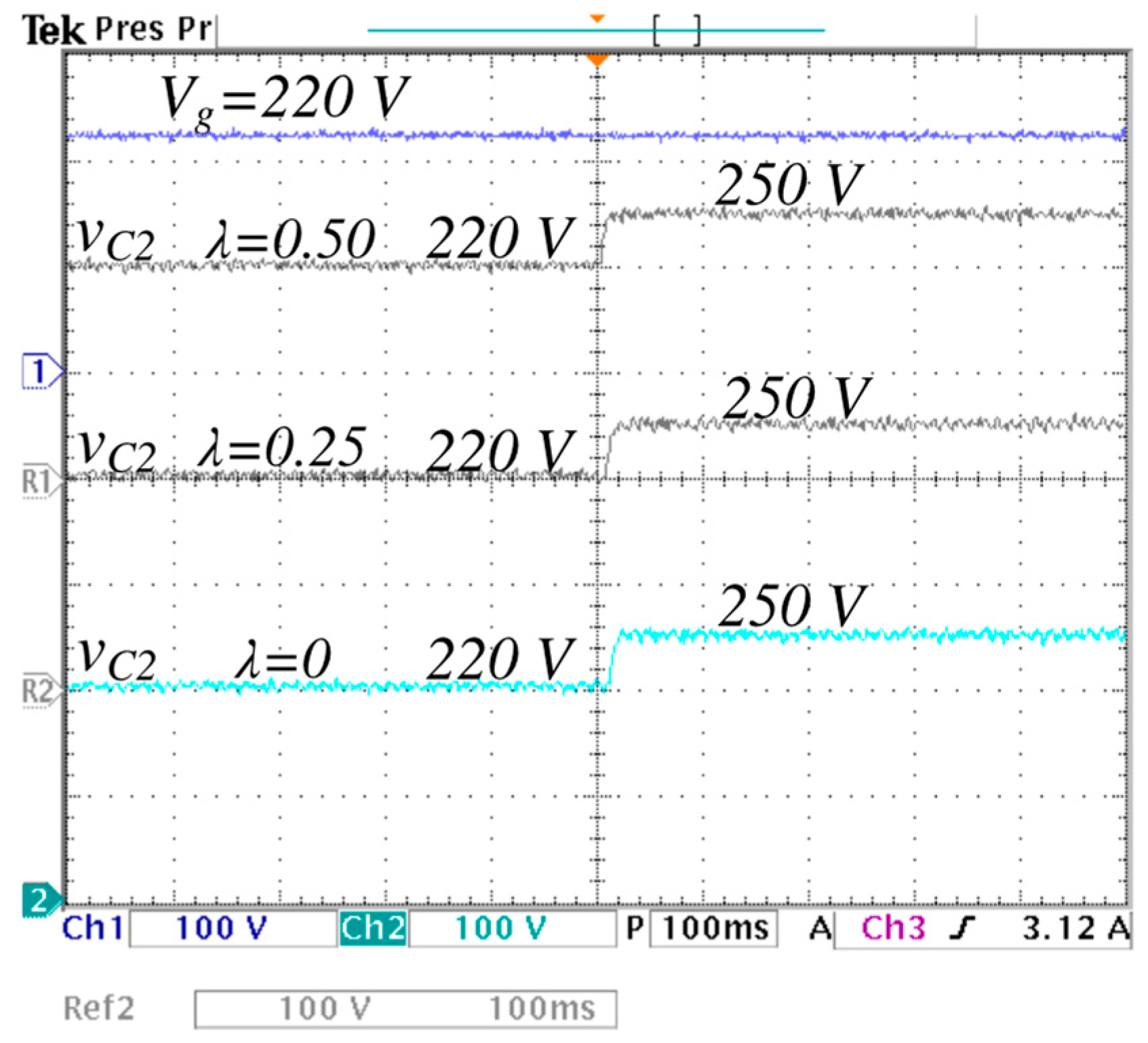
5.1. Selection of λ for the Practical Case
5.2. Parameters of the Controller
5.3. Steady-State Validations
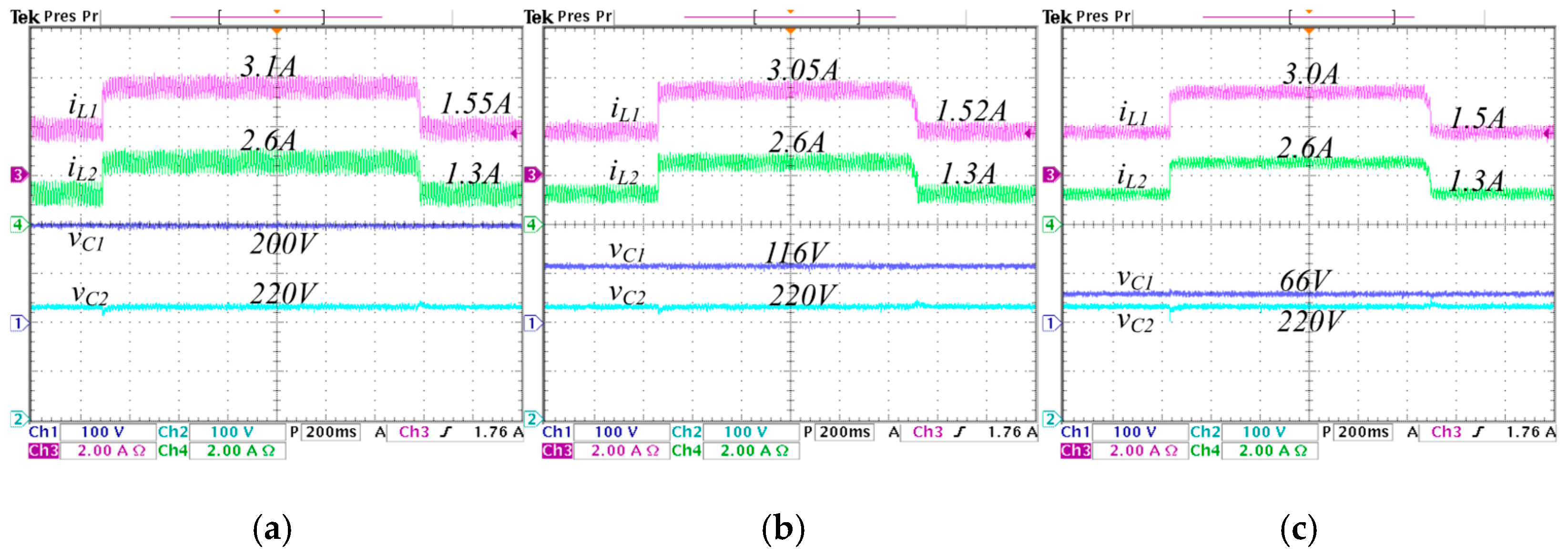
5.4. Stepwise Changes in the Load
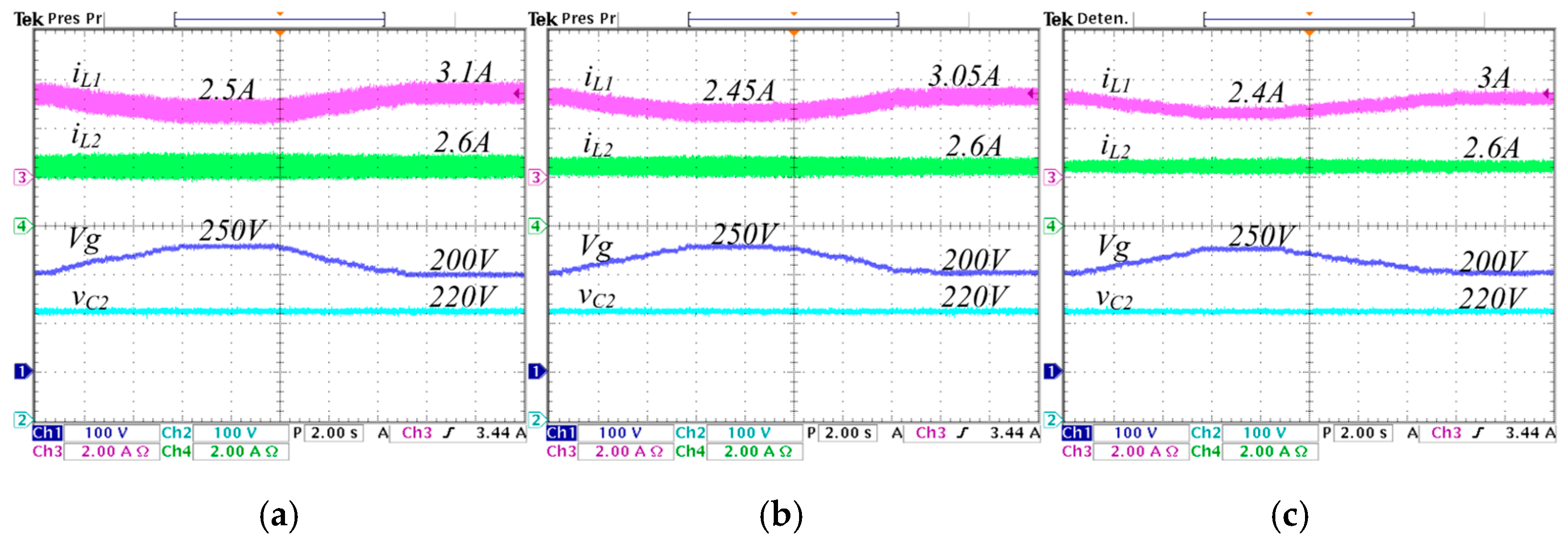
5.5. Changes in the Input Voltage
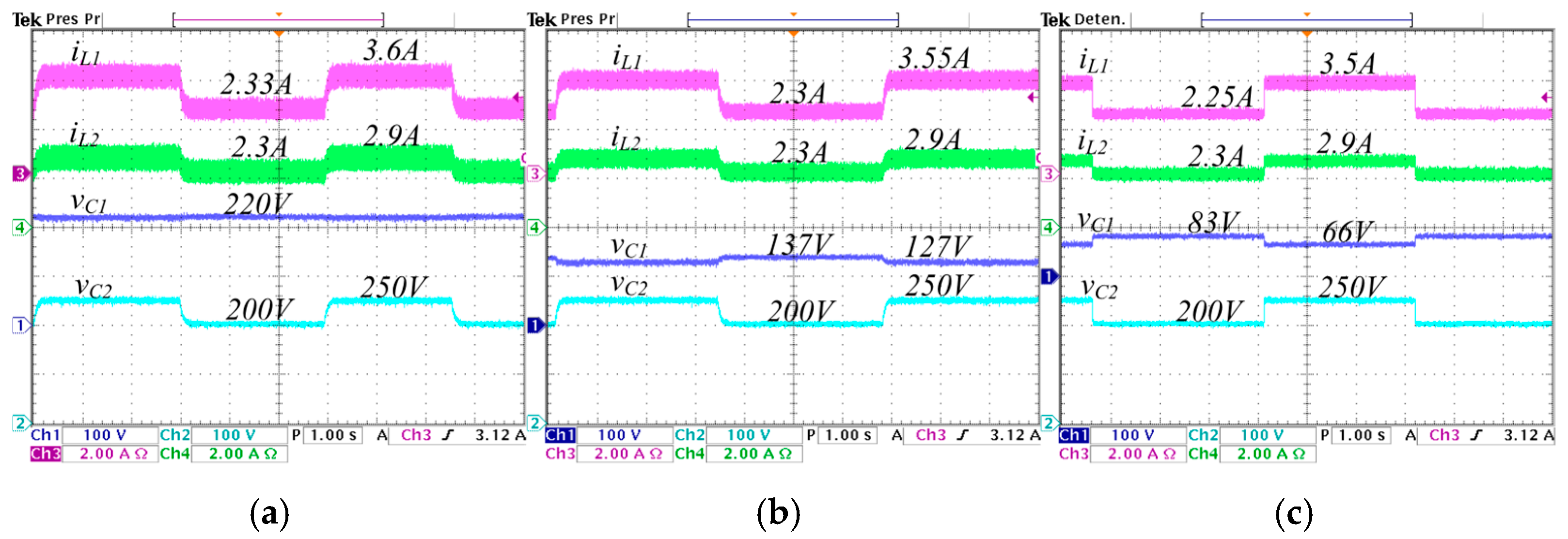
5.6. Stepwise Changes in the Voltage Reference
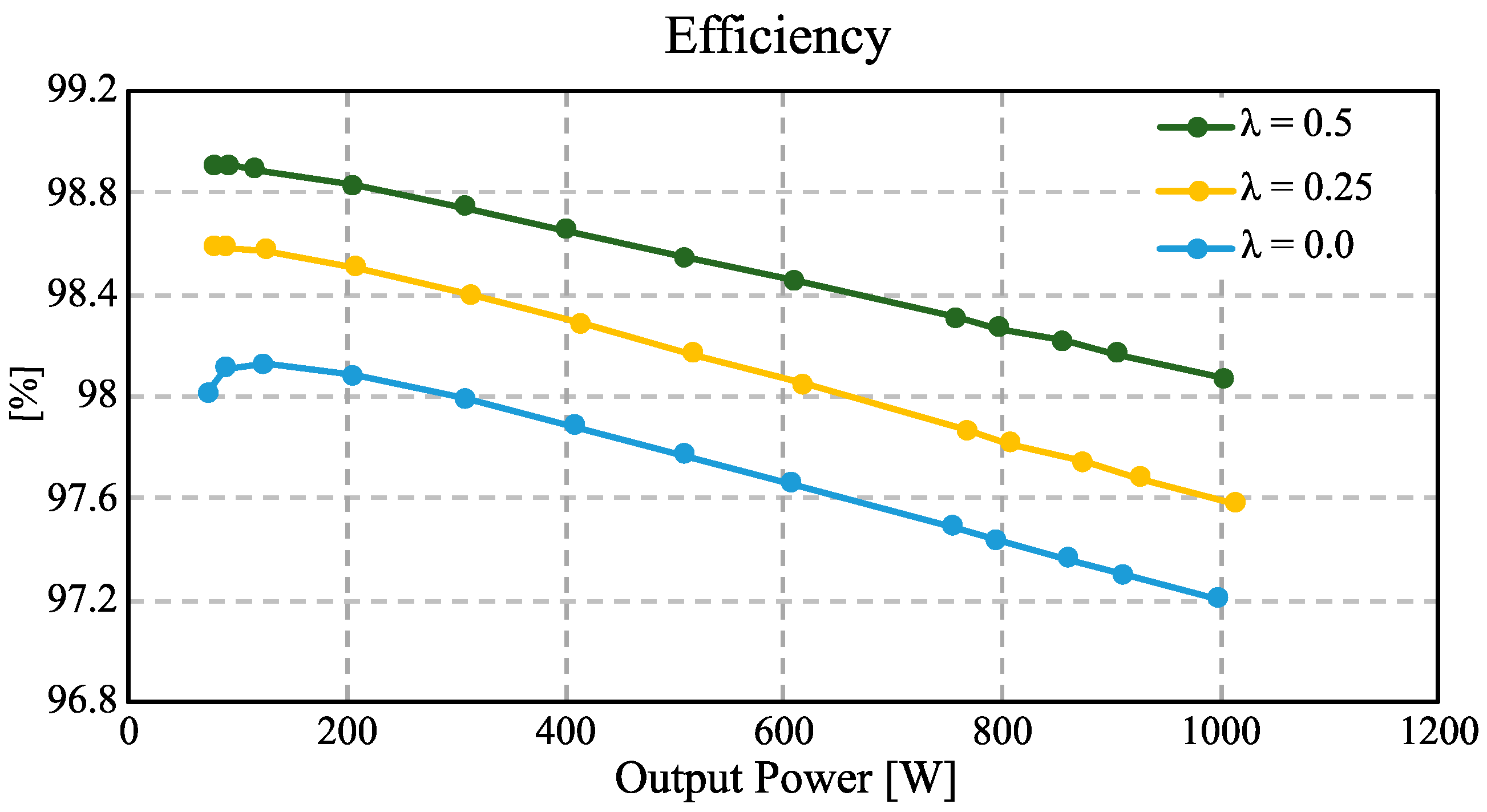
5.7. Efficiency Analysis
5.8. Comparison with Other Converters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mohan, N. Power Electronics: A First Course, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2023. [Google Scholar]
- Rashid, M.H. Power Electronics, Circuits, Devices, and Applications, 4th ed.; Pearson Education, Inc.: San Francisco, CA, USA, 2013. [Google Scholar]
- Shadoul, M.; Yousef, H.; Al Abri, R.; Al-Hinai, A. Adaptive Fuzzy Approximation Control of PV Grid-Connected Inverters. Energies 2021, 14, 942. [Google Scholar] [CrossRef]
- Fernández-Guillamón, A.; Gómez-Lázaro, E.; Muljadi, E.; Molina-García, Á. Power Systems with High Renewable Energy Sources: A Review of Inertia and Frequency Control Strategies over Time. Renew. Sustain. Energy Rev. 2019, 115, 109369. [Google Scholar] [CrossRef]
- Raghavendra, K.V.G.; Zeb, K.; Muthusamy, A.; Krishna, T.N.V.; Kumar, S.V.S.V.P.; Kim, D.-H.; Kim, M.-S.; Cho, H.-G.; Kim, H.-J. A Comprehensive Review of DC–DC Converter Topologies and Modulation Strategies with Recent Advances in Solar Photovoltaic Systems. Electronics 2020, 9, 31. [Google Scholar] [CrossRef]
- Islam, R.; Rafin, S.M.S.H.; Mohammed, O.A. Comprehensive Review of Power Electronic Converters in Electric Vehicle Applications. Forecasting 2023, 5, 22–80. [Google Scholar] [CrossRef]
- Safayatullah, M.; Elrais, M.T.; Ghosh, S.; Rezaii, R.; Batarseh, I. A Comprehensive Review of Power Converter Topologies and Control Methods for Electric Vehicle Fast Charging Applications. IEEE Access 2022, 10, 40753–40793. [Google Scholar] [CrossRef]
- S. Sánchez, A.G.; Soto-Vega, J.; Tlelo-Cuautle, E.; Rodríguez-Licea, M.A. Fractional-Order Approximation of PID Controller for Buck–Boost Converters. Micromachines 2021, 12, 591. [Google Scholar] [CrossRef] [PubMed]
- Ado, M.; BinArif, M.S.; Jusoh, A.; Mutawakkil, A.U.; Danmallam, I.M. Buck-boost converter with simple gate control for renewable energy applications. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 46, 17021–17033. [Google Scholar] [CrossRef]
- Rajavel, A.; Rathina Prabha, N. Fuzzy logic controller-based boost and buck-boost converter for maximum power point tracking in solar system. Trans. Inst. Meas. Control 2020, 43, 945–957. [Google Scholar] [CrossRef]
- Gheisarnejad, M.; Farsizadeh, H.; Tavana, M.R.; Khooban, M.H. A Novel Deep Learning Controller for DC/DC Buck-Boost Converters in Wireless Power Transfer Feeding CPLs. IEEE Trans. Ind. Electron. 2020, 68, 6379–6384. [Google Scholar] [CrossRef]
- Sarikhani, A.; Allahverdinejad, B.; Hamzeh, M. A Non-Isolated Buck-Boost DC-DC Converter with Continuous Input Current for Photovoltaic Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 804–811. [Google Scholar] [CrossRef]
- Mishra, A.; De Smedt, V. A Novel Hybrid Buck-Boost Converter Topology for Li-ion Batteries with Increased Efficiency. In Proceedings of the 27th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Glasgow, UK, 23–25 November 2020. [Google Scholar]
- Villanueva-Loredo, J.A.; Ortiz-Lopez, M.G.; Leyva-Ramos, J.; Diaz-Saldierna, L.H. Switching regulator based on switched-inductor SEPIC DC-DC converter with a continuous input current for lithium-ion batteries. IET Power Electron. 2021, 14, 982–991. [Google Scholar] [CrossRef]
- Wu, Y. Lithium-Ion Batteries: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Villanueva-Loredo, J.A.; Ortiz-Lopez, M.G.; Leyva-Ramos, J.; Diaz-Saldierna, L.H. Switching Regulator Based on a Non-Inverting Step-Down/Up DC–DC Converter for Lithium-Ion Battery Applications. Micromachines 2023, 14, 1144. [Google Scholar] [CrossRef] [PubMed]
- Koundi, M.; El Idrissi, Z.; El Fadil, H.; Belhaj, F.Z.; Lassioui, A.; Gaouzi, K.; Rachid, A.; Giri, F. State-Feedback Control of Interleaved Buck–Boost DC–DC Power Converter with Continuous Input Current for Fuel Cell Energy Sources: Theoretical Design and Experimental Validation. World Electr. Veh. J. 2022, 13, 124. [Google Scholar] [CrossRef]
- Huang, P.C.; Wu, W.Q.; Ho, H.H.; Chen, K.H. Hybrid Buck–Boost Feedforward and Reduced Average Inductor Current Techniques in Fast Line Transient and High-Efficiency Buck–Boost Converter. IEEE Trans. Power Electron. 2010, 25, 719–730. [Google Scholar] [CrossRef]
- Valdez-Resendiz, J.E.; Sanchez, V.M.; Rosas-Caro, J.C.; Mayo-Maldonado, J.C.; Sierra, J.M.; Barbosa, R. Continuous input-current buck-boost DC-DC converter for PEM fuel cell applications. Int. J. Hydrogen Energy 2017, 42, 30389–30399. [Google Scholar] [CrossRef]
- Mayo-Maldonado, J.C.; Valdez-Resendiz, J.E.; Garcia-Vite, P.M.; Rosas-Caro, J.C.; Rivera-Espinosa, M. del Rosario.; Valderrabano-Gonzalez, A. Quadratic Buck–Boost Converter With Zero Output Voltage Ripple at a Selectable Operating Point. IEEE Trans. Ind. Appl. 2019, 55, 2813–2822. [Google Scholar] [CrossRef]
- Bacha, S.; Munteanu, I.; Bratcu, A.I. Power Electronic Converters Modeling and Control: With Case Studies; Springer: London, UK, 2014. [Google Scholar]
- Leyva-Ramos, J.; Ortiz-Lopez, M.G.; Diaz-Saldierna, L.H.; Martinez-Cruz, M. Average current controlled switching regulators with cascade boost converters. IET Power Electron. 2011, 4, 1–10. [Google Scholar] [CrossRef]
- Leyva-Ramos, J.; Mota-Varona, R.; Ortiz-Lopez, M.G.; Diaz-Saldierna, L.H.; Langarica-Cordoba, D. Control Strategy of a Quadratic Boost Converter With Voltage Multiplier Cell for High-Voltage Gain. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1761–1770. [Google Scholar] [CrossRef]
- Maddi, H.L.R.; Yu, S.; Zhu, S.; Liu, T.; Shi, L.; Kang, M.; Xing, D.; Nayak, S.; White, M.H.; Agarwal, A.K. The Road to a Robust and Affordable SiC Power MOSFET Technology. Energies 2021, 14, 8283. [Google Scholar] [CrossRef]
- Rodriguez-Cortes, C.J.; Martinez-Rodriguez, P.R.; Sosa-Zuniga, J.M.; Langarica-Cordoba, D.; Cisneros-Montoya, R.; Vazquez-Guzman, G.; Reyes-Cruz, D. Comparative analysis and control design of two non-isolated DC–DC converters with high reduction ratio. Electr. Eng. 2025, 107, 2329–2345. [Google Scholar] [CrossRef]


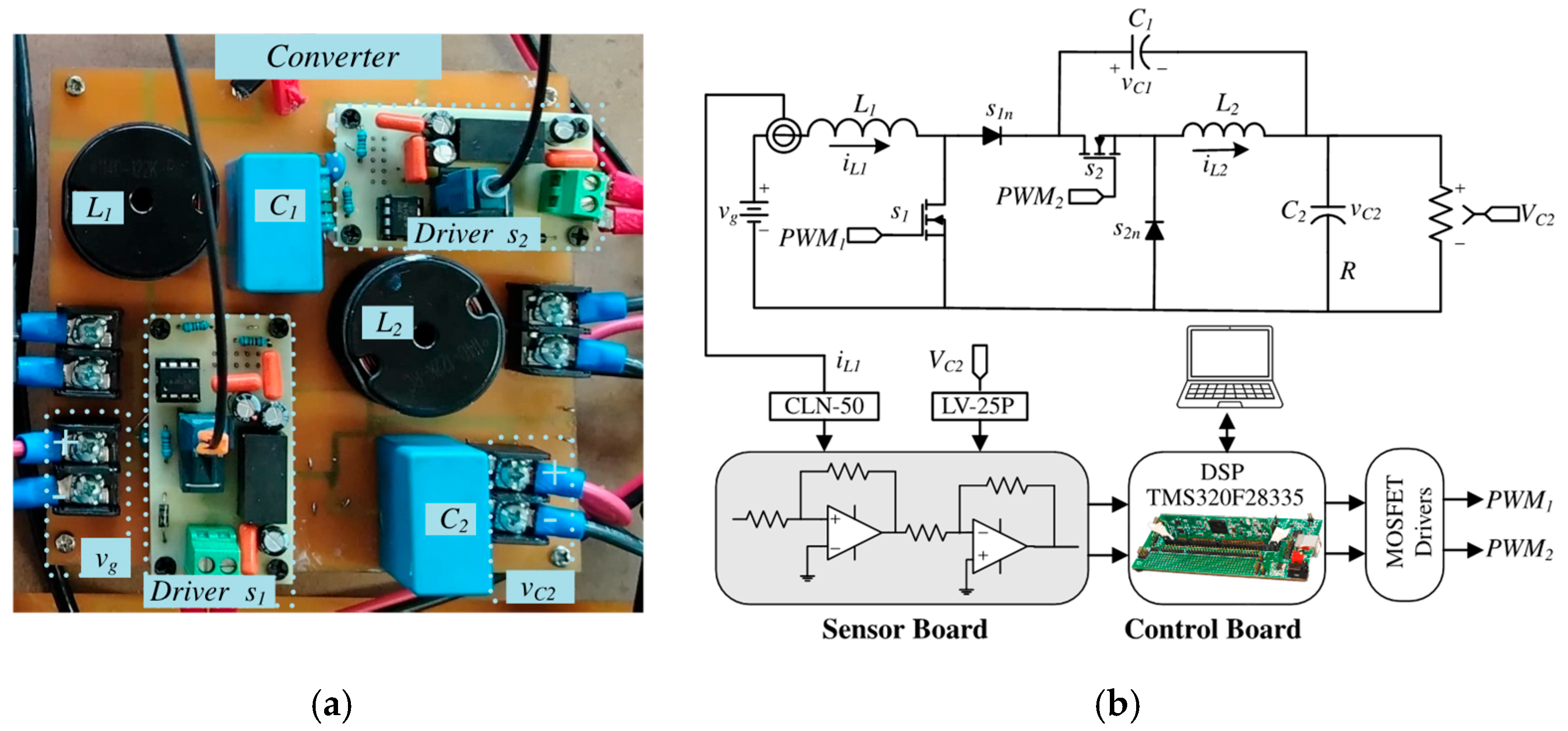
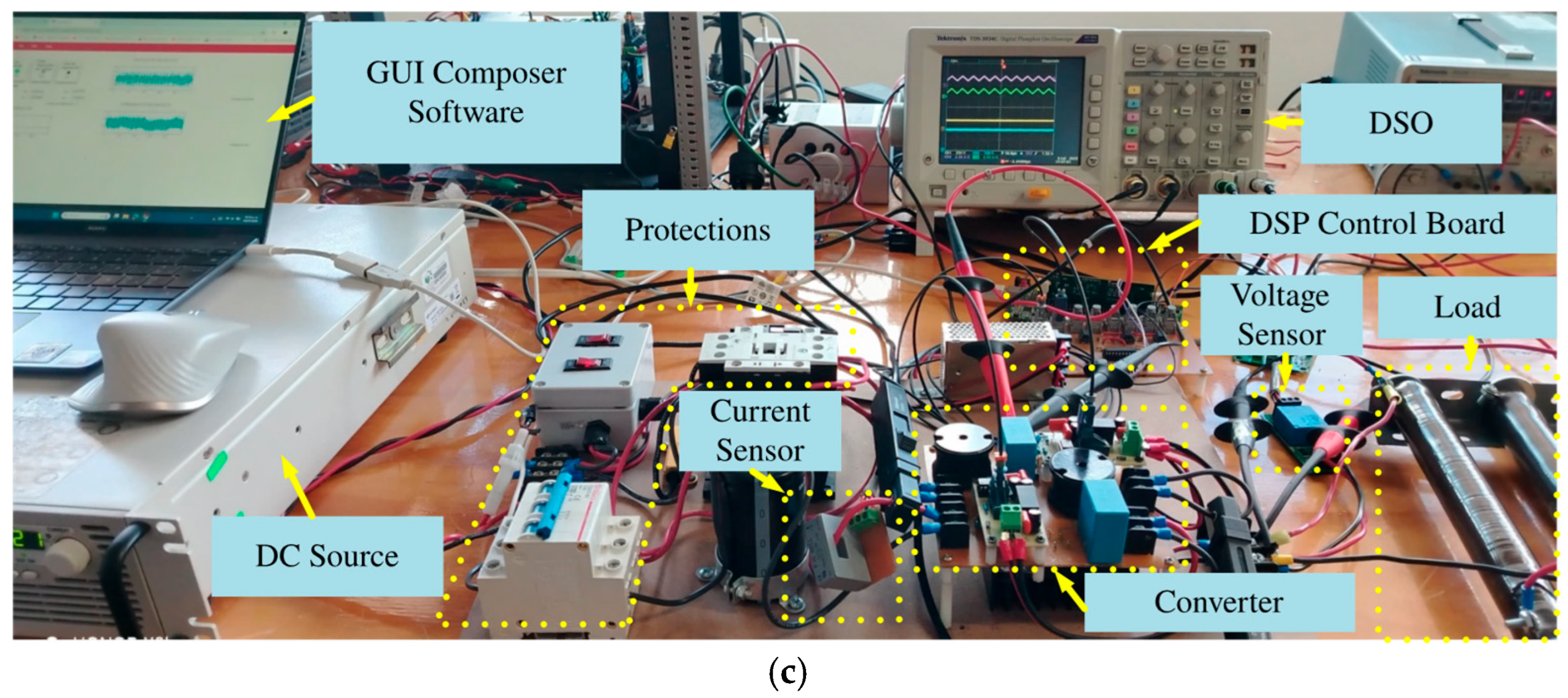




| Coefficient | Value |
|---|---|
| Parameter | Value | Part Number |
|---|---|---|
| Input voltage, Vg | 220V nominal (200–250 V) | --- |
| Reference voltage, Vref | 220 V | --- |
| Switching frequency, fS | 100 kHz | --- |
| 570 W | --- | |
| Load, R | 75 Ω | --- |
| 1.2 mH | 1140–122 K | |
| 1.2 mH | 1140–122 K | |
| 2.2 µF | B32923C3225M000 | |
| 2.2 µF | B32923C3225M000 | |
| 1200 V, 17 A | IPP026NIONF25 | |
| 650 V, 21 A | SCT3120ALGC11 | |
| 650 V, 15 A | SCS315AHGC9 | |
| 650 V, 15 A | SCS315AHGC9 |
| Step-Down Mode Tests Results | Step-Up Mode Tests Results | |||||
|---|---|---|---|---|---|---|
| V | | |||||
| λ = 0 | λ = 0.25 | λ = 0.5 | λ = 0 | λ = 0.25 | λ = 0.5 | |
| 0.47 | 0.34 | 0.2 | 0.52 | 0.40 | 0.28 | |
| λ | 0.47 | 0.59 | 0.7 | 0.52 | 0.65 | 0.78 |
| 2.5 A | 2.45 A | 2.4 A | 3.1 A | 3.05 A | 3.0 A | |
| 2.6 A | 2.6 A | 2.6 A | 2.6 A | 2.6 A | 2.6 A | |
| 250 V | 156 V | 94 V | 200 V | 120 | 60 | |
| 220 V | 220 V | 220 V | 220 V | 220 V | 220 V | |
| 1 A | 0.7 A | 0.4 A | 0.9 A | 0.67 A | 0.48 A | |
| 1 A | 0.75 A | 0.55 A | 1 A | 0.63 A | 0.4 A | |
| 5.5 V | 4 V | 2.4 V | 6.2 V | 4.8 V | 3.4 V | |
| 5.5 V | 4 V | 2.4 V | 6.2 V | 4.8 V | 3.4 V | |
| 472 V | 376 V | 312 V | 420 V | 336 V | 280 V | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villanueva-Loredo, J.A.; Rosas-Caro, J.C.; Martinez-Rodriguez, P.R.; Rodriguez-Cortes, C.J.; Langarica-Cordoba, D.; Vazquez-Guzman, G. Improved Operation of the Modified Non-Inverting Step-Down/Up (MNI-SDU) DC-DC Converter. Micromachines 2025, 16, 1063. https://doi.org/10.3390/mi16091063
Villanueva-Loredo JA, Rosas-Caro JC, Martinez-Rodriguez PR, Rodriguez-Cortes CJ, Langarica-Cordoba D, Vazquez-Guzman G. Improved Operation of the Modified Non-Inverting Step-Down/Up (MNI-SDU) DC-DC Converter. Micromachines. 2025; 16(9):1063. https://doi.org/10.3390/mi16091063
Chicago/Turabian StyleVillanueva-Loredo, Juan A., Julio C. Rosas-Caro, Panfilo R. Martinez-Rodriguez, Christopher J. Rodriguez-Cortes, Diego Langarica-Cordoba, and Gerardo Vazquez-Guzman. 2025. "Improved Operation of the Modified Non-Inverting Step-Down/Up (MNI-SDU) DC-DC Converter" Micromachines 16, no. 9: 1063. https://doi.org/10.3390/mi16091063
APA StyleVillanueva-Loredo, J. A., Rosas-Caro, J. C., Martinez-Rodriguez, P. R., Rodriguez-Cortes, C. J., Langarica-Cordoba, D., & Vazquez-Guzman, G. (2025). Improved Operation of the Modified Non-Inverting Step-Down/Up (MNI-SDU) DC-DC Converter. Micromachines, 16(9), 1063. https://doi.org/10.3390/mi16091063









