Charge Trapping Effects on n−MOSFET Current Mirrors Under TID Radiation
Abstract
1. Introduction
2. Hole Trapping Models and Flat−Band Voltage Shift
2.1. Hole Trapping
2.2. Time−Dependent Hole Trap Density and Transconductance
3. Reliability Analyses of Total Ionizing Dose Effects on n−MOSFET Current Mirrors
3.1. TID−Induced Electrical Degradation of an n−MOSFET
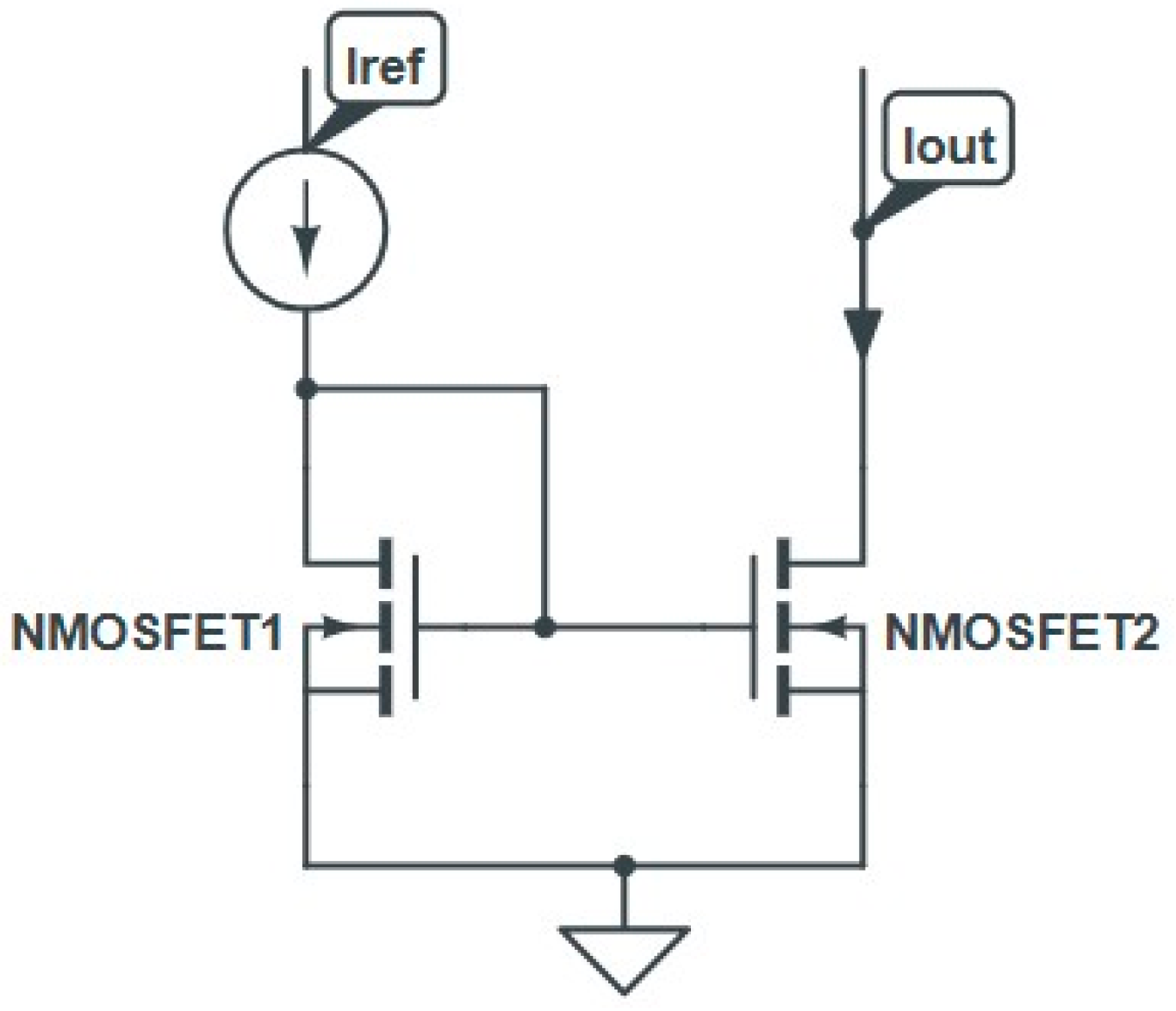
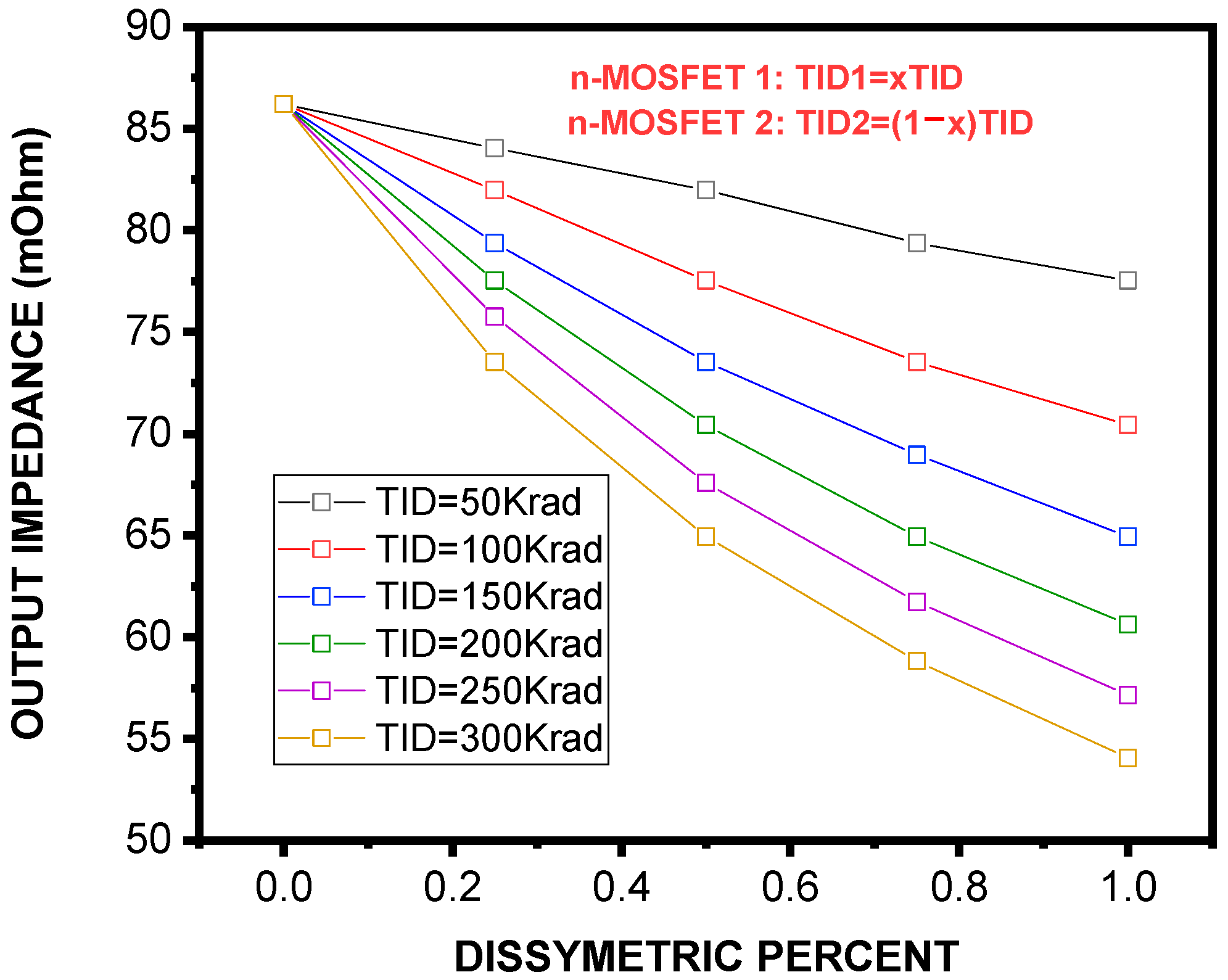
3.2. Electrical Degradation Mechanisms in n−MOSFET Current Mirrors
3.3. Comparative Analysis with Literature
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, S.; Shi, J.; Wang, J.L. Satellite on-board failure statistics and analysis. Spacecr. Eng. 2010, 19, 41–46. [Google Scholar]
- Cao, Y.; Wang, M.; Zheng, X.; Zhang, E.; Lv, L.; Wang, L.; Ma, M.; Lv, H.; Wang, Z.; Wang, Y.; et al. Combined Effect of TID eadiation and Electrical Stress on NMOSFETs. Micromachines 2022, 13, 1860. [Google Scholar] [CrossRef]
- Gao, T.; Yin, C.; Chen, Y.; Chen, R.; Yan, C.; Liu, H. Simulation of Total Ionizing Dose Effects Technique for CMOS Inverter Circuit. Micromachines 2023, 14, 1438. [Google Scholar] [CrossRef]
- Bonaldo, S. TID effects in highly scaled gate-all-around Si nanowire CMOS transistors irradiated to ultrahigh doses. IEEE Trans. Nucl. Sci. 2022, 69, 1444–1452. [Google Scholar] [CrossRef]
- Wang, S. Research and Modeling of Irradiation Characteristics of Ultra-Deep Submicron Devices. Ph.D. Thesis, Changchun University of Technology, Changchun, China, 2010. [Google Scholar]
- Zeng, C.; Li, X.; Gao, L. Research on High Temperature Characteristics of 28 nm Ultra-Thin FDSOI. Microelectronics 2021, 51, 577–581. [Google Scholar]
- Solano, J.; Spear, M.; Wallace, T.; Wilson, D.; Forman, F.; Esqueda, I.S. Total Ionizing Dose Response of Commercial 22nm FD-SOI CMOS Technology. In Proceedings of the 2022 IEEE Radiation Effects Data Workshop (REDW) (in conjunction with 2022 NSREC), Provo, UT, USA, 18–22 July 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Schrimpf, R.D.; Fleetwood, D.M. Radiation Effects and Soft Errors in Integrated Circuits and Electronic Devices; World Scientific: Singapore, 2004. [Google Scholar]
- Nasr, A.; Ashour, M. Experimental Studies for the Evaluation of Non-Ionizing Radiation Levels. In Proceedings of the Second All African IRPA Regional Radiation Protection Congress, Ismailia, Egypt, 22–26 April 2007; p. 223. [Google Scholar]
- Nasr, A. Effect of ionizing radiation on the characteristics of photodetectors. In Proceedings of the Second All African IRPA Regional Radiation Protection Congress, Ismailia, Egypt, 22–26 April 2007; p. 231. [Google Scholar]
- Prakash, G.; Ganesh, P.; Nagesha, Y.N.; Umakanth, D.; Arora, S.K.; Siddappa, K. Effect of 30 MeV Li3+ ion and 8 MeV electron irradiation on N-channel MOSFETs. Radiat. Eff. Defects Solids 2002, 157, 323. [Google Scholar] [CrossRef]
- Oldham, T.; McLean, F. Total ionizing dose effects in MOS oxides and devices. IEEE Trans. Nucl. Sci. 2003, 50, 483–499. [Google Scholar] [CrossRef]
- Chen, D.; Forney, J.D.; Pease, R.L.; Phan, A.M.; Carts, M.A.; Cox, S.R.; Kruckmeyer, K.; Burns, S.; Albarian, R.; Holcombe, B.; et al. The Effects of ELDRS at UltraLow Dose Rates. In Proceedings of the 2010 IEEE Radiation Effects Data Workshop, Denver, CO, USA, 20–23 July 2010. [Google Scholar] [CrossRef]
- Grasser, T. Stochastic charge trapping in oxides: From random telegraph noise to bias temperature instabilities. Microelectron. Reliab. 2012, 52, 39–70. [Google Scholar] [CrossRef]
- Vashishtha, P.; Kofler, C.; Verma, A.K.; Giridhar, S.P.; Tollerud, J.O.; Dissanayake, N.S.L.; Gupta, T.; Sehrawat, M.; Aggarwal, V.; Mayes, E.L.; et al. Epitaxial Interface-Driven Photoresponse Enhancement in Monolayer WS2-MoS2 Lateral Heterostructures. Adv. Funct. Mater. 2025, e12962. [Google Scholar] [CrossRef]
- Guérin, C.; Huard, V.; Bravaix, A. General framework about defect creation at the Si/SiO2 interface. J. Appl. Phys. 2009, 105, 114513. [Google Scholar] [CrossRef]
- Rauch, S.E.; La Rosa, G. The energy-driven paradigm of NMOSFET hot-carrier effects. IEEE Trans. Device Mater. Reliab. 2005, 5, 701–705. [Google Scholar] [CrossRef]
- Tyaginov, S.; Jech, M.; Franco, J.; Sharma, P.; Kaczer, B.; Grasser, T. Understanding and Modeling the Temperature Behavior of Hot-Carrier Degradation in SiON nMOSFETs. IEEE Electron Device Lett. 2016, 37, 84–87. [Google Scholar] [CrossRef]
- Wu, Z.; Franco, J.; Truijen, B.; Philippe, R.; Tyaginov, S.; Vandemaele, M.; Bury, E.; Groeseneken, G.; Linten, D.; Kaczer, B. Physics-based device aging modelling framework for accurate circuit reliability assessment. In Proceedings of the 2021 IEEE International Reliability Physics Symposium (IRPS), Monterey, CA, USA, 21–25 March 2021. [Google Scholar]
- Schroder, D.K.; Babcock, J.A. Negative bias temperature instability: Road to cross in deep submicron silicon semiconductor manufacturing. J. Appl. Phys. 2003, 94, 1–18. [Google Scholar] [CrossRef]
- Ullmann, B.; Jech, M.; Tyaginov, S.; Waltl, M.; Lllarionov, Y.Y.; Grill, A.; Puschkarsky, K.; Reisinger, H.; Grasser, T. The impact of mixed negative bias temperature instability and hot carrier stress on single oxide defects. In Proceedings of the 2017 IEEE International Reliability Physics Symposium, Monterey, CA, USA, 2–6 April 2017; pp. XT-10.1–XT-10.6. [Google Scholar]
- Jech, M.; Ullmann, B.; Rzepa, G.; Tyaginov, S.; Grill, A.; Waltl, M.; Jabs, D.; Jungemann, C.; Grasser, T. Impact of mixed negative bias temperature instability and hot carrier stress on MOSFET characteristics—Part II: Theory. IEEE Trans. Elec. Dev. 2019, 66, 241–248. [Google Scholar] [CrossRef]
- Zhou, X.J.; Fleetwood, D.M.; Felix, J.A.; Gusev, E.P.; Emic, D. Bias-temperature instabilities and radiation effects in MOS devices. IEEE Trans. Nucl. Sci. 2006, 52, 2231–2238. [Google Scholar] [CrossRef]
- Zhao, X.; Gan, P.; Zhao, Q.; Liang, D.; Cao, Y.; Pan, X.; Bermak, A. A 124 fj/Bit cascode current mirror array based PUF with 1.50% native unstable bit ratio. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 3494–3503. [Google Scholar] [CrossRef]
- Qin, Z.; Shintani, M.; Kuribara, K.; Ogasahara, Y.; Sato, T. Organic Current Mirror PUF for Improved Stability Against Device Aging. IEEE Sens. J. 2020, 20, 7569–7578. [Google Scholar] [CrossRef]
- Lin, Z.; Fang, Y.; Peng, C.; Lu, W.; Li, X.; Wu, X.; Chen, J. Current mirror based compensation circuit for multi-row read inmemory computing. Electron. Lett. 2019, 55, 1176–1178. [Google Scholar] [CrossRef]
- Maloberti, F. Analog Design for CMOS VLSI Systems; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Sedra, A.S.; Smith, K.C.; Chandokar, A.N. Microelectronic Circuits—Theory and Applications; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Carusone, T.C.; David, A. Analog Integrated Circuit Design; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Ning, T.H. Capture cross section and trap concentration of holes in silicon dioxide. J. Appl. 1976, 47, 1079–1081. [Google Scholar] [CrossRef]
- Amor, S.; André, N.; Kilchytska, V.; Tounsi, F.; Mezghani, B.; Gérard, P.; Ali, Z.; Udrea, F.; Flandre, D.; Francis, L.A. In situ-Thermal Annealing of On-Membrane SOI Semiconducteur-Based Devices After High Gamma Dose irradiation. Nanotechnology 2017, 28, 16. [Google Scholar] [CrossRef]
- Viswanathan, C.R.; Maserjian, J. Model for thickness dependence of radiation charging in MOS structures. IEEE Trans. Nucl. Sci. 1976, 23, 1540–1545. [Google Scholar] [CrossRef]
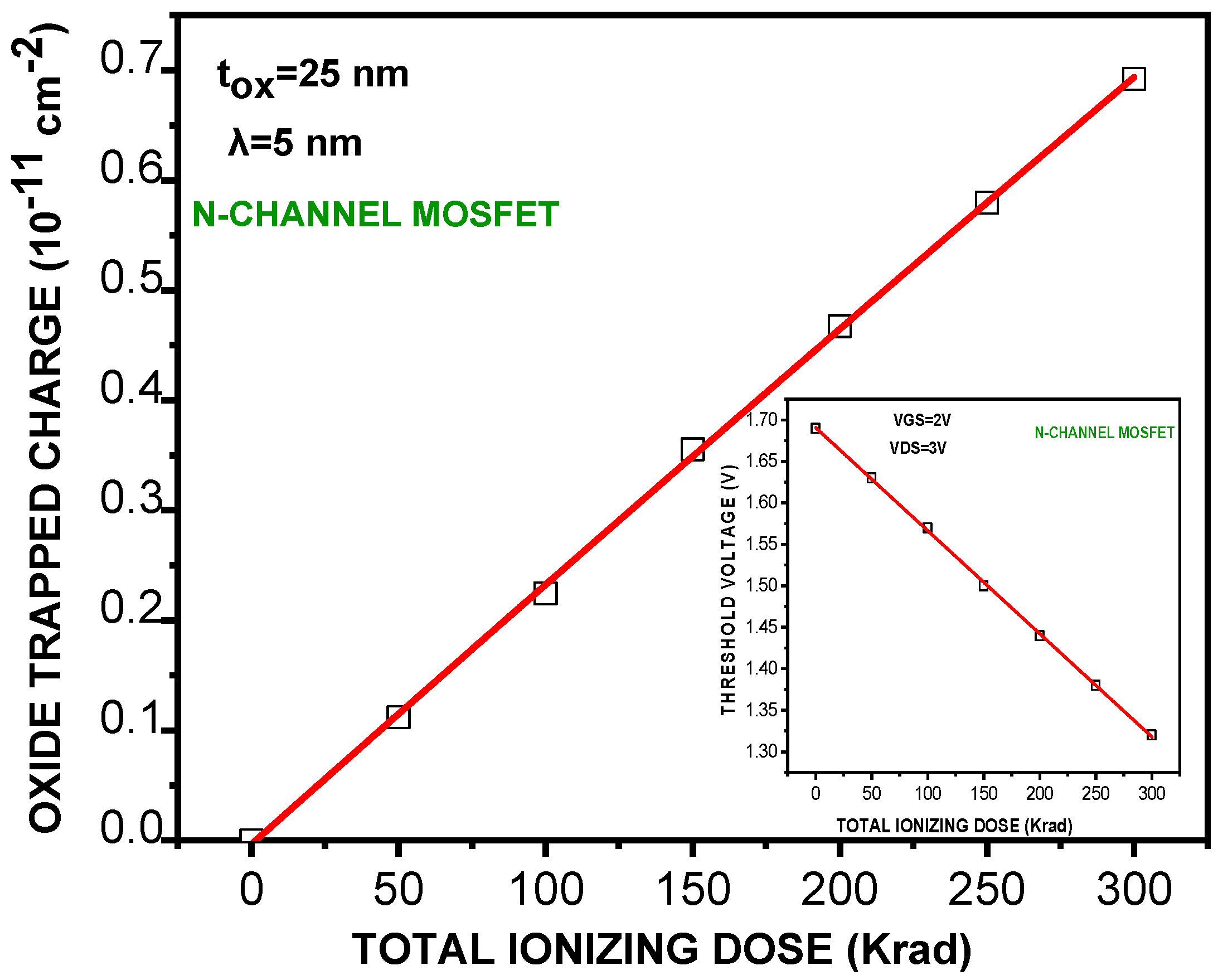




| TID Dose (krad(Si)) | Threshold Voltage Vth (V) | Transconductance gm (µS) |
|---|---|---|
| 0 | 1.69 | 1.099 |
| 50 | 1.63 | 1.16 |
| 100 | 1.57 | 1.24 |
| 150 | 1.50 | 1.28 |
| 200 | 1.44 | 1.32 |
| 250 | 1.38 | 1.38 |
| 300 | 1.32 | 1.40 |
| Study/Reference | Device Type | TID Range (krad(Si)) | Observed ΔVth (V) | Observed gm Change | Notes/Key Findings |
|---|---|---|---|---|---|
| This work | n−MOSFET current mirror, SOI, L = 1 µm, W = 24 µm | 50–300 | −0.37 (1.69 → 1.32) | +27% (1.099 → 1.40 µS) | Charge trapping in oxide, TID−induced degradation of current mirror accuracy |
| Cao et al., 2022 [2] | n−MOSFET | 0–300 | −0.3 approx. | +20% | Combined TID and electrical stress effects studied |
| Gao et al., 2023 [3] | CMOS inverter | 0–150 | −0.15 | +10% | Simulation study of TID effects in inverter circuits |
| Bonaldo, 2022 [4] | GAA Si nanowire CMOS | 0–500 | −0.4 | +25% | Ultra−high TID, highly scaled devices, significant ΔVth observed |
| Dubois et al., 2023 [7] | FDSOI 22 nm | 0–200 | −0.12 | +8% | Modeling TID effects |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguir, D.; Amor, S.; Francis, L.A.; Machhout, M. Charge Trapping Effects on n−MOSFET Current Mirrors Under TID Radiation. Micromachines 2025, 16, 1064. https://doi.org/10.3390/mi16091064
Aguir D, Amor S, Francis LA, Machhout M. Charge Trapping Effects on n−MOSFET Current Mirrors Under TID Radiation. Micromachines. 2025; 16(9):1064. https://doi.org/10.3390/mi16091064
Chicago/Turabian StyleAguir, Dorsaf, Sedki Amor, Laurent A. Francis, and Mohsen Machhout. 2025. "Charge Trapping Effects on n−MOSFET Current Mirrors Under TID Radiation" Micromachines 16, no. 9: 1064. https://doi.org/10.3390/mi16091064
APA StyleAguir, D., Amor, S., Francis, L. A., & Machhout, M. (2025). Charge Trapping Effects on n−MOSFET Current Mirrors Under TID Radiation. Micromachines, 16(9), 1064. https://doi.org/10.3390/mi16091064







