Atomic Insight into the Nano-Grinding Mechanism of Reaction-Bonded Silicon Carbide: Effect of Abrasive Size
Abstract
1. Introduction
2. Methodology
3. Results and Discussion
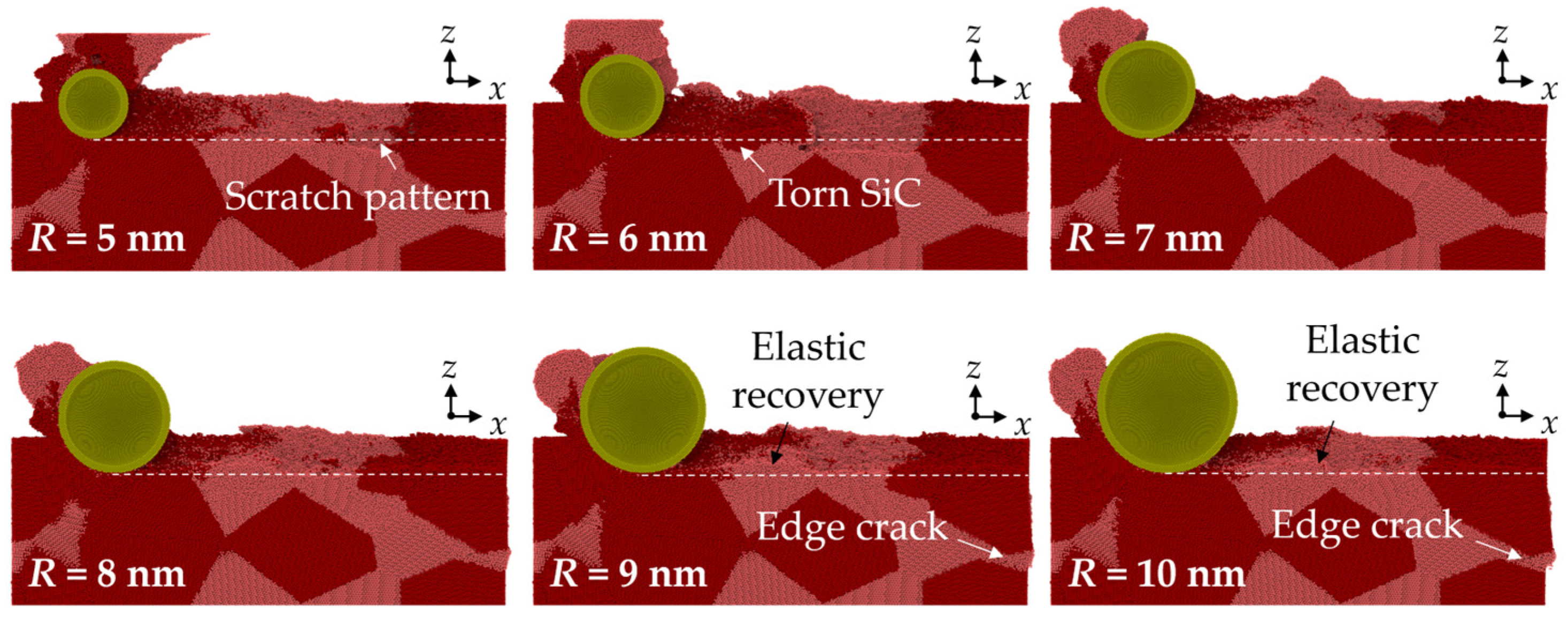
3.1. Surface Morphology
3.2. Deformation Behavior
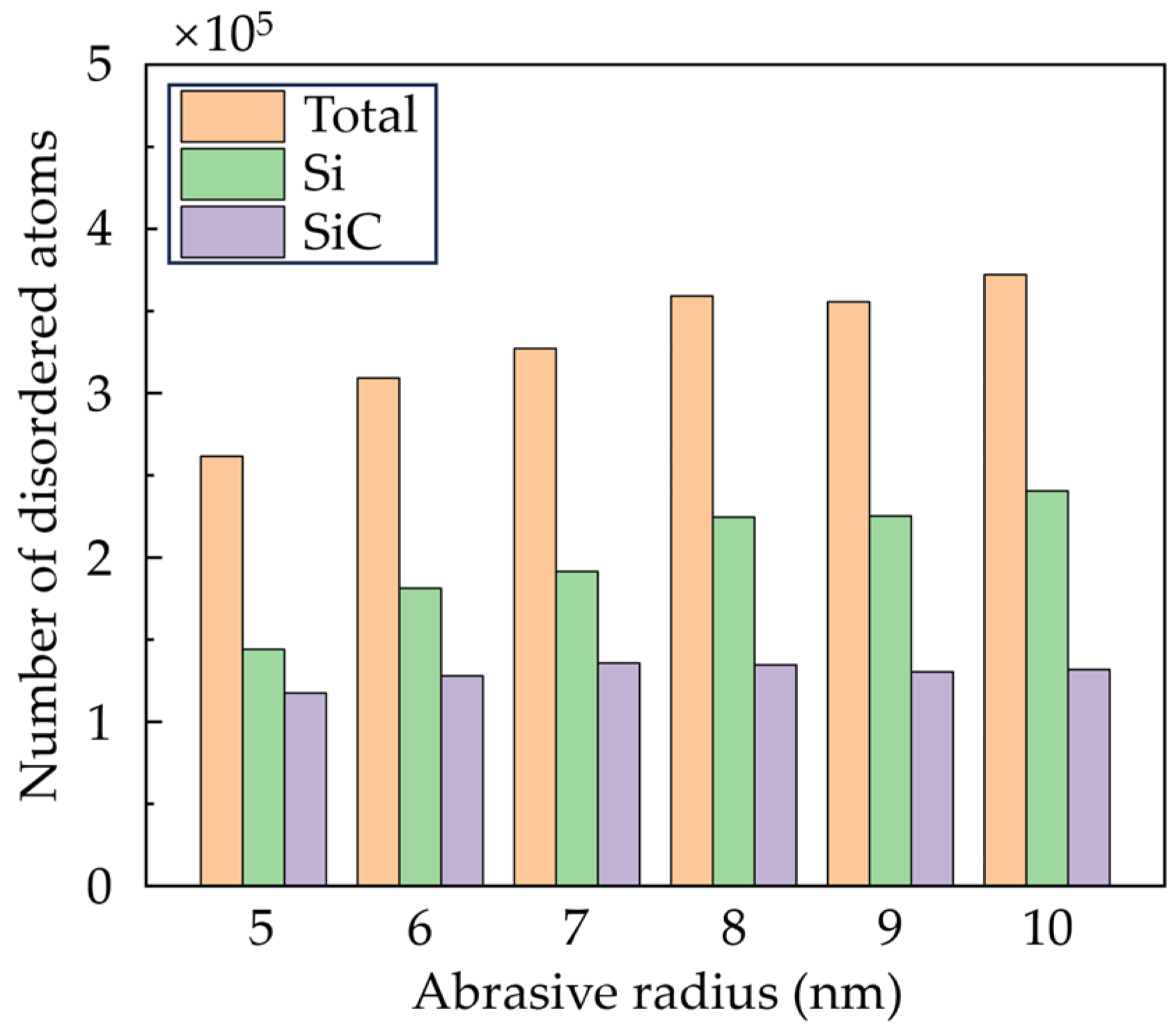
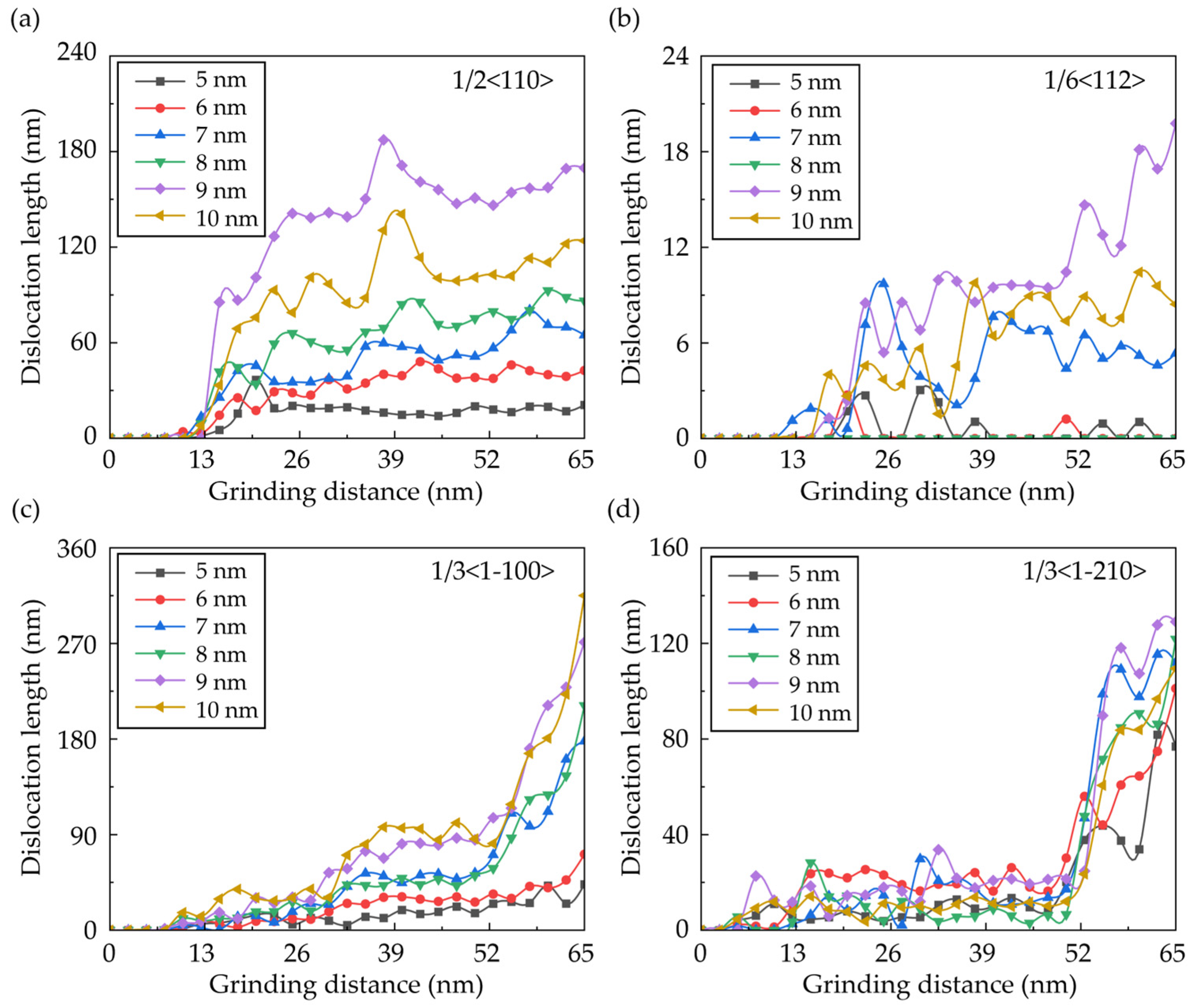
3.3. Dislocation Analysis
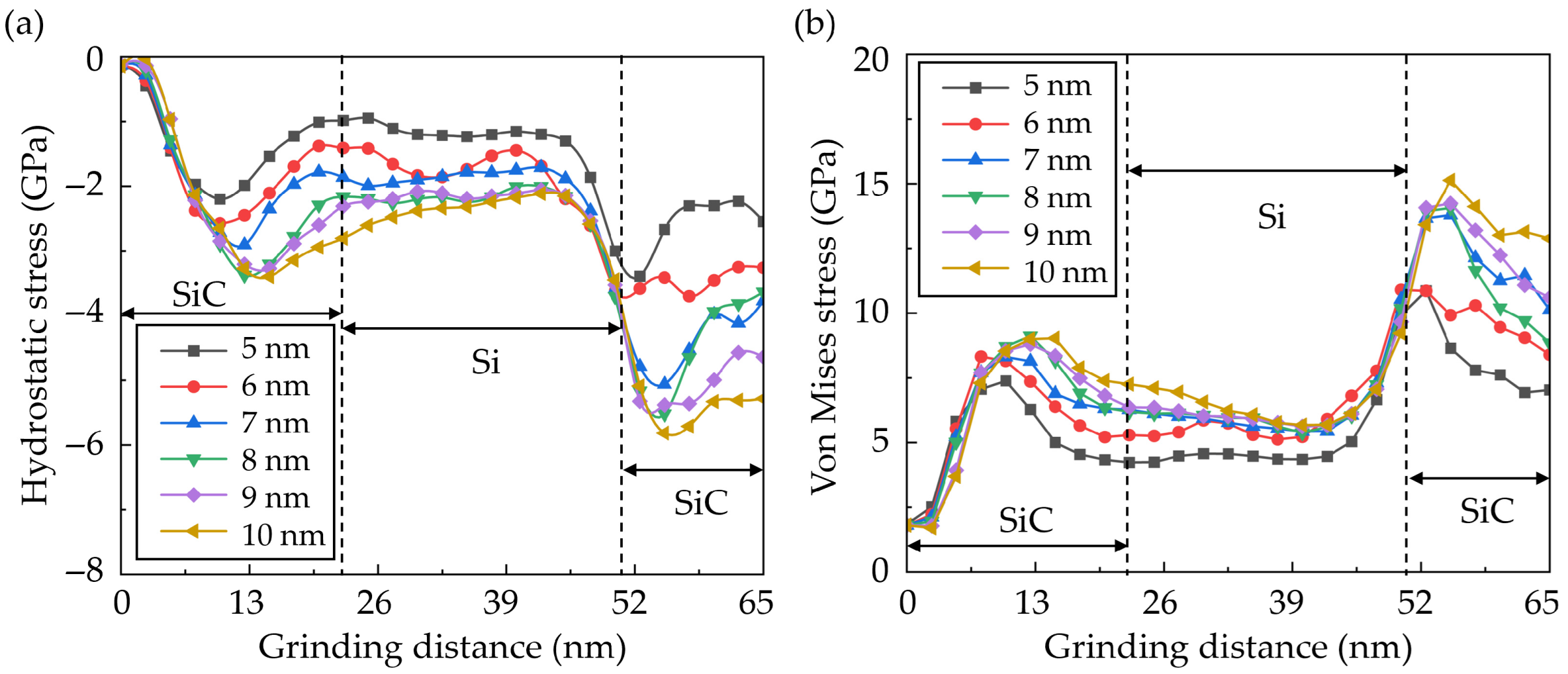
3.4. Internal Stress
4. Conclusions
- When small abrasives are used, surface swelling of SiC is observed due to the bending and tearing of SiC at the interfaces. As the abrasive radius increases, the surface swelling is mainly formed by Si atoms, which is mainly identified as elastic recovery. The surface roughness shows an increasing trend as the abrasive size increases, indicating the significance of elastic recovery on the overall surface roughness.
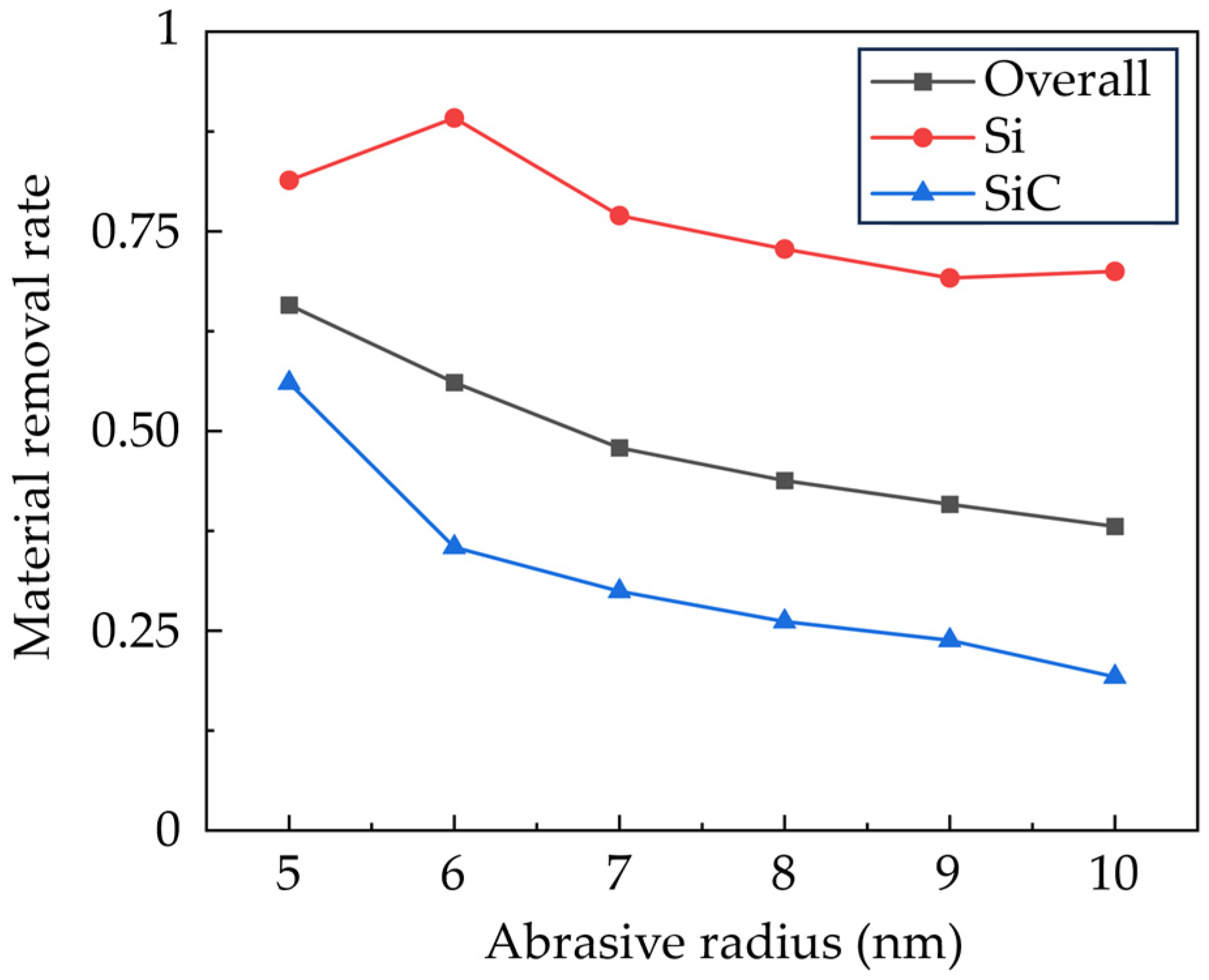
- During nano-grinding, Si has a higher material removal rate than SiC. As the abrasive size increases, the material removal rate gradually decreases, and the depth of plastic deformation is obviously increased. Stocking of Si is more apparent at the interface, and more plastic deformation patterns are observed inside the SiC grains. Furthermore, an obvious sliding of the grains is observed, forming edge cracks at the margin of the workpiece.
- In the subsurface workpiece, the disordered Si atoms can be stocked and squeezed into the phase boundaries. When large abrasives are used, the HPPT of Si is promoted, and the squeeze of the disordered Si becomes more obvious. More disordered Si atoms are generated, while variation in the disordered SiC atoms is slight.
- As the abrasive size increases, compression of the workpiece material is significantly enhanced, and more dislocations are formed in the subsurface of the workpiece. The bending of SiC becomes more apparent with an obvious increase in von Mises stress when machining from SiC to Si. Meanwhile, the von Mises stress can be increased by the enhanced extrusion of Si as the abrasive moves from Si to SiC.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Hu, H.; Wang, X.; Luo, X.; Zhang, G.; Zhao, W.; Wang, X.; Liu, Z.; Xiong, L.; Qi, E.; et al. Challenges and strategies in high-accuracy manufacturing of the world’s largest SiC aspheric mirror. Light Sci. Appl. 2022, 11, 310. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Cheung, C.F.; Zang, Y.; Wang, C.; Liu, C. Material removal rate optimization with bayesian optimized differential evolution based on deep learning in robotic polishing. J. Manuf. Syst. 2025, 78, 178–186. [Google Scholar] [CrossRef]
- Wang, H.; Dong, Z.; Kang, R.; Gao, S. Surface characteristics and material removal mechanisms during nano-grinding on C-face and Si-face of 4H-SiC crystals: Experimental and molecular dynamics insights. Appl. Surf. Sci. 2024, 665, 160293. [Google Scholar] [CrossRef]
- Liu, C.; Chu, J.; Zhang, J.; Zhang, J.; Chen, X.; Xiao, J.; Xu, J. Effect of tool rake angle on the material removal mechanism transition of single-crystal silicon: A molecular dynamics study. Int. J. Adv. Manuf. Technol. 2021, 115, 3631–3644. [Google Scholar] [CrossRef]
- Liu, C.; Chen, X.; Ke, J.; She, Z.; Zhang, J.; Xiao, J.; Xu, J. Numerical investigation on subsurface damage in nanometric cutting of single-crystal silicon at elevated temperatures. J. Manuf. Process. 2021, 68, 1060–1071. [Google Scholar] [CrossRef]
- Chavoshi, S.Z.; Xu, S.; Luo, X. Dislocation-mediated plasticity in silicon during nanometric cutting: A molecular dynamics simulation study. Mater. Sci. Semicond. Process. 2016, 51, 60–70. [Google Scholar] [CrossRef]
- Liu, C.; Xu, W.; Zhang, J.; Xiao, J.; Chen, X.; Xu, J. Numerical investigation on the temperature effect in nanometric cutting of polycrystalline silicon. Int. J. Mech. Sci. 2022, 220, 107172. [Google Scholar] [CrossRef]
- Geng, R.; Yang, X.; Xie, Q.; Zhang, R.; Zhang, W.; Qiu, H.; Mu, R.; Yang, W.; Li, R. Investigation of surface integrity and material removal mechanism of single-crystal Si subjected to micro-laser-assisted machining. Infrared Phys. Technol. 2021, 118, 103868. [Google Scholar] [CrossRef]
- Liu, C.; Chen, X.; Zhang, J.; Zhang, J.; Chu, J.; Xiao, J.; Xu, J. Molecular dynamic simulation of tool groove wear in nanoscale cutting of silicon. AIP Adv. 2020, 10, 015327. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Fang, F.; Chen, R. A numerical study on the material removal and phase transformation in the nanometric cutting of silicon. Appl. Surf. Sci. 2018, 455, 608–615. [Google Scholar] [CrossRef]
- Meng, B.; Yuan, D.; Xu, S. Study on strain rate and heat effect on the removal mechanism of SiC during nano-scratching process by molecular dynamics simulation. Int. J. Mech. Sci. 2019, 151, 724–732. [Google Scholar] [CrossRef]
- Sahoo, S.; Mannan, S.; Tiwari, U.; Kaware, R.R.; Ye, Z.; Gosvami, N.N.; Krishnan, N.M.A. Atomistic insights into scratch-induced structural evolution of silica glass. Acta Mater. 2025, 282, 120459. [Google Scholar] [CrossRef]
- Bhamra, J.S.; Ewen, J.P.; Ayestarán Latorre, C.; Bomidi, J.A.R.; Bird, M.W.; Dini, D. Atomic-scale insights into the tribochemical wear of diamond on quartz surfaces. Appl. Surf. Sci. 2023, 639, 158152. [Google Scholar] [CrossRef]
- Pradhan, T.; Pal, S.; Deng, C. Investigation on wear-resistance of nanocrystalline Pt-Au by molecular dynamics simulations. Tribol. Int. 2023, 189, 108966. [Google Scholar] [CrossRef]
- Goel, S.; Kovalchenko, A.; Stukowski, A.; Cross, G. Influence of microstructure on the cutting behaviour of silicon. Acta Mater. 2016, 105, 464–478. [Google Scholar] [CrossRef]
- Liu, Y.; Li, B.; Kong, L. Molecular dynamics simulation of silicon carbide nanoscale material removal behavior. Ceram. Int. 2018, 44, 11910–11913. [Google Scholar] [CrossRef]
- Meng, B.; Qiu, P.; Yuan, D.; Xu, S. Influence of microstructure on the diamond-machinability of hot-pressed silicon carbide: A molecular dynamics study. Ceram. Int. 2019, 45, 22872–22879. [Google Scholar] [CrossRef]
- Liu, C.; Ke, J.; Yin, T.; Yip, W.S.; Zhang, J.; To, S.; Xu, J. Cutting mechanism of reaction-bonded silicon carbide in laser-assisted ultra-precision machining. Int. J. Mach. Tools Manuf. 2024, 203, 104219. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, J.; Zhang, J.; Chu, J.; Chen, X.; Xiao, J.; Xu, J. Numerical investigation on material removal mechanism in elliptical vibration cutting of single-crystal silicon. Mater. Sci. Semicond. Process. 2021, 134, 106019. [Google Scholar] [CrossRef]
- Ameli Kalkhoran, S.N.; Vahdati, M.; Yan, J. Effect of relative tool sharpness on subsurface damage and material recovery in nanometric cutting of mono-crystalline silicon: A molecular dynamics approach. Mater. Sci. Semicond. Process. 2020, 108, 104868. [Google Scholar] [CrossRef]
- Voronoi, G. Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs. J. Für Die Reine Und Angew. Math. (Crelles J.) 1908, 134, 198–287. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Goel, S.; Luo, X.; Agrawal, A.; Reuben, R.L. Diamond machining of silicon: A review of advances in molecular dynamics simulation. Int. J. Mach. Tools Manuf. 2015, 88, 131–164. [Google Scholar] [CrossRef]
- Erhart, P.; Albe, K. Analytical potential for atomistic simulations of silicon, carbon, and silicon carbide. Phys. Rev. B 2005, 71, 035211. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, J.; Zhang, J.; Chen, X.; Xiao, J.; Xu, J. A simulation investigation on elliptical vibration cutting of single-crystal silicon. Int. J. Adv. Manuf. Technol. 2020, 108, 2231–2243. [Google Scholar] [CrossRef]
- Liu, C.; He, W.; Chu, J.; Zhang, J.; Chen, X.; Xiao, J.; Xu, J. Molecular Dynamics Simulation on Cutting Mechanism in the Hybrid Machining Process of Single-Crystal Silicon. Nanoscale Res. Lett. 2021, 16, 66. [Google Scholar] [CrossRef]
- Chavoshi, S.Z.; Luo, X. Molecular dynamics simulation study of deformation mechanisms in 3C–SiC during nanometric cutting at elevated temperatures. Mater. Sci. Eng. A 2016, 654, 400–417. [Google Scholar] [CrossRef]
- Chavoshi, S.Z.; Goel, S.; Luo, X. Influence of temperature on the anisotropic cutting behaviour of single crystal silicon: A molecular dynamics simulation investigation. J. Manuf. Process. 2016, 23, 201–210. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Chen, J.; Liu, C.; Liu, H.; Zhang, B.; To, S. Atomic insight into the speed effect on deformation mechanisms in nano-scratching of monocrystalline iron. Precis. Eng. 2024, 92, 219–230. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, J.; Zhang, J.; Chen, X.; He, W.; Xiao, J.; Xu, J. Influence of micro grooves of diamond tool on silicon cutting: A molecular dynamic study. Mol. Simul. 2020, 46, 92–101. [Google Scholar] [CrossRef]
- Chen, X.; Chu, J.; Zhu, Z.; Liu, C. Effect of temperature on surface morphology of single-crystal silicon in nanometric cutting. Appl. Surf. Sci. 2025, 684, 161957. [Google Scholar] [CrossRef]
- Maras, E.; Trushin, O.; Stukowski, A.; Ala-Nissila, T.; Jónsson, H. Global transition path search for dislocation formation in Ge on Si(001). Comput. Phys. Commun. 2016, 205, 13–21. [Google Scholar] [CrossRef]
- Dai, H.; Zhou, Y.; Zhang, F. Atomistic simulation of influence of laser nano-structured diamond abrasive on the polishing behavior of silicon. Mater. Sci. Semicond. Process. 2020, 105, 104706. [Google Scholar] [CrossRef]
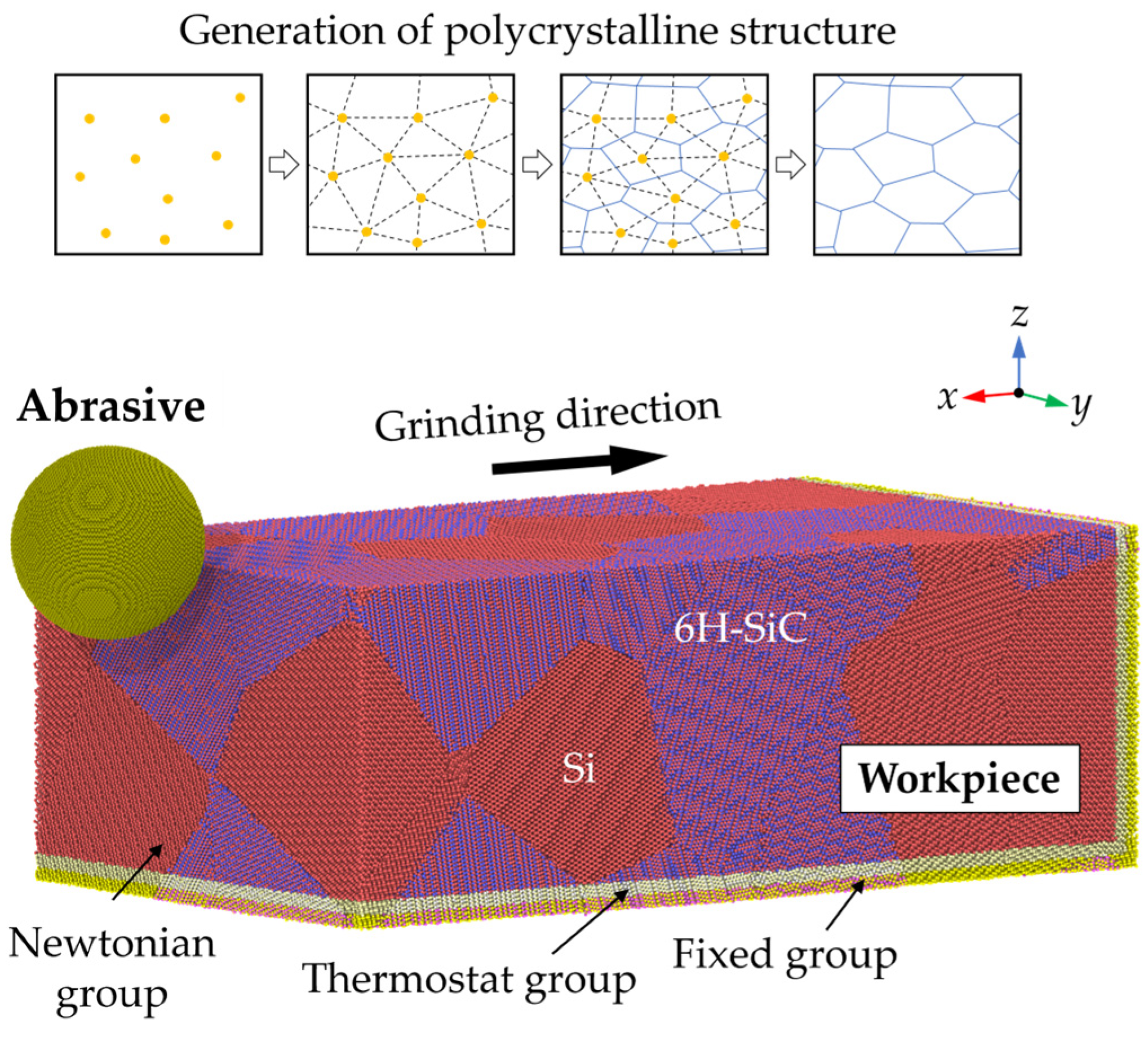



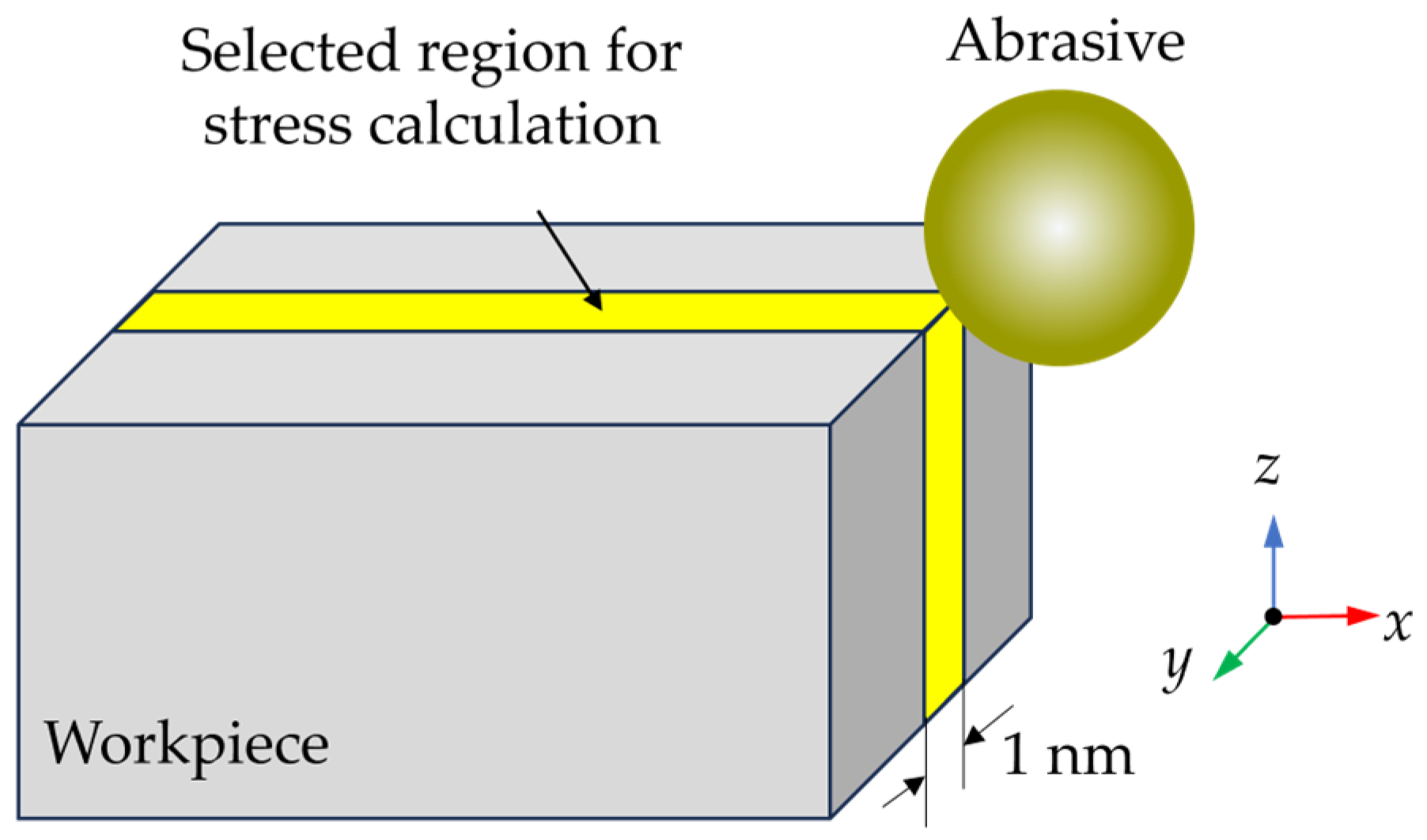
| Si | C | |
|---|---|---|
| D0 (eV) | 3.24 | 6.00 |
| r0 (Å) | 2.232 | 1.4276 |
| S | 1.842 | 2.167 |
| β (Å−1) | 1.4761 | 2.0099 |
| R (Å) | 2.82 | 2.00 |
| D (Å) | 0.14 | 0.15 |
| γ | 0.114354 | 0.11233 |
| c | 2.00494 | 181.910 |
| d | 0.81472 | 6.28433 |
| h | 0.259 | 0.5556 |
| 2μ (Å−1) | 0.0 | 0.0 |
| Parameters | Value |
|---|---|
| Workpiece dimension (x × y × z) | 70 nm × 40 nm × 25 nm |
| Number of workpiece atoms | About 5 million |
| Abrasive radius (R) | 5 nm, 6 nm, 7 nm, 8 nm, 9 nm, 10 nm |
| Grinding speed | 50 m/s |
| Grinding depth | 5 nm |
| Grinding distance | 65 nm |
| Grinding temperature | 300 K |
| Number of grains in workpiece | 20 (10 Si grains and 10 SiC grains) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, H.; Chen, X.; Luo, C.; Cai, X. Atomic Insight into the Nano-Grinding Mechanism of Reaction-Bonded Silicon Carbide: Effect of Abrasive Size. Micromachines 2025, 16, 1049. https://doi.org/10.3390/mi16091049
Mo H, Chen X, Luo C, Cai X. Atomic Insight into the Nano-Grinding Mechanism of Reaction-Bonded Silicon Carbide: Effect of Abrasive Size. Micromachines. 2025; 16(9):1049. https://doi.org/10.3390/mi16091049
Chicago/Turabian StyleMo, Honglei, Xie Chen, Cui Luo, and Xiaojiang Cai. 2025. "Atomic Insight into the Nano-Grinding Mechanism of Reaction-Bonded Silicon Carbide: Effect of Abrasive Size" Micromachines 16, no. 9: 1049. https://doi.org/10.3390/mi16091049
APA StyleMo, H., Chen, X., Luo, C., & Cai, X. (2025). Atomic Insight into the Nano-Grinding Mechanism of Reaction-Bonded Silicon Carbide: Effect of Abrasive Size. Micromachines, 16(9), 1049. https://doi.org/10.3390/mi16091049





