Morph and Function: Exploring Origami-Inspired Structures in Versatile Robotics Systems
Abstract
1. Introduction
1.1. The History of Origami
1.2. From Classic Origami to Engineering Applications
1.3. Significant Contributions of Origami-Inspired Structures in Robotics
2. Fundamental and Theoretical Background
2.1. Fundamentals of Origami
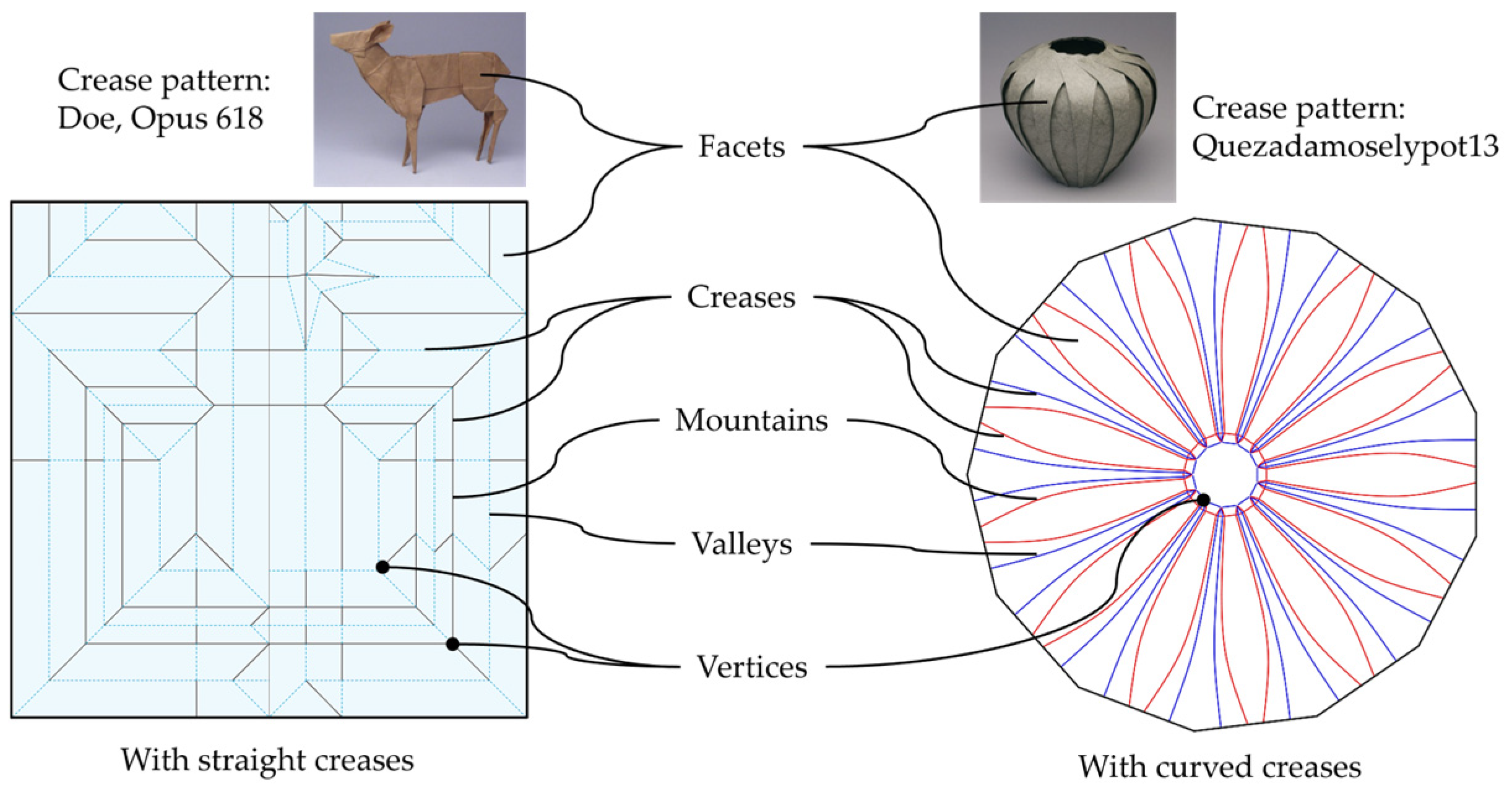
2.1.1. Anatomy of Origami
2.1.2. Crease Pattern Rules
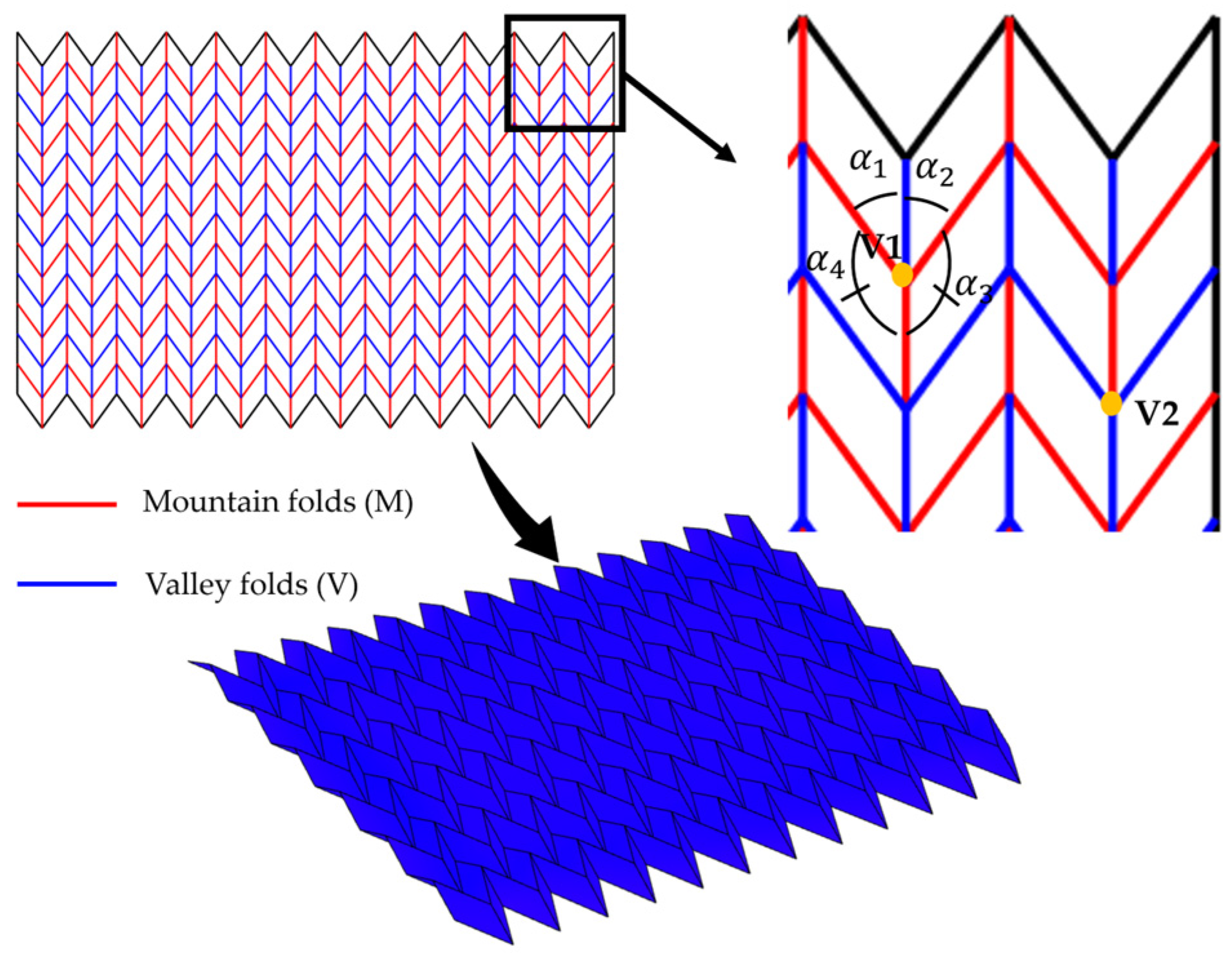
2.1.3. Mechanism of Folds
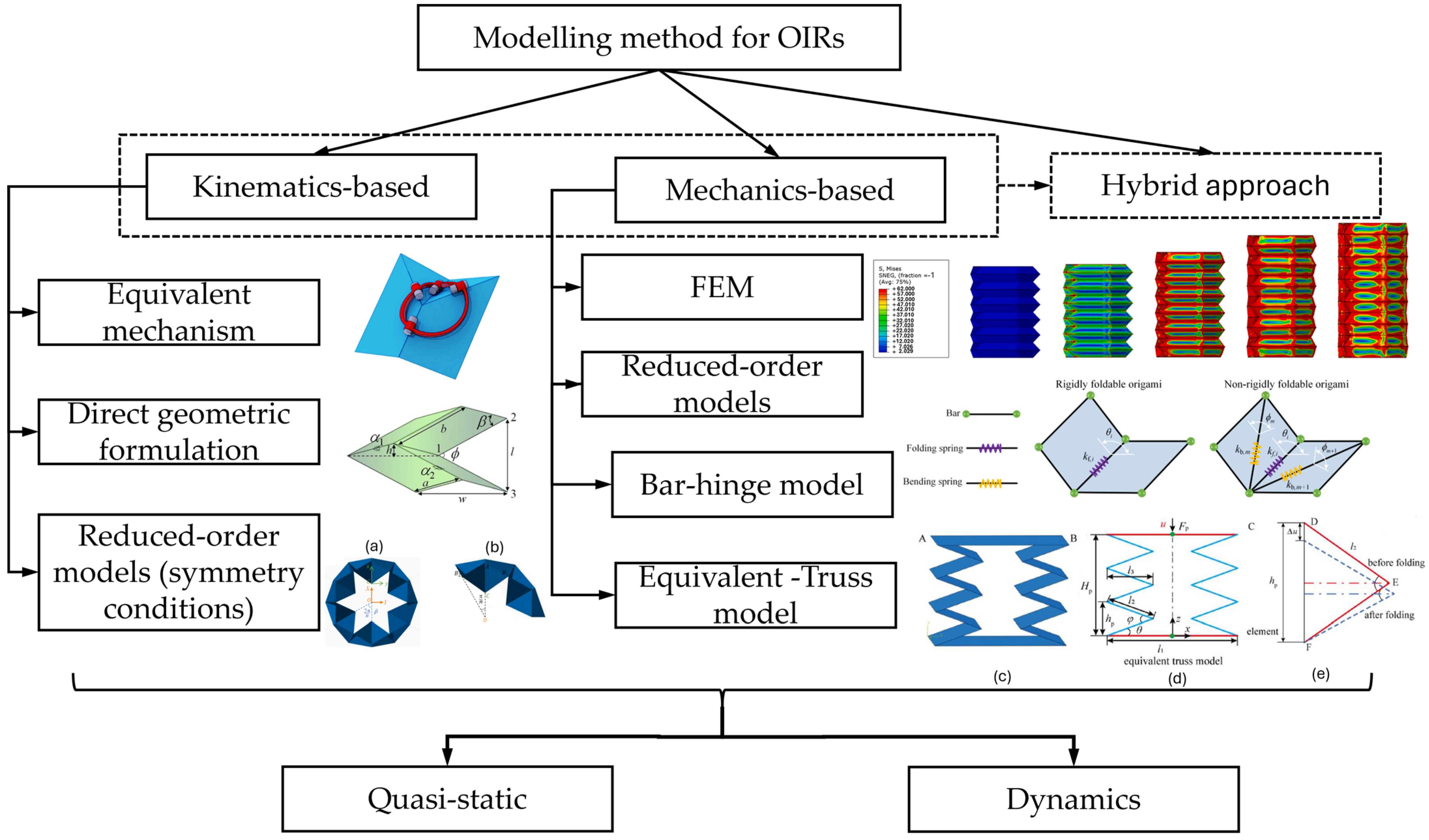
2.2. Design Methods and Tools
2.2.1. Kinematics-Based Methods
2.2.2. Mechanics-Based Methods
2.2.3. Hybrid Approaches
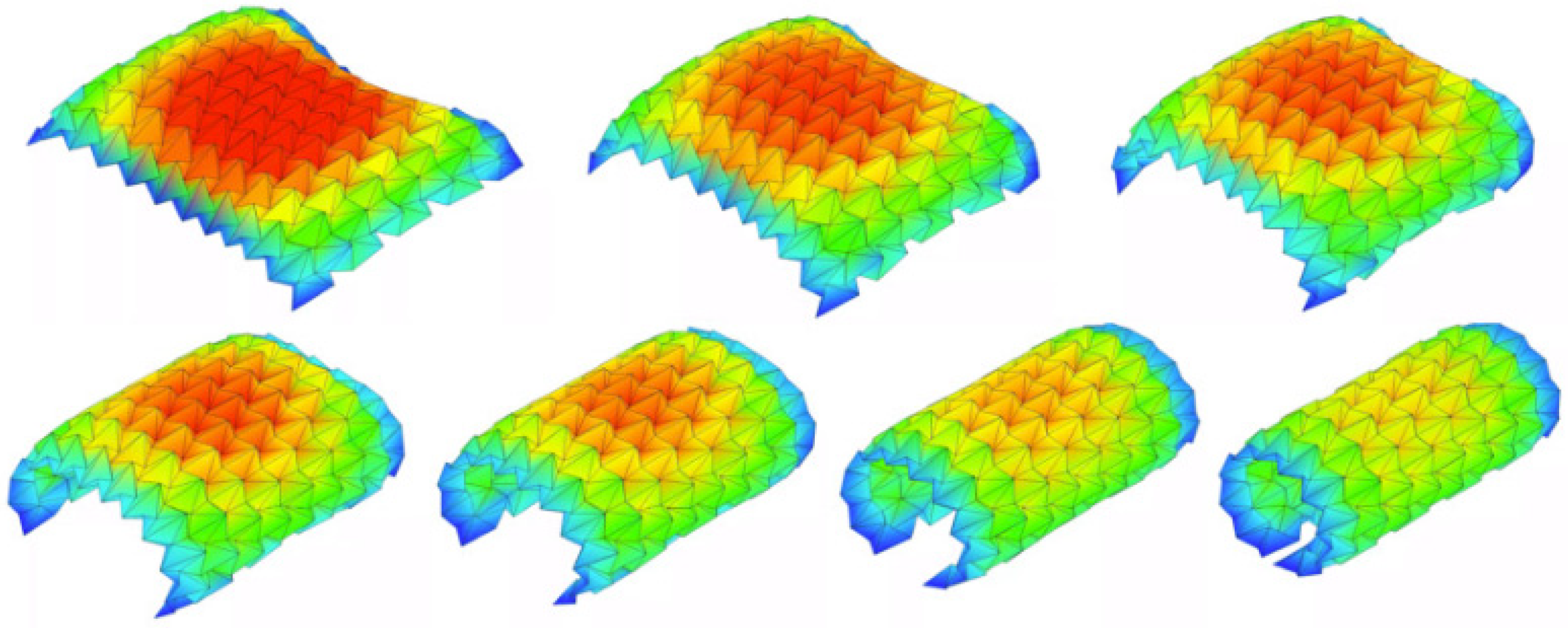
2.2.4. Quasi-Static and Dynamic Modelling Approaches
2.2.5. Tools for Origami Designs
3. Design of Origami-Inspired Robot (OIR)
3.1. Design Methodologies
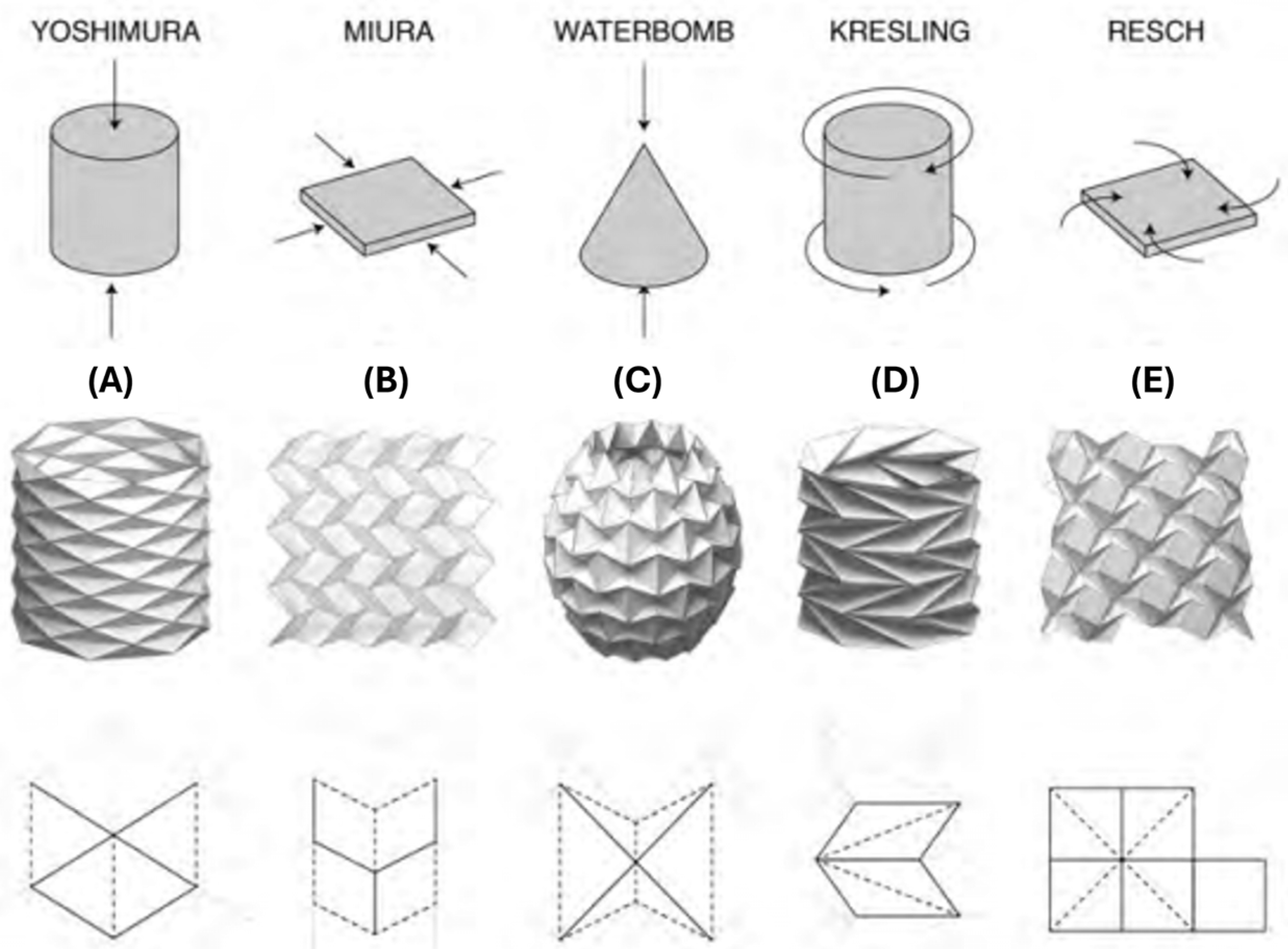
3.1.1. Traditional Tessellation Patterns
3.1.2. Single-Vertex Patterns
3.1.3. Modular Unit Cells Design
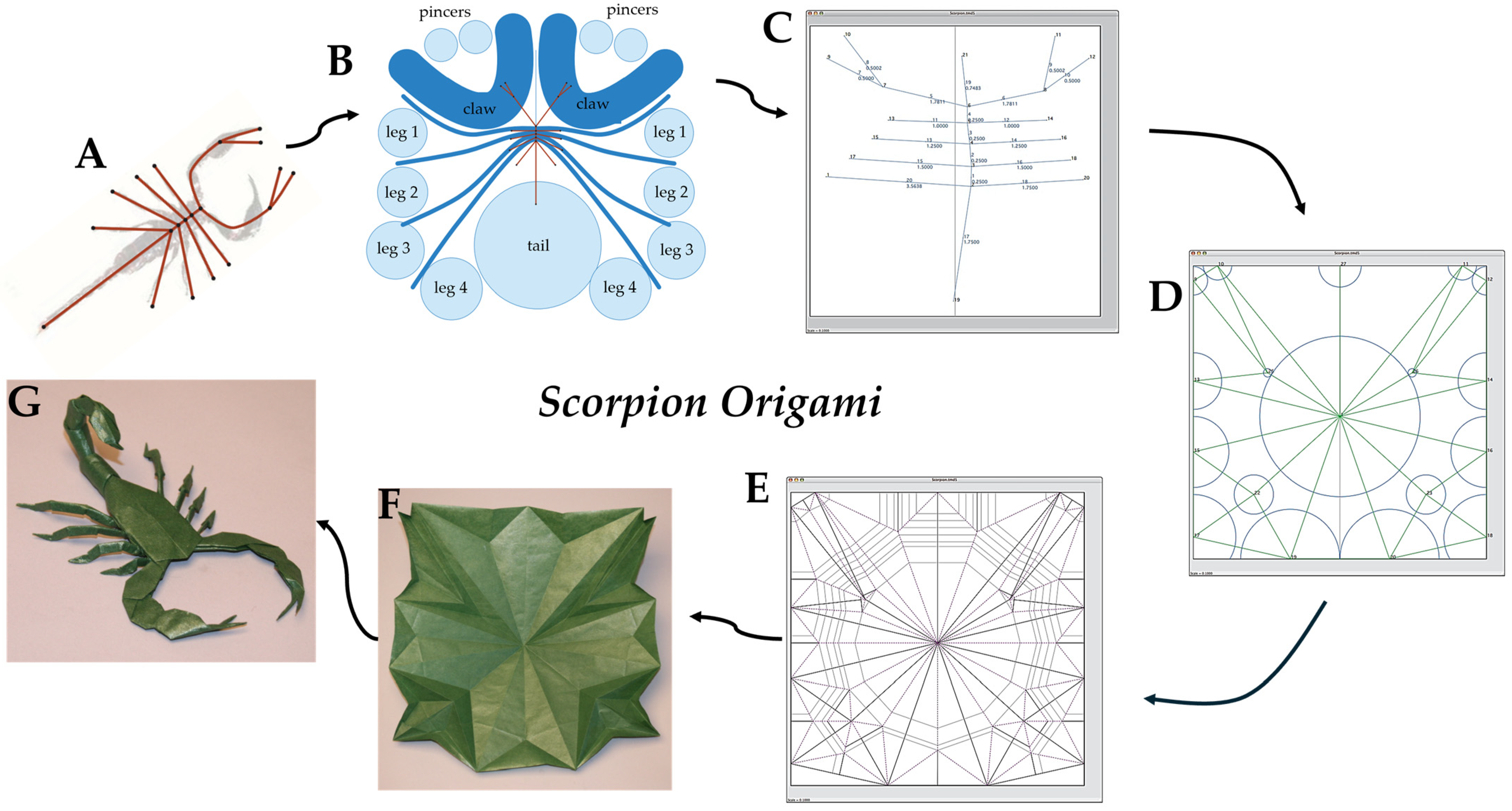
3.1.4. Custom Crease Design
3.2. Designs Toward Applications
3.2.1. Morphological Capability
3.2.2. Multi-Degree-of-Freedom (DOF) Motion
3.2.3. Mechanical Compliance
3.2.4. Simplified Deployment
4. Fabrication Techniques for Origami-Inspired Robotics
4.1. Materials Selection
4.2. Fabrication and Folding Methods
4.3. Advanced Manufacturing Techniques
5. Actuation and Control Strategies
5.1. Mechanical Actuation
5.1.1. Motors
5.1.2. Tendon/Cable-Driven
5.1.3. Bistable Snap Mechanism
5.2. Fluidic Actuation
5.2.1. Pneumatics
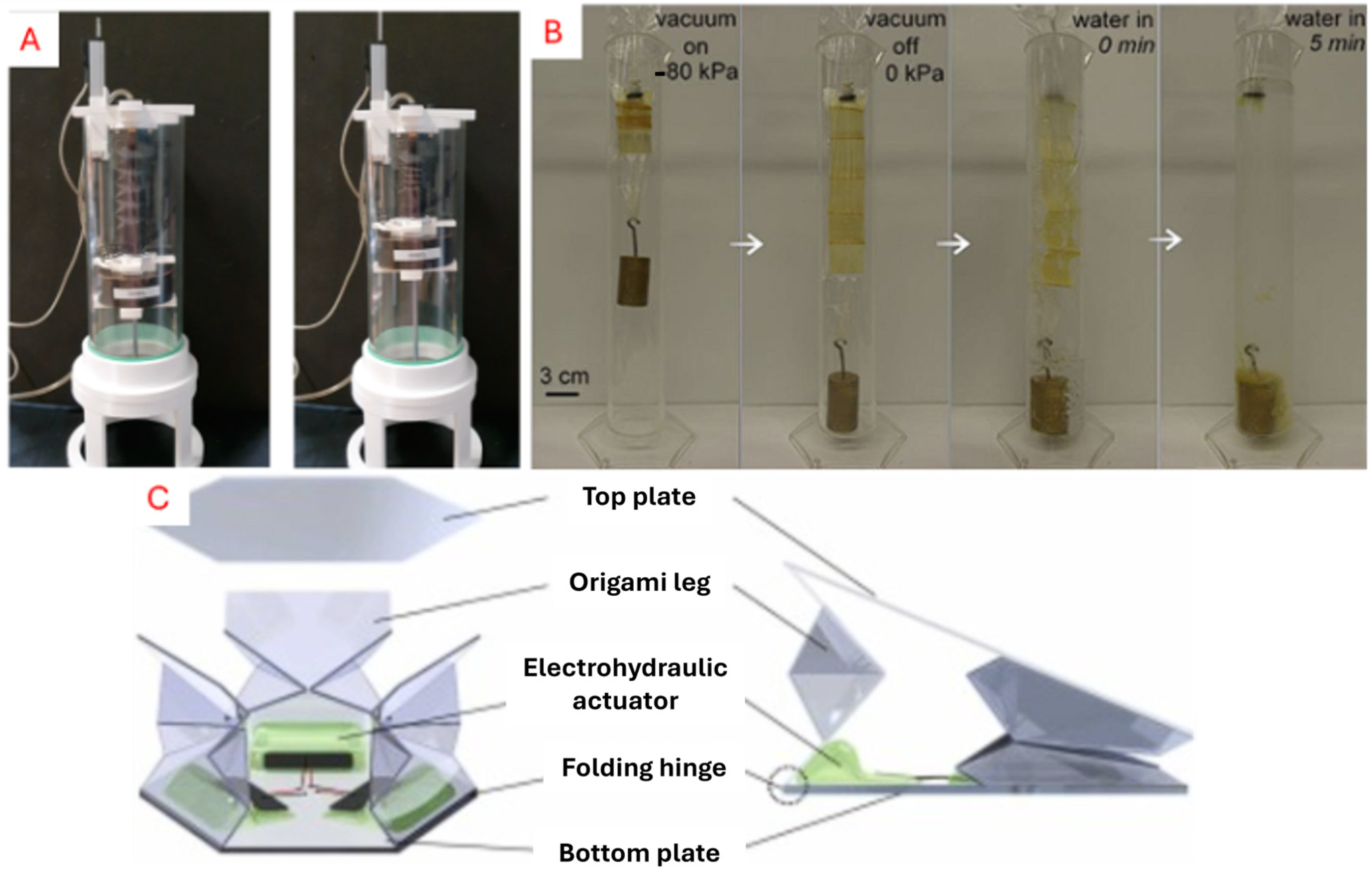
5.2.2. Hydraulics
5.3. Embedded Actuation
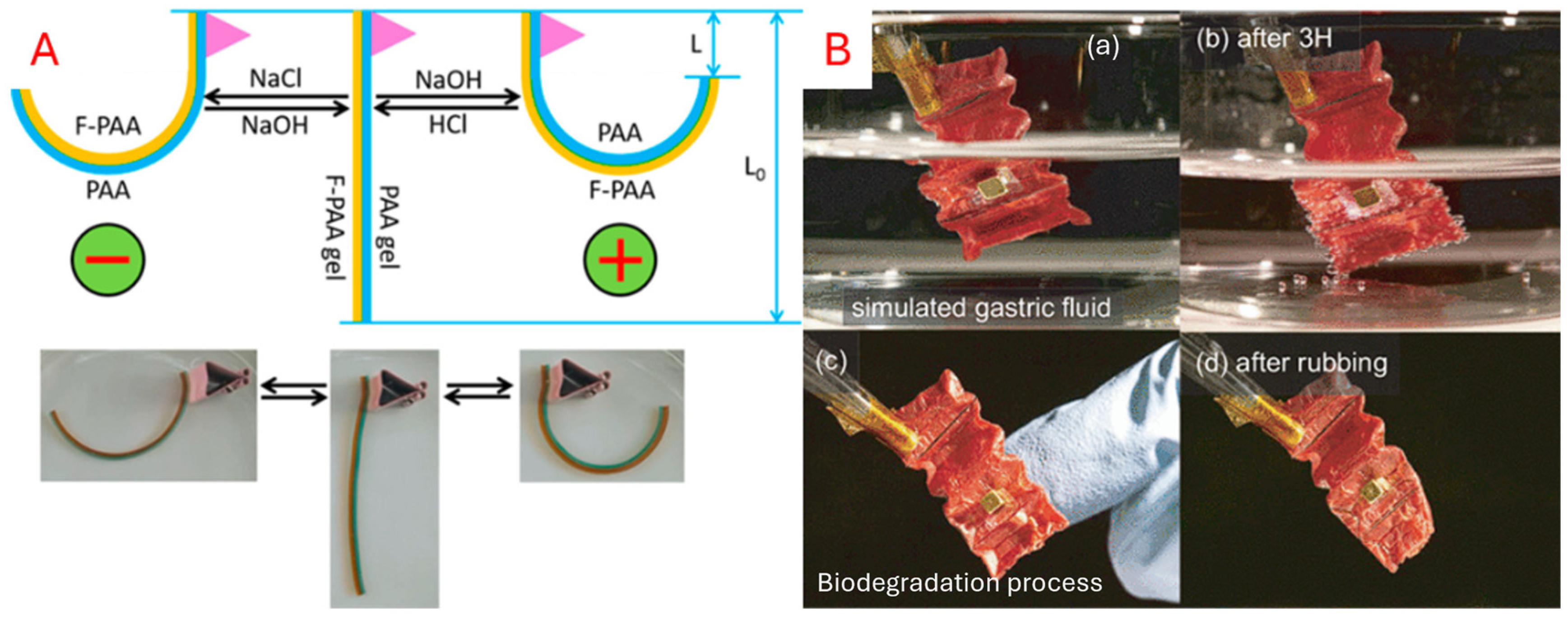
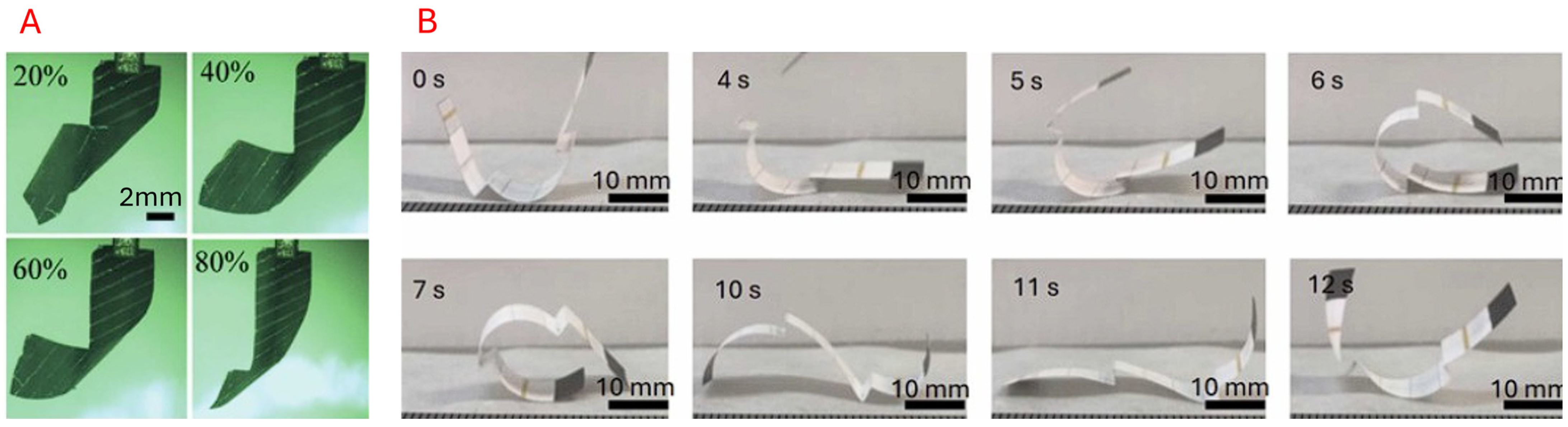
5.3.1. Chemoresponsive
5.3.2. Photoresponsive
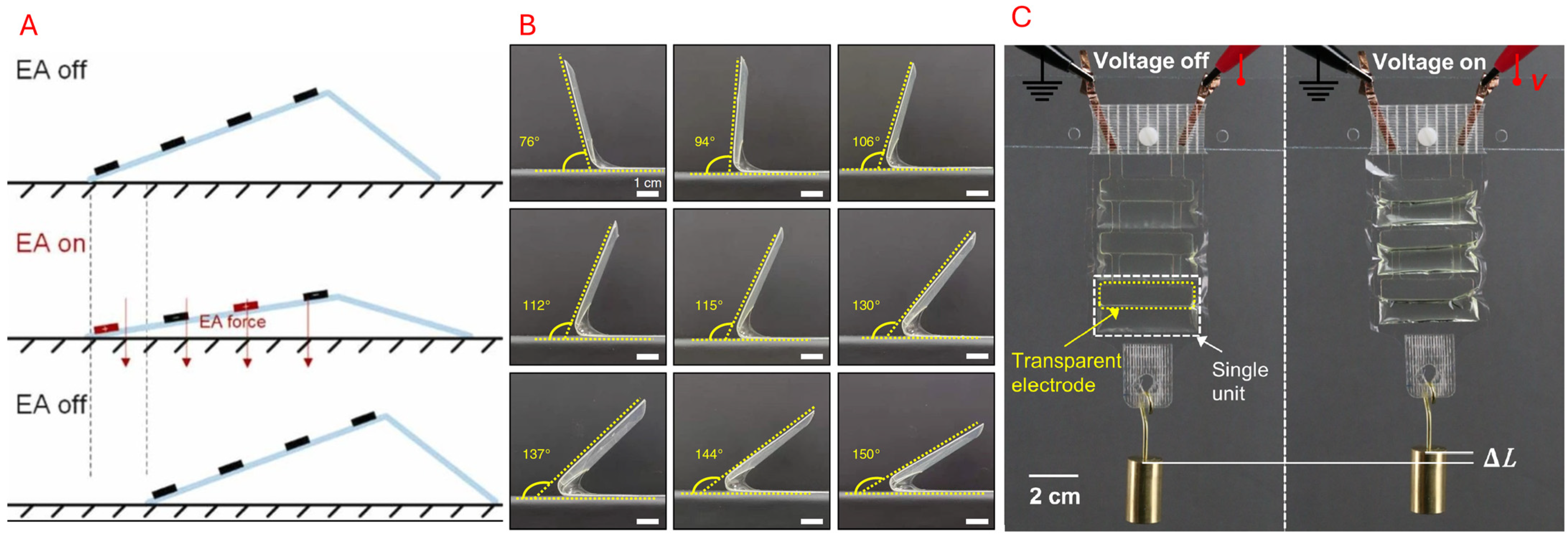
5.3.3. Electroresponsive
5.3.4. Magnetoresponsive
5.3.5. Thermoresponsive
5.3.6. Humidity-Responsive
6. Application of Origami-Inspired Robots
6.1. Small-Scale
6.2. Medium-Scale
6.3. Large-Scale
7. Challenges and Outlooks
7.1. Reliability and Robustness
7.2. Complexity in Modelling and Analysis
7.3. Integration with Emerging Technologies and Control Strategies
7.4. Artificial Intelligence (AI) Tools in OIRs
7.5. Transition from Lab Prototyping to Real-World Applications
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AM | Additive Manufacturing |
| CFRP | Carbon Fibre Reinforced Polymer |
| DOF | Degree of freedom |
| FDM | Fused Deposition Modelling |
| FEM | Finite Element Method |
| MEMS | Micro-Electro-Mechanical Systems |
| OIR | Origami-Inspired Robot |
| OMS | Origami Multiplexed Switch |
| PET | Polyethylene terephthalate |
| PLA | Polylactic Acid |
| PPy | Polypyrrole |
| TPU | Thermoplastic polyurethane |
References
- Hull, T. Origami. In Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures; Springer: Dordrecht, The Netherlands, 2008; pp. 1797–1800. [Google Scholar]
- Akira, Y.; Kiyo, Y.; Robert, J.L. Akira Yoshizawa, Japan’s Greatest Origami Master: Featuring over 60 Models and 1000 Diagrams by the Master; Tuttle Publishing: North Clarendon, VT, USA, 2016. [Google Scholar]
- Ben-Ari, M. The Axioms of Origami. In Mathematical Surprises; Springer International Publishing: Cham, Switzerland, 2022; pp. 113–130. [Google Scholar]
- Demaine, E.D.; O’Rourke, J. Geometric Folding Algorithms; Cambridge University Press (CUP): Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Koryo, M. The Application of Origami Science to Map and Atlas Design. In Origami 3; Hull, T., Ed.; A K Peters/CRC Press: Boca Raton, FL, USA, 2002; pp. 137–146. [Google Scholar]
- Lang, R.J. A computational algorithm for origami design. In Proceedings of the Twelfth Annual Symposium on Computational Geometry–SCG’96, Philadelphia, PA, USA, 24–26 May 1996; pp. 98–105. [Google Scholar] [CrossRef]
- Tachi, T. Freeform Origami Software. 2010. Available online: https://origami.c.u-tokyo.ac.jp/~tachi/software/ (accessed on 15 July 2025).
- Tachi, T. Rigid-Foldable Thick Origami. In Origami 5; A K Peters/CRC Press: Boca Raton, FL, USA, 2011; pp. 253–263. [Google Scholar]
- Rus, D.; Sung, C. Spotlight on origami robots. Sci. Robot. 2018, 3, eaat0938. [Google Scholar] [CrossRef]
- Misseroni, D.; Pratapa, P.P.; Liu, K.; Kresling, B.; Chen, Y.; Daraio, C.; Paulino, G.H. Origami engineering. Nat. Rev. Methods Primers 2024, 4, 40. [Google Scholar] [CrossRef]
- Ahmed, A.R.; Gauntlett, O.C.; Camci-Unal, G. Origami-Inspired Approaches for Biomedical Applications. ACS Omega 2021, 6, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Jian, B.; Jin, L.; Wang, R.; Ge, Q. Origami Robots: Design, Actuation, and 3D Printing Methods. Adv. Mater. Technol. 2025, 10, e00278. [Google Scholar] [CrossRef]
- Xiang, X.; Lu, G.; You, Z. Energy absorption of origami inspired structures and materials. Thin-Walled Struct. 2020, 157, 107130. [Google Scholar] [CrossRef]
- Hussain, K.F.; Cantwell, W.J.; Khan, K.A. Review of Recent Advances in Origami-Inspired Structures for Enhanced Energy Absorption: Trends and Engineering Applications. Arab. J. Sci. Eng. 2025. [Google Scholar] [CrossRef]
- Yue, S. A Review of Origami-Based Deployable Structures in Aerospace Engineering. J. Phys. Conf. Ser. 2023, 2459, 012137. [Google Scholar] [CrossRef]
- Meloni, M.; Cai, J.; Zhang, Q.; Sang-Hoon Lee, D.; Li, M.; Ma, R.; Parashkevov, T.E.; Feng, J. Engineering Origami: A Comprehensive Review of Recent Applications, Design Methods, and Tools. Adv. Sci. 2021, 8, 2000636. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, J.; Feng, J. Geometric and Kinematic Analyses and Novel Characteristics of Origami-Inspired Structures. Symmetry 2019, 11, 1101. [Google Scholar] [CrossRef]
- Fonseca, L.M.; Rodrigues, G.V.; Savi, M.A. An overview of the mechanical description of origami-inspired systems and structures. Int. J. Mech. Sci. 2022, 223, 107316. [Google Scholar] [CrossRef]
- Yan, P.; Huang, H.; Meloni, M.; Li, B.; Cai, J. Mechanical Properties Inside Origami-Inspired Structures: An Overview. Appl. Mech. Rev. 2025, 77, 011001. [Google Scholar] [CrossRef]
- Peraza-Hernandez, E.A.; Hartl, D.J.; Malak, R.J., Jr.; Lagoudas, D.C. Origami-inspired active structures: A synthesis and review. Smart Mater. Struct. 2014, 23, 094001. [Google Scholar] [CrossRef]
- Ning, X.; Wang, X.; Zhang, Y.; Yu, X.; Choi, D.; Zheng, N.; Kim, D.S.; Huang, Y.; Zhang, Y.; Rogers, J.A. Assembly of Advanced Materials into 3D Functional Structures by Methods Inspired by Origami and Kirigami: A Review. Adv. Mater. Interfaces 2018, 5, 1800284. [Google Scholar] [CrossRef]
- Leanza, S.; Wu, S.; Sun, X.; Qi, H.J.; Zhao, R.R. Active Materials for Functional Origami. Adv. Mater. 2024, 36, e2302066. [Google Scholar] [CrossRef]
- Ai, C.; Chen, Y.; Xu, L.; Li, H.; Liu, C.; Shang, F.; Xia, Q.; Zhang, S. Current Development on Origami/Kirigami-Inspired Structure of Creased Patterns toward Robotics. Adv. Eng. Mater. 2021, 23, 2100473. [Google Scholar] [CrossRef]
- Rus, D.; Tolley, M.T. Design, fabrication and control of origami robots. Nat. Rev. Mater. 2018, 3, 101–112. [Google Scholar] [CrossRef]
- Song, K.; Li, H.; Li, Y.; Ma, J.; Zhou, X. A review of curved crease origami: Design, analysis, and applications. Front. Phys. 2024, 12, 1393435. [Google Scholar] [CrossRef]
- Gilewski, W.; Pełczyński, J.; Stawarz, P. A Comparative Study of Origami Inspired Folded Plates. Procedia Eng. 2014, 91, 220–225. [Google Scholar] [CrossRef]
- Robert, L. Robert Lang Origami. Available online: https://langorigami.com/artworks/ (accessed on 15 July 2025).
- Alfattani, R.; Lusk, C. Design of a Bistable Origami Reverse-Fold Using Spherical Kinematics. Volume 5B: 41st Mechanisms and Robotics Conference. In Proceedings of the ASME 2017 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Cleveland, OH, USA, 6–9 August 2017. [Google Scholar] [CrossRef]
- Zhai, J.; Zhang, D.; Li, M.; Cui, C.; Cai, J. Out-of-plane energy absorption and crush behavior of origami honeycomb. Thin-Walled Struct. 2022, 181, 109966. [Google Scholar] [CrossRef]
- Krishnapuram, S.; Xiao, X.; Ren, H. Comparative Study of Mechanical Scaling Effects of Origami-Inspired Motion Generation Mechanisms with Multi-Degree Vertices. Actuators 2024, 13, 266. [Google Scholar] [CrossRef]
- Barreto, R.L.P.; Morlin, F.V.; de Souza, M.B.; Carboni, A.P.; Martins, D. Multiloop origami inspired spherical mechanisms. Mech. Mach. Theory 2021, 155, 104063. [Google Scholar] [CrossRef]
- Lv, C.; Krishnaraju, D.; Konjevod, G.; Yu, H.; Jiang, H. Origami based mechanical metamaterials. Sci. Rep. 2014, 4, srep05979. [Google Scholar] [CrossRef] [PubMed]
- Schenk, M.; Guest, S.D. Geometry of Miura-folded metamaterials. Proc. Natl. Acad. Sci. USA 2013, 110, 3276–3281. [Google Scholar] [CrossRef]
- Wickeler, A.L.; Naguib, H.E. Novel origami-inspired metamaterials: Design, mechanical testing and finite element modelling. Mater. Des. 2020, 186, 108242. [Google Scholar] [CrossRef]
- Woodruff, S.R.; Filipov, E.T. A bar and hinge model formulation for structural analysis of curved-crease origami. Int. J. Solids Struct. 2020, 204–205, 114–127. [Google Scholar] [CrossRef]
- Masana, R.; Dalaq, A.S.; Khazaaleh, S.; Daqaq, M.F. The Kresling origami spring: A review and assessment. Smart Mater. Struct. 2024, 33, 043002. [Google Scholar] [CrossRef]
- Filipov, E.; Liu, K.; Tachi, T.; Schenk, M.; Paulino, G. Bar and hinge models for scalable analysis of origami. Int. J. Solids Struct. 2017, 124, 26–45. [Google Scholar] [CrossRef]
- Xue, W.; Jin, L.; Jian, B.; Ge, Q. Origami-Based Flexible Robotic Grippers via Hard-Soft Coupled Multimaterial 3D Printing. Soft Robot. 2025. [Google Scholar] [CrossRef]
- Wo, Z.; Filipov, E.T. Stiffening multi-stable origami tubes by outward popping of creases. Extrem. Mech. Lett. 2023, 58, 101941. [Google Scholar] [CrossRef]
- Tang, D.; Zhang, C.; Sun, H.; Dai, H.; Xie, J.; Fu, J.; Zhao, P. Origami-inspired magnetic-driven soft actuators with programmable designs and multiple applications. Nano Energy 2021, 89, 106424. [Google Scholar] [CrossRef]
- Zhu, Y.; Filipov, E.T. Rapid multi-physics simulation for electro-thermal origami systems. Int. J. Mech. Sci. 2021, 202–203, 106537. [Google Scholar] [CrossRef]
- Ario, I.; Nakazawa, M. Non-linear dynamic behaviour of multi-folding microstructure systems based on origami skill. Int. J. Non-Linear Mech. 2010, 45, 337–347. [Google Scholar] [CrossRef]
- Zhang, X.; Karagiozova, D.; Lu, G.; Durandet, Y.; Wang, S. Analytical and finite element analyses on axial tensile behaviour of origami bellows with polygonal cross-section. Thin-Walled Struct. 2023, 193, 111234. [Google Scholar] [CrossRef]
- Hu, J.; Pan, H. Design of constant-force mechanisms using origami. Adv. Mech. Eng. 2024, 16, 1–12. [Google Scholar] [CrossRef]
- Lang, R.J. Mathematical Algorithms for Origami Design. Symmetry Cult. Sci. 1994, 5, 115–152. [Google Scholar]
- Demaine, E.D.; Tachi, T. Origamizer: A Practical Algorithm for Folding Any Polyhedron. In Proceedings of the 33rd International Symposium on Computational Geometry (SoCG 2017), Brisbane, Australia, 4–7 July 2017; pp. 34:1–34:16. [Google Scholar] [CrossRef]
- Tachi, T. Origamizing Polyhedral Surfaces. IEEE Trans. Vis. Comput. Graph. 2010, 16, 298–311. [Google Scholar] [CrossRef]
- Tachi, T. Freeform Rigid-Foldable Structure using Bidirectionally Flat-Foldable Planar Quadrilateral Mesh. In Advances in Architectural Geometry 2010; Springer: Vienna, Austria, 2010; pp. 87–102. [Google Scholar] [CrossRef]
- Amanda, G.; Sasaki, K.; Erik, D. Origami Simulator. 2017. Available online: https://origamisimulator.org/ (accessed on 22 July 2025).
- Ghassaei, A.; Demaine, E.D.; Gershenfeld, N. Fast, Interactive Origami Simulation Using GPU Computation. In Proceedings of the 7th International Meeting on Origami in Science, Mathematics and Education (7OSME), Oxford, UK, 5–7 September 2018; pp. 1–16. Available online: https://erikdemaine.org/papers/OrigamiSimulator_Origami7/paper.pdf (accessed on 14 July 2025).
- Tomohiro, T. Freeform Variations of Origami. J. Geom. Graph. 2010, 14, 203–215. Available online: https://www.tsg.ne.jp/TT/cg/TachiFreeformOrigami2010.pdf (accessed on 14 July 2025).
- Schenk, M.; Guest, S.D. Origami Folding: A Structural Engineering Approach. In Proceedings of the 5th International Conference on Origami in Science, Mathematics and Education, Singapore, 13–17 July 2010; pp. 291–304. Available online: https://www3.eng.cam.ac.uk/~sdg/preprint/5OSME.pdf (accessed on 14 July 2025).
- Sasaki, K.; Mitani, J. Simple implementation and low computational cost simulation of curved folds based on ruling-aware triangulation. Comput. Graph. 2022, 102, 213–219. [Google Scholar] [CrossRef]
- Lang, R.J. Mathematical Methods in Origami Design. In Proceedings of the Bridges 2009: Mathematics, Music, Art, Architecture, Culture, Banff, AB, Canada, 26–29 July 2009; pp. 11–20. Available online: http://www.langorigami.com (accessed on 22 July 2025).
- Miura, K. Miura-ori, Basics for Designing its Folding Machines. Proc. Int. Cartogr. Assoc. 2019, 2, 86. [Google Scholar] [CrossRef][Green Version]
- Resch, R.D. The topological design of sculptural and architectural systems. In Proceedings of the National Computer Conference and Exposition—AFIPS’73, New York, NY, USA, 4–8 June 1973; pp. 643–650. [Google Scholar] [CrossRef]
- Kresling, B. Natural twist buckling in shells: From the hawkmoth’s bellows to the deployable Kresling-pattern and cylindrical Miura-ori. In Proceedings of the 6th International Conference on Computation of Spatial Structures IASS-IACM 2008: “Spanning Nano to Mega”, Ithaca, NY, USA, 28–31 May 2008; pp. 18–21. [Google Scholar]
- Yoshimura, Y. On the Mechanism of Buckling of a Circular Cylindrical Shell Under Axial Compression. Available online: https://ntrs.nasa.gov/citations/19930093840 (accessed on 15 July 2025).
- Wickeler, A.L.; McLellan, K.; Sun, Y.-C.; Naguib, H.E. 4D printed origami-inspired accordion, Kresling and Yoshimura tubes. J. Intell. Mater. Syst. Struct. 2023, 34, 2379–2392. [Google Scholar] [CrossRef]
- Ma, J.; You, Z. Modelling of the Waterbomb Origami Pattern and its Applications. Volume 5B: 38th Mechanisms and Robotics Conference. In Proceedings of the ASME 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Buffalo, NY, USA, 17–20 August 2014. [Google Scholar] [CrossRef]
- Gardiner, M.; Aigner, R.; Hanlon, R. Fold Mapping: Parametric Design of Origami Surfaces with Periodic Tessellations. In Proceedings of the 7th Origami Science Mathematics and Education Conference, Oxford, UK, 4–7 September 2018; pp. 105–118. [Google Scholar]
- Cao, H.; Zhou, J.; Chen, K.; He, Q.; Dou, Q.; Liu, Y. Design and Optimization of an Origami Gripper for Versatile Grasping and Manipulation. Adv. Intell. Syst. 2024, 6, 2400271. [Google Scholar] [CrossRef]
- Saito, K.; la Fuente, R.P.-D.; Arimoto, K.; Seong, Y.A.; Aonuma, H.; Niiyama, R.; You, Z. Earwig fan designing: Biomimetic and evolutionary biology applications. Proc. Natl. Acad. Sci. USA 2020, 117, 17622–17626. [Google Scholar] [CrossRef]
- Wang, R.; Sun, J.; Dai, J.S. Design analysis and type synthesis of a petal-inspired space deployable-foldable mechanism. Mech. Mach. Theory 2019, 141, 151–170. [Google Scholar] [CrossRef]
- Wang, S.; Gao, Y.; Huang, H.; Li, B.; Guo, H.; Liu, R. Design of deployable curved-surface rigid origami flashers. Mech. Mach. Theory 2022, 167, 104512. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, Y.; Han, B.; Dong, J.; Han, M.; Yao, J. Biomimetic Origami: Planar Single-Vertex Multi-Crease Mechanism Design and Optimization. Machines 2025, 13, 240. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, Z.; Peng, Y.; Zhang, Y.; An, S.; Wang, Y.; Zhai, Z.; Xu, Y.; Jiang, H. Plug & play origami modules with all-purpose deformation modes. Nat. Commun. 2023, 14, 4329. [Google Scholar] [CrossRef]
- Liu, J.; Pang, Z.; Li, Z.; Wen, G.; Su, Z.; He, J.; Liu, K.; Jiang, D.; Li, Z.; Chen, S.; et al. An origami-wheeled robot with variable width and enhanced sand walking versatility. Thin-Walled Struct. 2025, 206, 112645. [Google Scholar] [CrossRef]
- Guest, S.D.; Pellegrino, S. Inextensional wrapping of flat membranes. In Proceedings of the First International Seminar on Structural Morphology, Montpellier, France, 7–11 September 1992; pp. 203–215. [Google Scholar]
- Lee, D.-Y.; Jung, G.-P.; Sin, M.-K.; Ahn, S.-H.; Cho, K.-J. Deformable wheel robot based on origami structure. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 5612–5617. [Google Scholar] [CrossRef]
- Lee, D.-Y.; Kim, J.-S.; Kim, S.-R.; Koh, J.-S.; Cho, K.-J. The Deformable Wheel Robot Using Magic-Ball Origami Structure. Volume 6B: 37th Mechanisms and Robotics Conference. In Proceedings of the ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Portland, OR, USA, 4–7 August 2013. [Google Scholar] [CrossRef]
- Feng, Y.; Huang, X.; Qiu, X. Bistable morphology analysis of the flexible single-vertex origami unit cell. Extrem. Mech. Lett. 2023, 65, 102101. [Google Scholar] [CrossRef]
- Fang, H.; Li, S.; Ji, H.; Wang, K.W. Dynamics of a bistable Miura-origami structure. Phys. Rev. E 2017, 95, 052211. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Long, J.; Lu, G. Design and analysis of quadruple Waterbomb origami with multi-stability. Extrem. Mech. Lett. 2025, 75, 102295. [Google Scholar] [CrossRef]
- Miyashita, S.; Guitron, S.; Li, S.; Rus, D. Robotic metamorphosis by origami exoskeletons. Sci. Robot. 2017, 2, eaao4369. [Google Scholar] [CrossRef]
- Zhakypov, Z.; Paik, J. Design Methodology for Constructing Multimaterial Origami Robots and Machines. IEEE Trans. Robot. 2018, 34, 151–165. [Google Scholar] [CrossRef]
- Hanson, N.; Mensah, I.A.; Roberts, S.F.; Healey, J.; Wu, C.; Dorsey, K.L. Controlling the fold: Proprioceptive feedback in a soft origami robot. Front. Robot. AI 2024, 11, 1396082. [Google Scholar] [CrossRef]
- Onal, C.D.; Wood, R.J.; Rus, D. Towards printable robotics: Origami-inspired planar fabrication of three-dimensional mechanisms. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, S.; Deng, J.; Li, J.; Zhou, D.; Wang, D.; Liu, J.; Chen, W.; Liu, Y. High-Performance Twisted Nylon Actuators for Soft Robots. Research 2025, 8, 0642. [Google Scholar] [CrossRef]
- Vo, V.T.K.; Ang, M.H.; Koh, S.J.A. Maximal Performance of an Antagonistically Coupled Dielectric Elastomer Actuator System. Soft Robot. 2021, 8, 200–212. [Google Scholar] [CrossRef] [PubMed]
- Nugraha, M.I.; Rossiter, J.; Conn, A.T. A Low Cost Multi Degree of Freedom Capacitive Soft Sensor. IEEE Robot. Autom. Lett. 2025, 10, 3550–3557. [Google Scholar] [CrossRef]
- Mun, H.; Cortes, D.S.D.; Youn, J.-H.; Kyung, K.-U. Multi-Degree-of-Freedom Force Sensor Incorporated into Soft Robotic Gripper for Improved Grasping Stability. Soft Robot. 2024, 11, 628–638. [Google Scholar] [CrossRef]
- Rana, T.; Islam, S.; Rahman, A. Human-Centered Sensor Technologies for Soft Robotic Grippers: A Comprehensive Review. Sensors 2025, 25, 1508. [Google Scholar] [CrossRef]
- Mathew, B.P.; Devasia, F.; Asok, A.; Jayadevu, P.; Baby, R. Implementation of an origami inspired gripper robot for picking objects of variable geometry. Mater. Today Proc. 2022, 58, 176–183. [Google Scholar] [CrossRef]
- Yue, W.; Qi, J.; Song, X.; Fan, S.; Fortino, G.; Chen, C.-H.; Xu, C.; Ren, H. Origami-Inspired Structure with Pneumatic-Induced Variable Stiffness for Multi-DOF Force-Sensing. Sensors 2022, 22, 5370. [Google Scholar] [CrossRef]
- Wang, X.; Qu, H.; Li, X.; Kuang, Y.; Wang, H.; Guo, S.; Sharma, P. Multi-triangles cylindrical origami and inspired metamaterials with tunable stiffness and stretchable robotic arm. PNAS Nexus 2023, 2, pgad098. [Google Scholar] [CrossRef]
- Zhu, Y.; Filipov, E.T. Large-scale modular and uniformly thick origami-inspired adaptable and load-carrying structures. Nat. Commun. 2024, 15, 2353. [Google Scholar] [CrossRef]
- Kuribayashi, K.; Tsuchiya, K.; You, Z.; Tomus, D.; Umemoto, M.; Ito, T.; Sasaki, M. Self-deployable origami stent grafts as a biomedical application of Ni-rich TiNi shape memory alloy foil. Mater. Sci. Eng. A 2006, 419, 131–137. [Google Scholar] [CrossRef]
- Lee, D.-Y.; Kim, J.-K.; Sohn, C.-Y.; Heo, J.-M.; Cho, K.-J. High–load capacity origami transformable wheel. Sci. Robot. 2021, 6, eabe0201. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Ze, Q.; Dai, J.; Udipi, N.; Paulino, G.H.; Zhao, R. Stretchable origami robotic arm with omnidirectional bending and twisting. Proc. Natl. Acad. Sci. USA 2021, 118, e2110023118. [Google Scholar] [CrossRef]
- Zhang, Z.; Fan, W.; Long, Y.; Dai, J.; Luo, J.; Tang, S.; Lu, Q.; Wang, X.; Wang, H.; Chen, G. Hybrid-Driven Origami Gripper with Variable Stiffness and Finger Length. Cyborg Bionic Syst. 2024, 5, 0103. [Google Scholar] [CrossRef]
- Gage, T. MODeL-T Explores Origami-Inspired Foldable Flat Optics for Compact Lidar Missions; NASA’s Earth Science Technology Office. 10 February 2025. Available online: https://esto.nasa.gov/model-t-explores-origami-inspired-foldable-flat-optics-for-compact-lidar-missions/ (accessed on 24 July 2025).
- Li, S.; Vogt, D.M.; Rus, D.; Wood, R.J. Fluid-driven origami-inspired artificial muscles. Proc. Natl. Acad. Sci. USA 2017, 114, 13132–13137. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.-L.; Wang, D.-F.; Tachi, T.; Chuang, K.-C. An origami longitudinal–torsional wave converter. Extrem. Mech. Lett. 2022, 51, 101570. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, T.; Nian, G.; Shan, Y.; Liang, X.; Jiang, H.; Qu, S. Ron Resch Origami Pattern Inspired Energy Absorption Structures. J. Appl. Mech. 2018, 86, 011005. [Google Scholar] [CrossRef]
- Jayawardana, W.M.A.; Elder, T.; Twohig, T.; Croll, A.B. Switchable origami adhesives. Soft Matter 2024, 20, 3814–3822. [Google Scholar] [CrossRef]
- Felton, S.M.; Lee, D.-Y.; Cho, K.-J.; Wood, R.J. A passive, origami-inspired, continuously variable transmission. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2913–2918. [Google Scholar] [CrossRef]
- Fang, H.; Zhang, Y.; Wang, K.W. Origami-based earthworm-like locomotion robots. Bioinspir. Biomim. 2017, 12, 065003. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Hua, M.; Yan, Y.; Wu, S.; Alsaid, Y.; He, X. Stimuli-Responsive Polymers for Soft Robotics. Annu. Rev. Control Robot. Auton. Syst. 2022, 19, 515–545. [Google Scholar] [CrossRef]
- Yan, W.; Li, S.; Deguchi, M.; Zheng, Z.; Rus, D.; Mehta, A. Origami-based integration of robots that sense, decide, and respond. Nat. Commun. 2023, 14, 1553. [Google Scholar] [CrossRef]
- Qu, C.; Hu, J.; Liu, X.; Li, Z.; Ding, Y. Morphology and mechanical properties of polyimide films: The effects of UV irradiation on microscale surface. Materials 2017, 10, 1329. [Google Scholar] [CrossRef]
- Xiao, P.; He, X.; Lu, Q. Exceptionally High-Temperature-Resistant Kapton-Type Polyimides with Tg > 520 °C: Synthesis via Incorporation of Spirobis(indene)-bis(benzoxazole)-Containing Diamines. Polymers 2025, 17, 832. [Google Scholar] [CrossRef]
- A Robertson, M.; Kara, O.C.; Paik, J. Soft pneumatic actuator-driven origami-inspired modular robotic “pneumagami”. Int. J. Robot. Res. 2021, 40, 72–85. [Google Scholar] [CrossRef]
- Wang, D.H.; Tan, L.-S. Origami-Inspired Fabrication: Self-Folding or Self-Unfolding of Cross-Linked-Polyimide Objects in Extremely Hot Ambience. ACS Macro Lett. 2019, 8, 546–552. [Google Scholar] [CrossRef]
- Zhu, R.; Fan, D.; Wu, W.; He, C.; Xu, G.; Dai, J.S.; Wang, H. Soft Robots for Cluttered Environments Based on Origami Anisotropic Stiffness Structure (OASS) Inspired by Desert Iguana. Adv. Intell. Syst. 2023, 5, 2200301. [Google Scholar] [CrossRef]
- Wagner, M.A.; Huang, J.-L.; Okle, P.; Paik, J.; Spolenak, R. Hinges for origami-inspired structures by multimaterial additive manufacturing. Mater. Des. 2020, 191, 108643. [Google Scholar] [CrossRef]
- Lazarus, N.; Smith, G.L.; Dickey, M.D. Self-Folding Metal Origami. Adv. Intell. Syst. 2019, 1, 1900059. [Google Scholar] [CrossRef]
- Onal, C.D.; Wood, R.J.; Rus, D. An origami-inspired approach to worm robots. IEEE/ASME Trans. Mechatron. 2012, 18, 430–438. [Google Scholar] [CrossRef]
- Koh, J.-S.; Cho, K.-J. Omega-Shaped Inchworm-Inspired Crawling Robot with Large-Index-and-Pitch (LIP) SMA Spring Actuators. IEEE/ASME Trans. Mechatron. 2013, 18, 419–429. [Google Scholar] [CrossRef]
- Xiang, X.; Lu, G.; Ruan, D.; You, Z.; Zolghadr, M. Large deformation of an arc-Miura structure under quasi-static load. Compos. Struct. 2017, 182, 209–222. [Google Scholar] [CrossRef]
- An, B.; Miyashita, S.; Ong, A.; Tolley, M.T.; Demaine, M.L.; Demaine, E.D.; Wood, R.J.; Rus, D. An End-to-End Approach to Self-Folding Origami Structures. IEEE Trans. Robot. 2018, 34, 1409–1424. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, P.; Bai, Y.; Li, J.; Feng, J.; Sareh, P. Engineered origami crease perforations for optimal mechanical performance and fatigue life. Thin-Walled Struct. 2023, 185, 110572. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, P.; Bai, Y.; Li, J.; Feng, J.; Sareh, P. Effects of perforated creases on the mechanical behavior and fatigue life of thick origami structures. Mech. Based Des. Struct. Mach. 2024, 52, 6525–6538. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, D.; Levine, D.J.; Sung, C. Origami-Inspired Robot That Swims via Jet Propulsion. IEEE Robot. Autom. Lett. 2021, 6, 7145–7152. [Google Scholar] [CrossRef]
- Ze, Q.; Wu, S.; Dai, J.; Leanza, S.; Ikeda, G.; Yang, P.C.; Iaccarino, G.; Zhao, R.R. Spinning-enabled wireless amphibious origami millirobot. Nat. Commun. 2022, 13, 3118. [Google Scholar] [CrossRef]
- Lee, S.; Cha, Y. Analysis of Kresling origami bellows for pneumatic pump. Sens. Actuators A Phys. 2025, 391, 116631. [Google Scholar] [CrossRef]
- Liu, M.; Wang, C.; Shi, C.; Guo, H.; Liu, R. Bio-inspired deployable cable-driven origami gripper with variable finger length for space capture. Aerosp. Sci. Technol. 2025, 158, 109844. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, G.; Wu, H.; Kong, L.; Wang, H. A Pneumatic/Cable-driven Hybrid Linear Actuator with Combined Structure of Origami Chambers and Deployable Mechanism. IEEE Robot. Autom. Lett. 2020, 5, 3564–3571. [Google Scholar] [CrossRef]
- Kim, J.; Im, E.; Lee, Y.; Cha, Y. Quadrupedal robot with tendon-driven origami legs. Sens. Actuators A Phys. 2024, 378, 115769. [Google Scholar] [CrossRef]
- Salerno, M.; Zhang, K.; Menciassi, A.; Dai, J.S. A Novel 4-DOF Origami Grasper with an SMA-Actuation System for Minimally Invasive Surgery. IEEE Trans. Robot. 2016, 32, 484–498. [Google Scholar] [CrossRef]
- Liu, W.; Bai, X.; Yang, H.; Bao, R.; Liu, J. Tendon Driven Bistable Origami Flexible Gripper for High-Speed Adaptive Grasping. IEEE Robot. Autom. Lett. 2024, 9, 5417–5424. [Google Scholar] [CrossRef]
- Kim, S.-J.; Lee, D.-Y.; Jung, G.-P.; Cho, K.-J. An origami-inspired, self-locking robotic arm that can be folded flat. Sci. Robot. 2018, 3, eaar2915. [Google Scholar] [CrossRef]
- Hoff, E.V.; Jeong, D.; Lee, K. OrigamiBot-I: A thread-actuated origami robot for manipulation and locomotion. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 1421–1426. [Google Scholar] [CrossRef]
- Lee, K.; Wang, Y.; Zheng, C. TWISTER Hand: Underactuated Robotic Gripper Inspired by Origami Twisted Tower. IEEE Trans. Robot. 2020, 36, 488–500. [Google Scholar] [CrossRef]
- Wang, J.; Yang, H.; Zhang, J.; Liu, H.; Zhong, Y.; Hu, Y.; Liu, Y.; Xia, C.; Wu, J. Versatile Rigid-Flexible Coupling Modules: Enhancing Soft Origami Structures with Cable-Driven Parallel Mechanisms. Adv. Intell. Syst. 2025, 7, 2401008. [Google Scholar] [CrossRef]
- Yeow, B.S.; Cai, C.J.; Kalairaj, M.S.; Hoo, F.W.; Lee, Z.X.; Tan, J.C.S.; Ho, J.R.; Ma, V.M.; Huang, H.; Ren, H. Origami-Inspired Snap-through Bistability in Parallel and Curved Mechanisms Through the Inflection of Degree Four Vertexes. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 10863–10869. [Google Scholar] [CrossRef]
- Zhang, L.; Pan, F.; Ma, Y.; Yang, K.; Guo, S.; Chen, Y. Bistable reconfigurable origami metamaterials with high load-bearing and low state-switching forces. Extrem. Mech. Lett. 2023, 63, 102064. [Google Scholar] [CrossRef]
- Morgan, M.R.; Lang, R.J.; Magleby, S.P.; Howell, L.L. Towards developing product applications of thick origami using the offset panel technique. Mech. Sci. 2016, 7, 69–77. [Google Scholar] [CrossRef]
- Buscicchio, A.; Alessandrino, G.; Troise, A.; Sironi, T.; Gloder, A. SolarCube: An Origami-Inspired Lightweight Deployable Solar Panel for Nanosatellites. In Proceedings of the 2023 13th European Space Power Conference (ESPC), Elche, Spain, 2–6 October 2023; pp. 1–9. [Google Scholar] [CrossRef]
- Yan, W.; Mehta, A. A crawling robot driven by a folded self-sustained oscillator. In Proceedings of the 2022 IEEE 5th International Conference on Soft Robotics (RoboSoft), Edinburgh, UK, 4–8 April 2022; pp. 455–460. [Google Scholar] [CrossRef]
- Zaghloul, A.; Bone, G.M. Origami-Inspired Soft Pneumatic Actuators: Generalization and Design Optimization. Actuators 2023, 12, 72. [Google Scholar] [CrossRef]
- Liu, J.; Ma, G.; Ma, Z.; Zuo, S. Origami-inspired soft-rigid hybrid contraction actuator and its application in pipe-crawling robot. Smart Mater. Struct. 2023, 32, 065015. [Google Scholar] [CrossRef]
- Yoon, C.; Xiao, R.; Park, J.; Cha, J.; Nguyen, T.D.; Gracias, D.H. Functional stimuli responsive hydrogel devices by self-folding. Smart Mater. Struct. 2014, 23, 094008. [Google Scholar] [CrossRef]
- Schmitt, F.; Piccin, O.; Barbé, L.; Bayle, B. An Origami-Inspired Flexible Pneumatic Actuator. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 436–441. [Google Scholar] [CrossRef]
- Caiyang, E.; Wang, B.; Guo, Z.; Zhang, H.; Xu, Q.; Chen, J. An origami-inspired 3D-printed soft foldable actuator with large contraction deformation and strong actuation capability. Smart Mater. Struct. 2025, 34, 045019. [Google Scholar] [CrossRef]
- Martinez, R.; Fish, C.; Chen, X.; Whitesides, G.M. Elastomeric Origami: Programmable Paper-Elastomer Composites as Pneumatic Actuators. Adv. Funct. Mater. 2012, 22, 1376–1384. [Google Scholar] [CrossRef]
- Yi, J.; Chen, X.; Song, C.; Wang, Z. Fiber-Reinforced Origamic Robotic Actuator. Soft Robot. 2018, 5, 81–92. [Google Scholar] [CrossRef]
- Kim, S.; Kang, J.; Yoo, S.; Cha, Y. Soft origami tripod based on electrohydraulic actuator for twisting motion. Sens. Actuators A Phys. 2025, 393, 116814. [Google Scholar] [CrossRef]
- Onorati, S.; Semproni, F.; Paternò, L.; Casagrande, G.; Iacovacci, V.; Menciassi, A. A hydraulic soft robotic detrusor based on an origami design. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 6817–6822. [Google Scholar]
- Kellaris, N.; Venkata, V.G.; Smith, G.M.; Mitchell, S.K.; Keplinger, C. Peano-HASEL actuators: Muscle-mimetic, electrohydraulic transducers that linearly contract on activation. Sci. Robot. 2018, 3, eaar3276. [Google Scholar] [CrossRef]
- Geckeler, C.; Pizzani, B.A.; Mintchev, S. Biodegradable Origami Gripper Actuated with Gelatin Hydrogel for Aerial Sensor Attachment to Tree Branches. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 5324–5330. [Google Scholar]
- Huang, Z.; Wei, C.; Dong, L.; Wang, A.; Yao, H.; Guo, Z.; Mi, S. Fluid-driven hydrogel actuators with an origami structure. iScience 2022, 25, 104674. [Google Scholar] [CrossRef] [PubMed]
- Ionov, L. 3D microfabrication using stimuli-responsive self-folding polymer films. Polym. Rev. 2013, 53, 92–107. [Google Scholar] [CrossRef]
- Gracias, D.H. Stimuli responsive self-folding using thin polymer films. Curr. Opin. Chem. Eng. 2013, 2, 112–119. [Google Scholar] [CrossRef]
- Huang, H.-W.; Tibbitt, M.W.; Huang, T.-Y.; Nelson, B.J. Matryoshka-Inspired Micro-Origami Capsules to Enhance Loading, Encapsulation, and Transport of Drugs. Soft Robot. 2019, 6, 150–159. [Google Scholar] [CrossRef]
- Aggarwal, A.; Li, C.; Stupp, S.I.; de la Cruz, M.O. Controlling the Shape Morphology of Origami-Inspired Photoresponsive Hydrogels. Soft Matter 2022, 18, 2193–2202. [Google Scholar] [CrossRef]
- Li, C.; Xue, Y.; Han, M.; Palmer, L.C.; Rogers, J.A.; Huang, Y.; Stupp, S.I. Synergistic photoactuation of bilayered spiropyran hydrogels for predictable origami-like shape change. Matter 2021, 4, 1377–1390. [Google Scholar] [CrossRef]
- Patel, H.; Chen, J.; Hu, Y.; Erturk, A. Photo-responsive hydrogel-based re-programmable metamaterials. Sci. Rep. 2022, 12, 13033. [Google Scholar] [CrossRef] [PubMed]
- Ikejiri, S.; Takashima, Y.; Osaki, M.; Yamaguchi, H.; Harada, A. Solvent-Free Photoresponsive Artificial Muscles Rapidly Driven by Molecular Machines. J. Am. Chem. Soc. 2018, 140, 17308–17315. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhang, T. Modeling and Characterizing Two Dielectric Elastomer Folding Actuators for Origami-Inspired Robot. IEEE Robot. Autom. Lett. 2022, 7, 11775–11782. [Google Scholar] [CrossRef]
- Xiang, C.; Sun, H.; Wu, T.; Wu, B.; Guan, Y.; Zou, T. Electroadhesion-driven crawling robots based on origami mechanism. Sens. Actuators A Phys. 2024, 377, 115684. [Google Scholar] [CrossRef]
- Sun, Y.; Li, D.; Wu, M.; Yang, Y.; Su, J.; Wong, T.; Xu, K.; Li, Y.; Li, L.; Yu, X.; et al. Origami-inspired folding assembly of dielectric elastomers for programmable soft robots. Microsyst. Nanoeng. 2022, 8, 37. [Google Scholar] [CrossRef]
- Kirkman, S.; Rothemund, P.; Acome, E.; Keplinger, C. Electromechanics of planar HASEL actuators. Extrem. Mech. Lett. 2021, 48, 101408. [Google Scholar] [CrossRef]
- Rothemund, P.; Kellaris, N.; Mitchell, S.K.; Acome, E.; Keplinger, C. HASEL Artificial Muscles for a New Generation of Lifelike Robots—Recent Progress and Future Opportunities. Adv. Mater. 2020, 33, e2003375. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Lahondes, Q.; Esendag, K.; Damian, D.; Miyashita, S. Origami Robot Self-folding by Magnetic Induction. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23–27 October 2022; pp. 2519–2525. [Google Scholar] [CrossRef]
- These origami robots could one day deliver drugs inside your body. AAAS Articles DO Group. March 2021. Available online: https://www.science.org/content/article/these-origami-robots-could-one-day-deliver-drugs-inside-your-body (accessed on 22 July 2025).
- Miyashita, S.; Guitron, S.; Yoshida, K.; Li, S.; Damian, D.D.; Rus, D. Ingestible, controllable, and degradable origami robot for patching stomach wounds. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 909–916. [Google Scholar] [CrossRef]
- Yuk, H.; Kim, D.; Lee, H.; Jo, S.; Shin, J.H. Shape memory alloy-based small crawling robots inspired by C. elegans. Bioinspir. Biomim. 2011, 6, 046002. [Google Scholar] [CrossRef] [PubMed]
- Na, J.; Evans, A.A.; Bae, J.; Chiappelli, M.C.; Santangelo, C.D.; Lang, R.J.; Hull, T.C.; Hayward, R.C. Programming Reversibly Self-Folding Origami with Micropatterned Photo-Crosslinkable Polymer Trilayers. Adv. Mater. 2015, 27, 79–85. [Google Scholar] [CrossRef]
- Kotikian, A.; McMahan, C.; Davidson, E.C.; Muhammad, J.M.; Weeks, R.D.; Daraio, C.; Lewis, J.A. Untethered soft robotic matter with passive control of shape morphing and propulsion. Sci. Robot. 2019, 4, eaax7044. [Google Scholar] [CrossRef]
- Zuo, J.; Chen, H.; Gu, J.; Zhang, W.; Zhang, Z.; Huang, G. A facile method for fabricating humidity-sensitive bilayer actuators with programmable deformation. Sens. Actuators A Phys. 2023, 352, 114208. [Google Scholar] [CrossRef]
- Mustapa, A.; Abdullah, A.H.; Idris, W.F.W.; Ismail, Z. Pencil yourself a humidity-driven continuous roll Paperbot. Sens. Actuators B Chem. 2025, 444, 138363. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.; Li, Q. Hydrogel-driven origami metamaterials for tunable swelling behavior. Mater. Des. 2021, 207, 109819. [Google Scholar] [CrossRef]
- Okuzaki, H.; Kuwabara, T.; Funasaka, K.; Saido, T. Humidity-Sensitive Polypyrrole Films for Electro-Active Polymer Actuators. Adv. Funct. Mater. 2013, 23, 4400–4407. [Google Scholar] [CrossRef]
- Trivedi, D.; Rahn, C.D.; Kier, W.M.; Walker, I.D. Soft Robotics: Biological Inspiration, State of the Art, and Future Research. Appl. Bionics Biomech. 2008, 5, 99–117. [Google Scholar] [CrossRef]
- Pujada-Gamarra, E.; Lavayen-Farfán, D.; Olivera-Oliva, D.; Rodríguez-Hernández, J. Origami-Inspired Photovoltaic Modules—Development of Ecofriendly Solutions for Naval and Mining Operations. Eng. Proc. 2025, 83, 26. [Google Scholar] [CrossRef]
- Blumenschein, L.H.; Coad, M.M.; Haggerty, D.A.; Okamura, A.M.; Hawkes, E.W. Design, Modeling, Control, and Application of Everting Vine Robots. Front. Robot. AI 2020, 7, 548266. [Google Scholar] [CrossRef] [PubMed]
- Stokes, A.A.; Shepherd, R.F.; Morin, S.A.; Ilievski, F.; Whitesides, G.M. A Hybrid Combining Hard and Soft Robots. Soft Robot. 2014, 1, 70–74. [Google Scholar] [CrossRef]
- Bellinger, A.M.; Jafari, M.; Grant, T.M.; Zhang, S.; Slater, H.C.; Wenger, E.A.; Mo, S.; Lee, Y.-A.L.; Mazdiyasni, H.; Kogan, L.; et al. Oral, ultra–long-lasting drug delivery: Application toward malaria elimination goals. Sci. Transl. Med. 2016, 8, 365ra157. [Google Scholar] [CrossRef]
- Seyidoğlu, B.; Rafsanjani, A. A textile origami snake robot for rectilinear locomotion. Device 2024, 2, 100226. [Google Scholar] [CrossRef]
- Zhakypov, Z.; Falahi, M.; Shah, M.; Paik, J. The design and control of the multi-modal locomotion origami robot, Tribot. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 4349–4355. [Google Scholar] [CrossRef]
- Hu, Q.; Chen, Z.; Dong, E.; Sun, D. Design and Control of a Modular, Untethered Soft Origami Robot Driven by SMA Coils. IEEE Trans. Ind. Electron. 2025, 72, 8208–8218. [Google Scholar] [CrossRef]
- Yang, D.; Mishra, S.; Aukes, D.M.; Zhang, W. Design, Planning, and Control of an Origami-inspired Foldable Quadrotor. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019. [Google Scholar] [CrossRef]
- Hu, J.; Li, H.; Chen, W. A squid-inspired swimming robot using folding of origami. J. Eng. 2021, 2021, 630–639. [Google Scholar] [CrossRef]
- Hu, B.; Zhou, Z.; Qu, H.; Hu, H.; Wang, X.; Wang, H.; Liu, W.; Guo, S. Kirigami-based soft actuators and tendon-driven robots. Sens. Actuators A Phys. 2025, 393, 116864. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Y.; Liu, K.; Zhang, H.; Tong, X.; Chen, D.; Wang, L.; Paik, J. Ultra-tunable bistable structures for universal robotic applications. Cell Rep. Phys. Sci. 2023, 4, 101365. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, D.; Wu, H.; Bao, Y.; Chai, G. Non-contact magnetic driving bioinspired Venus flytrap robot based on bistable anti-symmetric CFRP structure. Compos. Struct. 2016, 135, 17–22. [Google Scholar] [CrossRef]
- Kang, J.; Kim, S.; Cha, Y. Soft origami tripod based on electrohydraulic actuator for multimodal motions. Sens. Actuators A Phys. 2024, 372, 115334. [Google Scholar] [CrossRef]
- Gao, K.; Xu, K. Advancements and Prospects of pH-Responsive Hydrogels in Biomedicine. Gels 2025, 11, 293. [Google Scholar] [CrossRef]
- Zhao, L.; Huang, J.; Zhang, Y.; Wang, T.; Sun, W.; Tong, Z. Programmable and Bidirectional Bending of Soft Actuators Based on Janus Structure with Sticky Tough PAA-Clay Hydrogel. ACS Appl. Mater. Interfaces 2017, 9, 11866–11873. [Google Scholar] [CrossRef]
- Ding, M.; Jing, L.; Yang, H.; Machnicki, C.; Fu, X.; Li, K.; Wong, I.; Chen, P.-Y. Multifunctional soft machines based on stimuli-responsive hydrogels: From freestanding hydrogels to smart integrated systems. Mater. Today Adv. 2020, 8, 100088, Erratum in Mater. Today Adv. 2021, 9, 100130. [Google Scholar] [CrossRef]
- Derkowska-Zielińska, B.; Guerchi, A.; Kowalska, D.; Smokal, V.; Czaplicki, R. New azobenzene-containing light-responsive polymers for soft robotics. In Proceedings of the Soft Mechatronics and Wearable Systems 2025 (Volume PC13434), Vancouver, BC, Canada, 17–20 March 2025; p. PC134340R. [Google Scholar] [CrossRef]
- Kim, D.; Lee, H.; Kwon, S.; Sung, Y.J.; Song, W.K.; Park, S. Bilayer Hydrogel Sheet-Type Intraocular Microrobot for Drug Delivery and Magnetic Nanoparticles Retrieval. Adv. Health Mater. 2020, 9, e2000118. [Google Scholar] [CrossRef]
- Jin, Y.; Li, J.; Liu, S.; Cao, G.; Liu, J. A worm-inspired robot based on origami structures driven by the magnetic field. Bioinspir. Biomim. 2023, 18, 046008. [Google Scholar] [CrossRef] [PubMed]
- Okuzaki, H.; Kunugi, T. Adsorption-induced chemomechanical behavior of polypyrrole films. J. Appl. Polym. Sci. 1997, 64, 383–388. [Google Scholar] [CrossRef]
- Okuzaki, H.; Funasaka, K. Electrically Driven Polypyrrole Film Actuator Working in Air. J. Intell. Mater. Syst. Struct. 1999, 10, 465–469. [Google Scholar] [CrossRef]
- Just Add Water—Blooming Flower Trick—YouTube. Available online: https://www.youtube.com/watch?v=DuhdLonimdU (accessed on 21 July 2025).
- Mackay, R.E.; Le, H.R.; Keatch, R.P. Design optimisation and fabrication of SU-8 based electro-thermal micro-grippers. J. Micro-Nano Mechatron. 2011, 6, 13–22. [Google Scholar] [CrossRef]
- Feng, B.; Liu, Y.; Zhang, J.; Qu, S.; Yang, W. Miniature origami robot for various biological micromanipulations. Nat. Commun. 2025, 16, 2633. [Google Scholar] [CrossRef]
- Kim, K.; Nilsen, E.; Huang, T.; Kim, A.; Ellis, M.; Skidmore, G.; Lee, J.-B. Metallic microgripper with SU-8 adaptor as end-effectors for heterogeneous micro/nano assembly applications. Microsyst. Technol. 2004, 10, 689–693. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, H.; Du, N.; Lyu, Y.; Xu, J.; Fu, H.; Guan, Y.; Nan, K. Drug origami: A computation-guided approach for customizable drug release kinetics of oral formulations. Matter 2025, 8, 101878. [Google Scholar] [CrossRef]
- Ze, Q.; Wu, S.; Nishikawa, J.; Dai, J.; Sun, Y.; Leanza, S.; Zemelka, C.; Novelino, L.S.; Paulino, G.H.; Zhao, R.R. Soft robotic origami crawler. Sci. Adv. 2022, 8, eabm7834. [Google Scholar] [CrossRef] [PubMed]
- Pagano, A.; Yan, T.; Chien, B.; Wissa, A.; Tawfick, S. A crawling robot driven by multi-stable origami. Smart Mater. Struct. 2017, 26, 094007. [Google Scholar] [CrossRef]
- Sadeghi, S.; Betsill, B.D.; Li, S. Design and Optimization of an Origami-Inspired Jumping Mechanism With Nonlinear Stiffness Properties. Volume 8: 31st Conference on Mechanical Vibration and Noise. In Proceedings of the ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Anaheim, CA, USA, 18–21 August 2019. [Google Scholar] [CrossRef]
- Hedayati, H.; Suzuki, R.; Rees, W.; Leithinger, D.; Szafir, D. Designing Expandable-Structure Robots for Human-Robot Interaction. Front. Robot. AI 2022, 9, 719639. [Google Scholar] [CrossRef]
- Tang, J.; Wei, F. Miniaturized Origami Robots: Actuation Approaches and Potential Applications. Macromol. Mater. Eng. 2021, 307, 2100671. [Google Scholar] [CrossRef]
- Suzuki, H.; Wood, R.J. Origami-inspired miniature manipulator for teleoperated microsurgery. Nat. Mach. Intell. 2020, 2, 437–446. [Google Scholar] [CrossRef]
- Yang, Y.; Vella, K.; Holmes, D.P. Grasping with Kirigami Shells. Available online: https://www.science.org/doi/10.1126/scirobotics.abd6426 (accessed on 22 July 2025).
- Li, D.; Yumbla, E.Q.; Olivas, A.; Sugar, T.; Ben Amor, H.; Lee, H.; Zhang, W.; Aukes, D.M. Origami-Inspired Wearable Robot for Trunk Support. IEEE/ASME Trans. Mechatron. 2023, 28, 1466–1476. [Google Scholar] [CrossRef]
- Carmona, D.; Xun, Q.; Jia, X.; Ren, H. A Novel Wearable Origami Device for Head and Cervical Spine Protection in Falls. In Proceedings of the 2022 2nd Asian Conference on Innovation in Technology (ASIANCON), Ravet, India, 26–28 August 2022; pp. 1–10. [Google Scholar] [CrossRef]
- Chen, Z.; Tighe, B.; Zhao, J. Origami-Inspired Modules Enable A Reconfigurable Robot with Programmable Shapes and Motions. IEEE/ASME Trans. Mechatron. 2022, 27, 2016–2025. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Li, K.; Su, L. Origami-inspired metamaterials hierarchical structure with tailorable crushing behavior. Constr. Build. Mater. 2022, 345, 128328. [Google Scholar] [CrossRef]
- Chen, B.; Ni, X.; Zhou, L.; Zi, B.; Li, E.; Zhang, D. Development of Bioinspired Five-DOF Origami for Robotic Spine Assistive Exoskeleton. IEEE Trans. Robot. 2025, 41, 3317–3334. [Google Scholar] [CrossRef]
- Nohooji, H.R.; Voos, H. Compliant Robotics in Space: A Prospective Review of Soft and Deformable Systems for Space Missions. Adv. Intell. Syst. 2025, 7, 2400785. [Google Scholar] [CrossRef]
- Jasim, B.; Taheri, P. An Origami-Based Portable Solar Panel System. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 1–3 November 2018; pp. 199–203. [Google Scholar] [CrossRef]
- Verzoni, A.; Rais-Rohani, M. Transition analysis of flat-foldable origami-inspired deployable shelter concepts. Eng. Struct. 2022, 273, 115074. [Google Scholar] [CrossRef]
- Zhu, Y.; Birla, M.; Oldham, K.R.; Filipov, E.T. Elastically and Plastically Foldable Electrothermal Micro-Origami for Controllable and Rapid Shape Morphing. Adv. Funct. Mater. 2020, 30, 2003741. [Google Scholar] [CrossRef]
- Tsuda, Y.; Mori, O.; Funase, R.; Sawada, H.; Yamamoto, T.; Saiki, T.; Endo, T.; Kawaguchi, J. Flight status of IKAROS deep space solar sail demonstrator. Acta Astronaut. 2011, 69, 833–840. [Google Scholar] [CrossRef]
- Moshtaghzadeh, M.; Izadpanahi, E.; Mardanpour, P. Prediction of fatigue life of a flexible foldable origami antenna with Kresling pattern. Eng. Struct. 2022, 251, 113399. [Google Scholar] [CrossRef]
- Fakhari, H.E.; Eslami, H.; Moshtaghzadeh, M.; Mardanpour, P. A comprehensive study of a new cylindrical flexible Miura-Ori origami: Kinematics, FEA, and fatigue assessments. Aerosp. Sci. Technol. 2024, 155, 109620. [Google Scholar] [CrossRef]
- Moshtaghzadeh, M.; Bakhtiari, A.; Izadpanahi, E.; Mardanpour, P. Stability and Fatigue Analysis of an Adaptive Origami Antenna Structure with Kresling Pattern. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Moshtaghzadeh, M.; Bakhtiari, A.; Mardanpour, P. Artificial Neural Network-based Finite Element method for assessing fatigue and stability of an origami-inspired structure. Eng. Struct. 2022, 272, 114965. [Google Scholar] [CrossRef]
- Son, H.; Park, Y.; Na, Y.; Yoon, C. 4D Multiscale Origami Soft Robots: A Review. Polymers 2022, 14, 4235. [Google Scholar] [CrossRef]
- Mathew, A.T.; Vo, T.V.K.; Koh, S.J.A. A molecular perspective to analytical modeling that reveals new instabilities in dielectric elastomer transducers. J. Mech. Phys. Solids 2019, 132, 103703. [Google Scholar] [CrossRef]
- Arora, N.; Chen, V.; Cherkasov, A.; Xiang, Y.; Juhl, A.; Buskohl, P.; Rudykh, S. Magnetically-Programmed Instability-Driven Pattern Transformations in Soft Materials. Adv. Funct. Mater. 2024, 34, 2401077. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, J.; Dong, Z.; Li, B.; Chang, C. Temperature-triggered inflatable hydrogel muscles with snap-through instability for untethered robots. Nat. Commun. 2025, 16, 3384. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Yu, Z.; Duan, A.; Tongne, A.; Li, Y.; Zhang, W. A Kresling origami-enabled soft robot toward autonomous obstacle avoidance and wall-climbing. Sens. Actuators B Chem. 2025, 438, 137792. [Google Scholar] [CrossRef]
- Robert, J.L. Paper. Robert Lang Origami. 9 August 2011. Available online: https://langorigami.com/article/paper/ (accessed on 23 July 2025).









| Design Methods | Patterns | Typical Applications | Source |
|---|---|---|---|
| Tessellations | Miura-Ori | Morphable wheel | [68] |
| High-DOF robotic arm and manipulation | [31,93] | ||
| Kresling | High-DOF motions | [67,90] | |
| Tunable stiffness | [39,86] | ||
| Shock absorber | [36] | ||
| Wave-mode converter | [94] | ||
| Waterbomb | Deformable wheel | [71] | |
| Compliant Gripper | [84] | ||
| Yoshimura | Compliant gripper | [38] | |
| Resch | Energy absorption | [95] | |
| Stiffness switching | [96] | ||
| Honeycomb | Out-of-plane energy absorption | [29] | |
| Vertex-centre patterns | Petal | Deformable wheel | [70] |
| Deployable solar array and truss-antenna | [64] | ||
| Flasher Pattern | Thick-panel deployable curved-surface | [65] | |
| Various transmission wheel | [97] | ||
| Custom designs | Origami exoskeletons | Self-reconfiguring robot with multi-tasking | [75] |
| Tribot | Multigait robot | [76] | |
| Diamond cutouts | Multi-DOF force sensing | [85] |
| Category | Sub-Type | Reference |
|---|---|---|
| Mechanical actuation | Motors | [68,114,115] |
| Tendons/cable-driven | [114,116,117,118,119,120,121,122,123,124,125] | |
| Bistable snap mechanism | [121,126,127,128,129,130] | |
| Fluidic actuation | Pneumatics | [67,118,125,131,132,133,134,135,136,137] |
| Hydraulics | [67,93,138,139,140] | |
| Embedded actuation | Chemoresponsive | [141,142,143,144,145] |
| Photoresponsive | [146,147,148,149] | |
| Electroresponsive | [76,144,150,151,152,153,154] | |
| Magnetoresponsive | [40,90,155,156,157] | |
| Thermoresponsive | [88,155,158,159,160] | |
| Humidity-responsive | [75,161,162,163,164] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vo, T.V.K.; Quah, T.K.N.; Chua, L.T.; Li, K.H.H. Morph and Function: Exploring Origami-Inspired Structures in Versatile Robotics Systems. Micromachines 2025, 16, 1047. https://doi.org/10.3390/mi16091047
Vo TVK, Quah TKN, Chua LT, Li KHH. Morph and Function: Exploring Origami-Inspired Structures in Versatile Robotics Systems. Micromachines. 2025; 16(9):1047. https://doi.org/10.3390/mi16091047
Chicago/Turabian StyleVo, Tran Vy Khanh, Tan Kai Noel Quah, Li Ting Chua, and King Ho Holden Li. 2025. "Morph and Function: Exploring Origami-Inspired Structures in Versatile Robotics Systems" Micromachines 16, no. 9: 1047. https://doi.org/10.3390/mi16091047
APA StyleVo, T. V. K., Quah, T. K. N., Chua, L. T., & Li, K. H. H. (2025). Morph and Function: Exploring Origami-Inspired Structures in Versatile Robotics Systems. Micromachines, 16(9), 1047. https://doi.org/10.3390/mi16091047