Accelerated Super-Resolution Reconstruction for Structured Illumination Microscopy Integrated with Low-Light Optimization
Abstract
1. Introduction
2. Methods and System
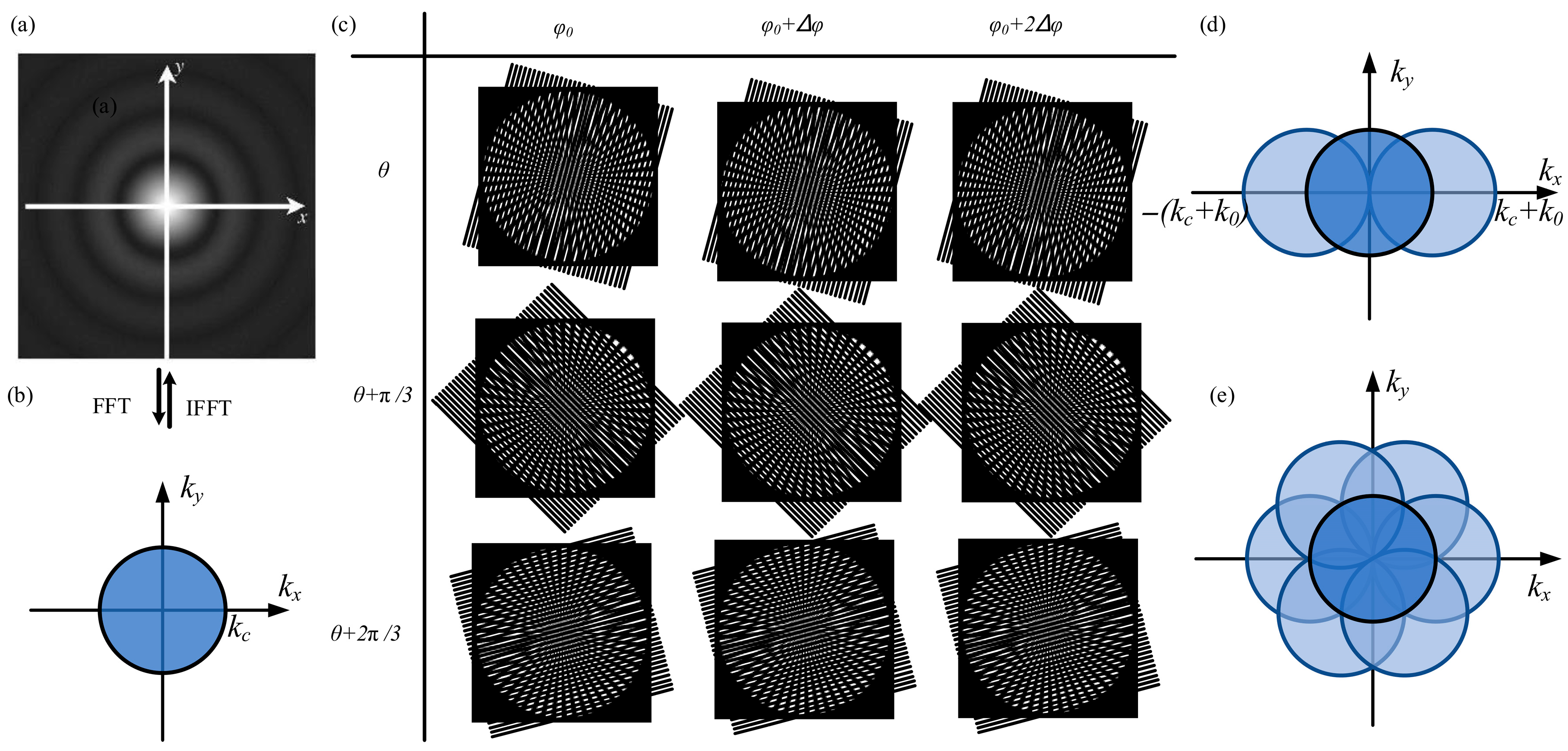
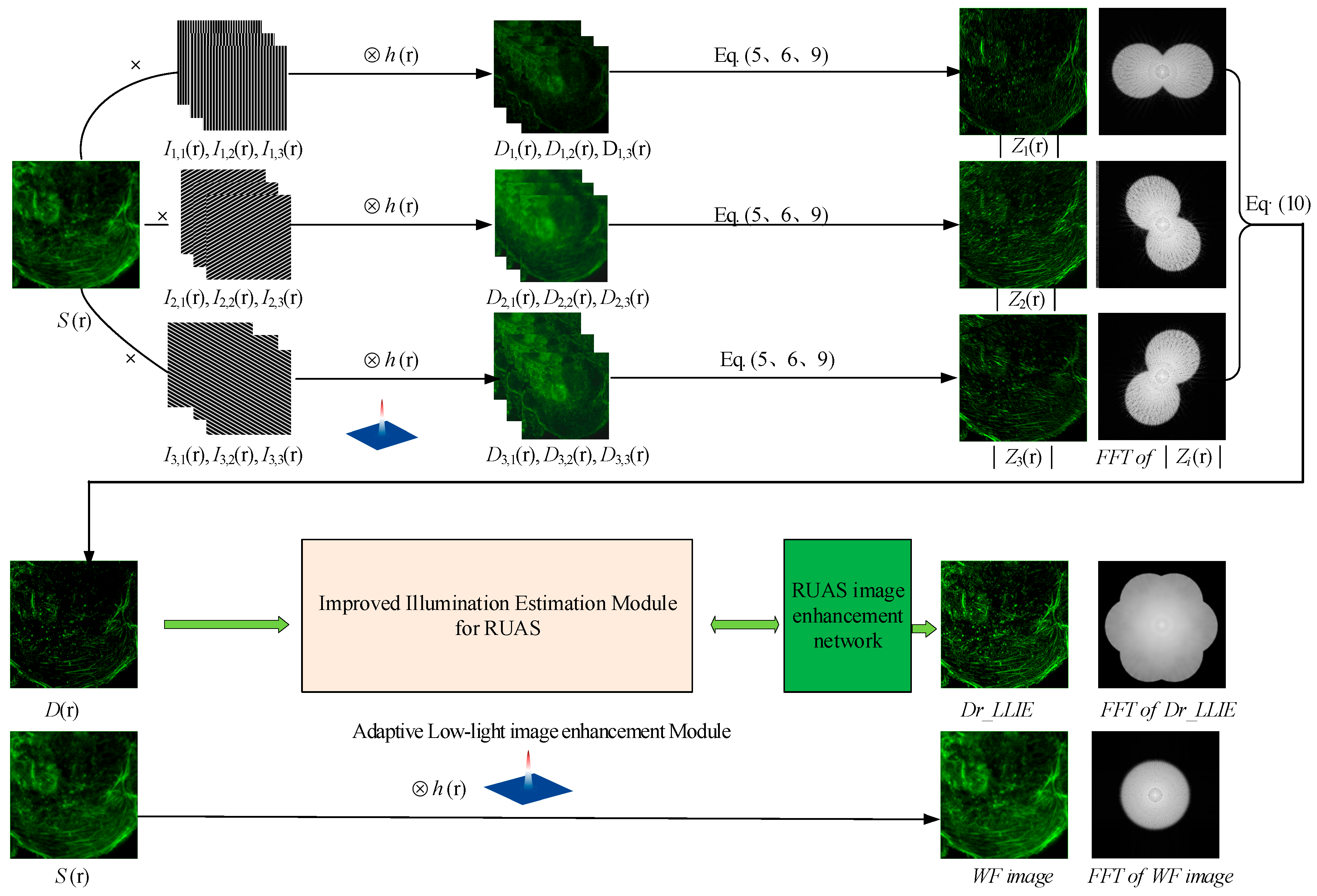
2.1. Principle of DM-SIM
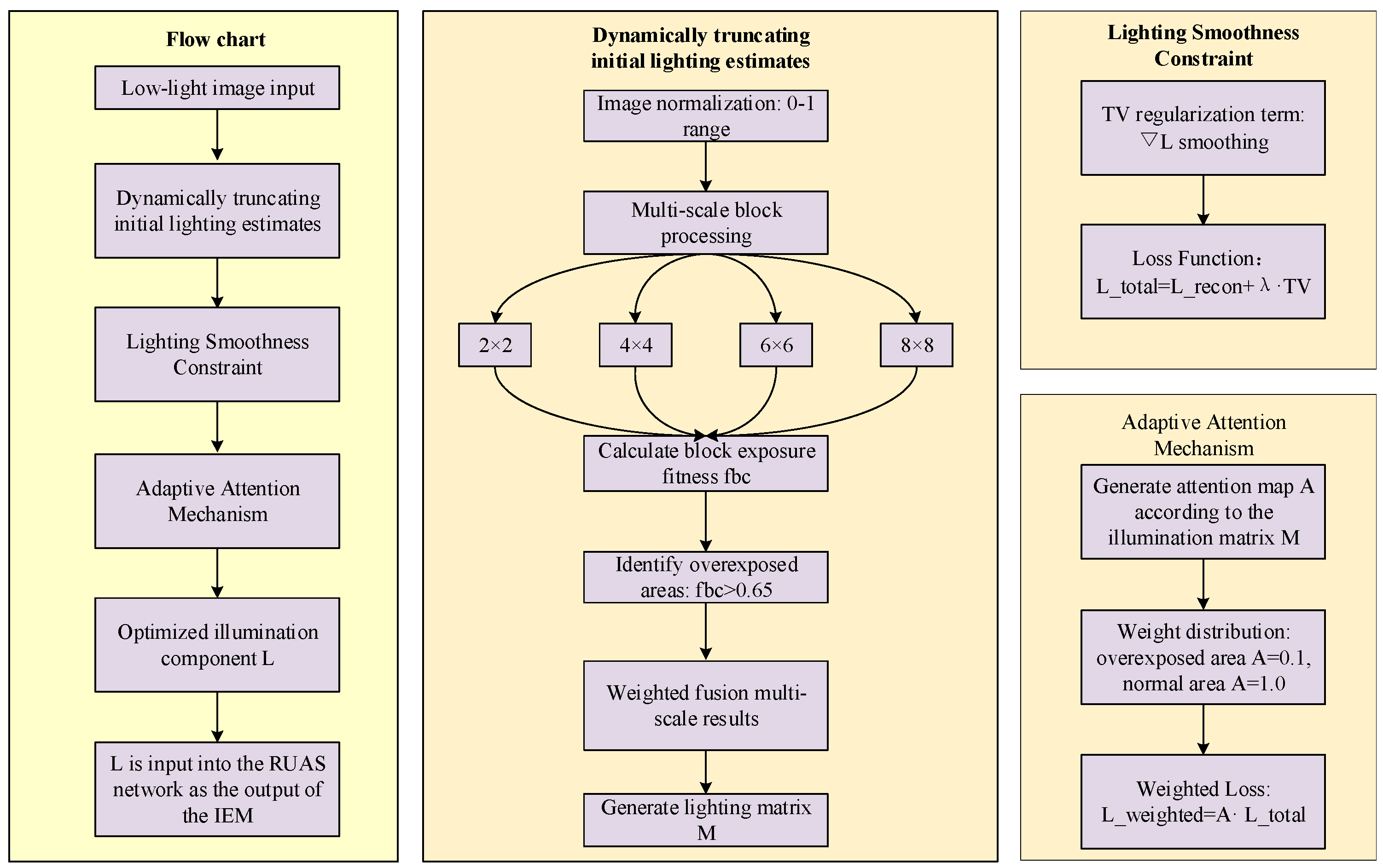
2.2. LLIE Principle and Improved Illumination Estimation Method
- Local overexposure problem: Under non-uniform illumination conditions, the local maximum may correspond to the pixel value of the overexposed area. Directly using these values as the initial illumination estimation will cause the overexposed area to be over-magnified during the enhancement process, resulting in local overexposure.
- Insufficient illumination smoothness: The spatial change of illumination components should have a certain smoothness, but the local maximum estimation method of the RUAS algorithm cannot effectively constrain the smooth transition of illumination components, and it is easy to produce mutations in local areas, further exacerbating the overexposure problem.
2.3. Flowchart of DM-SIM-LLIE Method
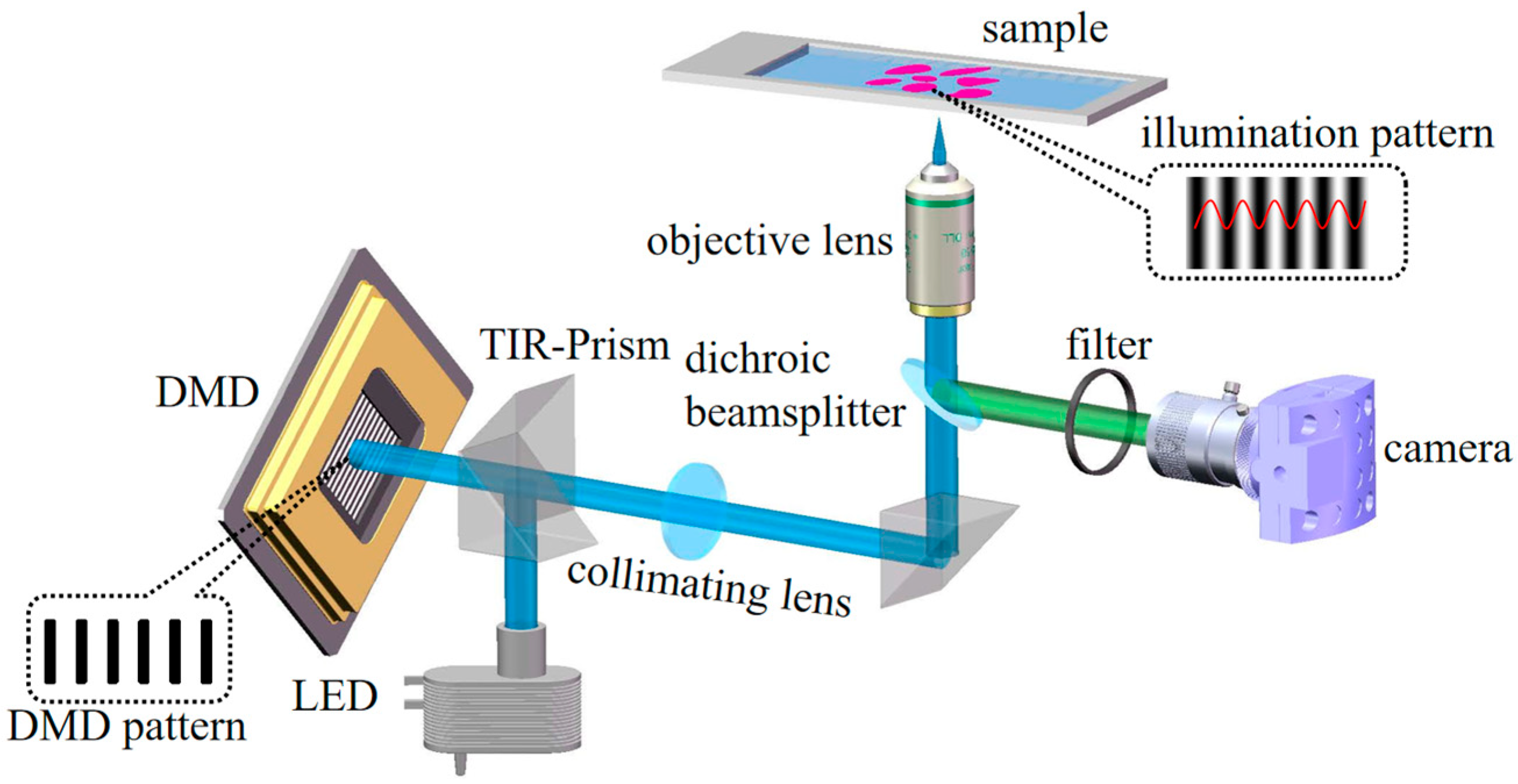
3. Experimental System Setup
4. Results and Discussion
4.1. Improved Lateral Resolution Results and Analysis
4.2. Low-Light Image Enhancement Verification
4.3. Image Reconstruction Results After Combining the LLIE Process
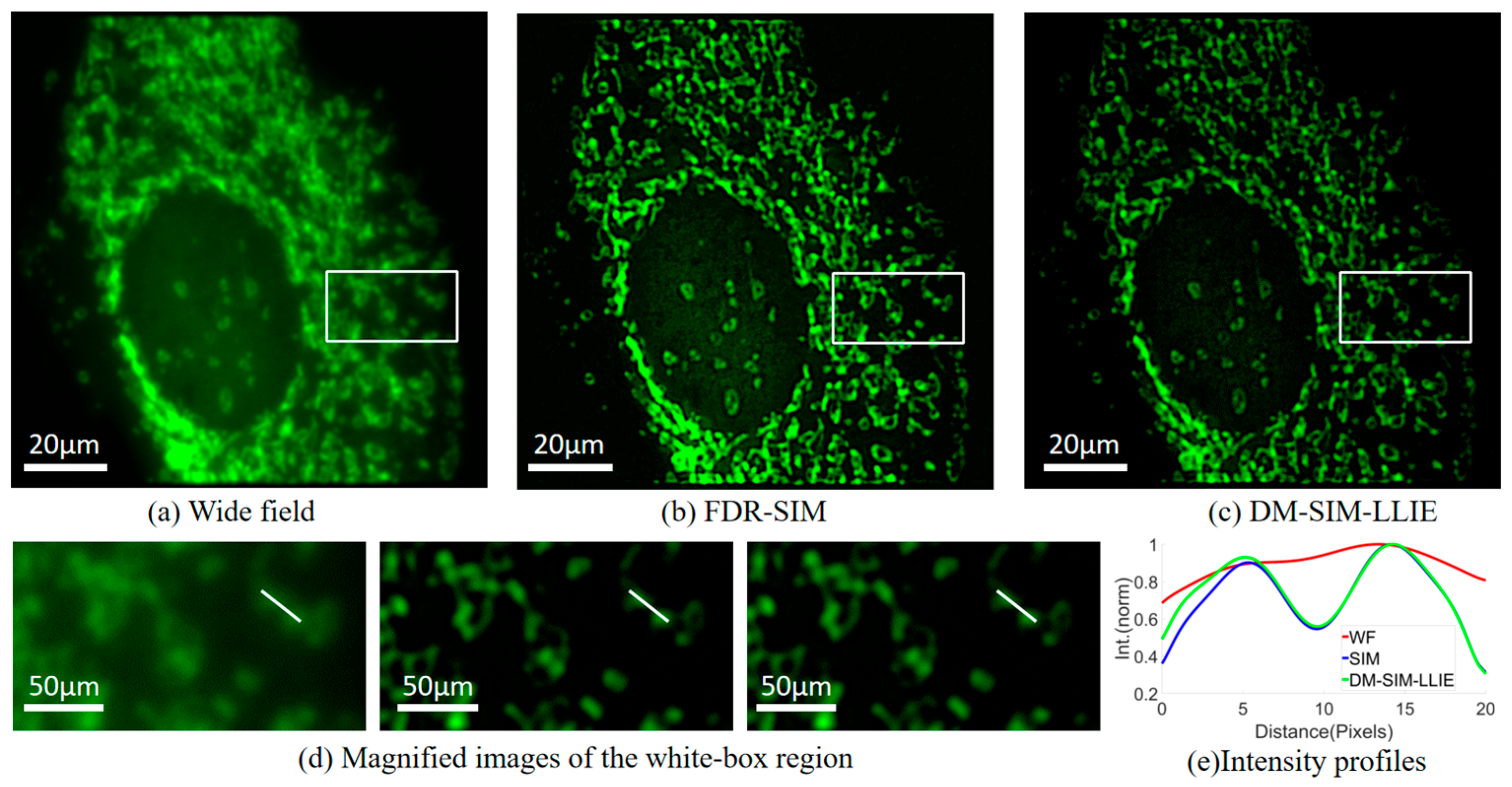
4.4. Comparison of DM-SIM-LLIE with FDR-SIM
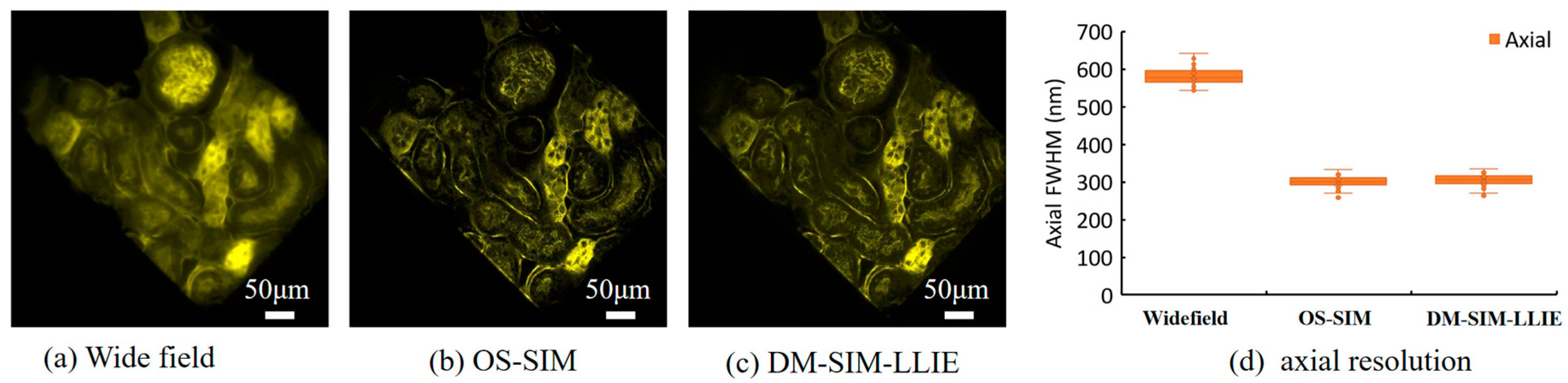
4.5. Improved Axial Resolution Results and Analysis
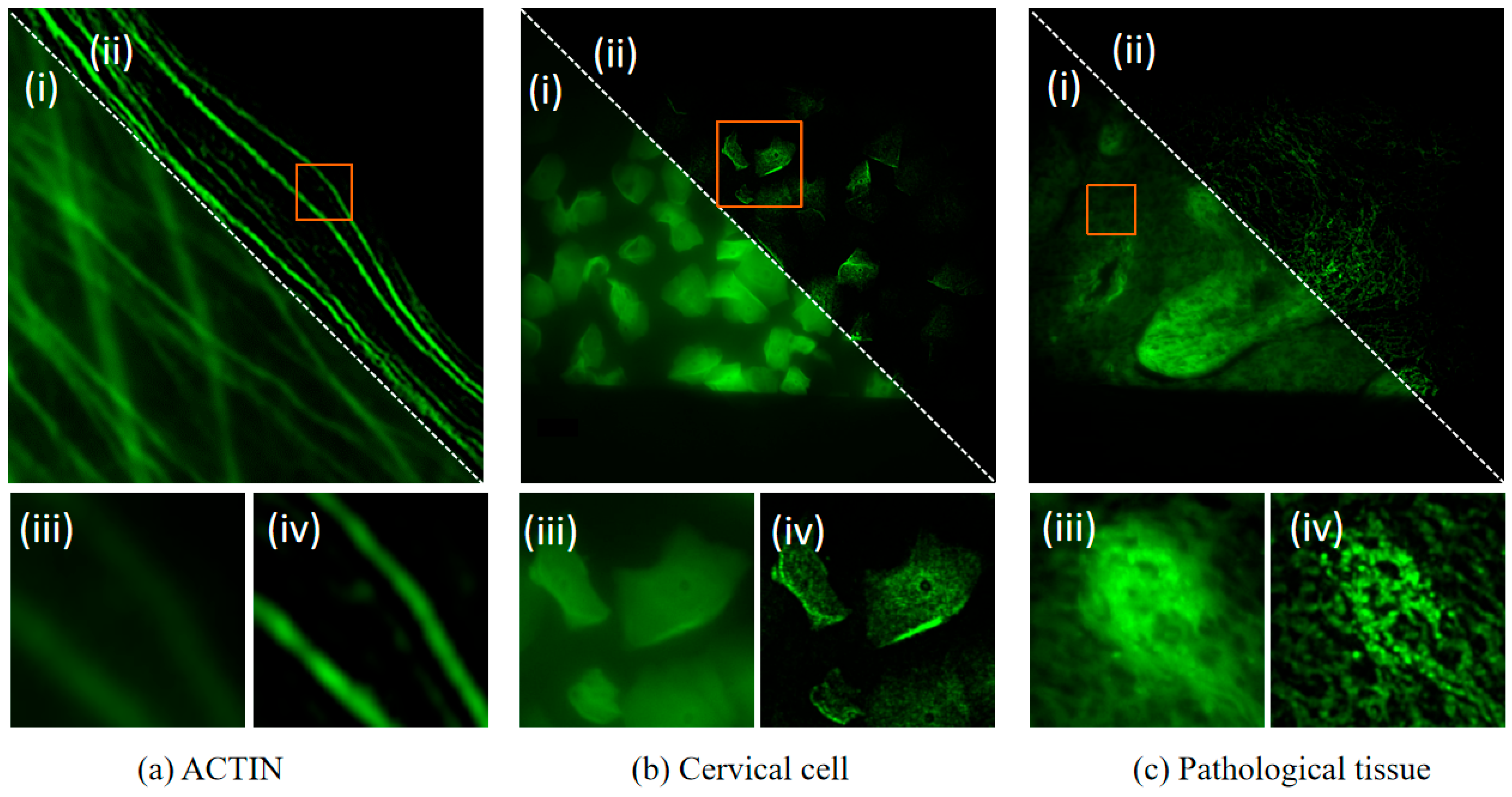
4.6. Experimental Evaluation on Different Samples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbe, E. Beiträge zur Theorie des Mikroskops und der mikroskopischen Wahrnehmung. Arch. Mikrosk. Anat. 1873, 9, 456–468. [Google Scholar] [CrossRef][Green Version]
- Gustafsson, M.G. Nonlinear structured-illumination microscopy: Wide-field fluorescence imaging with theoretically unlimited resolution. Proc. Natl. Acad. Sci. USA 2005, 102, 13081–13086. [Google Scholar] [CrossRef]
- Chen, X.; Zhong, S.; Hou, Y.; Cao, R.; Wang, W.; Li, D.; Dai, Q.; Kim, D.; Xi, P. Superresolution structured illumination microscopy reconstruction algorithms: A review. Light Sci. Appl. 2023, 12, 172. [Google Scholar] [CrossRef] [PubMed]
- Prakash, K.; Diederich, B.; Reichelt, S.; Heintzmann, R.; Schermelleh, L. Super-resolution structured illumination microscopy: Past, present and future. Philos. Trans. R. Soc. A 2021, 379, 20200143. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Wen, K.; Liu, M.; Zheng, J.; Chu, K.; Smith, Z.J.; Liu, L.; Gao, P. Recent advances in structured illumination microscopy. J. Phys. Photonics 2021, 3, 024009. [Google Scholar] [CrossRef]
- Prakash Singh, S.; Raja, S.; Mahalingam, S. Lentiviral Vpx induces alteration of mammalian cell nuclear envelope integrity. Biochem. Biophys. Res. Commun. 2019, 511, 192–198. [Google Scholar] [CrossRef]
- Wang, Y.; Guan, M.; Wang, H.; Li, Y.; Zhang, K.; Xi, P.; Zhang, Y. The largest isoform of Ankyrin-G is required for lattice structure of the axon initial segment. Biochem. Biophys. Res. Commun. 2021, 578, 28–34. [Google Scholar] [CrossRef]
- Dan, D.; Wang, Z.; Zhou, X.; Lei, M.; Zhao, T.; Qian, J.; Yu, X.; Yan, S.; Min, J.; Bianco, P.R.; et al. Rapid Image Reconstruction of Structured Illumination Microscopy Directly in the Spatial Domain. IEEE Photonics J. 2021, 13, 1–11. [Google Scholar] [CrossRef]
- Shroff, S.A.; Fienup, J.R.; Williams, D.R. Phase-shift estimation in sinusoidally illuminated images for lateral superresolution. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2009, 26, 413–424. [Google Scholar] [CrossRef]
- Wicker, K. Non-iterative determination of pattern phase in structured illumination microscopy using auto-correlations in Fourier space. Opt. Express 2013, 21, 24692. [Google Scholar] [CrossRef]
- Zhou, X.; Lei, M.; Dan, D.; Yao, B.; Yang, Y.; Qian, J.; Chen, G.; Bianco, P.R. Image recombination transform algorithm for superresolution structured illumination microscopy. J. Biomed. Opt. 2016, 21, 096009. [Google Scholar] [CrossRef]
- Li, M.; Li, Y.; Liu, W.; Lal, A.; Jiang, S.; Jin, D.; Yang, H.; Wang, S.; Zhang, K.; Xi, P. Structured illumination microscopy using digital micro-mirror device and coherent light source. Appl. Phys. Lett. 2020, 116, 233702. [Google Scholar] [CrossRef]
- Dong, S.; Liao, J.; Guo, K.; Bian, L.; Suo, J.; Zheng, G. Resolution doubling with a reduced number of image acquisitions. Biomed. Opt. Express 2015, 6, 2946–2952. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Q.; Zhang, J.; Ye, Z.; Ye, H.; Zhu, Y.; Kuang, C.; Chen, Y.; Liu, W. Deep learning enables contrast-robust super-resolution reconstruction in structured illumination microscopy. Opt. Express 2024, 32, 3316–3328. [Google Scholar] [CrossRef]
- Ling, C.; Zhang, C.; Wang, M.; Meng, F.; Du, L.; Yuan, X. Fast structured illumination microscopy via deep learning. Photonics Res. 2020, 8, 1350–1359. [Google Scholar] [CrossRef]
- Song, L.; Liu, X.; Xiong, Z.; Ahamed, M.; An, S.; Zheng, J.; Ma, Y.; Gao, P. Super-resolution reconstruction of structured illumination microscopy using deep-learning and sparse deconvolution. Opt. Lasers Eng. 2024, 174, 107968. [Google Scholar] [CrossRef]
- Li, X.R.; Chen, J.J.; Wang, M.T. Advancement in Structured Illumination Microscopy Based on Deep Learning. Chin. J. Lasers-Zhongguo Jiguang 2024, 51, 2107103. [Google Scholar]
- Qian, J.; Wang, C.; Wu, H.; Chen, Q.; Zuo, C. Ensemble deep learning-enabled single-shot composite structured illumination microscopy (eDL-cSIM). PhotoniX 2025, 6, 1–21. [Google Scholar] [CrossRef]
- Chen, X.; Qiao, C.; Jiang, T.; Liu, J.; Meng, Q.; Zeng, Y.; Chen, H.; Qiao, H.; Li, D.; Wu, J. Self-supervised denoising for multimodal structured illumination microscopy enables long-term super-resolution live-cell imaging. PhotoniX 2024, 5, 4. [Google Scholar] [CrossRef]
- Saurabh, A.; Brown, P.T.; Bryan, J.S., IV; Fox, Z.R.; Kruithoff, R.; Thompson, C.; Kural, C.; Shepherd, D.P.; Pressé, S. Approaching maximum resolution in structured illumination microscopy via accurate noise modeling. Npj Imaging 2025, 3, 5. [Google Scholar] [CrossRef] [PubMed]
- Tu, S.; Liu, Q.; Liu, X.; Liu, W.; Zhang, Z.; Luo, T.; Kuang, C.; Liu, X.; Hao, X. Fast reconstruction algorithm for structured illumination microscopy. Opt. Lett. 2020, 45, 1567–1570. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Hao, H.; Wang, Z.; Liang, Y.; Feng, K.; He, M.; Yun, X.; Bianco, P.R.; Sun, Y.; Yao, B.; et al. Multi-color structured illumination microscopy for live cell imaging based on the enhanced image recombination transform algorithm. Biomed. Opt. Express 2021, 12, 3474–3484. [Google Scholar] [CrossRef]
- Tang, H.; Zhu, H.; Fei, L.; Wang, T.; Cao, Y.; Xie, C. Low-illumination image enhancement based on deep learning techniques: A brief review. Photonics 2023, 10, 198. [Google Scholar] [CrossRef]
- Liu, R.; Ma, L.; Zhang, J.; Fan, X.; Luo, Z. Retinex-inspired unrolling with cooperative prior architecture search for low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 2 November 2021. [Google Scholar]
- Liu, P.; Wang, Y.; Yang, J.; Li, W. An adaptive enhancement method for gastrointestinal low-light images of capsule endoscope. In Proceedings of the ICASSP 2023—2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023. [Google Scholar]
- Dan, D.; Yao, B.; Lei, M. Structured illumination microscopy for super-resolution and optical sectioning. Chin. Sci. Bull. 2014, 59, 1291–1307. [Google Scholar] [CrossRef]
- Lal, A.; Shan, C.; Xi, P. Structured Illumination Microscopy Image Reconstruction Algorithm. IEEE J. Sel. Top. Quantum Electron. 2016, 22, 50–63. [Google Scholar] [CrossRef]
- Dan, D.; Ming, L.; Baoli, Y. DMD-based LED-illumination super-resolution and optical sectioning microscopy. Sci. Rep. 2013, 23, 1116. [Google Scholar] [CrossRef]
- Qiao, C.; Li, D. BioSR: A biological image dataset for super-resolution microscopy. Figshare 2020, 9, 13264793. [Google Scholar]
- Qiao, C.; Li, D.; Guo, Y.; Liu, C.; Jiang, T.; Dai, Q.; Li, D. Evaluation and development of deep neural networks for image super-resolution in optical microscopy. Nat. Methods 2021, 18, 194–202. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Ma, T.; Liu, R.; Fan, X.; Luo, Z. Toward fast, flexible, and robust low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Jiang, Y.; Gong, X.; Liu, D.; Cheng, Y.; Fang, C.; Shen, X.; Yang, J.; Zhou, P.; Wang, Z. Deep light enhancement without paired supervision. IEEE Trans. Image Process. 2021, 30, 2340–2349. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Guo, C.; Chen, C.L. Learning to enhance low-light image via zero-reference deep curve estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 4225–4238. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Guo, X.; Ma, J.; Liu, W.; Zhang, J. Beyond brightening low-light images. Int. J. Comput. Vis. 2021, 129, 1013–1037. [Google Scholar] [CrossRef]
- Wei, C.; Wang, W.; Yang, W.; Liu, J. Deep retinex decomposition for low-light enhancement. arXiv 2018, arXiv:1808.04560. [Google Scholar] [CrossRef]
- Wu, W.; Weng, J.; Zhang, P.; Wang, X.; Yang, W.; Jiang, J. Uretinex-net: Retinex-based deep unfolding network for low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Bai, J.; Yin, Y.; He, Q.; Li, Y.; Zhang, X. Retinexmamba: Retinex-based mamba for low-light image enhancement. arXiv 2024, arXiv:2405.03349. [Google Scholar]
- Müller, M.; Mönkemöller, V.; Hennig, S.; Hübner, W.; Huser, T. Open-source image reconstruction of super-resolution structured illumination microscopy data in ImageJ. Nat. Commun. 2016, 7, 10980. [Google Scholar] [CrossRef] [PubMed]

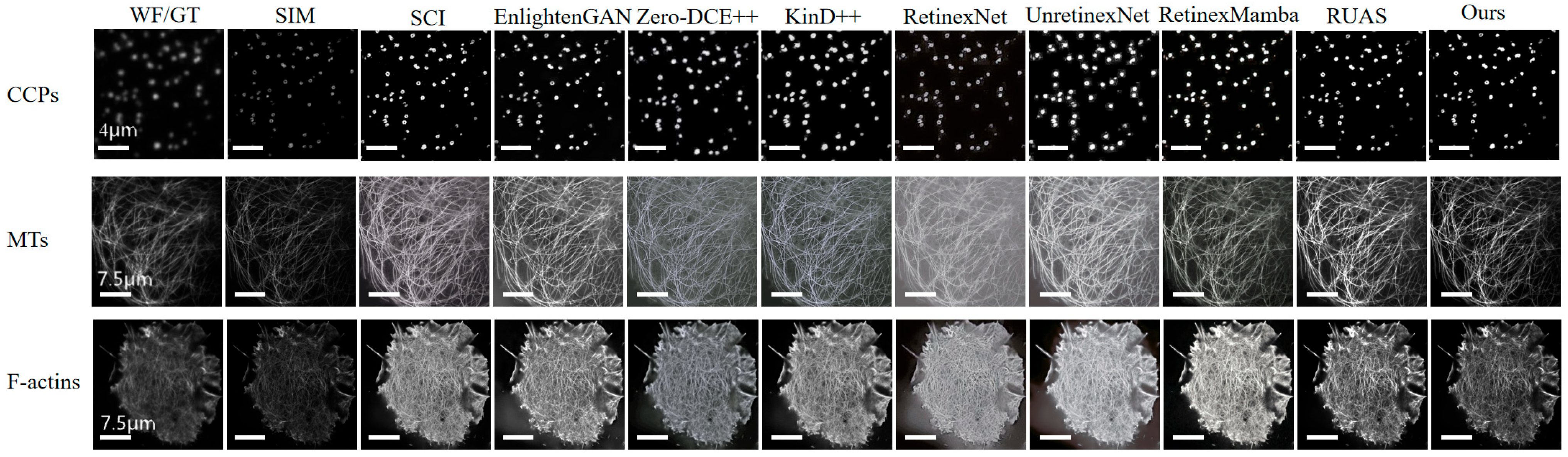

| Dataset | Metrics | SCI | EnGAN | ZeroDCE++ | Kind++ | RetinexNet | UnretNet | RetMamba | RUAS | Ours |
|---|---|---|---|---|---|---|---|---|---|---|
| CCPS | SSIM↑ | 0.856 | 0.159 | 0.509 | 0.677 | 0.061 | 0.582 | 0.193 | 0.878 | 0.893 |
| PSNR↑ | 19.941 | 19.477 | 14.958 | 16.263 | 16.714 | 15.586 | 16.440 | 20.255 | 20.490 | |
| CII↑ | 2.888 | 2.731 | 3.294 | 4.163 | 2.027 | 4.337 | 3.831 | 2.745 | 2.702 | |
| RMSE↓ | 25.673 | 27.081 | 45.568 | 39.206 | 37.225 | 42.386 | 38.415 | 24.763 | 24.102 | |
| MTs | SSIM↑ | 0.347 | 0.361 | 0.384 | 0.453 | 0.263 | 0.309 | 0.569 | 0.474 | 0.699 |
| PSNR↑ | 10.466 | 10.124 | 10.822 | 11.256 | 7.279 | 7.275 | 15.076 | 12.247 | 17.130 | |
| CII↑ | 2.809 | 2.393 | 1.868 | 2.003 | 1.450 | 2.436 | 2.125 | 3.086 | 2.101 | |
| RMSE↓ | 76.428 | 79.491 | 73.354 | 86.367 | 110.301 | 110.347 | 44.947 | 62.261 | 35.483 | |
| F-actions | SSIM↑ | 0.427 | 0.271 | 0.256 | 0.256 | 0.1799 | 0.295 | 0.274 | 0.576 | 0.782 |
| PSNR↑ | 11.126 | 10.363 | 10.441 | 11.472 | 8.603 | 7.549 | 8.582 | 12.926 | 18.451 | |
| CII↑ | 3.942 | 3.367 | 3.769 | 3.769 | 3.518 | 4.211 | 4.904 | 3.311 | 2.194 | |
| RMSE↓ | 70.831 | 77.340 | 76.640 | 76.369 | 94.708 | 106.917 | 94.928 | 57.578 | 30.478 |
| Algorithm | Time/s |
|---|---|
| FDR-SIM FDR-SIM-LLIE | 3.90 random |
| DM-SIM DM-SIM-LLIE | 0.71 2.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.; Yi, D.; Zhou, L. Accelerated Super-Resolution Reconstruction for Structured Illumination Microscopy Integrated with Low-Light Optimization. Micromachines 2025, 16, 1020. https://doi.org/10.3390/mi16091020
Huang C, Yi D, Zhou L. Accelerated Super-Resolution Reconstruction for Structured Illumination Microscopy Integrated with Low-Light Optimization. Micromachines. 2025; 16(9):1020. https://doi.org/10.3390/mi16091020
Chicago/Turabian StyleHuang, Caihong, Dingrong Yi, and Lichun Zhou. 2025. "Accelerated Super-Resolution Reconstruction for Structured Illumination Microscopy Integrated with Low-Light Optimization" Micromachines 16, no. 9: 1020. https://doi.org/10.3390/mi16091020
APA StyleHuang, C., Yi, D., & Zhou, L. (2025). Accelerated Super-Resolution Reconstruction for Structured Illumination Microscopy Integrated with Low-Light Optimization. Micromachines, 16(9), 1020. https://doi.org/10.3390/mi16091020








