Considering the Node Level in Error Correction for DMFBs †
Abstract
1. Introduction
2. Preliminaries
2.1. DMFB (Digital MicroFluidic Biochip)
2.1.1. Architecture
2.1.2. Dilution and Splitting Operations
2.1.3. Splitting Error
2.2. REMIA
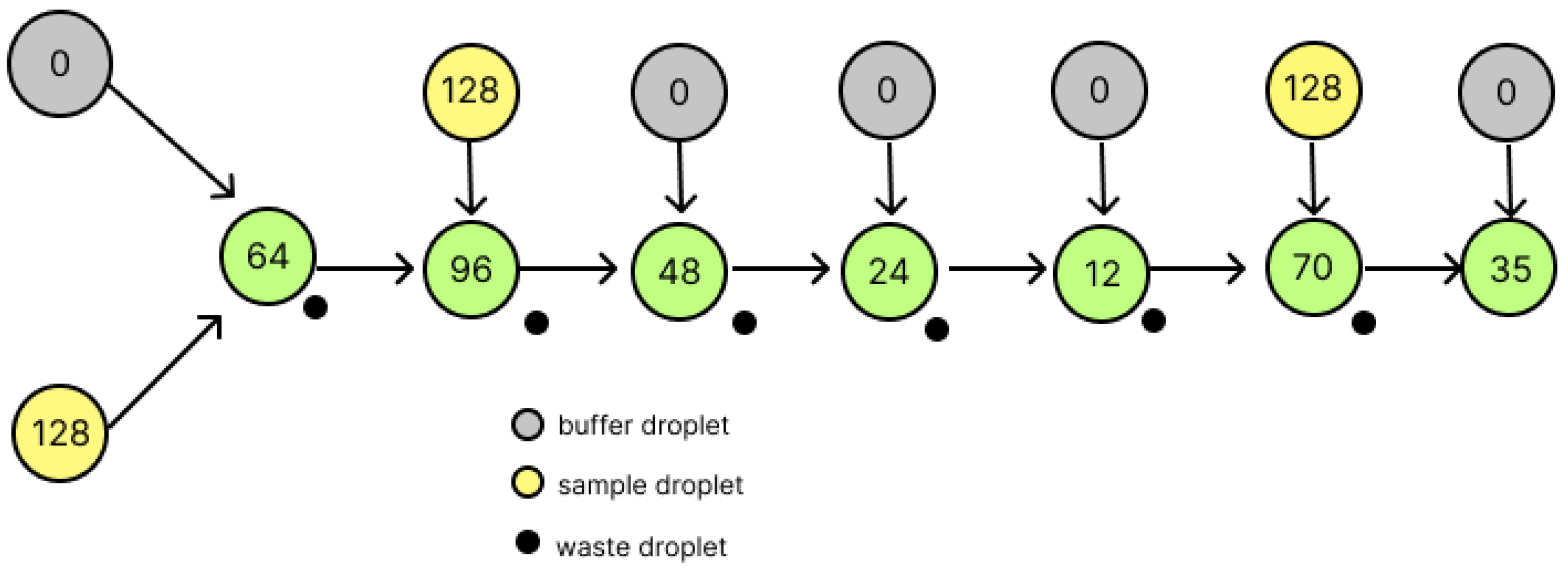
2.3. A Countermeasure Method for Division Errors by Wada et al.
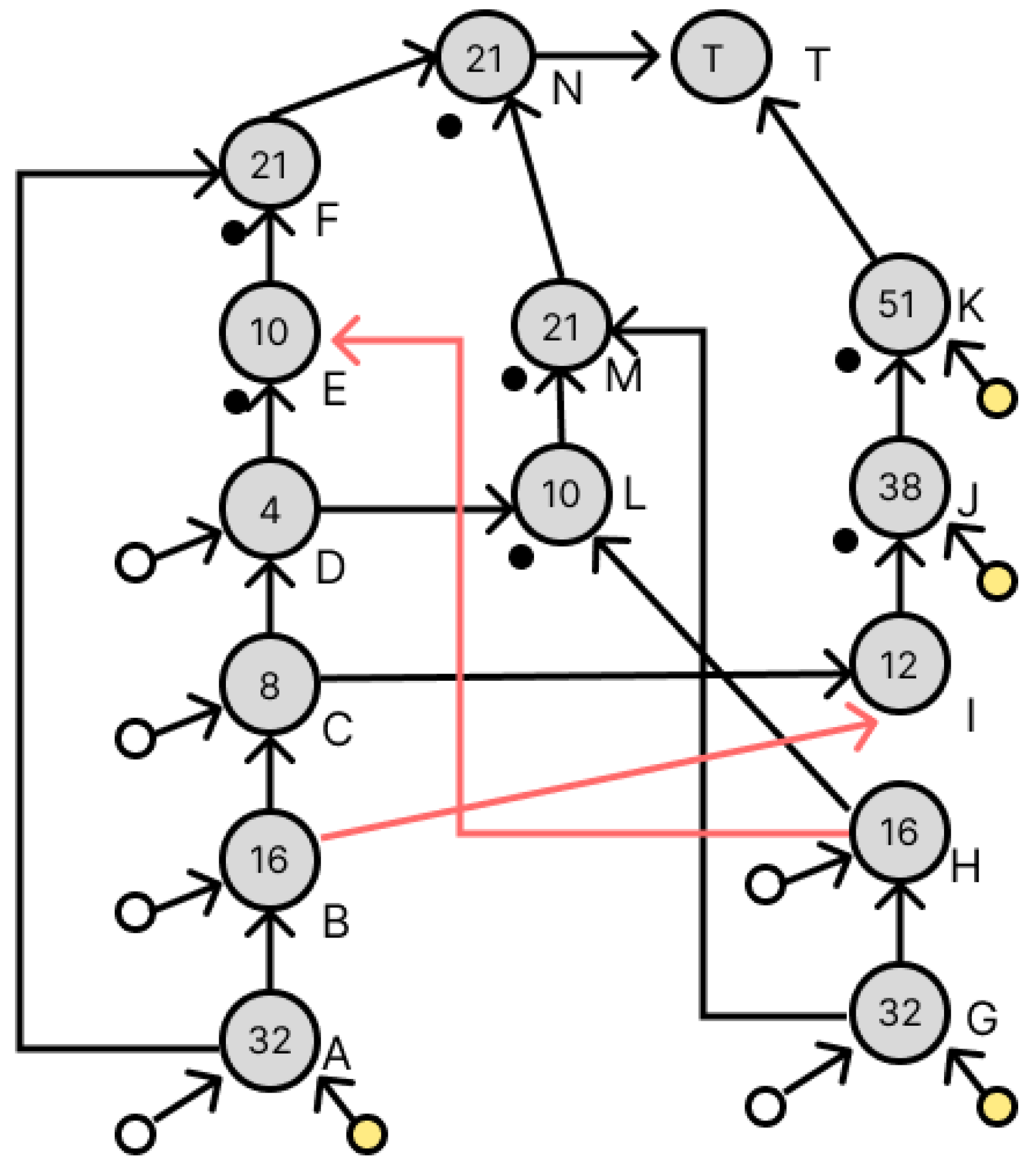
3. Error Correction Techniques Based on Node Redundancy with Node Level Consideration
3.1. Overview of the Proposed Method
3.2. Node Redundancy
3.2.1. Simple Redundancy
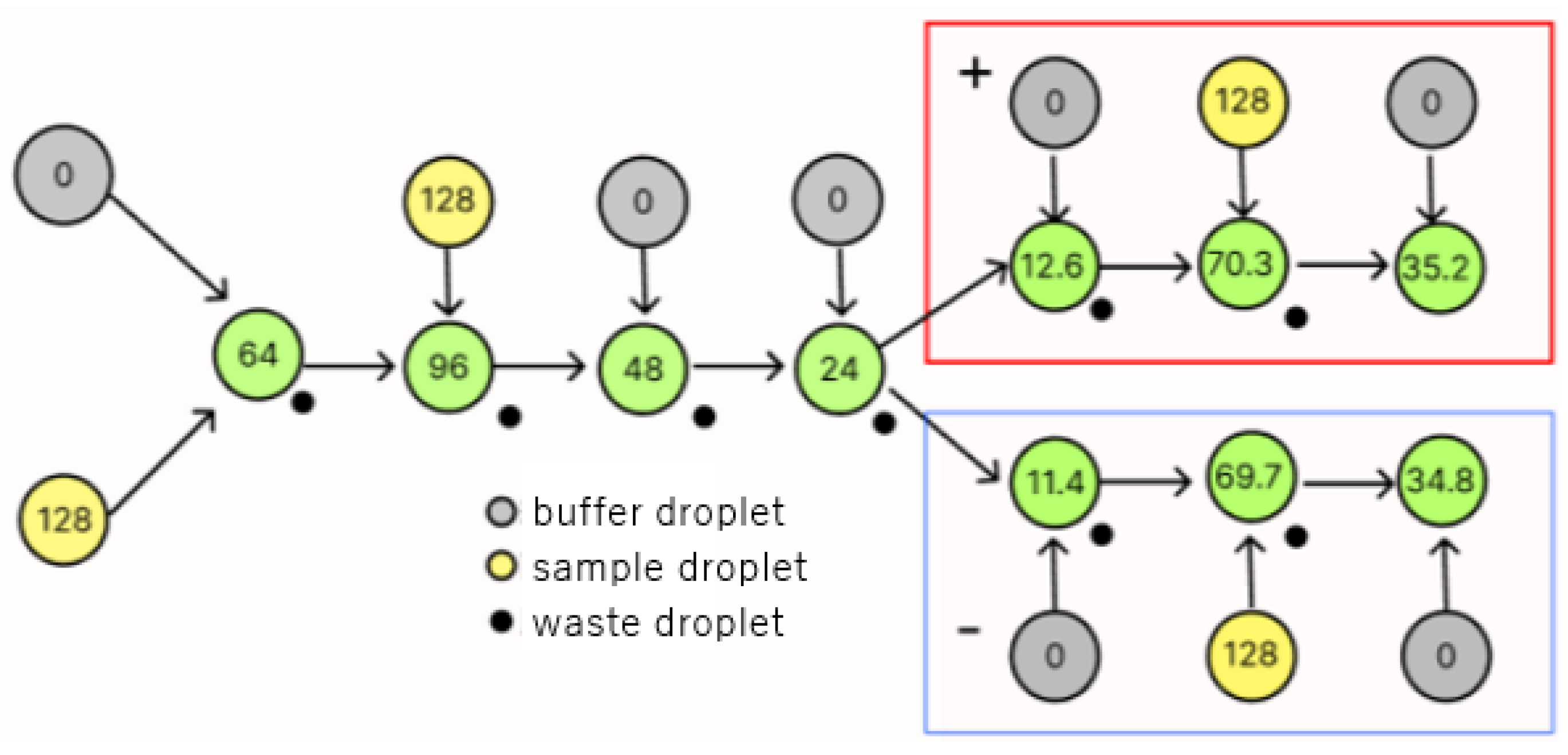
3.2.2. Redundancy Using Waste Droplets
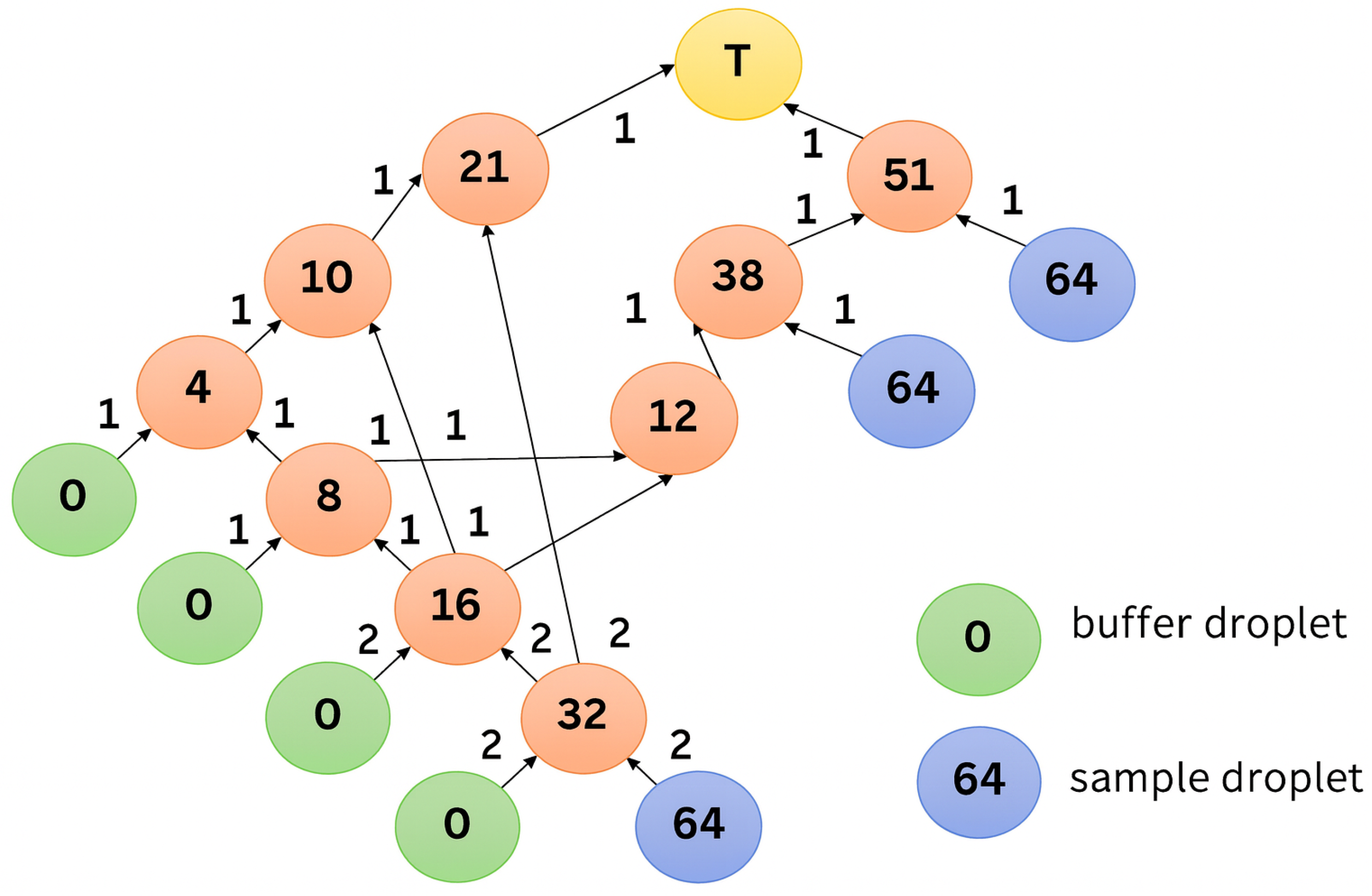
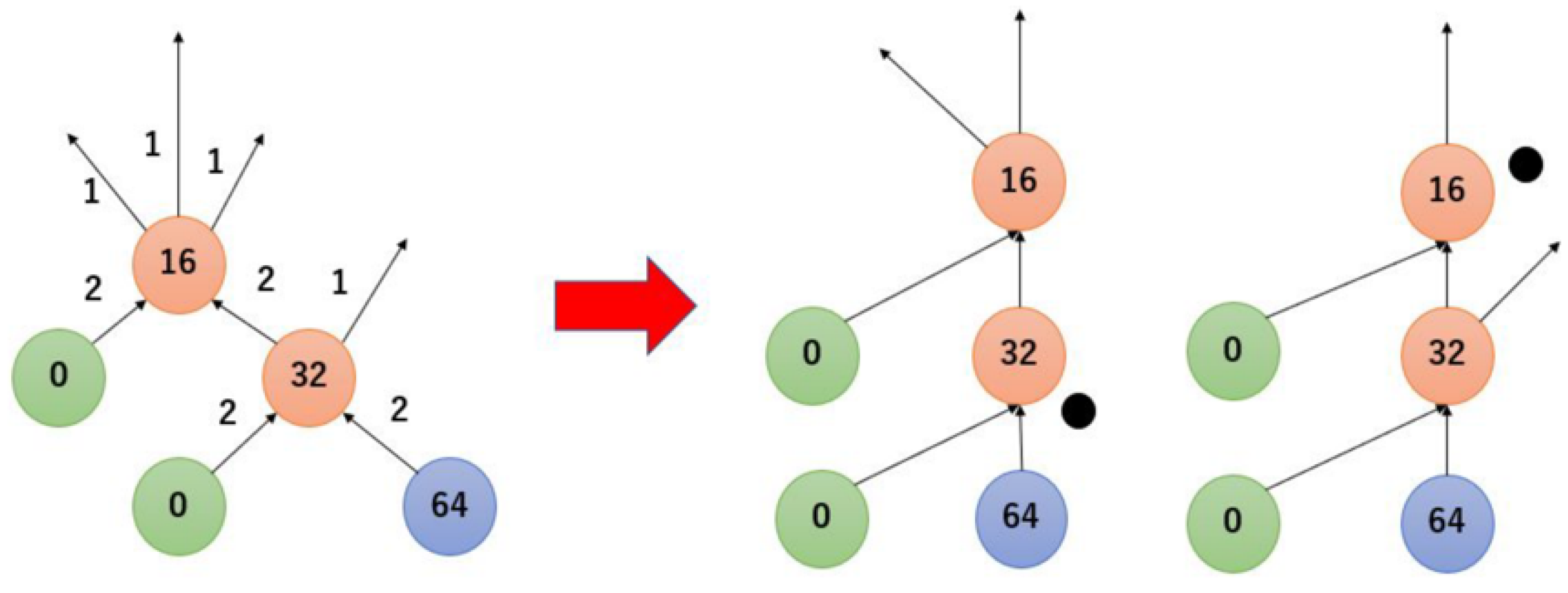
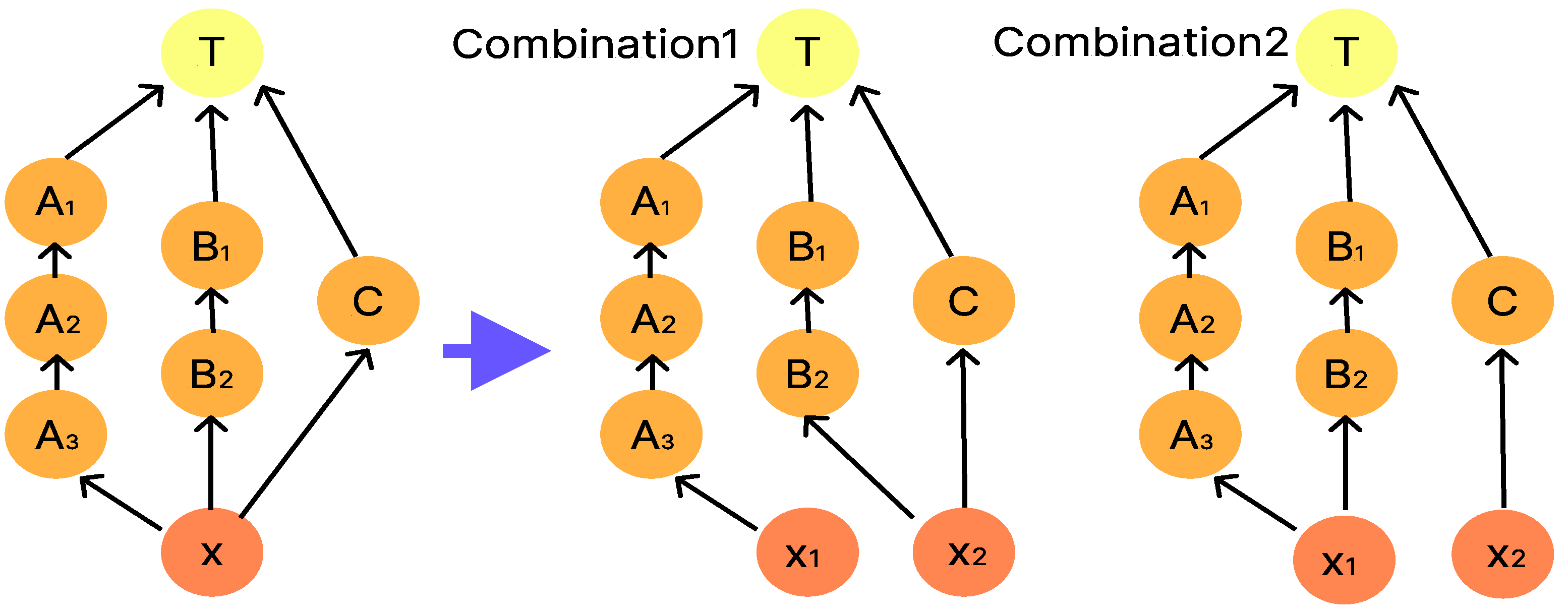
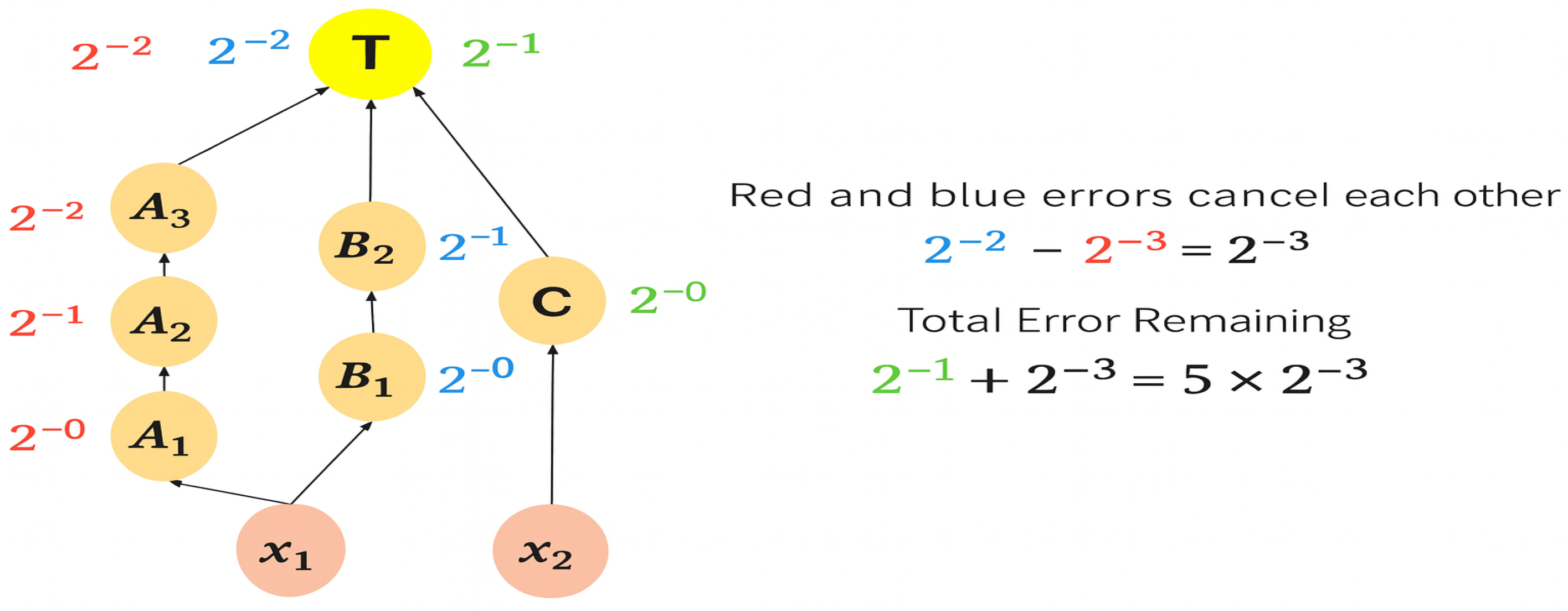
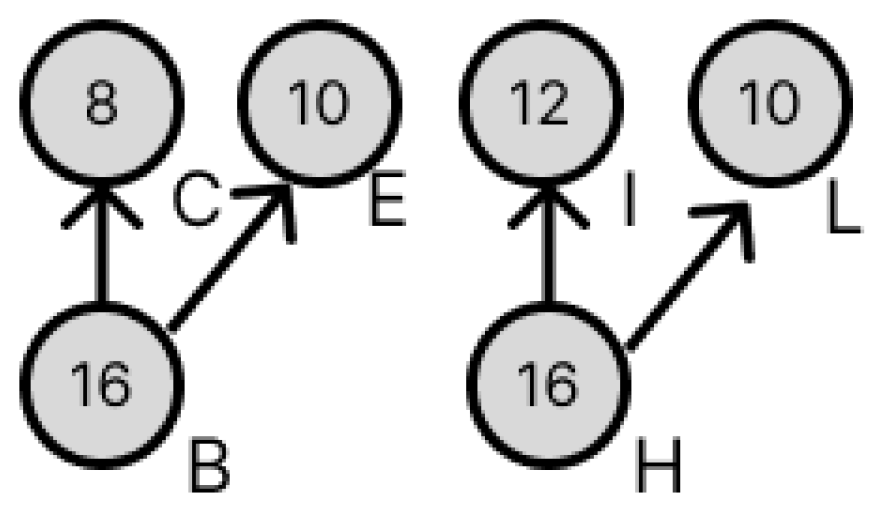
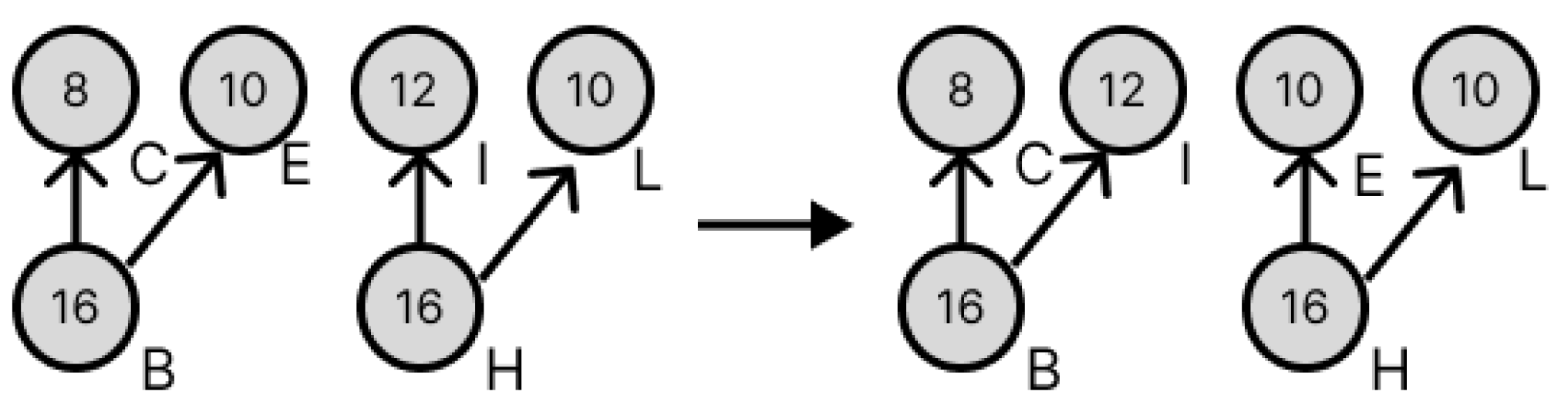
3.3. Transformation of Dilution Graphs Considering Node Level
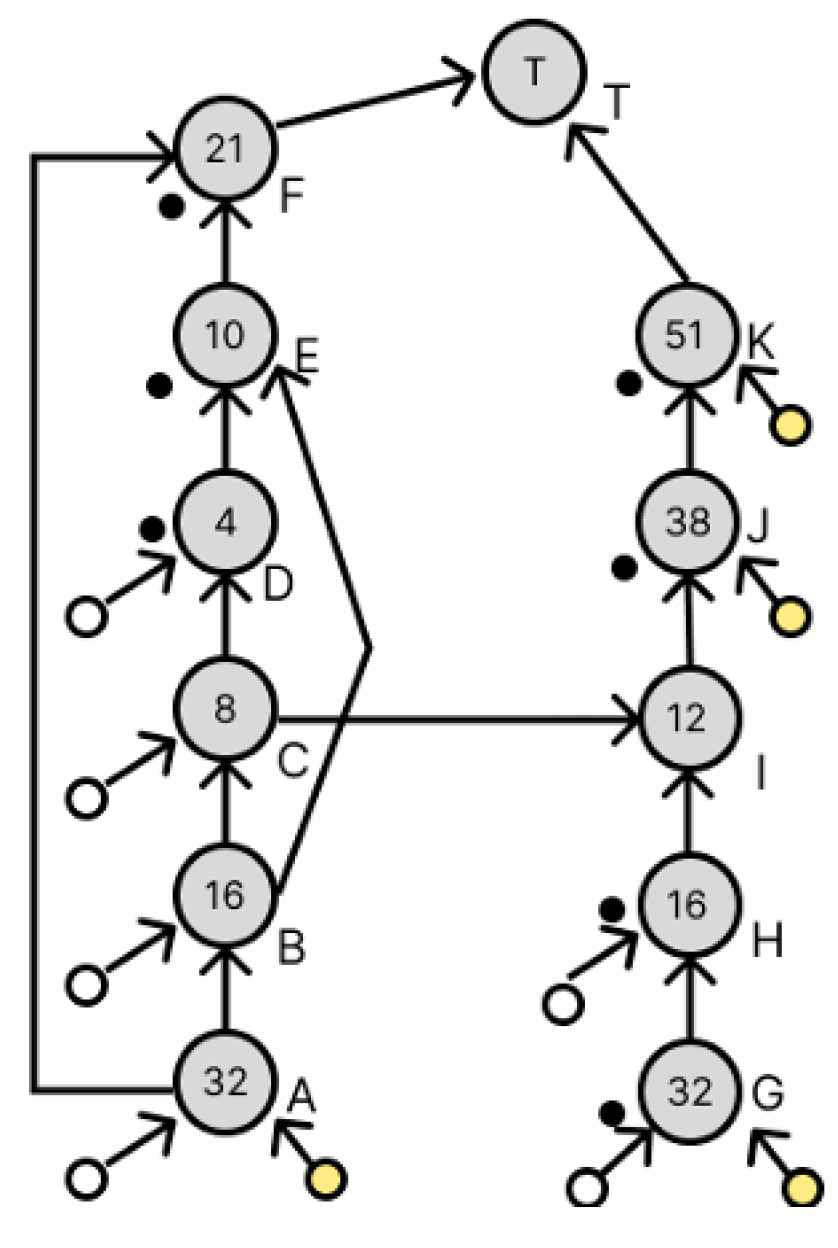
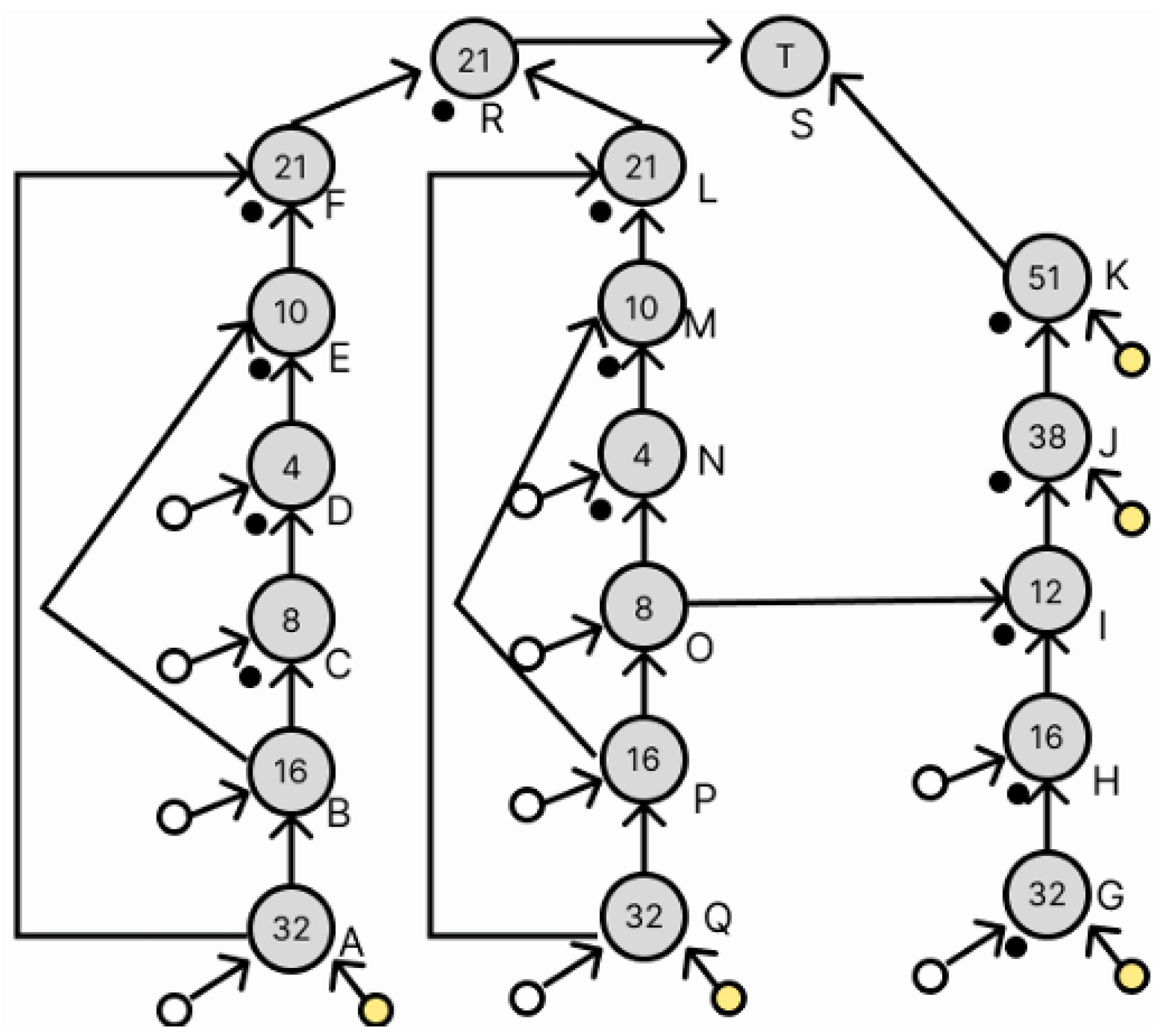
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nirmala, N.; Gracia Nirmala Rani, D.; Jeyapandi, R. Advancements and Challenges in Digital Microfluidic Biochip Applications: A Comprehensive Survey. J. Propuls. Technol. 2024, 45, 1735–1741. [Google Scholar]
- Li, Z.; Lai, K.Y.-T.; McCrone, J.; Yu, P.-H.; Chakrabarty, K.; Pajic, M.; Ho, T.-Y.; Lee, C.-Y. Efficient and adaptive error recovery in a micro-electrode-dot-array digital microfluidic biochip. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2017, 37, 601–614. [Google Scholar] [CrossRef]
- Fair, R.B. Digital microfluidics: Is a true lab-on-a-chip possible? Microfluid. Nanofluid. 2007, 3, 245–281. [Google Scholar] [CrossRef]
- Kolluri, R.; Phani Kumar, J.V.; Pyne, S. Heterogeneous earliest finish time based scheduling for digital microfluidic biochips. In Proceedings of the BIODEVICES 2019—12th International Conference on Biomedical Electronics and Devices, Prague, Czech Republic, 22–24 February 2019; pp. 175–182. [Google Scholar]
- Brindha, G.; Rohini, G.; Gnanakousalya, C. Genetic algorithm based optimization of single node in reformed-digital micro fluidic biochip. Indian J. Sci. Technol. 2015, 8, 1. [Google Scholar] [CrossRef]
- Keszocze, O.; Wille, R.; Drechsler, R. One-pass synthesis for digital microfluidic biochips: A survey. In Proceedings of the 2020 International Symposium on Devices, Circuits and Systems (ISDCS), Howrah, India, 4–6 March 2020; pp. 1–6. [Google Scholar]
- Poddar, S.; Wille, R.; Rahaman, H.; Bhattacharya, B.B. Erroroblivious sample preparation with digital microfluidic lab-on-chip. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 38, 1886–1899. [Google Scholar] [CrossRef]
- Poddar, S.; Ghoshal, S.; Chakrabarty, K.; Bhattacharya, B.B. Error-correcting sample preparation with cyberphysical digital microfluidic lab-on-chip. ACM Trans. Des. Autom. Electron. Syst. (TODAES) 2016, 22, 1–29. [Google Scholar] [CrossRef]
- Huang, J.-D.; Liu, C.-H.; Chiang, T.-W. Reactantminimization during sample preparation on digital microfluidicbiochips using skewed mixing trees. In Proceedings of the International Conference on Computer-Aided Design, San Jose, CA, USA, 5–8 November 2012; pp. 377–383. [Google Scholar]
- Wada, Y.; Yamashita, S. Minimizing the Impact of Unbalanced Splitting Errors on DMFBsWithout Any Overhead. In Proceedings of the 26th Euromicro Conference on Digital System Design (DSD) Conference, Golem, Albania, 6–8 September 2023; pp. 531–538. [Google Scholar]
- Song, L.-Y.; Chen, Y.-L.; Lei, Y.-C.; Huang, J.-D. Forecast-Based Sample Preparation Algorithm for Unbalanced Splitting Correction on DMFBs. In Proceedings of the 2019 IEEE 37th International Conference onComputer Design (ICCD), Abu Dhabi, United Arab Emirates, 17–20 November 2019; pp. 422–428. [Google Scholar]
- Ho, T.-Y.; Zeng, J.; Chakrabarty, K. Digital microfluidic biochips: A vision for functional diversity and more than more. In Proceedings of the 2010 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 7–11 November 2010; pp. 578–585. [Google Scholar]
- Thies, W.; Urbanski, J.P.; Thorsen, T.; Amarasinghe, S. Abstraction layers for scalable microfluidic biocomputing. Nat. Comput. 2008, 7, 255–275. [Google Scholar] [CrossRef]
- Roy, S.; Bhattacharya, B.B.; Chakrabarty, K. Optimization of dilution and mixing of biochemical samples using digital microfluidic biochips. IEEE Trans.-Comput.-Aided Design Integr. Circuits Syst. 2010, 29, 1696–1708. [Google Scholar] [CrossRef]



| Percentage of Split Errors | Frequency |
|---|---|
| 0% | 49.5% |
| 1% | 32.2% |
| 2% | 13.7% |
| 3% | 3.8% |
| 4% | 0.7% |
| 5% | 0.1% |
| Average Error | Worst Error | Number of Drops Used | Number of Dilution Operations | |
|---|---|---|---|---|
| Figure 9 (Wada et al. Method) | 0.0000467146% | 0.0202777646% | 10 | 12 |
| Figure 11 (Redundancy with Waste Droplets) | 0.0000317079% | 0.0187978745% | 10 | 15 |
| Figure 14 (Node Level Consideration) | 0.0000073830% | 0.0157602094% | 10 | 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suzuki, K.; Yamashita, S.; Tomiyama, H.; Gupta, A. Considering the Node Level in Error Correction for DMFBs. Micromachines 2025, 16, 1013. https://doi.org/10.3390/mi16091013
Suzuki K, Yamashita S, Tomiyama H, Gupta A. Considering the Node Level in Error Correction for DMFBs. Micromachines. 2025; 16(9):1013. https://doi.org/10.3390/mi16091013
Chicago/Turabian StyleSuzuki, Koki, Shigeru Yamashita, Hiroyuki Tomiyama, and Ankur Gupta. 2025. "Considering the Node Level in Error Correction for DMFBs" Micromachines 16, no. 9: 1013. https://doi.org/10.3390/mi16091013
APA StyleSuzuki, K., Yamashita, S., Tomiyama, H., & Gupta, A. (2025). Considering the Node Level in Error Correction for DMFBs. Micromachines, 16(9), 1013. https://doi.org/10.3390/mi16091013






