Passive Droplet Generation in T-Junction Microchannel: Experiments and Lattice Boltzmann Simulations
Abstract
1. Introduction
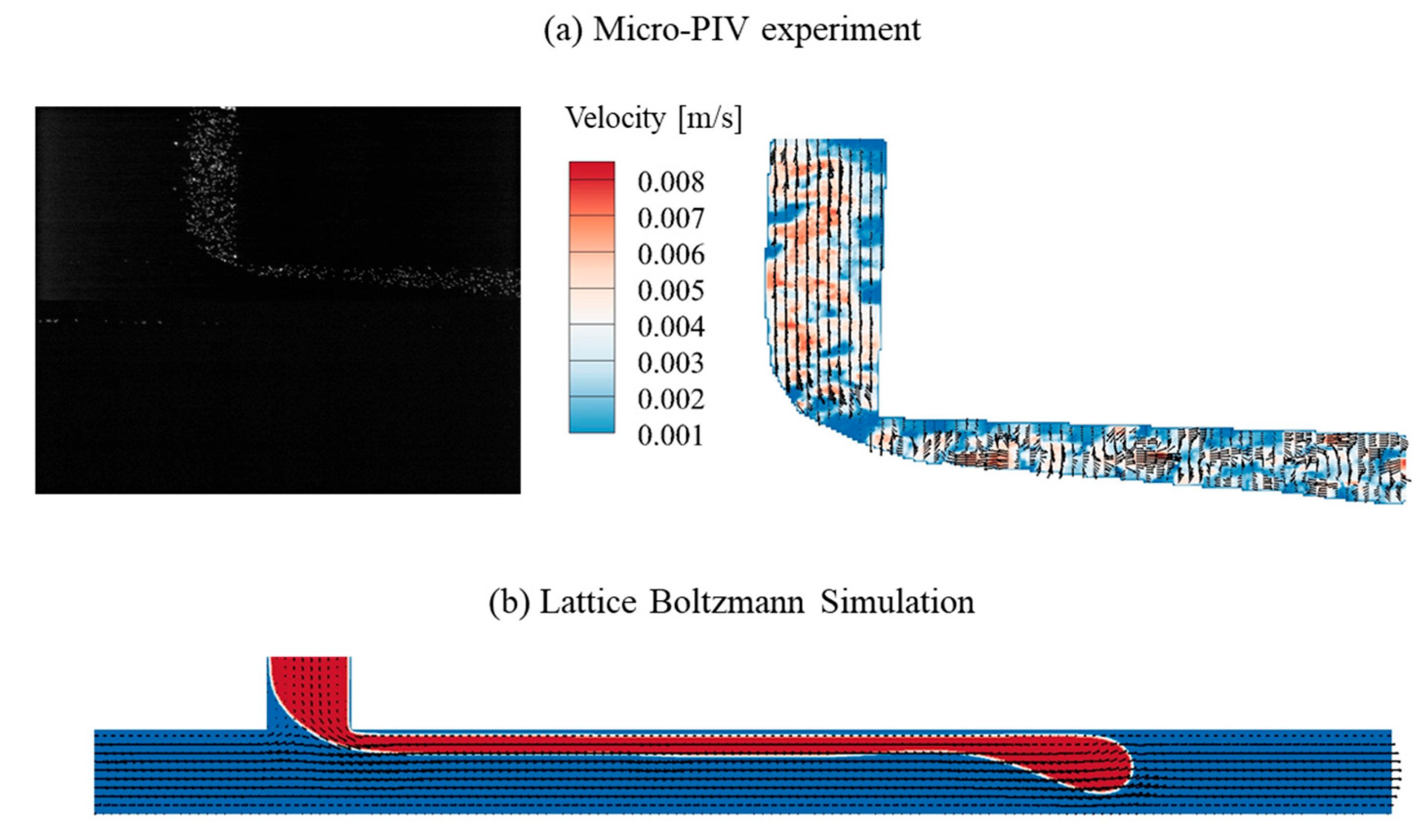
2. Experimental and Numerical Methodology
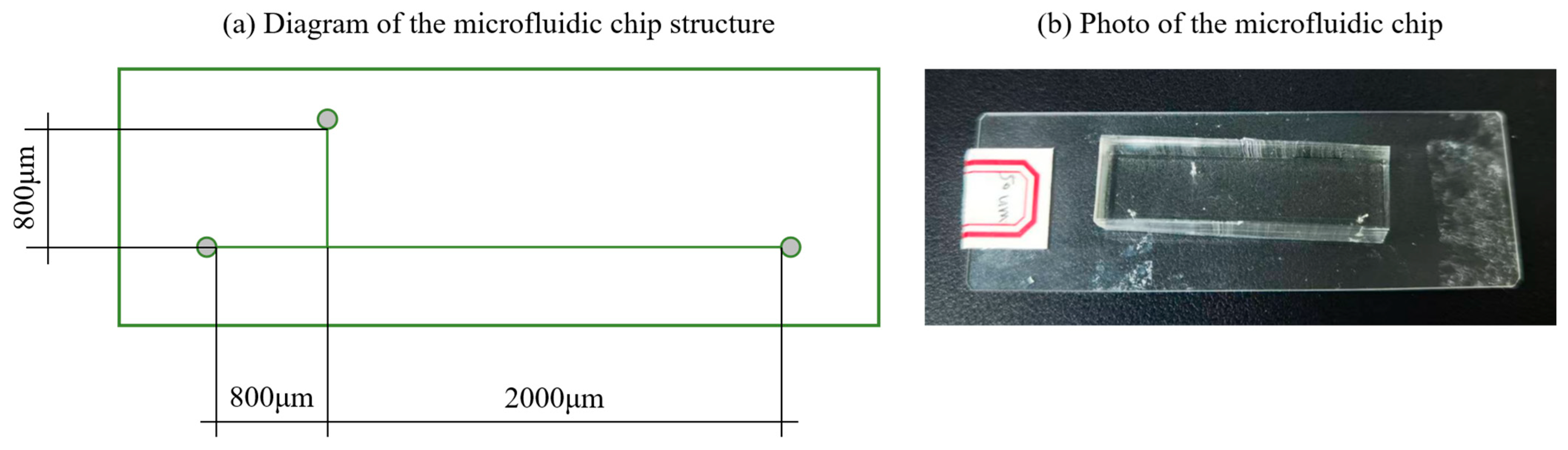
2.1. Fabrication of the T-Junction Microchannel
2.2. Experimental Setup
2.3. Governing Equations and Lattice Boltzmann Model
3. Results and Discussion
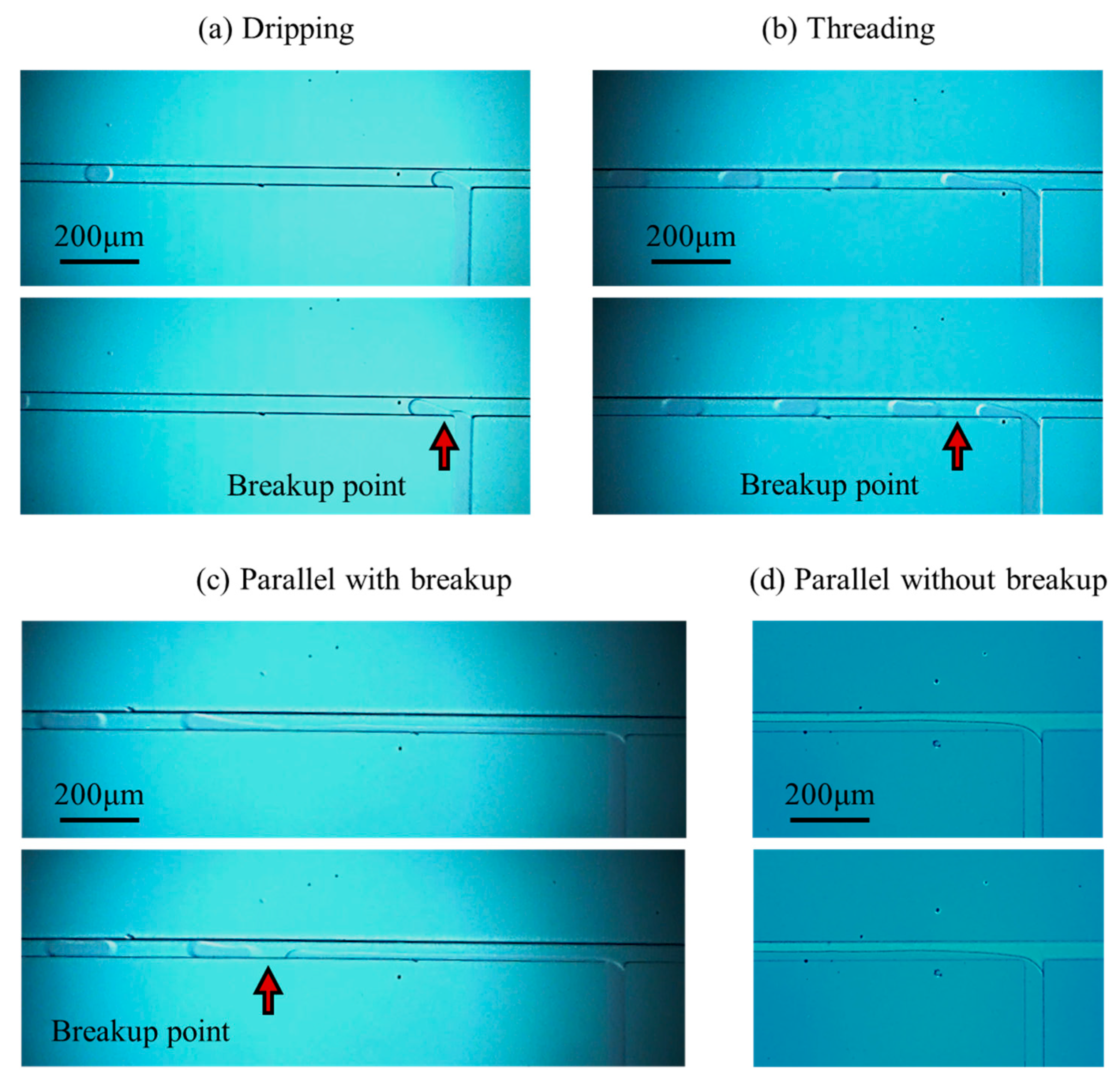
3.1. Flow Regimes and Their Transition Mechanisms
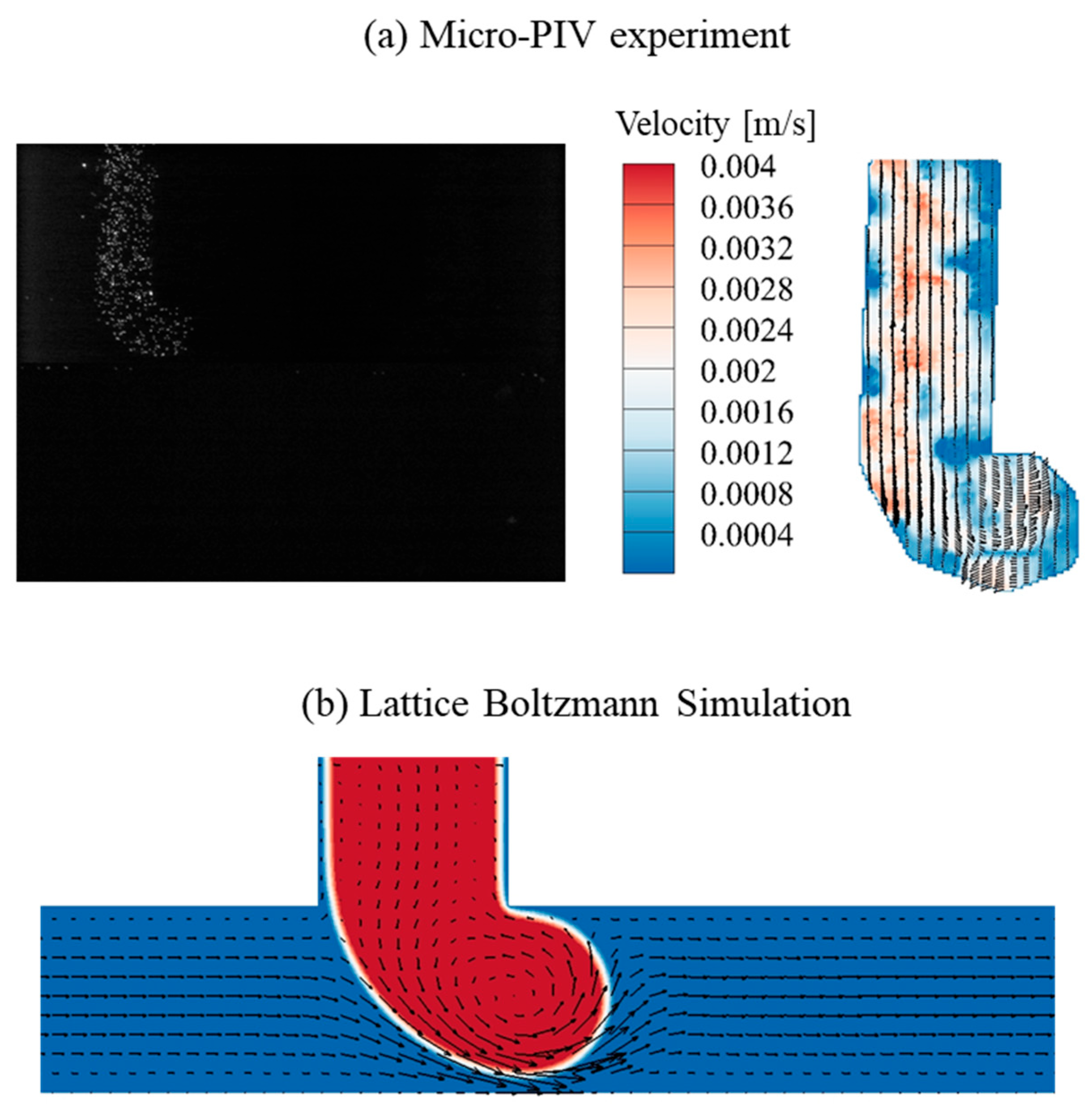
3.2. Mechanism of Microdroplet Generation
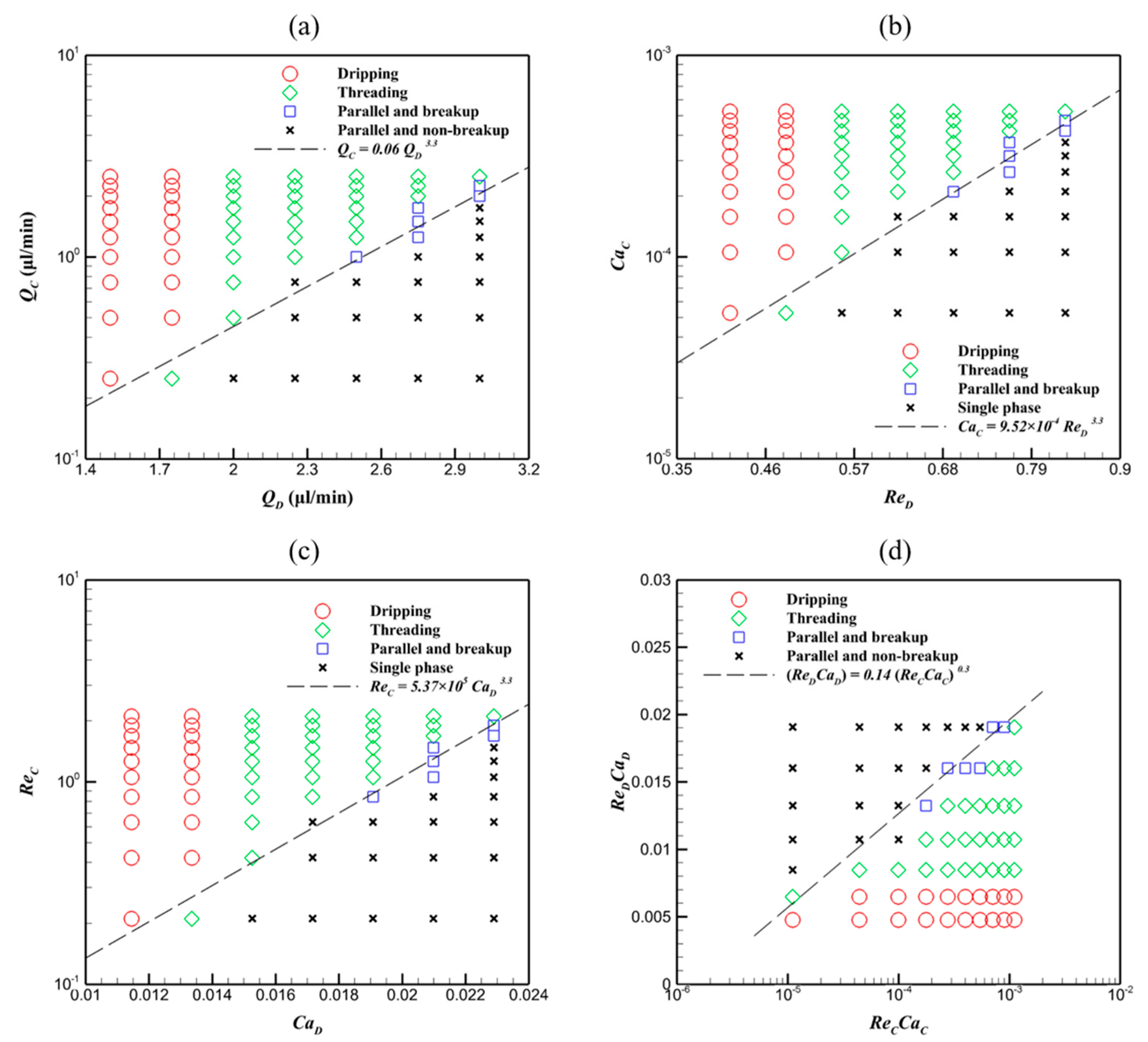
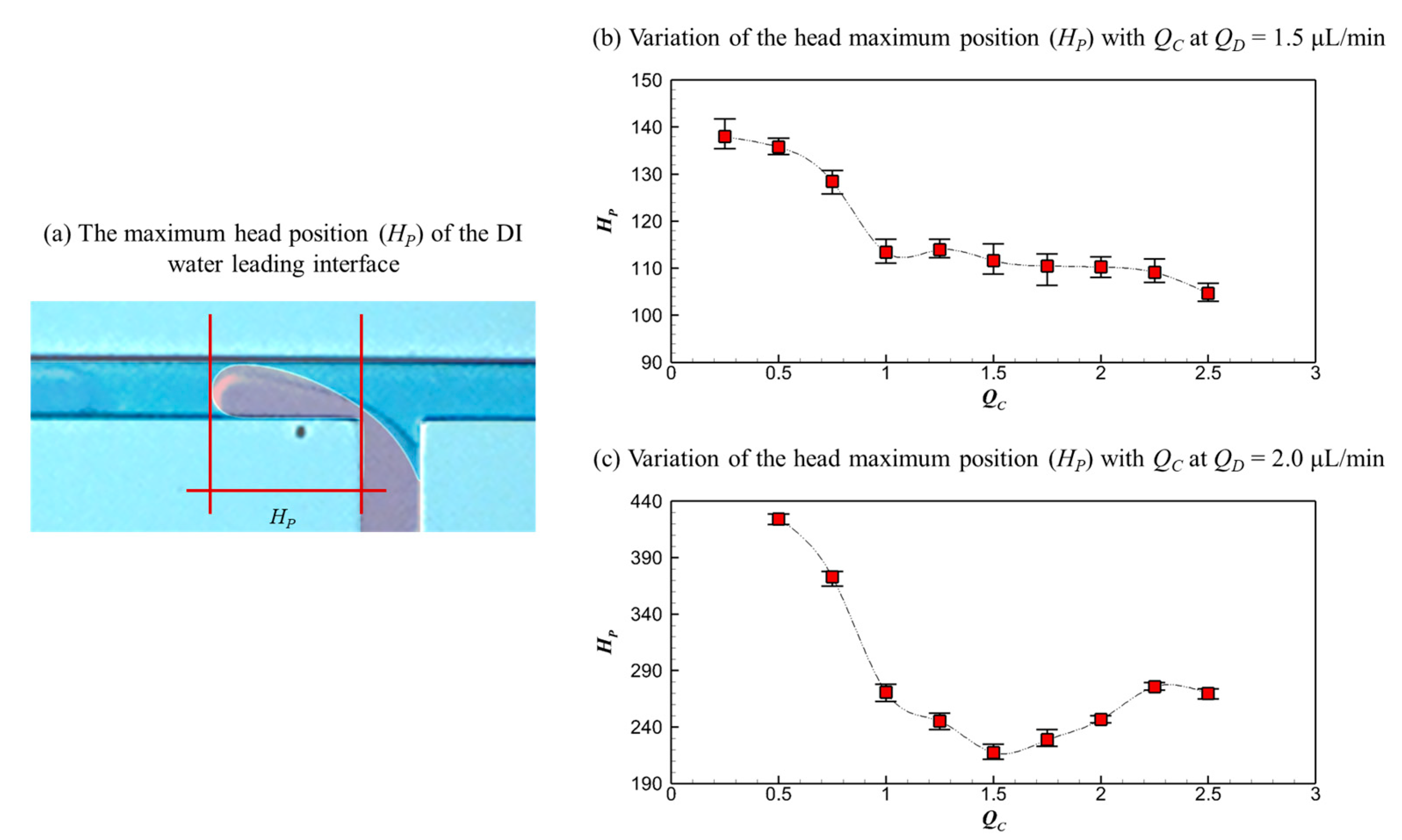
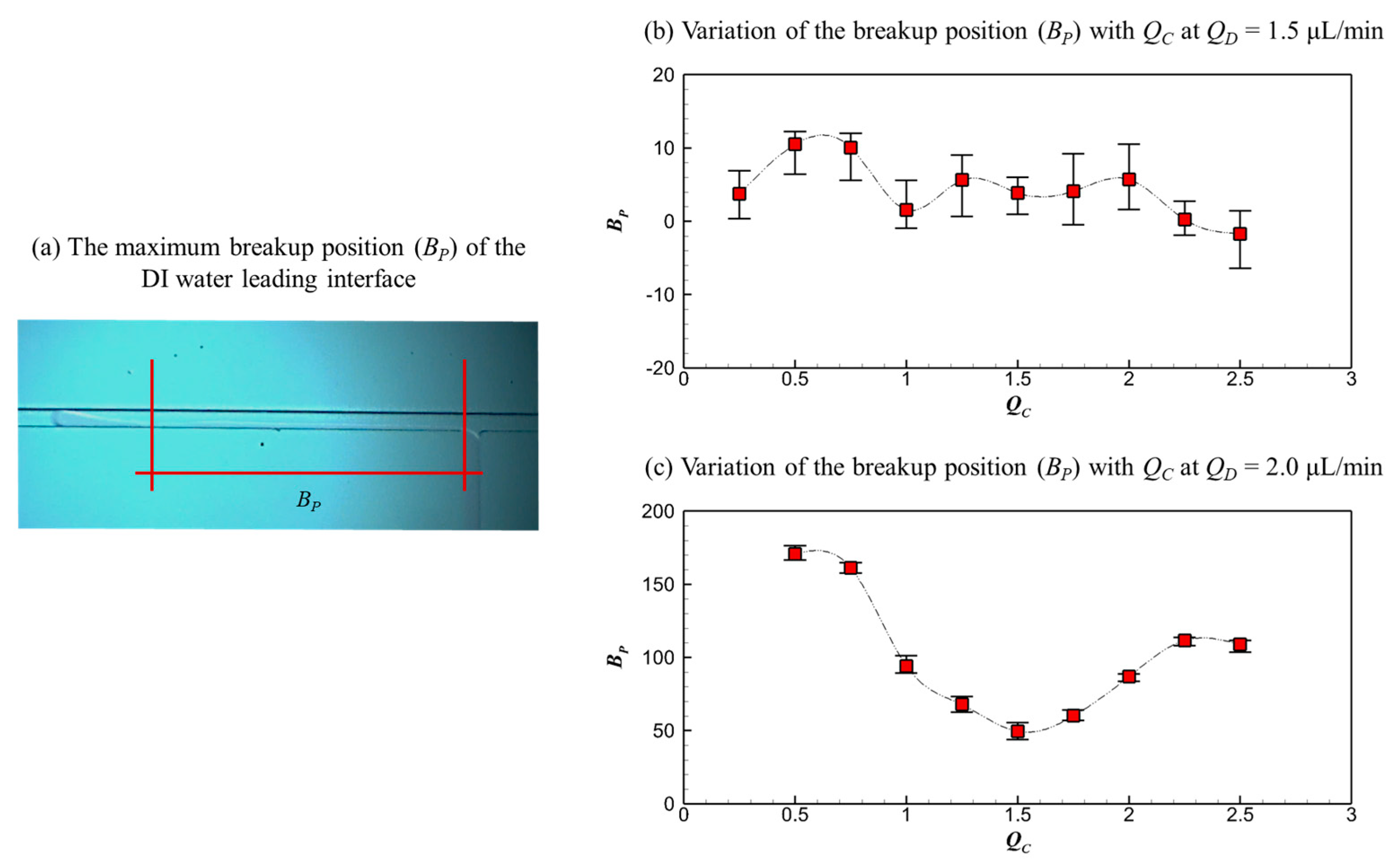
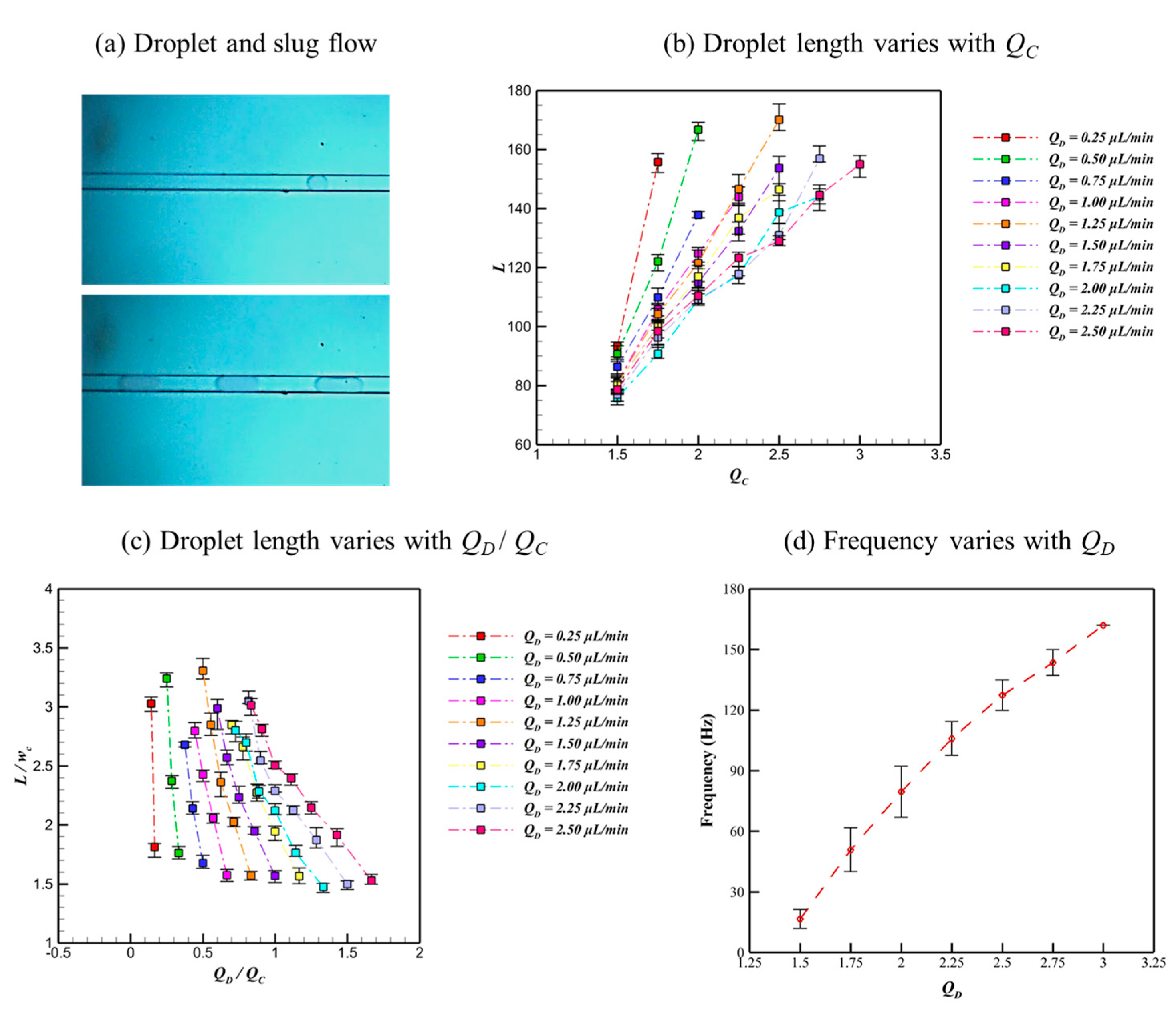
3.3. Quantitative Characterization of Microdroplet Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Iwai, K.; Wehrs, M.; Garber, M.; Sustarich, J.; Washburn, L.; Costello, Z.; Kim, P.W.; Ando, D.; Gaillard, W.R.; Hillson, N.J.; et al. Scalable and automated CRISPR-based strain engineering using droplet microfluidics. Microsyst. Nanoeng. 2022, 8, 31. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Ettelaie, R.; Li, T.; Yang, J.; Dong, L.; Xue, N.; Binks, B.P.; Cheng, F.; Yang, H. Pickering emulsion droplets and solid microspheres acting synergistically for continuous-flow cascade reactions. Nat. Catal. 2024, 7, 295–306. [Google Scholar] [CrossRef]
- Su, Y.-Y.; Pan, D.-W.; Zhang, T.-X.; Xie, R.; Ju, X.-J.; Liu, Z.; Deng, N.-N.; Wang, W.; Chu, L.-Y. Wetting-induced interfacial instability: A mechanism for droplet emission at air-liquid interfaces. Sci. Adv. 2025, 11, eads1065. [Google Scholar] [CrossRef]
- Zhu, P.; Wang, L. Passive and active droplet generation with microfluidics: A review. Lab A Chip 2017, 17, 34–75. [Google Scholar] [CrossRef]
- Aboutalebi, M.; Shafii, M.B.; Hannani, S.K. Numerical Study on the Ferrofluid Droplet Splitting in a T-junction with Branches of Unequal Widths using Asymmetric Magnetic Field. J. Appl. Comput. Mech. 2023, 9, 357–370. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, V.; Pathak, M. Droplet formation dynamics under perpendicular and head-on dispersed phase configuration in a microfluidic T-junction. Phys. Fluids 2024, 36, 113347. [Google Scholar] [CrossRef]
- Governo, A.F.L.; Murshed, S.M.S.; Semião, V. Microdroplet formation of water and alumina nanofluid in a T-junction microchannel. Phys. Fluids 2024, 36, 052008. [Google Scholar] [CrossRef]
- Kholardi, M.D.; Farhadi, M. Understanding droplet formation in T-shaped channels with magnetic field influence: A computational investigation. Phys. Fluids 2024, 36, 053302. [Google Scholar] [CrossRef]
- Zhu, L.; Zheng, L. Droplet breakup through triangular obstacle in T-junction microchannel. Phys. Fluids 2025, 37, 042005. [Google Scholar] [CrossRef]
- Deng, C.; Wang, H.; Huang, W.; Cheng, S. Numerical and experimental study of oil-in-water (O/W) droplet formation in a co-flowing capillary device. Colloids Surf. A Physicochem. Eng. Asp. 2017, 533, 1–8. [Google Scholar] [CrossRef]
- Sattari, A.; Hanafizadeh, P.; Keshtiban, M.M. Microfluidic preparation of double emulsions using a high aspect ratio double co-flow device. Colloids Surf. A Physicochem. Eng. Asp. 2021, 628, 127297. [Google Scholar] [CrossRef]
- Cubaud, T.; Mason, T.G. Capillary threads and viscous droplets in square microchannels. Phys. Fluids 2008, 20, 053302. [Google Scholar] [CrossRef]
- Yu, W.; Liu, X.; Zhao, Y.; Chen, Y. Droplet generation hydrodynamics in the microfluidic cross-junction with different junction angles. Chem. Eng. Sci. 2019, 203, 259–284. [Google Scholar] [CrossRef]
- Wu, Z.; Cao, Z.; Sunden, B. Flow patterns and slug scaling of liquid-liquid flow in square microchannels. Int. J. Multiph. Flow 2019, 112, 27–39. [Google Scholar] [CrossRef]
- Ramji, S.; Rakesh, A.; Pushpavanam, S. Modelling mass transfer in liquid-liquid slug flow in a microchannel. Chem. Eng. J. 2019, 364, 280–291. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, Y.; Wang, X.; Pang, Y.; Ren, Y.; Li, D. Experimental and theoretical studies on neck thinning dynamics of droplets in cross junction microchannels. Exp. Therm. Fluid Sci. 2022, 139, 110739. [Google Scholar] [CrossRef]
- Thorsen, T.; Roberts, R.W.; Arnold, F.H.; Quake, S.R. Dynamic Pattern Formation in a Vesicle-Generating Microfluidic Device. Phys. Rev. Lett. 2001, 86, 4163–4166. [Google Scholar] [CrossRef]
- Garstecki, P.; Fuerstman, M.J.; Whitesides, G.M. Nonlinear Dynamics of a Flow-Focusing Bubble Generator: An Inverted Dripping Faucet. Phys. Rev. Lett. 2005, 94, 234502. [Google Scholar] [CrossRef]
- Jena, S.K.; Srivastava, T.; Bahga, S.S.; Kondaraju, S. Effect of channel width on droplet generation inside T-junction microchannel. Phys. Fluids 2023, 35, 022107. [Google Scholar] [CrossRef]
- Shen, F.; Chen, J.; Li, C.; Yuan, Y.; Liu, Z. Easy Generation of Droplets in a Capillary Inserted Microchannel. Ind. Eng. Chem. Res. 2024, 63, 2021–2030. [Google Scholar] [CrossRef]
- Shen, F.; Yang, X.; Li, C.; Wang, J.; Wu, D.; Liu, Z. Evolution of symmetrical microvortices in a generating microdroplet during neck breakage stage in an altered T-shaped microchannel. Exp. Fluids 2024, 65, 179. [Google Scholar] [CrossRef]
- Dangla, R.; Kayi, S.C.; Baroud, C.N. Droplet microfluidics driven by gradients of confinement. Proc. Natl. Acad. Sci. USA 2013, 110, 853–858. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.; Jiao, S.; Zhao, S.; Lou, Y.; Zhang, L.; Wang, X.; Liu, Z. Droplet motions directed by an expansion section in the T-junctions. Phys. Fluids 2024, 36, 092036. [Google Scholar] [CrossRef]
- Wehking, J.D.; Gabany, M.; Chew, L.; Kumar, R. Effects of viscosity, interfacial tension, and flow geometry on droplet formation in a microfluidic T-junction. Microfluid. Nanofluid. 2014, 16, 441–453. [Google Scholar] [CrossRef]
- Yao, C.; Liu, Y.; Xu, C.; Zhao, S.; Chen, G. Formation of liquid–liquid slug flow in a microfluidic T-junction: Effects of fluid properties and leakage flow. AIChE J. 2018, 64, 346–357. [Google Scholar] [CrossRef]
- Du, W.; Fu, T.; Duan, Y.; Zhu, C.; Ma, Y.; Li, H.Z. Breakup dynamics for droplet formation in shear-thinning fluids in a flow-focusing device. Chem. Eng. Sci. 2018, 176, 66–76. [Google Scholar] [CrossRef]
- Kumari, P.; Atta, A. Insights into the dynamics of non-Newtonian droplet formation in a T-junction microchannel. Phys. Fluids 2022, 34, 062001. [Google Scholar] [CrossRef]
- Liu, Z.-M.; Liu, L.-K.; Shen, F. Effects of geometric configuration on droplet generation in Y-junctions and anti-Y-junctions microchannels. Acta Mech. Sin. 2015, 31, 741–749. [Google Scholar] [CrossRef]
- Jiang, X.; Deng, Z. Study of directional splitting characteristics of compound droplets containing solid core in Y-junction microchannel. Chem. Eng. Sci. 2025, 305, 121160. [Google Scholar] [CrossRef]
- Kovalev, A.V.; Pervunin, K.S.; Bilsky, A.V.; Yagodnitsyna, A.A. Influence of dispersed phase flow-rate pulsations on the liquid–liquid parallel flow in a T-junction microchannel. Chem. Eng. J. 2024, 488, 150734. [Google Scholar] [CrossRef]
- Xiong, Q.-Q.; Chen, Z.; Li, S.-W.; Wang, Y.-D.; Xu, J.-H. Micro-PIV measurement and CFD simulation of flow field and swirling strength during droplet formation process in a coaxial microchannel. Chem. Eng. Sci. 2018, 185, 157–167. [Google Scholar] [CrossRef]
- Kamalakshakurup, G.; Aghaamoo, M.; Ataei, M.; Zhang, N.; Lee, A.P. Shear-dependent microvortices in liquid–liquid flow-focusing geometry: A theoretical, numerical, and experimental study. Phys. Fluids 2021, 33, 032016. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Sotoudeh, F.; Lee, B.J.; Paydari, M.-R.; Karimi, N. Effect of hybrid wall contact angles on slug flow behavior in a T-junction microchannel: A numerical study. Colloids Surf. A Physicochem. Eng. Asp. 2022, 650, 129677. [Google Scholar] [CrossRef]
- Kumar, P.; Pathak, M. Dynamic wetting characteristics during droplet formation in a microfluidic T-junction. Int. J. Multiph. Flow 2022, 156, 104203. [Google Scholar] [CrossRef]
- Chaghagolani, H.O.; Kadivar, E. Numerical study of droplet sorting in an asymmetric Y-junction microfluidic by BEM and LS method. Microfluid. Nanofluid. 2023, 27, 14. [Google Scholar] [CrossRef]
- Li, X.; He, L.; Lv, S.; Xu, C.; Qian, P.; Xie, F.; Liu, M. Effects of wall velocity slip on droplet generation in microfluidic T-junctions. RSC Adv. 2019, 9, 23229–23240. [Google Scholar] [CrossRef]
- Bai, F.; He, X.; Yang, X.; Zhou, R.; Wang, C. Three dimensional phase-field investigation of droplet formation in microfluidic flow focusing devices with experimental validation. Int. J. Multiph. Flow 2017, 93, 130–141. [Google Scholar] [CrossRef]
- Zhang, T.; Dong, F.; Li, M.; Wu, J. Controlling gas–liquid flow and enhancing heat transfer in a T-junction microchannel by wettability-engineered walls. Phys. Fluids 2024, 36, 022101. [Google Scholar] [CrossRef]
- Liang, H.; Liu, H.; Chai, Z.; Shi, B. Lattice Boltzmann method for contact-line motion of binary fluids with high density ratio. Phys. Rev. E 2019, 99, 063306. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- He, X.; Zou, Q.; Luo, L.-S.; Dembo, M. Analytic solutions of simple flows and analysis of nonslip boundary conditions for the lattice Boltzmann BGK model. J. Stat. Phys. 1997, 87, 115–136. [Google Scholar] [CrossRef]
- Niu, X.D.; Shu, C.; Chew, Y.T. A lattice Boltzmann BGK model for simulation of micro flows. Eur. Lett. 2004, 67, 600–606. [Google Scholar] [CrossRef]
- Li, X.; Dong, Z.-Q.; Li, Y.; Wang, L.-P.; Niu, X.-D.; Yamaguchi, H.; Li, D.-C.; Yu, P. A fractional-step lattice Boltzmann method for multiphase flows with complex interfacial behavior and large density contrast. Int. J. Multiph. Flow 2022, 149, 103982. [Google Scholar] [CrossRef]
- Dong, Z.-Q.; Wang, L.-P.; Xian, T. Effects of the hidden errors in the bounce back scheme on the lattice Boltzmann simulation of the turbulent channel flow using the multiple-relaxation-time collision model. Phys. Fluids 2023, 35, 055107. [Google Scholar] [CrossRef]
- Zhang, X.-L.; Huang, J.-J. Study on wetting and spreading behaviors of compound droplets on wedge by lattice Boltzmann method. Acta Phys. Sin. 2023, 72, 024701. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y. Droplet formation in a T-shaped microfluidic junction. J. Appl. Phys. 2009, 106, 034906. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y. Lattice Boltzmann Simulation of Droplet Generation in a Microfluidic Cross-Junction. Commun. Comput. Phys. 2011, 9, 1235–1256. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Chen, L.; Shen, L.; Cui, H. Modelling the passive breakup of a surfactant-contaminated droplet in a T-junction microchannel. J. Fluid Mech. 2024, 986, A23. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Deng, Z.; Chen, Y. Asymmetric droplet splitting in a T-junction under a pressure difference. Int. J. Multiph. Flow 2024, 180, 104967. [Google Scholar] [CrossRef]
- Niu, X.D.; Li, Y.; Ma, Y.R.; Chen, M.F.; Li, X.; Li, Q.Z. A mass-conserving multiphase lattice Boltzmann model for simulation of multiphase flows. Phys. Fluids 2018, 30, 013302. [Google Scholar] [CrossRef]
- Li, X.; Yu, P.; Niu, X.-D.; Li, D.-C.; Yamaguchi, H. A magnetic field coupling lattice Boltzmann model and its application on the merging process of multiple-ferrofluid-droplet system. Appl. Math. Comput. 2021, 393, 125769. [Google Scholar] [CrossRef]
- Li, X.; Dong, Z.-Q.; Wang, L.-P.; Niu, X.-D.; Yamaguchi, H.; Li, D.-C.; Yu, P. A magnetic field coupling fractional step lattice Boltzmann model for the complex interfacial behavior in magnetic multiphase flows. Appl. Math. Model. 2023, 117, 219–250. [Google Scholar] [CrossRef]
- Ding, H.; Spelt, P.D.M.; Shu, C. Diffuse interface model for incompressible two-phase flows with large density ratios. J. Comput. Phys. 2007, 226, 2078–2095. [Google Scholar] [CrossRef]
- Carrier, O.; Ergin, F.G.; Li, H.-Z.; Watz, B.B.; Funfschilling, D. Time-resolved mixing and flow-field measurements during droplet formation in a flow-focusing junction. J. Micromech. Microeng. 2015, 25, 084014. [Google Scholar] [CrossRef]
- Rausch, M.H.; Kretschmer, L.; Will, S.; Leipertz, A.; Fröba, A.P. Density, Surface Tension, and Kinematic Viscosity of Hydrofluoroethers HFE-7000, HFE-7100, HFE-7200, HFE-7300, and HFE-7500. J. Chem. Eng. Data 2015, 60, 3759–3765. [Google Scholar] [CrossRef]


| Type | Material | Density (ρ) | Viscosity [56] (μ) | Surface Tension (σ) |
|---|---|---|---|---|
| Dispersed fluid | DI water | |||
| Continuous fluid | HFE-7100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wu, W.; Dong, Z.; Wang, Y.; Yu, P. Passive Droplet Generation in T-Junction Microchannel: Experiments and Lattice Boltzmann Simulations. Micromachines 2025, 16, 1011. https://doi.org/10.3390/mi16091011
Li X, Wu W, Dong Z, Wang Y, Yu P. Passive Droplet Generation in T-Junction Microchannel: Experiments and Lattice Boltzmann Simulations. Micromachines. 2025; 16(9):1011. https://doi.org/10.3390/mi16091011
Chicago/Turabian StyleLi, Xiang, Weiran Wu, Zhiqiang Dong, Yiming Wang, and Peng Yu. 2025. "Passive Droplet Generation in T-Junction Microchannel: Experiments and Lattice Boltzmann Simulations" Micromachines 16, no. 9: 1011. https://doi.org/10.3390/mi16091011
APA StyleLi, X., Wu, W., Dong, Z., Wang, Y., & Yu, P. (2025). Passive Droplet Generation in T-Junction Microchannel: Experiments and Lattice Boltzmann Simulations. Micromachines, 16(9), 1011. https://doi.org/10.3390/mi16091011





