The Multi-Objective Optimization of a Dual C-Type Gold Ribbon Interconnect Structure Considering Its Geometrical Parameter Fluctuation
Abstract
1. Introduction
2. Simulation and Verification
2.1. Parametric Configuration Characterization
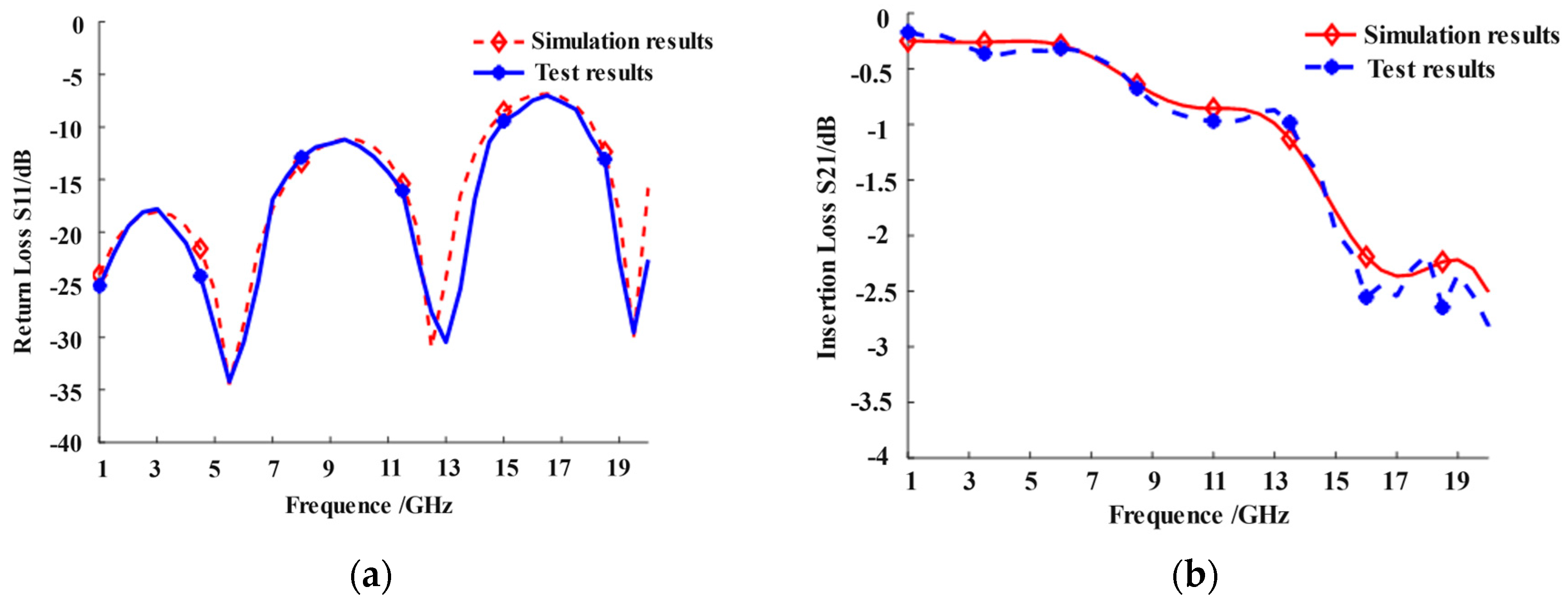
2.2. Electromagnetic Simulation and Experiment Verification
3. Calculation of Fluctuation Range of Configuration Parameters
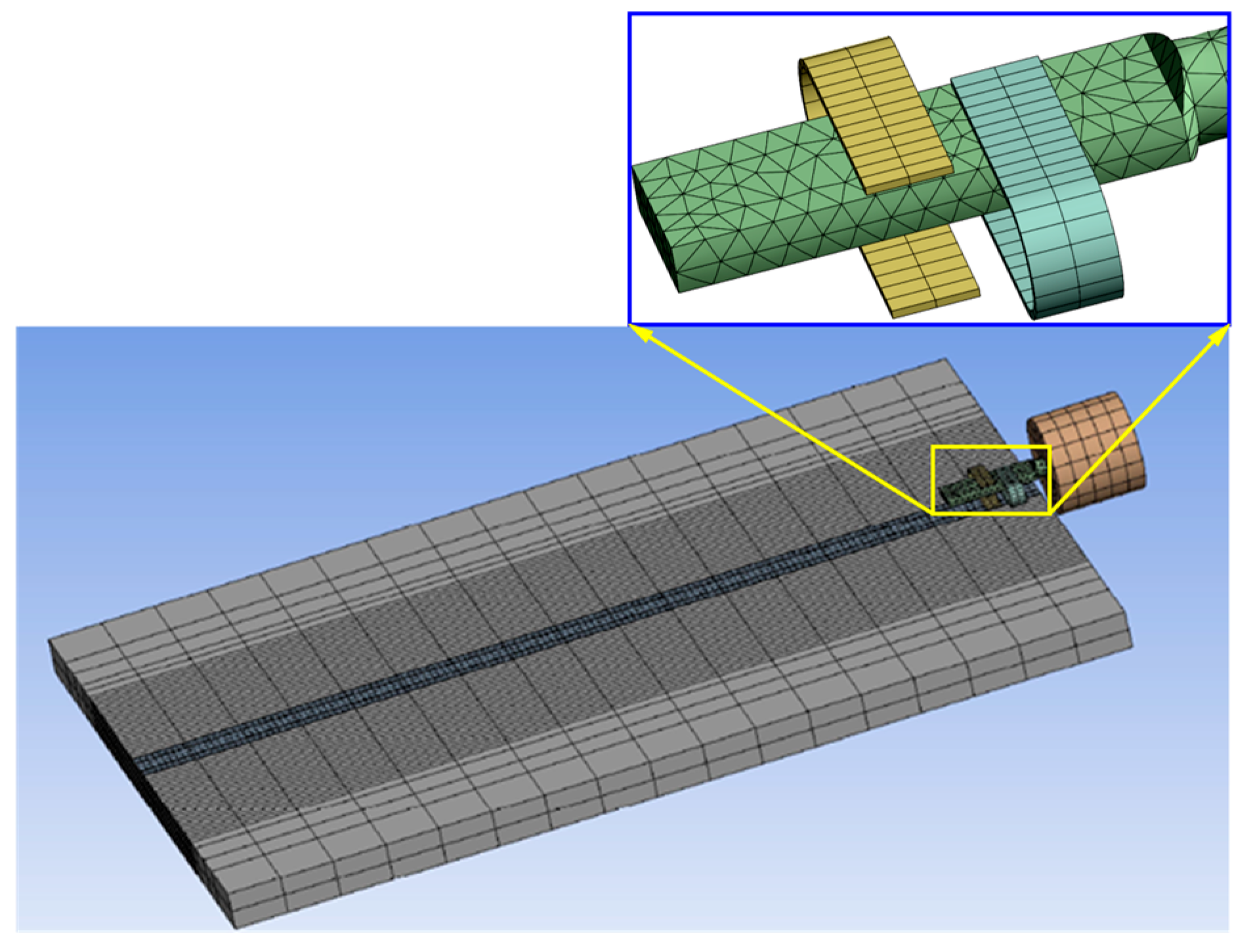
3.1. FEA Model
3.2. FEA Under Random Vibration Loads
3.3. FEA Under Thermal Loads
3.4. Calculation
4. Experimental Analysis and Structure Optimization
4.1. Orthogonal Experimental Analysis
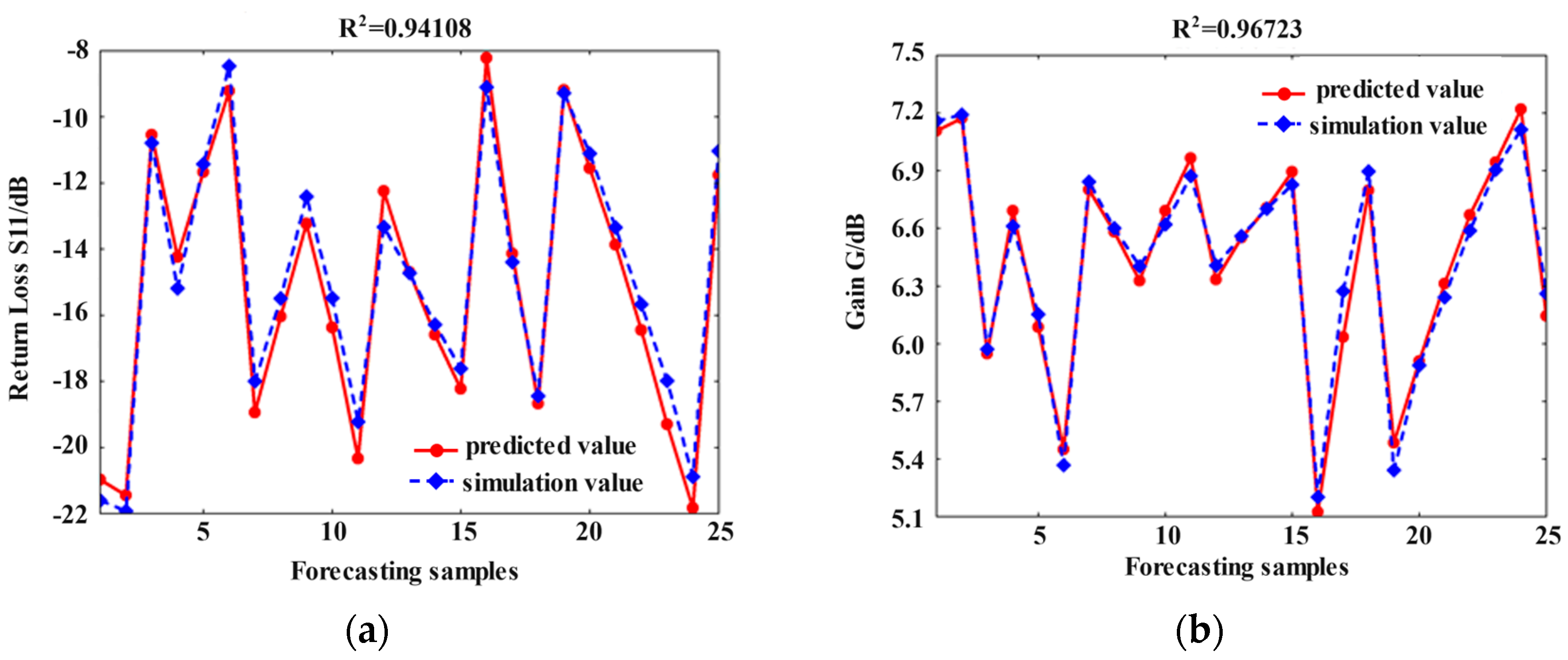
4.2. Performance Prediction and Parameter Optimization
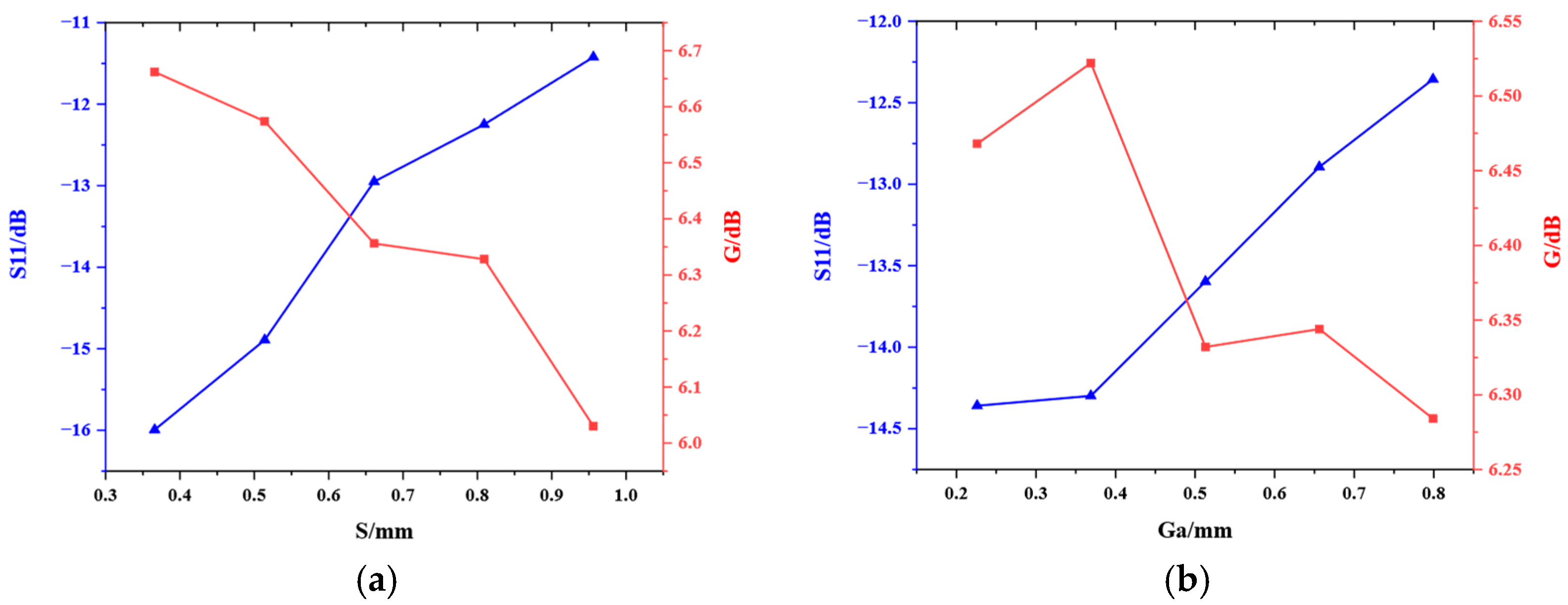
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
Abbreviations
| LHS | Latin hypercube sampling |
| BP | Back propagation neural network |
| CFAWOA | Chaos feedback adaptive whale optimization algorithm |
| MORBMOA | Multi-objective red-billed blue magpie optimization algorithm |
References
- Nauman, P.; Sands, T. Micro-satellite systems design, Integration, and flight. Micromachines 2024, 15, 455. [Google Scholar] [CrossRef]
- Tian, M.M.; Huang, P.; Ma, G.B.; Li, W.; Li, X.M. Intelligent Management of Satellite Ground System. In Proceedings of the 33rd Chinese Control and Decision Conference, Kunming, China, 23–25 May 2021. [Google Scholar]
- Nawaz, A.A.; Khan, W.T.; Ulusoy, A.C. Organically Packaged Components and Modules: Recent Advancements for Microwave and mm-Wave Applications. IEEE Microw. Mag. 2019, 20, 49–72. [Google Scholar] [CrossRef]
- Tung, W.S.; Chiang, W.-Y.; Liu, C.-K.; Chen, C.-A.; Rao, P.-Z.; Abu, P.A.R.; Chen, W.-M.; Asadi, F.; Chen, S.-L. Low cost AIP design in 5G flexible antenna phase array system application. Micromachines 2020, 11, 851. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Q.; Zhou, G.; Wang, Z.; Pang, J.; Sun, T.; Keqing, O. Multi-chips High-density Interconnection Design on InFO Platform. In Proceedings of the 22nd International Conference on Electronic Packaging Technology, Xiamen, China, 14 September 2021. [Google Scholar]
- Prerna; Ramalingam, N.; Mulla, Z.Z.; Ganeshan, A.; Balakrishnan, R.; Karunan, A. Artificial Intelligence based advanced Signal Integrity prediction. In Proceedings of the Electrical Design of Advanced Packaging and Systems, Urbana, IL, USA, 12–14 December 2022. [Google Scholar]
- Wang, C.S.; Wang, Y.; Wang, Z.; Wang, M.; Yuan, S.; Wang, W. Structural-electrical coupling optimisation for radiating and scattering performances of active phased array antenna. Int. J. Electron. 2018, 105, 586–597. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Dasgupta, B.; Jyoti, R. Design and analysis of ultrathin X-band frequency selective surface structure for gain enhancement of hybrid antenna. Int. J. RF Microw. Comput.-Aided Eng. 2020, 31, e22505. [Google Scholar] [CrossRef]
- Kumar, S.; Sharma, R. Chip-to-Chip Copper Interconnects with Rough Surfaces: Analytical Models for Parameter Extraction and Performance Evaluation. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 286–299. [Google Scholar] [CrossRef]
- Wang, Z.H.; Wang, L.; Yu, K.P.; Liu, S.Y.; Wang, C.S. Equivalent Circuit Based Performance Coupling Analysis Method for Lead Wire Interconnection with Defects. Electronics 2020, 9, 642. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Zhi, C.L.; Dong, G. Modeling and analysis of wide frequency band coaxial TSV transmission interconnect. Micromachines 2024, 15, 1127. [Google Scholar] [CrossRef]
- Chan, Y.-C.; Basu, N.; Chen, T.-W.; Tsai, Y.-T.; Lin, H.-Y.; Chen, S.-C.; Lee, M.-H.; Liao, M.-H. The Analysis of Multiwall Carbon Nanotubes as Through Silicon Via by Equivalent Circuit Model at Different Operating Temperatures in Multilayers Stacking Scheme. IEEE Trans. Electron. Devices 2023, 70, 3360–3364. [Google Scholar] [CrossRef]
- Lu, Q.; Zhu, Z.; Yang, Y.; Ding, R.; Li, Y. High-Frequency Electrical Model of Through-Silicon Vias for 3-D Integrated Circuits Considering Eddy Current and Proximity Effects. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 2036–2044. [Google Scholar] [CrossRef]
- Cheng, H.C.; Hong, R.Y.; Chen, W.H. Assessment of Elastic-Plastic and Electrical Properties of Printed Silver-Based Interconnects for Flexible Electronics. ASME J. Electron. Packag. 2018, 140, 041007. [Google Scholar] [CrossRef]
- Lu, M.C. Hybrid Bonding for Ultra-High-Density Interconnect. ASME J. Electron. Packag. 2024, 146, 030802. [Google Scholar] [CrossRef]
- Li, C.Q.; Liang, Z.M.; Lu, H.H.; Cheng, L.X. Study on the Electrothermal Properties of Cu-CNT TSV Interconnects Under Multiphysics Field Coupling. IEEE Trans. Compon. Packag. Manuf. Technol. 2024, 14, 2309–2320. [Google Scholar] [CrossRef]
- Liu, S.Y.; Xue, S.; Huang, J.L.; Wang, H.; Wang, Z.H.; Wang, C.S. A Data-Driven Approach to Collaborative Optimization for Enhancing TSV Multiphysics Performance. IEEE Trans. Compon. Packag. Manuf. Technol. 2025, 15, 253–262. [Google Scholar] [CrossRef]
- Bondarik, A.; Forsberg, T.; Sjoberg, D.; Sjoland, H.; Tormanen, M. A bond wire connection implementation at mm-wave active microstrip antenna. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 427–429. [Google Scholar] [CrossRef]
- Guo, J.L.; Shih, Y.C.; Shekhi, R.B.; You, J.P.; Shi, F.G. Semiconductor Chip Electrical Interconnection and Bonding by Nano-Locking with Ultra-Fine Bond-Line Thickness. Nanomaterials 2021, 11, 1901. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Cho, J.; Cho, K.; Park, J.; Kim, S.; Kim, D.-H.; Park, G.; Sitaraman, S.; Raj, P.M.; Tummala, R.R.; et al. Glass-Interposer Electromagnetic Bandgap Structure with Defected Ground Plane for Broadband Suppression of Power/Ground Noise Coupling. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 1493–1505. [Google Scholar] [CrossRef]
- Watanabe, A.O.; Kanno, K.; Ito, H.; Tummala, R.R.; Swaminathan, M. High-density low-loss millimeter-wave package interconnects with the impact of dielectric-material surface roughness. Appl. Phys. Lett. 2022, 19, 134103. [Google Scholar] [CrossRef]
- Ge, C.Q.; Huang, C.P.; Huang, Z.L.; Zhao, G.L.; Long, H.L.; Zeng, Q. Research on the electrical performance of flexible metal arrays. In Proceedings of the 24th International Conference on Electronic Packaging Technology, Shihezi, China, 8–11 September 2023. [Google Scholar]
- Tian, J.; Wang, C.; Liu, S.; Xue, S.; Zhang, L.; Liu, J.; Wang, Z.; Yu, K.; Li, R. Electromechanical coupling parameter identification for flexible conductor wire interconnection considering interaction effect in microwave circuits. Electronics 2021, 10, 464. [Google Scholar] [CrossRef]
- Tian, J.; Wang, C.; Wang, Z.; Min, Z.; Yu, K.; Zhou, C.; Liu, J.; Liu, S.; Wang, Y.; Gao, W.; et al. A key parameters interval estimation method of the gold ribbon interconnect structure for the electrical performance of microwave modules. In Proceedings of the 21st International Conference on Electronic Packaging Technology, Guangzhou, China, 12–15 August 2020. [Google Scholar]
- Teng, Y.; Han, B.; Liu, S.; Liu, J.; Lin, K.; Xue, S.; Yao, S.; Zhang, D.; Wang, C. Polynomial based surrogate modeling of interconnection configuration and signal transmission performance of double C-type gold ribbon in microwave modules. In Proceedings of the 23rd International Conference on Electronic Packaging Technology, Dalian, China, 10–13 August 2022. [Google Scholar]
- Ridho, A.; Alamsyah, A. Chaotic whale optimization algorithm in hyperparameter selection in convolutional neural network algorithm. J. Adv. Inf. Syst. Technol. 2023, 4, 156–169. [Google Scholar] [CrossRef]
- Fu, S.; Li, K.; Huang, H.; Ma, C.; Fan, Q.; Zhu, Y. Red-billed blue magpie optimizer: A novel metaheuristic algorithm for 2D/3D UAV path planning and engineering design problems. Artif. Intell. Rev. 2024, 57, 134. [Google Scholar] [CrossRef]
- Trampler, M.E.; Lovato, R.E.; Gong, X. Dual-resonance continuously beam-scanning X-bond reflectarray antenna. IEEE Trans. Antennas Propag. 2020, 68, 6080–6087. [Google Scholar] [CrossRef]
- Wang, S.Q.; Chung, K.L.; Du, L.G.; Kong, F.M.; Li, K. Design and analysis of a compact frequency beam-scanning antenna based on composite FHMSIW/SSPP waveguide. IEEE Antennas Wirel. Propag. Lett. 2022, 21, 546–550. [Google Scholar] [CrossRef]
- Ordal, M.A.; Bell, R.J.; Alexander, R.W.; Long, L.L.; Querry, M.R. Optical-Properties of 14 Metals in the Infrared and Far Infrared: AL, CO, CU, AU, FE, PB, MO, NI, PD, PT, AG, TI, V, and W. Appl. Opt. 1985, 24, 4493. [Google Scholar] [CrossRef] [PubMed]









| Components | Material | Density (g/mm3) | Young’s Modulus (GPa) | CTE (K−1) | Thermal Conductivity (W/m K) | Poisson’s Ratio | Dielectric Loss | Relative Permittivity | Bulk Conductivity (S/m) |
|---|---|---|---|---|---|---|---|---|---|
| Microstrip conductor | Au | 19.32 | 78.3 | 14.2 × 10−6 | 317 | 0.42 | 0.0012 | 1 | 4.1 × 107 |
| Gold ribbon | |||||||||
| Coaxial lead | |||||||||
| Dielectric substrate | MIC | 3.5 | 380 | 7 × 10−6 | 20 | 0.26 | 0.0002 | 9.9 | - |
| Glass medium | SiO2 | 2.2 | 75 | 0.55 × 10−6 | 1.1 | 0.14 | 1.32 × 10−5 | 4 | - |
| Interval | Maximum Displacement (mm) | ||
|---|---|---|---|
| X-Direction | Y-Direction | Z-Direction | |
| 0.037607 | 0.011764 | 0.04271 | |
| Structure Parameters | Variable | Direction | Design Value (mm) | Random Vibration Deformation (mm) | Thermal Deformation (mm) |
|---|---|---|---|---|---|
| The width of the C-type gold ribbon | B | Y | 0.25 | [0, 0.011764] | [−7.85 × 10−3, 1.112 × 10−2]. |
| The bending length of the C-type gold ribbon | S | X | 0.625 | [0, 0.025071] | [−3.28 × 10−3, 5.27 × 10−3] |
| Distance between the two gold ribbons | b2 | Y | 0.1 | [0, 0.0156848] | [−6.569 × 10−3, 1.02 × 10−2] |
| Distance between the edge of the gold ribbon and the edge of the dielectric substrate | b1 | Y | 0.3 | [0, 0.0065353] | [−7.83 × 10−3, 8.06 × 10−3] |
| Lead drop | h | Z | 0.3 | [0, 0.04745] | [−4.08 × 10−3, 6.66 × 10−3] |
| Coaxial dielectric substrate module gap | Ga | Y | 0.5 | [0, 0.0039481] | [−8.89 × 10−3, 1.41 × 10−2] |
| Structure Parameters | Variable | Design Value (mm) | Range of the Max Deformation (mm) | Range of Manufacturing Error (mm) | Fluctuation Range of Parameters (mm) |
|---|---|---|---|---|---|
| The width of the C-type gold ribbon | B | 0.25 | [−2.09 × 10−2, 6.11 × 10−2] | [−0.1, 0.1] | [0.1291, 0.4111] |
| The bending length of the C-type gold ribbon | S | 0.625 | [−8.74 × 10−3, 8.08 × 10−2] | [−0.25, 0.25] | [0.3663, 0.9558] |
| Distance between the two gold ribbons | b2 | 0.1 | [−1.18 × 10−2, 2.01 × 10−2] | [−0.05, 0.05] | [0.0382, 0.1701] |
| Distance between the edge of the gold ribbon and the edge of the dielectric substrate | b1 | 0.3 | [−2.08 × 10−2, 3.92 × 10−2] | [−0.1, 0.1] | [0.1792, 0.4392] |
| Lead drop | h | 0.3 | [−1.09 × 10−2, 1.44 × 10−1] | [−0.1, 0.1] | [0.1891, 0.544] |
| Coaxial dielectric substrate module gap | Ga | 0.5 | [−2.37 × 10−2, 4.84 × 10−2] | [−0.25, 0.25] | [0.2263, 0.7984] |
| Performance | B/mm | S/mm | b2/mm | b1/mm | h/mm | Ga/mm | S11/dB | G/dB |
|---|---|---|---|---|---|---|---|---|
| Best value | 0.129 | 0.366 | 0.038 | 0.179 | 0.367 | 0.226 | −23.014 | 7.19 |
| Worst value | 0.411 | 0.956 | 0.071 | 0.374 | 0.455 | 0.799 | −12.8244 | 2.29 |
| Performance | Initial Design (dB) | Optimal Design (dB) | Improvement |
|---|---|---|---|
| Return loss S11 | −19.7147 | −25.0375 | 26.99% |
| Peak gain G | 6.9339 | 7.5324 | 8.63% |
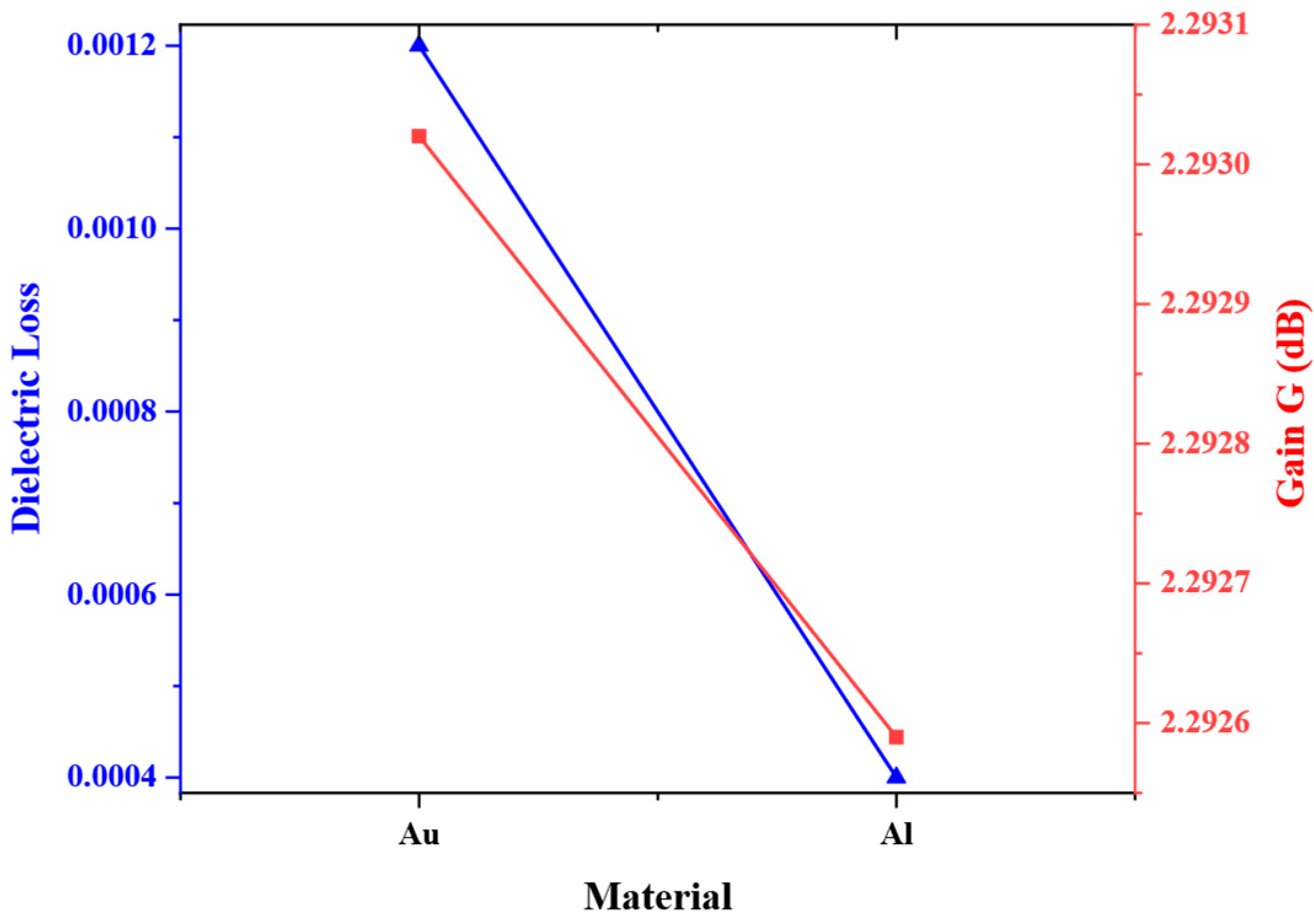
| Material | ||
|---|---|---|
| Au | 2.15 | 7.28 |
| Al | 6.6 | 11.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Xue, S.; Mu, J.; Liu, S.; Zhang, Q.; Wu, W.; Wang, Z.; Ma, Z.; Diwu, D.; Wang, C. The Multi-Objective Optimization of a Dual C-Type Gold Ribbon Interconnect Structure Considering Its Geometrical Parameter Fluctuation. Micromachines 2025, 16, 914. https://doi.org/10.3390/mi16080914
Li G, Xue S, Mu J, Liu S, Zhang Q, Wu W, Wang Z, Ma Z, Diwu D, Wang C. The Multi-Objective Optimization of a Dual C-Type Gold Ribbon Interconnect Structure Considering Its Geometrical Parameter Fluctuation. Micromachines. 2025; 16(8):914. https://doi.org/10.3390/mi16080914
Chicago/Turabian StyleLi, Guangmi, Song Xue, Jinyang Mu, Shaoyi Liu, Qiongfang Zhang, Wenzhi Wu, Zhihai Wang, Zhen Ma, Dongchao Diwu, and Congsi Wang. 2025. "The Multi-Objective Optimization of a Dual C-Type Gold Ribbon Interconnect Structure Considering Its Geometrical Parameter Fluctuation" Micromachines 16, no. 8: 914. https://doi.org/10.3390/mi16080914
APA StyleLi, G., Xue, S., Mu, J., Liu, S., Zhang, Q., Wu, W., Wang, Z., Ma, Z., Diwu, D., & Wang, C. (2025). The Multi-Objective Optimization of a Dual C-Type Gold Ribbon Interconnect Structure Considering Its Geometrical Parameter Fluctuation. Micromachines, 16(8), 914. https://doi.org/10.3390/mi16080914








