Influence of Design Parameters of Membrane-Type Flow Controller on Bearing Characteristics of Hydrostatic Guideways
Abstract
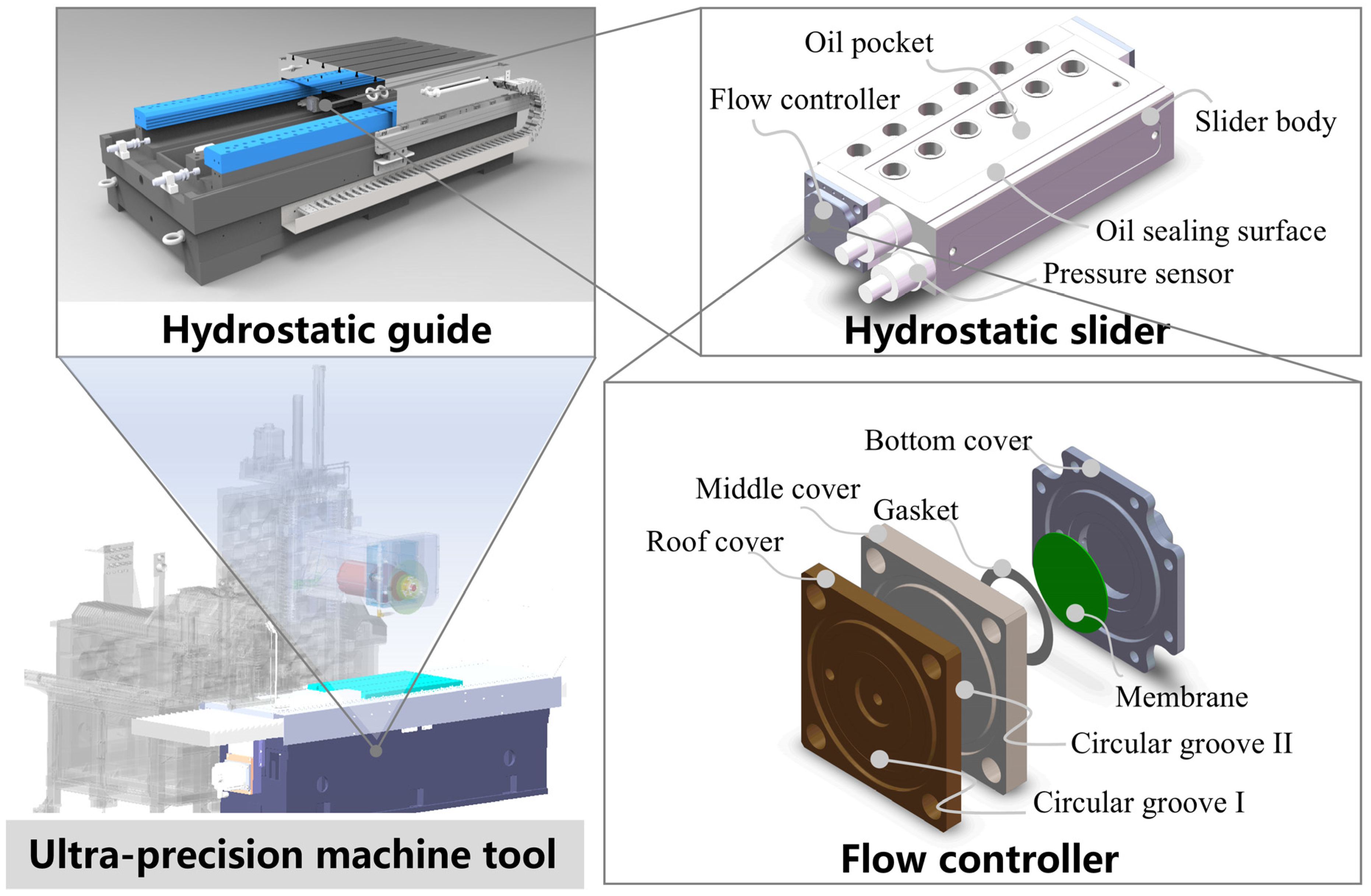
1. Introduction
2. Materials and Methods
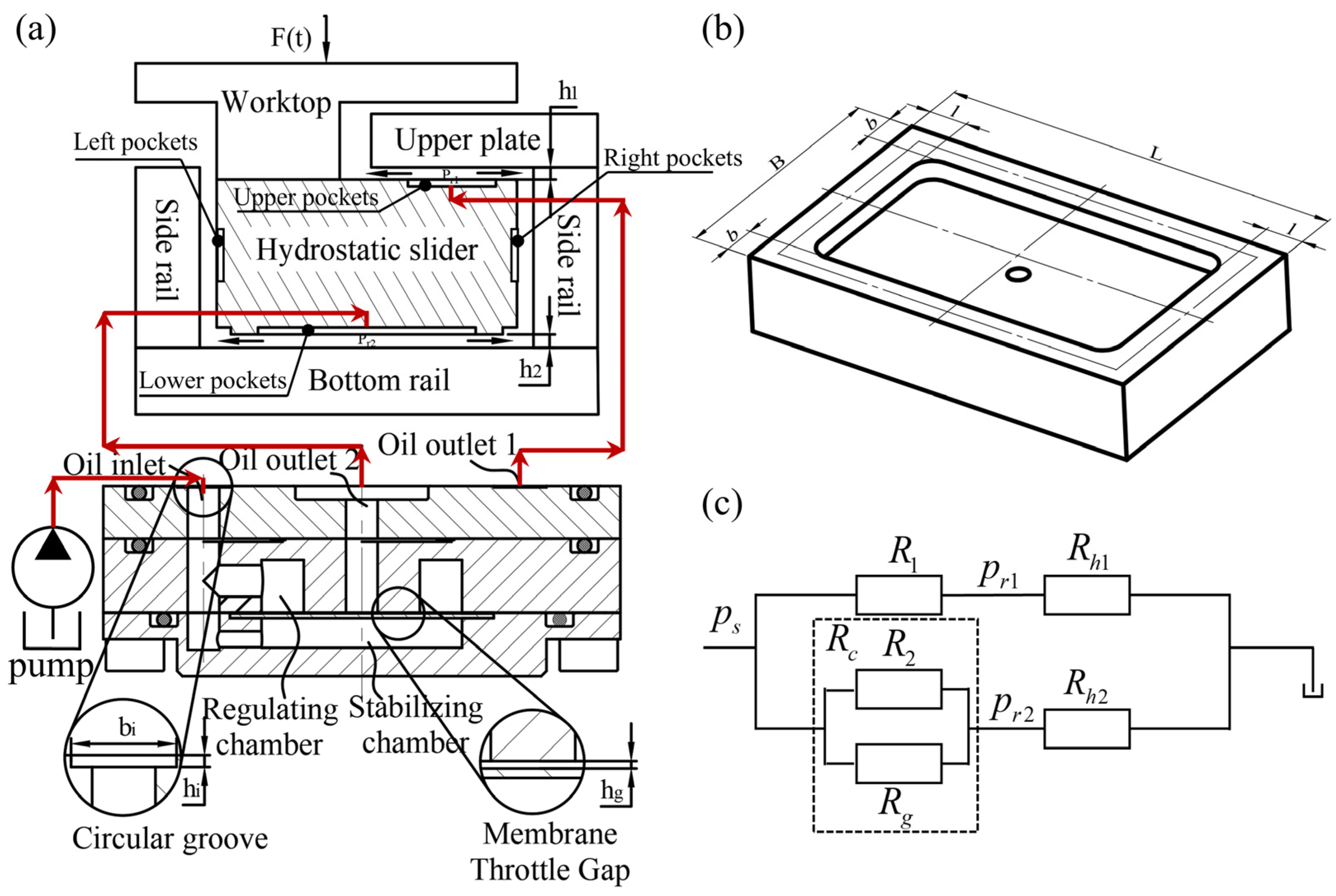
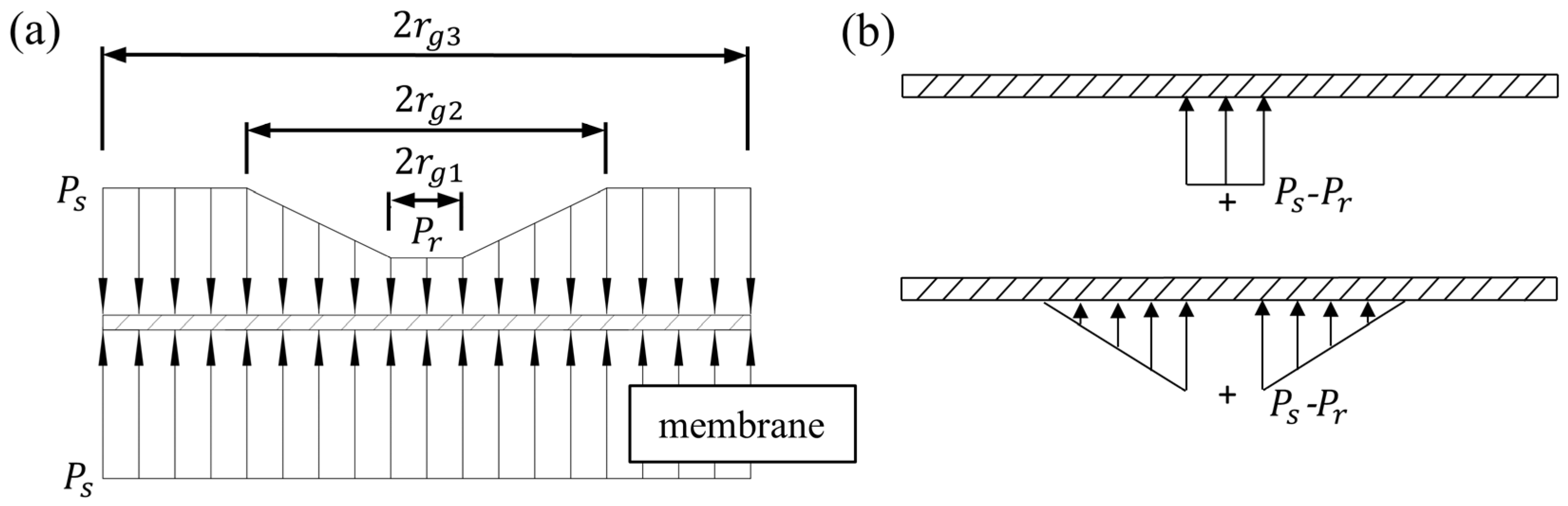
2.1. Structural Design and Theoretical Modeling of the Flow Controller
- (1)
- Assume that the hydrostatic guideway oil pocket pressure is uniformly distributed;
- (2)
- Assume that the guideway and flow controller are rigid;
- (3)
- Assume that the viscosity of the hydraulic oil remains constant and does not change due to temperature, flow rate, and other factors;
- (4)
- Assume that the flow state of the hydraulic oil is laminar;
- (5)
- Assume that the hydraulic fluid is incompressible.
- —Dynamic viscosity of hydraulic oil;
- —Thickness of oil film in upper and lower oil pocket;
- —Slide oil seal surface size parameters;
- —Oil pocket liquid resistance coefficient.
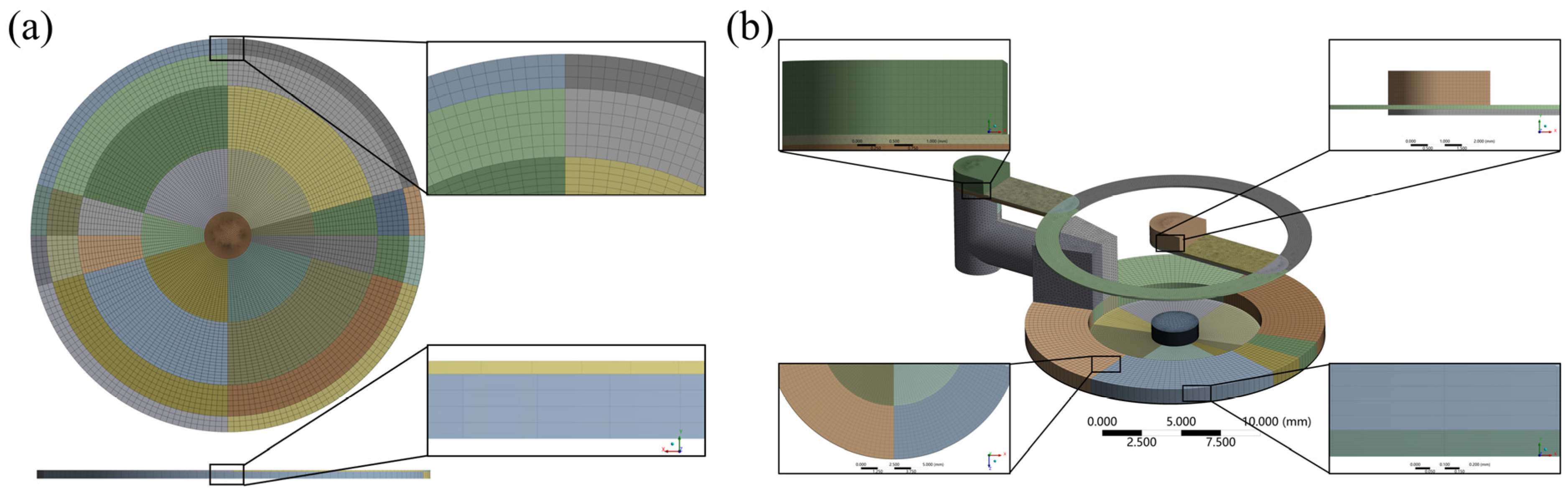
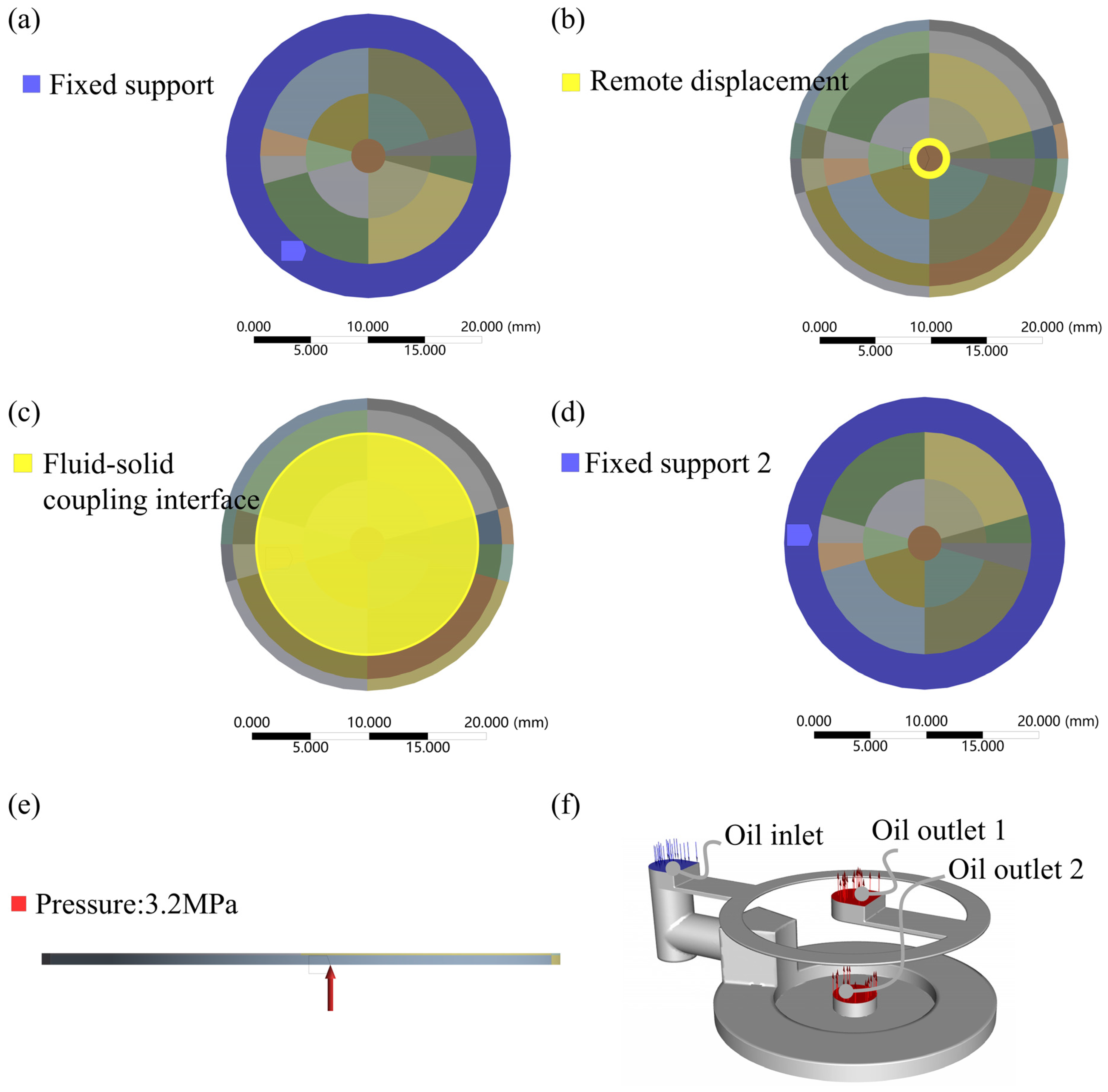
2.2. Simulation Modeling of Bidirectional Fluid-Solid Coupling
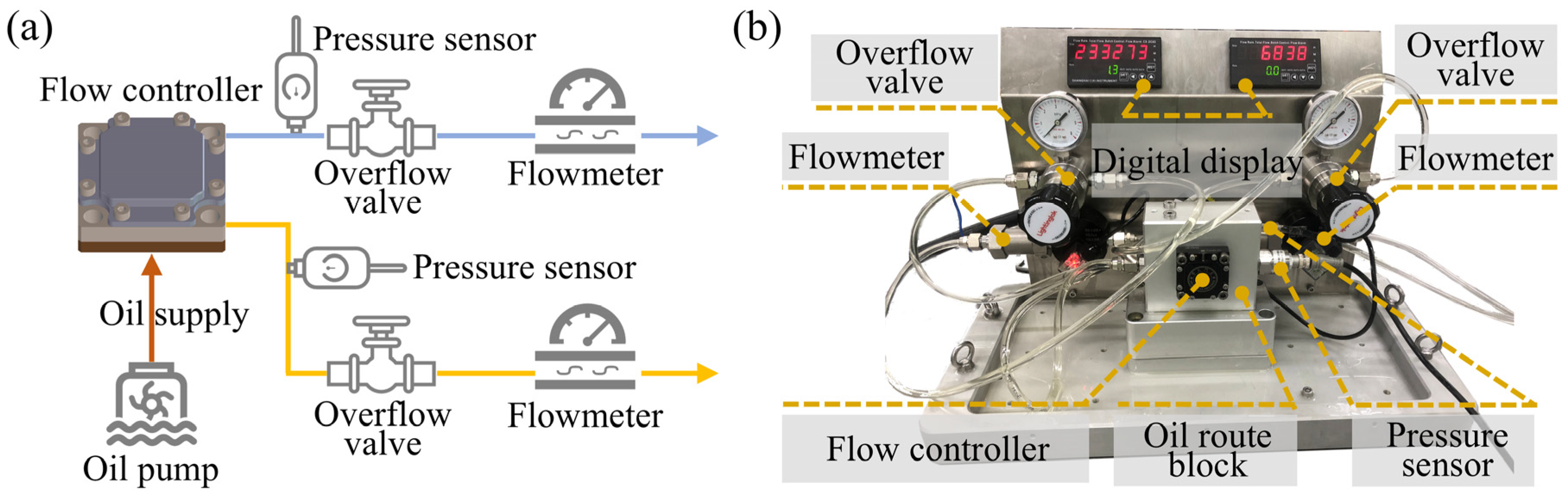
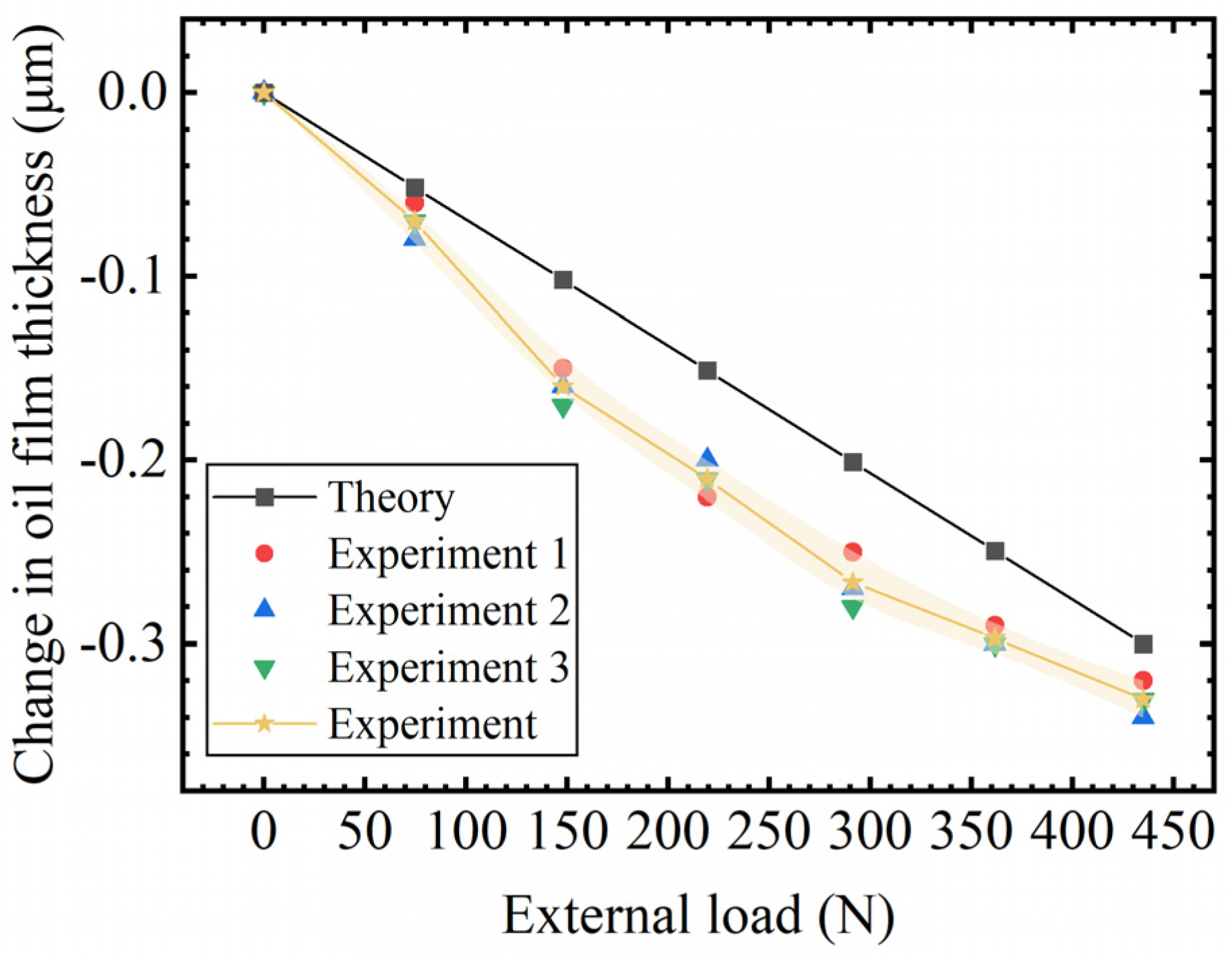
2.3. Flow and Bearing Characteristic Test Platforms
3. Results and Discussion
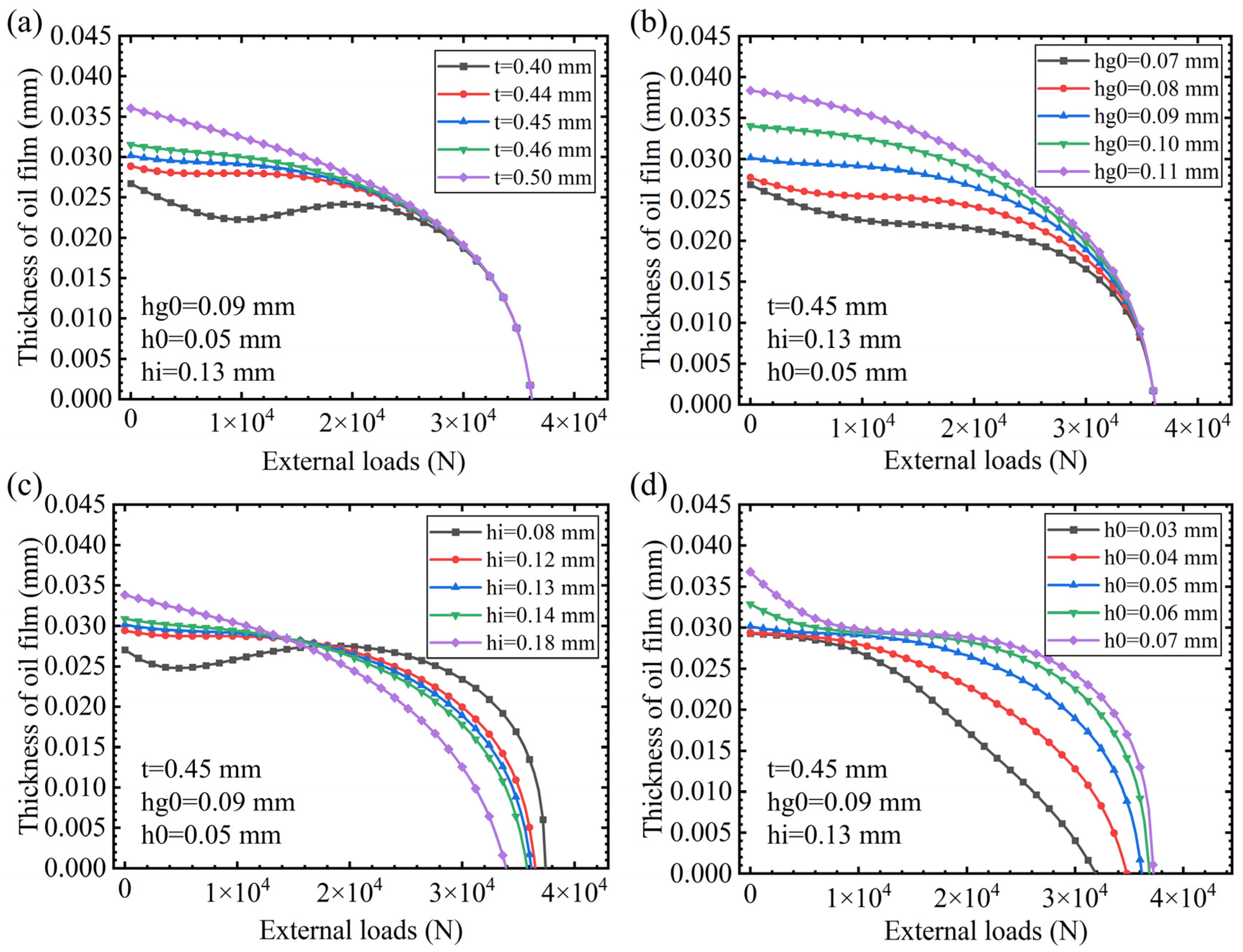
3.1. The Influence of Design Parameters on Bearing Characteristics
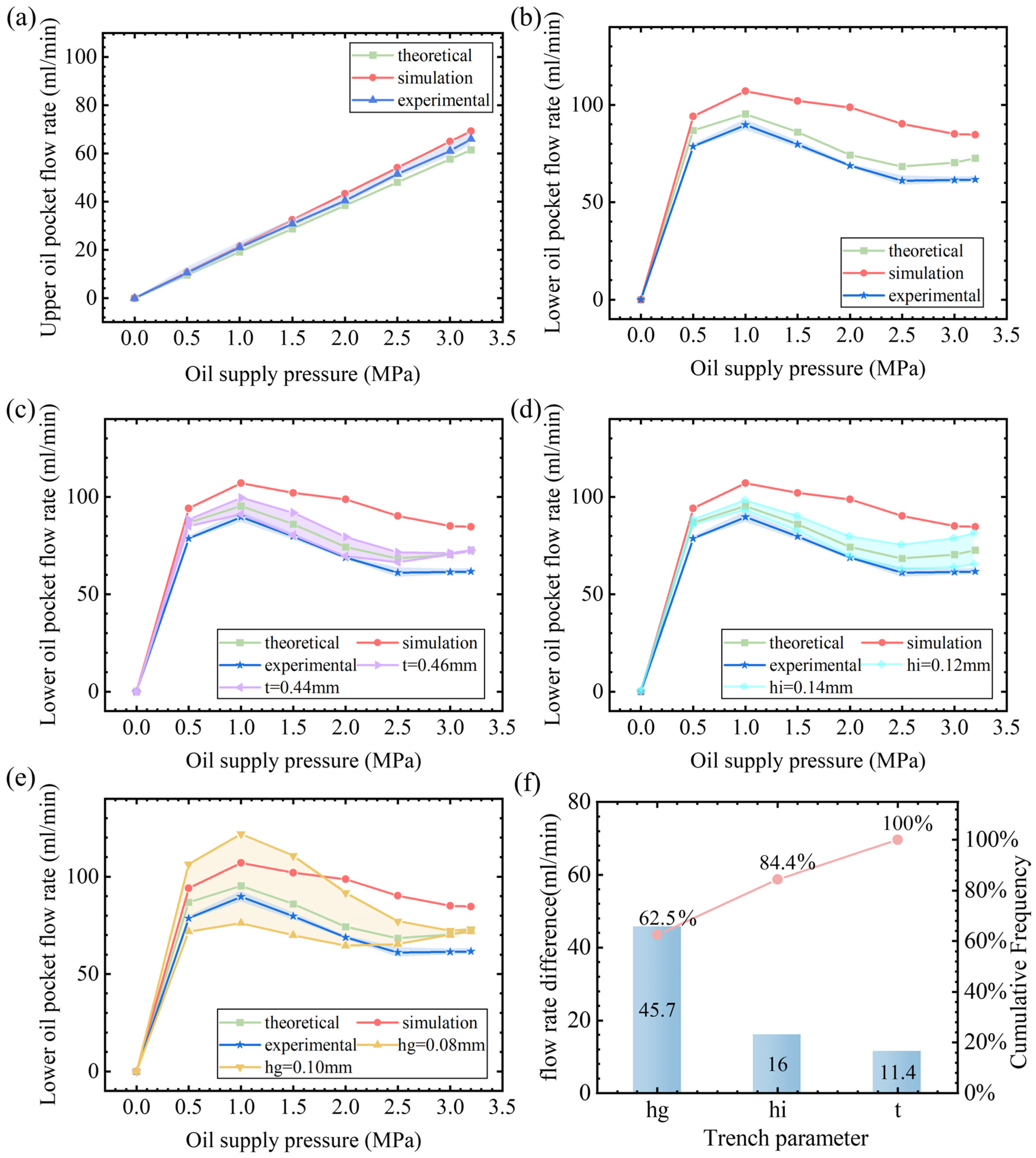
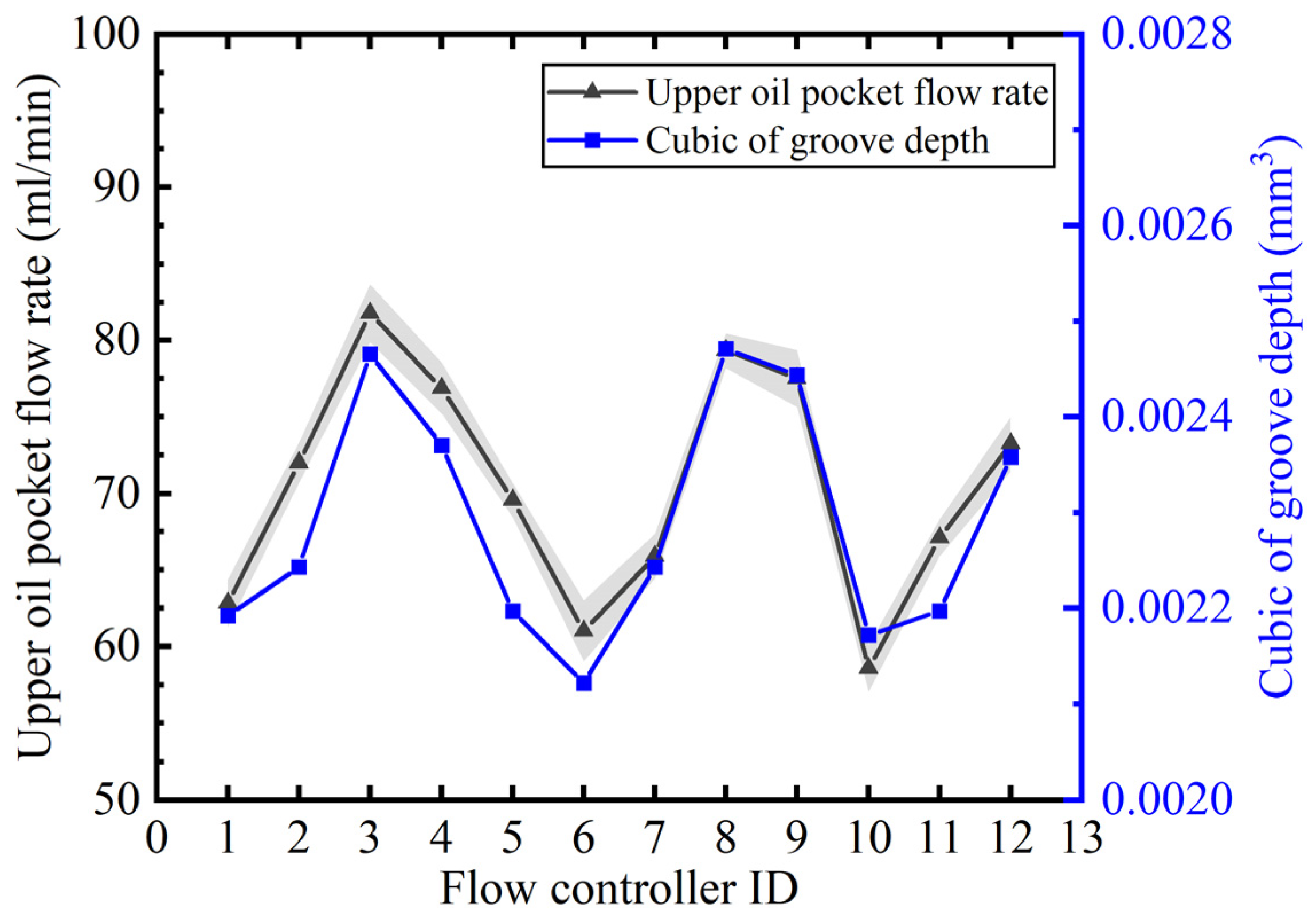
3.2. Initial Flow Rate of the Flow Controller
3.3. Bearing Characteristics of Closed Guideway
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xue, F.; Zhao, W.; Chen, Y.; Wang, Z. Research on error averaging effect of hydrostatic guideways. Precis. Eng. 2012, 36, 84–90. [Google Scholar] [CrossRef]
- Zha, J.; Cheng, K.; Xue, F.; Wu, D.; Liu, X. Hydrostatic guideways for precision machines: The state-of-the-art and future perspectives. Tribol. Int. 2024, 200, 110060. [Google Scholar] [CrossRef]
- Lei, P.; Wang, Z.; Shi, C.; Peng, Y.; Lu, F. Simulation, Modeling and Experimental Research on the Thermal Effect of the Motion Error of Hydrostatic Guideways. Micromachines 2021, 12, 1445. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, D.; Pan, W.; Rong, X.; Zhang, Y. Static and dynamic characteristics of large-span six-slider closed hydrostatic guideway considering pitch moment and yaw moment. Ind. Lubr. Tribol. 2024, 76, 392–404. [Google Scholar] [CrossRef]
- Shi, C.; Wang, Z.; Peng, Y.; Lei, P.; Li, C. Quasi-static kinematics model for motion errors of closed hydrostatic guideways in ultra-precision machining. Precis. Eng. 2021, 71, 90–102. [Google Scholar] [CrossRef]
- Song, L.; Zhang, Q.; Xu, L.; Zhao, X.; Sun, T. Investigation of the error averaging effect on design and assembly of external slider closed hydrostatic guideways. Tribol. Int. 2024, 199, 110036. [Google Scholar] [CrossRef]
- Singh, N.; Sharma, S.C.; Jain, S.C.; Sanjeeva Reddy, S. Performance of membrane compensated multirecess hydrostatic/hybrid flexible journal bearing system considering various recess shapes. Tribol. Int. 2004, 37, 11–24. [Google Scholar] [CrossRef]
- Pattnayak, M.R.; Pandey, R.K.; Dutt, J.K. Performance Improvement of an Oil-Lubricated Journal Bearing Using Bionic-Textures Fused Micro-Pockets. J. Tribol. 2021, 144, 041804. [Google Scholar] [CrossRef]
- Galda, L.; Dzierwa, A.; Sep, J.; Pawlus, P. The Effect of Oil Pockets Shape and Distribution on Seizure Resistance in Lubricated Sliding. Tribol. Lett. 2010, 37, 301–311. [Google Scholar] [CrossRef]
- Bouyer, J.; Wodtke, M.; Fillon, M. Experimental research on a hydrodynamic thrust bearing with hydrostatic lift pockets: Influence of lubrication modes on bearing performance. Tribol. Int. 2022, 165, 107253. [Google Scholar] [CrossRef]
- Chen, D.; Zhou, S.; Dong, L.; Fan, J. Performance evaluation and comparative analysis of hydrostatic spindle affect by the oil film slip. J. Manuf. Processes 2015, 20, 128–136. [Google Scholar] [CrossRef]
- Khatri, C.B.; Sharma, S.C. Analysis of textured multi-lobe non-recessed hybrid journal bearings with various restrictors. Int. J. Mech. Sci. 2018, 145, 258–286. [Google Scholar] [CrossRef]
- Liu, T.; Bei, Z.; Wang, H.; Duan, R.; Chen, F.; Zhang, J. Study on microgroove working surface in hydrostatic bearing for oil film heat suppression. Appl. Therm. Eng. 2025, 266, 125618. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Liu, J.T.; Yang, J.X. Design analysis on new thin film restrictor of liquid hydrostatic bearing. Bearing 2008, 3, 27–30. [Google Scholar]
- Sawano, H.; Nakamura, Y.; Yoshioka, H.; Shinno, H. High performance hydrostatic bearing using a variable inherent restrictor with a thin metal plate. Precis. Eng. 2015, 41, 78–85. [Google Scholar] [CrossRef]
- Lin, S.C.; Lo, Y.H.; Lin, Y.H.; Tung, W.T.; Lai, T.H. Design and Performance Analysis of Dual Membrane Restrictor for Hydrostatic Bearing. Lubricants 2022, 10, 179. [Google Scholar] [CrossRef]
- Renn, J.C.; Hsu, W.J.; Li, Y.R. An Innovative Spool-Type Pressure Feedback Restrictor for Hydrostatic Bearings. Smart Sci. 2016, 4, 203–208. [Google Scholar] [CrossRef]
- Kang, Y.; Peng, D.X.; Hung, Y.H.; Hu, S.Y.; Lin, C.S. Design for static stiffness of hydrostatic bearings: Double-action variable compensation of membrane-type restrictors and self-compensation. Ind. Lubr. Tribol. 2014, 66, 322–334. [Google Scholar] [CrossRef]
- Lai, T.H.; Lin, S.C. A Simulation Study for the Design of Membrane Restrictor in an Opposed-Pad Hydrostatic Bearing to Achieve High Static Stiffness. Lubricants 2018, 6, 71. [Google Scholar] [CrossRef]
- Ueda, H.; Saito, M.; Kawamura, Y.; Kawada, S.; Miyatake, M. Study on static and dynamic characteristics of water-lubricated hydrostatic thrust bearings—Effect of feed hole inlet shape on bearing characteristics. Tribol. Int. 2024, 191, 109127. [Google Scholar] [CrossRef]
- Kang, Y.; Shen, P.C.; Chen, C.H.; Chang, Y.P.; Lee, H.H. Modified determination of fluid resistance for membrane-type restrictors. Ind. Lubr. Tribol. 2007, 59, 123–131. [Google Scholar] [CrossRef]
- Kang, Y.; Shen, P.C.; Chang, Y.P.; Lee, H.H.; Chiang, C.P. Modified predictions of restriction coefficient and flow resistance for membrane-type restrictors in hydrostatic bearing by using regression. Tribol. Int. 2007, 40, 1369–1380. [Google Scholar] [CrossRef]
- Yang, Y.L.; Lo, Y.H.; Huang, T.T.; Lin, S.C. Numerical simulation analysis and design of membrane-type restrictor. In Proceedings of the 6th Asia International Conference on Tribology (ASIATRIB), Sarawak, Malaysia, 17–20 September 2018. [Google Scholar]
- Ding, Z. Fluid Hydrostatic Support Design, 1st ed.; Shanghai Scientific and Technical Publisher: Shanghai, China, 1989. [Google Scholar]
- Lu, F.; Wang, Z.Z.; Lei, P.L.; Chen, Y. Study on the static characteristics of a pre-pressure single-action membrane-type restrictor used in a single oil pad. Machines 2022, 10, 302. [Google Scholar] [CrossRef]
- Wu, Y.; Qiao, Z.; Ge, H.; Xue, J.; Wang, B. Application of direct coupling method to design problems of hydrostatic guideways accounting for fluid-structure interactions. Adv. Eng. Softw. 2023, 177, 103410. [Google Scholar] [CrossRef]

| Throttle Tabs/mm | Membrane Thickness/mm | Membrane Material /MPa | Gasket Thickness /mm | |||
| rg1 | rg2 | Rg3 | t | E | m | hg0 |
| 1.5 | 5.5 | 9.5 | 0.45 | 2 × 105 | 0.3 | 0.09 |
| Circular groove I/mm | Circular groove II/mm | Opposite oil pad gap/mm | ||||
| bI | hI | rI | bII | hII | rII | h0 |
| 5 | 0.13 | 15 | 1.5 | 0.13 | 8 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Xu, X.; Lin, Z.; Li, M.; Bi, G.; Wang, Z. Influence of Design Parameters of Membrane-Type Flow Controller on Bearing Characteristics of Hydrostatic Guideways. Micromachines 2025, 16, 891. https://doi.org/10.3390/mi16080891
Chen Y, Xu X, Lin Z, Li M, Bi G, Wang Z. Influence of Design Parameters of Membrane-Type Flow Controller on Bearing Characteristics of Hydrostatic Guideways. Micromachines. 2025; 16(8):891. https://doi.org/10.3390/mi16080891
Chicago/Turabian StyleChen, Yi, Xiaoyu Xu, Ziqi Lin, Maoyuan Li, Guo Bi, and Zhenzhong Wang. 2025. "Influence of Design Parameters of Membrane-Type Flow Controller on Bearing Characteristics of Hydrostatic Guideways" Micromachines 16, no. 8: 891. https://doi.org/10.3390/mi16080891
APA StyleChen, Y., Xu, X., Lin, Z., Li, M., Bi, G., & Wang, Z. (2025). Influence of Design Parameters of Membrane-Type Flow Controller on Bearing Characteristics of Hydrostatic Guideways. Micromachines, 16(8), 891. https://doi.org/10.3390/mi16080891








