Artificial Intelligence Control Methodologies for Shape Memory Alloy Actuators: A Systematic Review and Performance Analysis
Abstract
1. Introduction
- Non-linear Behavior: The relationship between temperature, stress, and strain in SMAs is highly non-linear, making it difficult to predict and control their response using conventional linear control techniques.
- Hysteresis: SMAs exhibit significant hysteresis, meaning that their current state depends not only on the present input but also on their previous states. This path-dependent behavior creates a memory effect that complicates control strategies.
- Temperature Dependence: The actuation of SMAs is fundamentally temperature-driven, making their performance sensitive to ambient temperature variations and thermal management challenges [20].
- Rate Dependence: The response rate of SMAs is limited by heating and cooling dynamics, resulting in relatively slow actuation speeds compared to conventional actuators [19].
- Section 3.1 analyzes sensing technologies and instrumentation approaches for SMA actuator systems;
- Section 3.2 provides a comprehensive evaluation of classical control strategies, including their architectural classifications, implementation characteristics, and performance analysis;
- Section 3.3 delivers an in-depth assessment of artificial intelligence techniques, encompassing feedforward neural networks, recurrent architectures, LSTM networks, and reinforcement learning approaches employed in SMA control, with particular emphasis on their training modalities, adaptability, and implementation efficacy.
2. SMA Actuators and Literature Review
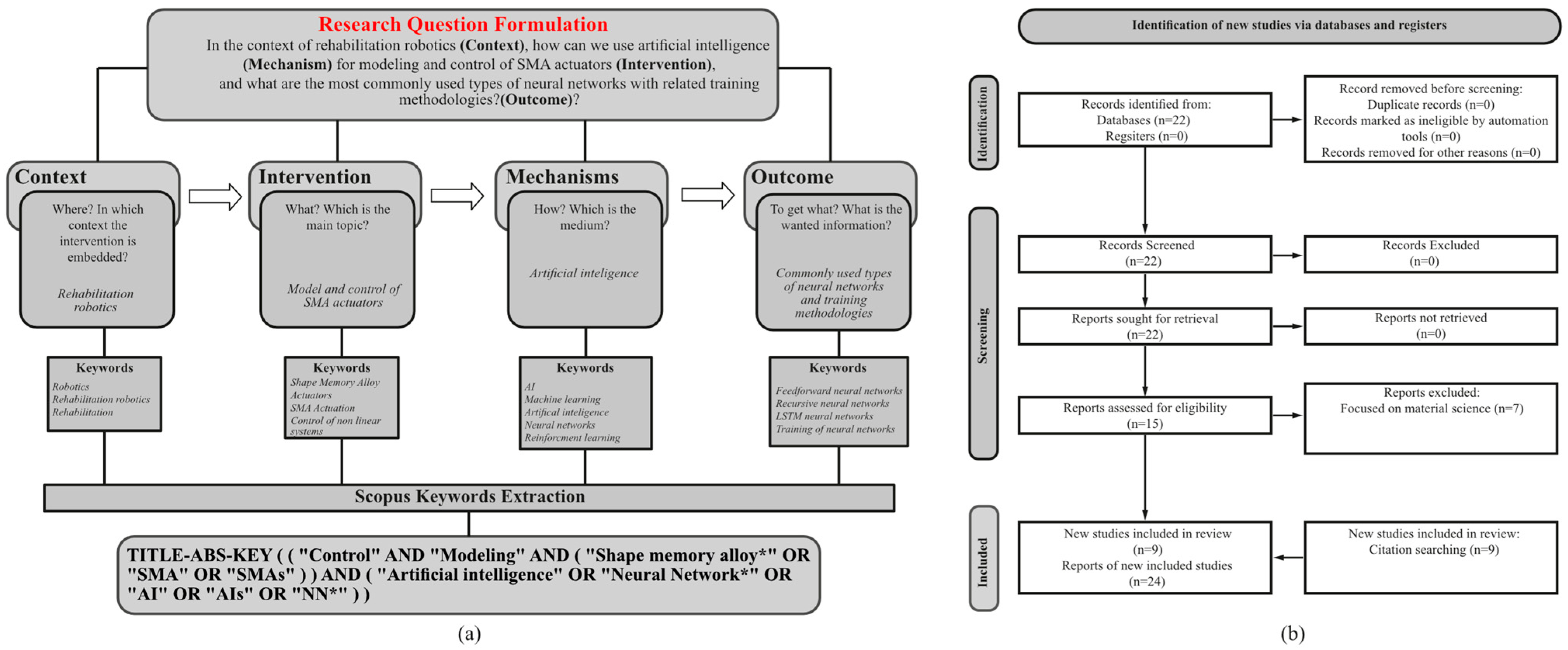
2.1. Literature Review: Methodology and Bibliometric Data
- Examining the fundamental principles and characteristics of SMAs that influence their control requirements;
- Analyzing conventional control approaches and their limitations when applied to SMA actuators;
- Investigating various AI-based control methodologies and their applications to SMA systems;
- Evaluating the performance of different AI control strategies through comparative analysis;
- Identifying current challenges, emerging trends, and future research directions in AI-controlled SMA actuators.
2.2. Shape Memory Alloy Fundamentals
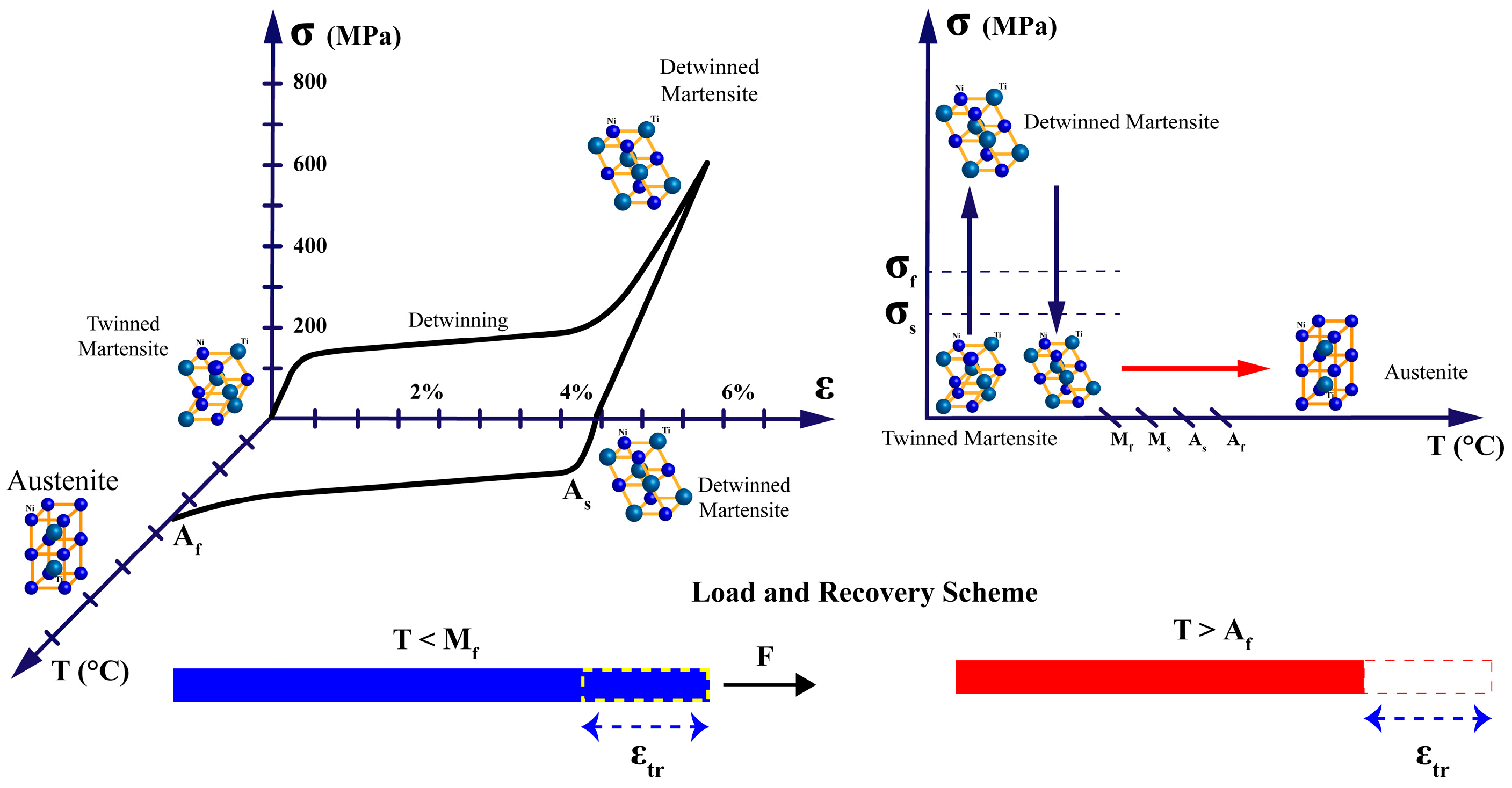
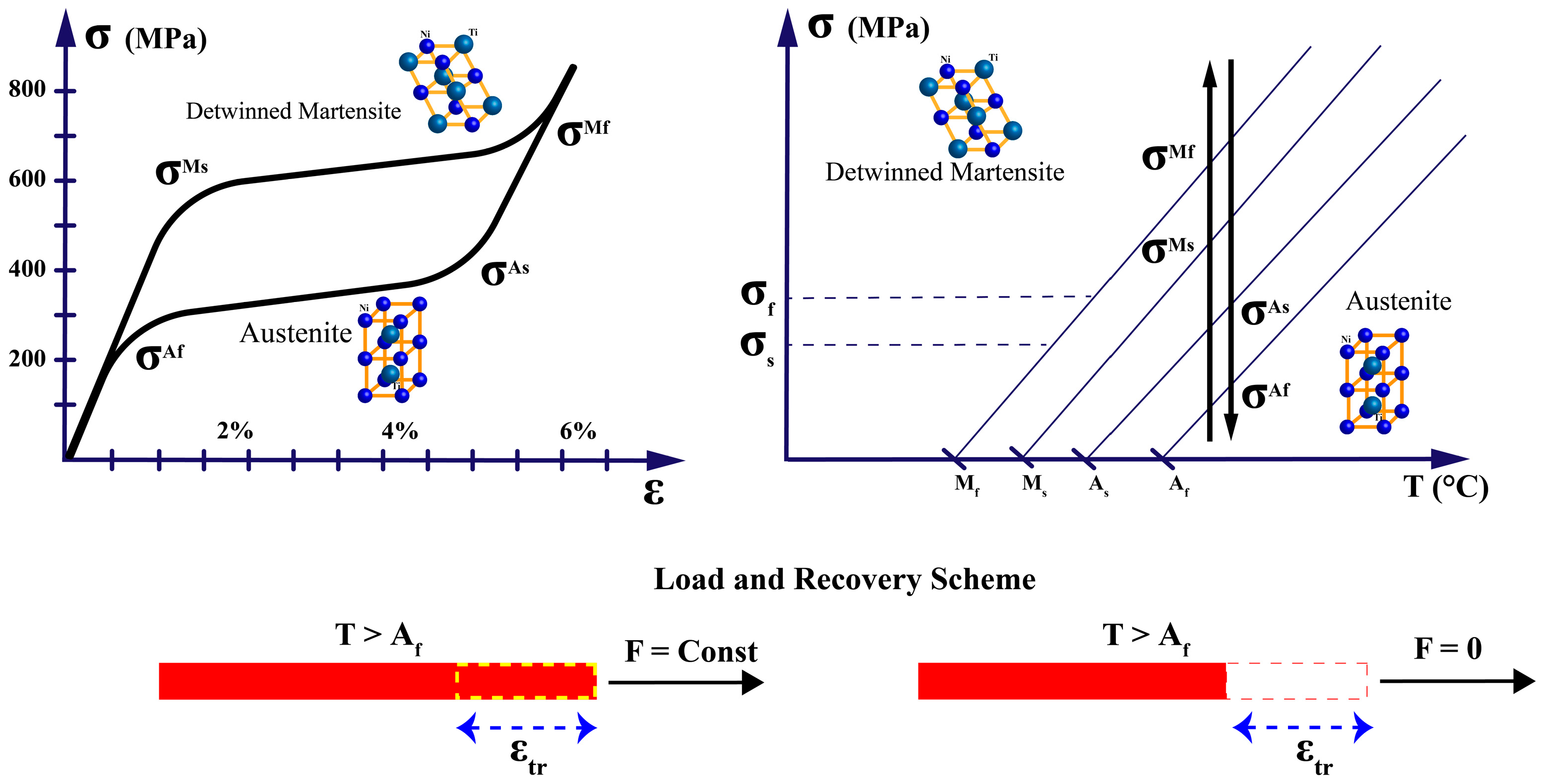
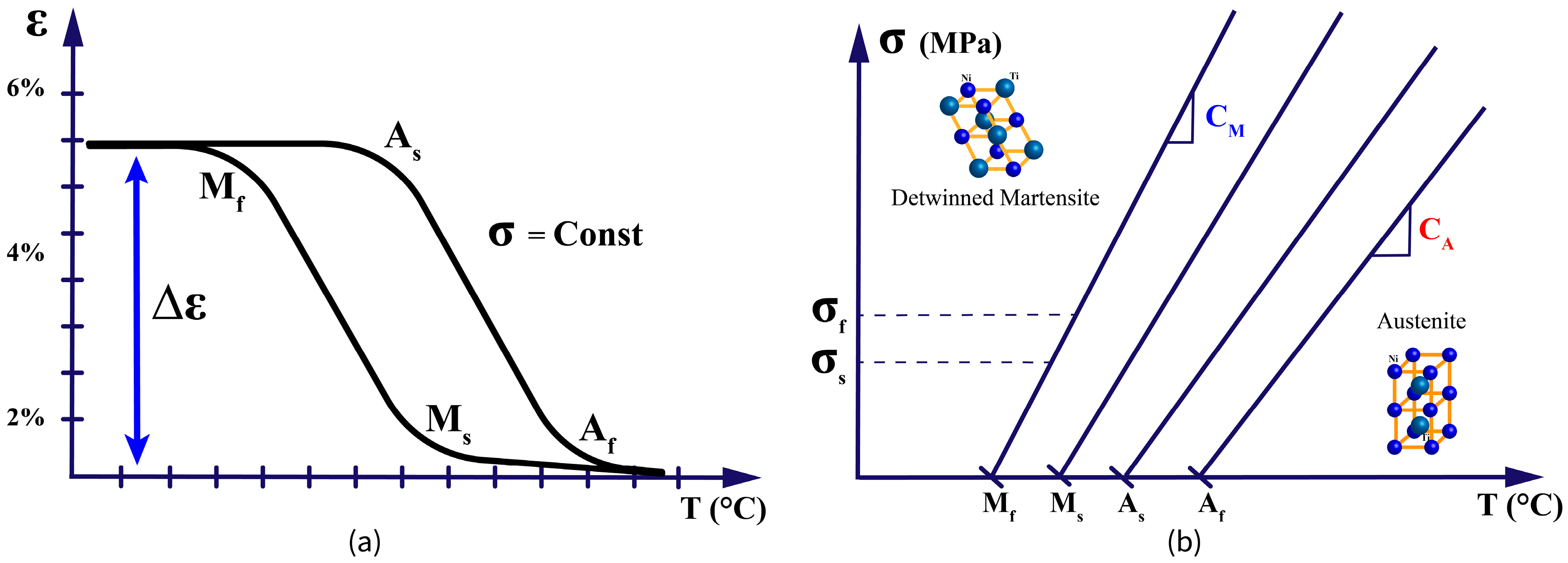
- Shape Memory Effect (SME): When a SMA in its martensitic phase is deformed and subsequently heated above its transformation temperature, it recovers its original shape as it transforms to austenite. Upon cooling, the material returns to martensite without macroscopic shape change unless external stress is applied, as in Figure 6. This one-way shape memory effect is the basis for most SMA actuator applications.
- Superelasticity (or Pseudoelasticity): When an SMA is at a temperature above its austenitic finish temperature, the application of mechanical stress can induce a transformation to stress-induced martensite. Upon removal of the stress, the material spontaneously reverts to austenite, recovering its original shape, as in Figure 7. This property allows SMAs to undergo large deformations (up to 8–10% strain) and return to their original shape without permanent deformation.
- Martensite start (Ms): Temperature at which martensite begins to form during cooling.
- Martensite finish (Mf): Temperature at which the transformation to martensite completes during cooling.
- Austenite start (As): Temperature at which austenite begins to form during heating.
- Austenite finish (Af): Temperature at which the transformation to austenite completes during heating.
- Below Mf: The material is fully martensitic and exhibits a detwinning plateau in its stress–strain curve, allowing for large recoverable deformations through the reorientation of martensite variants.
- Between Mf and Af: The material exists in a mixed-phase state, with the proportion of austenite increasing with temperature. The mechanical properties in this region are highly sensitive to temperature changes.
- Above Af: The material is fully austenitic and exhibits superelastic behavior, with stress-induced martensite forming under load and reverting to austenite upon unloading.
2.3. Types of SMA Actuators
- Wire actuators with bias spring represent the most prevalent configuration (11 documented cases), utilizing a mechanical spring to provide the restoring force necessary for shape recovery during cooling. When heated, the SMA wire contracts against the bias spring; upon cooling, the spring extends the wire to its original length. This configuration offers mechanical simplicity with predictable force-displacement relationships, though it introduces parasitic energy consumption as the SMA must work against spring resistance. Multiple geometric arrangements are possible:

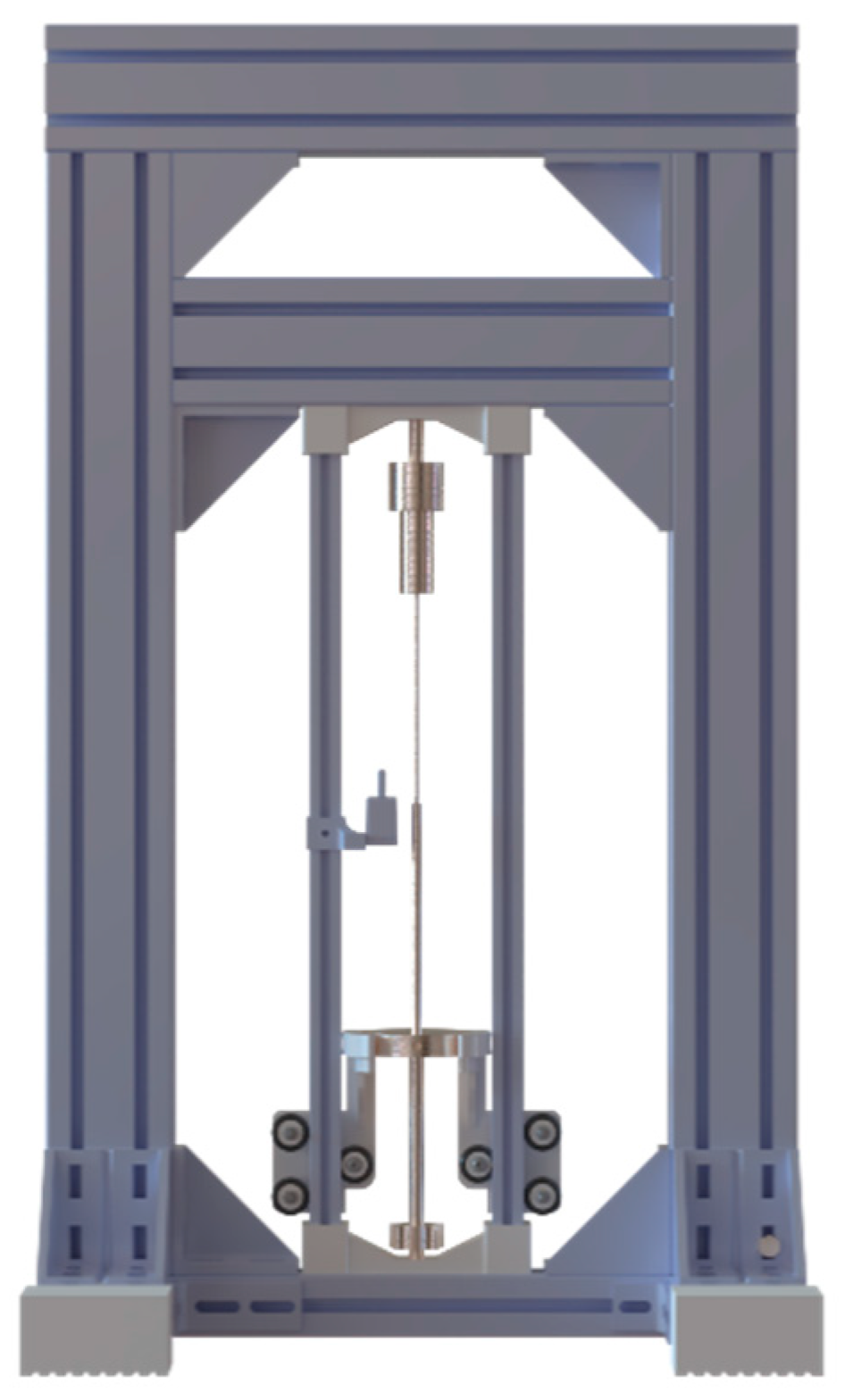
- Wire actuators with weight (three documented cases) employ gravitational loading as the resetting mechanism. This configuration improves thermomechanical efficiency by eliminating energy losses associated with working against variable spring resistance. However, it requires specific orientation considerations and offers limited implementation flexibility. These configurations are commonly employed in experimental setups due to their constant-force characteristics throughout the displacement range, Figure 11.
- Antagonistic wire configurations (three documented cases) utilize opposing SMA elements for bidirectional actuation without passive resetting mechanisms. Primary advantages include active bidirectional control capabilities and enhanced positioning precision, though with increased control complexity. Applications include the following:
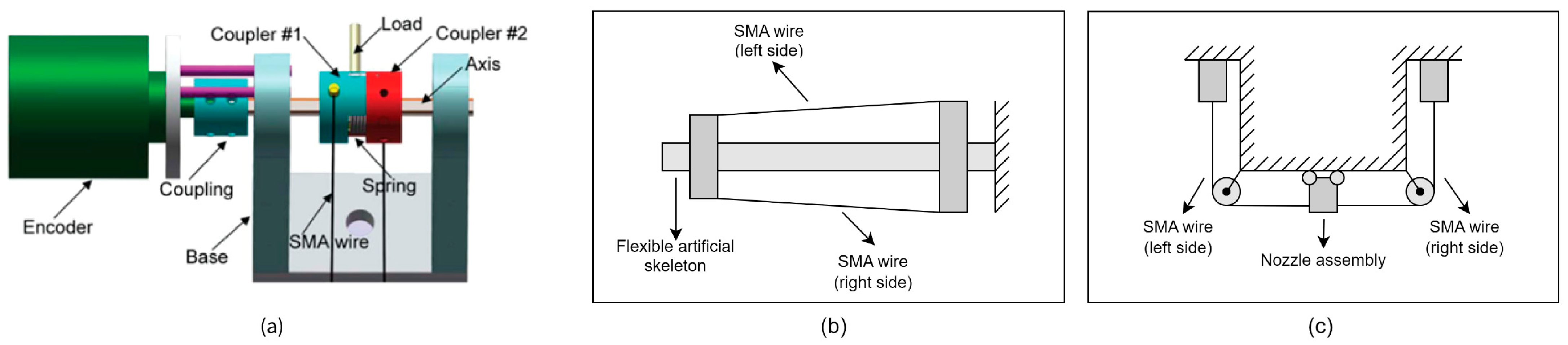
- Specialized actuator designs (one documented case) encompass various geometries addressing specific performance requirements. The documented example features an arc-shaped SMA element generating rotational motion without additional mechanical components (Figure 13) [35], demonstrating the adaptability of control methodologies across diverse geometrical configurations.
3. Conventional Control Methods for SMA Actuators
3.1. Sensing Technologies for SMA Actuators
3.1.1. Position Sensors
3.1.2. Alternative Sensing Methodologies
3.2. Classical Control Strategies
3.2.1. Control Architecture Classification
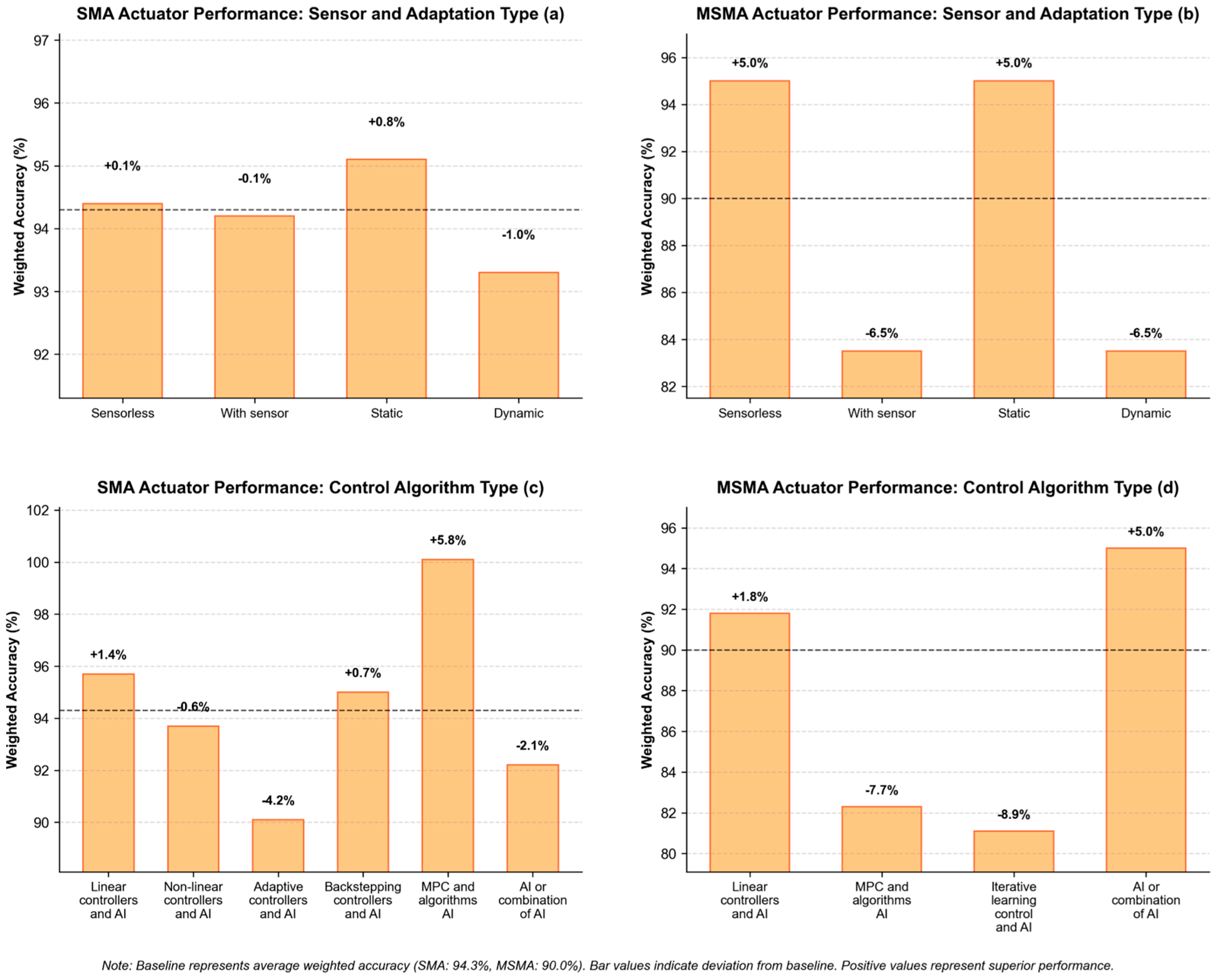
- Static vs. Dynamic Control: The temporal adaptation characteristics of control systems represent another critical distinction, with static controllers maintaining fixed parameters throughout operation and dynamic controllers implementing parameter adjustment mechanisms to accommodate system evolution over time. The literature exhibits a strong preference for dynamic controllers (13 of 16 closed-loop implementations) as reported in Figure 15a, which continuously adjust control parameters to adapt to the evolving hysteretic characteristics that develop during cyclic actuation [47]. All adaptive implementations rely on position sensor feedback for parameter updating, with no sensorless adaptive solutions identified in the current research landscape.
- Sensor Utilization: In more than half of the examined studies (16 of 24), position sensors provide essential feedback during controller operation, enabling real-time state monitoring and adjustment (Figure 15b). The remaining implementations (eight studies) utilize sensorless approaches that eliminate position sensors during operation, though these sensors remain present during the experimental characterization and control system calibration phases. Sensorless implementations offer significant advantages for miniaturized applications by eliminating bulky position sensors that reduce system flexibility and constrain integration potential.
- Open-Loop vs. Closed-Loop Control: The research corpus demonstrates a clear predominance of closed-loop control architectures, with only 8 of the 24 investigated studies implementing open-loop strategies. This distribution reflects the inherent limitations of open-loop approaches, which apply predefined actuation signals without compensating for system state variations or external disturbances, thereby providing limited effectiveness in addressing the non-linearities and hysteresis inherent to SMA actuators [28,38].
- Feedforward control: open-loop controllers employed in SMA systems typically implement feedforward architectures that incorporate predictive compensation for system uncertainties, particularly hysteresis phenomena. A notable subset of these controllers (five of eight open-loop implementations) integrate estimator modules, predominantly neural network structures, to evaluate actuator displacement without physical sensors, thereby creating virtual feedback loops that enable closed-loop operational characteristics while maintaining the implementation advantages of sensorless operation (Figure 15c).
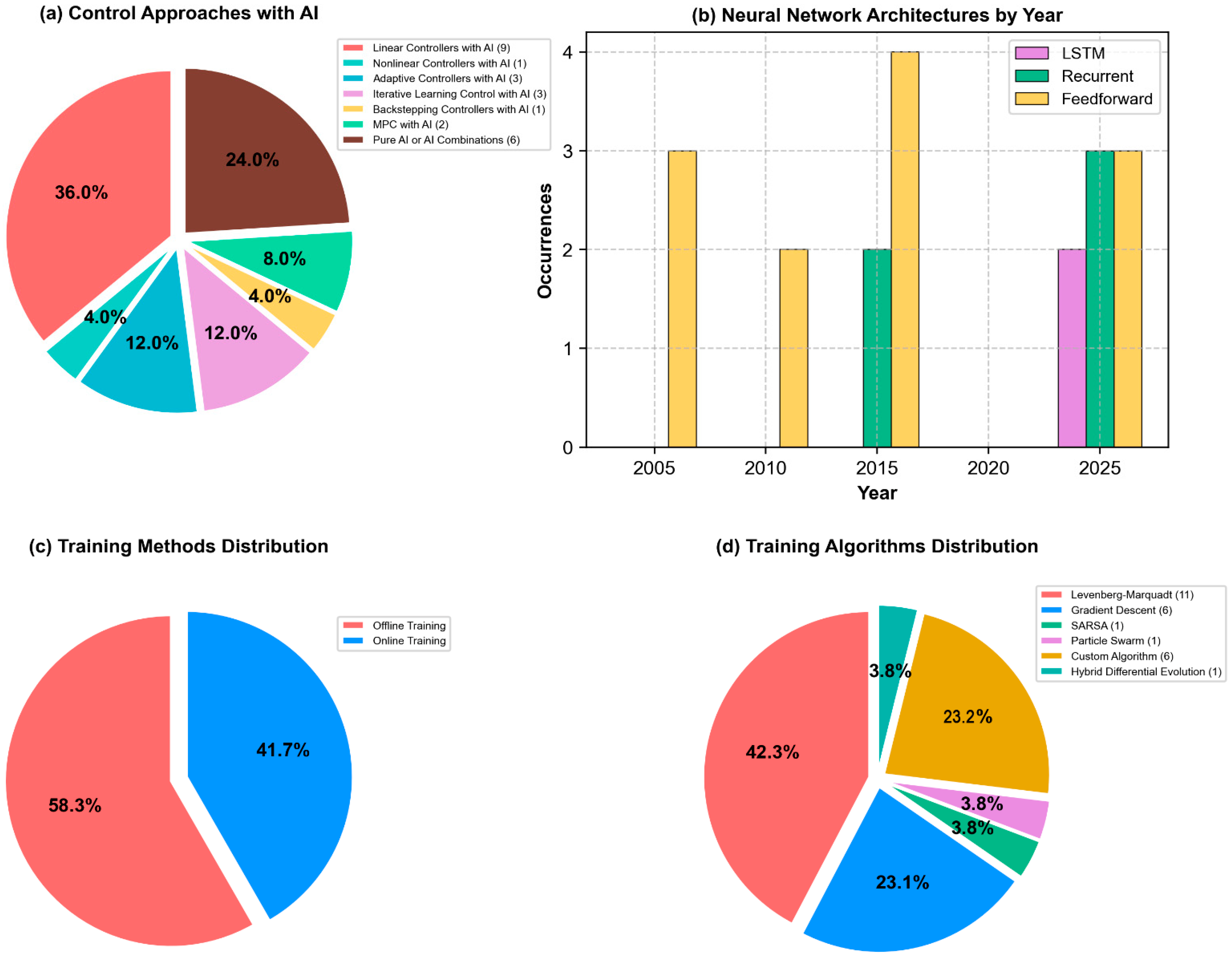
- Linear Controllers with AI Integration: The most prevalent approach combines classical linear controllers with artificial intelligence algorithms, leveraging the stability characteristics of conventional control while addressing non-linearities through AI-based compensation mechanisms.
- Pure AI Controllers: Control systems based exclusively on artificial intelligence methodologies represent the second most common implementation strategy, employing various neural network architectures to capture the complex behavior of SMA systems.
- Non-Linear Control with AI Enhancement: Several studies implement non-linear control techniques such as Sliding Mode Control (SMC) in conjunction with AI algorithms, capitalizing on the robustness of SMC approaches while mitigating their limitations through intelligent adaptation.
- Specialized Control Methodologies: Less common implementations include adaptive controllers, Iterative Learning Control (ILC), backstepping controllers, and Model Predictive Control (MPC), each offering specific advantages for particular operational requirements.
3.2.2. Type of Control Strategies
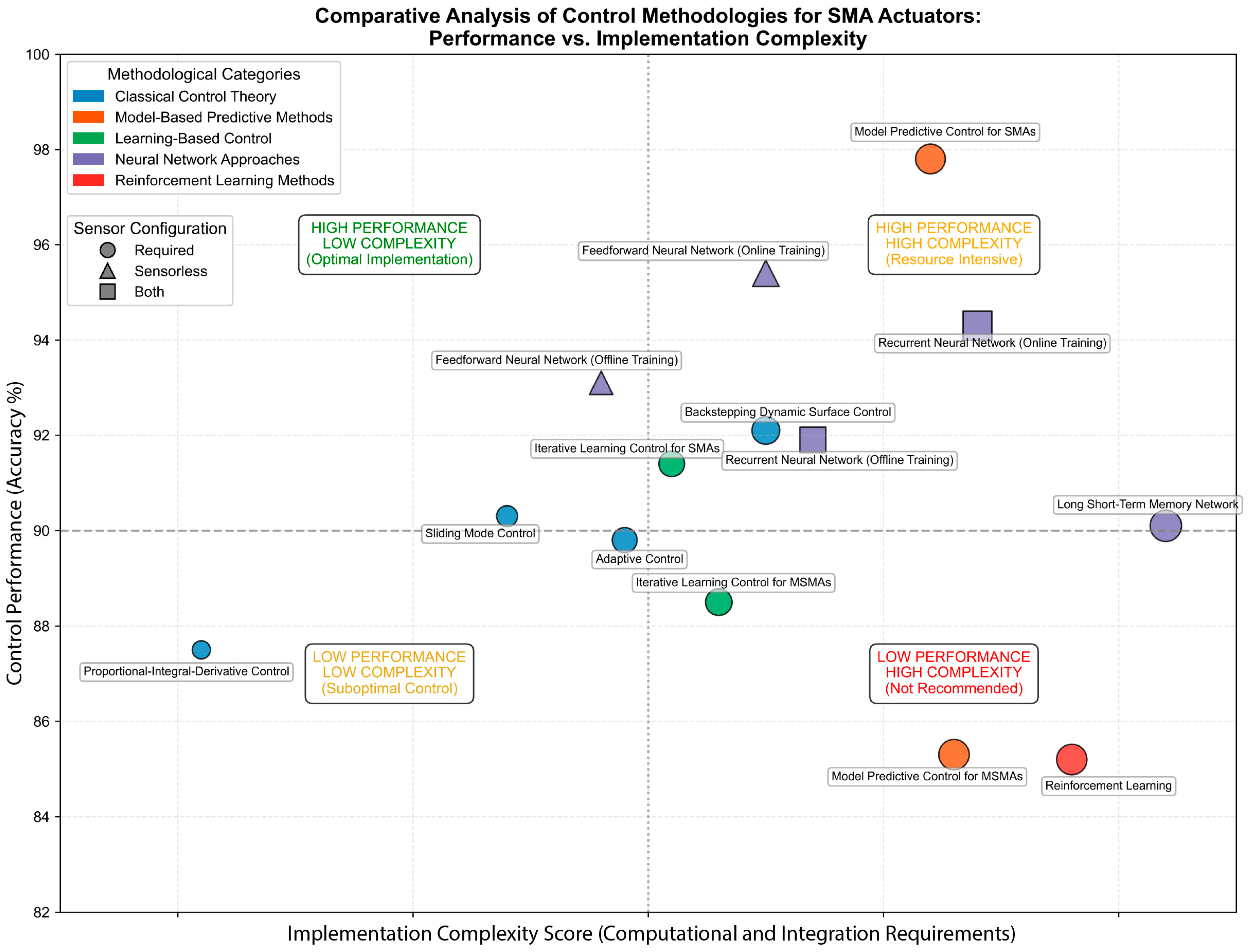
3.2.3. Control Strategy Performance Analysis
- Periodic Signal Testing: Implemented as a baseline evaluation metric present across all studies;
- Signal Typology Diversity: Presence of multiple reference trajectories with distinct morphological characteristics;
- Amplitude Variation: Implementation of variable amplitude parameters within testing protocols;
- Frequency Modulation: Incorporation of frequency variability within reference trajectories;
- Load Variation: Post-calibration performance assessment under diverse loading conditions;
- External Disturbance Introduction: Explicit incorporation of input/output perturbations.
3.3. Types of Artificial Intelligence
3.3.1. Feedforward Neural Networks
- Offline Training: Model parameters are established using historical data before deployment, with limited adaptation capability during operation.
- Online Training: Continuous parameter updates based on real-time operational data, enabling adaptation to changing system dynamics.
- Gradient descent method: an iterative method that updates the weights in the opposite direction to that of the cost function gradient [55]. The most common cost function is the MSE. Its speed is regulated by the learning rate, but high values can cause overshooting. It is often modified for online training. The gradient descent algorithm can be modified to be used online, by iteratively applying the training method to subsequent batches of data after the initial training [48].
- Levenberg–Marquadt (LM): the most widely used algorithm. It is a combination of the gradient descent method with the Newton–Raphson method, an alternative method which considers curvature of the cost function through its Hessian matrix to update the weights. The LM algorithm combines the robustness of gradient descent with the convergence speed of Newton–Raphson [35].
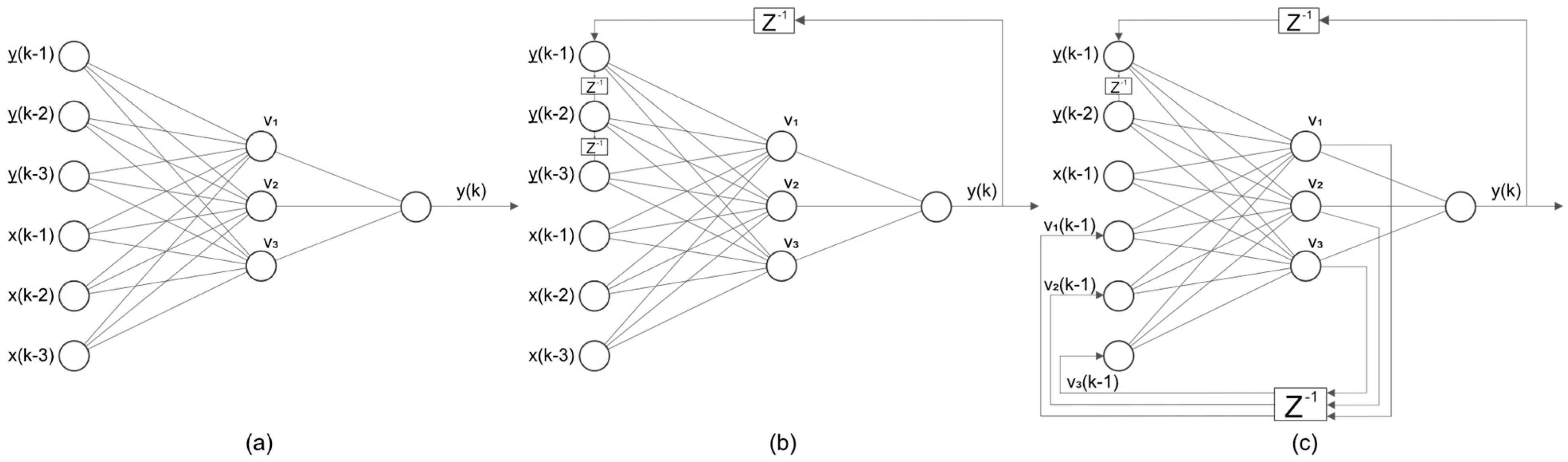
3.3.2. Recurrent Neural Networks
- Elman Network: Feedback from the hidden layer;
- Jordan–Elman Network: Feedback from both hidden and output layers, Figure 19c.
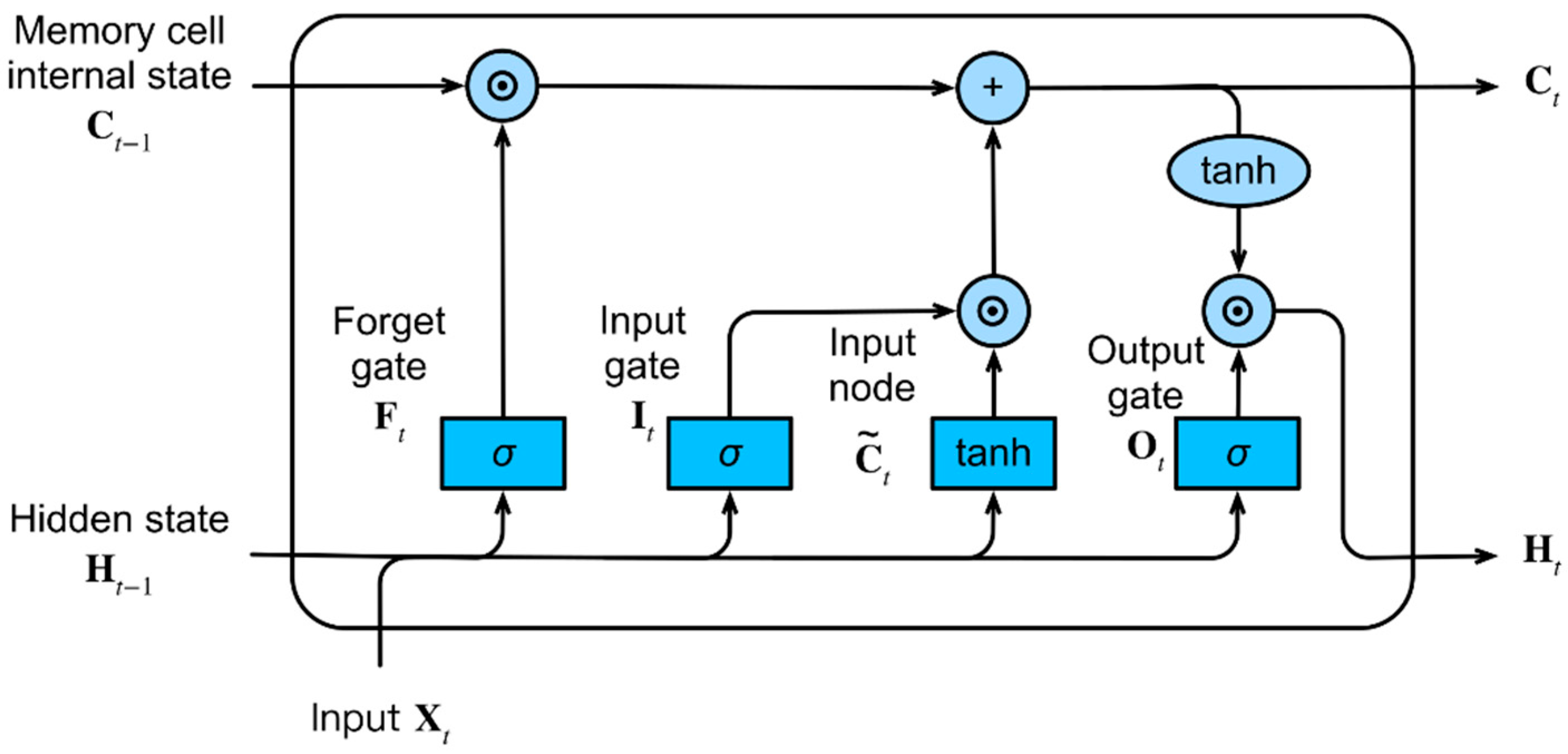
3.3.3. LSTM (Long Short-Term Memory) Networks
- Forget Gate: A sigmoid activation function is applied to the previous operation’s result, yielding a value between 0 and 1. This output is multiplied with the long-term memory from the previous timestep. The purpose of this gate is to modify long-term memory, determining which values should be “remembered.”
- Input Gate: The combination of short-term memory and outputs from the previous layer serves as input to two activation functions sigmoid (producing values between 0 and 1) and hyperbolic tangent (producing values between −1 and 1). The results are multiplied, and this product is added to the long-term memory modified by the forget gate, producing an updated long-term memory value.
- Output Gate: The updated long-term memory undergoes modification through a hyperbolic tangent activation function, while the short-term signal is modified through a sigmoid activation function. These outputs are multiplied to produce a modified short-term memory signal.
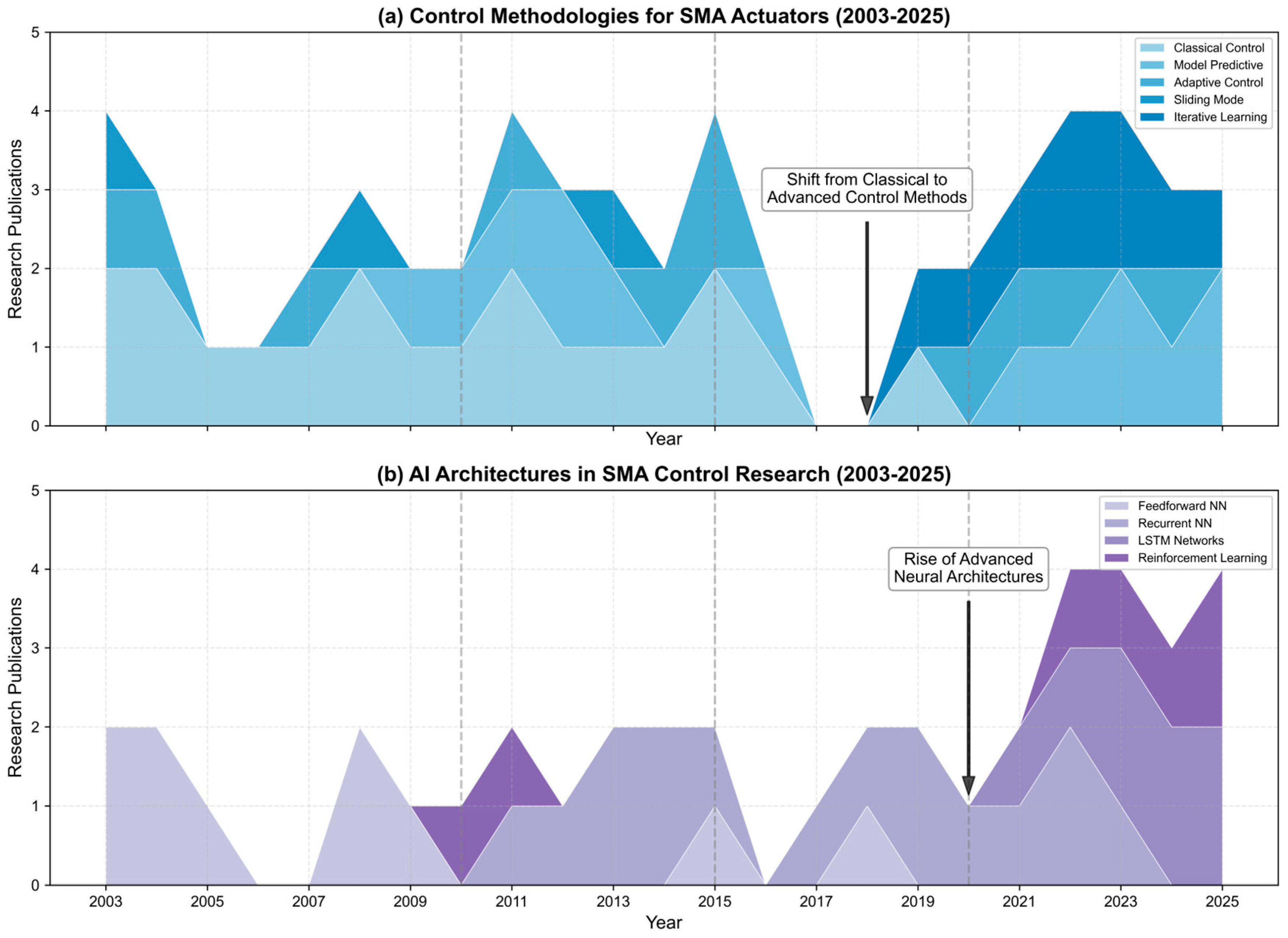
3.3.4. Reinforcement Learning
3.3.5. Artificial Intelligence Model Performance Analysis
- Material Behavior Modeling and Hysteresis Compensation [37]: Neural networks provide accurate mathematical representations of complex thermomechanical coupling phenomena.
- Feedforward Control Systems [55]: Direct neural network control without intermediate conventional control elements.
- Closed-Loop Control Through Reinforcement Learning [41]: Adaptation through environmental interaction rather than explicit mathematical modeling.
- Feedforward Neural Networks: The earliest and most prevalent architecture, characterized by unidirectional information flow from input to output layers.
- Recurrent Neural Networks: Enhanced architectures incorporating feedback connections to capture temporal dependencies crucial for modeling hysteresis effects.
- Long Short-Term Memory (LSTM) Networks: Advanced recurrent architectures with specialized memory cells designed to model long-term dependencies in sequential data.
3.3.6. AI Control Limitations and Future Research Roadmap in SMA Actuated Systems
- Computational Resource Requirements: Real-time AI control, particularly online learning approaches, demands significant computational resources that may exceed the capabilities of embedded control systems. This limitation becomes critical in applications requiring rapid response times or operating under strict power consumption constraints, regardless of the specific SMA actuation mechanism employed.
- Training Data Quality and Comprehensiveness: Neural network-based controllers require extensive, high-quality training datasets that capture the full operational envelope of SMA behavior. Experimental generation of such datasets is time-intensive and resource-demanding, often requiring sophisticated testing apparatus and precise environmental control. Poor training data quality directly compromises controller performance across all SMA system variants.
- Black-Box Behavior and Interpretability: AI controllers, particularly deep neural networks, operate as black-box systems where the relationship between inputs and outputs lacks physical interpretability. This opacity creates challenges for system validation, fault diagnosis, and safety certification in critical applications where understanding the control logic is essential.
- Hysteresis Model Limitations: While AI approaches demonstrate superior hysteresis compensation compared to linear methods, they struggle with complex, multi-loop hysteresis characteristics that can emerge under specific loading conditions or after extended cycling. The path-dependent nature of severe hysteresis can exceed the modeling capabilities of current neural network architectures.
- Real-Time Adaptation Constraints: Online learning algorithms face the exploration–exploitation trade-off, where the controller must balance learning new behaviors against maintaining stable performance. In safety-critical applications, excessive exploration can lead to system instability or performance degradation.
- Model Degradation Over Time: SMA materials exhibit property evolution due to thermal cycling, mechanical fatigue, and microstructural changes. AI controllers trained on initial material properties may gradually lose accuracy as material characteristics evolve, requiring periodic retraining or adaptive mechanisms that current implementations inadequately address.
- Integration with Physical Constraints: Many AI approaches lack explicit incorporation of fundamental physical limits such as maximum transformation strain, critical stress thresholds, or thermal damage temperatures. This can result in control commands that, while mathematically optimal, are physically unrealistic or potentially damaging to the actuator system.
- Immediate Research Priorities (1–3 years):
- Development of standardized benchmarking datasets incorporating diverse SMA compositions, hysteresis characteristics, and operational conditions for systematic AI algorithm comparison;
- Investigation of lightweight neural architectures achieving <2% RMSE while reducing computational requirements by 80% for embedded microcontroller deployment;
- Systematic comparison of physics-informed neural networks vs. purely data-driven approaches to establish optimal integration strategies for SMA control;
- Creation of unified performance metrics combining tracking accuracy, energy efficiency, and robustness for meaningful cross-study comparisons;
- Development of adaptive fatigue compensation algorithms addressing the current gap in material degradation management over extended cycling.
- Medium-term Research Goals (3–7 years):
- Integration of multi-physics thermomechanical modeling with AI control architectures for improved performance prediction and compensation;
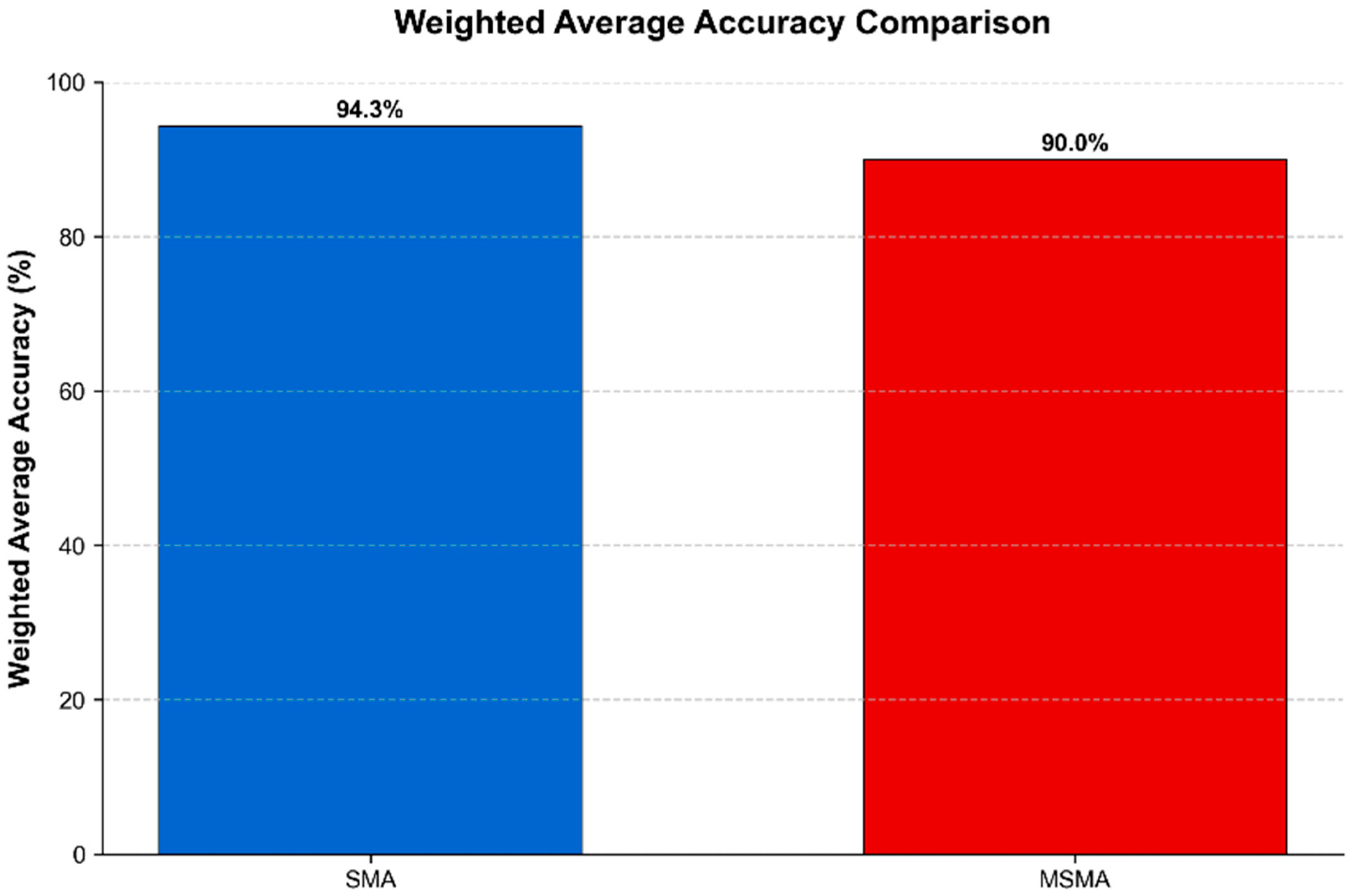
- Development of material-specific neural architecture search algorithms addressing the observed performance differentials between SMA (+5.8%) and MSMA (−7.7%) systems;
- Exploration of federated learning approaches enabling cross-system knowledge transfer between different SMA actuator configurations and applications;
- Implementation of multi-modal sensor fusion frameworks combining electrical resistance, temperature, force, and vision-based measurements for enhanced state estimation;
- Creation of safe online learning algorithms with formal stability guarantees addressing the current limitation where only 46% of implementations utilize real-time adaptation.
- Long-term Research Vision (7+ years):
- Autonomous SMA system design using AI-driven optimization for actuator geometry, material selection, and control architecture co-design;
- Integration of SMA control with broader smart material ecosystems enabling coordinated multi-actuator systems for complex applications;
- Development of explainable AI approaches providing real-time control decision insights for safety-critical aerospace and biomedical applications;
- Creation of digital twin frameworks incorporating material evolution models for predictive maintenance and performance optimization;
- Establishment of industry-standard AI control platforms enabling plug-and-play SMA actuator integration across diverse engineering applications.
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lagoudas, D.C. Shape memory Alloys: Modeling And Engineering Applications. In Springer Ebook Collection/Chemistry and Materials Science 2005–2008; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Shreekrishna, S.; Radhika, N.; Nair, V.S. A review on shape memory alloys and their prominence in automotive technology. J. Intell. Mater. Syst. Struct. 2022, 34, 499–524. [Google Scholar] [CrossRef]
- Csank, J.; Thomas, G. Dynamic analysis for a geared turbofan engine with variable area fan nozzle. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017. [Google Scholar] [CrossRef]
- Petrini, L.; Migliavacca, F. Biomedical Applications of Shape Memory Alloys. J. Metall. 2011, 2011, 1–15. [Google Scholar] [CrossRef]
- Zainal, M.; Sahlan, S.; Ali, M. Micromachined Shape-Memory-Alloy Microactuators and Their Application in Biomedical Devices. Micromachines 2015, 6, 879–901. [Google Scholar] [CrossRef]
- Lester, B.T.; Baxevanis, T.; Chemisky, Y.; Lagoudas, D.C. Review and perspectives: Shape memory alloy composite systems. Acta Mech. 2015, 226, 3907–3960. [Google Scholar] [CrossRef]
- Hartl, D.J.; Mooney, J.T.; Lagoudas, D.C.; Calkins, F.T.; Mabe, J.H. Use of a Ni60Ti shape memory alloy for active jet engine chevron application: II. Experimentally validated numerical analysis. Smart Mater. Struct. 2010, 19, 015021. [Google Scholar] [CrossRef]
- Copaci, D.; Blanco, D.; Moreno, L.E. Flexible Shape-Memory Alloy-Based Actuator: Mechanical Design Optimization According to Application. Actuators 2019, 8, 63. [Google Scholar] [CrossRef]
- Rodinò, S.; Maletta, C. Design considerations and applications of shape memory alloy-based actuation in morphing structures: A systematic review. Prog. Eng. Sci. 2024, 1, 100021. [Google Scholar] [CrossRef]
- Elahinia, M.H.; Ashrafiuon, H. Nonlinear Control of a Shape Memory Alloy Actuated Manipulator. J. Vib. Acoust. 2002, 124, 566–575. [Google Scholar] [CrossRef]
- Hartl, D.J.; Lagoudas, D.C. Aerospace applications of shape memory alloys. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2007, 221, 535–552. [Google Scholar] [CrossRef]
- Rodinò, S.; Curcio, E.M.; Sgambitterra, E.; Maletta, C. SMA-Polymer Composite Made by 3D Printing: Modelling and Experiments. Procedia Struct. Integr. 2023, 47, 579–588. [Google Scholar] [CrossRef]
- Rodrigue, H.; Wang, W.; Han, M.-W.; Kim, T.J.Y.; Ahn, S.-H. An Overview of Shape Memory Alloy-Coupled Actuators and Robots. Soft Robot. 2017, 4, 3–15. [Google Scholar] [CrossRef]
- Wang, Z.; Hang, G.; Li, J.; Wang, Y.; Xiao, K. A micro-robot fish with embedded SMA wire actuated flexible biomimetic fin. Sens. Actuators Phys. 2008, 144, 354–360. [Google Scholar] [CrossRef]
- Kohl, M.; Dittmann, D.; Quandt, E.; Winzek, B. Thin film shape memory microvalves with adjustable operation temperature. Sens. Actuators Phys. 2000, 83, 214–219. [Google Scholar] [CrossRef]
- Song, S.-H.; Lee, J.-Y.; Rodrigue, H.; Choi, I.-S.; Kang, Y.J.; Ahn, S.-H. 35 Hz shape memory alloy actuator with bending-twisting mode. Sci. Rep. 2016, 6, 21118. [Google Scholar] [CrossRef]
- Stachiv, I.; Sittner, P.; Olejnicek, J.; Landa, M.; Heller, L. Exploiting NiTi shape memory alloy films in design of tunable high frequency microcantilever resonators. Appl. Phys. Lett. 2017, 111, 213105. [Google Scholar] [CrossRef]
- Sgambitterra, E.; Greco, C.; Rodinò, S.; Niccoli, F.; Furgiuele, F.; Maletta, C. Fully coupled electric-thermo-mechanical model for predicting the response of a SMA wire activated by electrical input. Sens. Actuators Phys. 2023, 362, 114643. [Google Scholar] [CrossRef]
- Rodinò, S.; Caroleo, G.; Sgambitterra, E.; Bruno, F.; Muzzupappa, M.; Maletta, C. A multiphysics dynamic model for shape memory alloy actuators. Sens. Actuators Phys. 2023, 362, 114602. [Google Scholar] [CrossRef]
- Rodinò, S.; Siciliano, M.; Curcio, E.M.; Lamonaca, F.; Carnì, D.L.; Carbone, G.; Maletta, C. Development of an Automated Experimental System for Thermomechanical and Electrical Characterization of NiTi Shape Memory Alloys. Exp. Mech. 2024, 64, 425–440. [Google Scholar] [CrossRef]
- Mammano, G.S.; Dragoni, E. Functional fatigue of shape memory wires under constant-stress and constant-strain loading conditions. Procedia Eng. 2011, 10, 3692–3707. [Google Scholar] [CrossRef]
- Maletta, C.; Sgambitterra, E.; Furgiuele, F.; Casati, R.; Tuissi, A. Fatigue properties of a pseudoelastic NiTi alloy: Strain ratcheting and hysteresis under cyclic tensile loading. Int. J. Fatigue 2014, 66, 78–85. [Google Scholar] [CrossRef]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; for the PRISMA Group. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. BMJ 2009, 339, b2535. [Google Scholar] [CrossRef]
- Bhattacharya, K. Microstructure of Martensite: Why It Forms and How It Gives Rise to the Shape-Memory Effect (Oxford); 2013. Disponibile su. Available online: https://api.semanticscholar.org/CorpusID:15502914 (accessed on 1 June 2025).
- Miyazaki, S.; Otsuka, K. Development of shape memory alloys. ISIJ Int. 1989, 29, 353–377. [Google Scholar] [CrossRef]
- Wollants, P.; Roos, J.R.; Delaey, L. Thermally- and stress-induced thermoelastic martensitic transformations in the reference frame of equilibrium thermodynamics. Prog. Mater. Sci. 1993, 37, 227–288. [Google Scholar] [CrossRef]
- Ma, N.; Song, G.; Lee, H.-J. Position control of shape memory alloy actuators with internal electrical resistance feedback using neural networks. Smart Mater. Struct. 2004, 13, 777–783. [Google Scholar] [CrossRef]
- Song, G.; Chaudhry, V.; Batur, C. A Neural Network Inverse Model for a Shape Memory Alloy Wire Actuator. J. Intell. Mater. Syst. Struct. 2003, 14, 371–377. [Google Scholar] [CrossRef]
- Malinga, B.; Buckner, G.D. 1 adaptive control of a shape memory alloy actuated flexible beam. Syst. Sci. Control Eng. 2015, 3, 460–471. [Google Scholar] [CrossRef]
- Tai, N.T.; Ahn, K.K. A hysteresis functional link artificial neural network for identification and model predictive control of SMA actuator. J. Process Control 2012, 22, 766–777. [Google Scholar] [CrossRef]
- Narayanan, P.; Elahinia, M. Control of a shape memory alloy–actuated rotary manipulator using an artificial neural network–based self-sensing technique. J. Intell. Mater. Syst. Struct. 2016, 27, 1885–1894. [Google Scholar] [CrossRef]
- Zhang, D.; Zhao, X.; Han, J.; Li, X.; Zhang, B. Active Modeling and Control for Shape Memory Alloy Actuators. IEEE Access 2019, 7, 162549–162558. [Google Scholar] [CrossRef]
- Ning, K.; Hartono, P.; Sawada, H. Using inverse learning for controlling bionic robotic fish with SMA actuators. MRS Adv. 2022, 7, 649–655. [Google Scholar] [CrossRef]
- Bhargaw, H.N.; Singh, S.; Botre, B.A.; Sinha, P. Differential resistance based self-sensing recurrent neural network model for position estimation and control of antagonistic Shape Memory Alloy actuator. Eng. Res. Express 2021, 3, 045018. [Google Scholar] [CrossRef]
- Khan, A.M.; Bijalwan, V.; Shin, B.; Kim, Y. Adaptive Neural Network Control Design and Analysis for Sma Actuators Having Dominant Shape Memory Effect. 2023. Available online: https://ssrn.com/abstract=4577203 (accessed on 1 June 2025).
- Song, G.; Chaudhry, V.; Batur, C. Precision tracking control of shape memory alloy actuators using neural networks and a sliding-mode based robust controller. Smart Mater. Struct. 2003, 12, 223–231. [Google Scholar] [CrossRef]
- Asua, E.; Etxebarria, V.; García-Arribas, A. Neural network-based micropositioning control of smart shape memory alloy actuators. Eng. Appl. Artif. Intell. 2008, 21, 796–804. [Google Scholar] [CrossRef]
- Asua, E.; Feutchwanger, J.; García-Arribas, A.; Etxebarria, V. Sensorless Control of SMA-based Actuators Using Neural Networks. J. Intell. Mater. Syst. Struct. 2010, 21, 1809–1818. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Cao, W.; Huang, X.; Zhang, X.; Zhou, M. Neural network based iterative learning control for magnetic shape memory alloy actuator with iteration-dependent uncertainties. Mech. Syst. Signal Process. 2023, 187, 109950. [Google Scholar] [CrossRef]
- Mai, H.; Song, G.; Liao, X. Adaptive online inverse control of a shape memory alloy wire actuator using a dynamic neural network. Smart Mater. Struct. 2013, 22, 015001. [Google Scholar] [CrossRef]
- Kirkpatrick, K.; Valasek, J. Active Length Control of Shape Memory Alloy Wires Using Reinforcement Learning. J. Intell. Mater. Syst. Struct. 2011, 22, 1595–1604. [Google Scholar] [CrossRef]
- Transducers Direct. Linear Position Transducer-6 to 56 Inch Stroke-TD390 2024. Available online: https://transducersdirect.com/products/linear-transducers/linear-position-transducer-6-to-56-inch-stroke-td390/?v=2ecd53e541df (accessed on 1 June 2025).
- Pan, Y.; Guo, Z.; Li, X.; Yu, H. Output-Feedback Adaptive Neural Control of a Compliant Differential SMA Actuator. IEEE Trans. Control Syst. Technol. 2017, 25, 2202–2210. [Google Scholar] [CrossRef]
- Son, N.N.; Anh, H.P.H. Adaptive displacement online control of shape memory alloys actuator based on neural networks and hybrid differential evolution algorithm. Neurocomputing 2015, 166, 464–474. [Google Scholar] [CrossRef]
- FreeD Technology Australia. Ascension Trakstar 3D Magnetic Tracking System. FreeD Technology Australia, 2024. Available online: https://freedspace.com.au/tracklab/products/brands/ndi/ascension-trakstar/ (accessed on 1 June 2025).
- Senthilkumar, P.; Umapathy, M. Use of load generated by a shape memory alloy for its position control with a neural network estimator. J. Vib. Control 2014, 20, 1707–1717. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Wang, E.; Zhou, M. Neural Network Adaptive Control of Magnetic Shape Memory Alloy Actuator With Time Delay Based on Composite NARMAX Model. IEEE Trans. Circuits Syst. Regul. Pap. 2023, 70, 3336–3346. [Google Scholar] [CrossRef]
- Khan, A.M.; Bijalwan, V.; Shin, B.; Kim, Y. Adaptive neural network controller for the rotating SMA actuator. Sens. Actuators Phys. 2024, 370, 115240. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Hoboken, NJ, USA, 1991; Available online: https://books.google.it/books?id=cwpRAAAAMAAJ (accessed on 1 June 2025).
- Yao, M.; Li, X.; Li, K. Backstepping Dynamic Surface Control of an SMA Actuator Based on Adaptive Neural Network. In Proceedings of the 2023 2nd International Conference on Innovations and Development of Information Technologies and Robotics (IDITR), Chengdu, China, 26–28 May 2023; pp. 70–77. [Google Scholar] [CrossRef]
- Su, L.; Zhang, C.; Yu, Y.; Zhang, X.-Y.; Su, C.-Y.; Zhou, M. Neural network-based nonlinear model predictive control with anti-dead-zone function for magnetic shape memory alloy actuator. Nonlinear Dyn. 2024, 113, 1315–1332. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Moore, K.L. An Introduction to Iterative Learning Control. Csm Eges 2006. Available online: https://www.researchgate.net/profile/Mohamed_Mourad_Lafifi/post/Is-is-possible-to-achieve-almost-perfect-step-tracking-for-a-system-with-inherent-delay-using-ITERATIVE-LEARNING-CONTROL-ILC/attachment/59d63da079197b807799a63e/AS%3A420689099149314%401477311505687/download/An+Introduction+to+Iterative+Learning+Control.pdf, (accessed on 1 June 2025).
- Wang, H.; Song, G. Innovative NARX recurrent neural network model for ultra-thin shape memory alloy wire. Neurocomputing 2014, 134, 289–295. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, Y.; Xu, R.; Zhang, Q.; Zhu, D. Feed-Forward Control for Magnetic Shape Memory Alloy Actuators Based on the Radial Basis Function Neural Network Model. J. Appl. Biomater. Funct. Mater. 2017, 15, 25–30. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, C.; Wang, Y.; Zhou, M. Neural-Network-Based Iterative Learning Control for Hysteresis in a Magnetic Shape Memory Alloy Actuator. IEEEASME Trans. Mechatron. 2022, 27, 928–939. [Google Scholar] [CrossRef]
- Zhou, M.; Su, L.; Zhang, C.; Liu, L.; Yu, Y.; Zhang, X.; Su, C.-Y. Neural Network Based Iterative Learning Control for Dynamic Hysteresis and Uncertainties in Magnetic Shape Memory Alloy Actuator. IEEE Trans. Circuits Syst. Regul. Pap. 2024, 71, 2885–2896. [Google Scholar] [CrossRef]
- MathWorks. Fitnet, Rete Neurale di Fitting Della Funzione 2025. Available online: https://it.mathworks.com/help/deeplearning/ref/fitnet.html (accessed on 1 June 2025).
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]



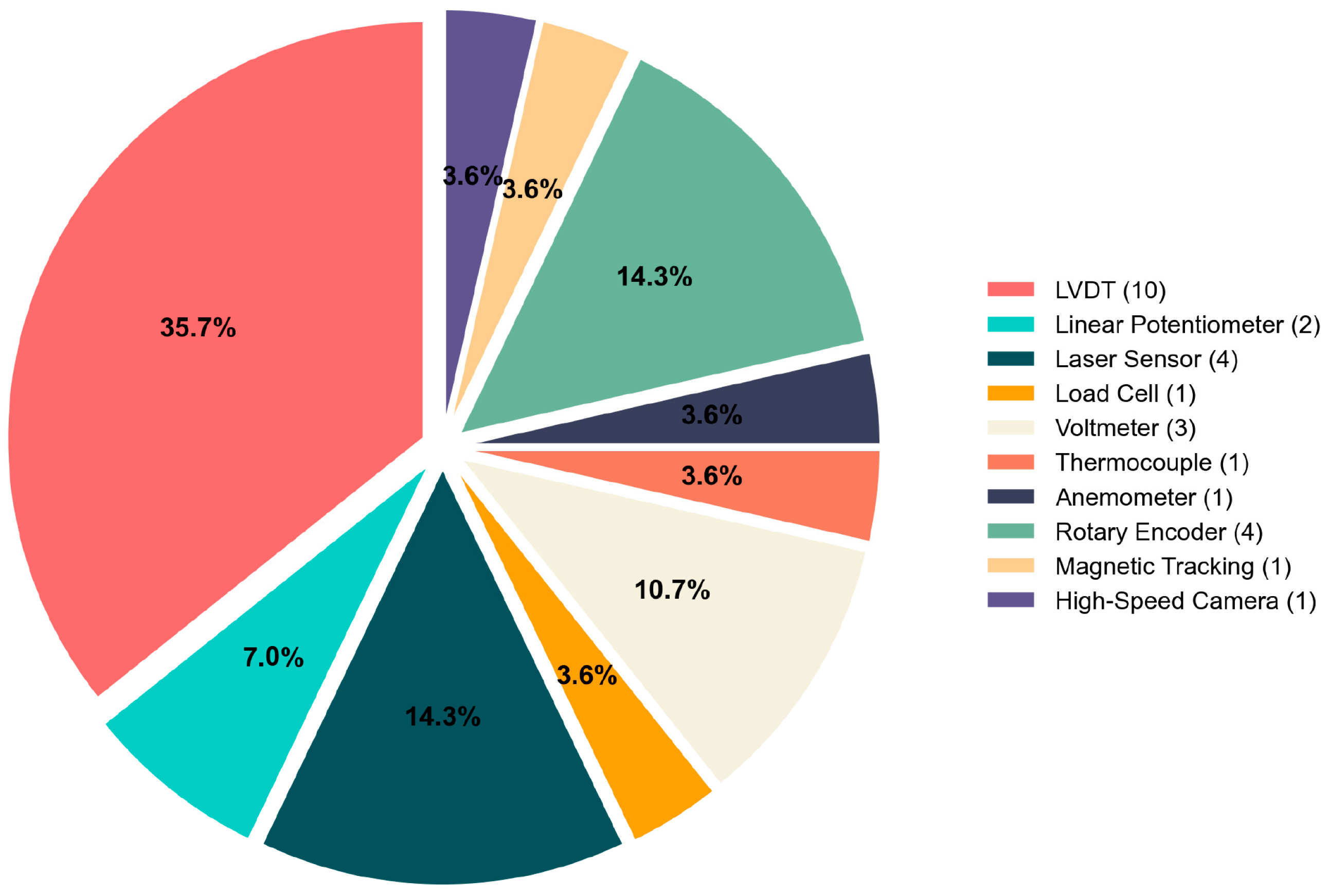



| Technology [References] | Measurement Principle | Characteristics | Precision | Applications | Limitations |
|---|---|---|---|---|---|
| Linear Variable Differential Transformer (LVDT) [36,37,38,39] | Electromagnetic induction with ferromagnetic core positioned within three coils (one primary AC-driven, two secondary connected in opposite phase); core displacement generates proportional voltage differential | Most widely deployed position sensing technology in SMA actuation systems; provides direct measurement of linear displacement | Dependent on output voltage assessment instrumentation | SMA contraction/expansion measurement [36]; MSMA displacement monitoring [39] | Form factor limitations for miniaturized or lightweight applications [38] |
| Laser Displacement Sensors [34,40] | Non-contact measurement evaluating position changes in laser beam reflected from mobile elements (typically reflective discs mounted at actuator endpoints) | Eliminates mechanical coupling with experimental apparatus; commercial implementations include Keyence IL series and IDEC MX1A/B models | Micron-level repeatability with application-specific measurement ranges | Longitudinal displacement measurement without mechanical interference [34,40] | Similar form factor challenges as LVDTs for miniaturized applications |
| Linear Potentiometers [41,42] | Resistive sensing determining probe position through internal electrical resistance variations | Commercial models (e.g., Linear Position Transducer) offer flexible measurement ranges (150–1420 mm) | Variable based on component specification | Rectilinear displacement measurement in larger-scale applications [41] | Lower precision than laser or LVDT alternatives |
| Rotary Encoders [31,43,44] | Patterned disc with transparent/opaque regions modulating light detection during rotation, generating electrical signals converted to angular position | Can provide direct rotational measurement or indirect translational monitoring when coupled with pulleys; can be integrated within robotic systems | Up to 2500 pulses per revolution (e.g., Omron E6B2-CWZ1X) | Direct angular position measurement [43]; indirect translational monitoring via pulleys [44]; robotic system integration [31] | Limited to rotational measurement without conversion mechanisms |
| Magnetic Tracking Systems [29,45] | Electromagnetic field detection for spatial positioning | Enables six-degree-of-freedom tracking through miniaturized sensors (e.g., trakSTAR 3D Magnetic Tracking System) | Sub-millimeter 3D positioning capability | Three-dimensional position assessment for complex actuation systems [29] | Susceptible to electromagnetic interference; requires specialized infrastructure |
| High-Speed Camera Systems [33] | Computer vision analysis with Kinovea kinematic software processing | Emerging methodology enabling non-contact multi-point tracking | Dependent on camera resolution and processing algorithms | Spatial position evaluation of robotic systems; trajectory and velocity characterization [33] | Requires line-of-sight; computationally intensive; lighting-dependent |
| Technology [References] | Measurement Principle | Implementation Methodologies | Advantages | Applications | Limitations |
|---|---|---|---|---|---|
| Electrical Resistance Monitoring (Self-Sensing) [27,34,38,46] | Exploitation of phase-dependent resistivity differential between martensitic (higher) and austenitic (lower) phases | Programmable Power Supply: Controls one electrical parameter while measuring another; applies Ohm’s law for resistance calculation. Series Resistor: In constant-voltage scenarios, uses calibrated resistor for indirect current measurement via voltage sensing | Eliminates external position sensor requirements; enables system miniaturization; leverages intrinsic material properties | Phase transformation monitoring [27]; position estimation during actuation [38]; antagonistic wire configuration assessment [34] | Requires continuous energization; extends cooling times; necessitates instrumentation integration with activation signal |
| Force Measurement [34,46] | Direct stress/strain quantification during phase transformation | Load cell integration within actuation train | Enables correlation between material deformation and actuator position; provides structural stress monitoring capabilities | Material deformation correlation [46]; structural stress monitoring [34] | Requires mechanical integration; introduces additional mass/complexity |
| Temperature Monitoring [41,46] | Direct thermal state assessment of SMA elements | Thermocouple attachment to SMA elements | Provides actuation state verification; enables temperature-based control signal generation | Control signal generation [41]; operational state verification [46] | Measurement bias related to attachment methodology; limited spatial resolution |
| Airflow Measurement [46] | Quantification of convective cooling conditions | Cup anemometer deployment within experimental setup | Enables characterization of cooling system influence on actuator response dynamics | Cooling system performance evaluation [46] | Limited to laboratory environments; primarily for experimental characterization |
| Data Acquisition Systems [28,30,31,33,35,37,41] | Analog-to-digital signal conversion and processing | Commercial systems (National Instruments [28], dSPACE [31], Advantech [30]); embedded approaches (Arduino Nano [33], Jetson Nano [35]) | Integrates sensor networks with control systems; enables real-time data processing and control implementation | Experimental characterization [37]; control system implementation [41]; miniaturized implementations [33,35] | System complexity; calibration requirements; platform constraints |
| Control Strategy [References] | Classification | Working Principle | Key Advantages | Limitations/Challenges | Applicability to SMA/MSMA |
|---|---|---|---|---|---|
| Proportional-Integral-Derivative (PID) [37,48] | Linear, feedback-based | Generates control signal based on error between setpoint and actual output; combines proportional response to current error, integral action on accumulated error, and derivative action based on rate of change | Established industrial standard; intuitive parameter tuning; responsive to transient disturbances; well-documented implementation protocols | Performance degradation in non-linear regimes; steady-state error persistence without integral component; susceptibility to derivative noise amplification; integral windup during saturation conditions | Limited efficacy for SMA/MSMA systems due to pronounced hysteresis and non-linear thermomechanical coupling; requires supplementary compensation mechanisms |
| Sliding Mode Control (SMC) [46,49] | Non-linear, robust | Constrains system state trajectory onto a predefined sliding manifold through discontinuous control actions; operates in sequential reaching and maintenance phases | Inherent robustness against parametric uncertainties and external disturbances; reduced-order equivalent control problem; rapid convergence characteristics; invariance to matched uncertainties | High-frequency oscillations (chattering) at control discontinuities; potential for actuator degradation due to rapid switching; requires accurate sliding surface design; sensitive to unmodeled dynamics | Highly compatible with SMA/MSMA actuators due to robust performance under thermomechanical uncertainties and phase transformation non-linearities |
| Backstepping Dynamic Surface Control (BDSC) [50] | Non-linear, recursive | Implements systematic stabilization through recursive Lyapunov-based design; decomposes complex non-linear systems into cascaded subsystems with virtual control variables; employs low-pass filtering for derivative estimation | Superior tracking precision; systematic design methodology for complex non-linear systems; analytical stability guarantees; robustness against bounded disturbances; reduced computational burden compared to standard backstepping | Requires comprehensive analytical system model; increased design complexity with system order; potential performance degradation under severe model uncertainties; non-trivial implementation requirements | Exceptionally suitable for SMA/MSMA actuators due to systematic handling of non-linearities and hysteresis effects; accommodates complex thermomechanical coupling phenomena |
| Adaptive Control [29,43] | Parameter-adjusting, dynamic | Modifies controller parameters systematically according to performance metrics and estimation algorithms; utilizes reference models (MRAC) or direct adaptation mechanisms; incorporates parameter convergence safeguards | Autonomously accommodates parametric variations and uncertainties; minimal a priori system knowledge requirements; performance preservation under time-varying conditions; resilience to gradual system degradation | Parameter convergence not universally guaranteed; potential instability during rapid adaptation; susceptibility to disturbance-induced parameter drift; complex stability analysis requirements | Highly effective for SMA/MSMA systems exhibiting parameter variations due to thermal cycling, fatigue, or environmental conditions; compensates for time-variant hysteresis characteristics |
| Model Predictive Control (MPC) [30,51,52] | Optimization-based, predictive | Formulates control as a receding horizon optimization problem; predicts future system behavior using dynamic models; minimizes cost functions subject to explicit constraints; implements only first element of optimal control sequence | Explicit constraint handling capability; multivariable system accommodation; anticipatory disturbance compensation; systematic performance-constraint trade-off management; optimality guarantees within prediction horizon | Substantial computational requirements for online optimization; performance critically dependent on model fidelity; implementation complexity increases with horizon length and constraint complexity; potential suboptimality under model-plant mismatch | Well-suited for SMA/MSMA applications requiring constraint enforcement (thermal, mechanical, electrical) while maintaining performance objectives; particularly effective when augmented with accurate thermomechanical models |
| Iterative Learning Control (ILC) [39,47,53] | Memory-based, repetitive | Exploits task repetition to progressively refine control signals; utilizes error information from previous iterations to improve subsequent performance; implements memory-based feedforward corrections derived from historical execution data | Progressive performance enhancement for repetitive tasks; minimal model dependence; effective compensation for repeatable disturbances; potential for perfect tracking under ideal conditions | Strictly limited to repetitive operations with consistent initial conditions; performance degradation under non-repetitive disturbances; potential error amplification without appropriate filtering; memory-intensive implementation | Particularly advantageous for cyclic SMA/MSMA applications with repetitive actuation requirements; effective for compensating repeatable hysteresis effects; suitable for precision positioning tasks |
| Author and Year [Reference] | Title | Position Sensor Utilization | Feedback | Static/Dynamic Methodology | Control Algorithm | Tracking Performance (RMSE%) |
|---|---|---|---|---|---|---|
| Song, G. et al., 2003 [28] | A Neural Network Inverse Model for a Shape Memory Alloy Wire Actuator | Sensorless | No | Static | AI or AI combination | Sinusoidal signal: 7%. Accuracy score: 0.93 |
| Song, G. et al., 2003 [36] | Precision tracking control of shape memory alloy actuators using neural networks and a sliding-mode based robust controller | With position sensor | Yes | Static | Non-linear controllers (SMC) and AI | Sinusoidal signals: 5.1%. Evaluation conducted with various amplitudes and frequencies. Accuracy score: 2.87 |
| Ma, N. et al., 2004 [27] | Position control of shape memory alloy actuators with internal electrical resistance feedback using neural networks | Sensorless | Yes | Static | Linear controllers (PD) and AI | Multistep signal: 7%. Accuracy score: 1.86 |
| Asua, E. et al., 2008 [37] | Neural network-based micropositioning control of smart shape memory alloy actuators | With position sensor | Yes | Static | Linear controllers (PI) and AI | Square wave and ramp signals: <1%. Accuracy score: 1.98 |
| Asua, E. et al., 2010 [38] | Sensorless Control of SMA-based Actuators Using Neural Networks | Sensorless | Yes | Static | Linear controllers (PID) and AI | Ramp and step signals: <6%. Accuracy score: 2.82 |
| Kirkpatrick, K. et al., 2011 [41] | Active Length Control of Shape Memory Alloy Wires Using Reinforcement Learning | With position sensor | Yes | Dynamic | AI or AI combination | Multistep signals: <18%. Accuracy score: 1.64 |
| Tai, N. et al., 2012 [30] | A hysteresis functional link artificial neural network for identification and model predictive control of SMA actuator | With position sensor | Yes | Dynamic | MPC and AI algorithms | Multistep and sinusoidal signals: <0.2%. Accuracy score: 2.99 |
| Mai, H. et al., 2013 [40] | Adaptive online inverse control of a shape memory alloy wire actuator using a dynamic neural network | With position sensor | Yes | Dynamic | Linear controllers (P) and AI | Sinusoidal signals: <1%. Evaluation conducted with various amplitudes and frequencies. Accuracy score: 1.98 |
| Wang, H. et al., 2014 [54] | Innovative NARX recurrent neural network model for ultra-thin shape memory alloy wire | With position sensor | Yes | Static | AI or AI combination | Sinusoidal signals: 3.5%. Evaluation conducted with various amplitudes. Accuracy score: 1.93 |
| Senthilkumar, P. et al., 2014 [46] | Use of load generated by a shape memory alloy for its position control with a neural network estimator | Sensorless | Yes | Static | Linear controllers (PI with gain scheduling) and AI | Multistep signal: <1.5%. Evaluation conducted with various signal types. Accuracy score: 1.97 |
| Son, N.N. et al., 2015 [44] | Adaptive displacement online control of shape memory alloys actuator based on neural networks and hybrid differential evolution algorithm | With position sensor | Yes | Dynamic | Linear controllers (PID) and AI | Sawtooth and trapezoidal signals: <7%. Evaluation conducted with various signal types. Accuracy score: 1.86 |
| Malinga, B. et al., 2015 [29] | 1 adaptive control of a shape memory alloy actuated flexible beam | With position sensor | Yes | Dynamic | Adaptive controllers and AI | Sawtooth or sinusoidal signals: <25%. Evaluation conducted with various signal types. Accuracy score: 1.5 |
| Narayanan, P. et al., 2016 [31] | Control of a shape memory alloy–actuated rotary manipulator using an artificial neural network–based self-sensing technique | Sensorless | Yes | Static | Linear controllers (PI with gain scheduling) and AI | Complex signal: 7%. Evaluation conducted with various signal types, with variable amplitude and frequency. Accuracy score: 3.72 |
| Zhou, M. et al., 2017 [55] | Feed-forward control for magnetic shape memory alloy actuators based on the radial basis function neural network model | Sensorless | No | Static | AI or AI combination | Complex signals: <1%. Evaluation conducted with various signal types, with variable amplitude and frequency. Accuracy score: 3.96 |
| Pan, Y. et al., 2017 [43] | Output-Feedback Adaptive Neural Control of a Compliant Differential SMA Actuator | With position sensor | Yes | Dynamic | Linear controllers (PD), adaptive and AI | Sinusoidal and complex signals: <2%. Evaluation conducted with various signal types, with variable amplitude and frequency. Accuracy score: 3.92 |
| Bhargaw, H.N. et al., 2021 [34] | Differential resistance based self-sensing recurrent neural network model for position estimation and control of antagonistic shape memory alloy actuator | Sensorless | Yes | Static | Linear controllers (PI) and AI | Multistep and sinusoidal signals: <5%. Evaluation conducted with various signal types, with variable amplitude and frequency. Accuracy score: 3.8 |
| Ning, K. et al., 2022 [33] | Using inverse learning for controlling bionic robotic fish with SMA actuators | Sensorless | No | Static | AI or AI combination | Not applicable. Experimental error evaluated on the achieved movement velocity <10%. |
| Yu, Y. et al., 2022 [56] | Neural-Network-Based Iterative Learning Control for Hysteresis in a Magnetic Shape Memory Alloy Actuator | With position sensor | Yes | Dynamic | Iterative Learning Control and AI | Sawtooth signals: <14%. Evaluation conducted with various amplitudes. Accuracy score: 1.72 |
| Yu, Y. et al., 2023 [47] | Neural Network Adaptive Control of Magnetic Shape Memory Alloy Actuator With Time Delay Based on Composite NARMAX Model | With position sensor | Yes | Dynamic | Adaptive controllers and AI algorithms | Sawtooth and complex signals: <4%. Evaluation conducted with various signal types, with variable amplitude and frequency. Accuracy score: 3.84 |
| Yao, M. et al., 2023 [50] | Backstepping Dynamic Surface Control of an SMA Actuator Based on Adaptive Neural Network | With position sensor | Yes | Dynamic | Backstepping controllers and AI | Sinusoidal signal: 5%. Comparison performed on system model. Accuracy score: 0.95 |
| Yu, Y. et al., 2023 [39] | Neural network based iterative learning control for magnetic shape memory alloy actuator with iteration-dependent uncertainties | With position sensor | Yes | Dynamic | Iterative Learning Control and AI | Complex signals: <15%. Evaluation conducted with various signal types, with variable amplitude and frequency, and variation in load level. Accuracy score: 4.25 |
| Khan, A.M. et al., 2024 [48] | Adaptive neural network controller for the rotating SMA actuator | With position sensor | Yes | Dynamic | AI or AI combination | Sinusoidal signals: <2%. Evaluation conducted with input and output disturbances. Accuracy score: 1.96 |
| Zhou, M. et al., 2024 [57] | Neural Network Based Iterative Learning Control for Dynamic Hysteresis and Uncertainties in Magnetic Shape Memory Alloy Actuator | With position sensor | Yes | Dynamic | Iterative Learning Control and AI | Complex signals: <13%. Evaluation conducted with various signal types, with variable amplitude and frequency. Accuracy score: 3.48 |
| Su, L. et al., 2025 [51] | Neural network-based non-linear model predictive control with anti-dead-zone function for magnetic shape memory alloy actuator | With position sensor | Yes | Dynamic | MPC and AI algorithms | Sinusoidal and sawtooth signals: <13%. Evaluation conducted with various signal types, with variable amplitude and frequency, and variation in load level. Accuracy score: 4.35 |
| Author and Year [Reference] | Training Approach | AI Type | Training Algorithm | Tracking Performance (RMSE%) |
|---|---|---|---|---|
| Song, G. et al., 2003 [28] | Offline | Feedforward Neural Network | Levenberg–Marquardt | Sinusoidal signal: 7% |
| Song, G. et al., 2003 [36] | Offline | Feedforward Neural Network | Levenberg–Marquardt | Sinusoidal signals: 5.1%. Evaluation performed with various amplitudes and frequencies. |
| Ma, N. et al., 2004 [27] | Offline | Feedforward Neural Network | Levenberg–Marquardt | Multistep signal: 7% |
| Asua, E. et al., 2008 [37] | Offline | Feedforward Neural Network | Levenberg–Marquardt | Square wave and ramp signals: <1% |
| Asua, E. et al., 2010 [38] | Offline | Feedforward Neural Network | Levenberg–Marquardt | Ramp and step signals: <6% |
| Kirkpatrick, K. et al., 2011 [41] | Online | Reinforcement Learning | N/A | Multistep signals: <18% |
| Tai, N. et al., 2012 [30] | Online | Recurrent Neural Network | Particle Swarm Optimization + Gradient descent | Multistep and sinusoidal signals: <0.2% |
| Mai, H. et al., 2013 [40] | Online | Recurrent Neural Network | Custom online algorithm | Sinusoidal signals: <1%. Evaluation performed with various amplitudes and frequencies. |
| Wang, H. et al., 2014 [54] | Offline | Recurrent Neural Network | Custom algorithm for recurrent neural network training | Sinusoidal signals: 3.5%. Evaluation performed with various amplitudes. |
| Senthilkumar, P. et al., 2014 [46] | Offline | Feedforward Neural Network | Levenberg–Marquardt | Multistep signal: <1.5% |
| Son, N.N. et al., 2015 [44] | Online | Recurrent Neural Network | Hybrid differential evolution | Sawtooth and trapezoidal signals: <7% |
| Malinga, B. et al., 2015 [29] | Offline | Recurrent Neural Network | Levenberg–Marquardt | Sawtooth or sinusoidal signals: <25% |
| Narayanan, P. et al., 2016 [31] | Offline | Feedforward Neural Network | Levenberg–Marquardt | Complex signal: 7% |
| Zhou, M. et al., 2017 [55] | Offline | Feedforward Neural Network | Gradient descent | Complex signals: <1% |
| Pan, Y. et al., 2017 [43] | Online | Feedforward Neural Network | Custom online algorithm | Sinusoidal and complex signals: <2%. Evaluation performed with various amplitudes and frequencies. |
| Bhargaw, H.N. et al., 2021 [34] | Offline | Recurrent Neural Network | Levenberg–Marquardt | Multistep and sinusoidal signals: <5% |
| Ning, K. et al., 2022 [33] | Offline | Feedforward Neural Network | Gradient descent | Not applicable. Experimental error evaluated on movement velocity: <10% |
| Yu, Y. et al., 2022 [56] | Offline | Recurrent Neural Network | Gradient descent | Sawtooth signals: <14%. Evaluation performed with various amplitudes. |
| Yu, Y. et al., 2023 [48] | Online | Recurrent Neural Network | Custom online algorithm | Sawtooth and complex signals: <4% |
| Yao, M. et al., 2023 [50] | Online | Feedforward Neural Network | Custom online algorithm | Sinusoidal signal: 5%. Comparison performed on system model. |
| Yu, Y. et al., 2023 [39] | Offline | Recurrent Neural Network | Gradient descent | Complex signals: <15%. Evaluation performed with different load levels applied to the actuator. |
| Khan, A.M. et al., 2024 [49] | Online | Feedforward Neural Network | Custom online algorithm | Sinusoidal signals: <2%. Evaluation performed with input and output disturbances. |
| Zhou, M. et al., 2024 [57] | Online | LSTM Neural Network | Gradient descent | Complex signals: <13% |
| Su, L. et al., 2025 [51] | Online | LSTM Neural Network | Gradient descent | Sinusoidal and sawtooth signals: <13% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodinò, S.; Rota, G.; Chiodo, M.; Corigliano, A.; Maletta, C. Artificial Intelligence Control Methodologies for Shape Memory Alloy Actuators: A Systematic Review and Performance Analysis. Micromachines 2025, 16, 780. https://doi.org/10.3390/mi16070780
Rodinò S, Rota G, Chiodo M, Corigliano A, Maletta C. Artificial Intelligence Control Methodologies for Shape Memory Alloy Actuators: A Systematic Review and Performance Analysis. Micromachines. 2025; 16(7):780. https://doi.org/10.3390/mi16070780
Chicago/Turabian StyleRodinò, Stefano, Giuseppe Rota, Matteo Chiodo, Antonio Corigliano, and Carmine Maletta. 2025. "Artificial Intelligence Control Methodologies for Shape Memory Alloy Actuators: A Systematic Review and Performance Analysis" Micromachines 16, no. 7: 780. https://doi.org/10.3390/mi16070780
APA StyleRodinò, S., Rota, G., Chiodo, M., Corigliano, A., & Maletta, C. (2025). Artificial Intelligence Control Methodologies for Shape Memory Alloy Actuators: A Systematic Review and Performance Analysis. Micromachines, 16(7), 780. https://doi.org/10.3390/mi16070780







