Research on Simulation Optimization of MEMS Microfluidic Structures at the Microscale
Abstract
1. Introduction
2. Working Principle of Microfluidic Systems
2.1. Working Principle and Features of Micropumps
2.2. Applications for Micropumps
3. Oscillatory Fluid Motion
3.1. Microscale Model Geometry
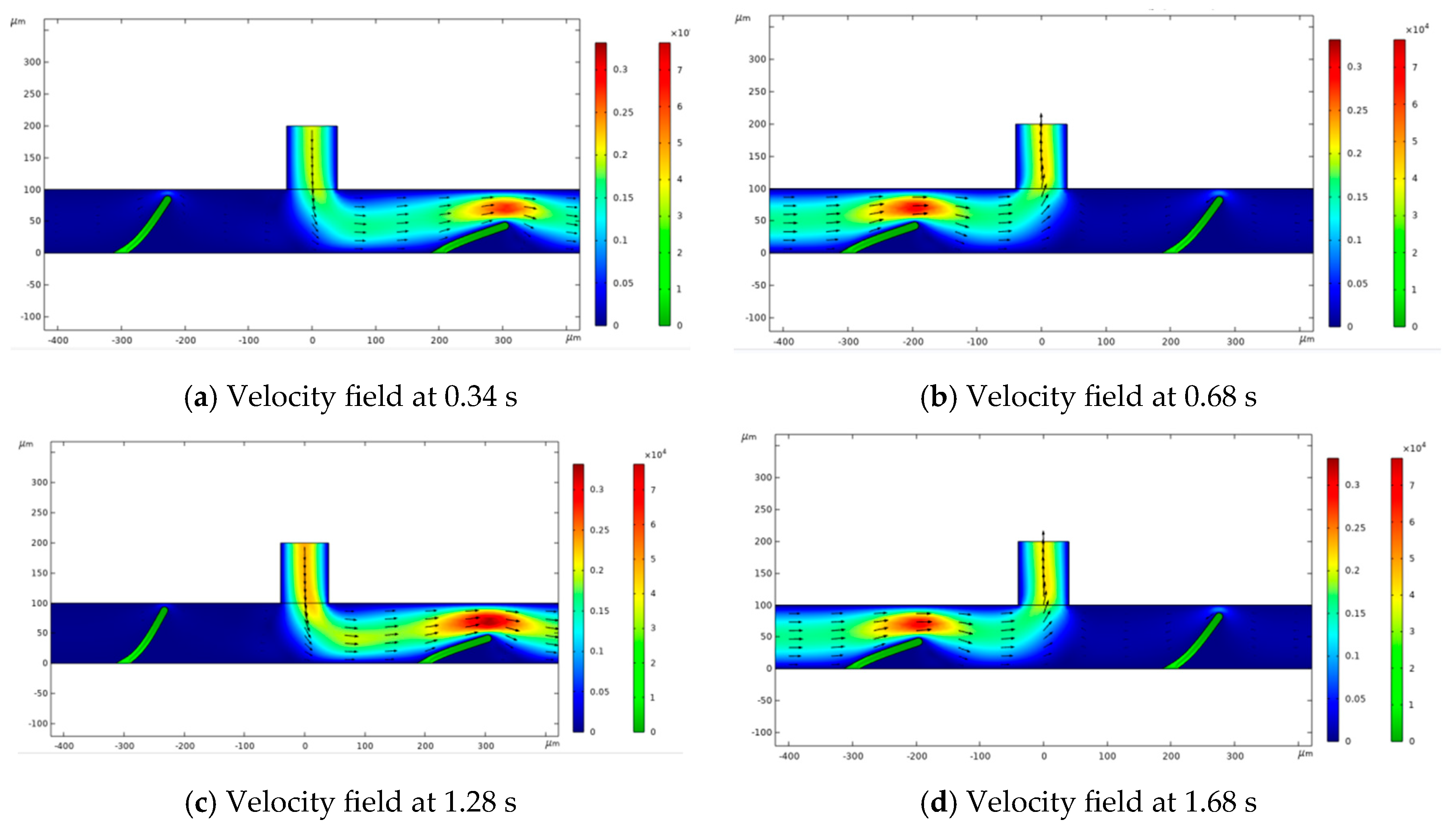
3.2. Flow Process Analysis
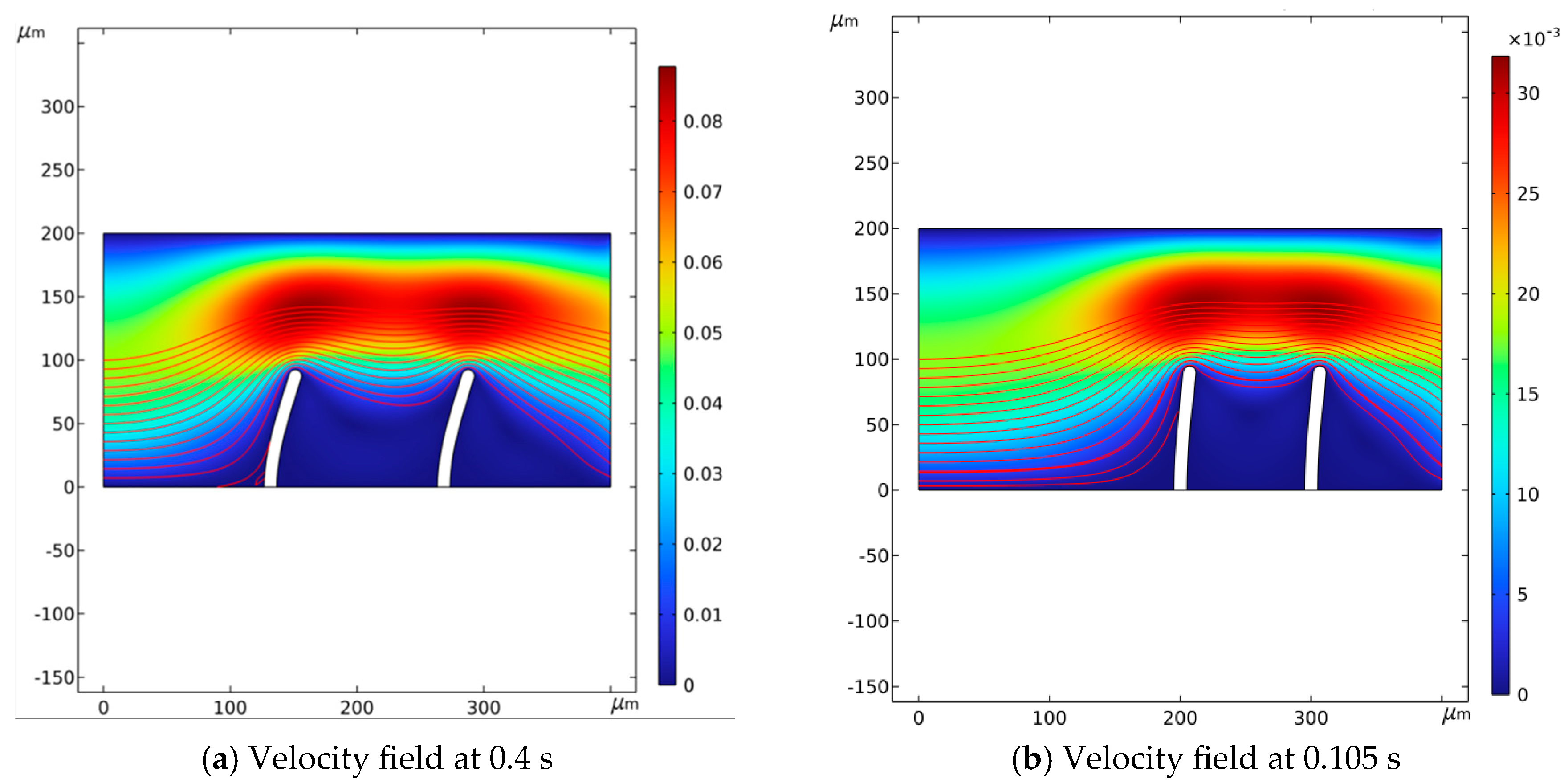
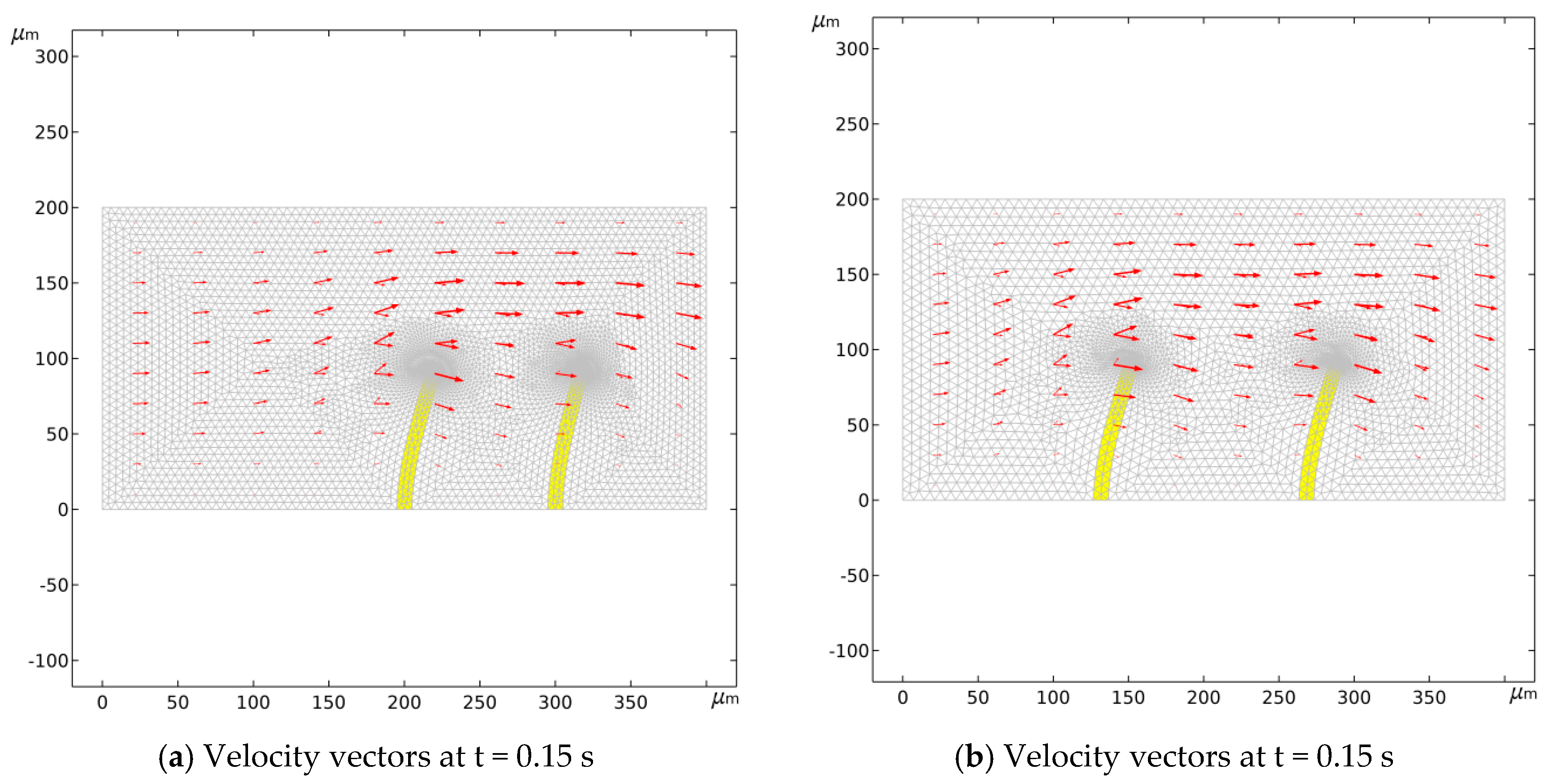
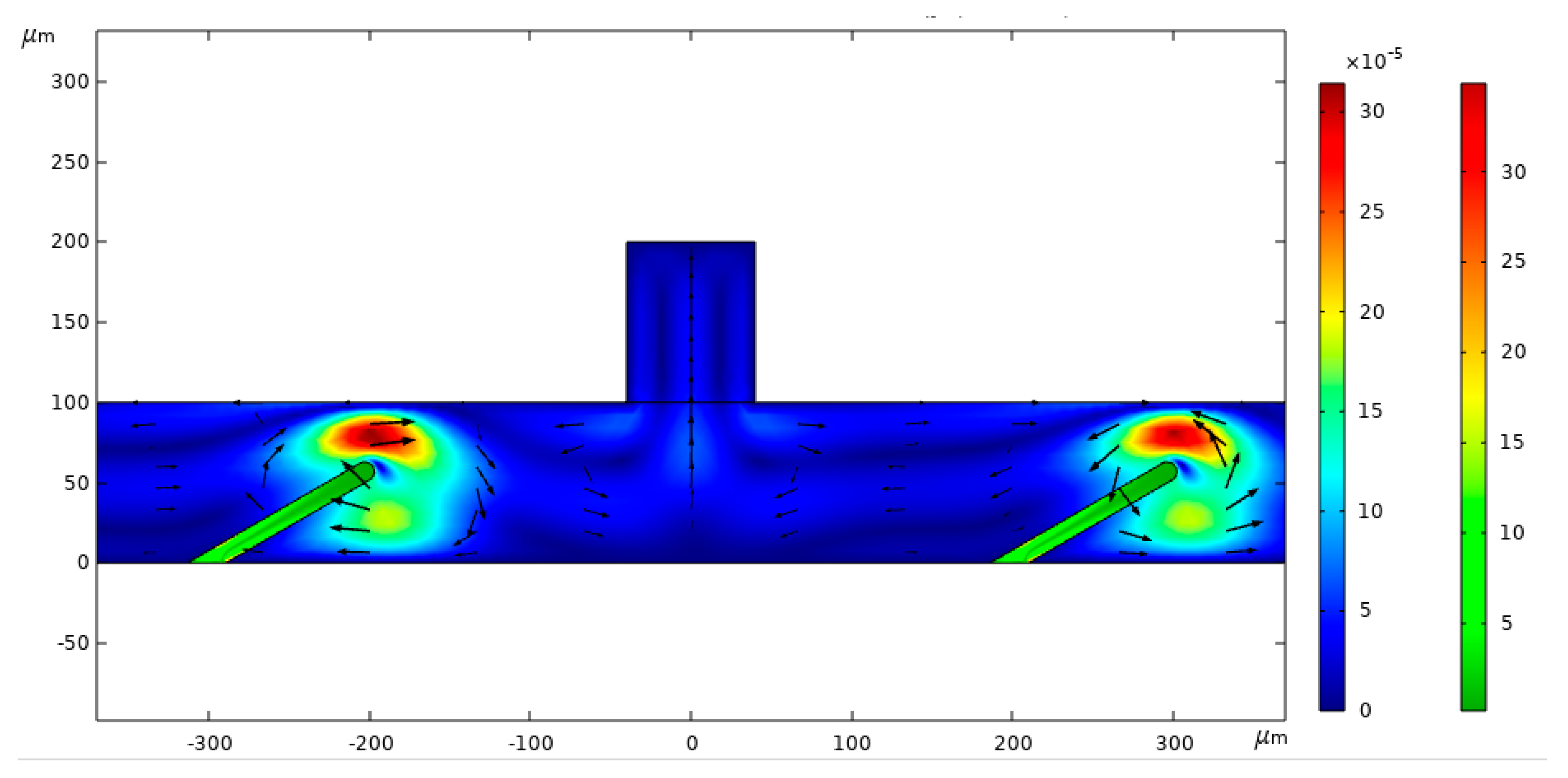
3.3. Analysis of Flow Process at Different Positions of the Valve Flaps
3.4. Experiment
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hardt, S.; Pennemann, H.; Schönfeld, F. Theoretical and experimental characterization of a low-reynolds number split-and-recombine mixer. Microfluid. Nanofluid. 2006, 2, 237–248. [Google Scholar] [CrossRef]
- Di Tommaso, P.; Chatzou, M.; Floden, E.W.; Barja, P.P.; Palumbo, E.; Notredame, C. Nextflow enables repro ducible computational workflows. Nat. Biotechnol. 2017, 35, 316–319. [Google Scholar] [CrossRef] [PubMed]
- Au, A.K.; Bhattacharjee, N.; Horowitz, L.F.; Chang, T.C.; Folch, A. 3D-printed microfluidic automation. Lab A Chip 2015, 15, 1934–1941. [Google Scholar] [CrossRef] [PubMed]
- Bonyar, A.; Santha, H.; Varga, M.; Ring, B.; Harsanyi, G. Characterization of rapid PDMS casting technique utilizing molding forms fabricated by 3D rapid prototyping technology (RPT). Int. J. Mater. Form. 2014, 7, 189–196. [Google Scholar] [CrossRef]
- Tan, Y.C.; Cristini, V.; Lee, A.P. Monodispersed microfluidic droplet generation by shear focusing microfluidic device. Sens. Actuators B Chem. 2006, 114, 350–356. [Google Scholar] [CrossRef]
- Ho, C.M.B.; Ng, S.H.; Li, K.H.H.; Yoon, Y. 3D printed microfluidics for biological applications. Lab A Chip 2015, 15, 3627–3637. [Google Scholar] [CrossRef] [PubMed]
- Lagally, E.T.; Emrich, C.A.; Mathies, R.A. Fully integrated PCR-capillary electrophoresis microsystem for DNA analysis. Lab A Chip 2001, 1, 102. [Google Scholar] [CrossRef] [PubMed]
- Tarn, M.D.; Lopez-Martinez, M.J.; Pamme, N. On-chip processing of particles and cells via multilaminar flow streams. Anal. Bioanal. Chem. 2014, 406, 139–161. [Google Scholar] [CrossRef]
- Alorabi, A.Q.; Tarn, M.D.; Gómez-Pastora, J.; Bringas, E.; Ortiz, I.; Paunov, V.N.; Pamme, N. On-chip polyelectrolyte coating onto magnetic droplets-Towards continuous flow assembly of drug delivery capsules. Lab A Chip 2017, 17, 3785–3795. [Google Scholar] [CrossRef]
- Tarn, M.D.; Pamme, N. On-Chip Magnetic Particle-Based Immunoassays Using Multilaminar Flow for Clinical Diagnostics. In Microchip Diagnostics; Humana Press: New York, NY, USA, 2017; pp. 69–83. [Google Scholar]
- Gómez-Pastora, J.; González-Fernández, C.; Fallanza, M.; Bringas, E.; Ortiz, I. Flow patterns and mass transfer performance of miscible liquidliquid flows in various microchannels: Numerical and experimental studies. Chem. Eng. J. 2018, 344, 487–497. [Google Scholar] [CrossRef]
- Zhao, W.; Cheng, R.; Lim, S.H.; Miller, J.R.; Zhang, W.; Tang, W.; Mao, L. Biocompatible and label-free separation of cancer cells from cell culture lines from white blood cells in ferrofluids. Lab A Chip 2017, 17, 2243–2255. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Wang, X. Ferrofluids lubrication: A status report. Lubr. Sci. 2016, 28, 3–26. [Google Scholar] [CrossRef]
- Torres-Díaz, I.; Rinaldi, C. Recent progress in ferrofluids research: Novel applications of magnetically controllable and tunable fluids. Soft Matter 2014, 10, 8584–8602. [Google Scholar] [CrossRef]
- Jiao, F.; Li, Q.; He, Y. Electromotive force induced by the moving non-magnetic phase in ferrofluids. Sens. Actuators A Phys. 2021, 317, 112472. [Google Scholar] [CrossRef]
- Jiao, F.; Li, Q.; Jiao, Y.; He, Y. Heat transfer of ferrofluids with magnetoviscous effects. J. Mol. Liq. 2021, 328, 115404. [Google Scholar] [CrossRef]
- Wang, W.; Su, Y.; Liu, Z.; Ju, X.; Xie, R.; Chu, L. Controllable microfluidic fabrication of microscale functional materials. Chem. Ind. Eng. Prog. 2019, 38, 421–433. [Google Scholar]
- Hongxia, C.H.E.N.; Hongyang, X.I.A.O.; Yuan, S.U.N. Experimental study on phase separation of slug flow in different T-type microchannels. J. Chem. Eng. Chin. Univ. 2020, 34, 912–918. [Google Scholar]
- Liu, L.; Zhu, C.; Ma, Y.; Fu, T. Progress on surfactant and interfacial transport phenomena in microchannels. CIESC J. 2021, 72, 783–798. [Google Scholar]
- Qian, J.; Li, X.; Wu, Z.; Chen, M.; Jin, Z.; Sundén, B. Research progress on flow regimes and mass transfer of liquid-liquid two-phase flow in microchannels. Chem. Ind. Eng. Prog. 2019, 38, 1624–1633. [Google Scholar]
- Sotowa, K.I. Fluid behavior and mass transport characteristics of gasliquid and liquid-liquid flows in microchannels. J. Chem. Eng. Jpn. 2014, 47, 213–224. [Google Scholar] [CrossRef]
- Wu, J.; Cao, W.; Wen, W.; Chang, D.C.; Sheng, P. Polydimethylsiloxane microfluidic chip with integrated microheater and thermal sensor. Biomicrofluidics 2009, 3, 012005. [Google Scholar] [CrossRef] [PubMed]
- Cerón, E.N.; Ortgies, D.H.; Del Rosal, B.; Ren, F.; Benayas, A.; Vetrone, F.; Rodríguez, E.M. Hybrid Nanostructures for High-Sensitivity Luminescence Nanothermometry in the Second Biological Window. Adv. Mater. 2015, 27, 4781–4787. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Wijethunga, P.A.L.; Moon, H.; Han, B. On-chip characterization of cryoprotective agent mixtures using an EWOD-based digital microfluidic device. Lab A Chip 2011, 11, 2212–2221. [Google Scholar] [CrossRef] [PubMed]
- Swain, J.E.; Lai, D.; Takayama, S.; Smith, G.D. Thinking big by thinking small: Application of microfluidic technology to improve ART. Lab A Chip 2013, 13, 1213–1224. [Google Scholar] [CrossRef]
- Newton, H.; Pegg, D.E.; Barrass, R.; Gosden, R.G. Osmotically inactive volume, hydraulic conductivity, and permeability to dimethyl sulphoxide of human mature oocytes. J. Reprod. Fertil. 1999, 117, 27–33. [Google Scholar] [CrossRef]
- Srinivasan, V.; Pamula, V.K.; Fair, R.B. An integrated digital microfluidic lab on-a-chip for clinical diagnostics on human physiological fluids. Lab A Chip 2004, 4, 310–315. [Google Scholar] [CrossRef] [PubMed]
- Gaver, D.P.; Kute, S.M. A Theoretical Model Study of the Influence of Fluid Stresses on a Cell Adhering to a Microchannel Wall. Biophys. J. 1998, 75, 721–733. [Google Scholar] [CrossRef]
- Cooley, M.; Sarode, A.; Hoore, M.; Fedosov, D.A.; Mitragotri, S.; Gupta, A.S. Influence of particle size and shape on their margination and wall-adhesion: Implications in drug delivery vehicle design across nanoto-micro scale. Nanoscale 2018, 10, 15350–15364. [Google Scholar] [CrossRef] [PubMed]
- Cucullo, L.; Hossain, M.; Puvenna, V.; Marchi, N.; Janigro, D. The role of shear stress in Blood-Brain Barrier endothelial physiology. BMC Neurosci. 2011, 12, 40. [Google Scholar] [CrossRef] [PubMed]
- Pang, Z.; Antonetti, D.A.; Tarbell, J.M. Shear stress regulates HUVEC hydraulic conductivity by occludin phosphorylation. Ann. Biomed. Eng. 2005, 33, 1536–1545. [Google Scholar] [CrossRef] [PubMed]
- Morigi, M.; Zoja, C.; Figliuzzi, M.; Foppolo, M.; Micheletti, G.; Bontempelli, M.; Remuzzi, A. Fluid shear stress modulates surface expression of adhesion molecules by endothelial cells. Blood 1995, 85, 1696–1703. [Google Scholar] [CrossRef] [PubMed]
- Terrell-Hall, T.B.; Ammer, A.G.; Griffith, J.I.; Lockman, P.R. Permeability across a novel microfluidic blood tumor barrier model. Fluids Barriers CNS 2017, 14, 3. [Google Scholar] [CrossRef] [PubMed]
- Boedicker, J.Q.; Vincent, M.E.; Ismagilov, R.F. Microfluidic Confinement of Single Cells of Bacteria in Small Volumes Initiates High-Density Behavior of Quorum Sensing and Growth and Reveals Its Variability. Angew. Chem. Int. Ed. 2009, 48, 5908–5911. [Google Scholar] [CrossRef] [PubMed]
- Chin, C.D.; Linder, V.; Sia, S.K. Commercialization of microfluidic point-of-care diagnostic devices. Lab A Chip 2012, 12, 2118–2134. [Google Scholar] [CrossRef] [PubMed]
- Shields, C.W.; Ohiri, K.A.; Szott, L.M.; Lo’pez, G.P. Translating microfluidics: Cell separation technologies and their barriers to commercialization. Cytom. Part B Clin. Cytom. 2017, 92, 115–125. [Google Scholar] [CrossRef] [PubMed]
- Macdonald, N.P.; Cabot, J.M.; Smejkal, P.; Guijt, R.M.; Paull, B.; Breadmore, M.C. Comparing Microfluidic Performance of Three-Dimensional (3D) Printing Platforms. Anal. Chem. 2017, 89, 3858–3866. [Google Scholar] [CrossRef] [PubMed]
- Bragheri, F.; Martinez Vazquez, R.; Osellame, R. Microfluidics. In Three-Dimensional Microfabrication Using Two-Photon Polymerization: Fundamentals, Technology, and Applications; William Andrew: Norwich, NY, USA, 2016; pp. 310–334. [Google Scholar]
- Brzeziński, M.; Socka, M.; Makowski, T.; Kost, B.; Cieślak, M.; Kro’lewska-Golińska, K. Microfluidic assisted nanoprecipitation of biodegradable nanoparticles composed of PTMC/PCL(co)polymers tannic acid doxorubicin for cancer, treatment. Colloids Surf. B Biointerfaces 2021, 201, 111598. [Google Scholar] [CrossRef] [PubMed]
- Karnik, R.; Gu, F.; Basto, P.; Cannizzaro, C.; Dean, L.; Kyei-Manu, W.; Farokhzad, O.C. Microfluidic Platform for Controlled Synthesis of Polymeric Nanoparticles. Nano Lett. 2008, 8, 2906–2912. [Google Scholar] [CrossRef] [PubMed]
- Kimmerling, R.J.; Lee Szeto, G.; Li, J.W.; Genshaft, A.S.; Kazer, S.W.; Payer, K.R.; Manalis, S.R. A microfluidic platform enabling single-cell RNA-seq of multigenerational lineages. Nat. Commun. 2016, 7, 10220. [Google Scholar] [CrossRef] [PubMed]
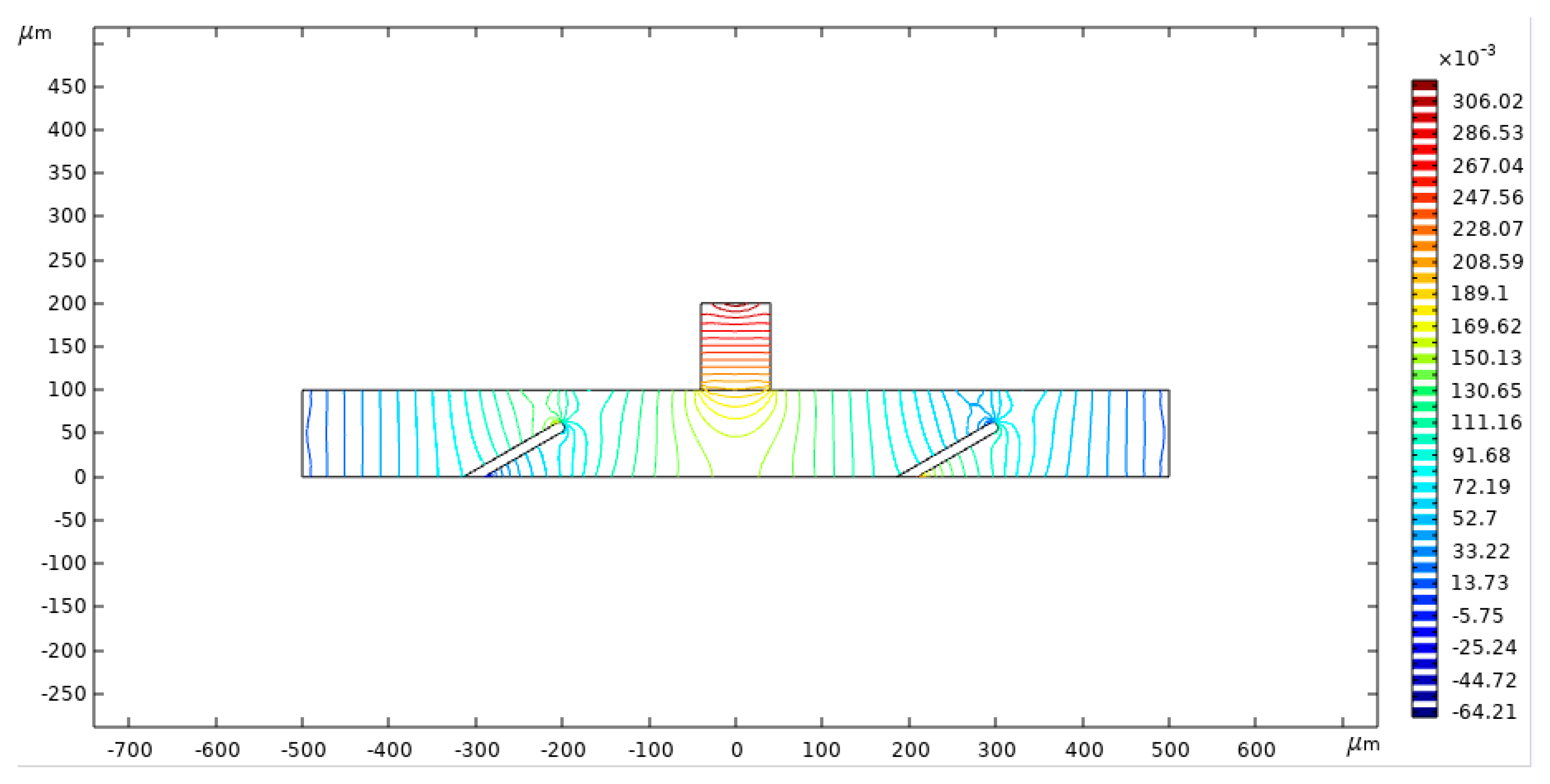

| Density | Dynamic Viscosity | Horizontal Channel Length | Horizontal Channel Height | Obstacle Width | Obstacle Height | Angle |
|---|---|---|---|---|---|---|
| 1000 kg/m3 | 0.001 Pa·s | 1000 μm | 100 μm | 6 μm | 56 μm | 60° |
| Channel | Sectional Shape | Width | Length | Height | Equivalent Diameter | Ratio of Length to Equivalent Diameter | Turning Point |
|---|---|---|---|---|---|---|---|
| 1 | rectangle | 60 | 1000 | 100 | 75 | 13.3 | 800 |
| 2 | rectangle | 120 | 1000 | 100 | 109.1 | 9.2 | 700 |
| 3 | Semicircle | 200 | 1000 | 100 | 30.54 | 32.7 | 1000 |
| 4 | Semicircle | 100 | 1000 | 50 | 15.3 | 65.4 | 700 |
| 5 | triangle | 60 | 1000 | 100 | 44.6 | 22.4 | 900 |
| 6 | triangle | 120 | 1000 | 100 | 67.9 | 14.7 | 900 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Meng, W. Research on Simulation Optimization of MEMS Microfluidic Structures at the Microscale. Micromachines 2025, 16, 695. https://doi.org/10.3390/mi16060695
Wang C, Meng W. Research on Simulation Optimization of MEMS Microfluidic Structures at the Microscale. Micromachines. 2025; 16(6):695. https://doi.org/10.3390/mi16060695
Chicago/Turabian StyleWang, Changhu, and Weiyun Meng. 2025. "Research on Simulation Optimization of MEMS Microfluidic Structures at the Microscale" Micromachines 16, no. 6: 695. https://doi.org/10.3390/mi16060695
APA StyleWang, C., & Meng, W. (2025). Research on Simulation Optimization of MEMS Microfluidic Structures at the Microscale. Micromachines, 16(6), 695. https://doi.org/10.3390/mi16060695






