Multiple Ring Electrode-Based PMUT with Tunable Deflections
Abstract
1. Introduction
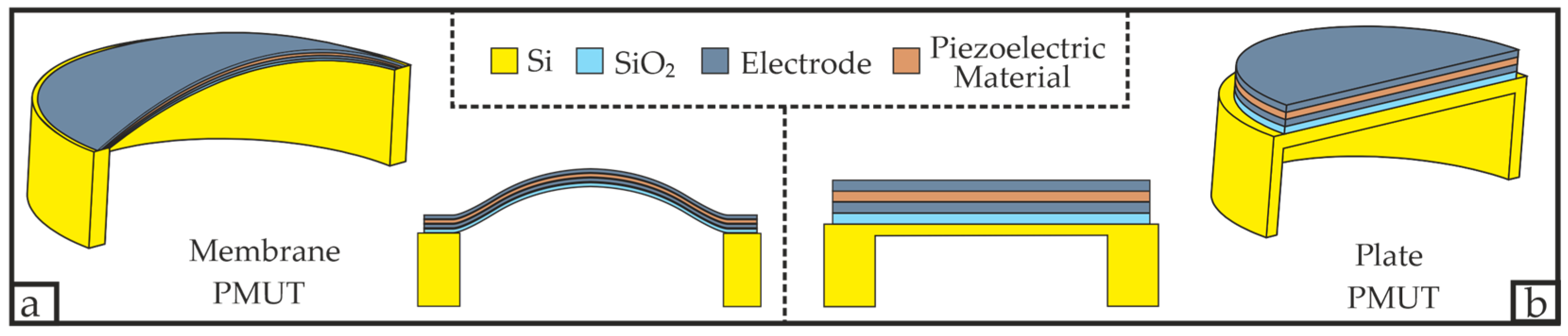
2. Device Fabrication and Material Characterization
2.1. PMUT Fabrication Process
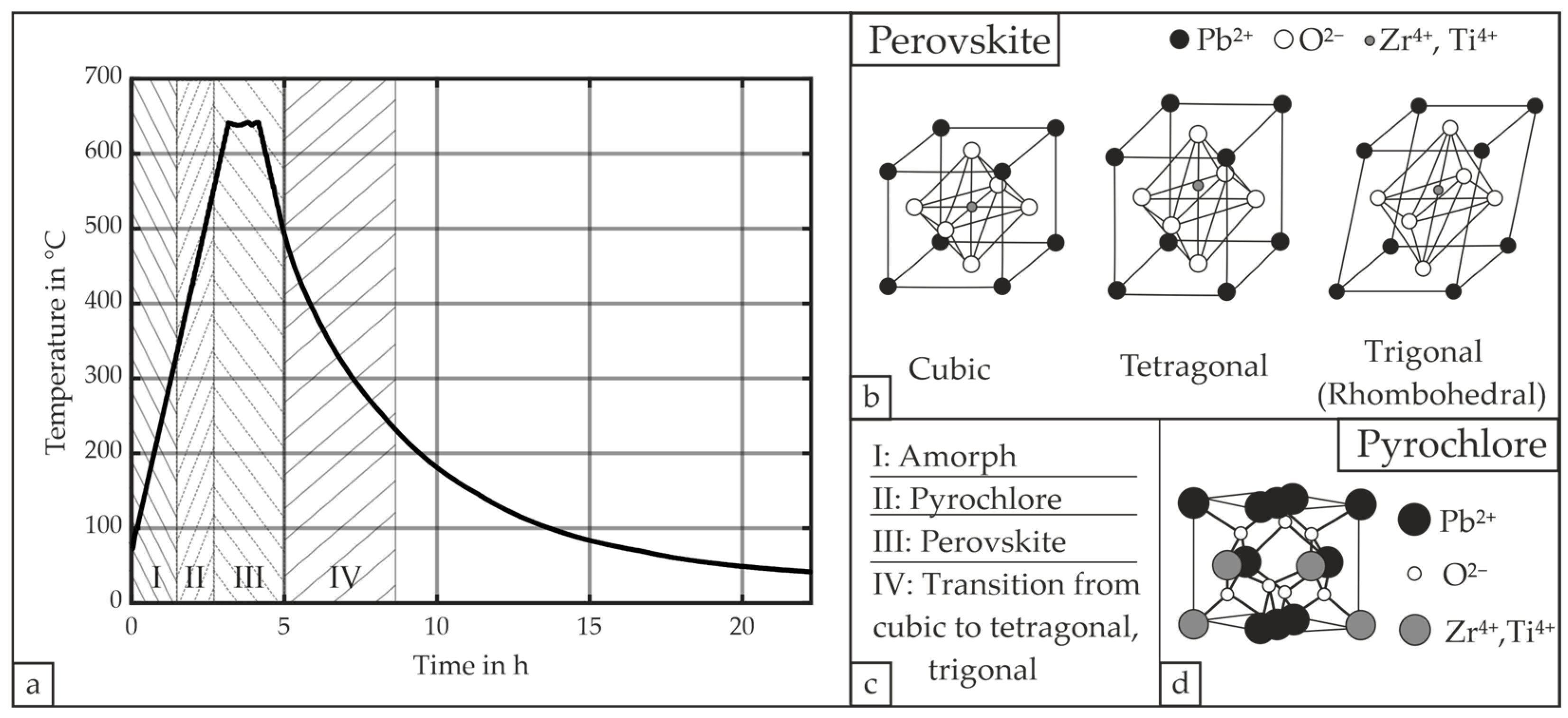
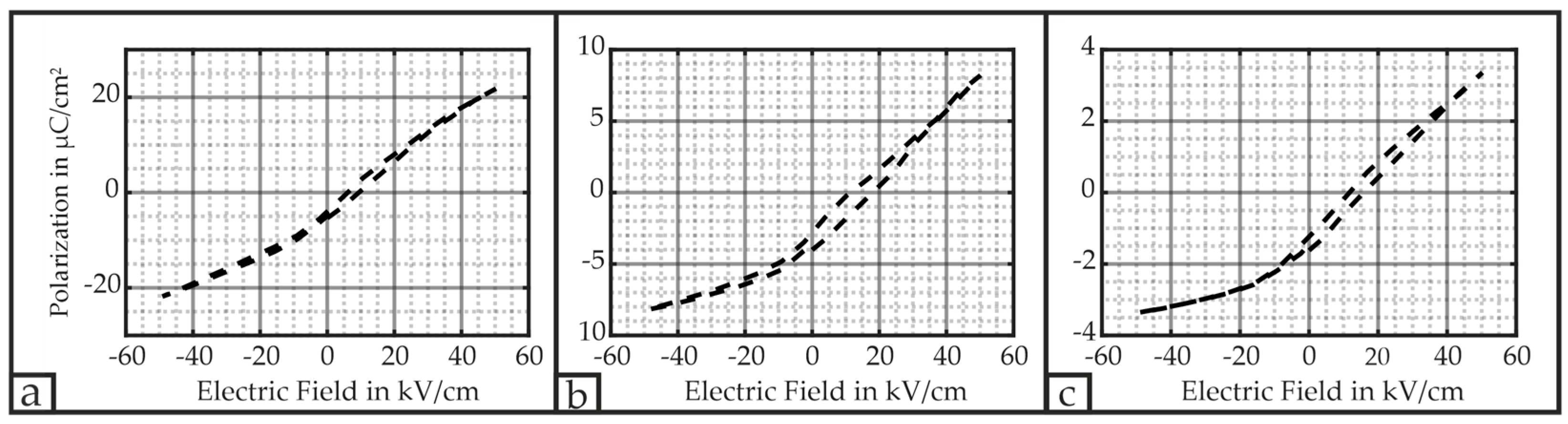
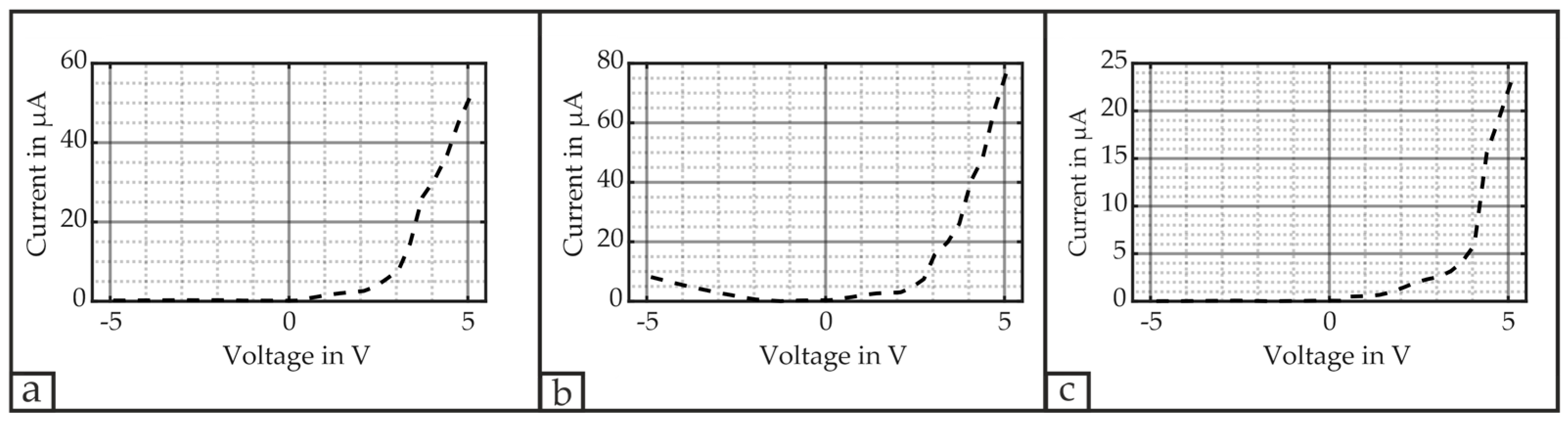
2.2. Material Characterization—Leakage Current and Polarization of the Piezoelectric Material
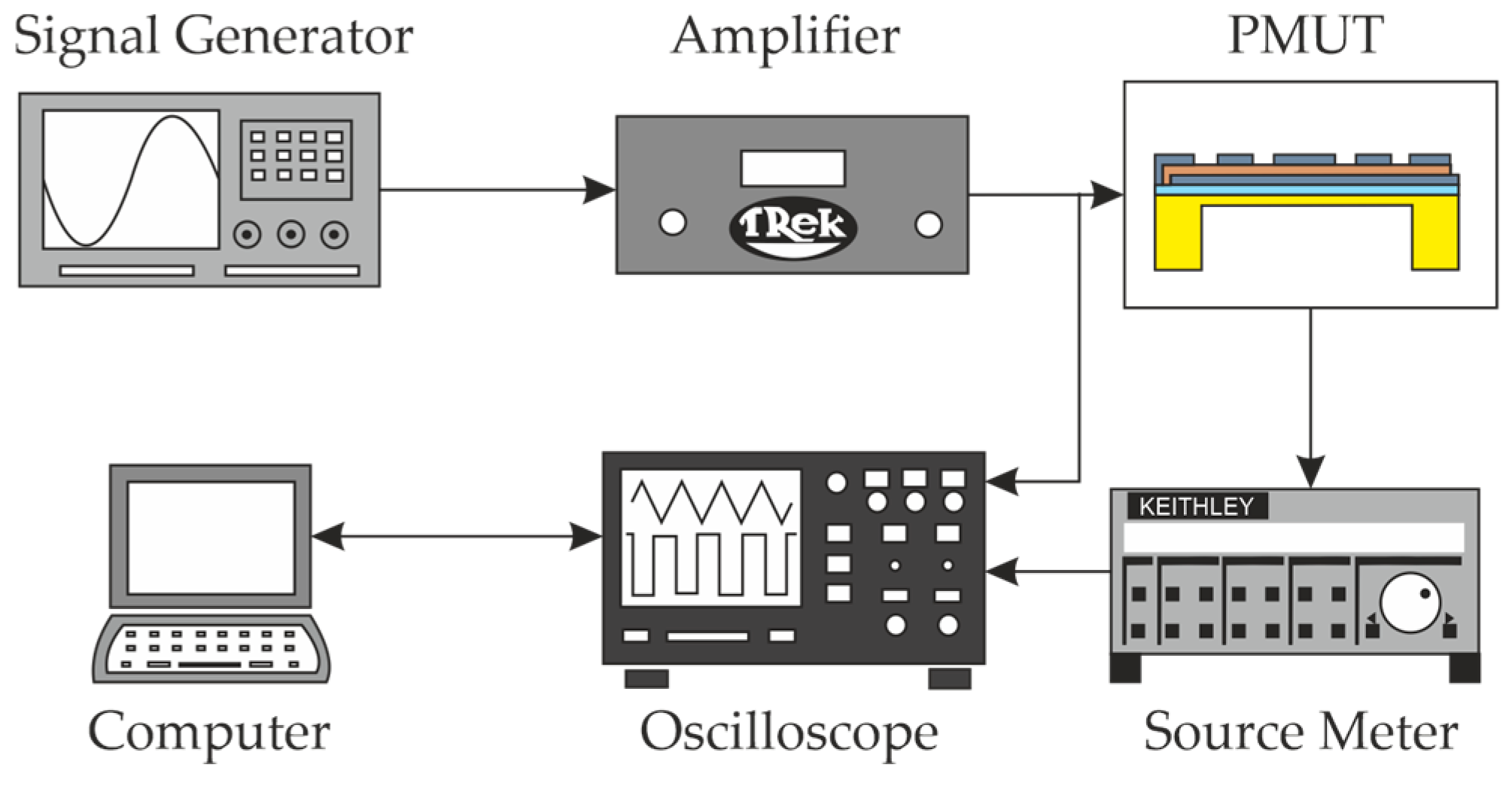
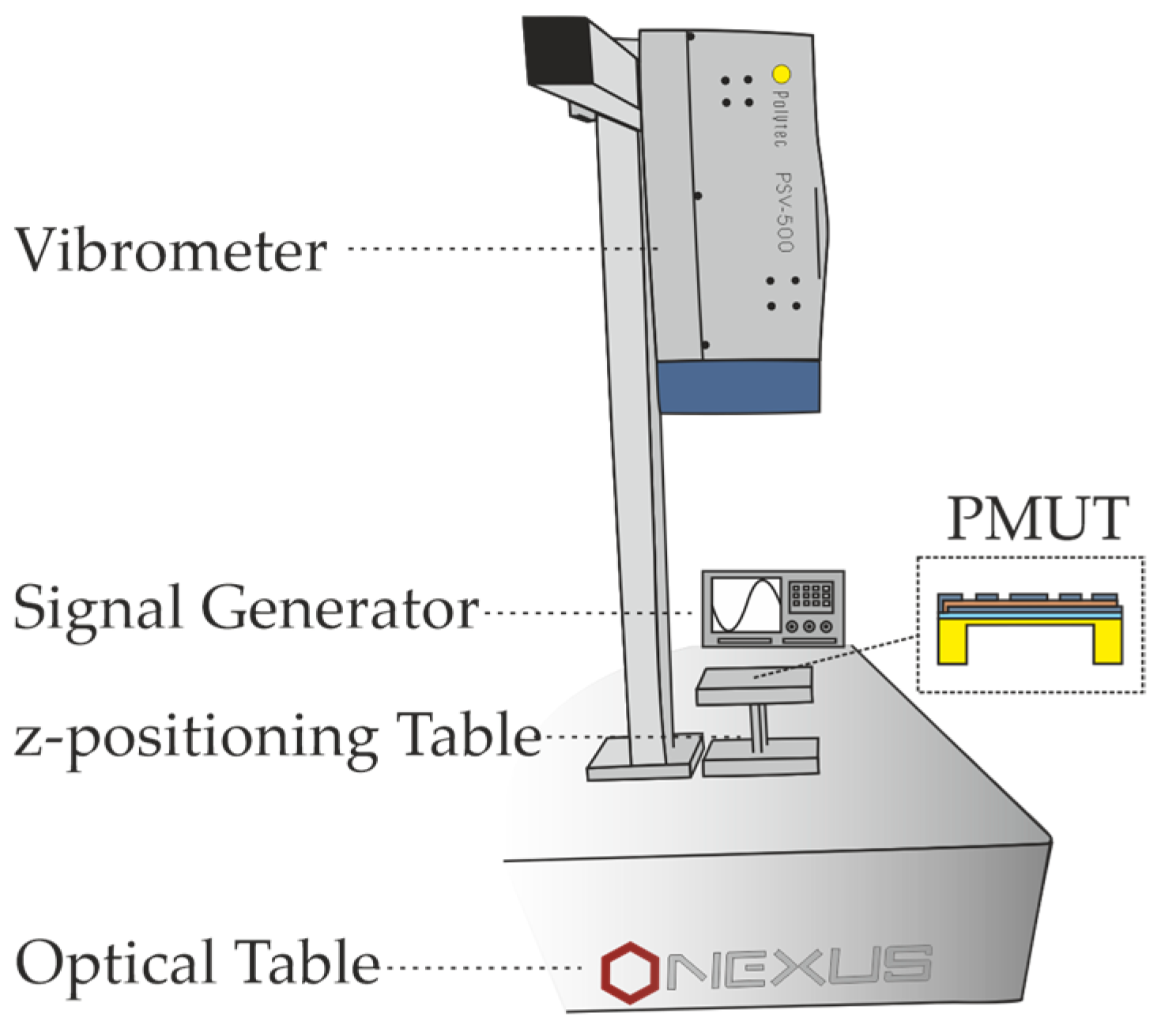
2.2.1. Experimental Setup for the Material Characterization
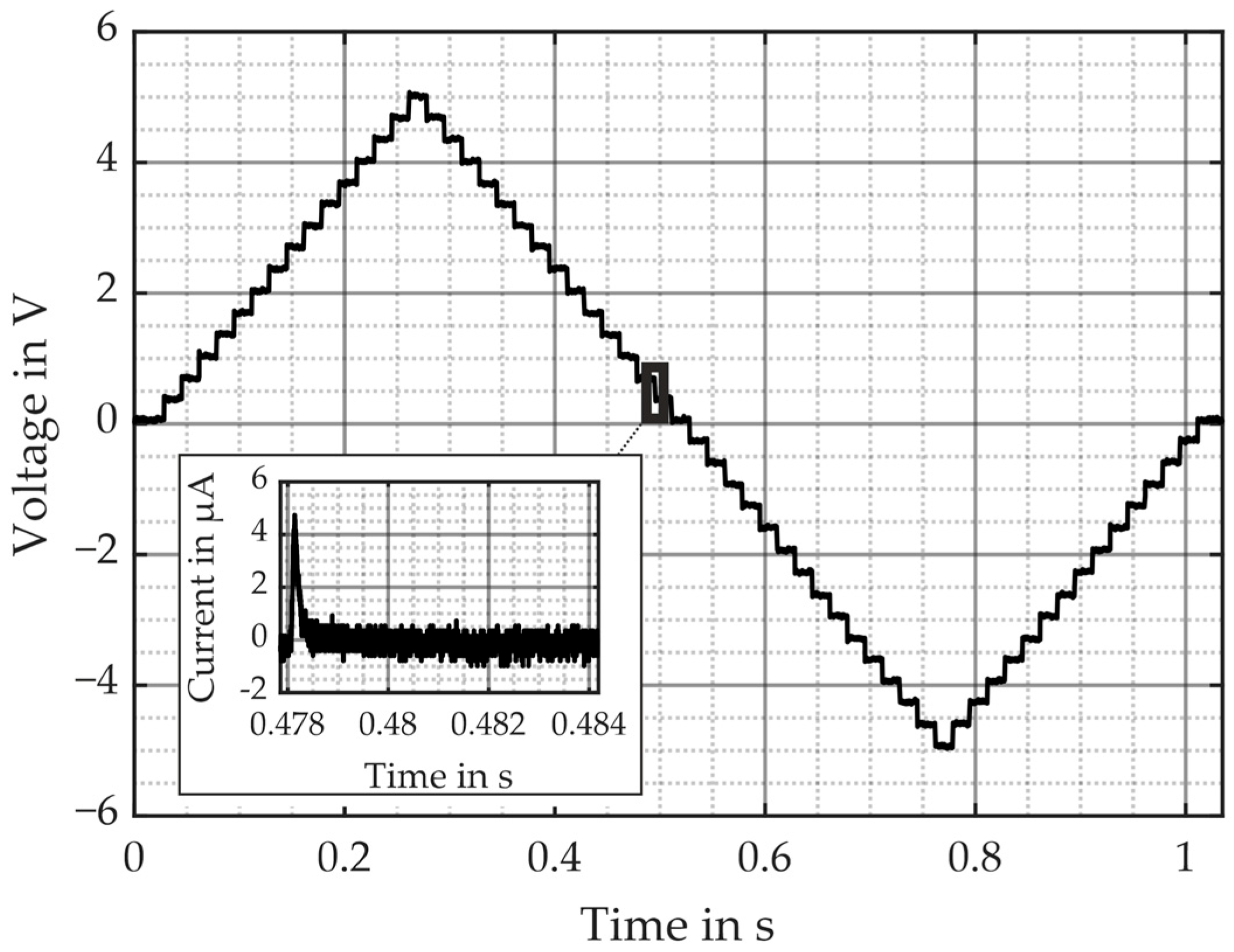
2.2.2. Results and Discussion
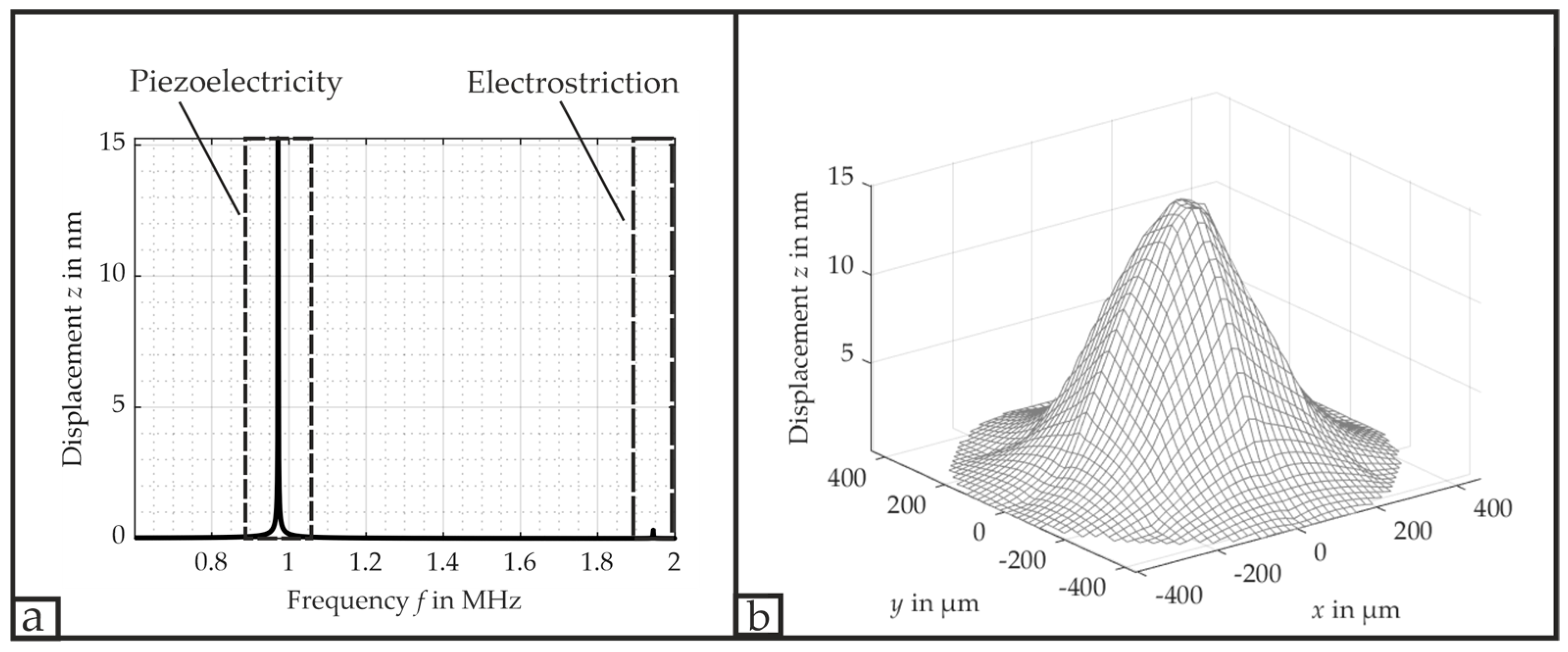
3. Displacement Dynamics
3.1. Experimental Setup for the Displacement Dynamics
- The excitation of all three electrodes simultaneously.
- Separate excitation of each electrode.
- Excitation of the primary electrode with the resonance frequency and applying different DC voltages at the 3rd electrode.
- A new concept which we will refer to as Ring Impinging (RI). The primary electrode and the 3rd electrode will each be excited with a different frequency still within their bandwidth B.
3.2. Simultaneous Excitation of All Three Electrodes and Separate Excitation of Each Electrode
3.3. Deflection Adjustment via the 3rd Electrode
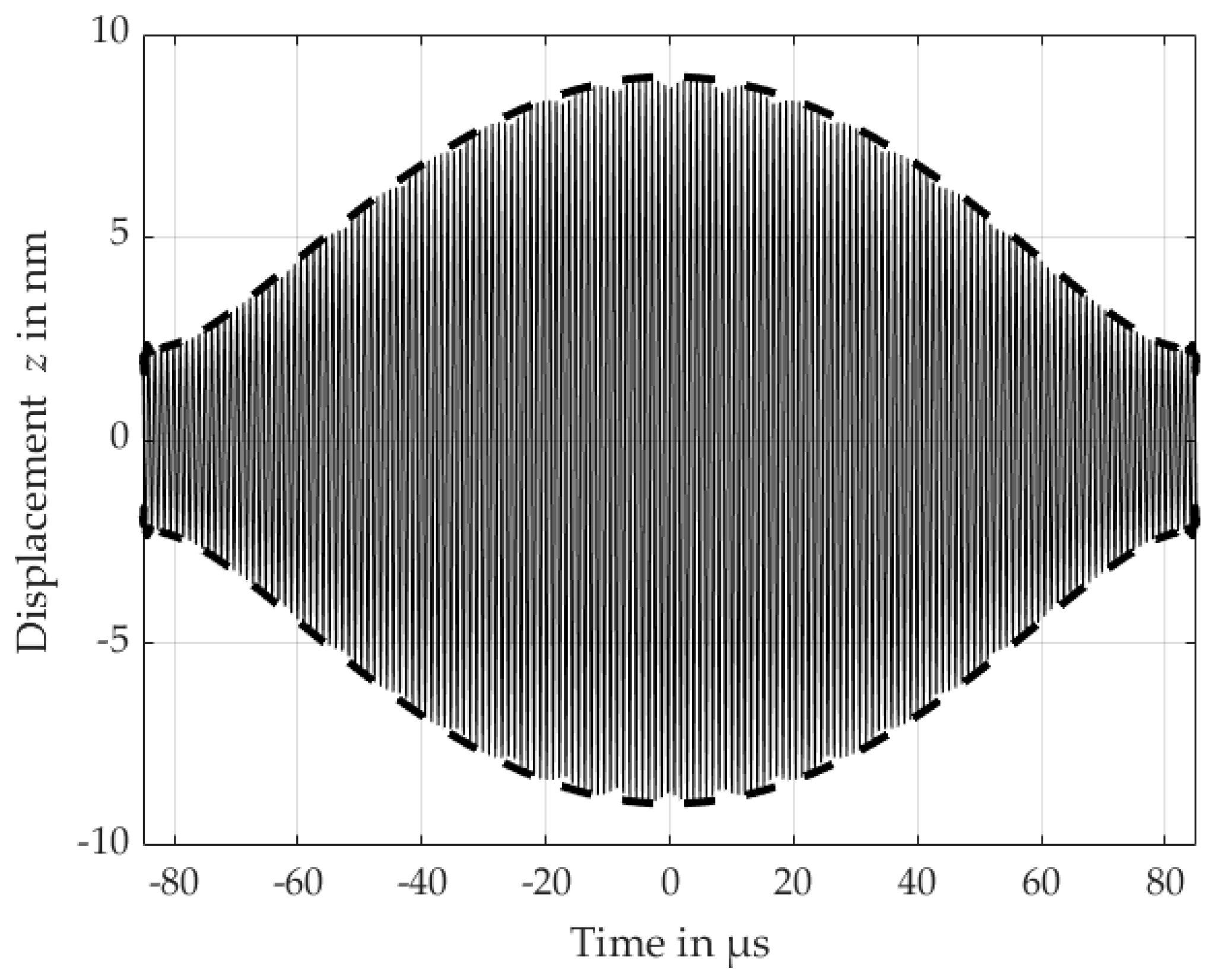
3.4. Ring Impinging (RI)
4. Summary, Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Area | |
| Amplitude | |
| Amplitude | |
| AIN | Aluminum Nitride |
| AMV | Actual Measured Voltage |
| Nondimensional Parameter | |
| Bandwidth | |
| BaTiO3 | Bariumtitanate |
| Capacitance | |
| CMOS | Complementary metal-oxide semiconductor |
| CMUT | Capacitive Micromachined Ultrasonic Transducer |
| Flexural Rigidity | |
| Thickness | |
| DSE | Deep Silicon Etching |
| Electric Field | |
| FFT | Fast Fourier Transform |
| Frequency | |
| Current | |
| Bessel Function | |
| j | Imaginary Unit |
| LDV | Laser Doppler Vibrometer |
| O | Oxygen |
| Polarization | |
| PMUT | Piezoelectric Micromachined Ultrasonic Transducer |
| PZT | Lead Zirconate Titanate |
| Pt | Platinum |
| Charge | |
| Radiation angle, phase | |
| Resistance | |
| Radius | |
| RI | Ring Impinging |
| Stiffness | |
| Si | Silicon |
| SiO2 | Silicon Dioxide |
| Time | |
| Tension | |
| Ti | Titanium |
| TiO2 | Titanium Dioxide |
| Voltage | |
| VSAG | Voltage Set at Generator |
| Acoustic Impedance | |
| ZnO | Zinc Oxide |
References
- Rupitsch, S.J. Piezoelectric Sensors and Actuators: Fundamentals and Applications; Topics in Mining, Metallurgy and Materials Engineering; Springer: Berlin/Heidelberg, Germany, 2019; ISBN 978-3-662-57532-1. [Google Scholar]
- Kou, Z.; Miller, R.J.; Singer, A.C.; Oelze, M.L. High Data Rate Communications In Vivo Using Ultrasound. IEEE Trans. Biomed. Eng. 2021, 68, 3308–3316. [Google Scholar] [CrossRef] [PubMed]
- George, B.; Fink, M.; Rupitsch, S.J.; Hiltl, P.-T.; Lee, G.; Ermert, H. Investigation of Inertial Cavitation Stimulation by Focused Ultrasound on Sonosensitive Nanoparticles for Drug Delivery Applications. In Proceedings of the 2019 IEEE International Ultrasonics Symposium (IUS), Glasgow, UK, 6–9 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1532–1535. [Google Scholar]
- Schaechtle, T.; Köhler, H.; Helmerich, J.; Fischer, G.K.J.; Gabbrielli, A.; Höflinger, F.; Rupitsch, S.J. Energieeffiziente akustische Kommunikation durch Metall für drahtlose Sensoranwendungen: Energy-aware ultrasonic communication through metal for wireless sensing applications. Tm-Tech. Mess. 2023, 90, 103–107. [Google Scholar] [CrossRef]
- Helmerich, J.; Schaechtle, T.; Wich, M.; Szabo, B.; Stieglitz, T.; Rupitsch, S.J. Implementation of an Ultrasonic-Based Link for Percutaneous Communications. Curr. Dir. Biomed. Eng. 2023, 9, 170–173. [Google Scholar] [CrossRef]
- Schaechtle, T.; Aftab, T.; Reindl, L.M.; Rupitsch, S.J. Wireless Passive Sensor Technology through Electrically Conductive Media over an Acoustic Channel. Sensors 2023, 23, 2043. [Google Scholar] [CrossRef]
- Birjis, Y.; Swaminathan, S.; Nazemi, H.; Raj, G.C.A.; Munirathinam, P.; Abu-Libdeh, A.; Emadi, A. Piezoelectric Micromachined Ultrasonic Transducers (PMUTs): Performance Metrics, Advancements, and Applications. Sensors 2022, 22, 9151. [Google Scholar] [CrossRef]
- Roy, K.; Lee, J.E.-Y.; Lee, C. Thin-Film PMUTs: A Review of over 40 Years of Research. Microsyst. Nanoeng. 2023, 9, 95. [Google Scholar] [CrossRef]
- Eccardt, P.C.; Niederer, K. Micromachined Ultrasound Transducers with Improved Coupling Factors from a CMOS Compatible Process. Ultrasonics 2000, 38, 774–780. [Google Scholar] [CrossRef]
- Kawasaki, S.; Saccher, M.; De Wijs, W.-J.; Van Den Brand, J.; Dekker, R. Ultrasound Imaging with Pre-Charged Collapse-Mode CMUTs. In Proceedings of the 2023 IEEE International Ultrasonics Symposium (IUS), Montreal, QC, Canada, 3–8 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–4. [Google Scholar]
- Roche, P.; Nadaud, K.; Galayko, D.; Calle, S.; Barcella, F.; Bunetel, J.-C.L.; Certon, D.; Poulin-Vittrant, G. A Discrete CMUT Self-Biasing Circuit towards Implanted Devices Application. Sens. Actuators Phys. 2024, 379, 115855. [Google Scholar] [CrossRef]
- Butaud, P.; Le Moal, P.; Bourbon, G.; Placet, V.; Ramasso, E.; Verdin, B.; Joseph, E. Towards a Better Understanding of the CMUTs Potential for SHM Applications. Sens. Actuators Phys. 2020, 313, 112212. [Google Scholar] [CrossRef]
- Moisello, E.; Novaresi, L.; Sarkar, E.; Malcovati, P.; Costa, T.L.; Bonizzoni, E. PMUT and CMUT Devices for Biomedical Applications: A Review. IEEE Access 2024, 12, 18640–18657. [Google Scholar] [CrossRef]
- Akhbari, S.; Voie, A.; Li, Z.; Eovino, B.; Lin, L. Dual-Electrode Bimorph Pmut Arrays for Handheld Therapeutic Medical Devices. In Proceedings of the 2016 IEEE 29th International Conference on Micro Electro Mechanical Systems (MEMS), Shanghai, China, 24–28 January 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1102–1105. [Google Scholar]
- Dangi, A.; Pratap, R. System Level Modeling and Design Maps of PMUTs with Residual Stresses. Sens. Actuators Phys. 2017, 262, 18–28. [Google Scholar] [CrossRef]
- Wah, T. Vibration of Circular Plates. J. Acoust. Soc. Am. 1962, 34, 275–281. [Google Scholar] [CrossRef]
- Royer, M.; Wurm, M.A.; Aadland, S.; Glenn, M. ZnO ON $1 Integrated Acoustic Sensor. Sens. Actuators 1983, 4, 357–362. [Google Scholar] [CrossRef]
- Udayakumar, K.R.; Chen, J.; Krupanidhi, S.B.; Cross, L.E. Sol-Gel Derived PZT Thin Films for Switching Applications. In Proceedings of the 1990 IEEE 7th International Symposium on Applications of Ferroelectrics, Urbana-Champaign, IL, USA, 6–8 June 1990; IEEE: Piscataway, NJ, USA, 1991; pp. 741–743. [Google Scholar]
- Udayakumar, K.R.; Bart, S.F.; Flynn, A.M.; Chen, J.; Tavrow, L.S.; Cross, L.E.; Brooks, R.A.; Ehrlich, D.J. Ferroelectric Thin Film Ultrasonic Micromotors. In Proceedings of the 1991 IEEE Micro Electro Mechanical Systems, Nara, Japan, 30 January–2 February 1991; IEEE: Piscataway, NJ, USA, 1991; pp. 109–113. [Google Scholar]
- Shelton, S.; Chan, M.-L.; Park, H.; Horsley, D.; Boser, B.; Izyumin, I.; Przybyla, R.; Frey, T.; Judy, M.; Nunan, K.; et al. CMOS-Compatible AlN Piezoelectric Micromachined Ultrasonic Transducers. In Proceedings of the 2009 IEEE International Ultrasonics Symposium, Rome, Italy, 20–23 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 402–405. [Google Scholar]
- Wang, Q.; Lu, Y.; Mishin, S.; Oshmyansky, Y.; Horsley, D.A. Design, Fabrication, and Characterization of Scandium Aluminum Nitride-Based Piezoelectric Micromachined Ultrasonic Transducers. J. Microelectromech. Syst. 2017, 26, 1132–1139. [Google Scholar] [CrossRef]
- Thao, P.N.; Yoshida, S.; Tanaka, S. Development of Mechanically-Robust Piezoelectric Micromachined Ultrasonic Transducer (pMUT) with Island-Shaped PZT Monocrystalline Thin Film. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 833–836. [Google Scholar]
- Wu, S.; Li, W.; Jiao, D.; Yang, H.; Wu, T.; Li, X. An Aluminum-Nitride PMUT with Pre-Concaved Membrane for Large Deformation and High Quality-Factor Performance. In Proceedings of the 2021 21st International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Orlando, FL, USA, 20–24 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 46–49. [Google Scholar]
- Horsley, D.A.; Lu, Y.; Tang, H.-Y.; Jiang, X.; Boser, B.E.; Tsai, J.M.; Ng, E.J.; Daneman, M.J. Ultrasonic Fingerprint Sensor Based on a PMUT Array Bonded to CMOS Circuitry. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–4. [Google Scholar]
- Ledesma, E.; Zamora, I.; Uranga, A.; Barniol, N. Tent-Plate AlN PMUT with a Piston-Like Shape Under Liquid Operation. IEEE Sens. J. 2020, 20, 11128–11137. [Google Scholar] [CrossRef]
- Sammoura, F.; Akhari, S.; Aqab, N.; Mahmoud, M.; Lin, L. Multiple Electrode Piezoelectric Micromachined Ultrasonic Transducers. In Proceedings of the IEEE International Ultrasonics Symposium, IUS, Chicago, IL, USA, 3–6 September 2014; IEEE Computer Society: Washington, DC, USA, 2014; pp. 305–308. [Google Scholar]
- Liu, K.; Lu, Y.; Wu, S.; Li, X.; Wu, T. Design of Piezoelectric Micromachined Ultrasonic Transducers Using High-Order Mode with High Performance and High Frequency. IEEE Open J. Ultrason. Ferroelectr. Freq. Control 2023, 3, 176–185. [Google Scholar] [CrossRef]
- Chare, C.; Gijsenbergh, P.; Jeong, Y.; Heremans, P.; Cheyns, D.; Genoe, J. Electromechanical Equivalent Circuit Model for Axisymmetric PMUTs with Elastic Boundary Conditions. J. Microelectromech. Syst. 2022, 31, 457–472. [Google Scholar] [CrossRef]
- Micro Restist Technology. Ma-N 400 and Ma-N 1400-Negative Tone Photoresists; Micro Restist Technology: Berlin, Germany, 2020. [Google Scholar]
- Suraj; Selvaraja, S.K. Sputter-Deposited PZT on Patterned Silicon Optimization for C-Band Electro-Optic Modulation. J. Opt. Soc. Am. B 2023, 40, 2321. [Google Scholar] [CrossRef]
- Piezoelectric MEMS Resonators; Bhugra, H., Piazza, G., Eds.; Microsystems and Nanosystems; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-28686-0. [Google Scholar]
- Abe, K.; Tomita, H.; Toyoda, H.; Motomasa Imai, M.I.; Yukari Yokote, Y.Y. PZT Thin Film Preparation on Pt-Ti Electrode by RF Sputtering. Jpn. J. Appl. Phys. 1991, 30, 2152. [Google Scholar] [CrossRef]
- Mardare, C.C.; Joanni, E.; Mardare, A.I.; Fernandes, J.R.A.; Sá, C.P.M.D.; Tavares, P.B. Effects of Adhesion Layer (Ti or Zr) and Pt Deposition Temperature on the Properties of PZT Thin Films Deposited by RF Magnetron Sputtering. Appl. Surf. Sci. 2005, 243, 113–124. [Google Scholar] [CrossRef]
- Ma, Y.; Song, J.; Wang, X.; Liu, Y.; Zhou, J. Synthesis, Microstructure and Properties of Magnetron Sputtered Lead Zirconate Titanate (PZT) Thin Film Coatings. Coatings 2021, 11, 944. [Google Scholar] [CrossRef]
- Aidam, R. Untersuchung des Epitaktischen Wachstums Dünner Pb(Zr0.52Ti0.48)O3-Schichten und ihre Anwendung in Ferroelektrischen Supraleitenden Feldeffekttransistoren; Forschungszentrum Karlsruhe: Karlsruhe, Germany, 1999. [Google Scholar]
- Byrne, C.; Fagan, R.; Hinder, S.; McCormack, D.E.; Pillai, S.C. New Approach of Modifying the Anatase to Rutile Transition Temperature in TiO2 Photocatalysts. RSC Adv. 2016, 6, 95232–95238. [Google Scholar] [CrossRef]
- Nam, H.-J.; Choi, D.-K.; Lee, W.-J. Formation of Hillocks in Pt/Ti Electrodes and Their Effects on Short Phenomena of PZT FIlms Deposited by Reactive Sputtering. Thin Solid Film. 2000, 371, 264–271. [Google Scholar] [CrossRef]
- Aungkavattana, P.; Haartz, B.; Ruud, C.O.; Trolier-McKinstry, S. In-Situ X-Ray Studies of Phase Transformations in Lead Zirconate Titanate Thin Films during Annealing. Thin Solid Film. 1995, 268, 102–107. [Google Scholar] [CrossRef]
- Xu, J.; Xi, R.; Xu, X.; Zhang, Y.; Feng, X.; Fang, X.; Wang, X. A2B2O7 Pyrochlore Compounds: A Category of Potential Materials for Clean Energy and Environment Protection Catalysis. J. Rare Earths 2020, 38, 840–849. [Google Scholar] [CrossRef]
- Subramanian, M.A.; Aravamudan, G.; Subba Rao, G.V. Oxide Pyrochlores—A Review. Prog. Solid State Chem. 1983, 15, 55–143. [Google Scholar] [CrossRef]
- Merz, W.J. Switching Time in Ferroelectric BaTiO3 and Its Dependence on Crystal Thickness. J. Appl. Phys. 1956, 27, 938–943. [Google Scholar] [CrossRef]
- Fujii, T.; Naono, T.; Mukaiyama, A.; Arakawa, T.; Hishinuma, Y.; Li, Y.; Birkmeyer, J. Preparation of Nb-Doped PZT Thin Film with High Piezoelectric Performance and Its Application to MEMS Devices; Fujifilm Dimatix, Inc.: Santa Clara, CA, USA, 2014. [Google Scholar]
- Beklešovas, B.; Iljinas, A.; Stankus, V.; Čyvienė, J.; Andrulevičius, M.; Ivanov, M.; Banys, J. Structural, Morphologic, and Ferroelectric Properties of PZT Films Deposited through Layer-by-Layer Reactive DC Magnetron Sputtering. Coatings 2022, 12, 717. [Google Scholar] [CrossRef]
- Kamenshchikov, M.V.; Solnyshkin, A.V.; Bogomolov, A.A.; Pronin, I.P. Electrical Conduction Mechanisms in PZT Thin Films Deposited by RF Magnetron Sputtering Method. Ferroelectrics 2013, 442, 101–106. [Google Scholar] [CrossRef]
- Hrib, L.M.; Boni, A.G.; Chirila, C.; Pasuk, I.; Pintilie, I.; Pintilie, L. Electrode Interface Control of the Schottky Diode-like Behavior in Epitaxial Pb(Zr0.2Ti0.8)O3 Thin Films: A Critical Analysis. J. Appl. Phys. 2013, 113, 214108. [Google Scholar] [CrossRef]
- Pintilie, L.; Vrejoiu, I.; Hesse, D.; LeRhun, G.; Alexe, M. Ferroelectric Polarization-Leakage Current Relation in High Quality Epitaxial Pb(Zr,Ti)O3 Films. Phys. Rev. B 2007, 75, 104103. [Google Scholar] [CrossRef]



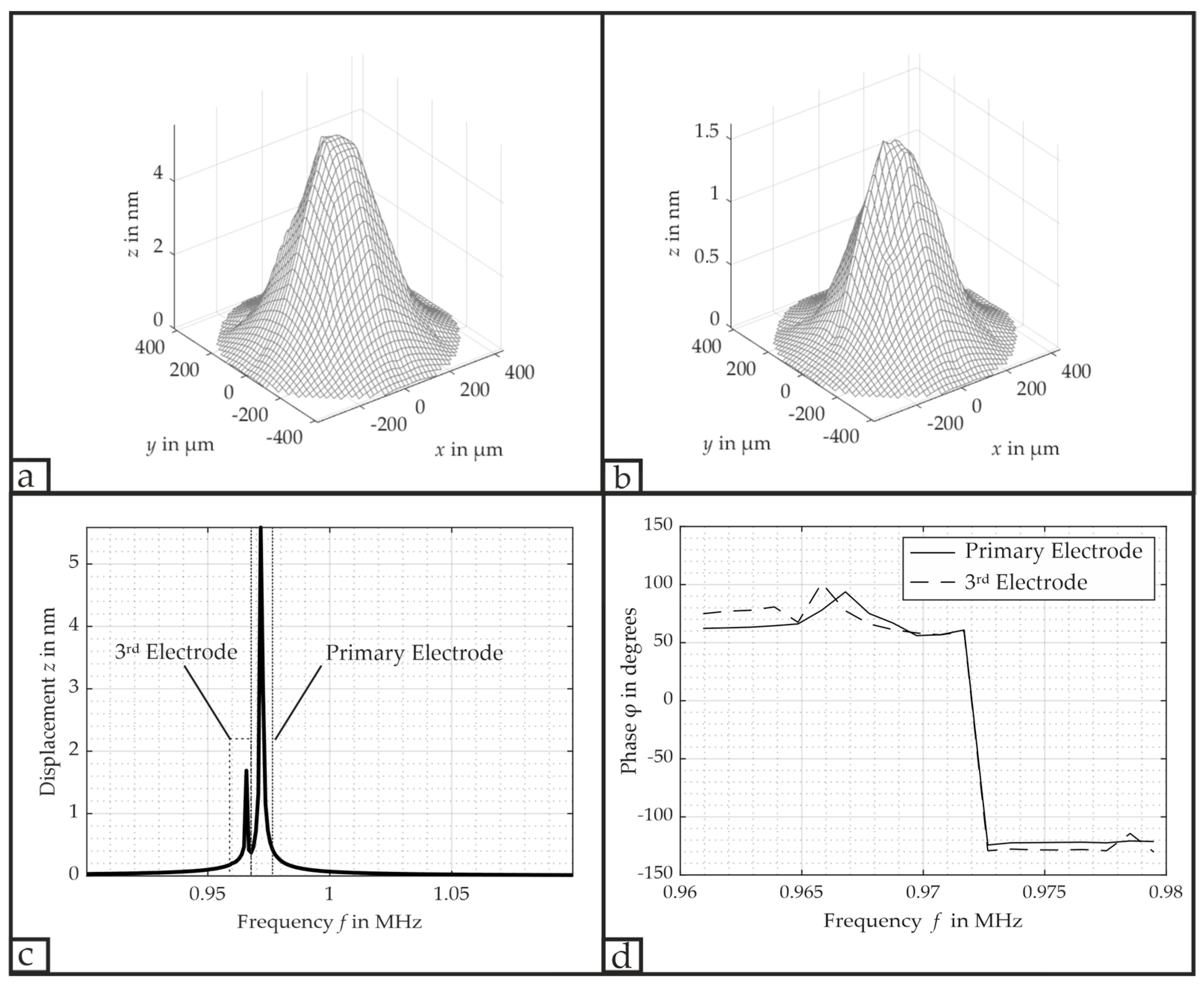
| Excited Electrodes | in kHz | in kHz | VSAG in | AMV in | |
|---|---|---|---|---|---|
| All three electrodes | 971.7 | 15.6 | 62.2 | 30.50 | 17.13 |
| Primary Electrode | 971.7 | 11.7 | 83.1 | 13.78 | 7.74 |
| 2nd Electrode | 971.7 | 9.8 | 99.1 | 26.04 | 14.63 |
| 3rd Electrode | 973.6 | 12.7 | 76.7 | 6.82 | 3.83 |
| Electrode | in | VSAG in | in | in |
|---|---|---|---|---|
| Primary Electrode | 21.8 | 13.78 | 3.14 · 10−4 | 2013 |
| 2nd Electrode | 8.2 | 26.04 | 6.8 · 10−4 | 4670 |
| 3rd Electrode | 3.4 | 6.82 | 1.2 · 10−3 | 1672 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Helmerich, J.; Wich, M.; Hofmann, A.; Schaechtle, T.; Rupitsch, S.J. Multiple Ring Electrode-Based PMUT with Tunable Deflections. Micromachines 2025, 16, 623. https://doi.org/10.3390/mi16060623
Helmerich J, Wich M, Hofmann A, Schaechtle T, Rupitsch SJ. Multiple Ring Electrode-Based PMUT with Tunable Deflections. Micromachines. 2025; 16(6):623. https://doi.org/10.3390/mi16060623
Chicago/Turabian StyleHelmerich, Jan, Manfred Wich, Annika Hofmann, Thomas Schaechtle, and Stefan Johann Rupitsch. 2025. "Multiple Ring Electrode-Based PMUT with Tunable Deflections" Micromachines 16, no. 6: 623. https://doi.org/10.3390/mi16060623
APA StyleHelmerich, J., Wich, M., Hofmann, A., Schaechtle, T., & Rupitsch, S. J. (2025). Multiple Ring Electrode-Based PMUT with Tunable Deflections. Micromachines, 16(6), 623. https://doi.org/10.3390/mi16060623






