Precision Molding Simulation Study of 3D Ultra-Thin Glass Components for Smartwatches
Abstract
1. Introduction
2. GMP Simulation Modeling
2.1. Geometric Dimensioning
2.2. Material Property
2.3. Boundary Conditions
2.4. Experimental Equipment
2.5. Scheme Design
3. Simulation Results and Analysis
3.1. Heating Process
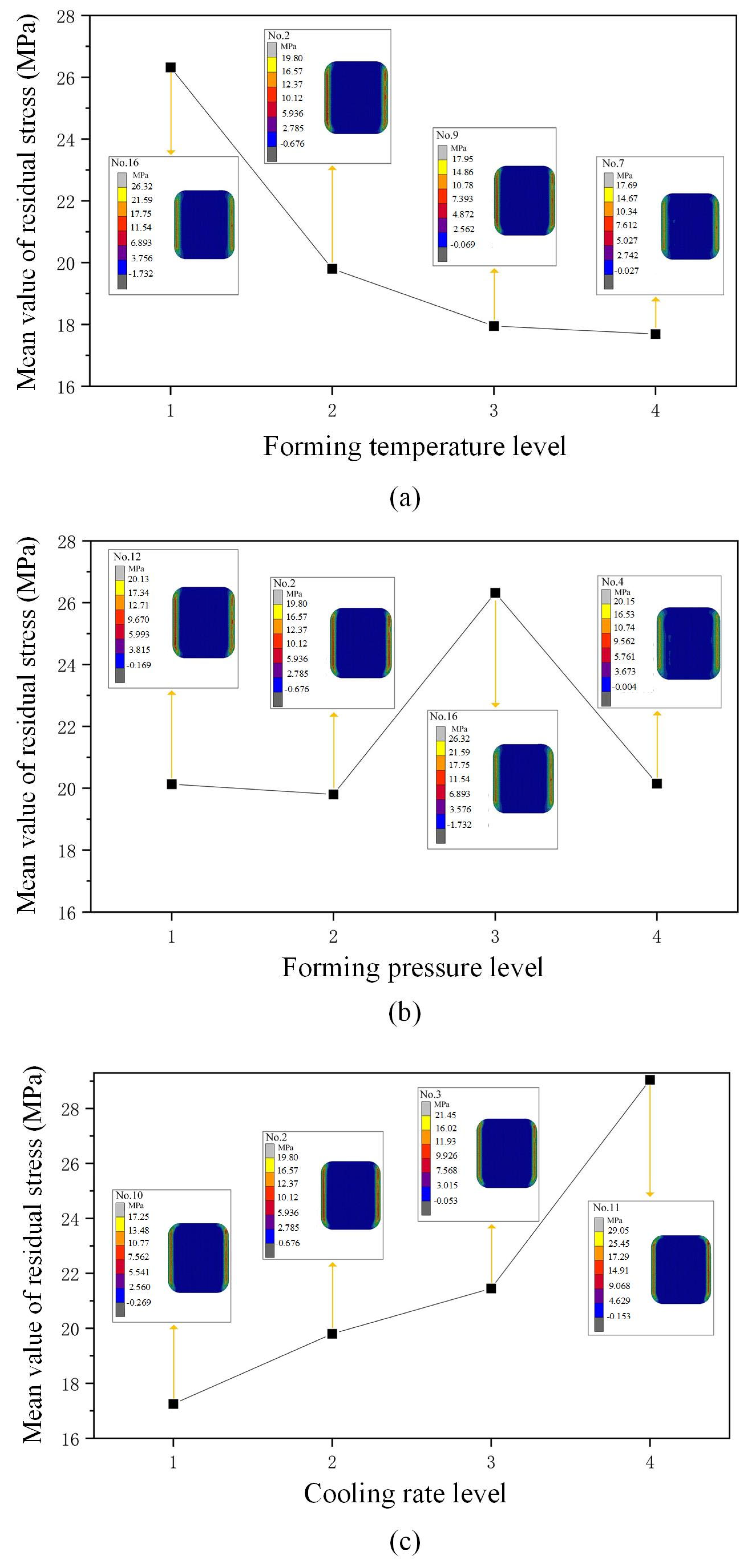
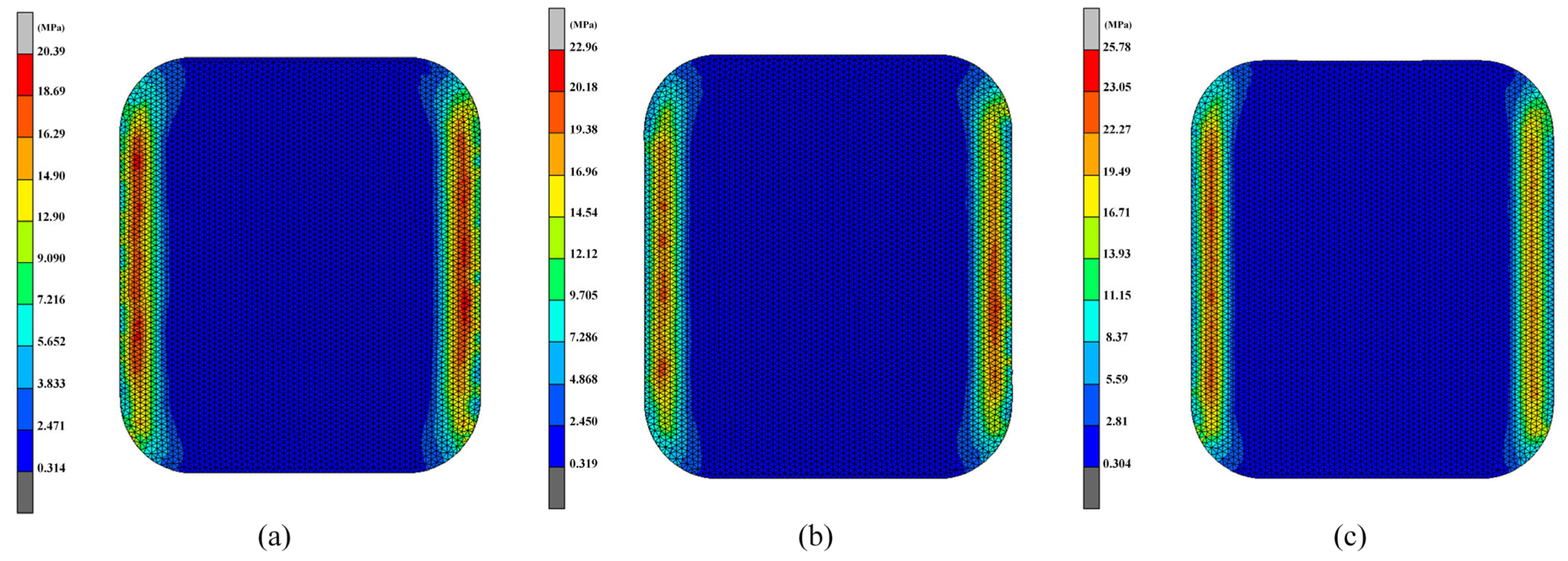
3.2. Residual Stress of Glass Components
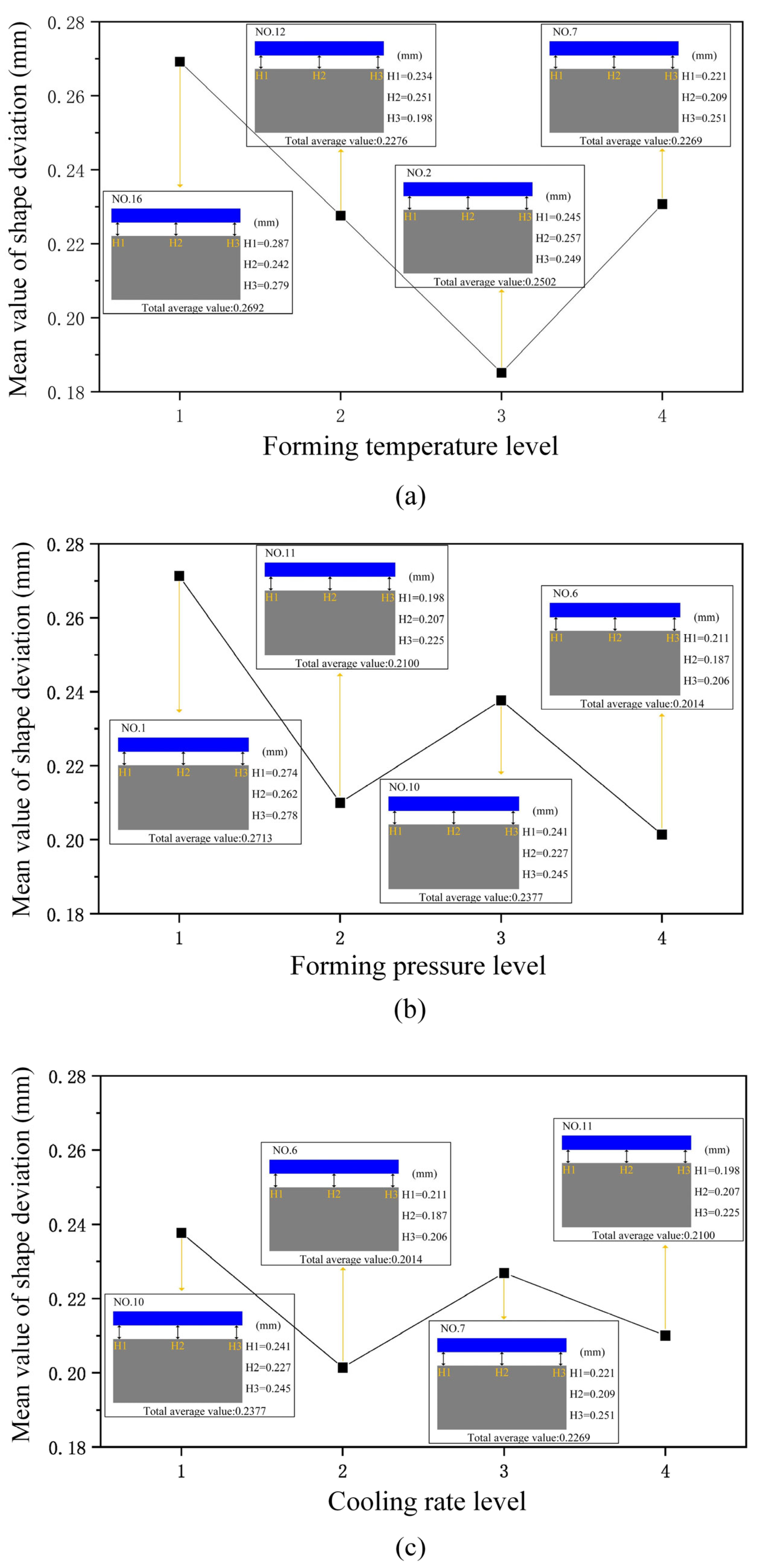
3.3. Shape Deviation of Glass Components
3.4. Energy Efficiency of Glass Components
4. Process Optimization for Molding
4.1. Regression Analysis-Based Model
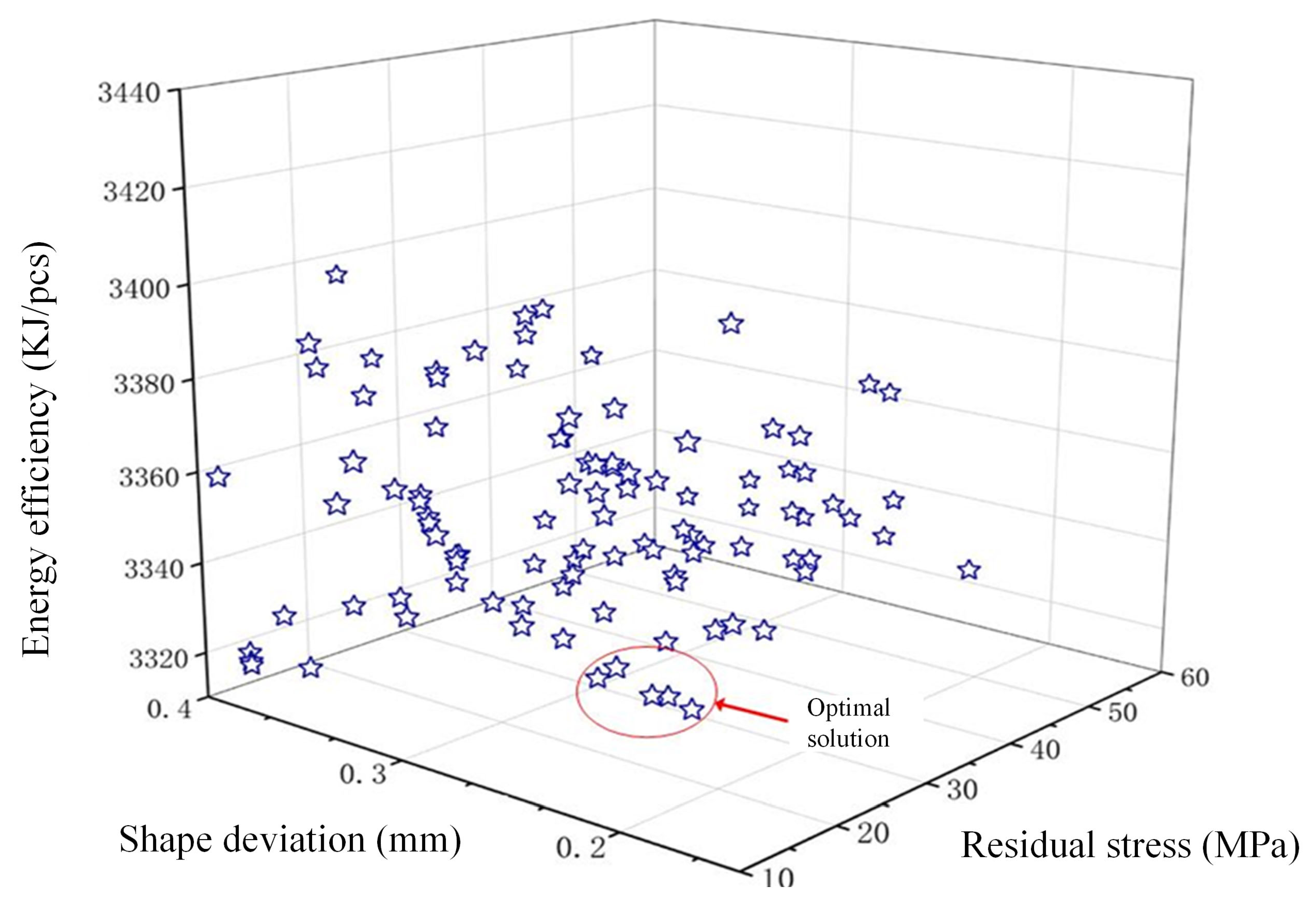
4.2. Multi-Objective Optimization
- (1)
- fmin = {Rs, Sd, Ee};
- (2)
- Population size = 100;
- (3)
- Iteration number = 500;
- (4)
- Stopped iterations = 500;
- (5)
- Value deviation of the fitness function = 1 × e−100;
- (6)
- Probability of crossover = 0.5;
- (7)
- Probability of mutation = 0.0005.
4.3. Experimental Validation
5. Discussion
6. Conclusions
- (1)
- A detailed simulation model of smartwatch glass component molding was established, simulating the heat transfer characteristics of the molding system. The results indicate that the maximum shape deviation occurs at the center of the glass component. Additionally, it was found that the primary concentration point of stress distribution lies in the curved deformation area of the molded component.
- (2)
- Under conditions of forming temperature at 630 °C, forming pressure at 0.25 MPa, and cooling rate at 0.25 °C/s, the residual stress in glass products is relatively low. Maintaining the forming temperature at 630 °C, increasing the forming pressure to 0.30MPa, and raising the cooling rate to 0.75 °C/s minimize shape deviation. Additionally, when the forming temperature of the glass component is 610 °C and the heating rate is 3 °C/s, the production energy efficiency during production is relatively low.
- (3)
- An analysis of a synergistic balance scheme between quality features and energy efficiency was conducted using the NSGA-II tri-objective optimization. With a maximum error of no more than 20%, which is within an acceptable range, the optimized projected results demonstrated good agreement with the simulation and experimental findings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ometov, A.; Shubina, V.; Klus, L.; Skibińska, J.; Saafi, S.; Pascacio, P.; Flueratoru, L.; Gaibor, D.Q.; Chukhno, N.; Chukhno, O.; et al. A Survey on Wearable Technology: History, State-of-the-Art and Current Challenges. Comput. Netw. 2021, 193, 108074. [Google Scholar] [CrossRef]
- Niknejad, N.; Ismail, W.B.; Mardani, A.; Liao, H.; Ghani, I. A Comprehensive Overview of Smart Wearables: The State of the Art Literature, Recent Advances, and Future Challenges. Eng. Appl. Artif. Intell. 2020, 90, 103529. [Google Scholar] [CrossRef]
- Siepmann, C.; Kowalczuk, P. Understanding Continued Smartwatch Usage: The Role of Emotional as Well as Health and Fitness Factors. Electron. Mark. 2021, 31, 795–809. [Google Scholar] [CrossRef]
- Celik, Y.; Godfrey, A. Bringing It All Together: Wearable Data Fusion. npj Digit. Med. 2023, 6, 149. [Google Scholar] [CrossRef]
- Bölen, M.C. Exploring the Determinants of Users’ Continuance Intention in Smartwatches. Technol. Soc. 2020, 60, 101209. [Google Scholar] [CrossRef]
- Cha, D.H.; Park, H.S.; Hwang, Y.; Kim, J.-H.; Kim, H.-J. Experimental Study of Glass Molding Process and Transcription Characteristics of Mold Surface in Molding of Aspheric Glass Lenses. Opt. Rev. 2011, 18, 241–246. [Google Scholar] [CrossRef]
- Zhou, T.; Du, Y.; Zhou, J.; Chen, Z.; Liang, Z.; Wang, X. High Efficiency Fabrication of 3D Curved Glass by Full-Motor-Driving Precision Molding. In Proceedings of the Optical Precision Manufacturing, Testing, and Applications, Beijing, China, 22–24 May 2018; SPIE: Bellingham, WA, USA, 2018; Volume 10847, pp. 265–270. [Google Scholar]
- Huang, H.; Yang, W.; Ming, W.; Zhang, G.; Xu, Y.; Zhang, Z. Mechanism of Springback Behavior in Ultra-Thin Glass Molding Process: A Molecular Dynamics Study. J. Non-Cryst. Solids 2022, 596, 121841. [Google Scholar] [CrossRef]
- Fotheringham, U.; Baltes, A.; Fischer, P.; Höhn, P.; Jedamzik, R.; Schenk, C.; Stolz, C.; Westenberger, G. Refractive Index Drop Observed After Precision Molding of Optical Elements: A Quantitative Understanding Based on the Tool–Narayanaswamy–Moynihan Model. J. Am. Ceram. Soc. 2008, 91, 780–783. [Google Scholar] [CrossRef]
- Ming, W.; Jia, H.; Huang, H.; Zhang, G.; Liu, K.; Lu, Y.; Cao, C. Study on Mechanism of Glass Molding Process for Fingerprint Lock Glass Plates. Crystals 2021, 11, 394. [Google Scholar] [CrossRef]
- Guloyan, Y.A. Glass Molding (Review). Glass Ceram. 2018, 74, 305–315. [Google Scholar] [CrossRef]
- Nelson, J.J. Overview of Glass Molding Processes. In Precision Lens Molding of Glass: A Process Perspective; Nelson, J.J., Ed.; Springer: Singapore, 2020; pp. 1–14. ISBN 9789811542381. [Google Scholar]
- Chen, Y.; Zhang, S.; Hu, S.; Zhao, Y.; Zhang, G.; Cao, Y.; Ming, W. Study of Heat Transfer Strategy of Metal Heating/Conduction Plates for Energy Efficiency of Large-Sized Automotive Glass Molding Process. Metals 2023, 13, 1218. [Google Scholar] [CrossRef]
- Axinte, E. Glasses as Engineering Materials: A Review. Mater. Des. 2011, 32, 1717–1732. [Google Scholar] [CrossRef]
- Chao, C.-L.; Huo, C.-B.; Chou, W.-C.; Lin, Y.-R.; Ma, K.-J.; Chien, H.-H. Study on the Design of Precious Metal Based Protective Films for Glass Moulding Process. Surf. Coat. Technol. 2013, 231, 567–572. [Google Scholar] [CrossRef]
- Chang, H.; Zhang, Z.; Wang, P.; Zhang, G. A Novel Composite Film with Superhydrophobic Graphene for Anti-Icing/Deicing via Chemical-Assisted Magnetically Controllable Picosecond Laser Writing. Mater. Today Phys. 2025, 54, 101726. [Google Scholar] [CrossRef]
- Tao, B.; Yuan, Y. FEM Simulation of the Effect of Coefficient of Thermal Expansion and Heat Capacity on Prediction of Residual Stresses of Compression Molded Glass Lenses. IOP Conf. Ser. Mater. Sci. Eng. 2017, 269, 012050. [Google Scholar] [CrossRef]
- Yan, J.; Zhou, T.; Masuda, J.; Kuriyagawa, T. Modeling High-Temperature Glass Molding Process by Coupling Heat Transfer and Viscous Deformation Analysis. Precis. Eng. 2009, 33, 150–159. [Google Scholar] [CrossRef]
- Su, L.; Wang, F.; He, P.; Dambon, O.; Klocke, F.; Yi, A.Y. An Integrated Solution for Mold Shape Modification in Precision Glass Molding to Compensate Refractive Index Change and Geometric Deviation. Opt. Lasers Eng. 2014, 53, 98–103. [Google Scholar] [CrossRef]
- Ming, W.; Jiang, Z.; Chen, Z.; He, W.; Li, X. Modelling and Analysis of Energy Consumption in Glass Molding Process for Smartphone Covers Using Different Heating Strategies. Int. J. Adv. Manuf. Technol. 2023, 124, 1491–1512. [Google Scholar] [CrossRef]
- Zhang, Z.; Ming, W.; Zhang, Y.; Yin, L.; Xue, T.; Yu, H.; Chen, Z.; Liao, D.; Zhang, G. Analyzing Sustainable Performance on High-Precision Molding Process of 3D Ultra-Thin Glass for Smart Phone. J. Clean. Prod. 2020, 255, 120196. [Google Scholar] [CrossRef]
- Ming, W.; Chen, Z.; Du, J.; Zhang, Z.; Zhang, G.; He, W.; Ma, J.; Shen, F. A Comprehensive Review of Theory and Technology of Glass Molding Process. Int. J. Adv. Manuf. Technol. 2020, 107, 2671–2706. [Google Scholar] [CrossRef]
- He, W.; Chen, Z.; Ming, W.; Du, J.; Cao, Y.; Ma, J.; Wei, A. Multi-Objective Optimization of Glass Multi-Station Bending Machining for Smartphone Curved Screen. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 476. [Google Scholar] [CrossRef]
- Liu, G.; Vu, A.-T.; Dambon, O.; Klocke, F. Glass Material Modeling and Its Molding Behavior. MRS Adv. 2017, 2, 875–885. [Google Scholar] [CrossRef]
- Dambon, O.; Wang, F.; Klocke, F.; Pongs, G.; Bresseler, B.; Chen, Y.; Yi, A.Y. Efficient Mold Manufacturing for Precision Glass Molding. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. Process. Meas. Phenom. 2009, 27, 1445–1449. [Google Scholar] [CrossRef]
- Ming, W.; Jia, H.; Liu, X.; Liu, X.; He, W.; Wei, A.; Chen, Z. Optimization of Process Parameters of GMP for 3D Ultrathin Glass Based on Cuckoo Search Algorithm. IOP Conf. Ser. Mater. Sci. Eng. 2020, 768, 042046. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, S.; Zhang, S.; Zhang, Q.; Zhang, Z.; Ming, W. Simulation and Experimental Study on the Precision Molding of Irregular Vehicle Glass Components. Micromachines 2023, 14, 1974. [Google Scholar] [CrossRef]
- Zhou, J.; Shi, T.; Hu, Y.; Ji, Y.; Li, M.; Shen, L. Numerical Simulation in Compression Molding of Glass Lens. In Proceedings of the 2013 IEEE International Conference on Automation Science and Engineering (CASE), Madison, WI, USA, 17–20 August 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 669–674. [Google Scholar]
- Soules, T.F.; Busbey, R.F.; Rekhson, S.M.; Markovsky, A.; Burke, M.A. Finite-Element Calculation of Stresses in Glass Parts Undergoing Viscous Relaxation. J. Am. Ceram. Soc. 1987, 70, 90–95. [Google Scholar] [CrossRef]
- Zhou, T.; Yan, J.; Masuda, J.; Kuriyagawa, T. Investigation on the Viscoelasticity of Optical Glass in Ultraprecision Lens Molding Process. J. Mater. Process. Technol. 2009, 209, 4484–4489. [Google Scholar] [CrossRef]
- Zhou, T.; Yan, J.; Kuriyagawa, T. Evaluating the Viscoelastic Properties of Glass above Transition Temperature for Numerical Modeling of Lens Molding Process. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2007: Optoelectronic System Design, Manufacturing, and Testing, Beijing, China, 9–12 September 2007; SPIE: Bellingham, WA, USA, 2008; Volume 6624, pp. 25–35. [Google Scholar]
- Storck, K.; Karlsson, M.; Loyd, D. Analysis of the Blank Mould—A Transient Heat Transfer Problem in Glass Forming. WIT Trans. Eng. Sci. 1970, 5, 8. [Google Scholar]
- Keijts, G.; Werff, K.V.D. Heat Transfer in Glass Container Production during the Final Blow. Glass Technol. 2001, 42, 104–108. [Google Scholar]
- Zhang, Y. Study on the Key Techniques. Ph.D. Thesis, Tianjin University, Tianjin, China, 2023. [Google Scholar]
- Zhang, Z.; Yang, W.; Ming, W.; Yin, L.; Liao, D.; Zhang, G. Surface Integrity Analysis of Ultra-Thin Glass Molding Process. Ceram. Int. 2021, 47, 30584–30597. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Tian, M.; Gong, X.; Yin, L.; Li, H.; Ming, W.; Zhang, Z.; Chen, J. Multi-Objective Optimization of Injection Molding Process Parameters in Two Stages for Multiple Quality Characteristics and Energy Efficiency Using Taguchi Method and NSGA-II. Int. J. Adv. Manuf. Technol. 2017, 89, 241–254. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, Z.; Ming, W.; Yin, L.; Zhang, G. Study on Shape Deviation and Crack of Ultra-Thin Glass Molding Process for Curved Surface. Ceram. Int. 2022, 48, 6767–6779. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Z.; Wei, S.; Hao, B.; Chang, H.; Huang, Y.; Zhang, G. Study on Plasma Behaviour, Ablation Mechanism, and Surface Morphology of CFRP by Underwater Laser-Induced Plasma Micro-Machining. J. Mater. Process. Technol. 2025, 338, 118757. [Google Scholar] [CrossRef]




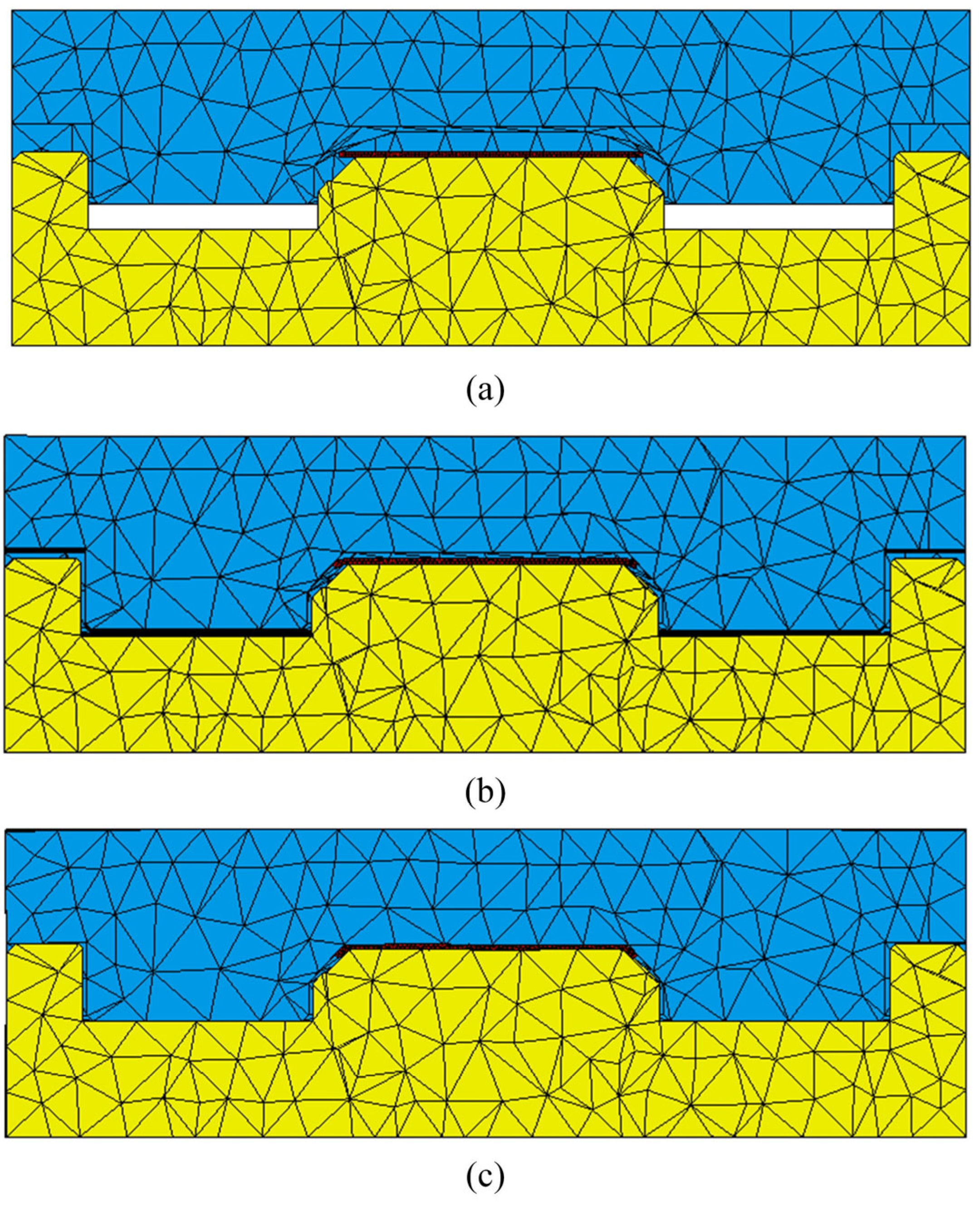

| Properties | Glass Material | Graphite Material |
|---|---|---|
| Young’s modulus E (GPa) | 72.6 | 10.2 |
| Poisson’s ratio v | 0.206 | 0.25 |
| Density (g/cm3) | 2.51 | 1.78 |
| Thermal conductivity K(W/m·K) | 1.1 | 151 |
| Specific heat Cp (J/kg·°C) | 858 | 720 |
| Thermal expansion coefficient (°C−1) | Liquid 3.43 × 10−5 Solid 1.143 × 10−5 | 4.8 × 10−6 |
| No. | Control Factors | ||||
|---|---|---|---|---|---|
| A (°C/s) | B (Hz) | C (°C) | D (MPa) | E (°C/s) | |
| 1 | 1.5 | 0 | 610 | 0.20 | 0.25 |
| 2 | 2 | 10 | 620 | 0.25 | 0.5 |
| 3 | 2.5 | 30 | 630 | 0.30 | 0.75 |
| 4 | 3 | 50 | 640 | 0.35 | 1 |
| No. | Control Factors | Residual Stress (MPa) | Shape Deviation (mm) | Energy Efficiency (kJ/pcs) | ||||
|---|---|---|---|---|---|---|---|---|
| A (°C/s) | B (Hz) | C (°C) | D (MPa) | E (°C/s) | ||||
| 1 | 1.5 | 0 | 610 | 0.20 | 0.25 | 18.65 | 0.2713 | 3365 |
| 2 | 1.5 | 10 | 620 | 0.25 | 0.5 | 19.80 | 0.2502 | 3432 |
| 3 | 1.5 | 30 | 630 | 0.30 | 0.75 | 21.45 | 0.1851 | 3450 |
| 4 | 1.5 | 50 | 640 | 0.35 | 1 | 20.15 | 0.2307 | 3493 |
| 5 | 2 | 0 | 620 | 0.30 | 1 | 28.72 | 0.1913 | 3408 |
| 6 | 2 | 10 | 610 | 0.35 | 0.75 | 28.58 | 0.2014 | 3365 |
| 7 | 2 | 30 | 640 | 0.20 | 0.5 | 17.69 | 0.2269 | 3469 |
| 8 | 2 | 50 | 630 | 0.25 | 0.25 | 15.21 | 0.2157 | 3426 |
| 9 | 2.5 | 0 | 630 | 0.35 | 0.5 | 17.95 | 0.1928 | 3401 |
| 10 | 2.5 | 10 | 640 | 0.30 | 0.25 | 17.25 | 0.2377 | 3444 |
| 11 | 2.5 | 30 | 610 | 0.25 | 1 | 29.05 | 0.2100 | 3341 |
| 12 | 2.5 | 50 | 620 | 0.20 | 0.75 | 20.13 | 0.2276 | 3383 |
| 13 | 3 | 0 | 640 | 0.25 | 1 | 20.85 | 0.1868 | 3420 |
| 14 | 3 | 10 | 630 | 0.20 | 0.75 | 21.18 | 0.2169 | 3401 |
| 15 | 3 | 30 | 620 | 0.35 | 0.25 | 18.84 | 0.2210 | 3359 |
| 16 | 3 | 50 | 610 | 0.30 | 0.5 | 26.32 | 0.2692 | 3341 |
| Stress Relaxation | Structural Relaxation | ||
|---|---|---|---|
| Shear Modulus (MPa) | Relaxation Times (s) | Weight Coefficient | Relaxation Times (s) |
| 12,566 | 0.0689 | 0.108 | 3.0 |
| 0.443 | 0.671 | ||
| 12,615 | 0.0065 | 0.166 | 0.247 |
| 0.161 | 0.091 | ||
| 4582 | 0.0001 | 0.046 | 0.033 |
| 0.077 | 0.008 | ||
| Level | A | B | C | D | E |
|---|---|---|---|---|---|
| 1 | 20.01 | 21.53 | 25.61 | 19.36 | 17.47 |
| 2 | 22.50 | 21.66 | 21.86 | 21.20 | 20.41 |
| 3 | 21.08 | 21.71 | 18.92 | 23.43 | 22.79 |
| 4 | 21.75 | 20.44 | 18.95 | 21.35 | 24.67 |
| Delta | 2.49 | 1.27 | 6.69 | 4.07 | 7.19 |
| Order | 4 | 5 | 2 | 3 | 1 |
| Level | A | B | C | D | E |
|---|---|---|---|---|---|
| 1 | 0.2247 | 0.2009 | 0.2284 | 0.2280 | 0.2268 |
| 2 | 0.1992 | 0.2169 | 0.2129 | 0.2061 | 0.2252 |
| 3 | 0.2074 | 0.2011 | 0.1930 | 0.2112 | 0.1981 |
| 4 | 0.2138 | 0.2262 | 0.2109 | 0.2018 | 0.1951 |
| Delta | 0.0255 | 0.0252 | 0.0353 | 0.0262 | 0.0317 |
| Order | 4 | 5 | 1 | 3 | 2 |
| Level | A | B | C | D | E |
|---|---|---|---|---|---|
| 1 | 3435 | 3399 | 3353 | 3405 | 3399 |
| 2 | 3417 | 3411 | 3396 | 3405 | 3411 |
| 3 | 3392 | 3405 | 3420 | 3411 | 3400 |
| 4 | 3380 | 3411 | 3457 | 3405 | 3416 |
| Delta | 55 | 12 | 104 | 6 | 17 |
| Order | 2 | 4 | 1 | 5 | 3 |
| No. | Control Factors | Residual Stress (MPa) | Shape Deviation (mm) | Energy Efficiency (kJ/pcs) | ||||
|---|---|---|---|---|---|---|---|---|
| A (°C/s) | B (Hz) | C (°C) | D (MPa) | E (°C/s) | ||||
| 1 | 1.64 | 43.13 | 609.4 | 0.2256 | 0.65 | 18.7 | 0.2605 | 3367 |
| 2 | 2.78 | 36.90 | 617.7 | 0.3350 | 0.45 | 17.7 | 0.2924 | 3339 |
| 3 | 1.67 | 43.20 | 611.1 | 0.2331 | 0.63 | 21.1 | 0.2506 | 3382 |
| 4 | 1.72 | 43.12 | 610.0 | 0.2343 | 0.56 | 21.6 | 0.2615 | 3369 |
| 5 | 1.78 | 42.89 | 608.9 | 0.2311 | 0.60 | 23.1 | 0.2537 | 3364 |
| 6 | 1.68 | 43.18 | 623.1 | 0.2739 | 0.66 | 29.8 | 0.2359 | 3396 |
| 7 | 1.82 | 43.20 | 608.9 | 0.2422 | 0.47 | 22.3 | 0.2609 | 3358 |
| Group | Control Factors | Simulation Results | Relative Error | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | Rs (MPa) | Sd (mm) | Ee (kJ/pcs) | Rs (%) | Sd (%) | Ee (%) | |
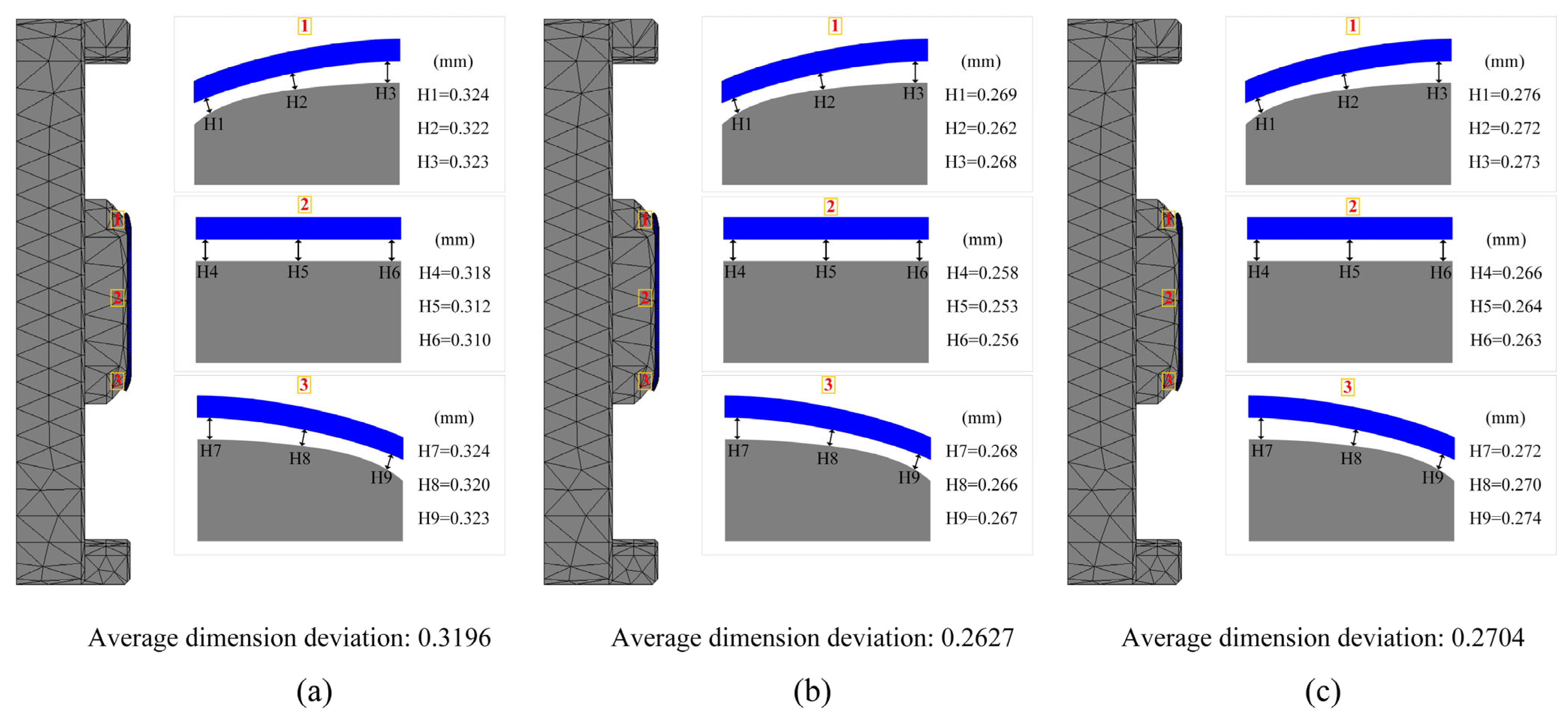
| 2 | 2.78 | 36.90 | 617.7 | 0.3350 | 0.45 | 20.39 | 0.3196 | 3348.7 | 13.2 | 8.5 | 2.9 |
| 3 | 1.67 | 43.20 | 611.1 | 0.2331 | 0.63 | 22.96 | 0.2627 | 3472.3 | 8.1 | 4.6 | 2.6 |
| 4 | 1.72 | 43.12 | 610.0 | 0.2343 | 0.56 | 25.78 | 0.2704 | 3634.3 | 16.2 | 3.3 | 7.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Hu, S.; Sun, P.; Ming, W. Precision Molding Simulation Study of 3D Ultra-Thin Glass Components for Smartwatches. Micromachines 2025, 16, 584. https://doi.org/10.3390/mi16050584
Zhao X, Hu S, Sun P, Ming W. Precision Molding Simulation Study of 3D Ultra-Thin Glass Components for Smartwatches. Micromachines. 2025; 16(5):584. https://doi.org/10.3390/mi16050584
Chicago/Turabian StyleZhao, Xinfeng, Shunchang Hu, Peiyan Sun, and Wuyi Ming. 2025. "Precision Molding Simulation Study of 3D Ultra-Thin Glass Components for Smartwatches" Micromachines 16, no. 5: 584. https://doi.org/10.3390/mi16050584
APA StyleZhao, X., Hu, S., Sun, P., & Ming, W. (2025). Precision Molding Simulation Study of 3D Ultra-Thin Glass Components for Smartwatches. Micromachines, 16(5), 584. https://doi.org/10.3390/mi16050584










