Random Lasers Based on Tellurite and Germanate Glasses and Glass-Ceramics Doped with Rare-Earth Ions
Abstract
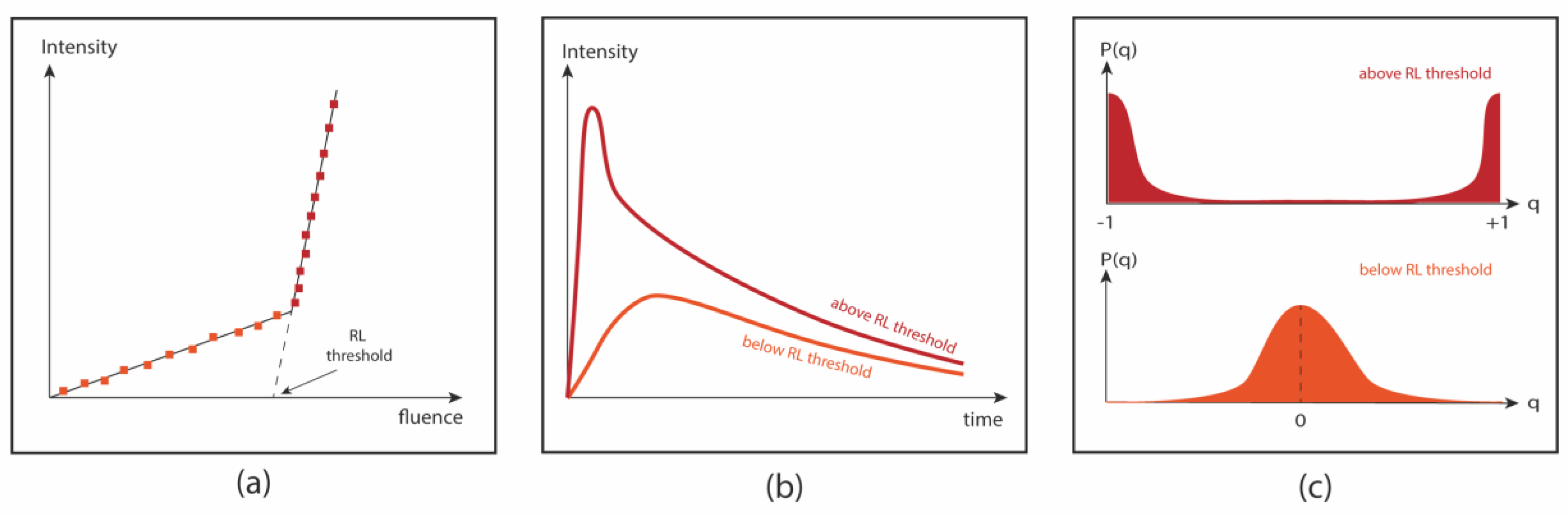
1. Introduction
2. Experimental Details
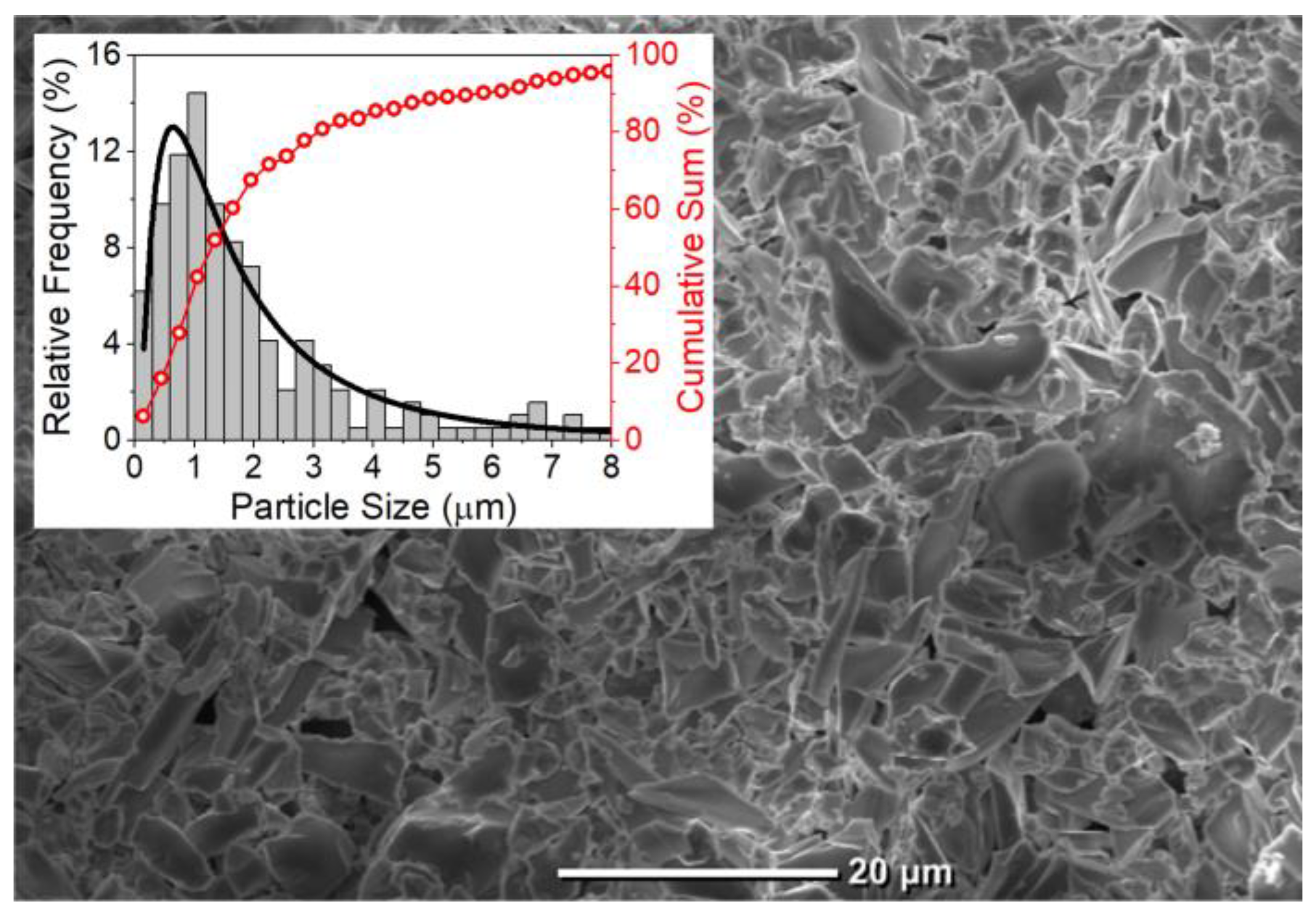
2.1. Fabrication of Tellurite and Germanate Glass and Glass-Ceramics
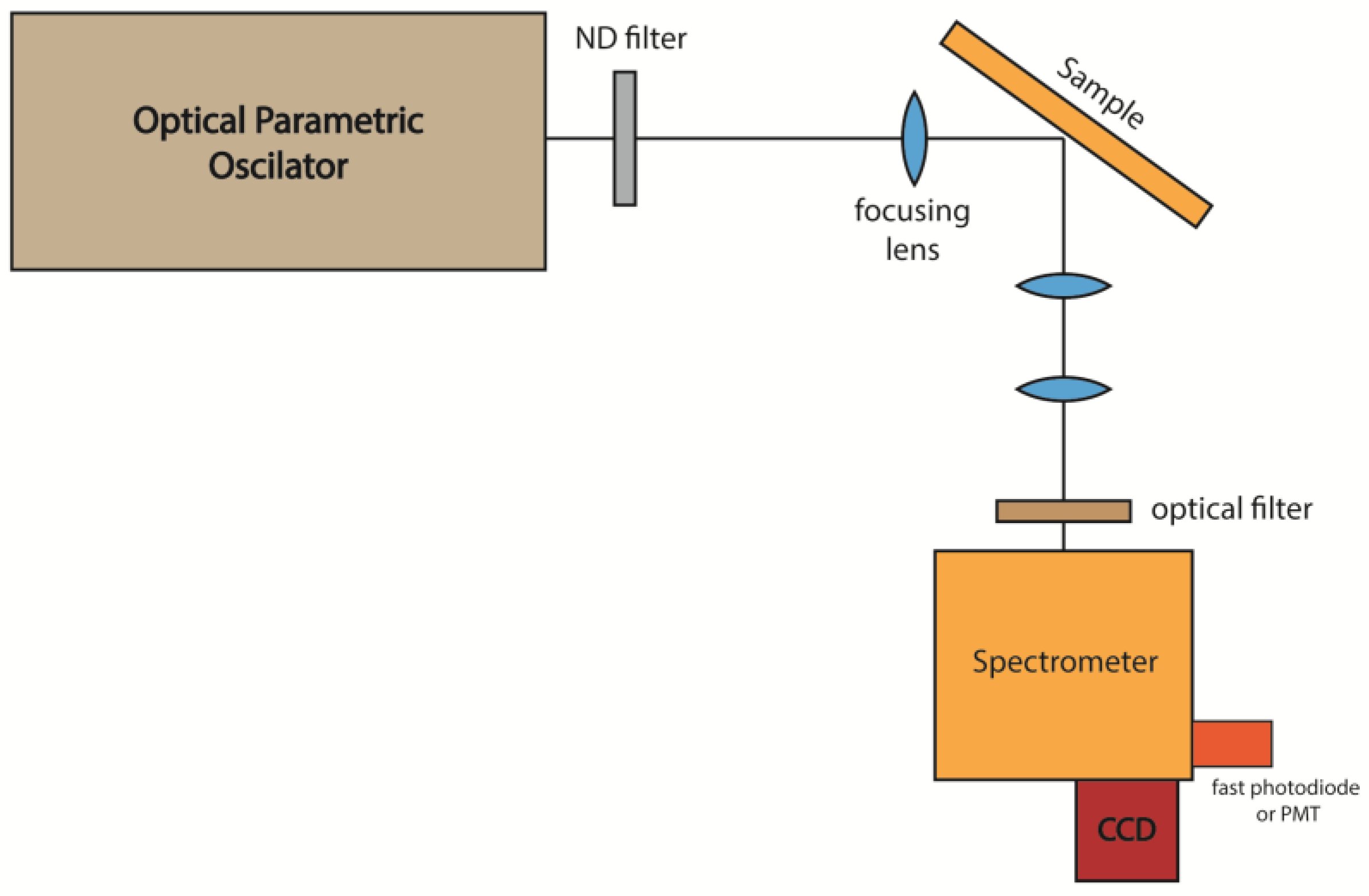
2.2. Optical Characterization of the Samples
3. Glass-Based Random Lasers
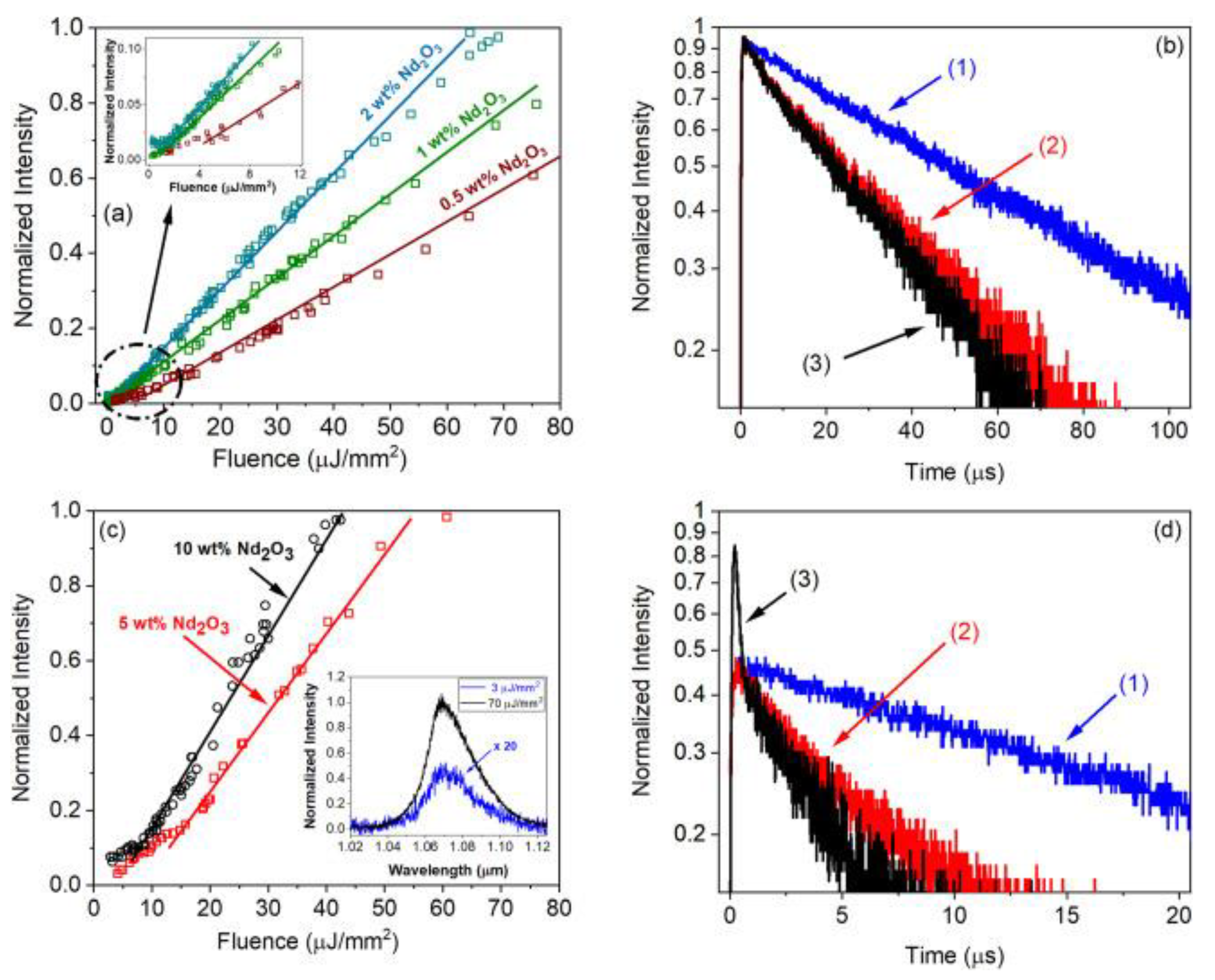
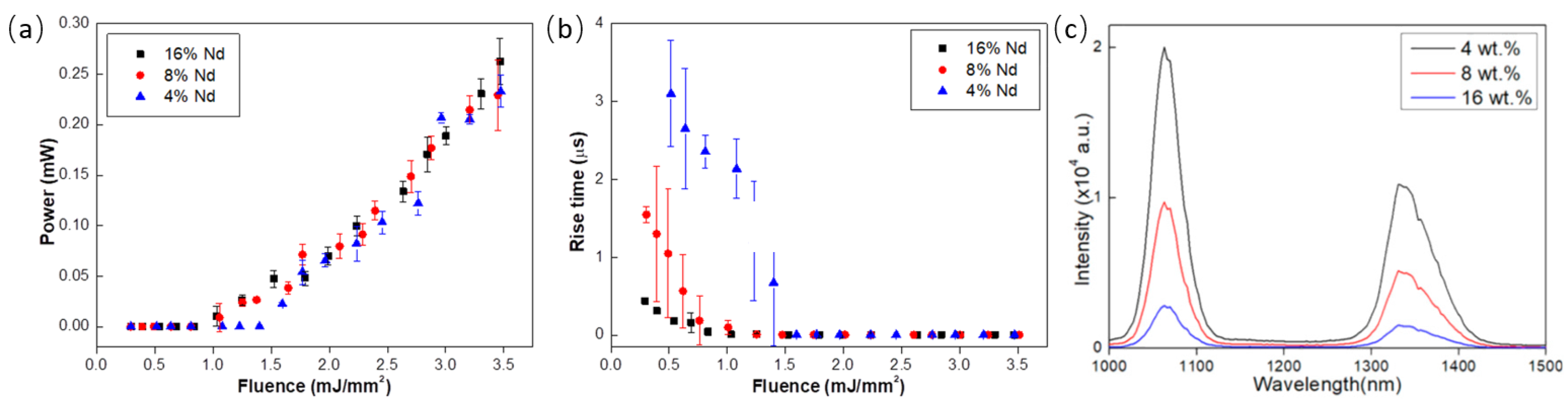
3.1. Nd 3+-Doped TeO2-ZnO (TZO)
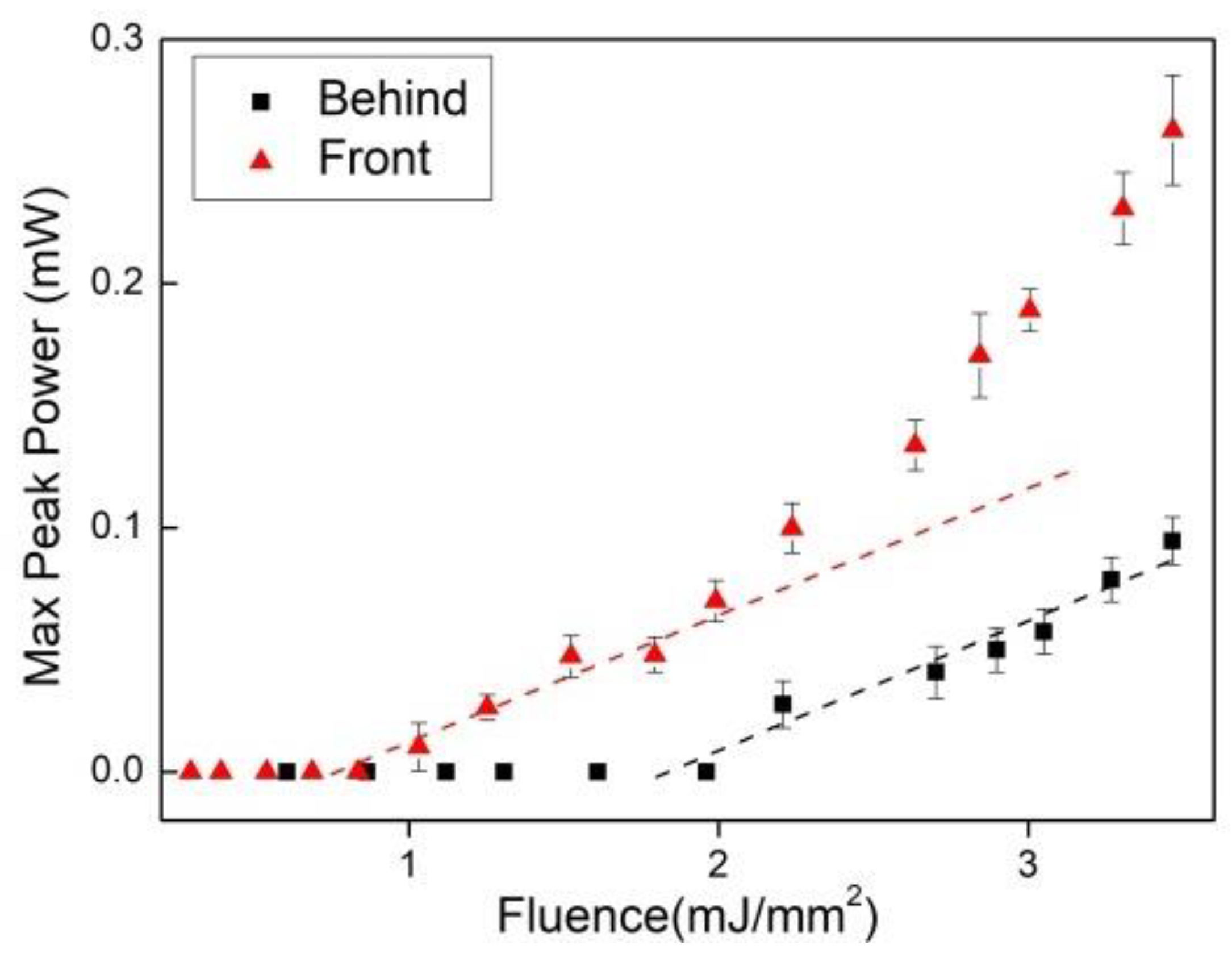
3.2. Nd 3+-Doped TeO2-ZnO-Al2O3 (TZA)
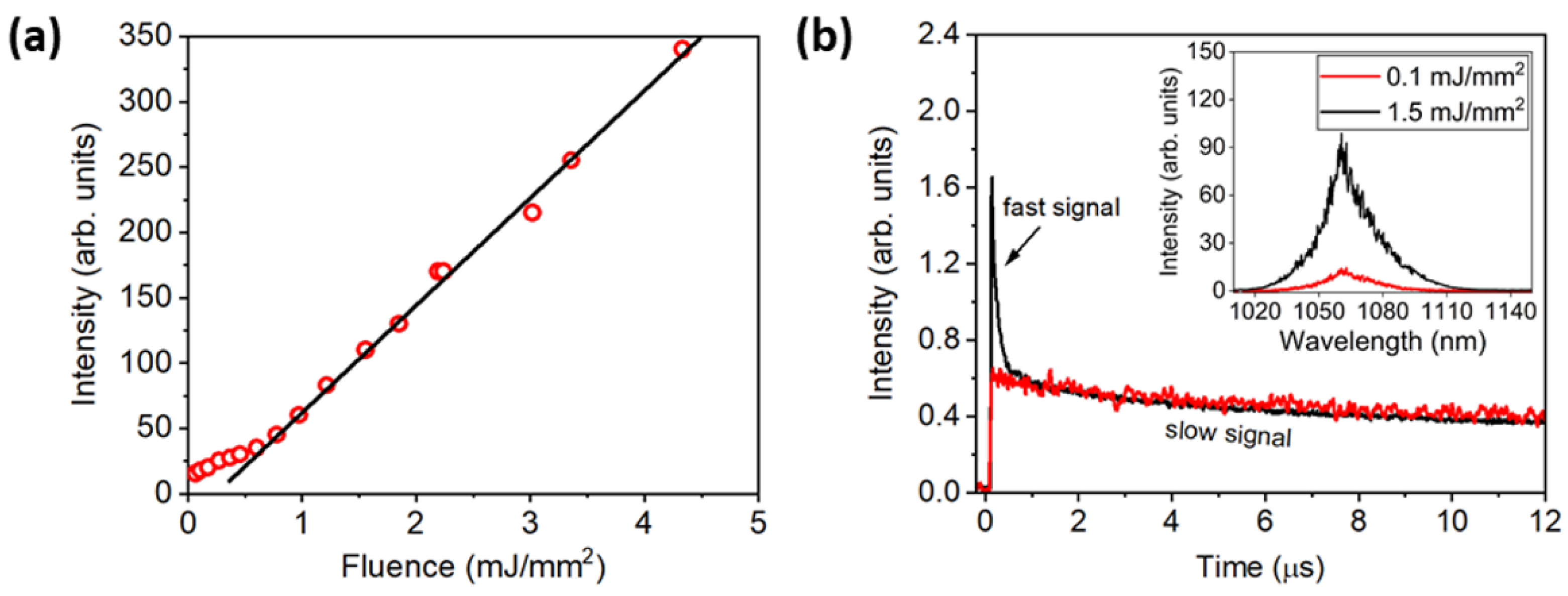
3.3. Nd3+ Doped GeO2-PbO-Al2O3 (GPA)
4. Glass-Ceramics-Based Random Lasers
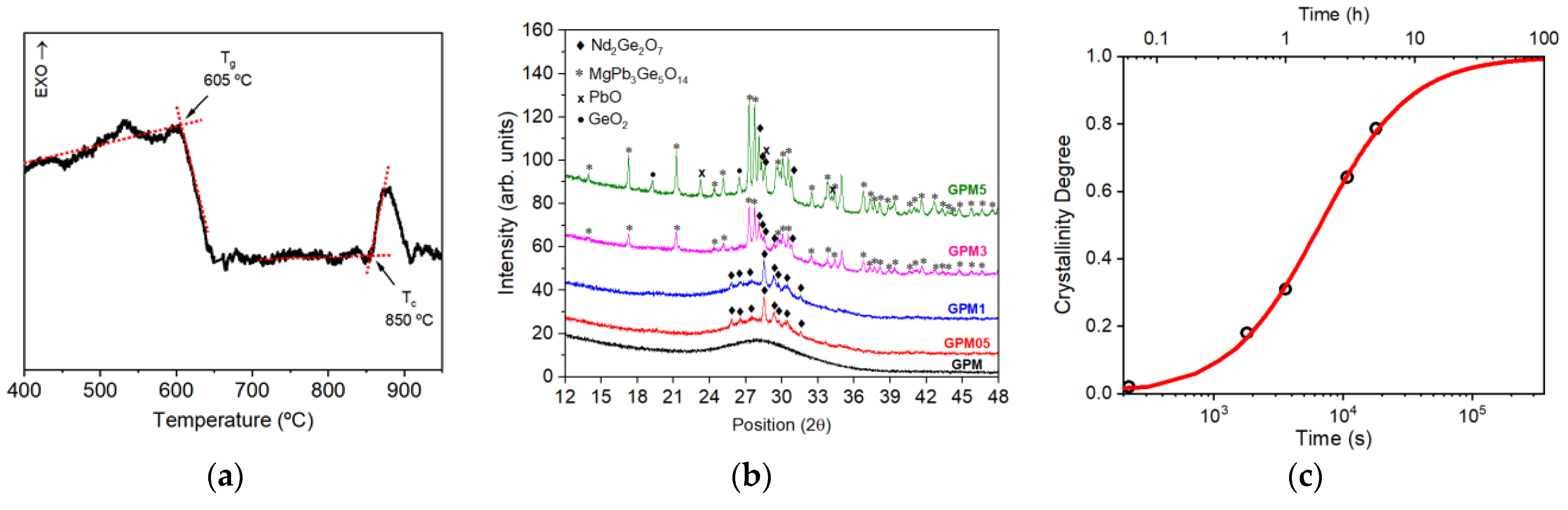
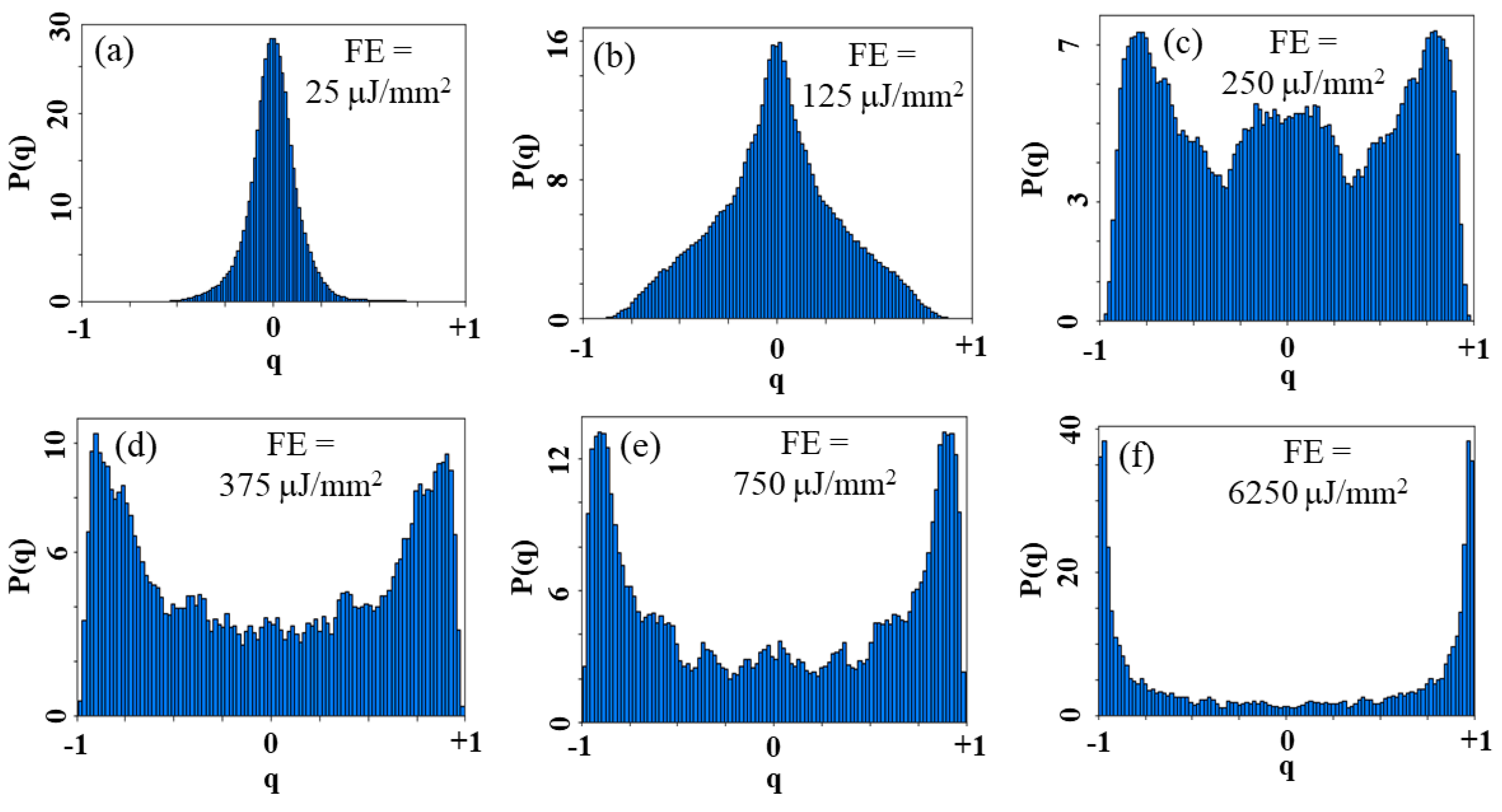
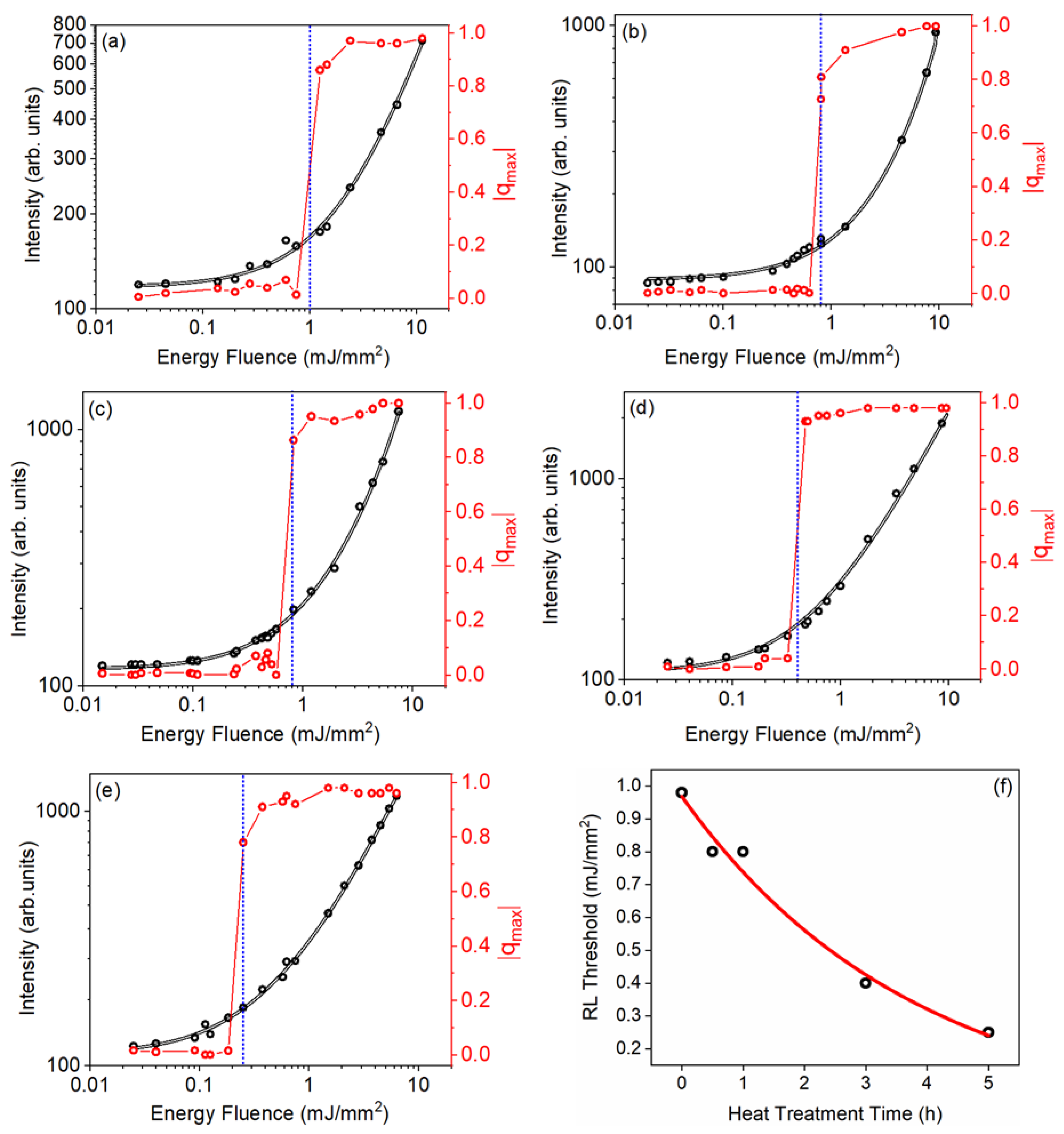
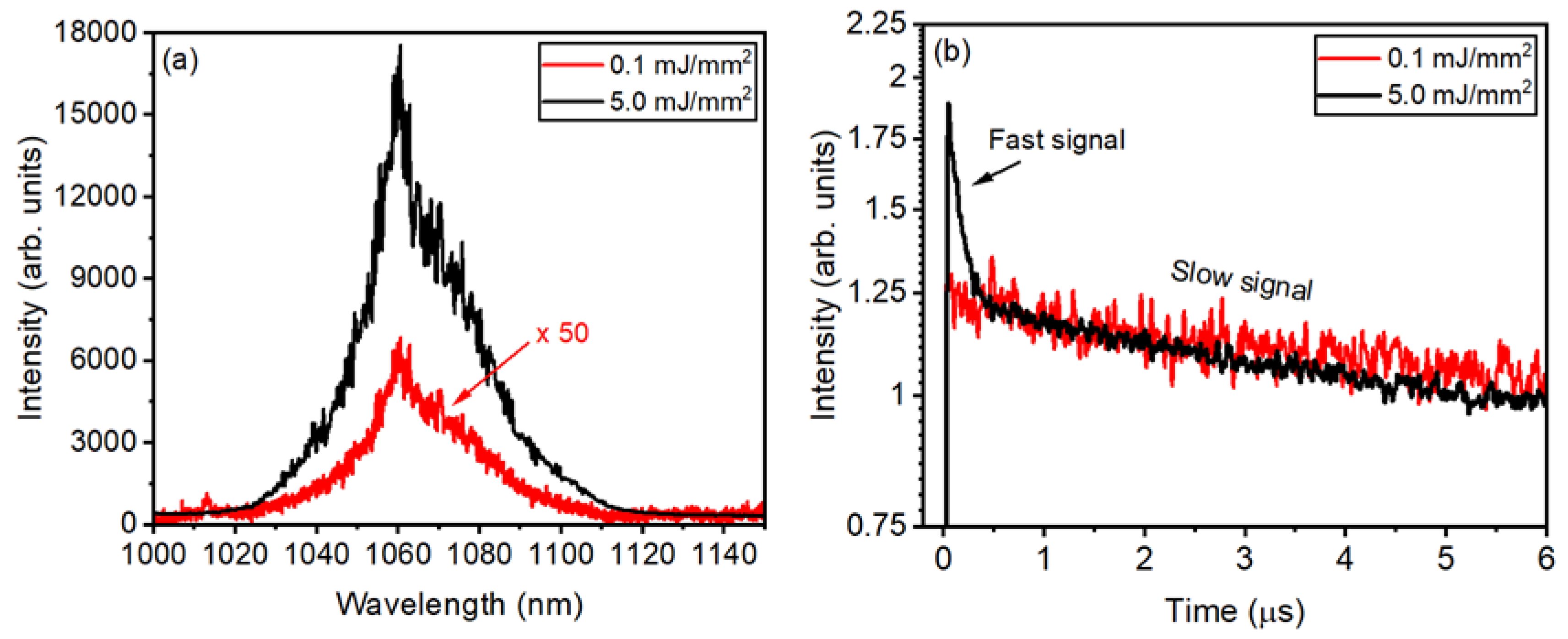
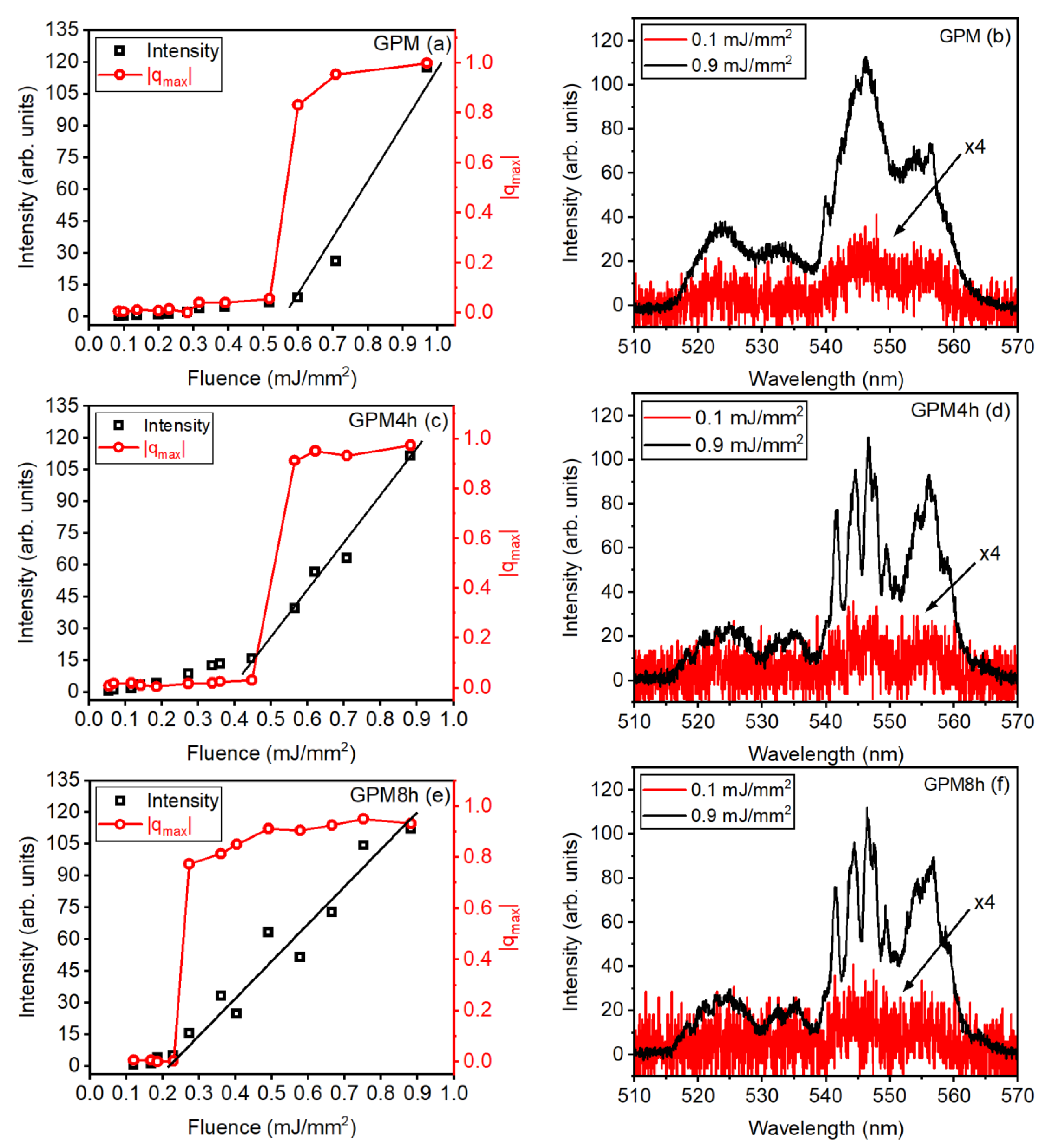
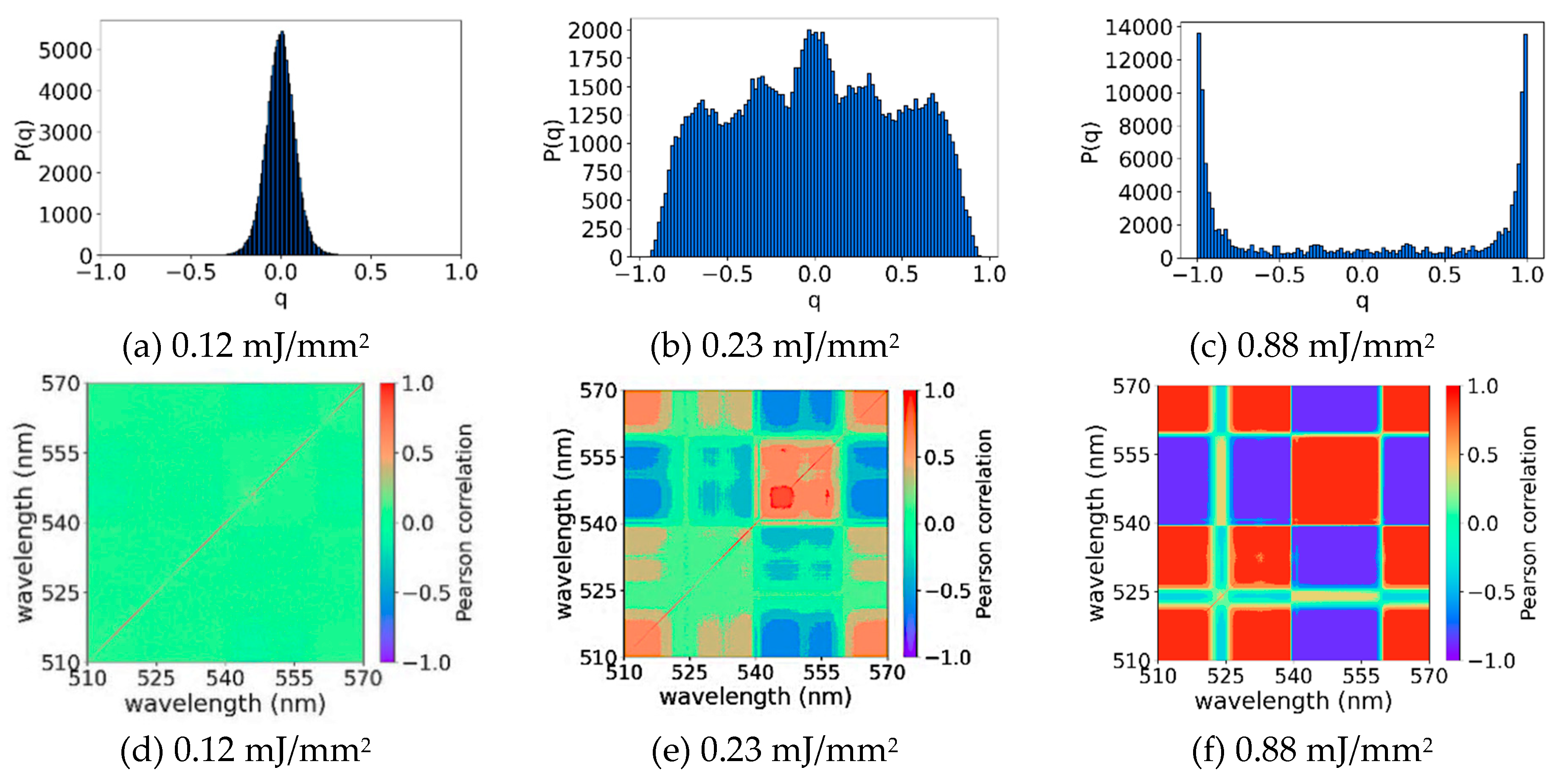
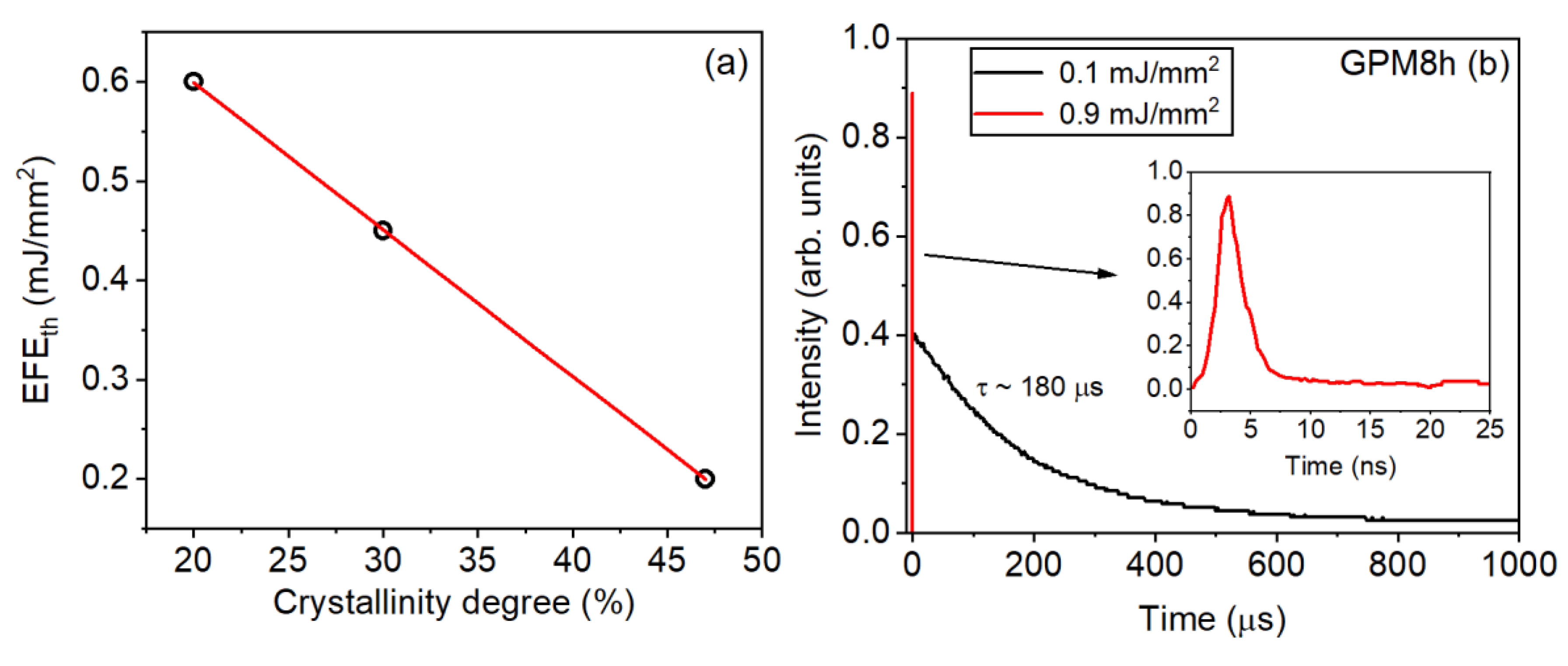
4.1. Nd3-Doped GeO2-PbO-MgO (GPM)
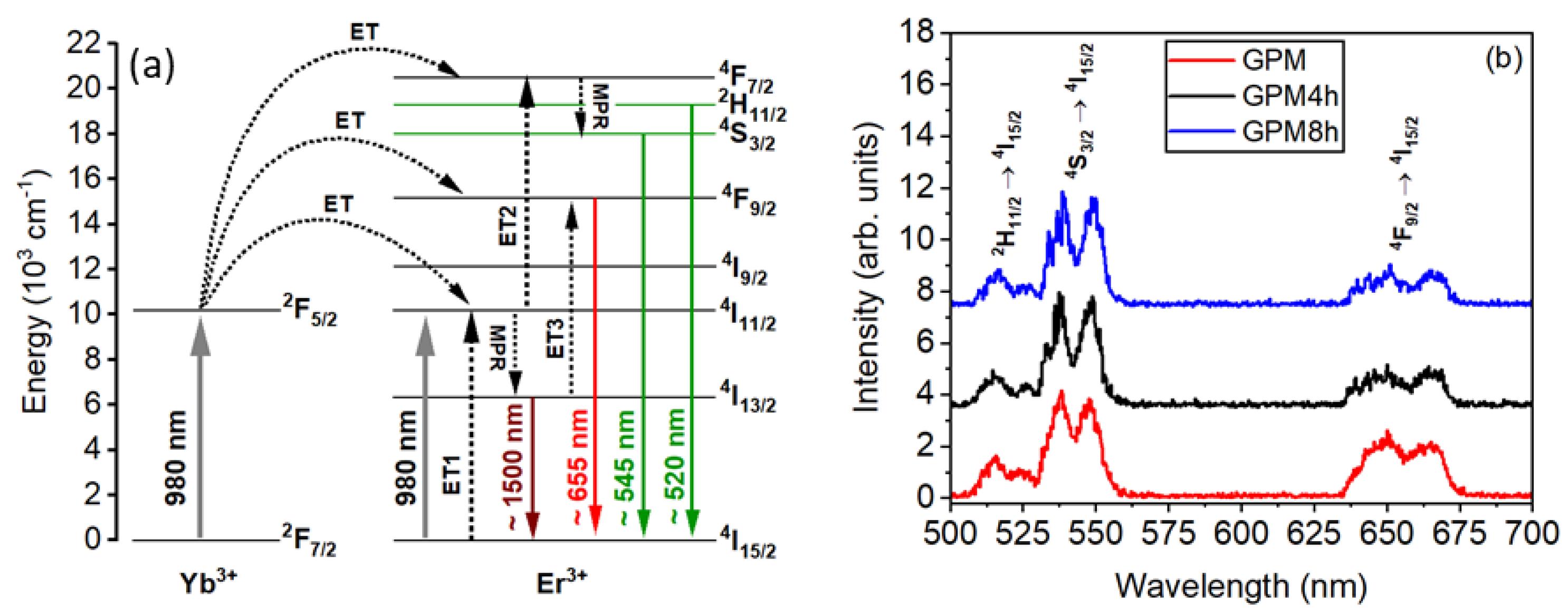
4.2. Er3+/Yb3+-Doped GeO2-PbO-MgO (GPM)
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ambartsumyan, R.V.; Basov, N.G.; Kryukov, P.G.; Lethokov, V.S. Laser with nonresonant feedback. JETP Lett. 1996, 3, 167–169. [Google Scholar]
- Gouedard, C.; Husson, D.; Sauteret, C.; Auzel, F.; Migus, A. Generation of spatially incoherent short pulses in laser-pumped neodymium stoichiometric crystals and powders. J. Opt. Soc. Am. B 1993, 10, 2358–2363. [Google Scholar] [CrossRef]
- Lawandy, N.M.; Balachandran, R.M.; Gomes, A.S.L.; Sauvian, E. Laser action in strongly scattering medium. Nature 1994, 368, 436–438. [Google Scholar] [CrossRef]
- Cao, H.; Zhao, Y.G.; Ho, S.T.; Seelig, E.W.; Wang, Q.H.; Chang, R.P.H. Random Laser Action in Semiconductor Powder. Phys. Rev. Lett. 1999, 82, 2278–2281. [Google Scholar] [CrossRef]
- Noginov, M.A. Solid-State Random Lasers; Springer: New York, NY, USA, 2005. [Google Scholar]
- Gomes, A.S.L.; Moura, A.L.; de Araújo, C.B.; Raposo, E.P. Recent advances and applications of random lasers and random fiber lasers. Prog. Quantum Electron. 2021, 78, 100343. [Google Scholar] [CrossRef]
- Gomes, A.L.S.; Valente, D.; de Oliveira, H.P.; Ribeiro, S.J.L.; de Araújo, C.B. Optical materials for flexible and stretchable random lasers. Opt. Mater. X 2022, 16, 100203. [Google Scholar] [CrossRef]
- Abdulhameed, A. ZnO-based random lasing and their sensing applications: A mini-review. Appl. Nanosci. 2024, 14, 985–995. [Google Scholar] [CrossRef]
- Azkargorta, J.; Iparraguirre, I.; Fernández, J.; Balda, R.; García-Revilla, S.; Barredo-Zurriarrain, M. Random Laser properties of Nd3+ crystal powders. Opt. Express 2018, 26, 11787–11803. [Google Scholar] [CrossRef]
- Azmi, A.N.; Wan Ismail, W.Z.; Abu Hassan, H.; Halim, M.M.; Zainal, N.; Muskens, O.L.; Wan Ahmad Kamil, W.M. Review of Open Cavity Random Lasers as Laser-Based Sensors. ACS Sens. 2022, 7, 914–928. [Google Scholar] [CrossRef]
- Padiyakkuth, N.; Thomas, S.; Antoine, R.; Kalarikkal, N. Recent progress and properties of random lasers using advanced materials. Mater. Adv. 2022, 3, 6687. [Google Scholar] [CrossRef]
- Li, X.; Chen, D.; Huang, F.; Chang, G.; Zhao, J.; Qiao, X.; Xu, X.; Du, J.; Yin, M. Phase-Selective Nanocrystallization of NaLnF4 in Aluminumsilicate Glass for Random Laser and 940 nm LED Excitable Upconverted Luminescence. Laser Photon. Rev. 2018, 12, 1800030. [Google Scholar] [CrossRef]
- Pisarski, W.A. Rare Earth Doped Glasses/Ceramics: Synthesis, Structure, Properties and their Optical Applications. Materials 2022, 15, 8099. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, S.; Li, Y.; Wu, C.; Zhang, W.; Zhang, H.; Xie, Z.; Zhou, S. Ultra-Broadband Random Laser and White-Light Emissive Carbon Dots/Crystal In-Situ Hybrids. Small 2022, 18, 2203152. [Google Scholar] [CrossRef]
- de Matos, C.J.; de SMenezes, L.; Brito-Silva, A.M.; Martinez Gámez, M.A.; Gomes, A.S.; de Araújo, C. Random Fiber Laser. Phys. Rev. Lett. 2007, 99, 153903. [Google Scholar] [CrossRef]
- Turitsyn, S.K.; Babin, S.A.; El-Taher, A.E.; Harper, P.; Churkin, D.V.; Kablukov, S.I.; Ania-Castañón, J.D.; Karalekas, V.; Podivilov, E.V. Random distributed feedback fibre laser. Nat. Photon. 2010, 4, 231–235. [Google Scholar] [CrossRef]
- Zhai, T.; Zhang, X.; Pang, Z.; Su, X.; Liu, H.; Feng, S.; Wang, L. Random laser based on waveguided plasmonic gain channels. Nano Lett. 2011, 11, 4295–4298. [Google Scholar] [CrossRef]
- Consoli, A.; Caselli, N.; López, C. Electrically driven random lasing from a modified Fabry-Perot laser diode. Nat. Photon. 2022, 16, 219–226. [Google Scholar] [CrossRef]
- Dominguez, C.T.; Lacroute, Y.; Chaumont, D.; Sacilotti, M.; de Araújo, C.B.; Gomes, A.S.L. Microchip Random Laser based on a disordered TiO2-nanomembranes arrangement. Opt. Express 2012, 20, 17380–17385. [Google Scholar] [CrossRef]
- Yi, J.; Yu, Y.; Shang, J.; An, X.; Tu, B.; Feng, G.; Zhou, S. Waveguide random laser based on a disordered ZnSe-nanosheets arrangement. Opt. Express 2016, 24, 5102–5109. [Google Scholar] [CrossRef]
- Moreira, L.M.; Anjos, V.; Bell, M.J.V.; Ramos, C.A.R.; Kassab, L.R.P.; Doualan, D.J.L.; Camy, P.; Moncorgé, R. The effects of Nd2O3 concentration in the laser emission of TeO2-ZnO glasses. Opt. Mater. 2016, 58, 84–88. [Google Scholar] [CrossRef]
- de Assumpção, T.A.A.; da Silva, D.M.; Camilo, M.E.; Kassab, L.R.P.; Gomes, A.S.L.; de Araújo, C.B.; Wetter, N.U. Frequency upconversion properties of Tm3+ doped TeO2–ZnO glasses containing silver nanoparticles. J. Alloys Compd. 2012, 536, S504–S506. [Google Scholar] [CrossRef]
- Bezerra, G.S.; Ocas, L.R.; Kumada, D.K.; Martins, W.S.; Kassab, L.R.P.; Reyna, A.S. Influence of plasmonic and thermo-optical effects of silver nanoparticles on near infrared optical thermometry in Nd3+-doped TeO2–ZnO glasses. J. Lumin. 2024, 265, 120222. [Google Scholar] [CrossRef]
- Bordon, C.D.S.; Dipold, J.; Freitas, A.Z.; Wetter, N.U.; de Rossi, W.; Kassab, L.R.P. A new double-line waveguide architecture for photonic applications using fs laser writing in Nd3+ doped GeO2-PbO glasses. Opt. Mater. 2022, 129, 112495. [Google Scholar] [CrossRef]
- Bontempo, L.; Filho, S.G.D.S.; Kassab, L.R.P. Conduction and reversible memory phenomena in Au-nanoparticles-incorporated TeO2–ZnO films. Thin Solid Film. 2016, 611, 21–26. [Google Scholar] [CrossRef]
- Bomfim, F.A.; Rangel, R.C.; da Silva, D.M.; Carvalho, D.O.; Melo, E.G.; Alayo, M.I.; Kassab, L.R.P. A new fabrication process of pedestal waveguides based on metal dielectric composites of Yb3+/Er3+ codoped PbO-GeO2 thin films with gold nanoparticles. Opt. Mater. 2018, 86, 433–440. [Google Scholar] [CrossRef]
- de Oliveira, M.A.S.; de Araújo, C.B.; Messaddeq, Y. Upconversion ultraviolet random lasing in Nd3+ doped fluoroindate glass powder. Opt. Express 2011, 19, 5620–5626. [Google Scholar] [CrossRef]
- Gomes, A.S.L.; Carvalho, M.T.; Dominguez, C.T.; de Araújo, C.B.; Prasad, P.N. Direct three-photon excitation of upconversion random laser emission in a weakly scattering organic colloidal system. Opt. Express 2014, 22, 14305–14310. [Google Scholar] [CrossRef]
- von der Weid, J.P.; Correia, M.M.; Tovar, P.; Gomes, A.S.L.; Margulis, W. A mode-locked random laser generating transform-limited optical pulses. Nat. Commun. 2024, 15, 177. [Google Scholar] [CrossRef]
- Câmara, J.G.; da Silva, D.M.; Kassab, L.R.P.; Silva-Neto, M.L.; Palacios, G.; de Araújo, C.B. Random lasing and replica symmetry breaking in GeO2-PbO-MgO glass–ceramics doped with neodymium. Sci. Rep. 2022, 12, 19438. [Google Scholar] [CrossRef]
- Nouri, M.; Tavoosi, M.; Alizadeh, P. Processing and optical properties of transparent GeO2-PbO-MgO-MgF2 glass-ceramics. Ceram. Int. 2016, 42, 17524–17529. [Google Scholar] [CrossRef]
- Dipold, J.; Bordon, C.D.S.; Magalhães, E.S.; Kassab, L.R.P.; Jimenez-Villar, E.; Wetter, N.U. 1337 nm Emission of a Nd3+-Doped TZA Glass Random Laser. Nanomaterials 2023, 13, 1972. [Google Scholar] [CrossRef] [PubMed]
- Câmara, J.G.; da Silva, D.M.; Kassab, L.R.P.; de Araújo, C.B. Random laser emission from neodymium doped alumina lead–germanate glass powder. Appl. Opt. 2023, 62, C59–C63. [Google Scholar] [CrossRef] [PubMed]
- Moura, A.L.; Maia, L.J.Q.; Jerez, V.; Gomes, A.S.L.; de Araújo, C.B. Random laser in Nd:YBO3 nanocrystalline powders presenting luminescence concentration quenching. J. Lumin. 2019, 214, 116543. [Google Scholar] [CrossRef]
- Yamane, M.; Asahara, Y. Glasses for Photonics; Cambridge University Press: Cambridge, CA, USA, 2000. [Google Scholar]
- Gunji, R.M.; Mattos, G.R.S.; Bordon, C.D.S.; Garcia, J.A.M.; Gómez-Malagón, L.A.; Kassab, L.R.P. Influence of the TiO2 nanoparticles on upconversion luminescence of Er3+-doped and Er3+/Yb3+-codoped GeO2-PbO glasses. J. Lumin. 2022, 251, 119240. [Google Scholar] [CrossRef]
- Camilo, M.E.; Silva, E.D.O.; Kassab, L.R.; Garcia, J.A.; De Araújo, C.B. White light generation controlled by changing the concentration of silver nanoparticles hosted by Ho3+/Tm3+/Yb3+ doped GeO2–PbO glasses. J. Alloys Comp. 2015, 644, 155–158. [Google Scholar] [CrossRef]
- Abo-Mosallam, H.A.; Mahdy, E.A. The influence of MgO on the crystallization behaviour and properties of SrO-rich phosphosilicate glasses. Ceram. Int. 2020, 46, 12009–12014. [Google Scholar] [CrossRef]
- Câmara, J.G.; da Silva, D.M.; Kassab, L.R.P.; Palacios, G.; de Araújo, C.B. Upconversion random lasing in Er3+/Yb3+co-doped germanate-lead-magnesium glass-ceramics. Opt. Mater. 2024, 157, 116387. [Google Scholar] [CrossRef]
- Câmara, J.G.; da Silva, D.M.; Kassab, L.R.P.; de Araújo, C.B.; Gomes, A.S.L. Random laser emission from neodymium doped zinc tellurite glass-powder presenting luminescence concentration quenching. J. Lumin. 2021, 233, 117936. [Google Scholar] [CrossRef]
- Shi, X.Y.; Chang, Q.; Tong, J.H.; Feng, Y.J.; Wang, Z.N.; Liu, D.H. Temporal profiles for measuring threshold of random lasers pumped by ns pulses. Sci. Rep. 2017, 7, 5325. [Google Scholar] [CrossRef]
- Gomes, A.S.L.; Moura, A.L.; de Araújo, C.B.; Raposo, E.P. (Eds.) Lévy Statistics and Spin Glass Behavior in Random Lasers; Jenny Stanford Publishing Ltd.: Singapore, 2023; ISBN 978-981-4968-55-3. [Google Scholar]
- Coronel, E.; Das, A.; González, I.R.R.; Gomes, A.S.L.; Margulis, W.; von der Weid, J.P.; Raposo, E.P. Evaluation of Pearson correlation coefficient and Parisi parameter of replica symmetry breaking in a hybrid electronically addressable random fiber laser. Opt. Express 2021, 29, 24422–24433. [Google Scholar] [CrossRef]
- Ghofraniha, N.; Viola, I.; Di Maria, F.; Barbarella, G.; Gigli, G.; Leuzzi, L.; Conti, C. Experimental evidence of replica symmetry breaking in random lasers. Nat. Commun. 2015, 6, 6058. [Google Scholar] [CrossRef] [PubMed]
- Mézard, M.; Parisi, G.; Virasoro, M.A. Spin Glass Theory and Beyond: An Introduction to the Replica Method and Its Applications; World Scientific Publishing: Singapore, 1987. [Google Scholar]
- Parisi, G. Nobel Lecture: Multiple Equilibria. Rev. Mod. Phys. 2023, 95, 030501. [Google Scholar] [CrossRef]
- Gomes, A.S.L.; Raposo, E.P.; Moura, A.L.; Fewo, S.I.; Pincheira, P.I.R.; Jerez, V.; Maia, L.J.Q.; de Araújo, C.B. Observation of Lévy distribution and replica symmetry breaking in random lasers from a single set of measurements. Sci. Rep. 2016, 6, 27987. [Google Scholar] [CrossRef] [PubMed]
- de Araújo, C.B.; Gomes, A.S.L.; Raposo, E.P. Lévy statistics and the Glassy Behavior of Light in Random Fiber Lasers. Appl. Sci. 2017, 7, 644. [Google Scholar] [CrossRef]
- Rivera, V.A.G.; Ferri, F.A.; Nunes, L.A.O.; Marega, E. White light generation via upconversion and blue tone in Er3+/Tm3+/Yb3+-doped zinc-tellurite glasses. Opt. Mater. 2017, 67, 25–31. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silva, D.M.; Câmara, J.G.; Wetter, N.U.; Dipold, J.; Kassab, L.R.P.; de Araújo, C.B. Random Lasers Based on Tellurite and Germanate Glasses and Glass-Ceramics Doped with Rare-Earth Ions. Micromachines 2025, 16, 550. https://doi.org/10.3390/mi16050550
da Silva DM, Câmara JG, Wetter NU, Dipold J, Kassab LRP, de Araújo CB. Random Lasers Based on Tellurite and Germanate Glasses and Glass-Ceramics Doped with Rare-Earth Ions. Micromachines. 2025; 16(5):550. https://doi.org/10.3390/mi16050550
Chicago/Turabian Styleda Silva, Davinson M., Josivanir G. Câmara, Niklaus U. Wetter, Jessica Dipold, Luciana R. P. Kassab, and Cid B. de Araújo. 2025. "Random Lasers Based on Tellurite and Germanate Glasses and Glass-Ceramics Doped with Rare-Earth Ions" Micromachines 16, no. 5: 550. https://doi.org/10.3390/mi16050550
APA Styleda Silva, D. M., Câmara, J. G., Wetter, N. U., Dipold, J., Kassab, L. R. P., & de Araújo, C. B. (2025). Random Lasers Based on Tellurite and Germanate Glasses and Glass-Ceramics Doped with Rare-Earth Ions. Micromachines, 16(5), 550. https://doi.org/10.3390/mi16050550









