Thermal Error Prediction in High-Power Grinding Motorized Spindles for Computer Numerical Control Machining Based on Data-Driven Methods
Abstract
1. Introduction
2. Mechanical Structure and Heat Source Calculation of the Motorized Spindle
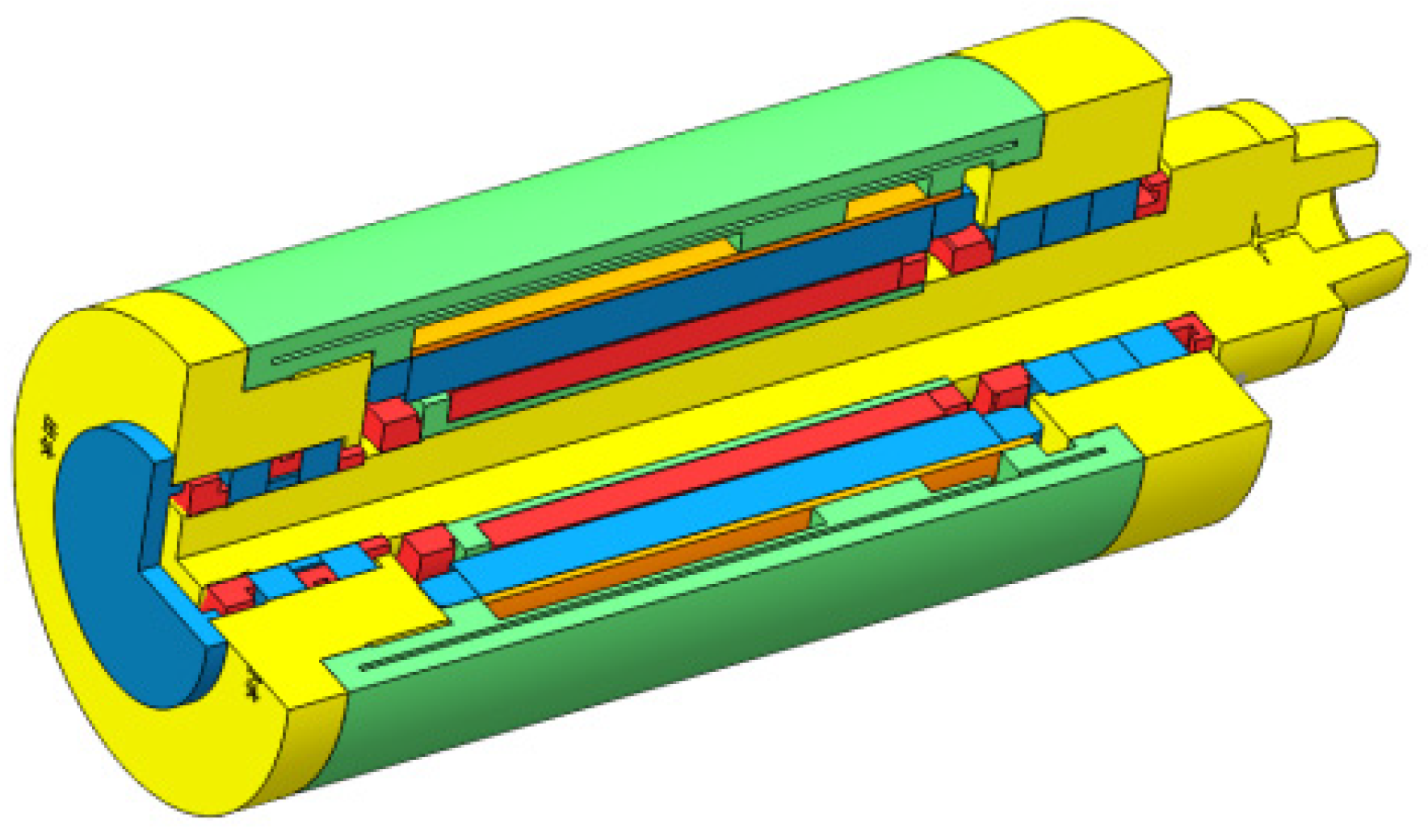
2.1. Structural Characteristics of the Motorized Spindle
2.2. Analysis and Calculation of Heat Generation in the Motorized Spindle
2.2.1. Analysis and Calculation of Motor Heat Generation
2.2.2. Analysis and Calculation of Bearing Heat Generation
2.3. Analysis and Calculation of Boundary Conditions in the Motorized Spindle
2.3.1. Convective Heat Transfer Between the Stator and the Coolant
2.3.2. Convective Heat Transfer Between the Spindle Housing and the Air
2.3.3. Heat Transfer in the Air Gap Between the Motor Stator and Motor Rotor
2.4. Simulation of the Thermal Characteristics of the Motorized Spindle
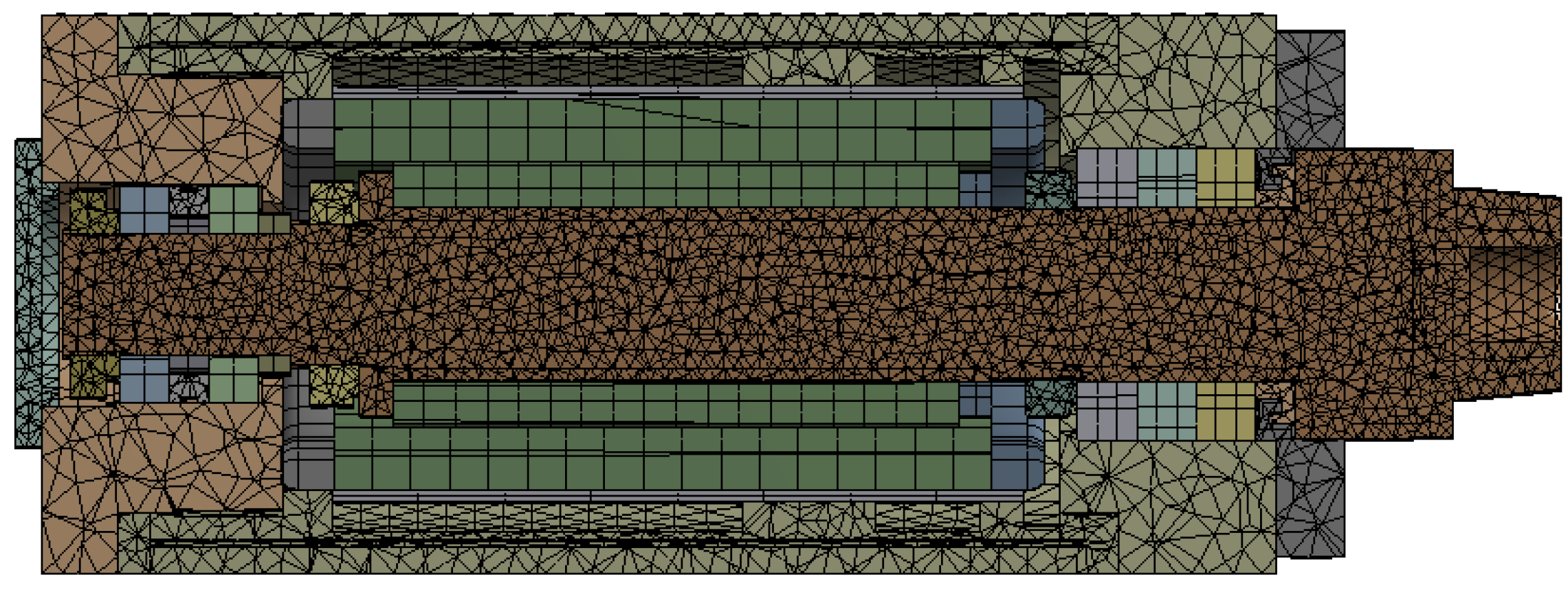
2.4.1. Establishment of a Finite Element Model
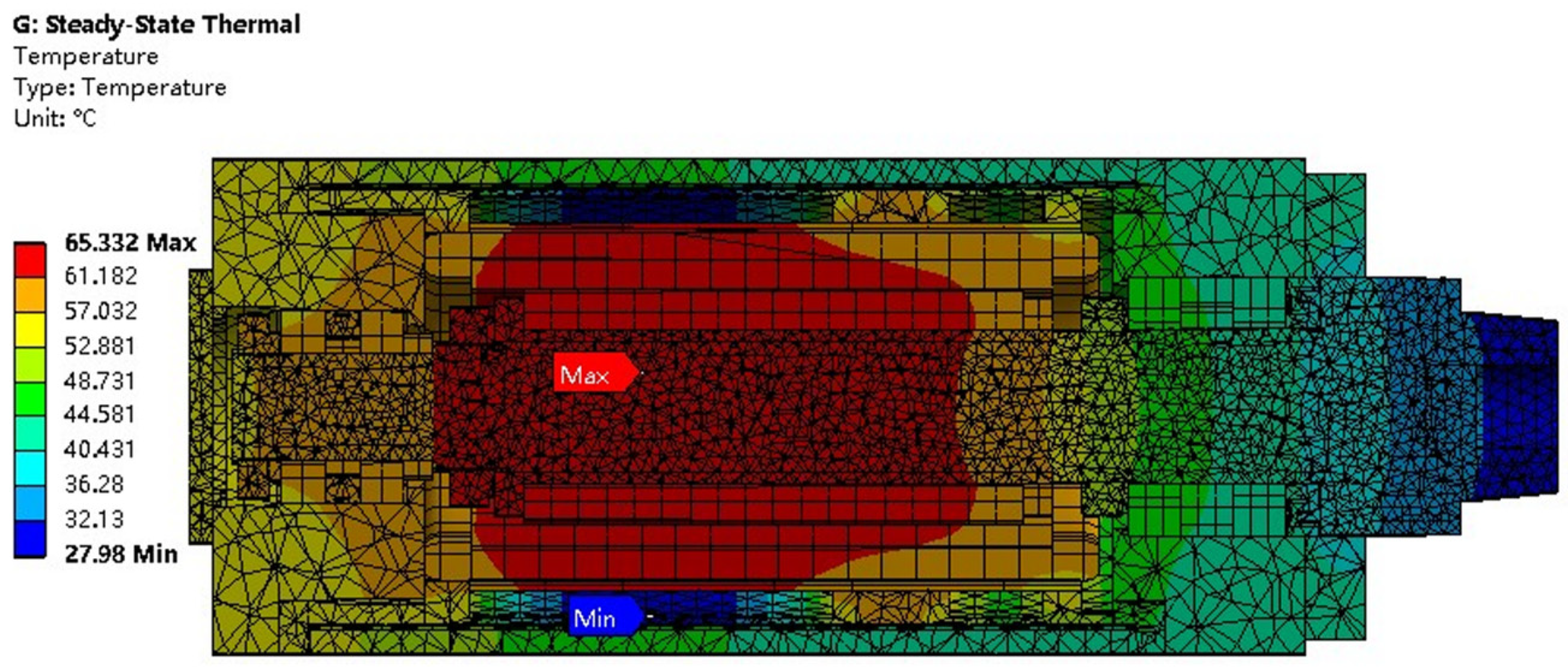
2.4.2. Steady-State Thermal Analysis of the Motorized Spindle
2.4.3. Transient Thermal Analysis of the Motorized Spindle
2.4.4. Thermal Deformation Analysis of the Motorized Spindle
3. Experiments of Thermal Error
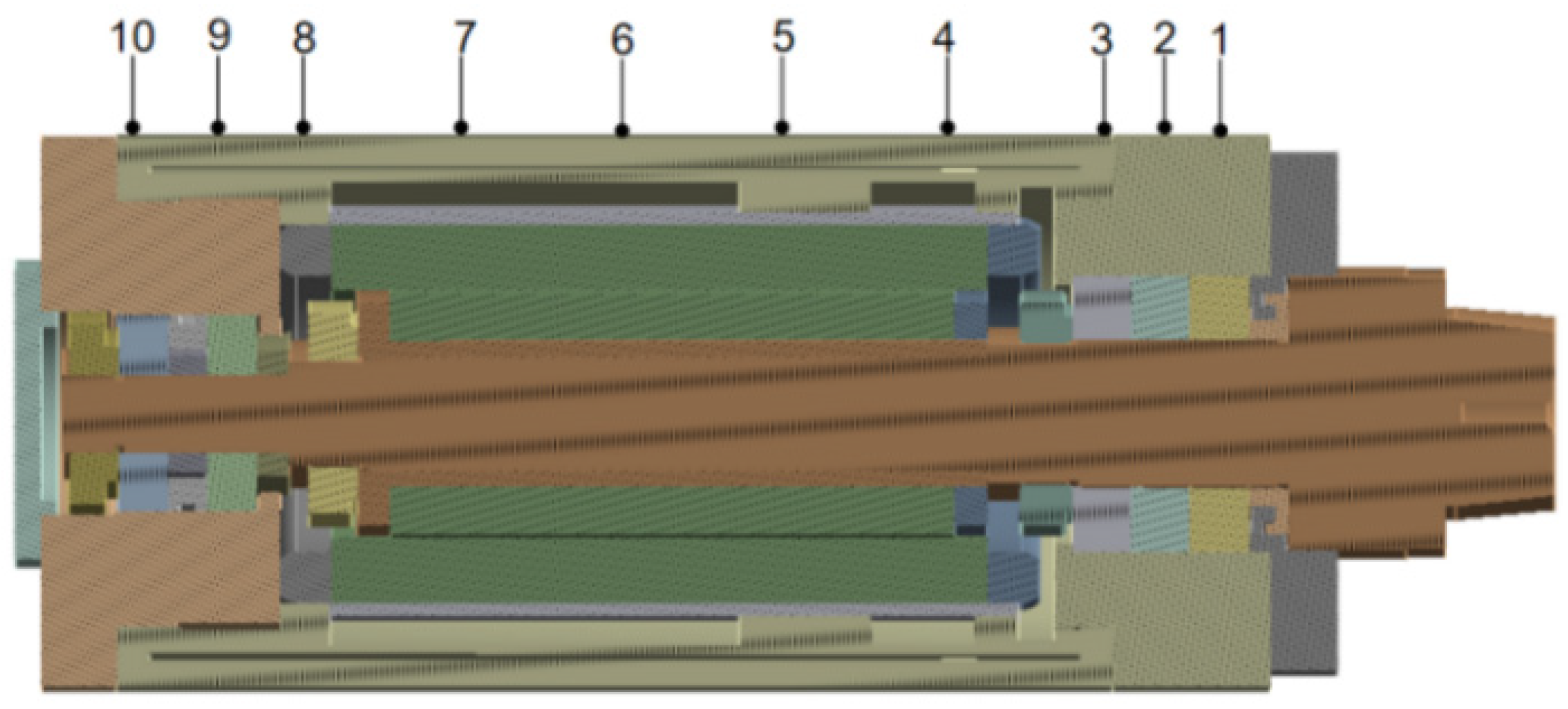
3.1. Arrangement of Temperature and Displacement Sensors
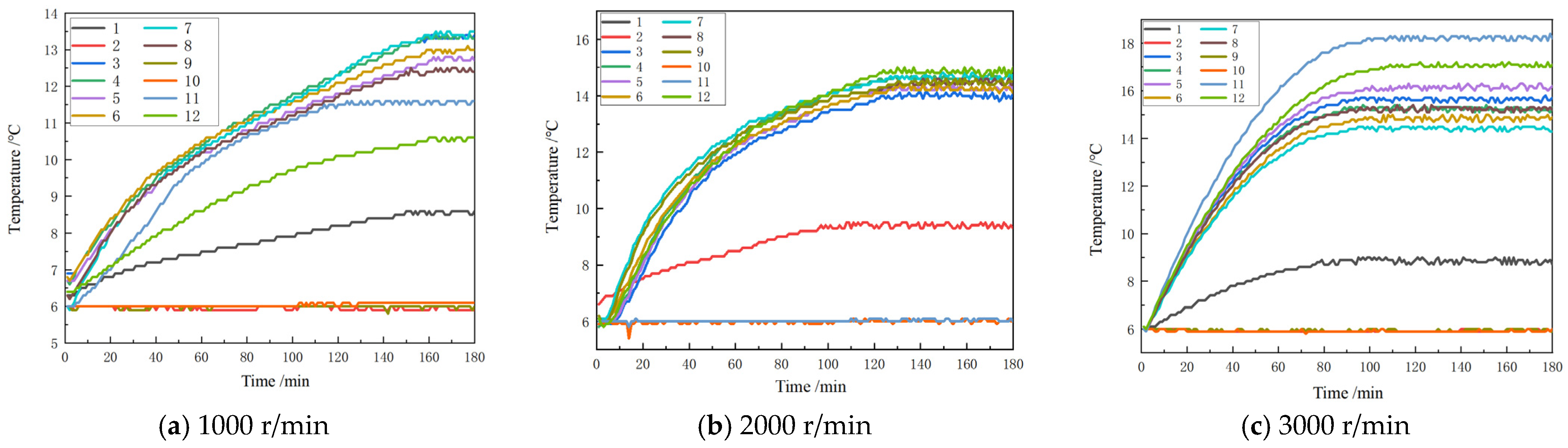
3.2. Experimental Data Collection and Analysis
4. Modeling and Verification of the Thermal Error Based on Ensemble Learning
4.1. Principle of the Ensemble Learning Thermal Characteristic Prediction Model
4.1.1. Foundational Concepts
- (1)
- Multiple linear regression
- (2)
- BP neural network
- (3)
- RBF neural network
4.1.2. Principle of an Ensemble Learning Model
4.2. Thermal Error Prediction and Validation of Ensemble Learning Models
4.2.1. Thermal Error Prediction of an Ensemble Learning Model
4.2.2. Model Accuracy Verification
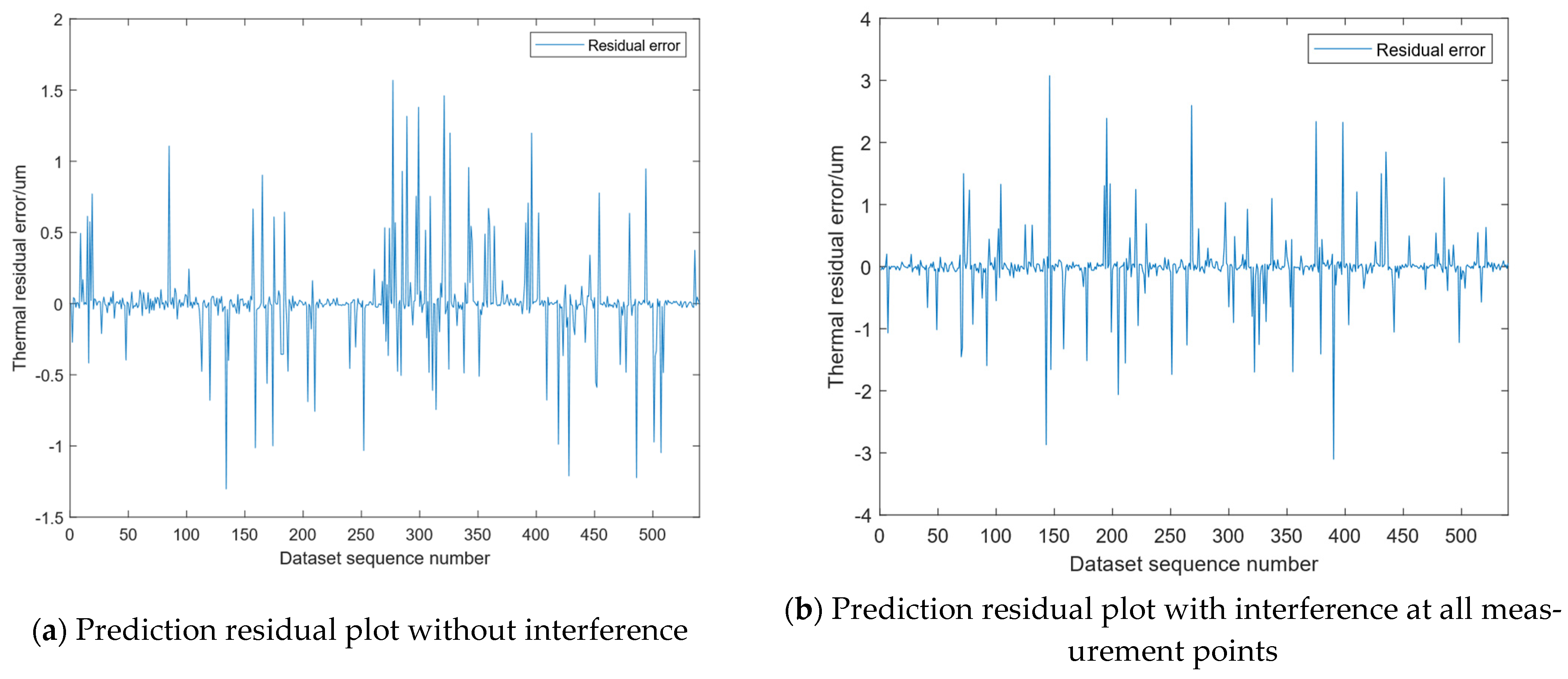
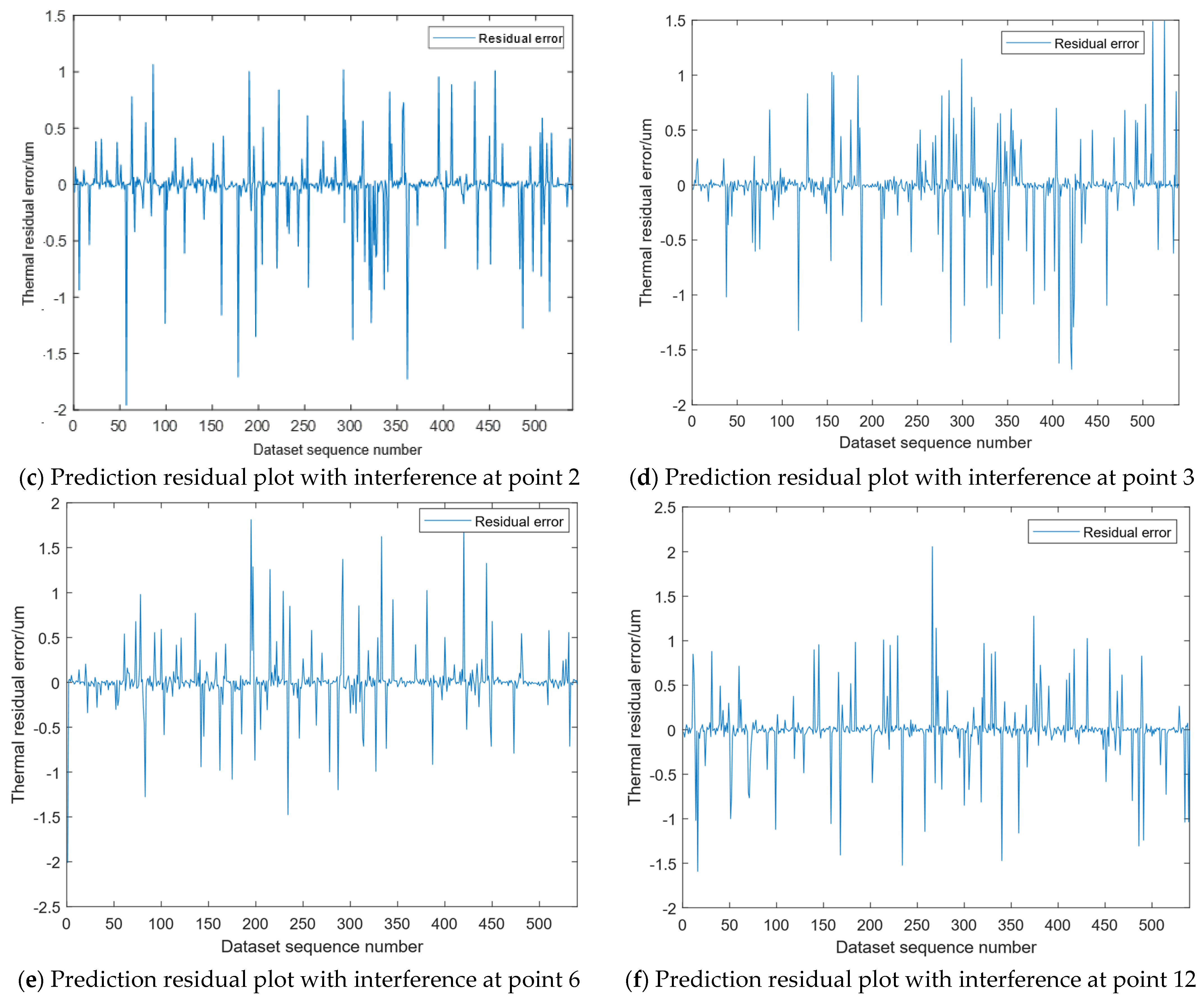
4.2.3. Testing Model Robustness
4.3. Comparative Modeling Methods
5. Conclusions
- (1)
- Three different types of commonly used regression algorithms are selected as weak learners for ensemble learning algorithms, and their modeling principles and implementation steps are introduced. The three models are trained using datasets, and the predicted values from the three trained models are combined and input into the metamodel as input datasets. The Stacking ensemble learning algorithm is used to integrate different weak learners to form a new ensemble learning model.
- (2)
- The training of the ensemble learning model is complete, and the accuracy of the model is verified through a validation set. The results show that the model has high accuracy, the strong robustness of ensemble learning, and better prediction accuracy than weak learners. The proposed ensemble learning model can significantly improve predictive performance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdulshahed, A.M.; Longstaff, A.P.; Fletcher, S.; Myers, A. Thermal error modelling of machine tools based on ANFIS with fuzzy c-means clustering using a thermal imaging camera. Appl. Math. Model. 2015, 39, 1837–1852. [Google Scholar] [CrossRef]
- Mayr, J.; Jedrzejewski, J.; Uhlmann, E.; Donmez, M.A.; Knapp, W.; Härtig, F.; Wendt, K.; Moriwaki, T.; Shore, P.; Schmitt, R. Thermal Issues in Machine Tools. CIRP Ann. 2012, 61, 771–791. [Google Scholar] [CrossRef]
- Jiang, Z.Y.; Huang, X.Z.; Chang, M.X.; Li, C.; Ge, Y. Thermal error prediction and reliability sensitivity analysis of motorized spindle based on Kriging model. Eng. Fail. Anal. 2021, 127, 105558. [Google Scholar] [CrossRef]
- Sun, S.W.; Qiao, Y.F.; Gao, Z.T.; Wang, J.J.; Bian, Y.C. A thermal error prediction model of the motorized spindles based on ABHHO-LSSVM. Int. J. Adv. Manuf. Technol. 2023, 127, 2257–2271. [Google Scholar] [CrossRef]
- Dai, Y.; Tao, X.S.; Xuan, L.Y.; Qu, H.; Wang, G. Thermal error prediction model of a motorized spindle considering variable preload. Int. J. Adv. Manuf. Technol. 2023, 121, 4745–4756. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, Y.X.; Meng, Q.Y.; Xin, X.C.; Ming, S.S. Improved thermal resistance network model of motorized spindle system considering temperature variation of cooling system. Adv. Manuf. 2018, 6, 384–400. [Google Scholar] [CrossRef]
- Zhou, C.J.; Qu, Z.F.; Hu, B.; Li, S.B. Thermal network model and experimental validation for a motorized spindle including thermal–mechanical coupling effect. Int. J. Adv. Manuf. Technol. 2021, 115, 487–501. [Google Scholar] [CrossRef]
- Yin, Q.; Tan, F.; Chen, H.X.; Yin, G.F. Spindle thermal error modeling based on selective ensemble BP neural networks. Int. J. Adv. Manuf. Technol. 2019, 101, 1699–1713. [Google Scholar] [CrossRef]
- Li, Z.L.; Zhu, W.M.; Zhu, B.; Wang, B.D.; Wang, Q.H. Thermal error modeling of motorized spindle based on particle swarm optimization-SVM neural network. Int. J. Adv. Manuf. Technol. 2022, 121, 7215–7227. [Google Scholar] [CrossRef]
- Li, B.; Tian, X.T.; Zhang, M. Thermal error modeling of machine tool spindle based on the improved algorithm optimized BP neural network. Int. J. Adv. Manuf. Technol. 2019, 105, 1497–1505. [Google Scholar] [CrossRef]
- Li, Z.L.; Wang, Q.H.; Zhu, B.; Wang, B.D.; Zhu, W.M. Thermal error modeling of high-speed motorized spindle based on Aquila Optimizer optimized least squares support vector machine. Case Stud. Therm. Eng. 2022, 39, 102432. [Google Scholar] [CrossRef]
- Li, Z.L.; Wang, B.D.; Zhu, B.; Wang, Q.H.; Zhu, W.M. Thermal error modeling of electrical spindle based on optimized ELM with marine predator algorithm. Case Stud. Therm. Eng. 2022, 38, 102326. [Google Scholar] [CrossRef]
- Wu, C.Y.; Xiang, S.T.; Xiang, W.S. Spindle thermal error prediction approach based on thermal infrared images: A deep learning method. J. Manuf. Syst. 2021, 59, 67–80. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Wang, L.P.; Li, X.K. Modeling for CNC Machine Tool Thermal Error Based on Genetic Algorithm Optimization Wavelet Neural Networks. J. Mech. Eng. 2019, 55, 215–220. [Google Scholar] [CrossRef]
- Abdulshahed, A.M.; Longstaff, A.P.; Fletcher, S. The application of ANFIS prediction models for thermal error compensation on CNC machine tools. Appl. Soft Comput. 2022, 27, 158–168. [Google Scholar] [CrossRef]
- Zimmermann, N.; Buechi, T.; Mayr, J.; Wegener, K. Self-optimizing thermal error compensation models with adaptive inputs using Group-LASSO for ARX-models. J. Manuf. Syst. 2022, 64, 615–625. [Google Scholar] [CrossRef]
- Li, Z.L.; Zhu, B.; Dai, Y.; Zhu, W.M.; Wang, Q.H.; Wang, B.D. Thermal error modeling of motorized spindle based on Elman neural network optimized by sparrow search algorithm. Int. J. Adv. Manuf. Technol. 2022, 121, 349–366. [Google Scholar] [CrossRef]
- Guo, Q.; Fan, S.; Xu, R.; Cheng, X.; Zhao, G.Y.; Yang, J.G. Spindle Thermal Error Optimization Modeling of a Five-axis Machine Tool. Chin. J. Mech. Eng. 2017, 30, 746–753. [Google Scholar] [CrossRef]
- Bao, L.; Xu, Y.L.; Zhou, Q.; Guo, P.; Guo, X.X.; Jiang, H. Thermal Error Modeling of Numerical Control Machine Based on Beetle Antennae Search Back-propagation Neural Networks. Int. J. Comput. Int. Syst. 2023, 16, 84. [Google Scholar] [CrossRef]
- Fu, G.Q.; Zhou, L.F.; Lei, G.Q.; Lu, C.J.; Deng, X.L.; Xie, L.F. A universal ensemble temperature-sensitive point combination model for spindle thermal error modeling. Int. J. Adv. Manuf. Technol. 2022, 119, 3377–3393. [Google Scholar] [CrossRef]
- Fan, J.W.; Wang, P.T.; Tao, H.H.; Pan, R. A thermal deformation prediction method for grinding machine’ spindle. Int. J. Adv. Manuf. Technol. 2022, 118, 1125–1139. [Google Scholar] [CrossRef]
- Cheng, Y.N.; Zhang, X.P.; Zhang, G.X.; Jiang, W.Q.; Li, B.W. Thermal error analysis and modeling for high-speed motorized spindles based on LSTM-CNN. Int. J. Adv. Manuf. Technol. 2023, 121, 3243–3257. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, N.; Dai, W.; Zhu, G.; Wen, J. Turbofan Engine Health Prediction Model Based on ESO-BP Neural Network. Appl. Sci. 2024, 14, 1996. [Google Scholar] [CrossRef]
- Zhong, D.F.; Zhang, G.B.; Zhang, Y.C.; Liang, G.A.; Huang, Y.M. Prediction of Industrial Boiler Energy Efficiency Using Stacking Ensemble Learning. J. Phys. Conf. Ser. 2023, 2562, 012068. [Google Scholar] [CrossRef]
- Li, M.; Yan, C.; Liu, W. The network loan risk prediction model based on convolutional neural network and stacking fusion model. Appl. Soft Comput. 2021, 113, 107961. [Google Scholar] [CrossRef]
- Liu, H.; Miao, E.M.; Wei, X.Y.; Zhuang, X.D. Robust modeling method for thermal error of CNC machine tools based on ridge regression algorithm. Int. J. Mach. Tools Manuf. 2017, 113, 35–48. [Google Scholar] [CrossRef]
- Feng, Z.; Min, X.; Jiang, W.; Song, F.; Li, X. Study on thermal error modeling for CNC machine tools based on the improved radial basis function neural network. Appl. Sci. 2023, 13, 5299. [Google Scholar] [CrossRef]















| Corresponding Parts | Material | Elastic Modulus (GPa) | Density (kg/m3) | Specific Heat Capacity (J/(kg·°C)) | Poisson’s Ratio | Thermal Conductivity (W/(m·°C)) | Thermal Expansion Coefficient (°C−1) |
|---|---|---|---|---|---|---|---|
| Arbors, bearing caps, housings, etc. | 45 | 210 | 7830 | 465 | 0.265 | 49.8 | 12.2 × 10−6 |
| Motor rotor | Coppper alloy | 110 | 8300 | 385 | 0.34 | 401 | 18.3 × 10−6 |
| Motor stator | 45Cr | 200 | 7852 | 434 | 0.29 | 60.5 | 4.8 × 10−6 |
| Bearing | GCr15 | 205 | 7810 | 553 | 0.3 | 40.11 | 13.3 × 10−6 |
| Spindle Parts | Heat Generation Coefficient (W/m3) |
|---|---|
| Front bearing | 9.824 × 104 |
| Rear bearing | 1.175 × 104 |
| Motor stator | 8.633 × 105 |
| Motor rotor | 1.279 × 106 |
| Parameter | Heat Transfer Coefficient (W/(m2·°C)) |
|---|---|
| Front end of the rotor | 68.42 |
| Rear end of the rotor | 61.28 |
| Rotor head and air | 133.2 |
| Motor stator and coolant | 400.51 |
| Motorized spindle shell and air heat | 9.7 |
| Motor stator and rotor and air gap | 138.6 |
| Spindle Speed (r/min) | 1000 | 2000 | 3000 |
|---|---|---|---|
| Time (min) | 180 | 180 | 180 |
| Evaluating Indicator | R | R2 | RMSE | MAE |
|---|---|---|---|---|
| No interference | 0.9998 | 0.9996 | 0.2019 | 0.0408 |
| Interference at measurement point 2 | 0.9995 | 0.9990 | 0.6538 | 0.1264 |
| Interference at measurement point 3 | 0.9995 | 0.9989 | 0.6890 | 0.1314 |
| Interference at measurement point 6 | 0.9995 | 0.9990 | 0.6859 | 0.1301 |
| Interference at measurement point 12 | 0.9994 | 0.9989 | 0.7136 | 0.1377 |
| All measurement points have interference | 0.9975 | 0.9949 | 0.6830 | 0.2448 |
| Model | R | R2 | RMSE | MAE |
|---|---|---|---|---|
| Ensemble learning Model | 0.9975 | 0.9949 | 0.6830 | 0.2448 |
| Multiple linear regression model | 0.9823 | 0.9650 | 1.7963 | 1.4443 |
| RBF neural network model | 0.9845 | 0.9890 | 1.0062 | 0.7896 |
| BP neural network model | 0.9833 | 0.9545 | 2.0476 | 1.6087 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Li, Y.; Lin, Z.; Pan, B.; Gu, D.; Luo, H. Thermal Error Prediction in High-Power Grinding Motorized Spindles for Computer Numerical Control Machining Based on Data-Driven Methods. Micromachines 2025, 16, 563. https://doi.org/10.3390/mi16050563
Wu Q, Li Y, Lin Z, Pan B, Gu D, Luo H. Thermal Error Prediction in High-Power Grinding Motorized Spindles for Computer Numerical Control Machining Based on Data-Driven Methods. Micromachines. 2025; 16(5):563. https://doi.org/10.3390/mi16050563
Chicago/Turabian StyleWu, Quanhui, Yafeng Li, Zhengfu Lin, Baisong Pan, Dawei Gu, and Hailin Luo. 2025. "Thermal Error Prediction in High-Power Grinding Motorized Spindles for Computer Numerical Control Machining Based on Data-Driven Methods" Micromachines 16, no. 5: 563. https://doi.org/10.3390/mi16050563
APA StyleWu, Q., Li, Y., Lin, Z., Pan, B., Gu, D., & Luo, H. (2025). Thermal Error Prediction in High-Power Grinding Motorized Spindles for Computer Numerical Control Machining Based on Data-Driven Methods. Micromachines, 16(5), 563. https://doi.org/10.3390/mi16050563





