Particle and Cell Separation in Deterministic Lateral Displacement Arrays with Inverse L-Shaped Pillars
Abstract
1. Introduction
2. Simulation Method and Models
2.1. Dissipative Particle Dynamics Simulation
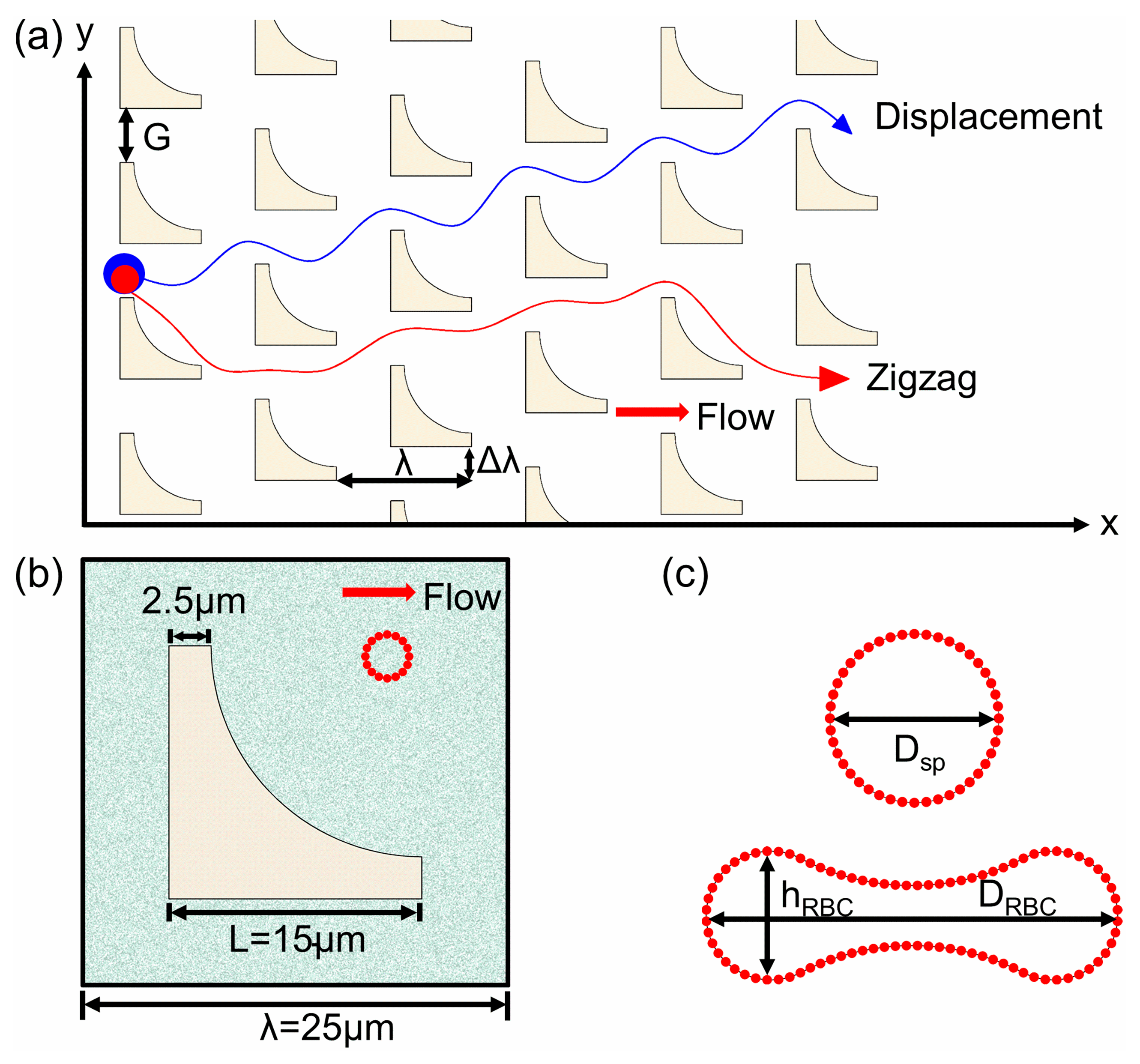
2.2. Models and Simulation Settings
3. Results and Discussion
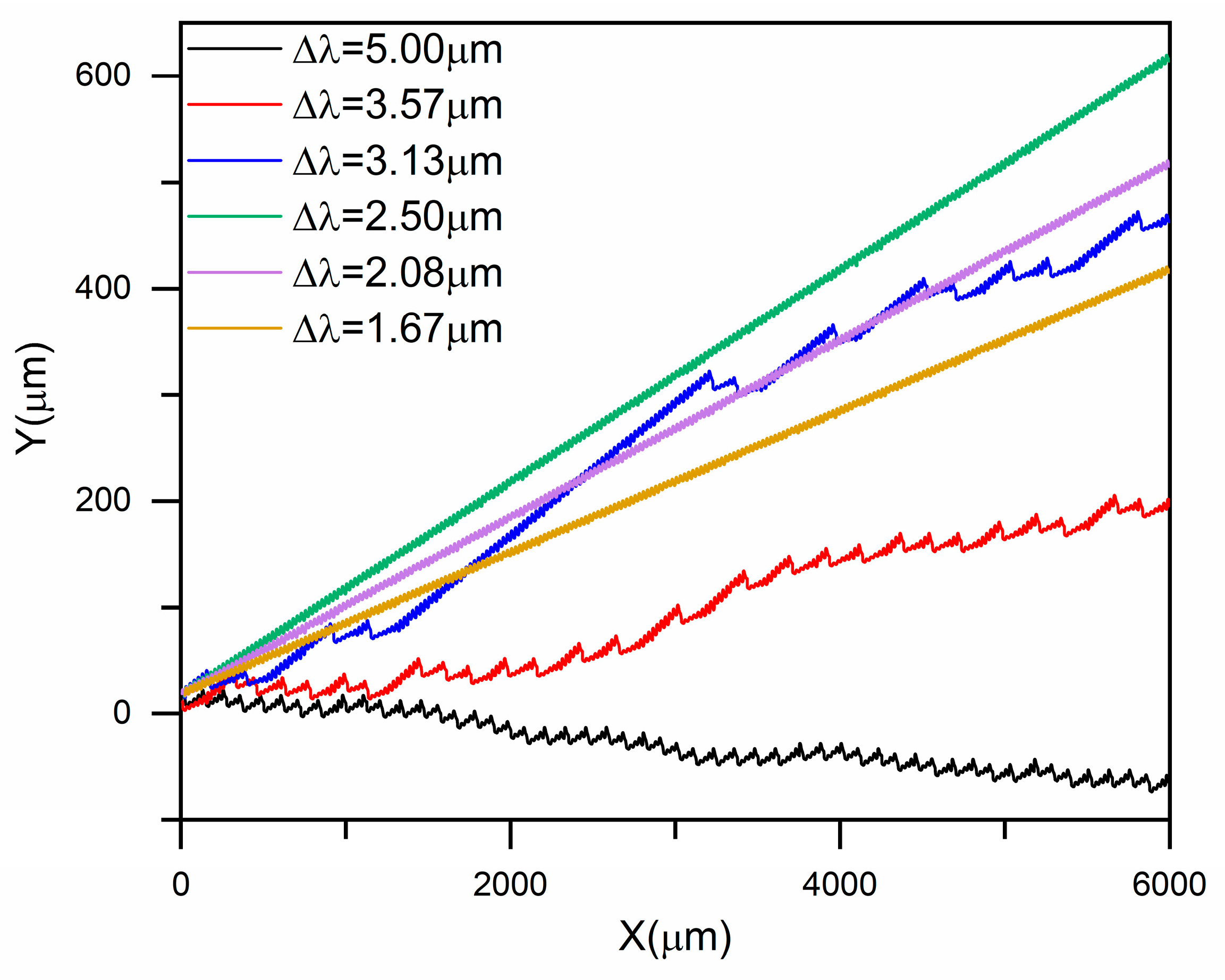
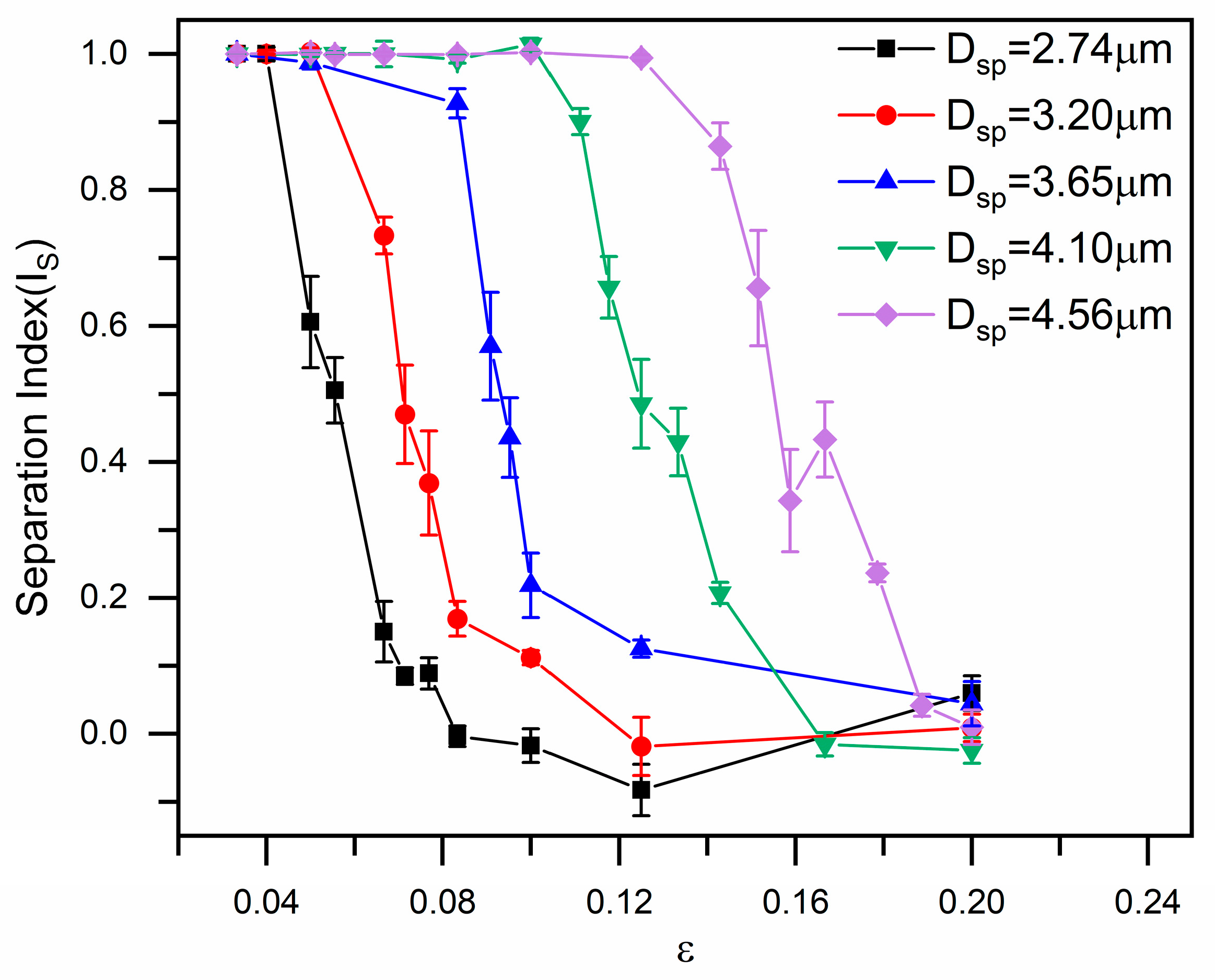
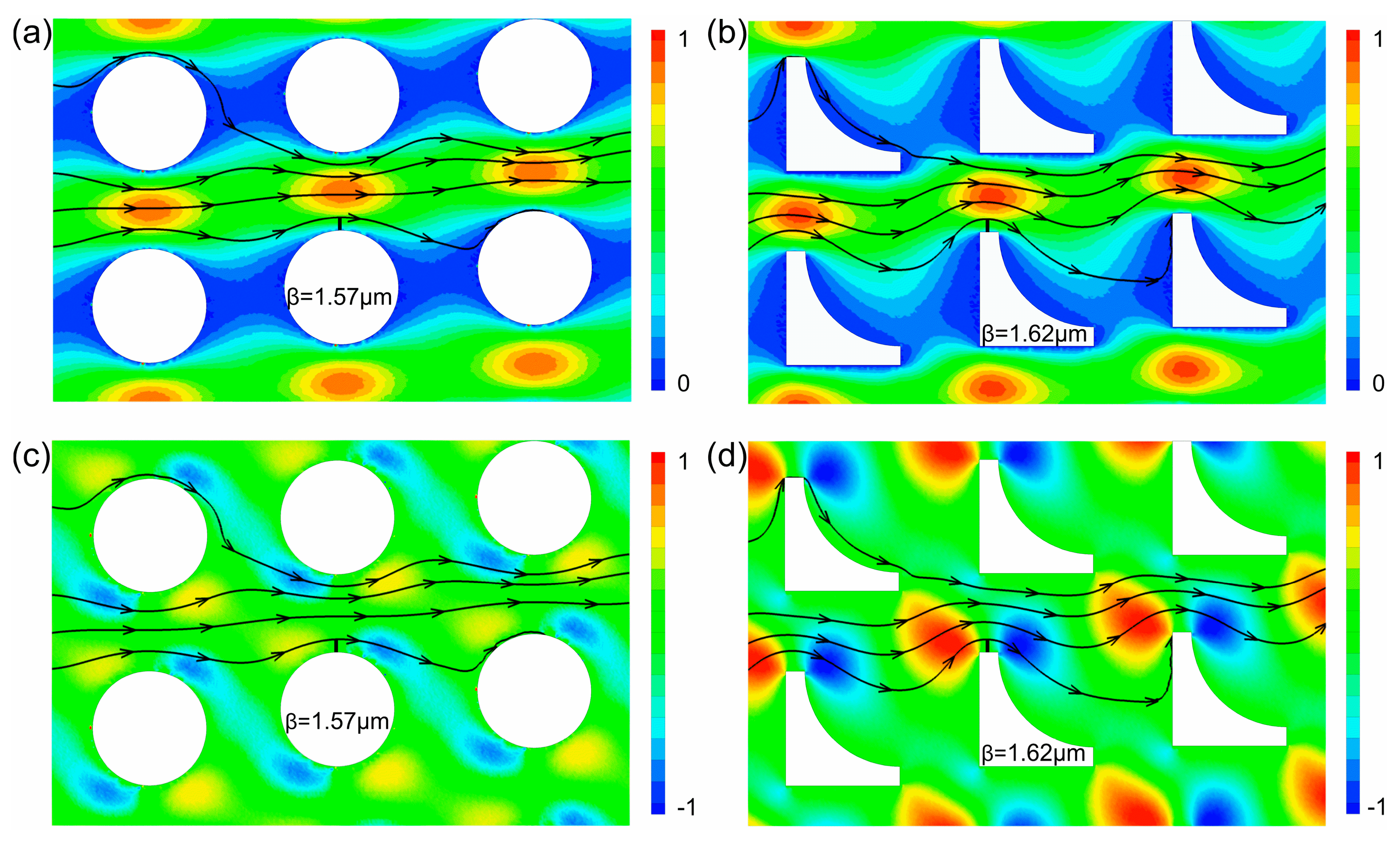
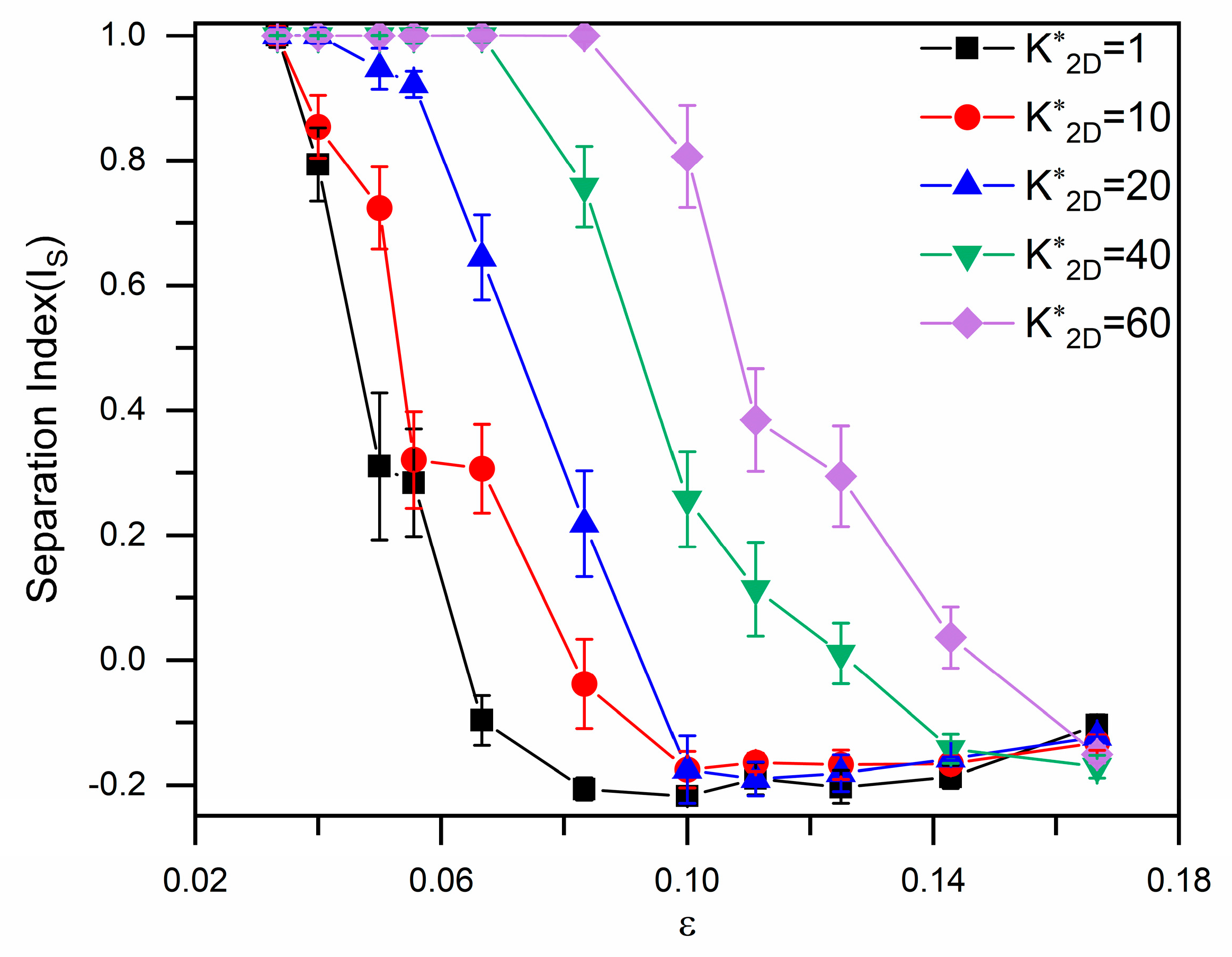
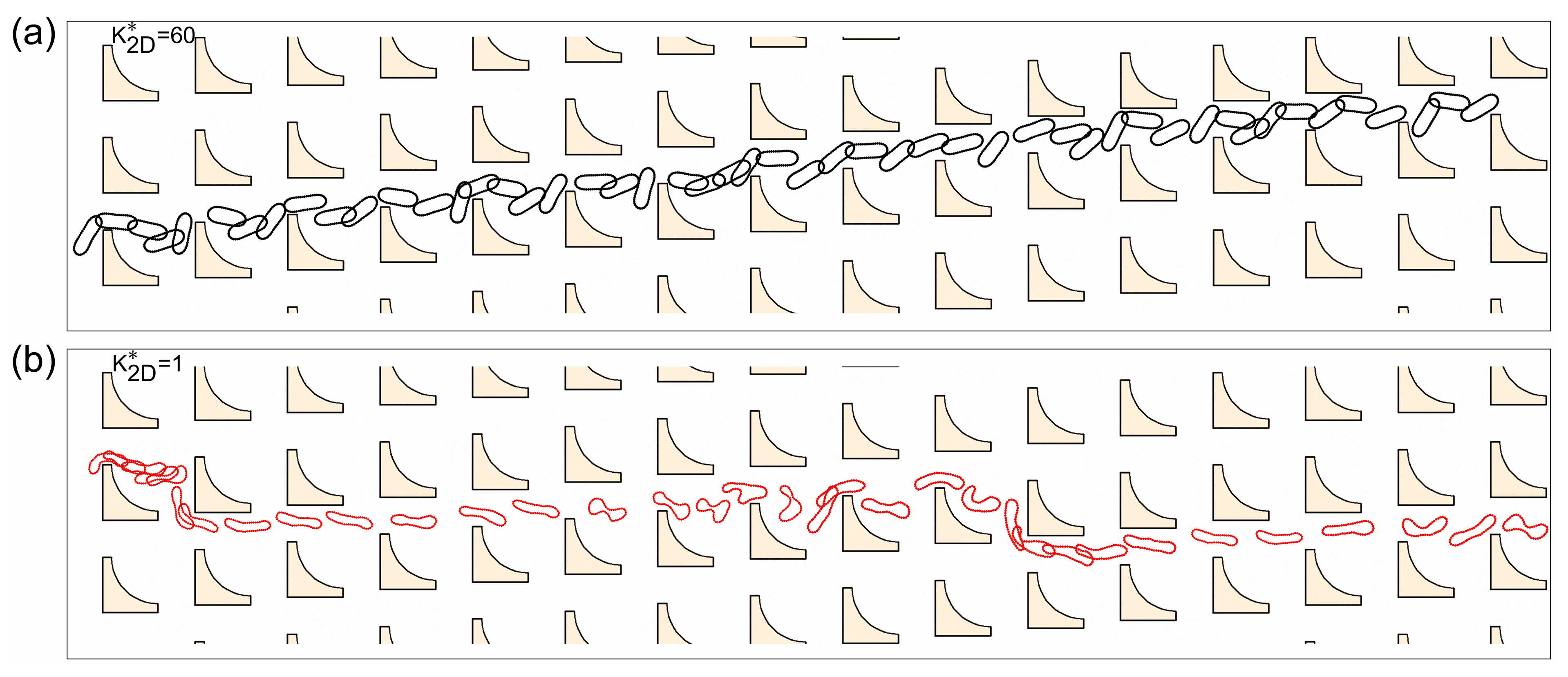
3.1. Size-Based Particle Separation
3.2. Deformability-Based Cell Sorting
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DLD | Deterministic Lateral Displacement |
| DPD | Dissipative Particle Dynamics |
| RBC | Red Blood Cell |
References
- Huang, L.R.; Cox, E.C.; Austin, R.H.; Sturm, J.C. Continuous Particle Separation Through Deterministic Lateral Displacement. Science 2004, 304, 987–990. [Google Scholar] [CrossRef]
- McGrath, J.; Jimenez, M.; Bridle, H. Deterministic lateral displacement for particle separation: A review. Lab Chip 2014, 14, 4139–4158. [Google Scholar]
- Salafi, T.; Zhang, Y.; Zhang, Y. A Review on Deterministic Lateral Displacement for Particle Separation and Detection. Nano-Micro Lett. 2019, 11, 77. [Google Scholar]
- Hochstetter, A.; Vernekar, R.; Austin, R.H.; Becker, H.; Beech, J.P.; Fedosov, D.A.; Gompper, G.; Kim, S.C.; Smith, J.T.; Stolovitzky, G.; et al. Deterministic Lateral Displacement: Challenges and Perspectives. ACS Nano 2020, 14, 10784–10795. [Google Scholar] [CrossRef] [PubMed]
- Karabacak, N.M.; Spuhler, P.S.; Fachin, F.; Lim, E.J.; Pai, V.; Ozkumur, E.; Martel, J.M.; Kojic, N.; Smith, K.; Chen, P.-i.; et al. Microfluidic, marker-free isolation of circulating tumor cells from blood samples. Nat. Protoc. 2014, 9, 694–710. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, Y.; Liang, W.; Bai, J.; Feng, H.; Fang, Z.; Tian, G.; Zhu, Y.; Zhang, H.; Wang, Y.; et al. Cascaded filter deterministic lateral displacement microchips for isolation and molecular analysis of circulating tumor cells and fusion cells. Lab Chip 2021, 21, 2881–2891. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, R.; Kumar, R.; Al-Turjman, F. A Novel Approach for Tuning of Fluidic Resistance in Deterministic Lateral Displacement Array for Enhanced Separation of Circulating Tumor Cells. Cogn. Comput. 2022, 14, 1660–1676. [Google Scholar]
- Davis, J.A.; Inglis, D.W.; Morton, K.J.; Lawrence, D.A.; Huang, L.R.; Chou, S.Y.; Sturm, J.C.; Austin, R.H. Deterministic hydrodynamics: Taking blood apart. Proc. Natl. Acad. Sci. USA 2006, 103, 14779–14784. [Google Scholar] [CrossRef]
- Beech, J.P.; Holm, S.H.; Adolfsson, K.; Tegenfeldt, J.O. Sorting cells by size, shape and deformability. Lab Chip 2012, 12, 1048–1051. [Google Scholar]
- Henry, E.; Holm, S.H.; Zhang, Z.; Beech, J.P.; Tegenfeldt, J.O.; Fedosov, D.A.; Gompper, G. Sorting cells by their dynamical properties. Sci. Rep. 2016, 6, 34375. [Google Scholar] [CrossRef]
- Holm, S.H.; Beech, J.P.; Barrett, M.P.; Tegenfeldt, J.O. Separation of parasites from human blood using deterministic lateral displacement. Lab Chip 2011, 11, 1326–1332. [Google Scholar] [PubMed]
- Holm, S.H.; Beech, J.P.; Barrett, M.P.; Tegenfeldt, J.O. Simplifying microfluidic separation devices towards field-detection of blood parasites. Anal. Methods 2016, 8, 3291–3300. [Google Scholar] [CrossRef]
- Beech, J.P.; Ho, B.D.; Garriss, G.; Oliveira, V.; Henriques-Normark, B.; Tegenfeldt, J.O. Separation of pathogenic bacteria by chain length. Anal. Chim. Acta 2018, 1000, 223–231. [Google Scholar]
- Kulrattanarak, T.; van der Sman, R.G.M.; Lubbersen, Y.S.; Schroën, C.G.P.H.; Pham, H.T.M.; Sarro, P.M.; Boom, R.M. Mixed motion in deterministic ratchets due to anisotropic permeability. J. Colloid. Interf. Sci. 2011, 354, 7–14. [Google Scholar] [CrossRef]
- Zhang, Z.; Henry, E.; Gompper, G.; Fedosov, D.A. Behavior of rigid and deformable particles in deterministic lateral displacement devices with different post shapes. J. Chem. Phys. 2015, 143, 243145. [Google Scholar] [CrossRef] [PubMed]
- Inglis, D.W.; Davis, J.A.; Austin, R.H.; Sturm, J.C. Critical particle size for fractionation by deterministic lateral displacement. Lab Chip 2006, 6, 655–658. [Google Scholar]
- Zhang, J.; Liu, H.; Tang, H.; Zhang, J.; Zhang, Z. A layout-dependent formula for the critical separation size of parallelogram-type deterministic lateral displacement arrays. Phys. Fluids 2023, 35, 052007. [Google Scholar]
- Ranjan, S.; Zeming, K.K.; Jureen, R.; Fisher, D.; Zhang, Y. DLD pillar shape design for efficient separation of spherical and non-spherical bioparticles. Lab Chip 2014, 14, 4250–4262. [Google Scholar] [CrossRef]
- Tang, H.; Niu, J.; Jin, H.; Lin, S.; Cui, D. Geometric structure design of passive label-free microfluidic systems for biological micro-object separation. Microsyst. Nanoeng. 2022, 8, 62. [Google Scholar]
- Razaulla, T.M.; Young, O.M.; Alsharhan, A.; Sochol, R.D.; Warren, R. Deterministic Lateral Displacement Using Hexagonally Arranged, Bottom-Up-Inspired Micropost Arrays. Anal. Chem. 2022, 94, 1949–1957. [Google Scholar] [CrossRef]
- Al-Fandi, M.; Al-Rousan, M.; Jaradat, M.A.K.; Al-Ebbini, L. New design for the separation of microorganisms using microfluidic deterministic lateral displacement. Robot. Comput.-Integr. Manuf. 2011, 27, 237–244. [Google Scholar]
- Ahasan, K.; Landry, C.M.; Chen, X.; Kim, J.-H. Effect of angle-of-attacks on deterministic lateral displacement (DLD) with symmetric airfoil pillars. Biomed. Microdevices 2020, 22, 42. [Google Scholar] [PubMed]
- Zeming, K.K.; Ranjan, S.; Zhang, Y. Rotational separation of non-spherical bioparticles using I-shaped pillar arrays in a microfluidic device. Nat. Commun. 2013, 4, 1625. [Google Scholar]
- Zhang, Z.; Chien, W.; Henry, E.; Fedosov, D.A.; Gompper, G. Sharp-edged geometric obstacles in microfluidics promote deformability-based sorting of cells. Phys. Rev. Fluids 2019, 4, 024201. [Google Scholar]
- Zeming, K.K.; Sato, Y.; Yin, L.; Huang, N.-J.; Wong, L.H.; Loo, H.L.; Lim, Y.B.; Lim, C.T.; Chen, J.; Preiser, P.R.; et al. Microfluidic label-free bioprocessing of human reticulocytes from erythroid culture. Lab Chip 2020, 20, 3445–3460. [Google Scholar]
- Zeming, K.K.; Vernekar, R.; Chua, M.T.; Quek, K.Y.; Sutton, G.; Kruger, T.; Kuan, W.S.; Han, J. Label-Free Biophysical Markers from Whole Blood Microfluidic Immune Profiling Reveal Severe Immune Response Signatures. Small 2021, 17, 2006123. [Google Scholar]
- Tan Kwan Zen, N.; Zeming, K.K.; Teo, K.L.; Loberas, M.; Lee, J.; Goh, C.R.; Yang, D.H.; Oh, S.; Hui Hoi Po, J.; Cool, S.M.; et al. Scalable mesenchymal stem cell enrichment from bone marrow aspirate using deterministic lateral displacement (DLD) microfluidic sorting. Lab Chip 2023, 23, 4313–4323. [Google Scholar]
- Espanol, P.; Warren, P.B. Perspective: Dissipative particle dynamics. J. Chem. Phys. 2017, 146, 150901. [Google Scholar]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, H.; Zhang, J.; Zhang, Z. Mesoscopic simulation of multi-scheme particle separation in deterministic lateral displacement devices using two-piece hybrid pillars. J. Chromatogr. A 2023, 1711, 464434. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Zhang, F.; Fan, Z.; Zhang, C.; Zhang, Z. Particle and Cell Separation in Deterministic Lateral Displacement Arrays with Inverse L-Shaped Pillars. Micromachines 2025, 16, 546. https://doi.org/10.3390/mi16050546
Jiang H, Zhang F, Fan Z, Zhang C, Zhang Z. Particle and Cell Separation in Deterministic Lateral Displacement Arrays with Inverse L-Shaped Pillars. Micromachines. 2025; 16(5):546. https://doi.org/10.3390/mi16050546
Chicago/Turabian StyleJiang, Hao, Fengyang Zhang, Zhou Fan, Chundong Zhang, and Zunmin Zhang. 2025. "Particle and Cell Separation in Deterministic Lateral Displacement Arrays with Inverse L-Shaped Pillars" Micromachines 16, no. 5: 546. https://doi.org/10.3390/mi16050546
APA StyleJiang, H., Zhang, F., Fan, Z., Zhang, C., & Zhang, Z. (2025). Particle and Cell Separation in Deterministic Lateral Displacement Arrays with Inverse L-Shaped Pillars. Micromachines, 16(5), 546. https://doi.org/10.3390/mi16050546





