Design, Analysis, and Manufacturing of Diffractive Achromatic Optical Systems
Abstract
1. Introduction
2. Principles and Design Methods
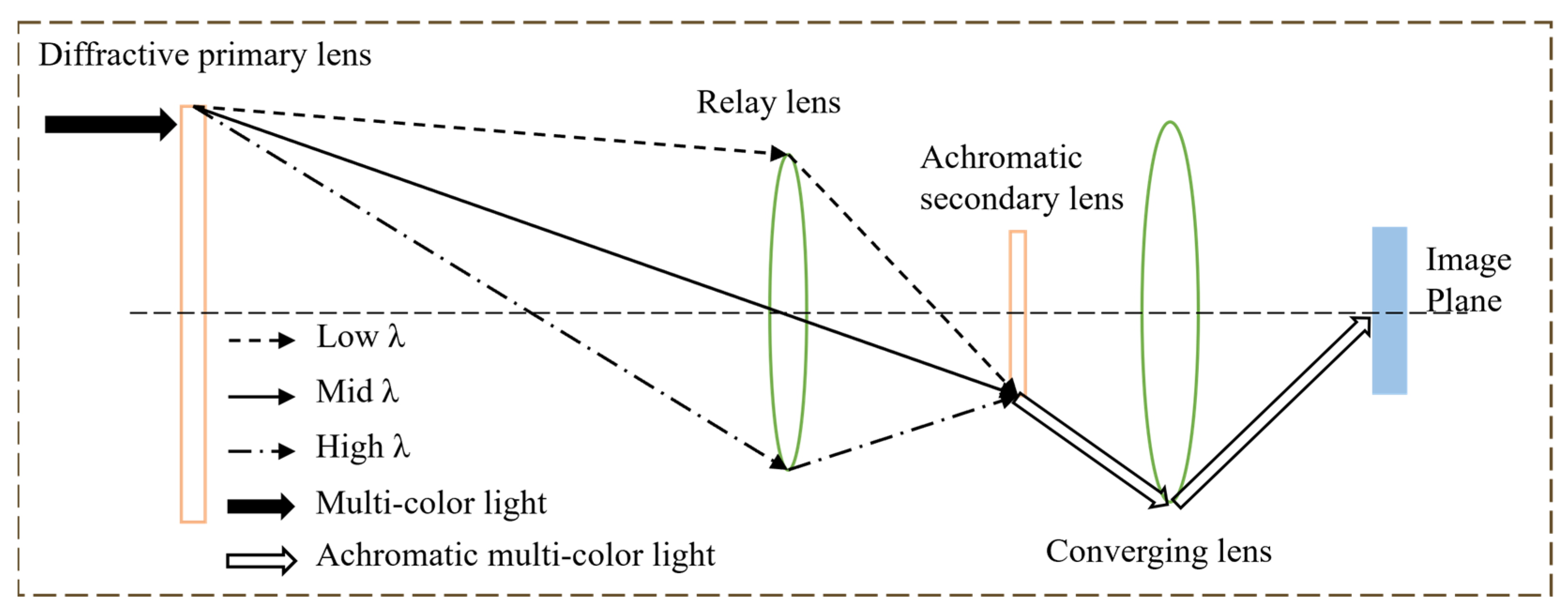
2.1. Principle of Schupmann Achromatic Model
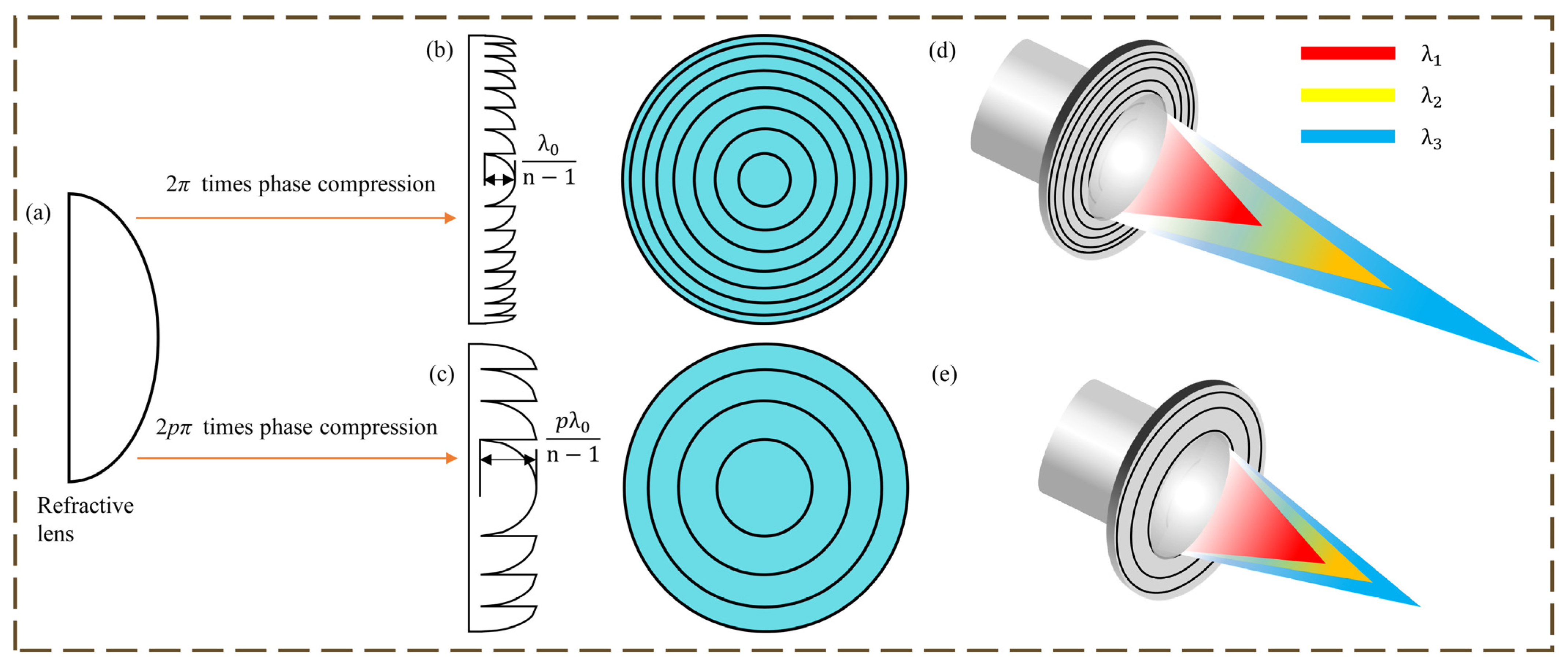
2.2. Principles of DOE and HDOE
2.3. Methodology for the Design of Broad-Band Diffractive Imaging Optical Systems
3. Optical Design and Experimentation
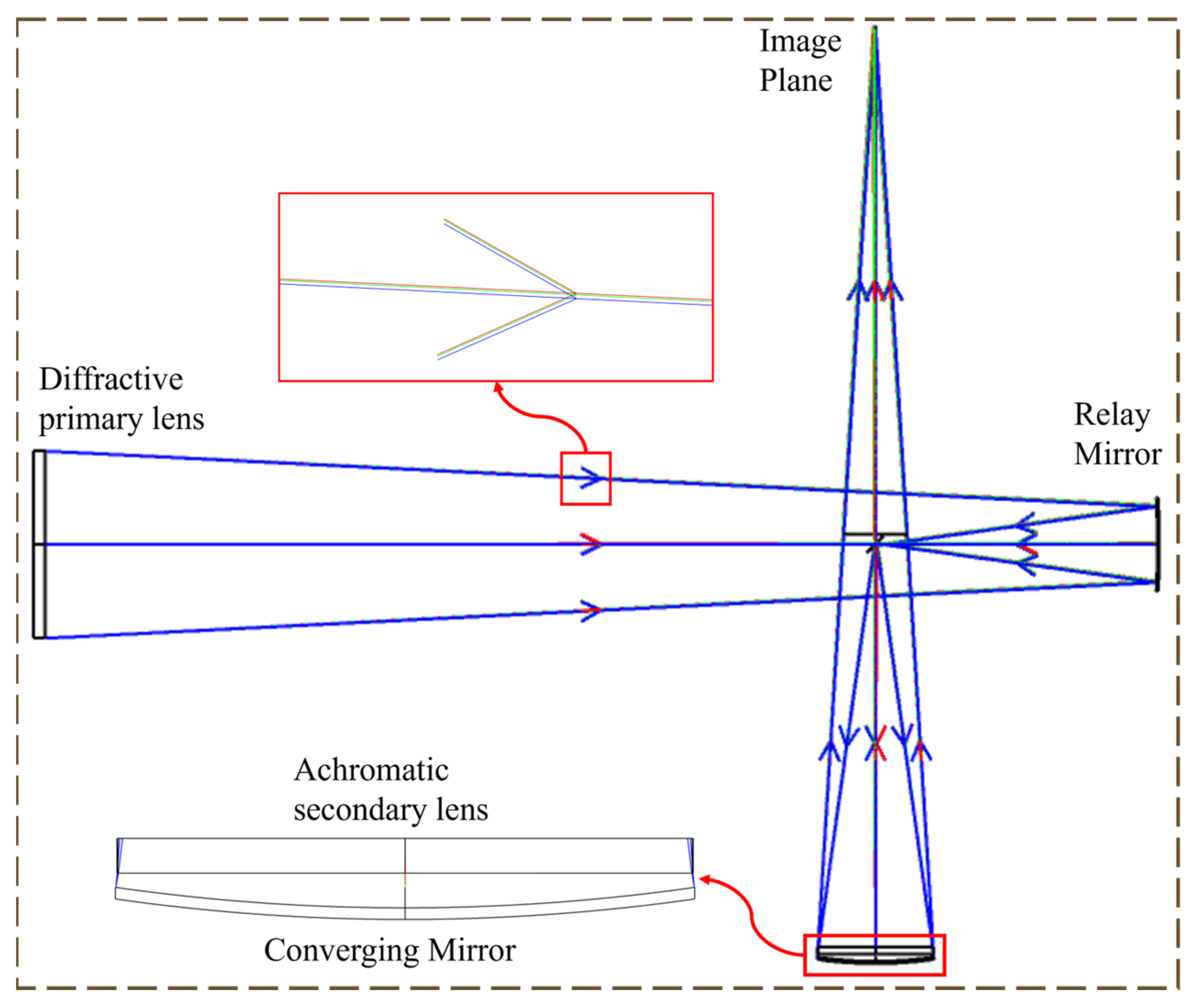
3.1. Optical Design
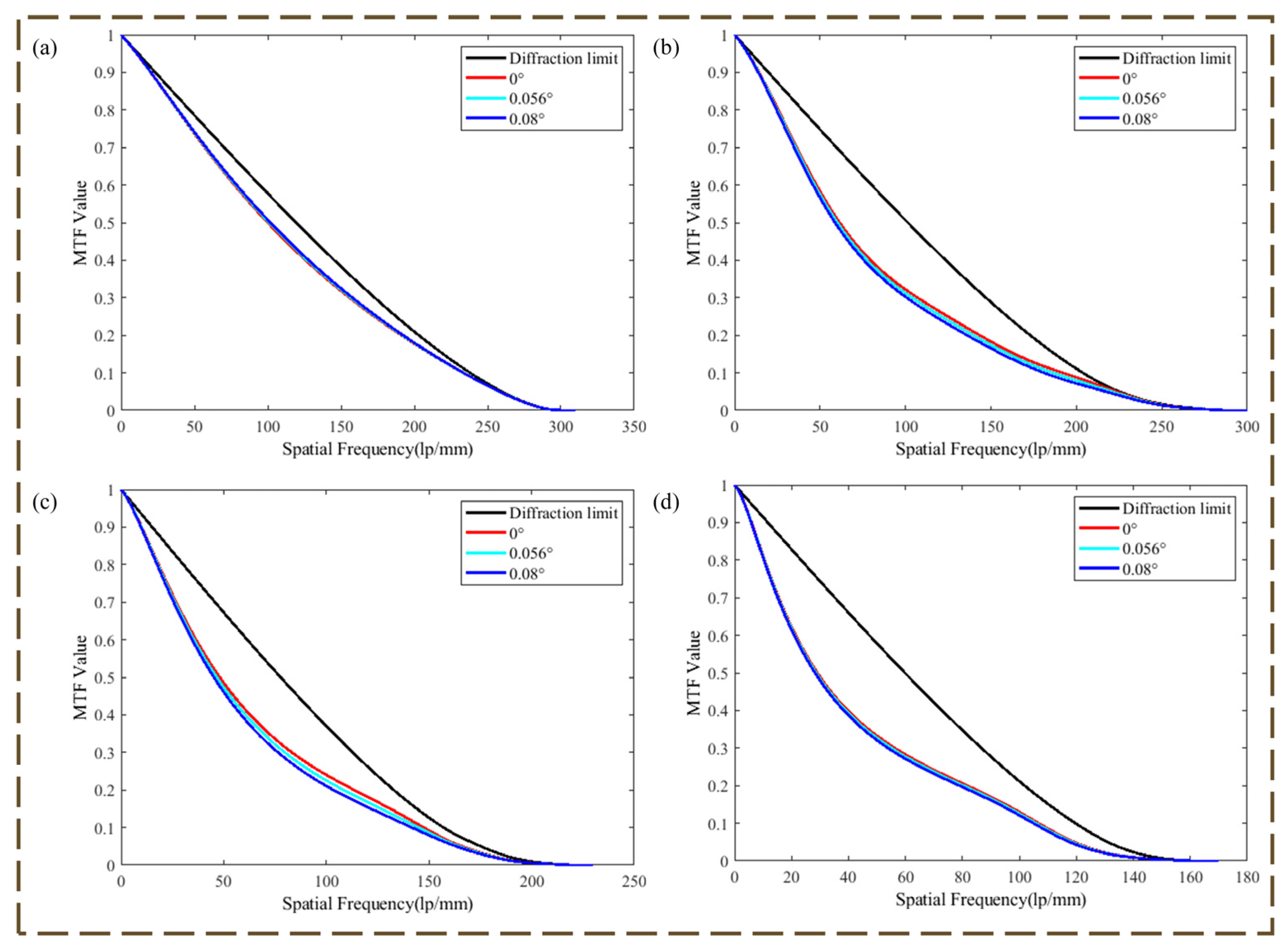
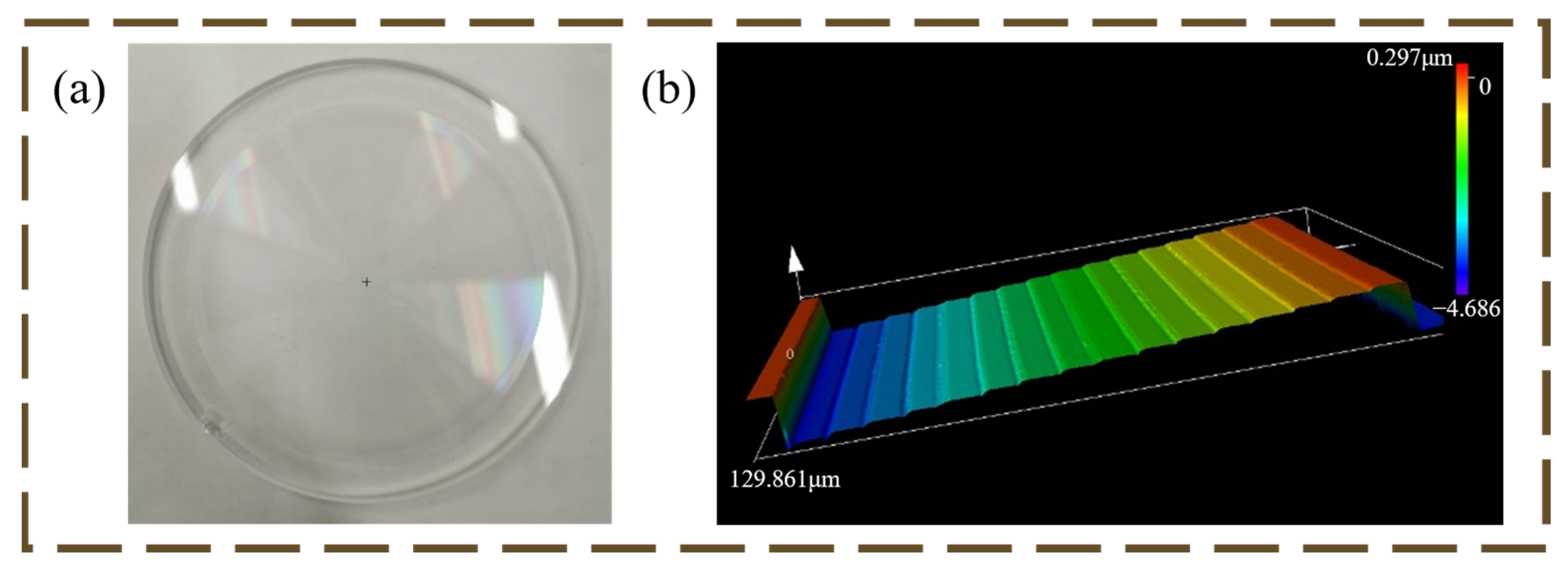
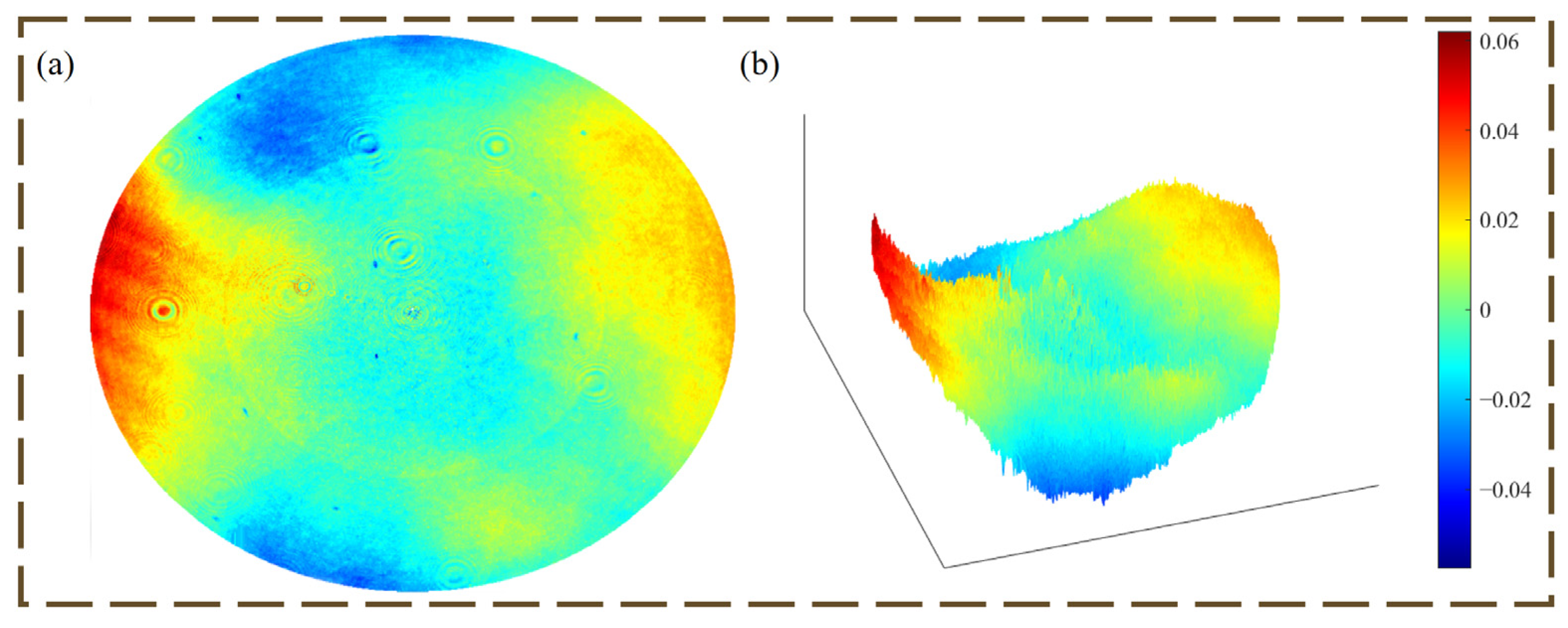
3.2. Experiment of Optical Imaging
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lord Rayleigh, F.R.S. XXXI. Investigations in optics, with special reference to the spectroscope. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1879, 8, 261–274. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Zhou, S.; Jiang, L. Modern description of Rayleigh’s criterion. Phys. Rev. A 2019, 99, 013808. [Google Scholar] [CrossRef]
- Zhang, Q.; He, Z.; Xie, Z.; Tan, Q.; Sheng, Y.; Jin, G.; Cao, L.; Yuan, X. Diffractive optical elements 75 years on: From micro-optics to metasurfaces. Photonics Insights 2023, 2, R09. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Hou, X.; Chen, L.; Liu, X.; Yang, J.; Zheng, Y. Hybrid diffractive-refractive lens for chromatic confocal measurement system. Opt. Express 2024, 32, 20128–20135. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Liu, T.; Wang, Z.; Hu, C.; Shi, J.; Chen, M.; Ye, M.; Wang, H.; Xie, C.; Zhang, X. Thz beam shaping based on diffractive transformation for forming patterned simulation lightfields and wavefronts. Infrared Phys. Technol. 2022, 124, 104225. [Google Scholar] [CrossRef]
- Mínguez-Vega, G.; Mendoza-Yero, O.; Lancis, J.; Gisbert, R.; Andrés, P. Diffractive optics for quasi-direct space-to-time pulse shaping. Opt. Express 2008, 16, 16993–16998. [Google Scholar] [CrossRef] [PubMed]
- Bouzid, O.; Haddadi, S.; Fromager, M.; Cagniot, E.; Ferria, K.; Forbes, A.; Ait-Ameur, K. Focusing anomalies with binary diffractive optical elements. Appl. Opt. 2017, 56, 9735–9741. [Google Scholar] [CrossRef] [PubMed]
- Sweeney, D.W.; Sommargren, G.E. Harmonic diffractive lenses. Appl. Opt. 1995, 34, 2469–2475. [Google Scholar] [CrossRef] [PubMed]
- Faklis, D.; Morris, G.M. Spectral properties of multiorder diffractive lenses. Appl. Opt. 1995, 34, 2462–2468. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Twardowski, P.; Gérard, P.; Yu, W.; Fontaine, J. Chromatic analysis of harmonic Fresnel lenses by FDTD and angular spectrum methods. Appl. Opt. 2018, 57, 5281–5287. [Google Scholar] [CrossRef] [PubMed]
- Swanson, G.J. Binary Optics Technology: The Theory and Design of Multi-Level Diffractive Optical Elements; Lincoln Laboratory Cambridge, Massachusetts Institute of Technology: Cambridge, MA, USA, 1989; Volume 854. [Google Scholar]
- Arieli, Y.; Ozeri, S.; Eisenberg, N.; Noach, S. Design of a diffractive optical element for wide spectral bandwidth. Opt. Lett. 1998, 23, 823–824. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Ren, D.; Wang, C.; Mao, C.; Yang, L. Design of high-efficiency diffractive optical elements towards ultrafast mid-infrared time-stretched imaging and spectroscopy. J. Mod. Opt. 2018, 65, 255–261. [Google Scholar] [CrossRef]
- Hyde, R.A.; Dixit, S.N.; Weisberg, A.H.; Rushford, M.C. Eyeglass: A very large aperture diffractive space telescope. In Highly Innovative Space Telescope Concepts; SPIE: Bellingham, WA, USA, 2002; pp. 28–39. [Google Scholar]
- Hyde, R.A. Eyeglass. 1. Very large aperture diffractive telescopes. Appl. Opt. 1999, 38, 4198–4212. [Google Scholar] [CrossRef] [PubMed]
- Atcheson, P.D.; Stewart, C.; Domber, J.; Whiteaker, K.; Cole, J.; Spuhler, P.; Seltzer, A.; Britten, J.A.; Dixit, S.N.; Farmer, B. MOIRE: Initial demonstration of a transmissive diffractive membrane optic for large lightweight optical telescopes. In Proceedings of the Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, Amsterdam, The Netherlands, 1–6 July 2012; pp. 729–742. [Google Scholar]
- Early, J.T.; Hyde, R.; Baron, R.L. Twenty-meter space telescope based on diffractive Fresnel lens. In UV/Optical/IR Space Telescopes: Innovative Technologies and Concepts; SPIE: Bellingham, WA, USA, 2004; pp. 148–156. [Google Scholar]
- Tandy, W.; Atcheson, P.; Domber, J.; Seltzer, A. MOIRE gossamer space telescope-structural challenges and solutions. In 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 2012: Honolulu, Hawaii, USA, 23–26 April 2012; [and Co-Located Conferences: 20th AIAA/ASME/AHS Adaptive Structures Conference, 14th AIAA Non-Deterministic Approaches Conference, 13th AIAA Gossamer Systems Forum, and 8th AIAA Multidisciplinary Design Optimization Specialist Conference (MDO)]; AIAA: Reston, VA, USA, 2012; p. 1670. [Google Scholar]
- Koechlin, L.; Serre, D.; Deba, P.; Pelló, R.; Peillon, C.; Duchon, P.; Gomez de Castro, A.I.; Karovska, M.; Désert, J.-M.; Ehrenreich, D. The Fresnel interferometric imager. Exp. Astron. 2009, 23, 379–402. [Google Scholar] [CrossRef]
- Andersen, G.; Tullson, D. Broadband antihole photon sieve telescope. Appl. Opt. 2007, 46, 3706–3708. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Zhang, J.; Zhou, C.; Xu, Y. Research on dispersion performance of harmonic diffractive lenses. J. Phys. Conf. Ser. 2006, 48, 897. [Google Scholar] [CrossRef]


| Wavelength | Field of View | Aperture | Focal Length | F/# |
|---|---|---|---|---|
| 400–900 nm | 0.16° | 80 mm | 656.2 mm | 8.18 |
| Thickness | Aperture | A2 | A4 | A6 | A8 | A10 |
|---|---|---|---|---|---|---|
| 5 mm | 80 mm | −2.071 | 8.11 × 10−7 | −6.35 × 10−13 | 6.56 × 10−19 | −9.36 × 10−24 |
| Number | Center Wavelength | Diffraction Order | Spectral Range | Bandwidth |
|---|---|---|---|---|
| 1 | 946.4 nm | 2 | 750–900 nm | 150 nm |
| 2 | 632.8 nm | 3 | 550–750 nm | 200 nm |
| 3 | 476.4 nm | 4 | 420–550 nm | 130 nm |
| 4 | 379.7 nm | 5 | 400–420 nm | 20 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Du, J.; Lei, B.; Bian, J.; Wang, L.; Fan, B. Design, Analysis, and Manufacturing of Diffractive Achromatic Optical Systems. Micromachines 2025, 16, 322. https://doi.org/10.3390/mi16030322
Zheng Y, Du J, Lei B, Bian J, Wang L, Fan B. Design, Analysis, and Manufacturing of Diffractive Achromatic Optical Systems. Micromachines. 2025; 16(3):322. https://doi.org/10.3390/mi16030322
Chicago/Turabian StyleZheng, Yidi, Junfeng Du, Boping Lei, Jiang Bian, Lihua Wang, and Bin Fan. 2025. "Design, Analysis, and Manufacturing of Diffractive Achromatic Optical Systems" Micromachines 16, no. 3: 322. https://doi.org/10.3390/mi16030322
APA StyleZheng, Y., Du, J., Lei, B., Bian, J., Wang, L., & Fan, B. (2025). Design, Analysis, and Manufacturing of Diffractive Achromatic Optical Systems. Micromachines, 16(3), 322. https://doi.org/10.3390/mi16030322






