A MEMS Pirani Vacuum Gauge Based on Porous Silicon †
Abstract
1. Introduction
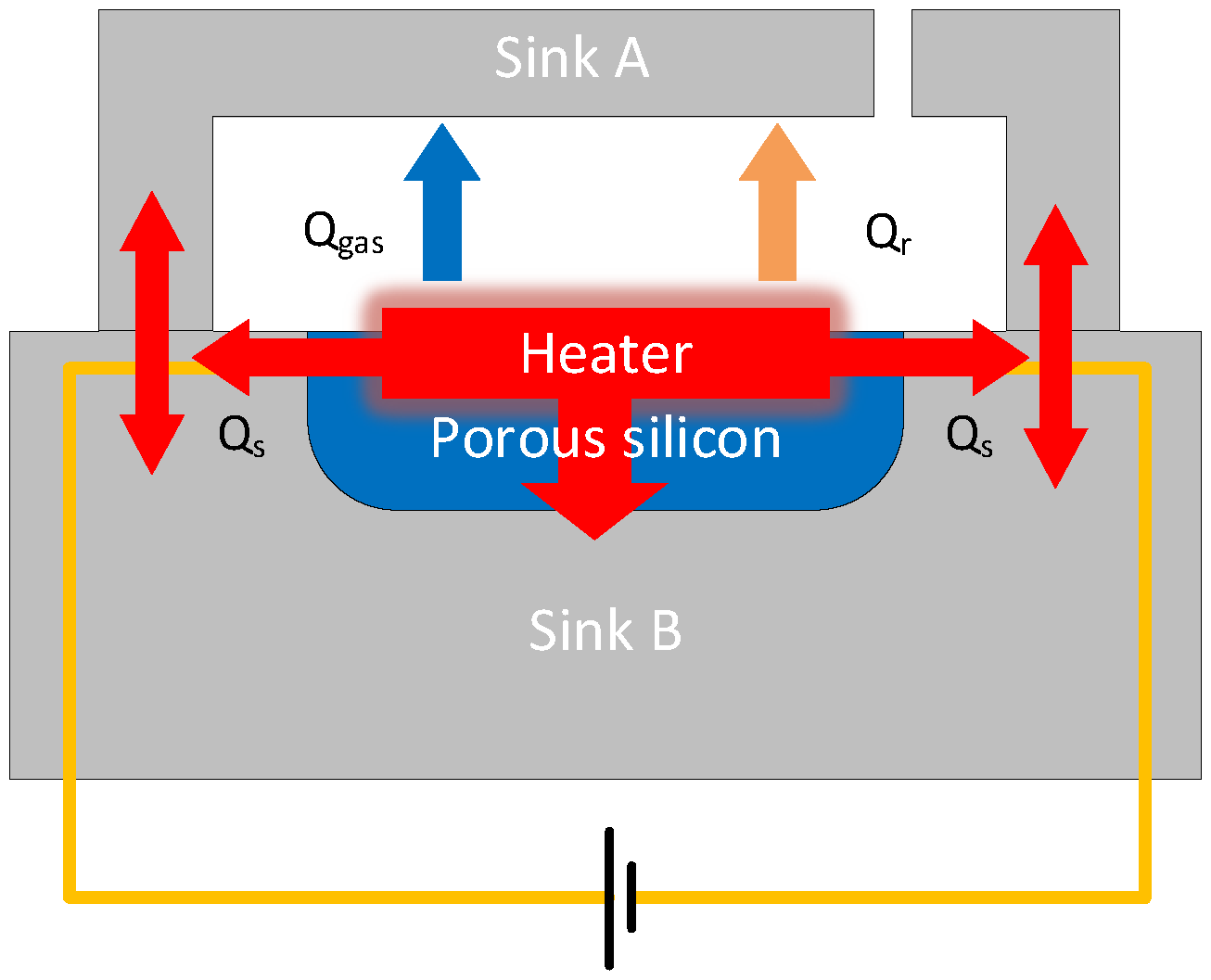
2. Principle and Theoretical Analysis
3. The Fabrication Process of Vacuum Gauge
- (1)
- Using a temperature control station to heat the porous silicon sample to 35 °C, 135 °C, 235 °C, and 335 °C in sequence.
- (2)
- (3)
- Scan the porous silicon sample with a high-power (5 mW) laser. Combined with the value of Tj to calculate λPS.
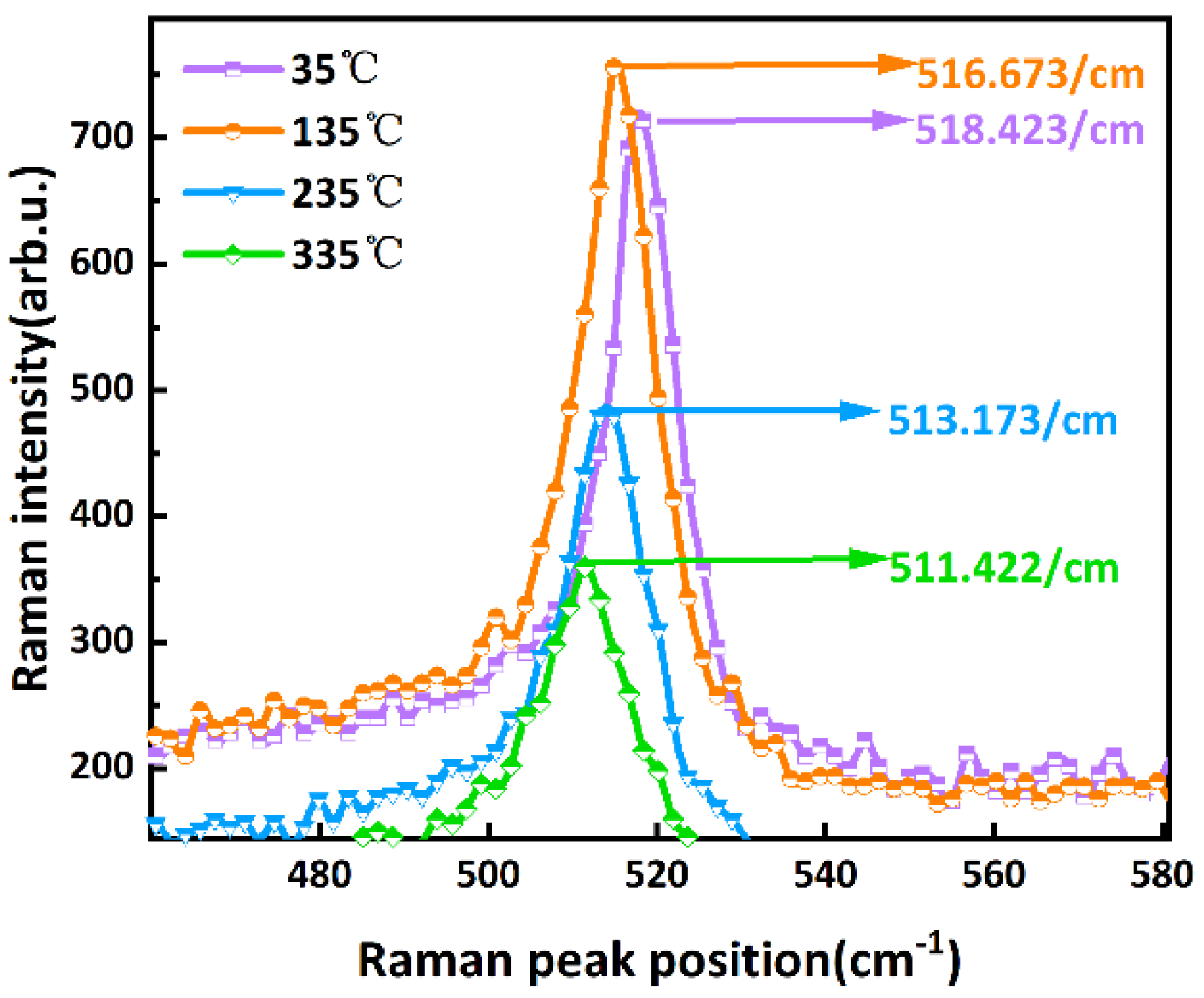
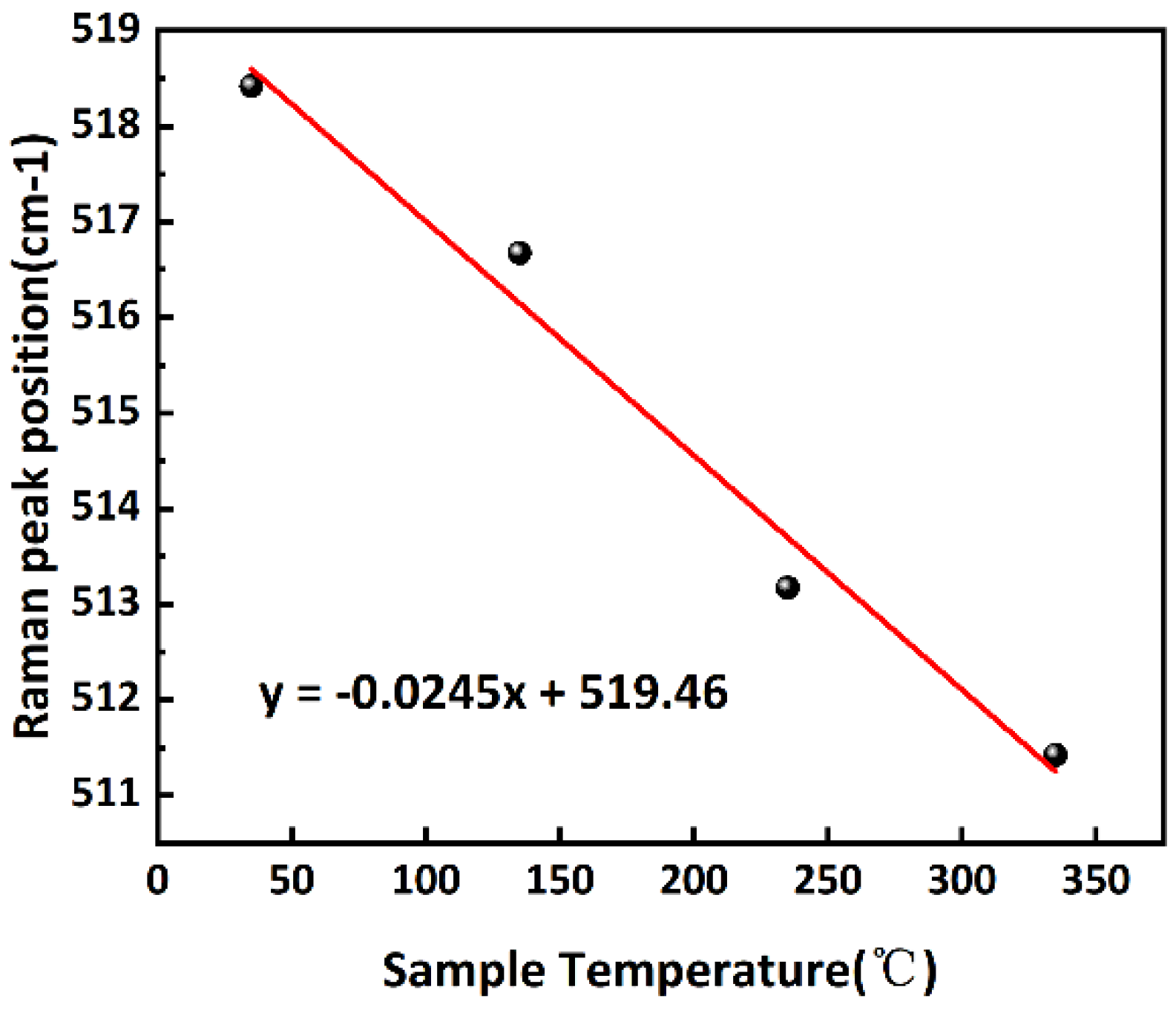
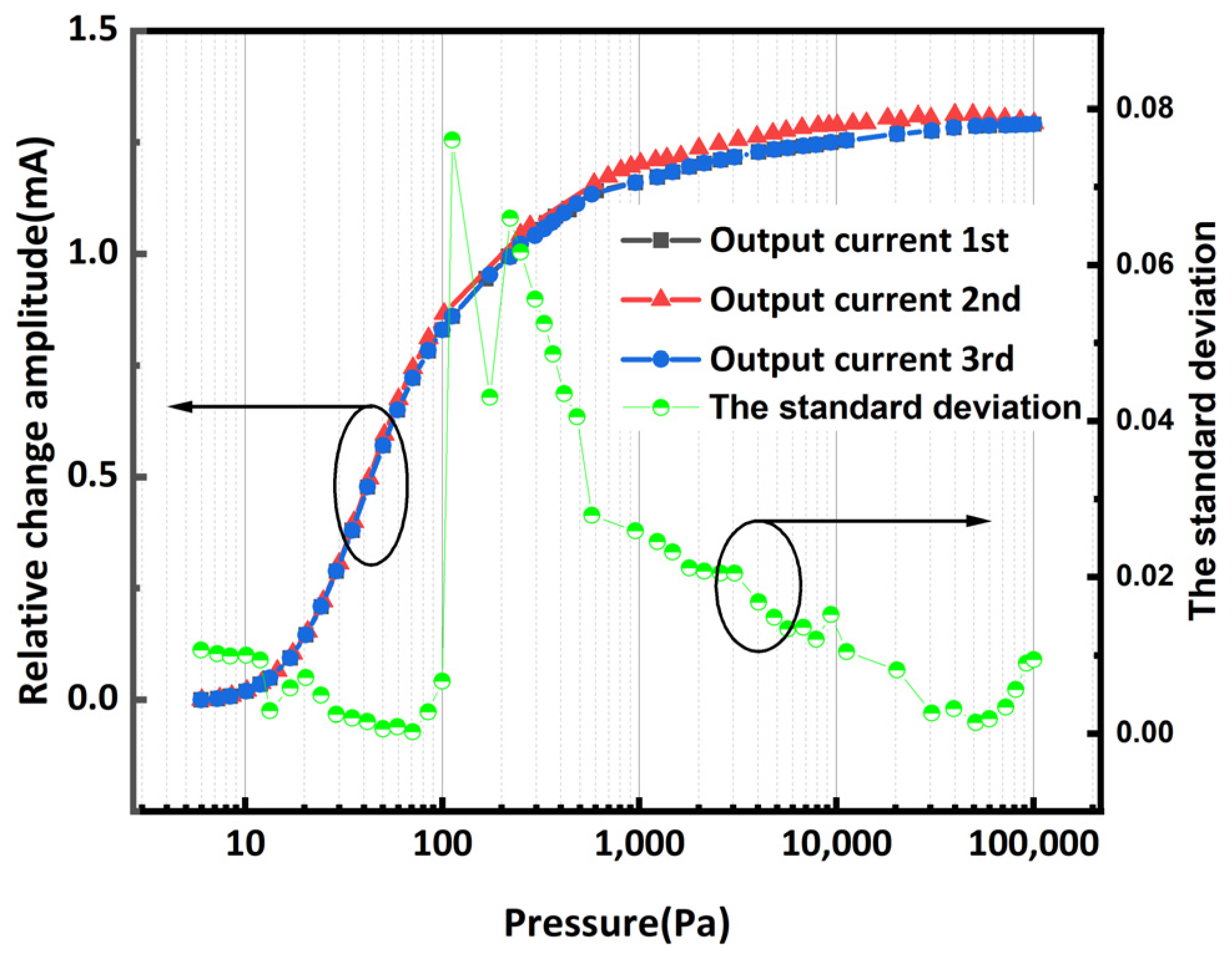
4. Measurement Results and Discussion
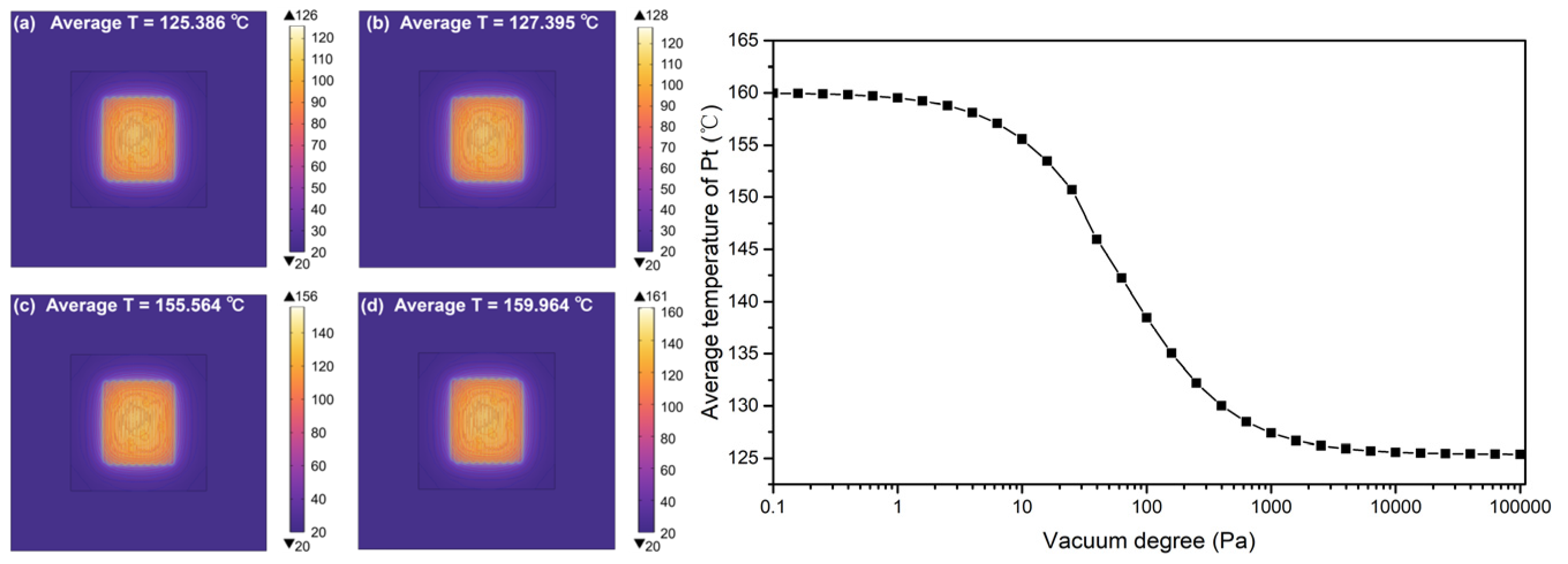
- (1)
- Place the chip to be tested in the vacuum chamber and apply 32 V and 24 V voltages to it with a DC power supply, respectively;
- (2)
- After using a molecular pump to pump the pressure in the vacuum chamber to the lowest pressure that can be pumped, the molecular pump is turned off, and the pressure value and output current value in the chamber are collected;
- (3)
- The pressure in the cavity is adjusted by the gas flow controller, and when the pressure to be measured is stabilized, the pressure value and output current value at this time are recorded.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Khosraviani, K.; Leung, A.M. The nanogap pirani—A pressure sensor with superior linearity in an atmospheric pressure range. J. Micromech. Microeng. 2009, 19, 045007. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, J.; Bai, S.; Guan, J.; Zhang, F.; Tang, Z. Size Effect of Heat Transport in Microscale Gas Gap. IEEE Trans. Ind. Electron. 2017, 64, 7387–7391. [Google Scholar] [CrossRef]
- Chae, J.; Stark, B.H.; Najafi, K. A micromachined Pirani gauge with dual heat sinks. IEEE Trans. Adv. Packag. 2005, 28, 619–625. [Google Scholar] [CrossRef]
- Lv, Y.; Zhou, Z.F.; Fu, J.; Li, Y. Macro-model extraction and system-level simulation of a thermopile-based MEMS vacuum sensor. J. Micromech. Microeng. 2025, 35, 025006. [Google Scholar] [CrossRef]
- Garg, M.; Arya, D.S.; Kumar, S.; Joshi, K.; Yousuf, M.; Chiu, Y.; Singh, P. Electrostatically actuated all metal MEMS Pirani gauge with tunable dynamic range. J. Micromech. Microeng. 2024, 34, 025003. [Google Scholar] [CrossRef]
- Song, X.; Huang, L.; Lin, Y.; Hong, L.; Xu, W. Surface Micromachined CMOS-MEMS Pirani Vacuum Gauge with Stacked Temperature Sensor. J. Microelectromech. Syst. 2024, 33, 274–281. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Qiu, J.; He, Y.; Li, Z.; Liu, P.; Wei, X. Micro-Pirani Pressure Sensor with Operation Range beyond Atmospheric Pressure based on Aligned Carbon Nanotube Films. IEEE Electron Device Lett. 2024, 45, 901–904. [Google Scholar] [CrossRef]
- Garg, M.; Singh, P.; Chiu, Y. Nanogap CMOS-MEMS Pirani Gauge Based on Titanium-Nitride Heating Element for Broad-Range Vacuum Characterization. IEEE Trans. Electron Devices 2023, 71, 1214–1219. [Google Scholar] [CrossRef]
- Garg, M.; Arya, D.S.; Kumar, S.; Yousuf, M.; Chiu, Y.; Singh, P. Stress engineered SU-8 dielectric-microbridge based polymer MEMS Pirani gauge for broad range hermetic characterization. J. Micromech. Microeng. 2022, 32, 075004. [Google Scholar] [CrossRef]
- Chen, S.J.; Wu, Y.C. A new macro-model of gas flow and parameter extraction for a CMOS-MEMS vacuum sensor. Symmetry 2020, 12, 1604. [Google Scholar] [CrossRef]
- Lai, J.; Kong, Y.; Jiao, B.; Ye, Y.; Yun, S.; Liu, R.; Ye, M.; Zhang, G. Study on fusion mechanisms for sensitivity improvement and measurable pressure limit extension of Pirani vacuum gauges with multi heat sinks. J. Microelectromech. Syst. 2020, 29, 100–108. [Google Scholar] [CrossRef]
- Mo, J.; Middelburg, L.M.; Morana, B.; van Zeijl, H.W.; Vollebregt, S.; Zhang, G. Surface-micromachined Silicon Carbide Pirani gauges for harsh environments. IEEE Sens. J. 2021, 21, 1350–1358. [Google Scholar] [CrossRef]
- Grau, M.; Völklein, F.; Meier, A.; Kunz, C.; Kaufmann, I.; Woias, P. Optimized MEMS pirani sensor with increased pressure measurement sensitivity in the fine and rough vacuum regimes. J. Vac. Sci. Technol. A Vac. Surf. Film 2014, 33, 021601. [Google Scholar] [CrossRef]
- Mastrangelo, C.H.; Muller, R.S. Microfabricated thermal absolute-pressure sensor with on-Chip Digital Front-End Processor. IEEE J. Solid-State Circuit 1991, 26, 1998–2007. [Google Scholar] [CrossRef]
- Lee, D.; Noh, Y.; Park, S.; Kumar, M.; Cho, Y.S. Performance enhancement of pirani gauge on silicon-on-insulator wafer with simple fabrication process. Sens. Actuator A-Phys. 2017, 263, 264–268. [Google Scholar] [CrossRef]
- Simon, I.; Billat, S.; Link, T.; Nommensen, P.; Auber, J.; Manoli, Y. In-situ pressure measurements of encapsulted gyroscopes. In Proceedings of the TRANSDUCERS 2007–2007 International Solid-State Sensors, Actuators and Microsystems Conference, Lyon, France, 10–14 June 2007. [Google Scholar] [CrossRef]
- Alvesteffer, W.J.; Jacobs, D.C.; Baker, D.H. Miniaturized thin film thermal vacuum sensor. J. Vac. Sci. Technol. A Vac. Surf. Film 1995, 13, 2980–2985. [Google Scholar] [CrossRef]
- Paul, O.; Baltes, H. Novel fully CMOS-compatible vacuum sensor. Sens. Actuator A-Phys. 1995, 46, 143–146. [Google Scholar] [CrossRef]
- Quednau, S.; Schlaak, H.F.; Völklein, F. B2.4—Numerical simulation of a MEMS pirani vacuum sensor. In Proceedings of the SENSOR 2013, Nürnberg, Germany, 14–16 May 2013. [Google Scholar] [CrossRef]
- Santagata, F.; Iervolino, E.; Mele, L.; van Herwaarden, A.W.; Creemer, J.F.; Sarro, P.M. An analytical model and verification for MEMS Pirani gauges. J. Micromech. Microeng. 2011, 21, 115007. [Google Scholar] [CrossRef]
- Jeon, G.-J.; Kim, W.Y.; Shim, H.B.; Lee, H.C. Nanoporous Pirani sensor based on anodic aluminum oxide. Appl. Phys. Lett. 2016, 109, 123505. [Google Scholar] [CrossRef]
- Zhang, Z.; Tao, J.; Li, Y. Design and evaluation of a highly robust MEMS Pirani vacuum gauge based on porous silicon thermal insulation layer. In Proceedings of the 2022 IEEE International Flexible Electronics Technology Conference (IFETC), Qingdao, China, 21–24 August 2022; pp. 1–2. [Google Scholar] [CrossRef]
- Périchon, S.; Lysenko, V.; Remaki, B.; Barbier, D.; Champagnon, B. Measurement of porous silicon thermal conductivity by micro-raman scattering. J. Appl. Phys. 1999, 86, 4700–4702. [Google Scholar] [CrossRef]

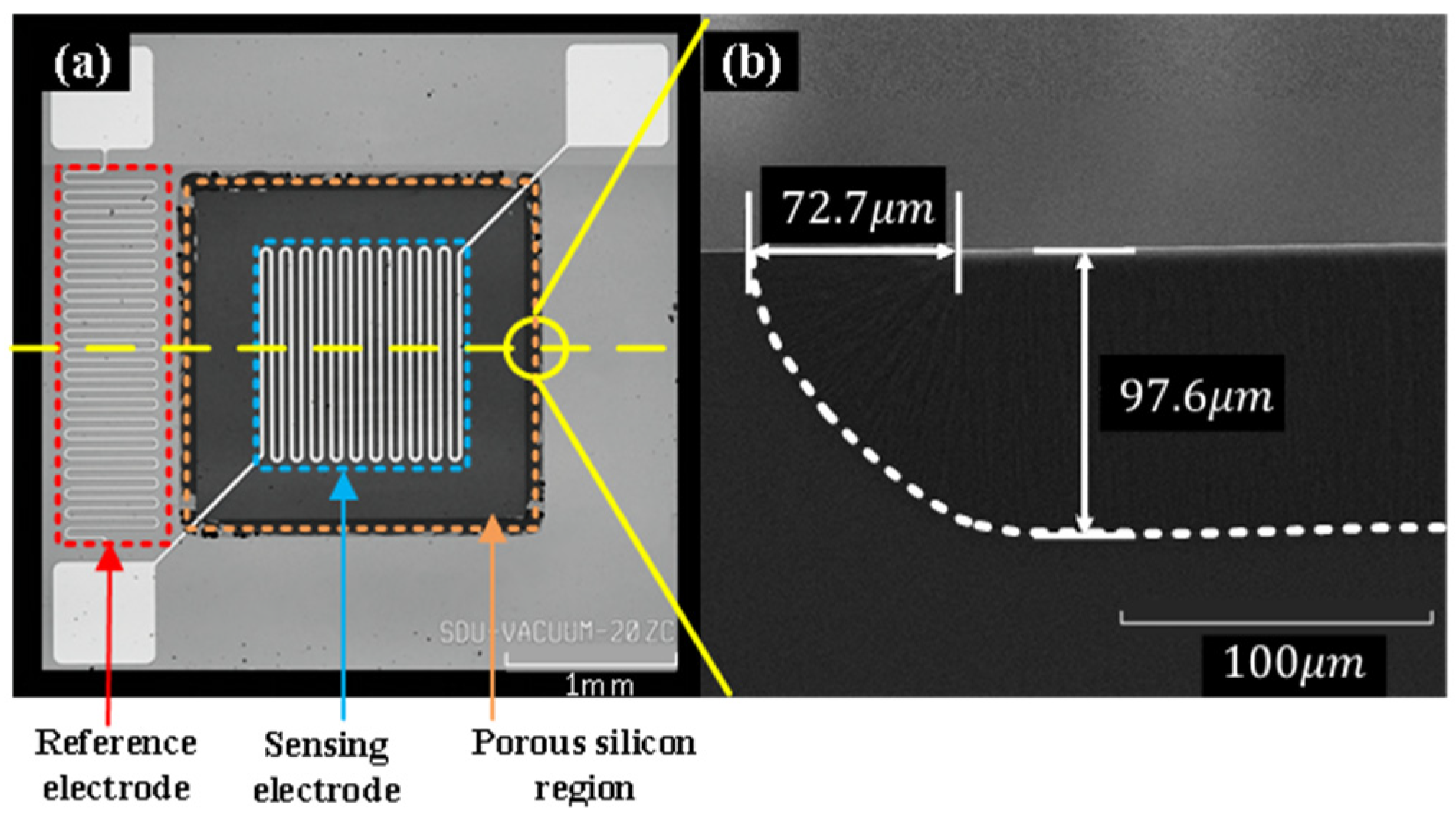
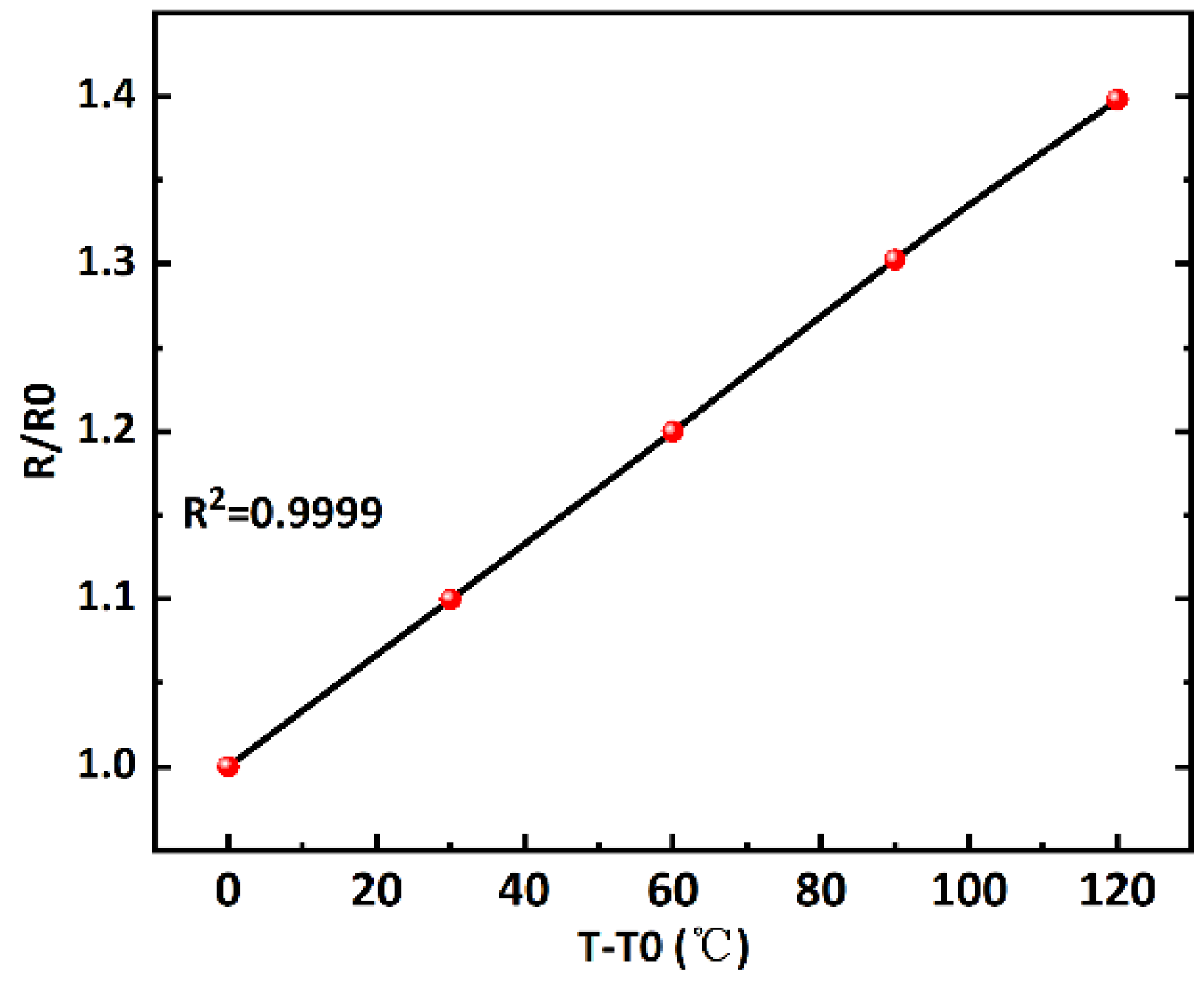
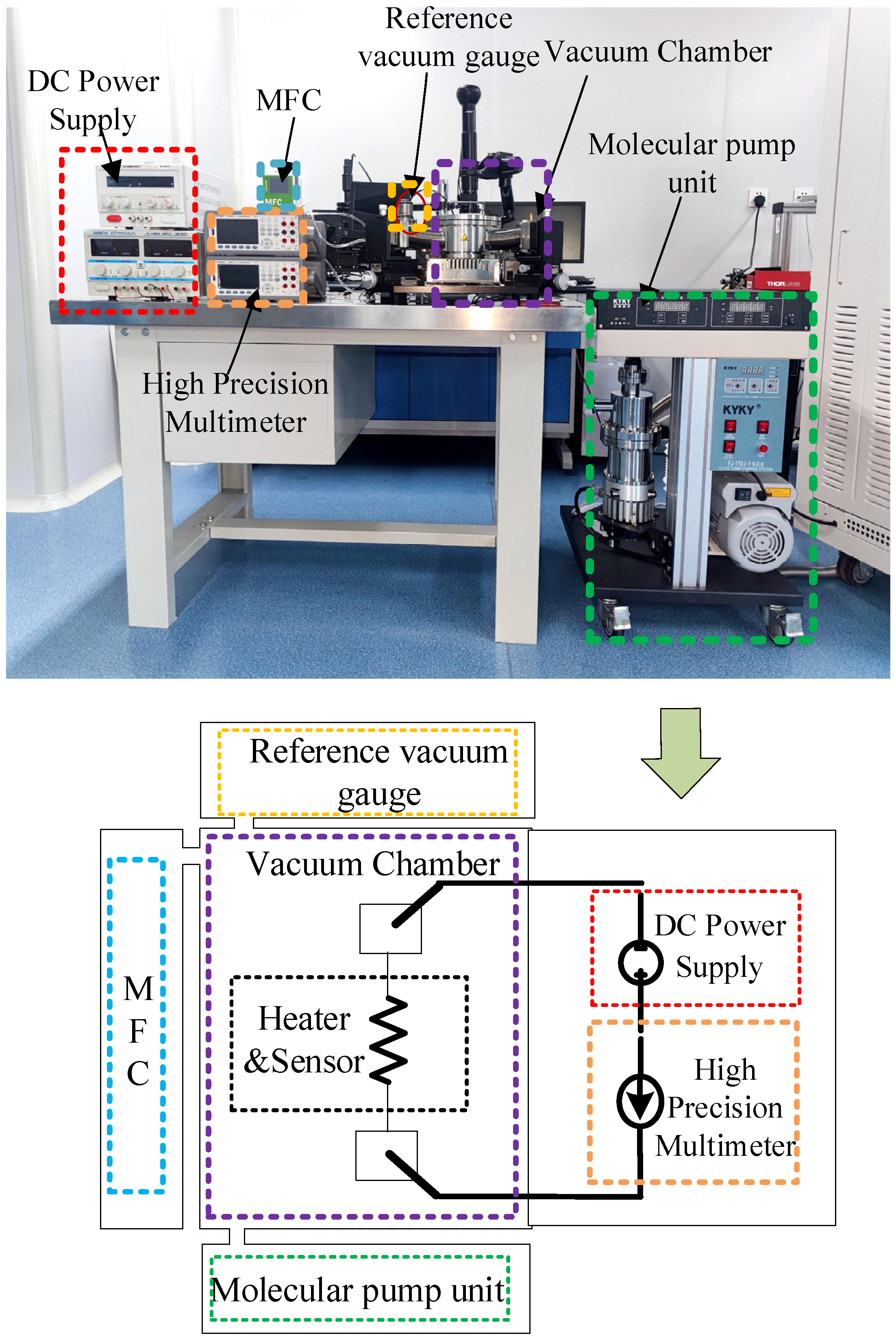
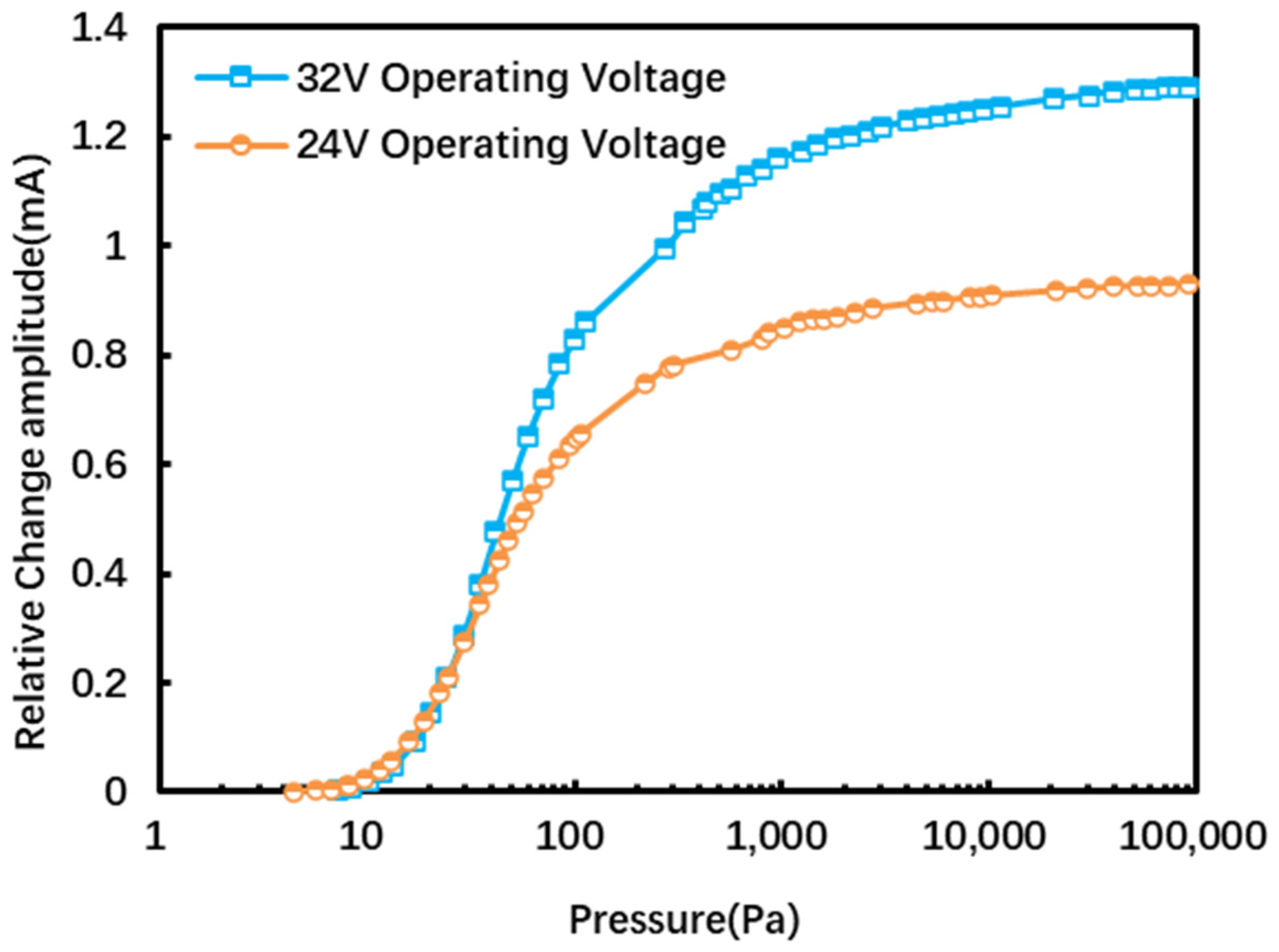

| Parameters | Design Value |
|---|---|
| The thickness of porous silicon (μm) | 100 |
| Resisitance (Ω) | 750 |
| Area of Porous Silicon (μm) | 1600 × 1600 |
| Size of a sensor (mm) | 3.2 × 3.2 × 0.5 |
| Thickness of Air Gap (μm) | 200 |
| Researcher | Structure | Pressure Range (Pa) | Year |
|---|---|---|---|
| Kourosh Khosraviani [1] | Membrane | 100–720,000 | 2009 |
| Y Lv [4] | Membrane | 0.001–1000 | 2025 |
| X. Song [6] | Membrane | 0.8–14,000 | 2024 |
| M Garg [8] | Membrane | 1–1,000,000 | 2024 |
| G.-J. Jeon [21] | Porous AAO | 0.013–101,324 | 2016 |
| This work | Porous silicon | 4–100,000 | 2025 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Zhang, Z.; Tao, J.; Wen, L. A MEMS Pirani Vacuum Gauge Based on Porous Silicon. Micromachines 2025, 16, 296. https://doi.org/10.3390/mi16030296
Lin Y, Zhang Z, Tao J, Wen L. A MEMS Pirani Vacuum Gauge Based on Porous Silicon. Micromachines. 2025; 16(3):296. https://doi.org/10.3390/mi16030296
Chicago/Turabian StyleLin, Yuzhe, Zichao Zhang, Jifang Tao, and Lianggong Wen. 2025. "A MEMS Pirani Vacuum Gauge Based on Porous Silicon" Micromachines 16, no. 3: 296. https://doi.org/10.3390/mi16030296
APA StyleLin, Y., Zhang, Z., Tao, J., & Wen, L. (2025). A MEMS Pirani Vacuum Gauge Based on Porous Silicon. Micromachines, 16(3), 296. https://doi.org/10.3390/mi16030296





