Investigation of Transient Thermal Behavior in Thyristors Under Pulse Conditions
Abstract
1. Introduction
2. Two-Dimensional Non-Uniform Model of Thyristors
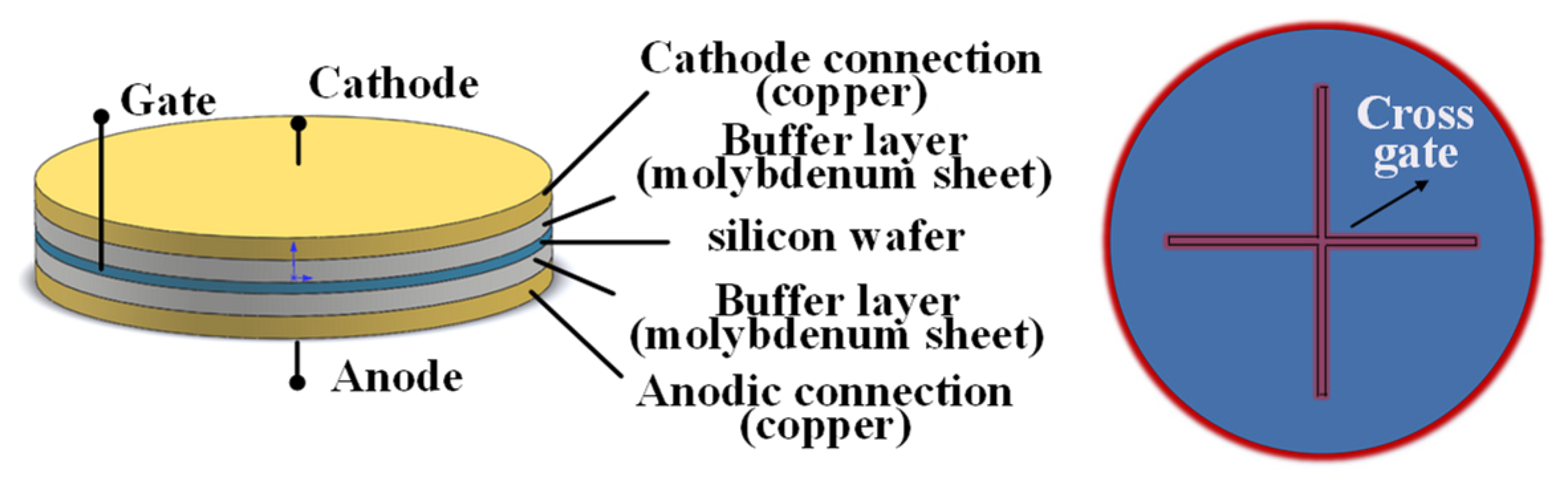
2.1. Establishment of the Model
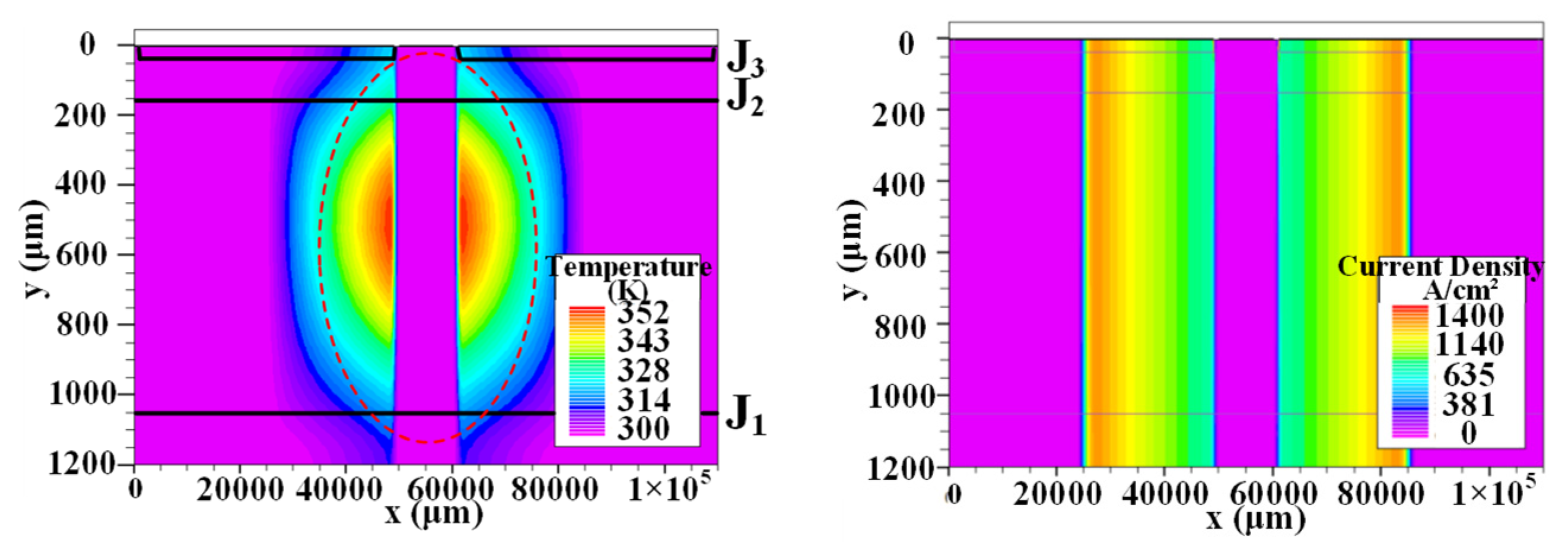
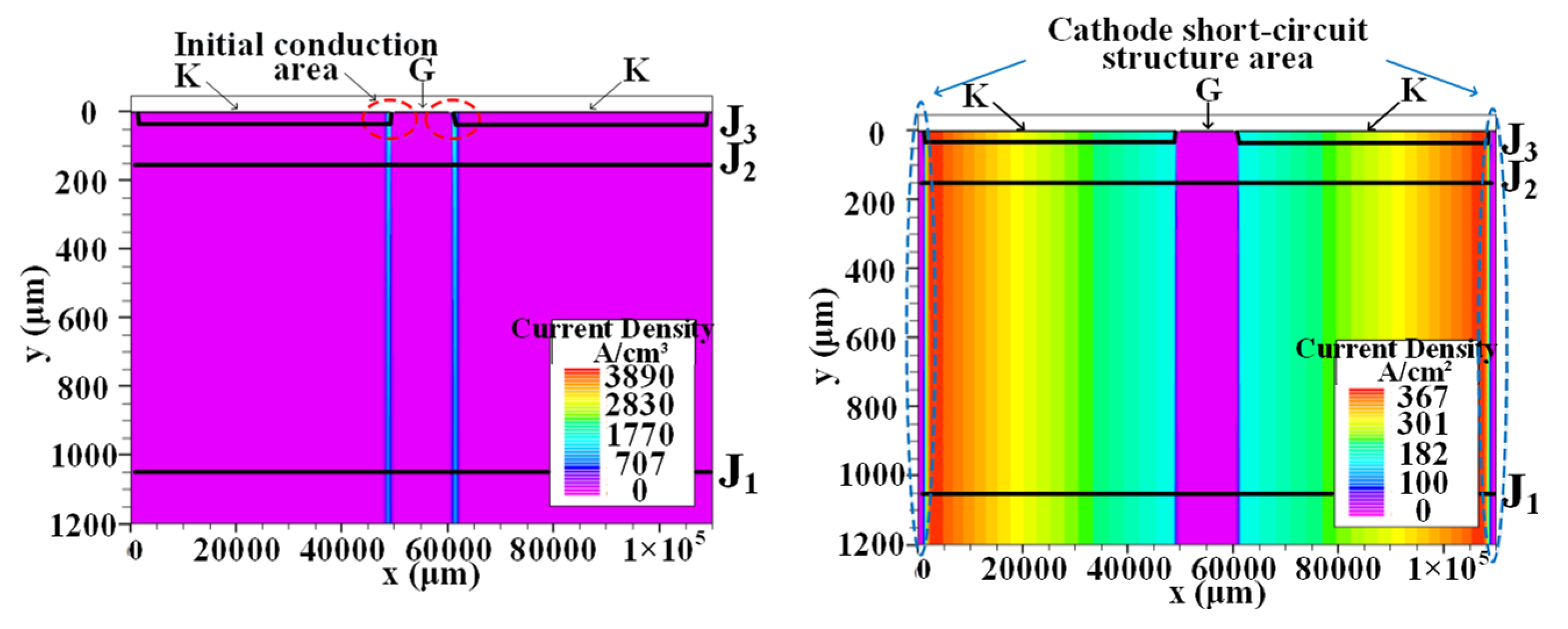
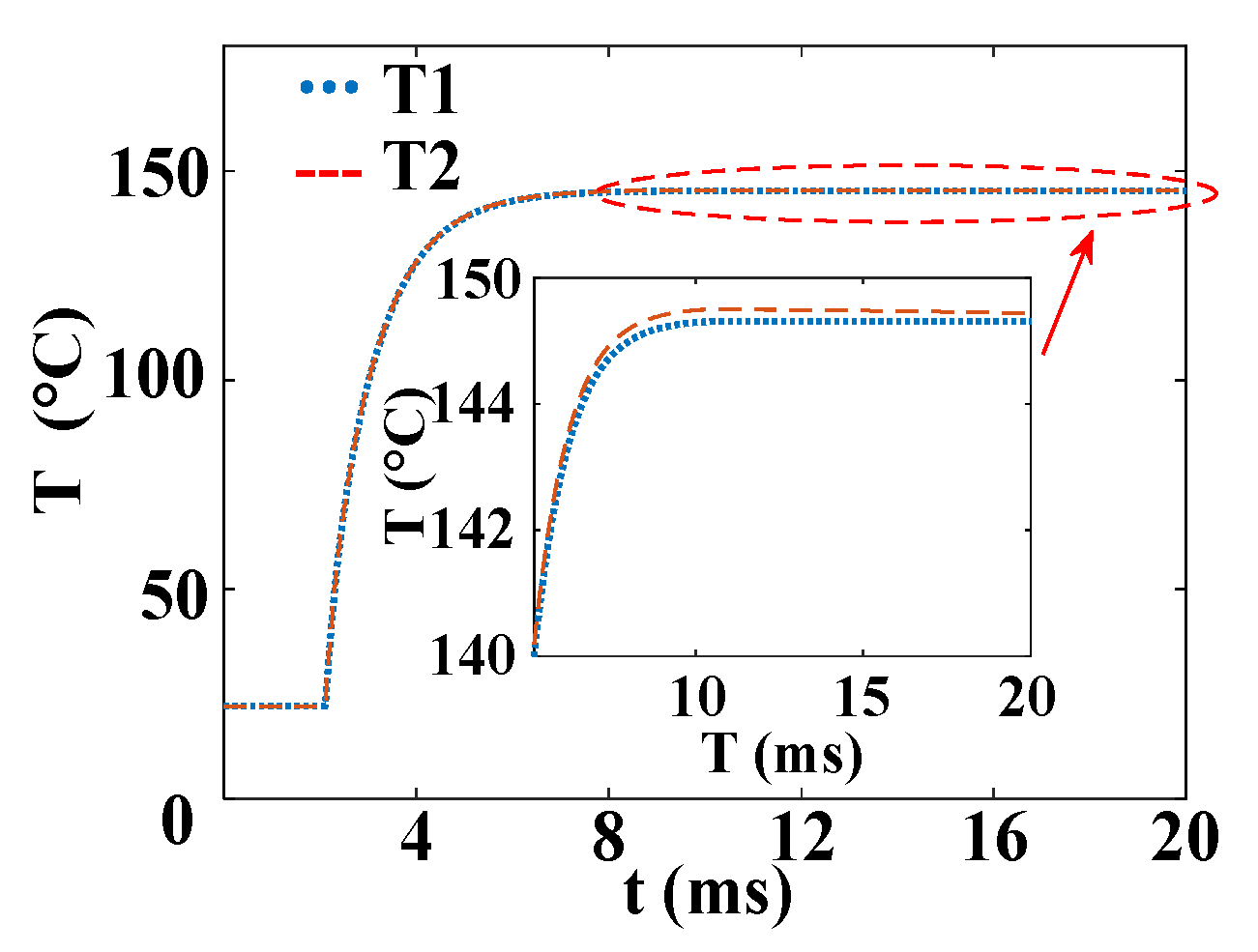
2.2. Solution and Analysis of the Model
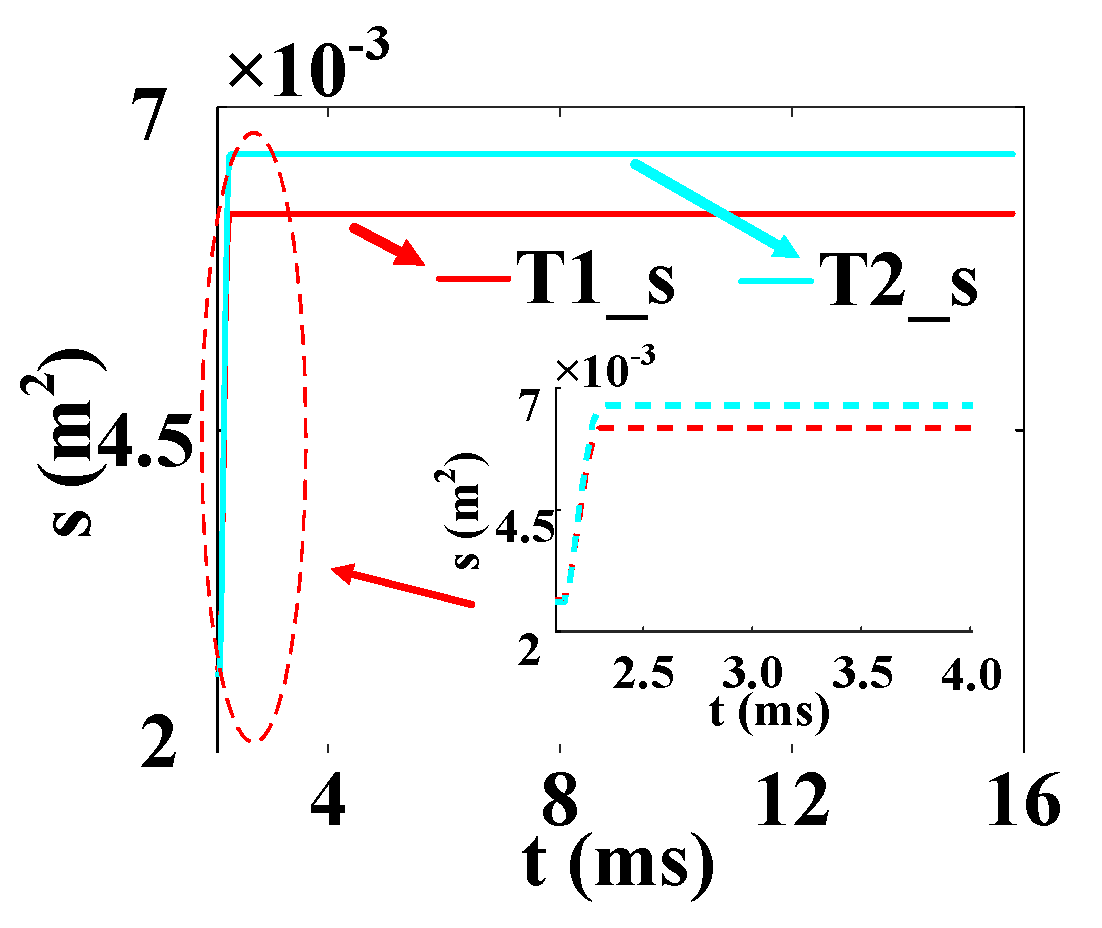
2.3. Extraction of Spread Velocity Equation
3. Establishment and Solution of Three-Dimensional Non-Uniform Model of Thyristor
3.1. Establishment of Three-Dimensional Finite Element Model
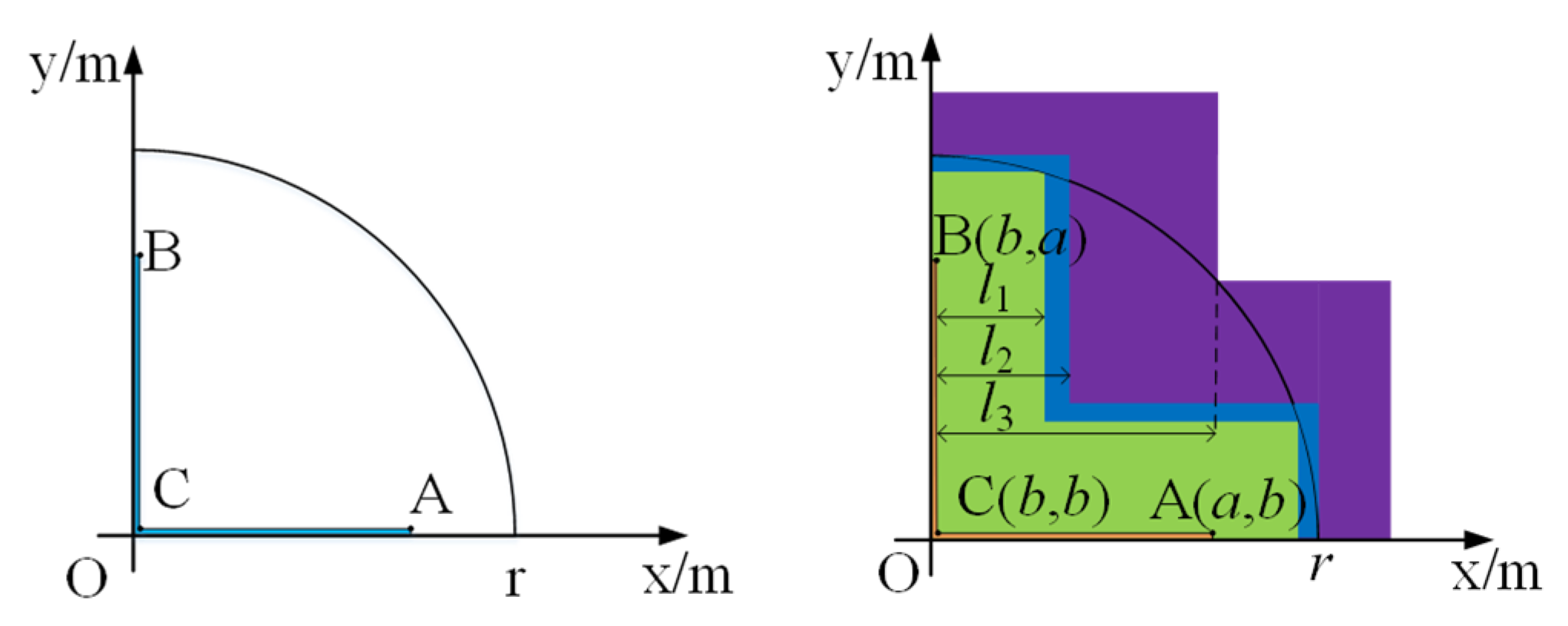
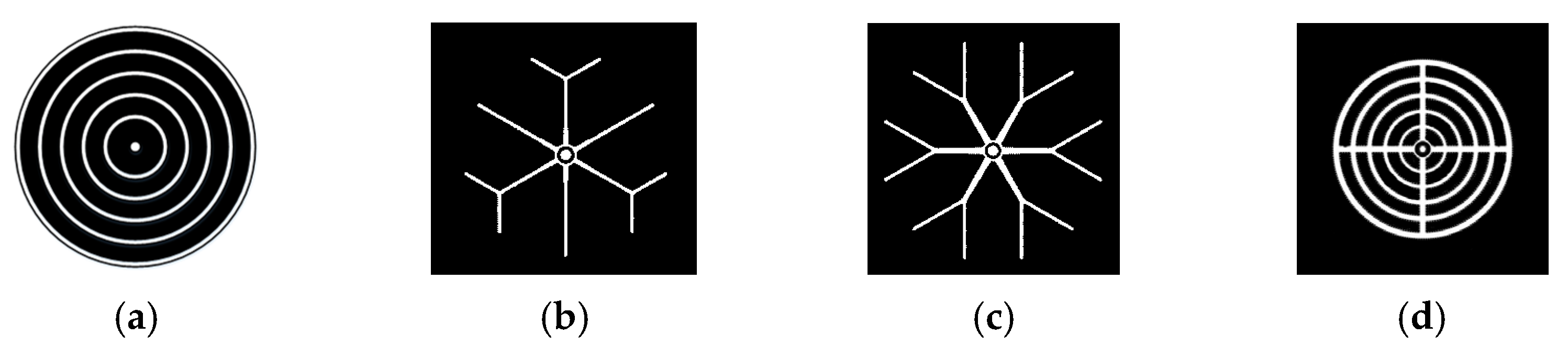
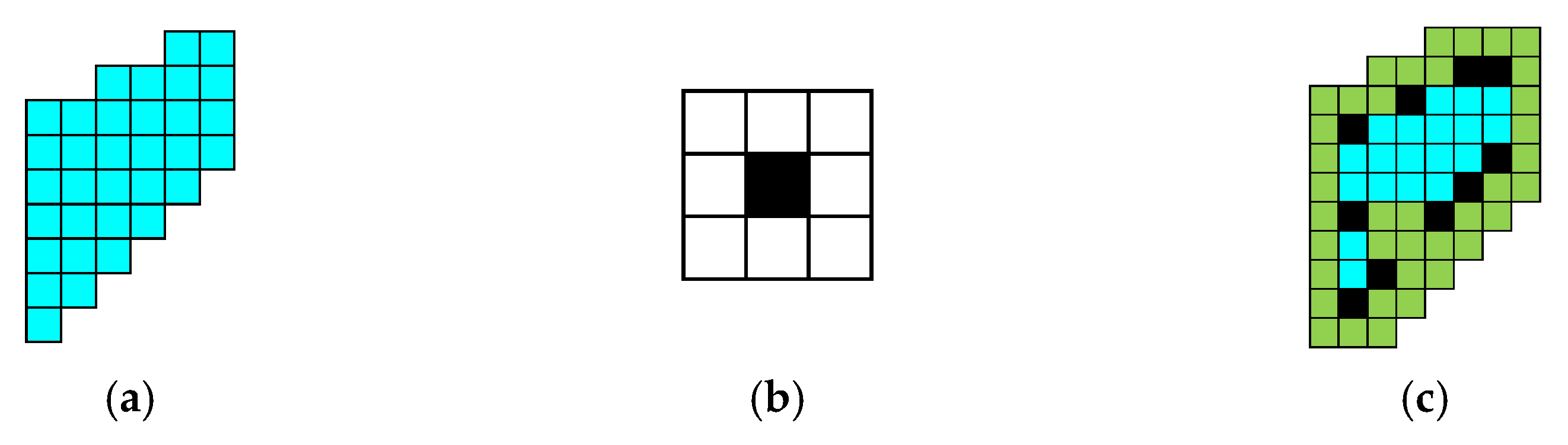
3.2. Establishment of Cross-Shaped Gate Model
- (1)
- When 0 ≤ l(ti) < l1, the following obtains:
- (2)
- When l1 ≤ l(ti) < l3, the following obtains:
- (3)
- When l3 ≤ l(ti), the following obtains:
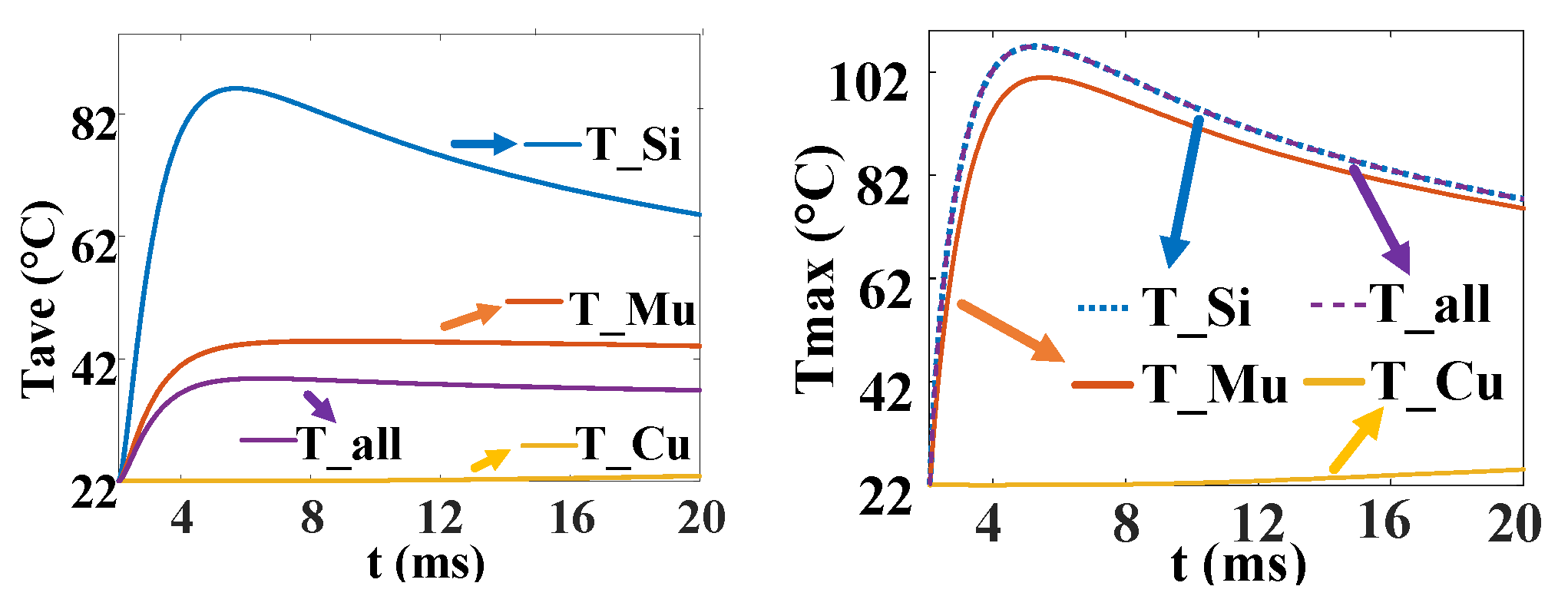
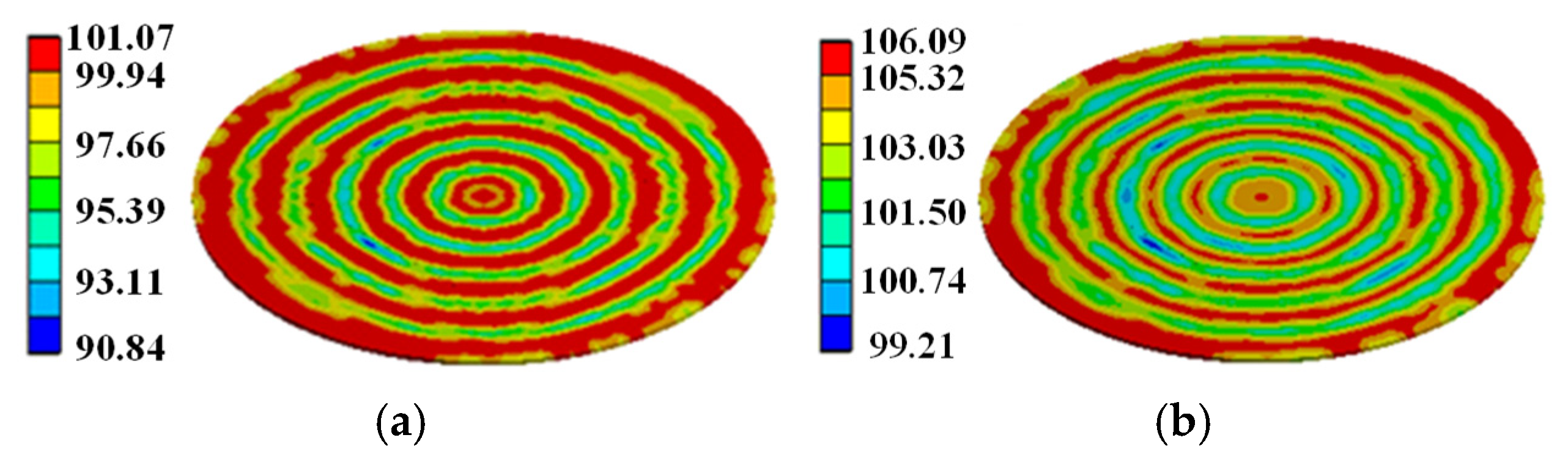
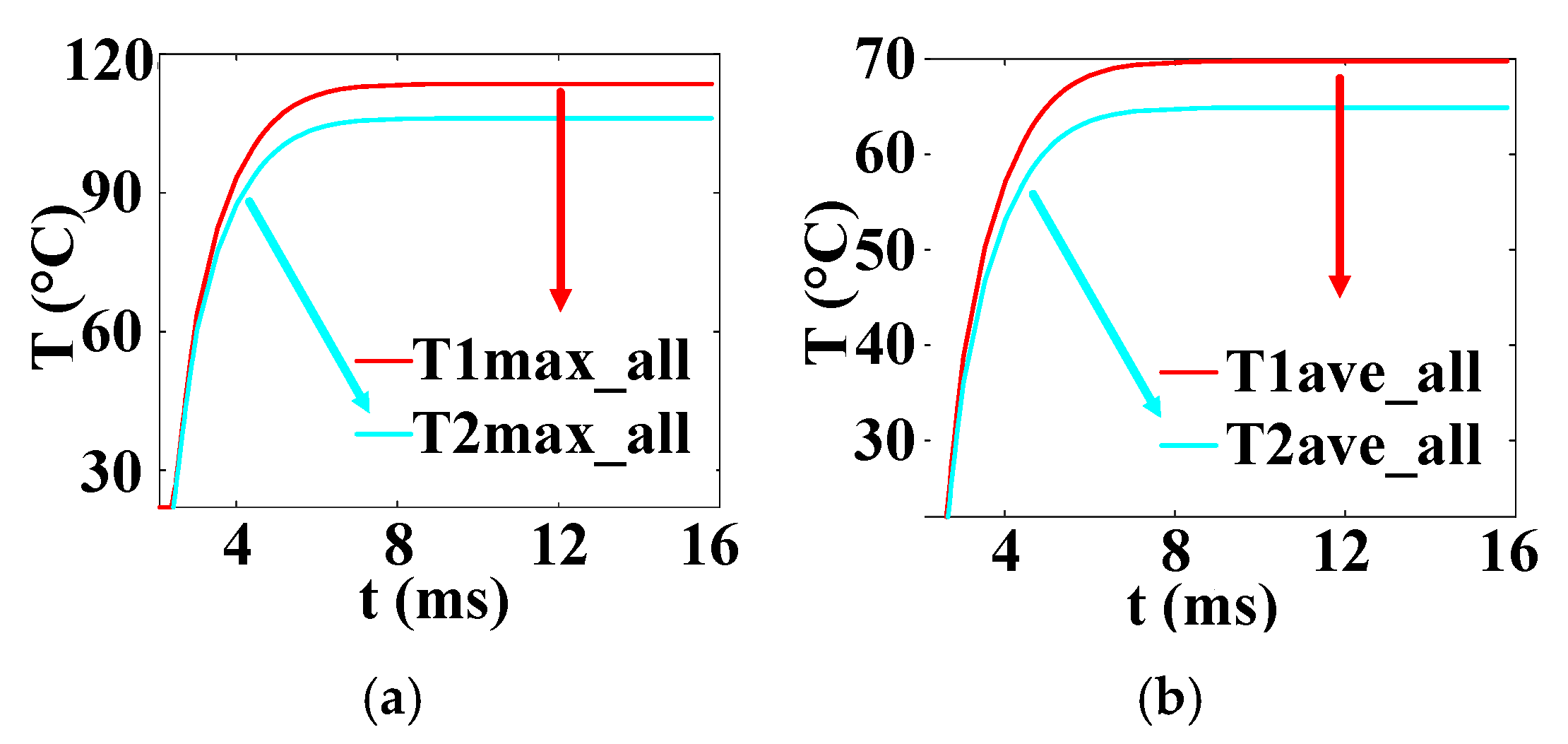
3.3. Solution and Analysis of the Model
3.4. Establishment of Complex Gate Model
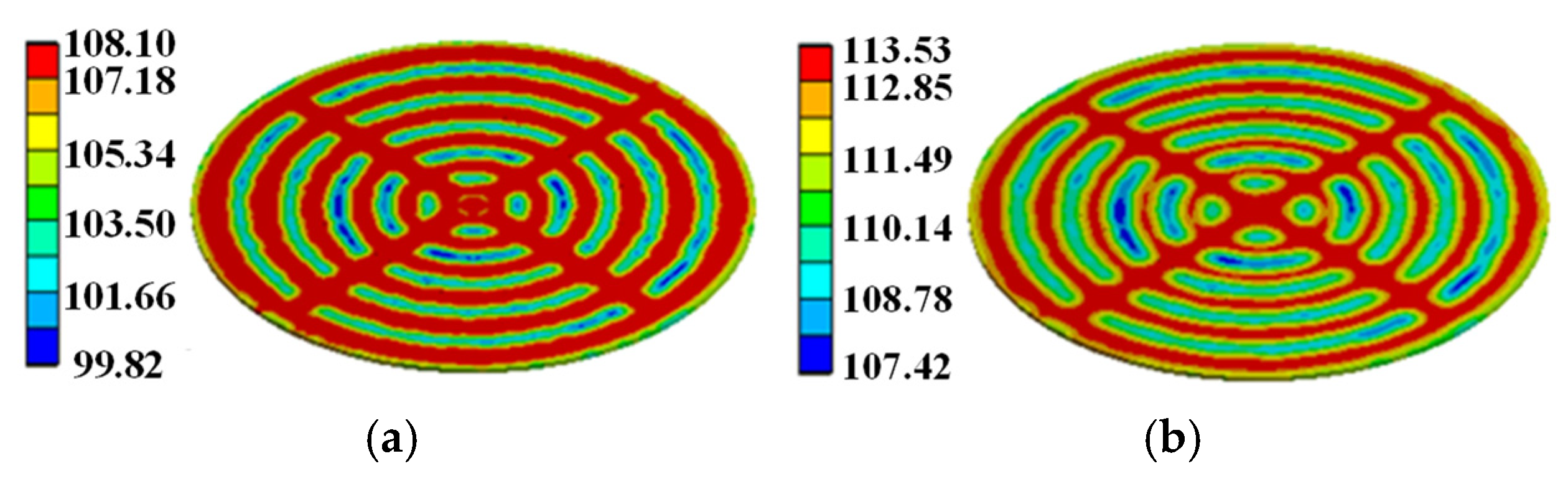
3.5. Solution and Analysis of the Model
4. Conclusions
- (1)
- In order to clarify the influence of different gate patterns on the thermal distribution of thyristors, a numerical model of expansion is established for simple and regular gate patterns such as cross patterns, and accurate numerical solutions can be obtained. Aiming at the irregular complex gate pattern, a general expansion model is established, which can accurately simulate the turn-on and expansion process of the complex gate pattern;
- (2)
- Considering the nonuniform distribution of current and temperature inside the silicon wafer, a three-dimensional finite element model of the thyristor is established. The transient temperature distribution in thyristors with cross–concentric-circle-, snowflake-, and branch-gate patterns during the turn-on process under pulse conditions is simulated. The results show that the branch-type thyristor has the lowest local and average temperature rise and the best thermal characteristics. The average temperature rise in the snowflake type is approximately equal to that in the branch type, and the maximum temperature rise is slightly higher than that in the branch type. The local and average temperature rise in the cross–concentric-circle type is the highest, and the thermal characteristics are the worst;
- (3)
- The cyclic surge current test was carried out on different types of thyristors. The cross–concentric-circle type evidenced thermal breakdown failure after dozens of times, while the leakage current test of the branch type and snowflake type was still normal after 5000 surge discharge cycles. Combined with the cyclic surge test and simulation results, the impact of the gate area on the temperature rise in the thyristor is further analyzed. Due to the decrease in the cathode area, the thyristor with a large gate area may have a higher temperature rise.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vobecký, J.; Schulze, H.J.; Streit, P.; Niedernostheide, F.J.; Botan, V.; Przybilla, J. Silicon thyristors for ultrahigh power (GW) applications. IEEE Trans. Electron Devices 2017, 64, 760–768. [Google Scholar] [CrossRef]
- Chaudhuri, D.; Dalvi, S.; Khatri, M.; Chatterjee, S.; Bhuvaneswari, G. Design of gate drive circuit for thyristor stack in electromagnetic railgun by load-line analysis. IEEE Trans. Plasma Sci. 2020, 49, 383–388. [Google Scholar] [CrossRef]
- Mojab, A.; Mazumder, S.K. Design and characterization of high-current optical Darlington transistor for pulsed-power applications. IEEE Trans. Electron Devices 2017, 64, 769–778. [Google Scholar] [CrossRef]
- Toulon, G.; Bourennane, A.; Isoird, K. Analysis and optimization of a thyristor structure using backside Schottky contacts suited for the high temperature. IEEE Trans. Electron Devices 2013, 60, 3814–3820. [Google Scholar] [CrossRef]
- Brand, H.; Selberherr, S. Two-dimensional simulation of thermal runaway in a nonplanar GTO-thyristor. IEEE Trans. Electron Devices 1995, 42, 2137–2146. [Google Scholar] [CrossRef]
- Fabis, P.M.; Shum, D.; Windischmann, H. Thermal modeling of diamond-based power electronics packaging. In Proceedings of the Fifteenth Annual IEEE Semiconductor Thermal Measurement and Management Symposium, San Diego, CA, USA, 9–11 March 1999; pp. 98–104. [Google Scholar] [CrossRef]
- Yang, S.; Bryant, A.; Mawby, P.; Xiang, D.; Ran, L.; Tavner, P. An industry-based survey of reliability in power electronic converters. IEEE Trans. Ind. Appl. 2011, 47, 1441–1451. [Google Scholar] [CrossRef]
- Marcantonio, V.; Monarca, D.; Colantoni, A.; Cecchini, M. Ultrasonic waves for materials evaluation in fatigue, thermal and corrosion damage: A review. Mech. Syst. Signal Process. 2019, 120, 32–42. [Google Scholar] [CrossRef]
- Walters, P.A. Step-like shifts in the voltage current characteristics of power thyristors and their effect on transient thermal impedance determinations. IEEE Trans. Electron Devices 1969, 16, 497–500. [Google Scholar] [CrossRef]
- Meng, H.; Zhu, A.; Zuo, L.; Luo, H.; Xin, Z.; Li, W. Online junction temperature extraction with gate voltage under non-trigger current for high-voltage thyristor. IEEE Trans. Power Electron. 2023, 38, 10574–10578. [Google Scholar] [CrossRef]
- Kuang, F.; Song, Z.; Mao, M.; Li, J.; Fu, P.; Li, C.; Yang, Y. Thermal Analysis of Power Thyristor Used in ITER Poloidal Field Converter. J. Fusion Energy 2016, 35, 214–220. [Google Scholar] [CrossRef]
- Arshad, M.; Jamil, E.; Shuja, A.; Qayyum, F.; Hassan, G. Modelling and simulation of design variants for the development of 4H-SiC thyristors. Silicon 2022, 14, 10313–10325. [Google Scholar] [CrossRef]
- Liu, H.; Wang, J.; Liang, S.; Yu, H.; Deng, G.; Wang, Y.; Shen, Z.J. Modeling and analysis of SiC GTO thyristor’s dynamic turn-on transient. IEEE Trans. Electron Devices 2022, 69, 6241–6248. [Google Scholar] [CrossRef]
- Bencic, Z.; Besic, A.; Damjanic, F.; Selih, J. Estimation of transient thermal impedance for constant current of a power thyristor using temperature field calculation. IEEE Trans. Electron Devices 1993, 40, 1885–1887. [Google Scholar] [CrossRef]
- Liang, N.; Tian, J.; Liu, C.; Gou, Y.; Zhuo, F.; Wang, F. Research on reliability assessment of thyristor in HVDC converter valve. J. Phys. Conf. Ser. 2019, 1187, 022016. [Google Scholar] [CrossRef]
- González, B.; Lazaro, A.; Rodríguez, R. Gate geometry-dependent thermal impedance of depletion mode HEMTs. IEEE Trans. Electron Devices 2023, 70, 5217–5222. [Google Scholar] [CrossRef]
- Yang, X.; Heng, K.; Dai, X.; Wu, X.; Liu, G. A temperature-dependent cauer model simulation of IGBT module with analytical thermal impedance characterization. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 3055–3065. [Google Scholar] [CrossRef]
- An, T.; Zhou, R.; Qin, F.; Dai, Y.; Gong, Y.; Chen, P. Comparative study of the parameter acquisition methods for the cauer thermal network model of an IGBT module. Electronics 2023, 12, 1650. [Google Scholar] [CrossRef]
- Wu, J.; Fu, X.; Lei, R.; Liu, S.; Wang, S.; Zhao, Y. Transient temperature field analysis of thyristor turn-on process under narrow pulse width and large current. IOP Conf. Ser. Earth Environ. Sci. 2019, 252, 032069. [Google Scholar] [CrossRef]
- Feng, B.; Liu, J.; Li, Y.; Fu, Y.; He, M. Thermal behaviors of thyristors in repetitive pulsed power applications. IEEE Trans. Plasma Sci. 2022, 50, 3659–3667. [Google Scholar] [CrossRef]
- Damjanovic, A. Protection of medium voltage SCR driven soft-starter from high-frequency switching transients. IEEE Trans. Ind. Appl. 2016, 52, 4652–4655. [Google Scholar] [CrossRef]
- Tsinghua University. Principle and Design of High Power Silicon Controlled Element; People’s Education Press: Beijing, China, 1975; pp. 39–64. [Google Scholar]
- Tang, L. Semiconductor Craft and Device Simulation Software Silvaco TCAD; Tsinghua University Press: Beijing, China, 2014; pp. 122–130. [Google Scholar]
- Schroder, D.K. The concept of generation and recombination lifetimes in semiconductors. IEEE Trans. Electron Devices 1982, 29, 1336–1338. [Google Scholar] [CrossRef]
- Klaassen, D.B.M. A Unified Mobility Model for Device Simulation-II. Temperature Dependence of Carrier Mobility and Lifetime. Solid-State Electron. 1992, 35, 961–967. [Google Scholar] [CrossRef]
- Klaassen, D.B.M. A unified mobility model for device simulation—I. Model equations and concentration dependence. Solid-State Electron. 1992, 35, 953–959. [Google Scholar] [CrossRef]
- Selberherr, S. Analysis and Simulation of Semiconductor Devices; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Van Overstraeten, R.; De Man, H. Measurement of the ionization rates in diffused silicon pn junctions. Solid-State Electron. 1970, 13, 583–608. [Google Scholar] [CrossRef]
- Slotboom, J.W.; Graaff, H.C.D. Measurements of Bandgap Narrowing in Si Bipolar Transistors. Solid State Electron. 1976, 19, 857–862. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, J.; Chen, R.; Li, D.; Yan, L.; Cheng, X.; Liu, J. Effects of Short Pulse on Lateral Current Spreading in Turn-on Process of Pulsed Thyristors Under Inductive Load. IEEE Trans. Plasma Sci. 2023, 51, 184–192. [Google Scholar] [CrossRef]
- Dodson, W.H.; Longini, R.L. Probed determination of turn-on spread of large area thyristors. IEEE Trans. Electron Devices 1966, 5, 478–484. [Google Scholar] [CrossRef]
- Ruhl, H.J. Spreading velocity of the active area boundary in a thyristor. IEEE Trans. Electron Devices 1970, 17, 672–680. [Google Scholar] [CrossRef]
- Bergman, G.D. The gate-triggered turn-on process in thyristors. Solid-State Electron. 1965, 8, 757–765. [Google Scholar] [CrossRef]
- Orhei, C.; Vasiu, R. An analysis of extended and dilated filters in sharpening algorithms. IEEE Access 2023, 11, 81449–81465. [Google Scholar] [CrossRef]
- Ma, S.Y.; Khalil, A.; Hajjdiab, H.; Eleuch, H. Quantum dilation and erosion. Appl. Sci. 2020, 10, 4040. [Google Scholar] [CrossRef]
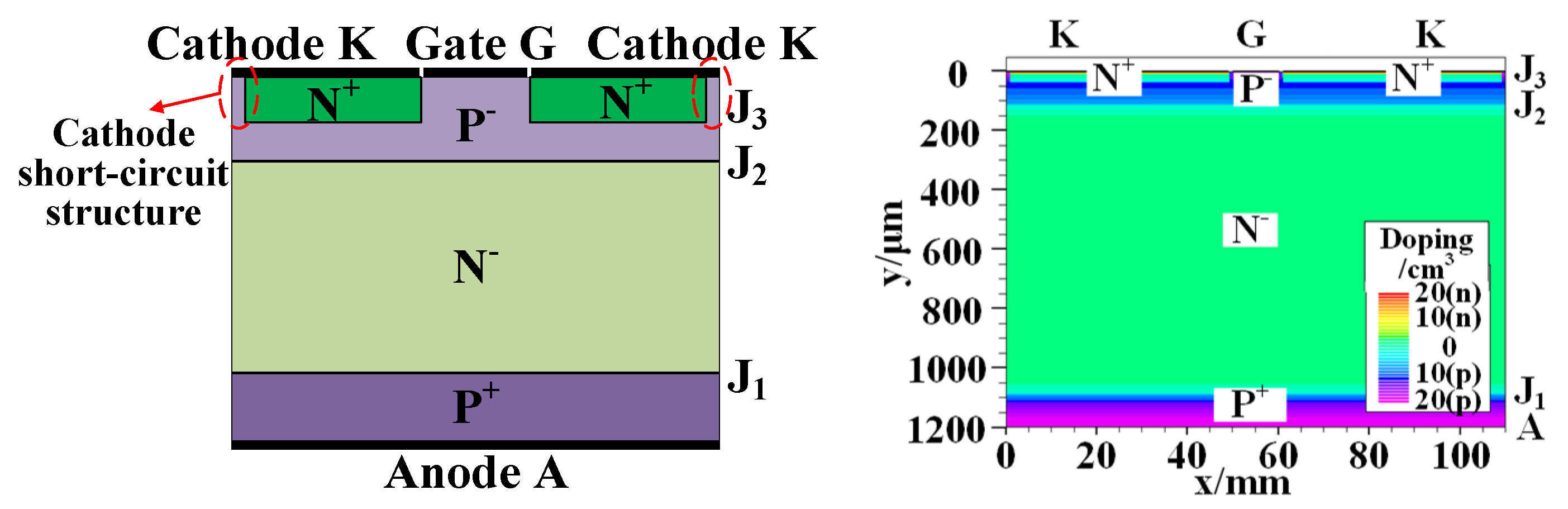
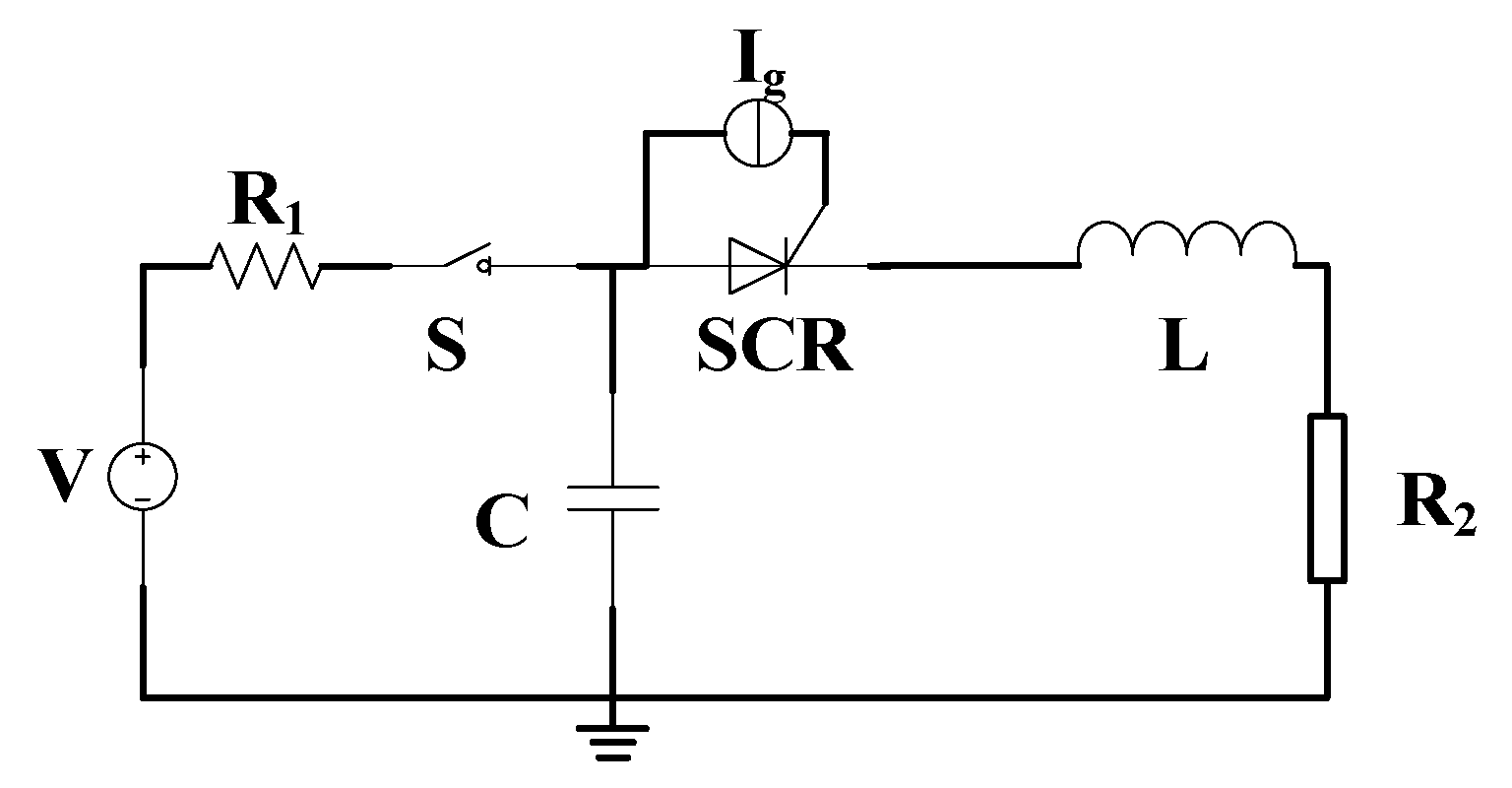
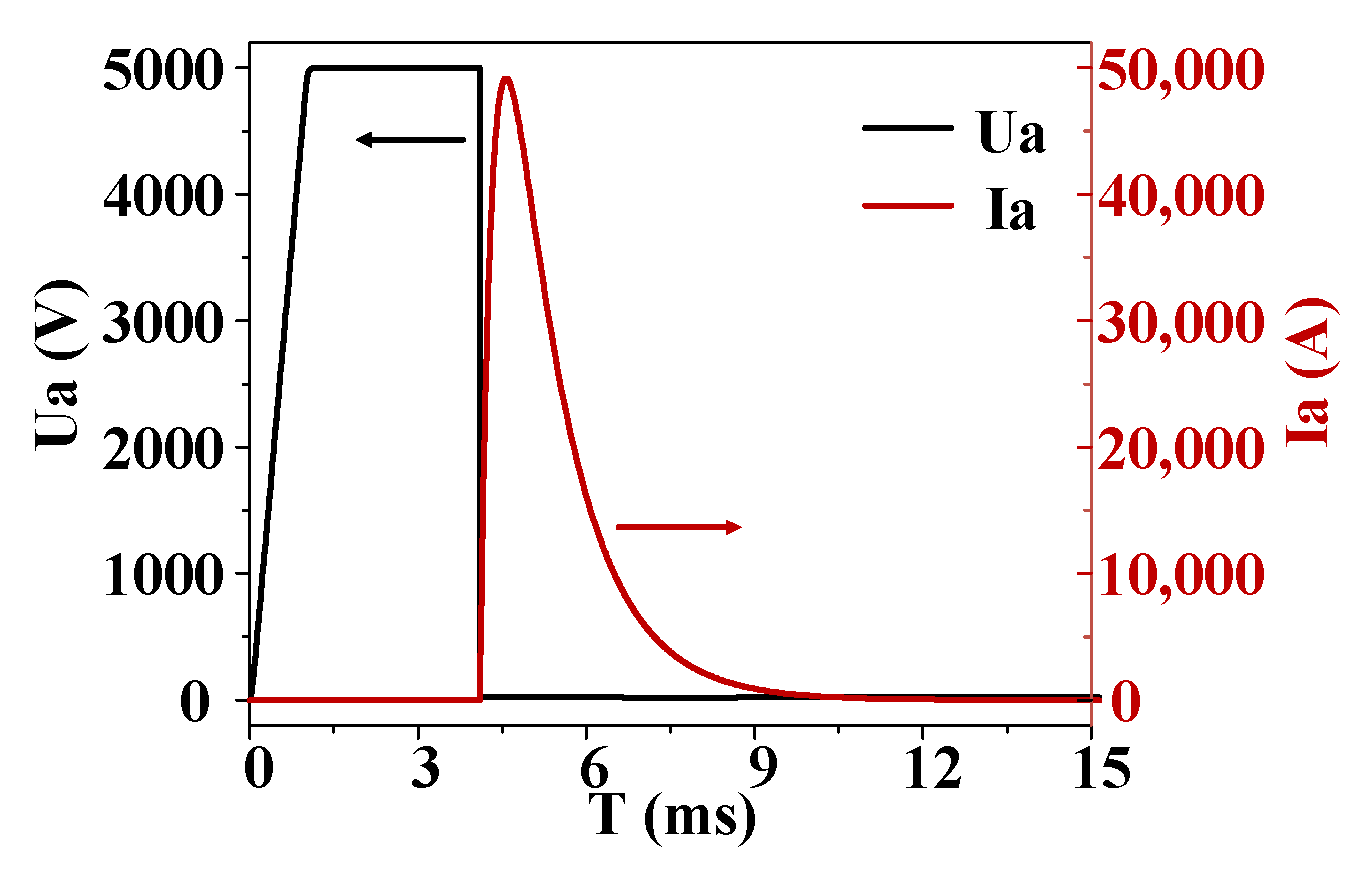
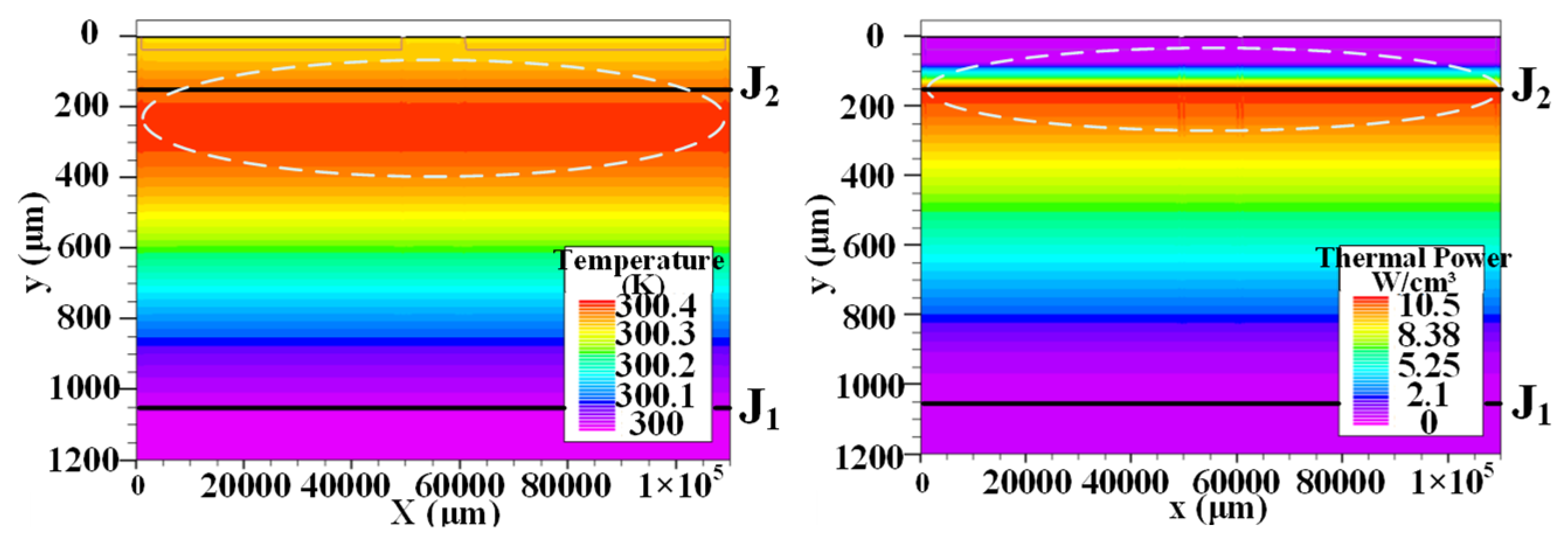






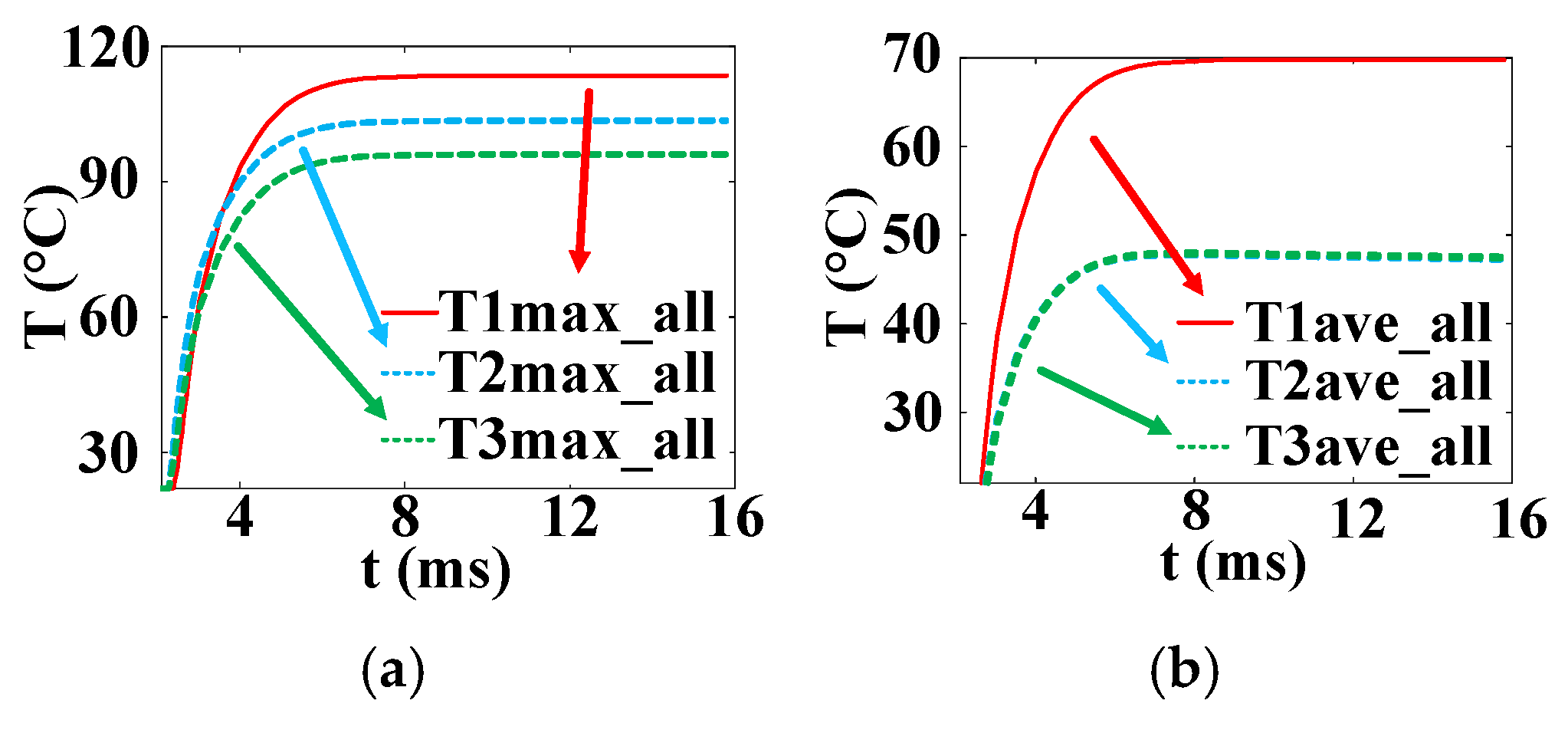
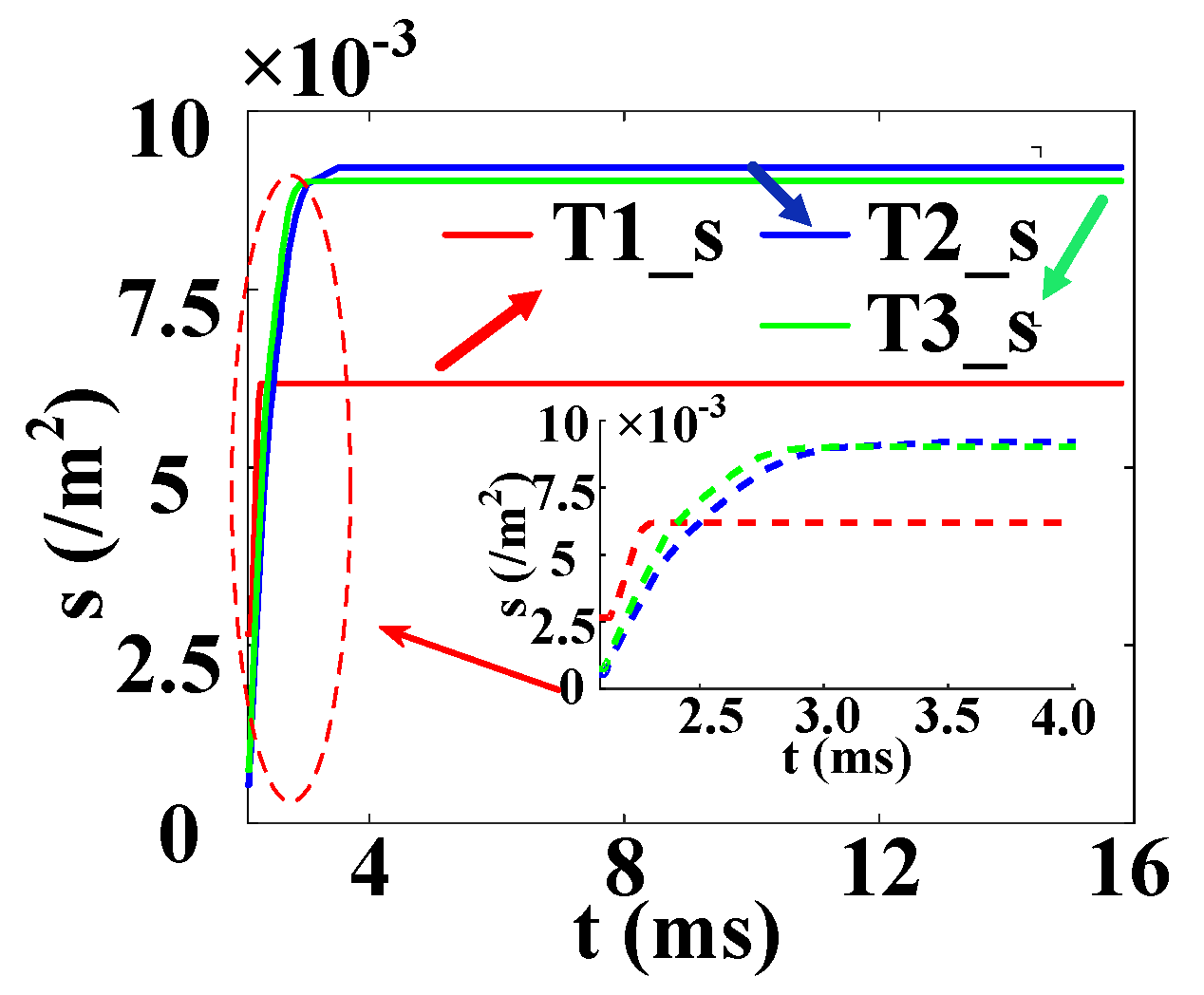
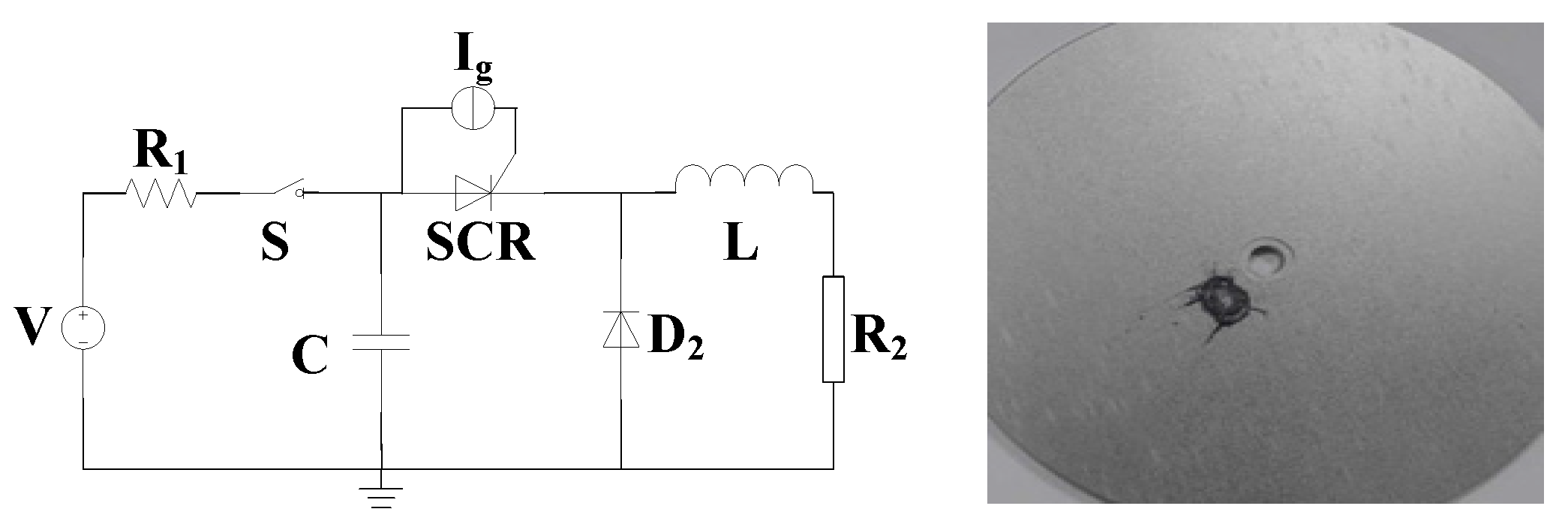
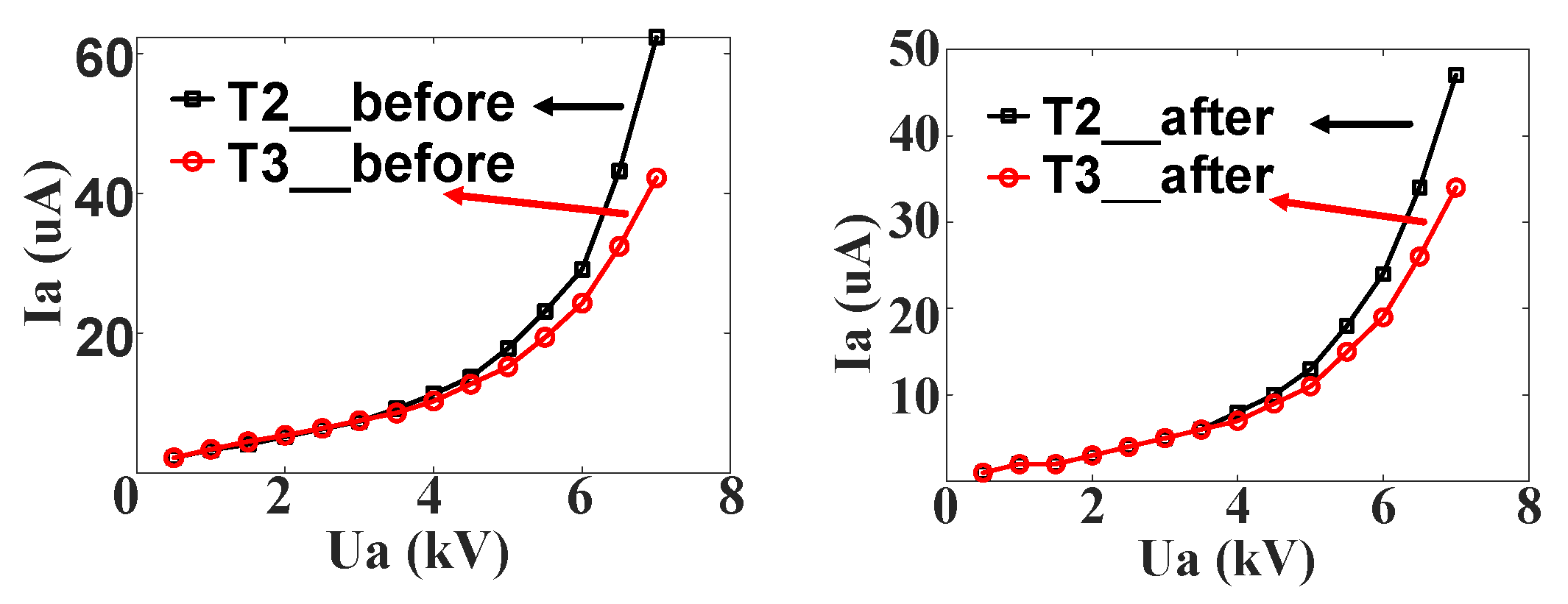
| Region | Length (μm) | Width (μm) | Doping Type | Max Doping (cm−3) |
|---|---|---|---|---|
| Anode (P+, bottom) | 110,000 | 150 | P | 1020 |
| Drift region (N−, base) | 110,000 | 900 | N | 1013 |
| Base region (P−, base) | 110,000 | 112 | P | 1017 |
| Cathode (N+, top) | 98,000 | 38 | N | 1020 |
| Parameter | Value | Physical Meaning | Unit |
|---|---|---|---|
| a | 0.75 | Constant | |
| c | 100 | Constant | |
| n | 4~6 | Constant | |
| A | 5.29 × 10−5 | Constant | |
| q | 1.60 × 10−19 | Electronic charge | C |
| Lp | The diffusion length of holes | cm | |
| VB | Avalanche breakdown voltage of PN junction | V | |
| VBF | Forward turning voltage | V | |
| ρn | The resistivity of the base region | Ω·cm | |
| Xm(N1) | Widening of the space charge region in the N− base region | cm | |
| Wn(N1) | The width of the N− base region | cm | |
| Nn | Doping concentration in the N− base region | cm−3 |
| Parameter | Value |
|---|---|
| Klaassen low-field mobility model | |
| Saturation velocity model | |
| Klaassen composite model | |
| Bandgap narrowing model | |
| Collision ionization model | |
| Lattice self-heating model |
| Symbol | Physical Meaning | Unit |
|---|---|---|
| μn0 (μp0) | The total mobility of low field electrons (holes) | cm2/V·s |
| μnL (μpL) | Electron (hole) mobility caused by lattice scattering | cm2/V·s |
| μnD (μpD) | Electron (hole) mobility caused by donor scattering | cm2/V·s |
| μnA (μpA) | Electron (hole) mobility caused by host scattering | cm2/V·s |
| μnp (μpn) | The effect of hole (electron) scattering on electron (hole) mobility | cm2/V·s |
| E | Local electric field | V/cm |
| VSATN (VSATP) | The saturation velocity of electrons (holes) | cm/s |
| τn (τp) | Concentration-dependent electron (hole) lifetime | s |
| τ0.n (τ0.p) | The intrinsic lifetime of electrons (holes) | s |
| n (p) | Concentration of electrons (holes) | cm−3 |
| CSRH.n (CSRH.p) | Electron (hole) SRH recombination coefficient | cm3/s |
| CAug.n (CAug.p) | Auger recombination coefficient of electrons (holes) | cm6/s |
| TL | Lattice temperature | K |
| N | Total doping concentration | cm−3 |
| ΔVg0 | Bandgap width | mV |
| αn(E) (αp(E)) | Electron (hole) ionization rate | cm−1 |
| C | Heat capacity per unit volume | J/K |
| λ | Thermal conductivity | W/(m·K) |
| H | Heat generation rate | W/m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Zhang, X.; Lu, J.; Dai, Y.; Ma, T.; Zhu, B. Investigation of Transient Thermal Behavior in Thyristors Under Pulse Conditions. Micromachines 2025, 16, 291. https://doi.org/10.3390/mi16030291
Zhang G, Zhang X, Lu J, Dai Y, Ma T, Zhu B. Investigation of Transient Thermal Behavior in Thyristors Under Pulse Conditions. Micromachines. 2025; 16(3):291. https://doi.org/10.3390/mi16030291
Chicago/Turabian StyleZhang, Guanxiang, Xiao Zhang, Junyong Lu, Yufeng Dai, Tao Ma, and Bofeng Zhu. 2025. "Investigation of Transient Thermal Behavior in Thyristors Under Pulse Conditions" Micromachines 16, no. 3: 291. https://doi.org/10.3390/mi16030291
APA StyleZhang, G., Zhang, X., Lu, J., Dai, Y., Ma, T., & Zhu, B. (2025). Investigation of Transient Thermal Behavior in Thyristors Under Pulse Conditions. Micromachines, 16(3), 291. https://doi.org/10.3390/mi16030291





