Analysis of Collapse–Snapback Phenomena in Capacitive Micromachined Ultrasound Transducers
Abstract
1. Introduction
2. Materials and Methods
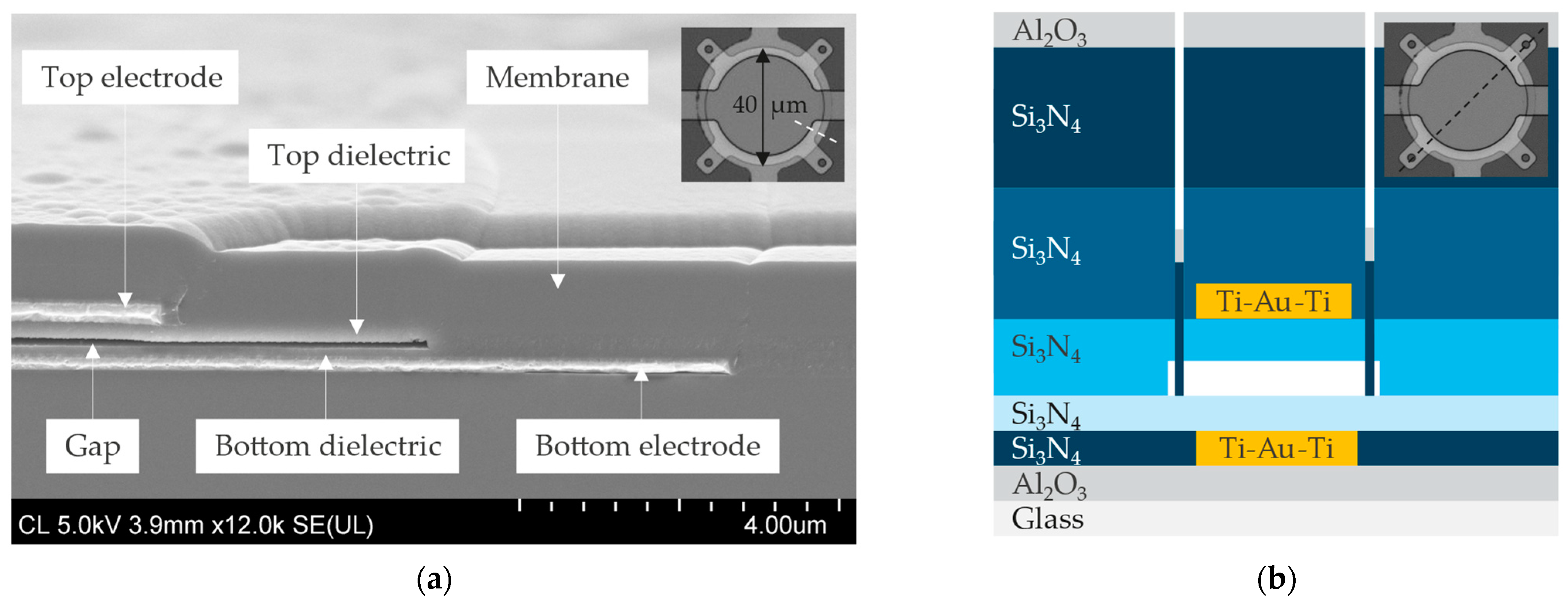
2.1. Fabrication Methods
2.2. Electrical Characterization Methods
2.3. Electromechanical Characterization Methods
2.4. Analytical Methods
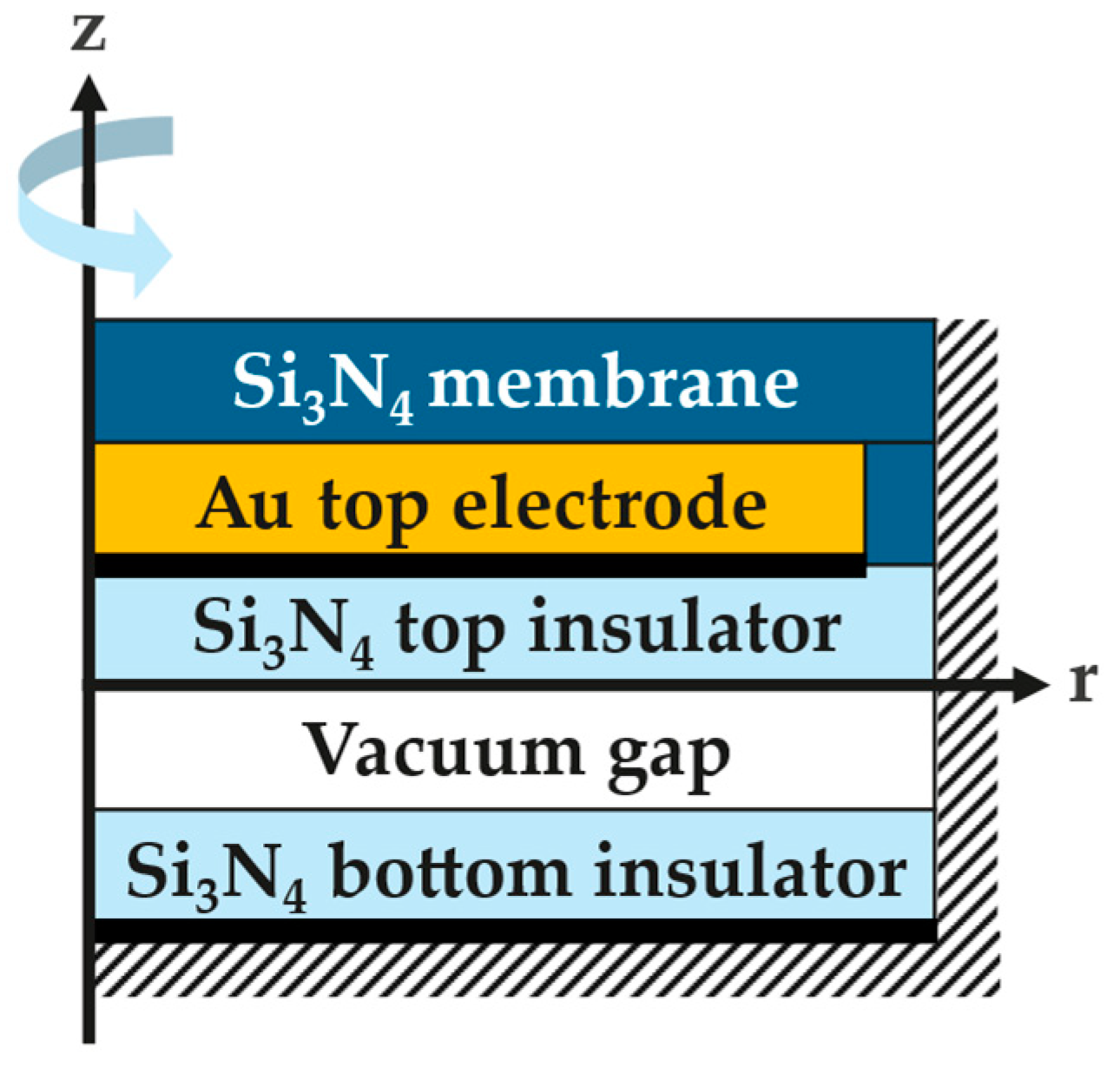
2.5. Simulation Methods
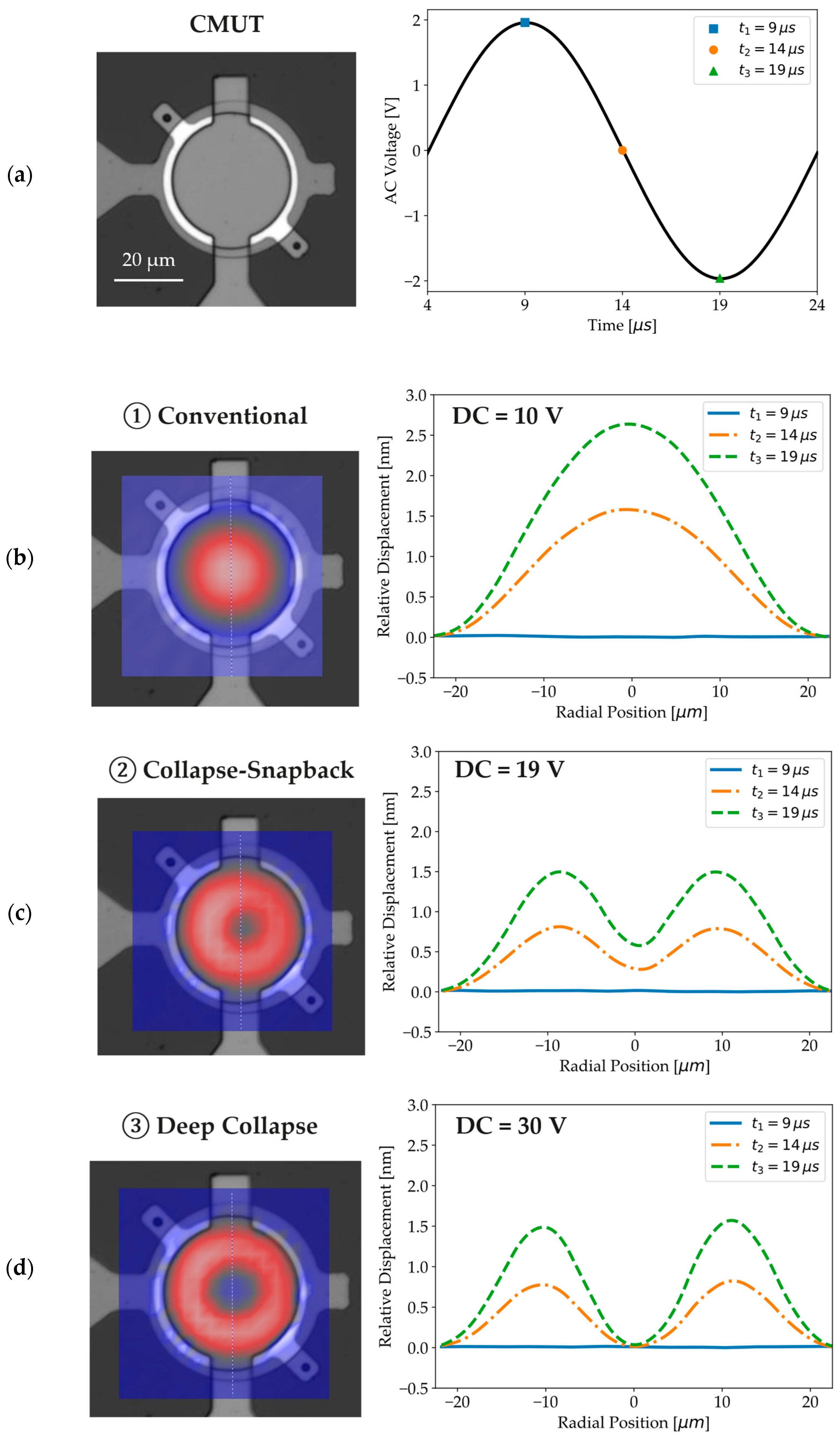
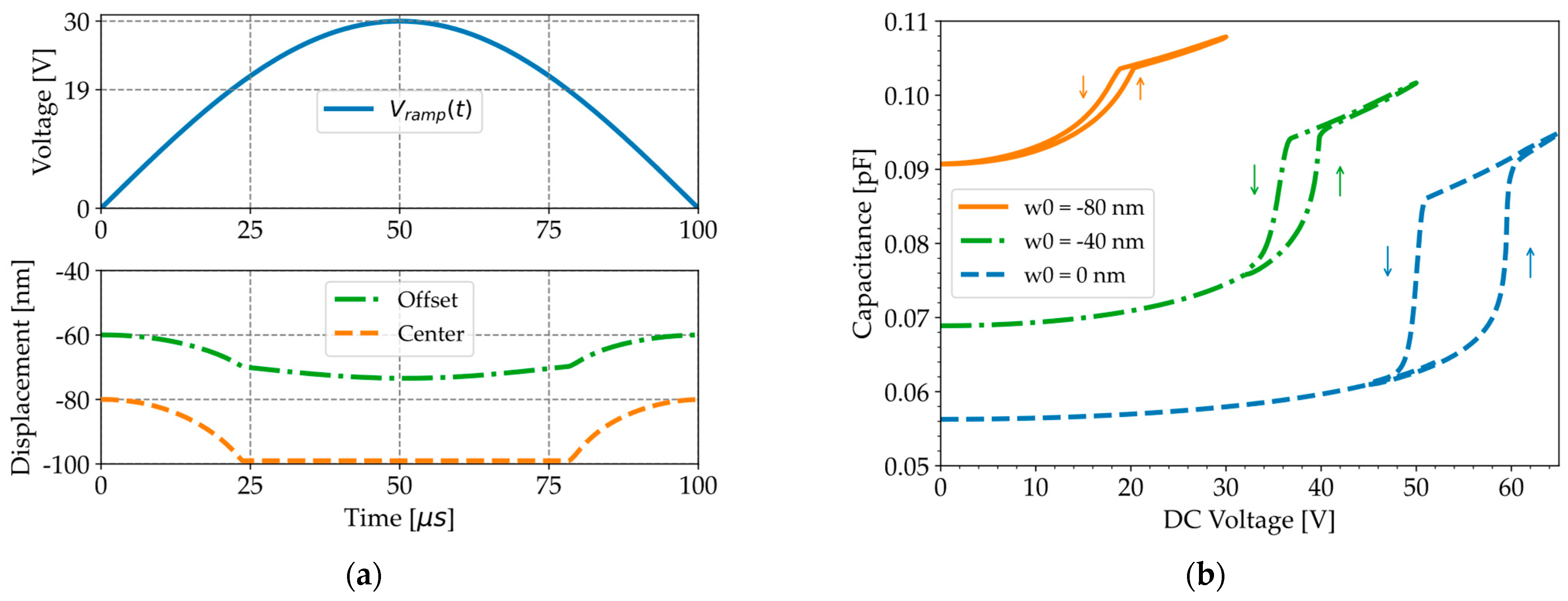
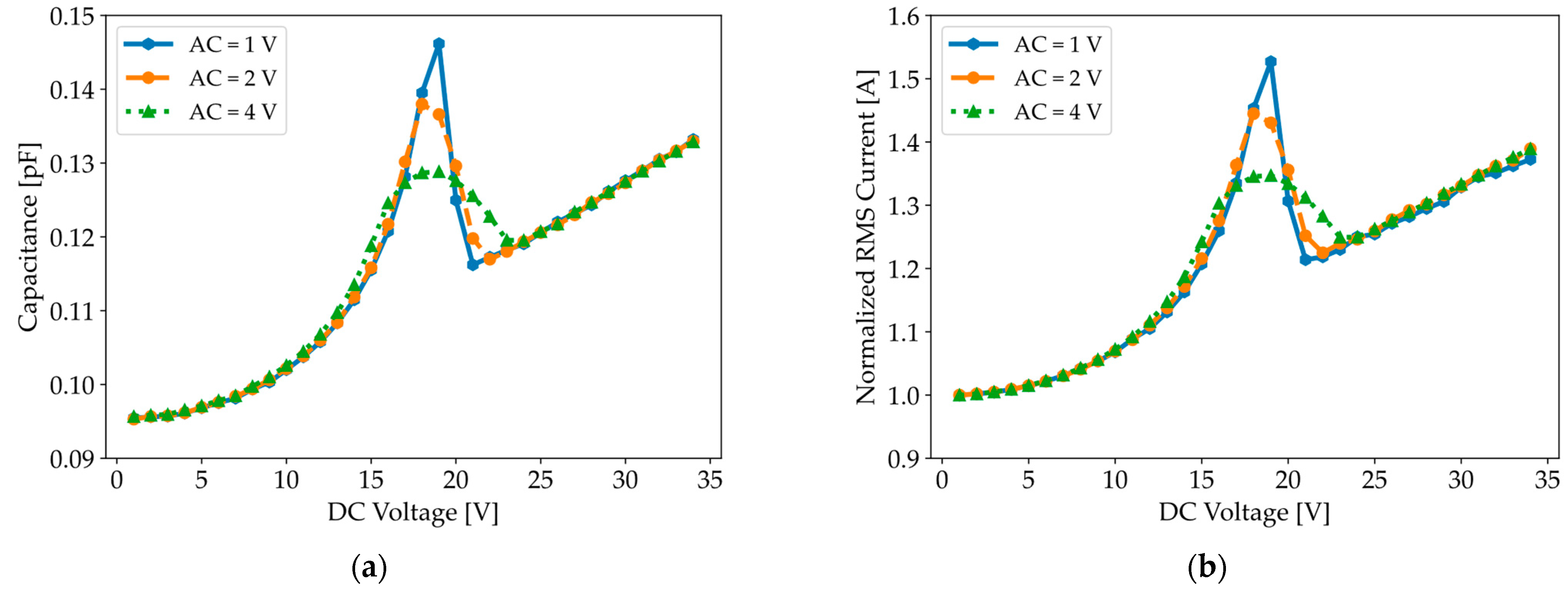
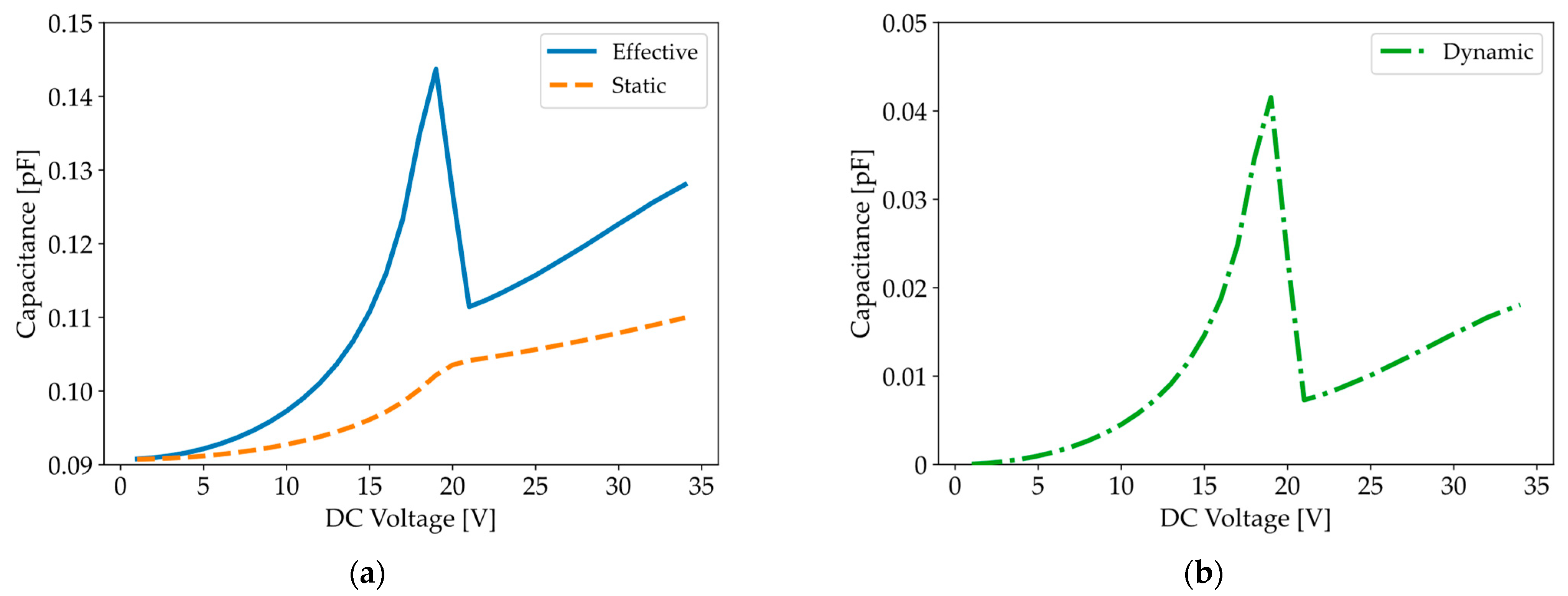
3. Results and Discussion
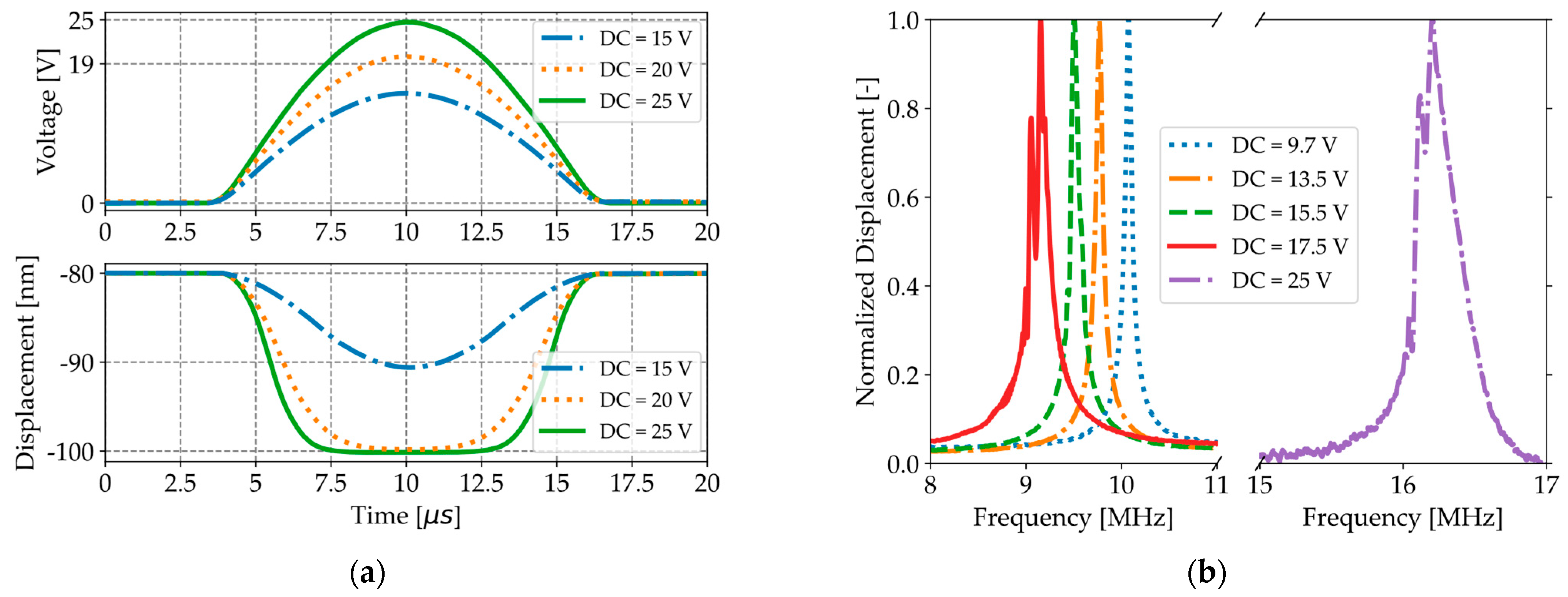
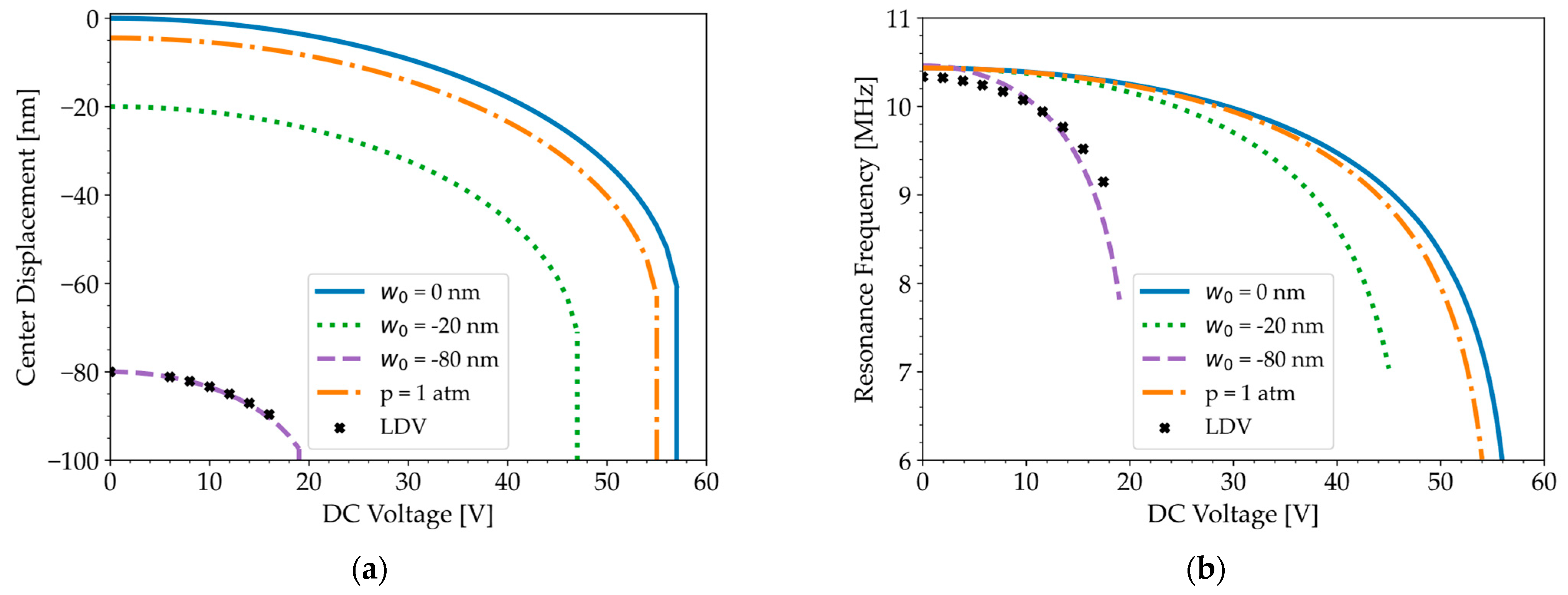
3.1. Validation of the COMSOL Model
3.2. C-V Curve and Mode Shapes: Experimental Results from LCR Meter and LDV
3.3. C-V Curve: Simulation Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, L.-F.; Huang, Q.-A.; Han, L. RF MEMS Switch. In Micro Electro Mechanical Systems; Huang, Q.-A., Ed.; Springer: Singapore, 2018; pp. 1039–1076. ISBN 978-981-10-5945-2. [Google Scholar]
- Park, K.K.; Oralkan, O.; Khuri-Yakub, B.T. Comparison of conventional and collapse-mode CMUT in 1-D array configuration. In Proceedings of the 2011 IEEE International Ultrasonics Symposium, Orlando, FL, USA, 18–21 October 2011; pp. 1000–1003. [Google Scholar]
- Olcum, S.; Yamaner, F.Y.; Bozkurt, A.; Atalar, A. Deep-collapse operation of capacitive micromachined ultrasonic transducers. IEEE Trans. Ultrason. Ferroelect. Freq. Contr. 2011, 58, 2475–2483. [Google Scholar] [CrossRef] [PubMed]
- Pekař, M.; Dittmer, W.U.; Mihajlović, N.; van Soest, G.; de Jong, N. Frequency Tuning of Collapse-Mode Capacitive Micromachined Ultrasonic Transducer. Ultrasonics 2017, 74, 144–152. [Google Scholar] [CrossRef] [PubMed]
- Merbeler, F.; Wismath, S.; Haubold, M.; Bretthauer, C.; Kupnik, M. Ultra-Low-Voltage Capacitive Micromachined Ultrasonic Transducers with Increased Output Pressure Due to Piston-Structured Plates. Micromachines 2022, 13, 676. [Google Scholar] [CrossRef] [PubMed]
- Yamaner, F.Y.; Zhang, X.; Oralkan, Ö. Fabrication of anodically bonded capacitive micromachined ultrasonic transducers with vacuum-sealed cavities. In Proceedings of the 2014 IEEE International Ultrasonics Symposium, Chicago, IL, USA, 3–6 September 2014; pp. 604–607. [Google Scholar]
- Park, K.K.; Oralkan, O.; Khuri-Yakub, B.T. A comparison between conventional and collapse-mode capacitive micromachined ultrasonic transducers in 10-MHz 1-D arrays. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2013, 60, 1245–1255. [Google Scholar] [CrossRef] [PubMed]
- Munir, J.; Ain, Q.; Lee, H.J. Reliability issue related to dielectric charging in capacitive micromachined ultrasonic transducers: A review. Microelectron. Reliab. 2019, 92, 155–167. [Google Scholar] [CrossRef]
- Elata, D.; Bamberger, H. On the Dynamic Pull-In of Electrostatic Actuators With Multiple Degrees of Freedom and Multiple Voltage Sources. J. Microelectromech. Syst. 2006, 15, 131–140. [Google Scholar] [CrossRef]
- Seeger, J.; Boser, B. Parallel-plate driven oscillations and resonant pull-in. In Proceedings of the Solid-State Sensor, Actuator and Microsystems Workshop, Hilton Head Island, SC, USA, 2–6 June 2002. [Google Scholar]
- Lin, D.-S.; Zhuang, X.; Wong, S.H.; Kupnik, M.; Khuri-Yakub, B.T. Encapsulation of Capacitive Micromachined Ultrasonic Transducers Using Viscoelastic Polymer. J. Microelectromech. Syst. 2010, 19, 1341–1351. [Google Scholar] [CrossRef]
- Park, K.K.; Kupnik, M.; Lee, H.J.; Oralkan, O.; Khuri-Yakub, B.T. Zero-bias resonant sensor with an oxide-nitride layer as charge trap. In Proceedings of the SENSORS, 2010 IEEE, Waikoloa, HI, USA, 1–4 November 2010; pp. 1024–1028. [Google Scholar] [CrossRef]
- Dew, E.B.; Kashani Ilkhechi, A.; Maadi, M.; Haven, N.J.M.; Zemp, R.J. Outperforming piezoelectric ultrasonics with high-reliability single-membrane CMUT array elements. Microsyst. Nanoeng. 2022, 8, 59. [Google Scholar] [CrossRef] [PubMed]
- Senturia, S.D. Microsystem Design; Springer: New York, NY, USA, 2001; ISBN 978-0-7923-7246-2. [Google Scholar]
- Bayram, B.; Haeggstrom, E.; Yaralioglu, G.G.; Khuri-Yakub, P. A new regime for operating capacitive micromachined ultrasonic transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2003, 50, 1184–1190. [Google Scholar] [CrossRef]
- Huang, Y.; Haeggstrom, E.; Bayram, B.; Zhuang, Z.; Ergun, A.S.; Cheng, C.H.; Khuri-Yakub, B.T. Collapsed regime operation of capacitive micromachined ultrasonic transducers based on wafer-bonding technique. In Proceedings of the IEEE Symposium on Ultrasonics, Honolulu, HI, USA, 5–8 October 2003; Volume 2, pp. 1161–1164. [Google Scholar]
- Pekař, M.; van Nispen, S.H.M.; Fey, R.H.B.; Shulepov, S.; Mihajlović, N.; Nijmeijer, H. A fluid-coupled transmitting CMUT operated in collapse mode: Semi-analytic modeling and experiments. Sens. Actuators A Phys. 2017, 267, 474–484. [Google Scholar] [CrossRef]
- Olçum, S. Deep collapse mode capacitive micromachined ultrasonic transducers. Dictoral Dissertation, Bilkent University, Ankara, Turkey, 2010. [Google Scholar]
- Roy, R.; Farhanieh, O.; Ergun, S.; Bozkurt, A. Fabrication of High-Efficiency CMUTs With Reduced Parasitics Using Embedded Metallic Layers. IEEE Sens. J. 2017, 17, 4013–4020. [Google Scholar] [CrossRef]
- Xu, T.; Tekes, C.; Degertekin, F. CMUTs with high-K atomic layer deposition dielectric material insulation layer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 2121–2131. [Google Scholar] [CrossRef] [PubMed]
- Robertson, J.; Wallace, R.M. High-K materials and metal gates for CMOS applications. Mater. Sci. Eng. R Rep. 2015, 88, 1–41. [Google Scholar] [CrossRef]
- Keysight E4980A/AL Precision LCR Meter User’s Guide. Available online: https://www.keysight.com/us/en/assets/9018-05655/user-manuals/9018-05655 (accessed on 14 January 2025).
- Keysight. Impedance Measurement Handbook. Available online: https://www.keysight.com/us/en/assets/7018-06840/application-notes/5950-3000.pdf (accessed on 19 December 2024).
- Keysight. Quasi-Static Capacitance Voltage Measurement Techniques. Available online: https://www.keysight.com/us/en/assets/7018-04703/application-notes/5992-0436.pdf (accessed on 28 December 2024).
- Engholm, M.; Pedersen, T.; Thomsen, E.V. Modeling of plates with multiple anisotropic layers and residual stress. Sens. Actuators A Phys. 2016, 240, 70–79. [Google Scholar] [CrossRef]
- El-Damak, D.R.; Hegazi, E.; Ragai, H.F. Analytical design of circular CMUT cells in immersion. In Proceedings of the 2010 IEEE International Ultrasonics Symposium, San Diego, CA, USA, 11–14 October 2010; pp. 1865–1868. [Google Scholar]
- Leissa, A.W. Vibration of Plates; Scientific and Technical Information Division, National Aeronautics and Space Administration: Washington, DC, USA, 1969.
- Pursula, P.; Saarilahti, J.; Paul, O.; Viikari, V. Analytical electromechanical model for CMUTs with multi-layered, non-uniform diaphragm. In Proceedings MME 2012; MME: Ilmenau, Germany, 2012. [Google Scholar]
- Zhang, W.; Zhang, H.; Du, F.; Shi, J.; Jin, S.; Zeng, Z. Pull-In Analysis of the Flat Circular CMUT Cell Featuring Sealed Cavity. Math. Probl. Eng. 2015, 2015, 150279. [Google Scholar] [CrossRef]
- Olcum, S.; Senlik, M.N.; Atalar, A. Optimization of the gain-bandwidth product of capacitive micromachined ultrasonic transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2005, 52, 2211–2219. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Pull-In and Pull-Out Analysis of a Biased Resonator—2D. Available online: https://www.comsol.com/model/pull-in-and-pull-out-analysis-of-a-biased-resonator-2d-22141 (accessed on 14 January 2025).
- Dutta, S.; Pandey, A. Overview of residual stress in MEMS structures: Its origin, measurement, and control. J. Mater. Sci. Mater. Electron. 2021, 32, 1–37. [Google Scholar] [CrossRef]
- Sheploak, M.; Dugundji, J. Large Deflections of Clamped Circular Plates Under Initial Tension and Transitions to Membrane Behavior. J. Appl. Mech. 1998, 65, 107–115. [Google Scholar] [CrossRef]
- Malatkar, P.; Wong, S.F.; Pringle, T.; Loh, W.K. Pitfalls an engineer needs to be aware of during vibration testing. In Proceedings of the 56th Electronic Components and Technology Conference, San Diego, CA, USA, 30 May–2 June 2006; pp. 1887–1892. [Google Scholar]
- Yaralioglu, G.G.; Ergun, S.; Bayram, B.; Haeggstrom, E.; Khuri-Yakub, P. Calculation and Measurement of Electromechanical Coupling Coefficient of Capacitive Micromachined Ultrasonic Transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2003, 50, 449–456. [Google Scholar] [CrossRef] [PubMed]




| DC Bias | Current Range | Voltage Step | Integration Time | |
|---|---|---|---|---|
| QSCV | 0 V–35 V | 10 pA | = 0.5 V | = 1 s |
| Geometrical Parameter | Variable | Unit | Value |
|---|---|---|---|
| Membrane radius | µm | 20 | |
| Membrane thickness | nm | 1050 | |
| Top electrode thickness | nm | 250 | |
| Top insulator thickness | nm | 200 | |
| Sacrificial layer thickness | nm | 100 | |
| Bottom insulator thickness | nm | 100 |
| Material Parameter | Variable | Unit | Si3N4 | Au |
|---|---|---|---|---|
| Young’s modulus | GPa | 210 | 70 | |
| Poisson’s ratio | - | 0.23 | 0.44 | |
| Density | kg/m3 | 3000 | 19,300 | |
| Dielectric constant | - | 7 | - |
| Resonance Frequency at DC = 0 V [MHz] | Resonance Frequency at DC = 17.5 V [MHz] | Pull-In Voltage [V] | |
|---|---|---|---|
| Analytical model | 10.33 | 10.18 | 56.38 |
| COMSOL without initial deflection with full top-electrode coverage | 10.19 | 10.04 | 55.68 |
| Relative error | 1% | 1% | 1% |
| COMSOL without initial deflection with 85% top-electrode coverage | 10.43 | 10.30 | 57.12 |
| COMSOL with initial deflection with 85% top-electrode coverage | 10.46 | 8.70 | 19.60 |
| Experimental characterization | 10.33 | 9.15 | 19 |
| Relative error | 1% | 5% | 3% |
| Initial Center Deflection | 0 nm | −40 nm | −80 nm |
|---|---|---|---|
| Contact radius after pull-in | 0.86 µm | 0.56 µm | 0.30 µm |
| Contact radius before pull-out | 0.31 µm | 0.20 µm | 0.09 µm |
| Difference in contact radius | 0.55 µm | 0.36 µm | 0.21 µm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Halbach, C.; Rochus, V.; Genoe, J.; Rottenberg, X.; Cheyns, D.; Heremans, P. Analysis of Collapse–Snapback Phenomena in Capacitive Micromachined Ultrasound Transducers. Micromachines 2025, 16, 160. https://doi.org/10.3390/mi16020160
Halbach C, Rochus V, Genoe J, Rottenberg X, Cheyns D, Heremans P. Analysis of Collapse–Snapback Phenomena in Capacitive Micromachined Ultrasound Transducers. Micromachines. 2025; 16(2):160. https://doi.org/10.3390/mi16020160
Chicago/Turabian StyleHalbach, Chloé, Veronique Rochus, Jan Genoe, Xavier Rottenberg, David Cheyns, and Paul Heremans. 2025. "Analysis of Collapse–Snapback Phenomena in Capacitive Micromachined Ultrasound Transducers" Micromachines 16, no. 2: 160. https://doi.org/10.3390/mi16020160
APA StyleHalbach, C., Rochus, V., Genoe, J., Rottenberg, X., Cheyns, D., & Heremans, P. (2025). Analysis of Collapse–Snapback Phenomena in Capacitive Micromachined Ultrasound Transducers. Micromachines, 16(2), 160. https://doi.org/10.3390/mi16020160












