A 3.0-V, High-Precision, High-PSRR BGR with High-Order Compensation and Improved FVF Pre-Regulation
Abstract
1. Introduction
2. Proposed Circuit Structure and Principles
2.1. Design Considerations
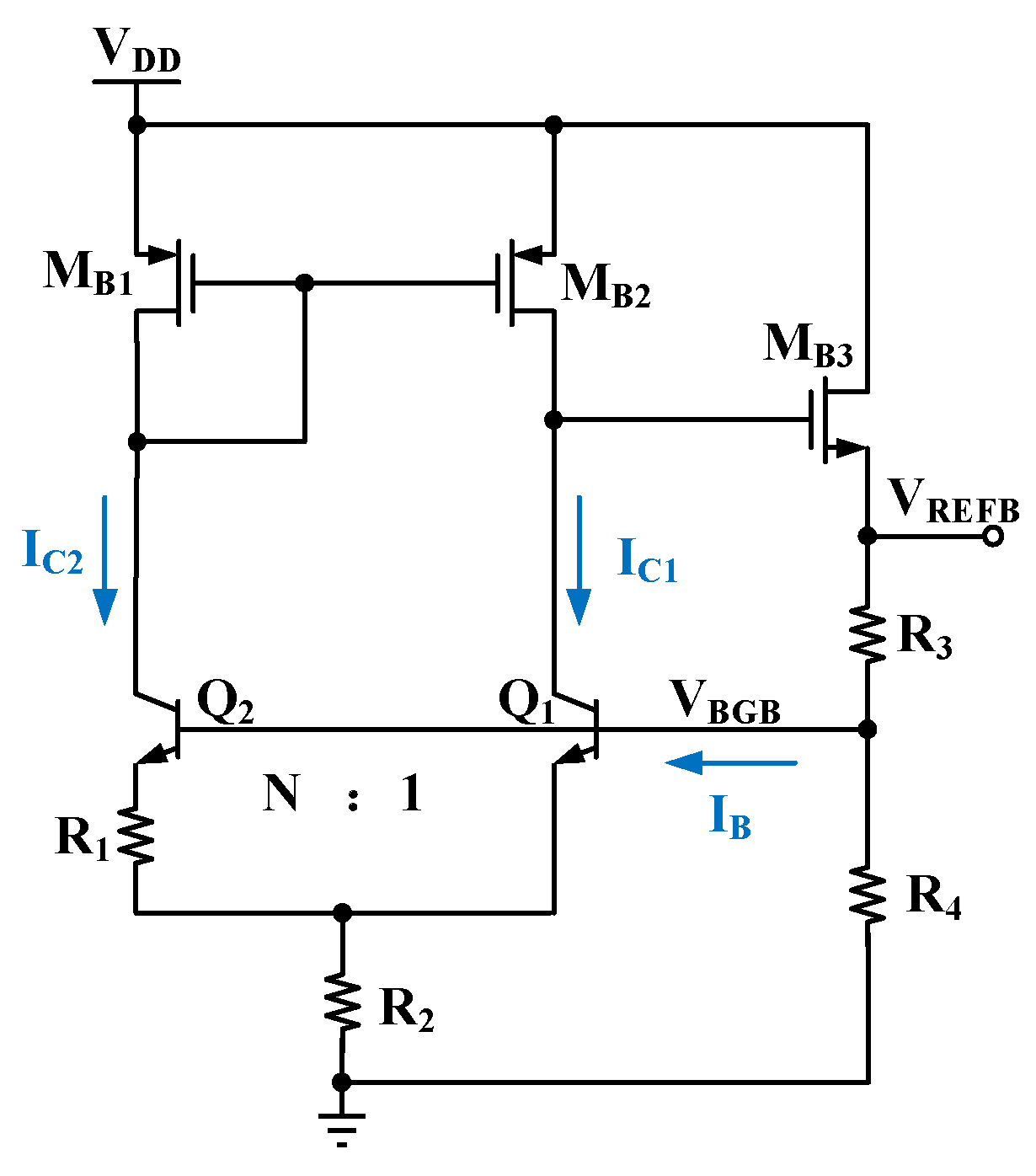
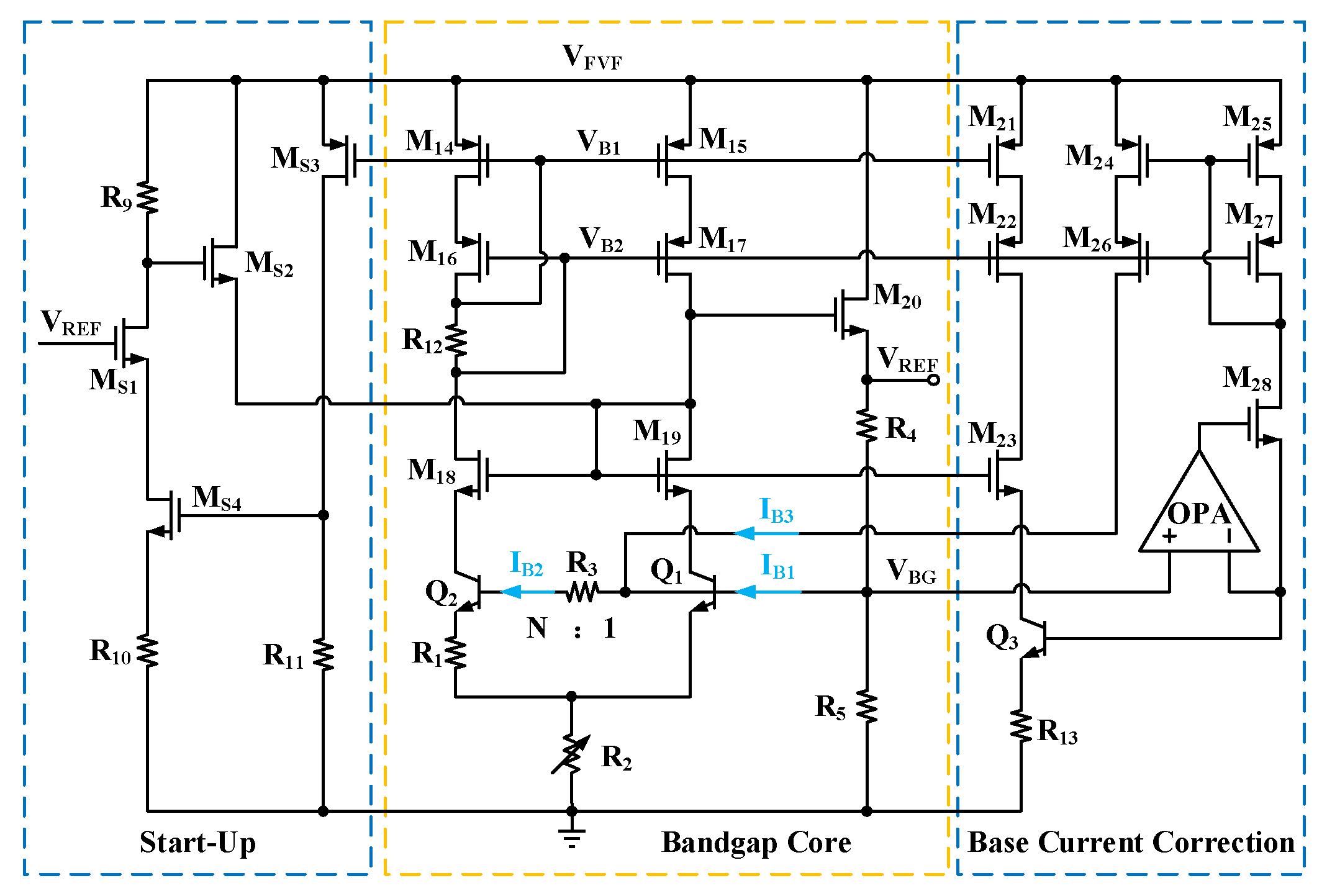
2.2. Bandgap Reference with Base Current Correction
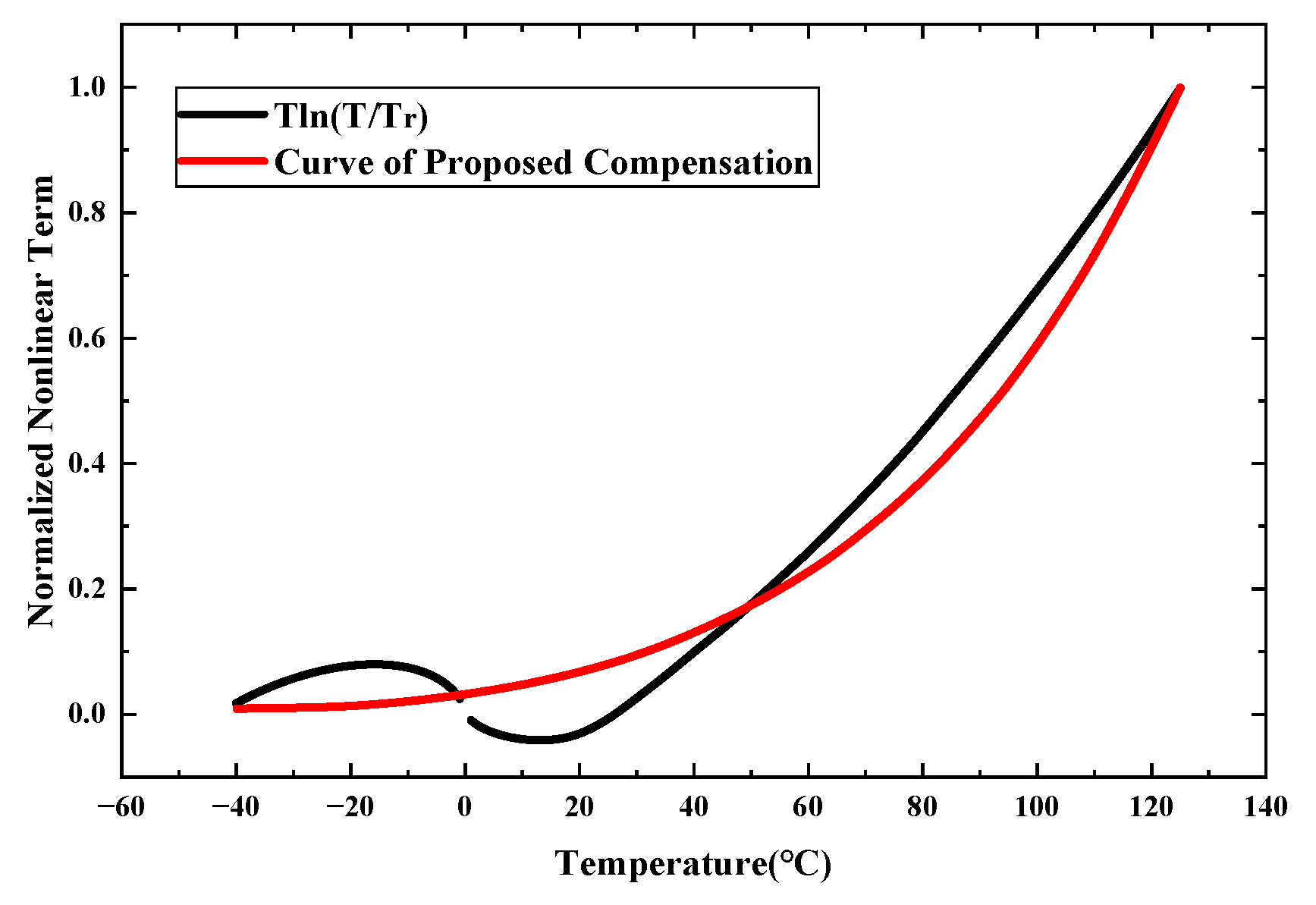
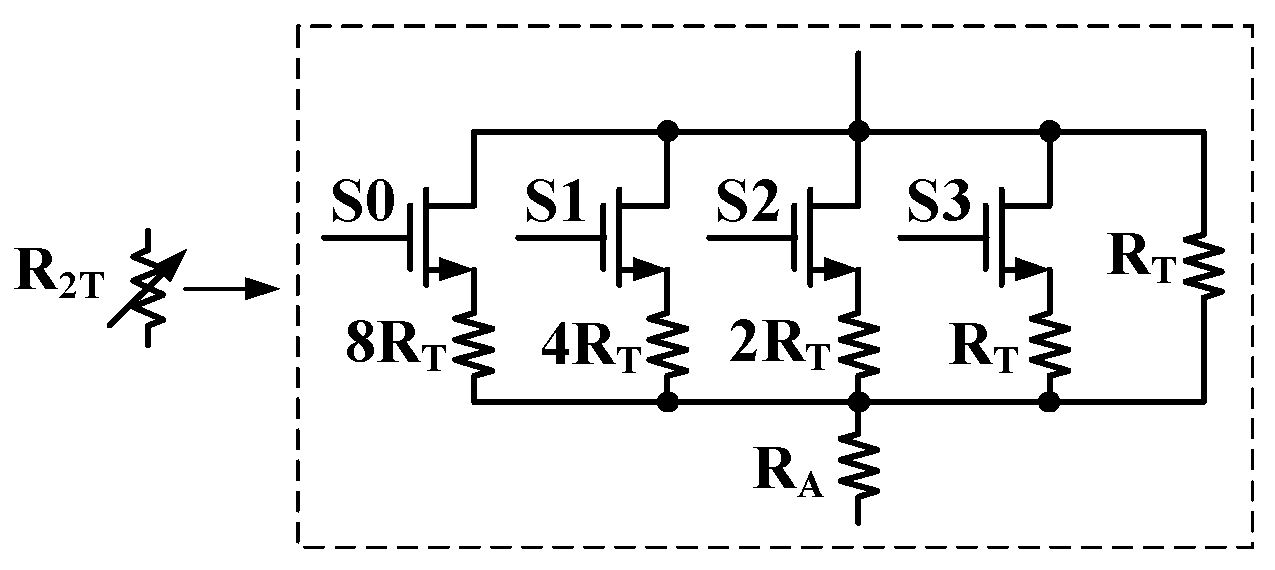
2.3. High-Order Compensation
2.4. FVF Structure with Improved PSRR
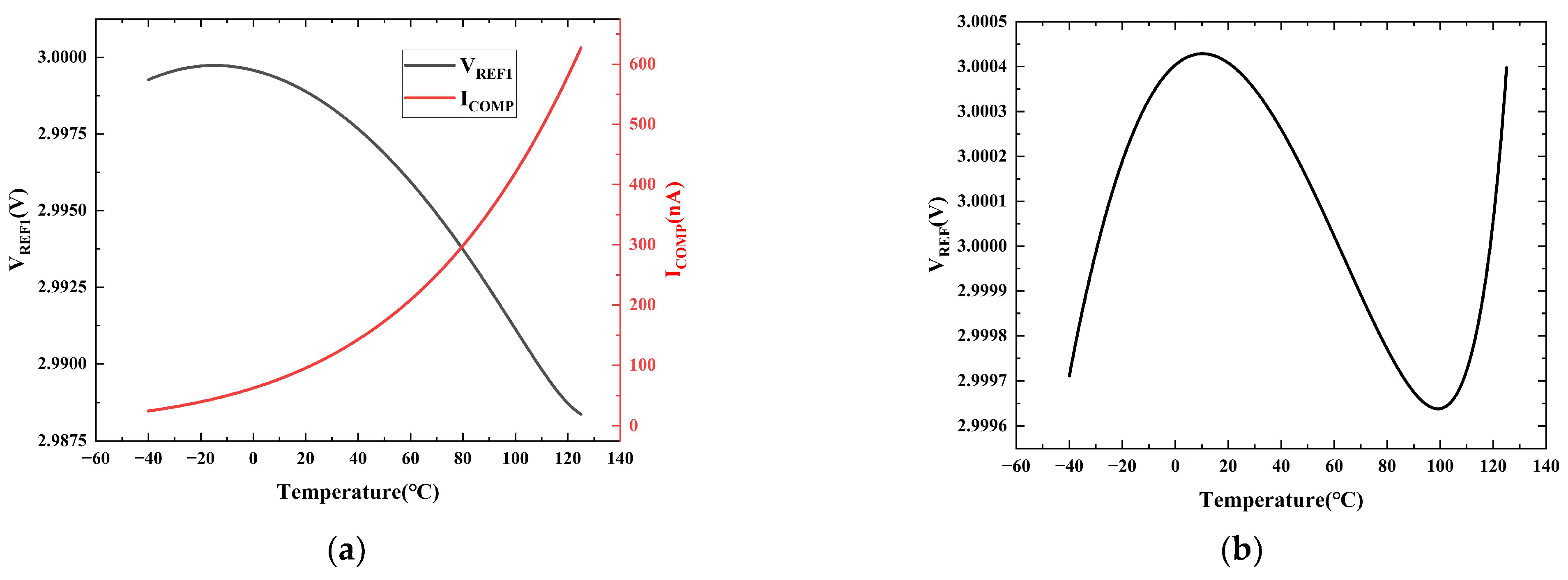
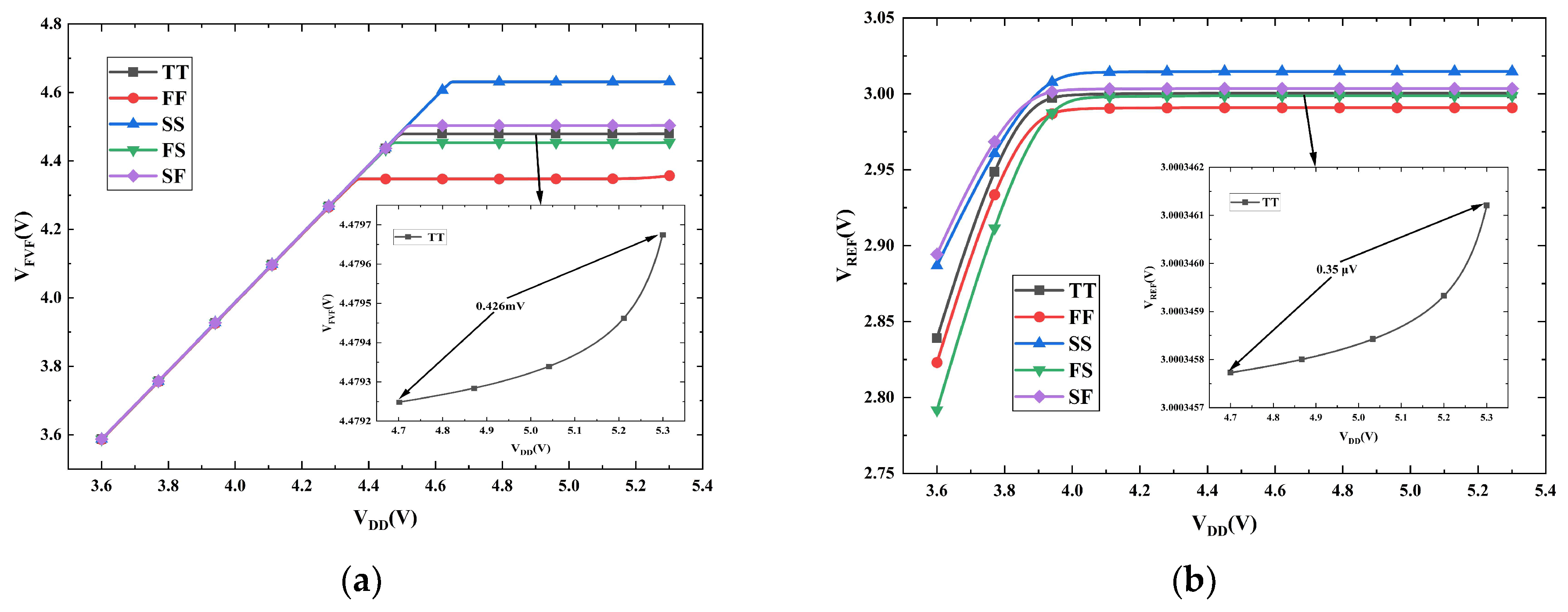
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boo, J.-H.; Cho, K.-I.; Kim, H.-J.; Lim, J.-G.; Kwak, Y.-S.; Lee, S.-H.; Ahn, G.-C. A Single-Trim Switched Capacitor CMOS Bandgap Reference with a 3 σ Inaccuracy of +0.02%, −0.12% for Battery-Monitoring Applications. IEEE J. Solid-State Circuits 2021, 56, 1197–1206. [Google Scholar] [CrossRef]
- Mu, S.; Chan, P.K. Design of Precision-Aware Subthreshold-Based MOSFET Voltage Reference. Sensors 2022, 22, 9466. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Yang, Y.; Zhang, Q. A 4.6-ppm/°C High-Order Curvature Compensated Bandgap Reference for BMIC. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 1492–1496. [Google Scholar] [CrossRef]
- Xue, W.; Yu, X.; Zhang, Y.; Ming, X.; Fang, J.; Ren, J. A 3.0-V 4.2-μA 2.23-ppm/°C BGR with Cross-Connected NPNs and Base-Current Compensation. Microelectron. J. 2024, 152, 106354. [Google Scholar] [CrossRef]
- Hunter, B.L.; Matthews, W.E. A ±3 ppm/°C Single-Trim Switched Capacitor Bandgap Reference for Battery Monitoring Applications. IEEE Trans. Circuits Syst. Regul. Pap. 2017, 64, 777–786. [Google Scholar] [CrossRef]
- Osaki, Y.; Hirose, T.; Kuroki, N.; Numa, M. 1.2-V Supply, 100-nW, 1.09-V Bandgap and 0.7-V Supply, 52.5-nW, 0.55-V Subbandgap Reference Circuits for Nanowatt CMOS LSIs. IEEE J. Solid-State Circuits 2013, 48, 1530–1538. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhan, C.; Wang, L.; Law, M.-K. A −40 °C–125 °C 0.4-μA Low-Noise Bandgap Voltage Reference with 0.8-mA Load Driving Capability Using Shared Feedback Resistors. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 4033–4037. [Google Scholar]
- Kim, M.; Cho, S. A 0.0082-mm2, 192-nW Single BJT Branch Bandgap Reference in 0.18-μm CMOS. IEEE Solid-State Circuits Lett. 2020, 3, 426–429. [Google Scholar] [CrossRef]
- Mu, J.; Liu, L.; Zhu, Z.; Yang, Y. A 58-ppm/°C 40-nW BGR at Supply from 0.5 V for Energy Harvesting IoT Devices. IEEE Trans. Circuits Syst. II Express Briefs 2017, 64, 752–756. [Google Scholar] [CrossRef]
- Huang, W.; Liu, L.; Zhu, Z. A Sub-200 nW All-in-One Bandgap Voltage and Current Reference Without Amplifiers. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 121–125. [Google Scholar]
- Huang, S.; Li, M.; Li, H.; Yin, P.; Shu, Z.; Bermak, A.; Tang, F. A Sub-1 ppm/°C Bandgap Voltage Reference with High-Order Temperature Compensation in 0.18-μm CMOS Process. IEEE Trans. Circuits Syst. Regul. Pap. 2022, 69, 1408–1416. [Google Scholar] [CrossRef]
- Yan, T.; Chi-Wa, U.; Law, M.K.; Lam, C.S. A −40 °C–125 °C, 1.08 ppm/°C, 918 nW Bandgap Voltage Reference with Segmented Curvature Compensation. Microelectron. J. 2020, 105, 104897. [Google Scholar] [CrossRef]
- Lee, C.-C.; Chen, H.-M.; Lu, C.-C.; Lee, B.-Y.; Huang, H.-C.; Fu, H.-S.; Lin, Y.-X. A High-Precision Bandgap Reference with a V-Curve Correction Circuit. IEEE Access 2020, 8, 62632–62638. [Google Scholar] [CrossRef]
- Zhou, Z.-K.; Shi, Y.; Wang, Y.; Li, N.; Xiao, Z.; Wang, Y.; Liu, X.; Wang, Z.; Zhang, B. A Resistorless High-Precision Compensated CMOS Bandgap Voltage Reference. IEEE Trans. Circuits Syst. Regul. Pap. 2019, 66, 428–437. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, C.; Hou, H.; Han, W. A Sub-1 ppm/°C Reference Voltage Source with a Wide Input Range. Micromachines 2024, 15, 1273. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.F.; Chi-Wa, U.; Martins, R.P.; Lam, C.S. A 0.5 V 22.5 ppm/°C Bandgap Voltage Reference with Leakage Current Injection for Curvature Correction. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 3897–3901. [Google Scholar]
- Liu, L.; Liao, X.; Mu, J. A 3.6 μVrms Noise, 3 ppm/◦C TC Bandgap Reference with Offset/Noise Suppression and Five-Piece Linear Compensation. IEEE Trans. Circuits Syst. Regul. Pap. 2019, 66, 3786–3796. [Google Scholar] [CrossRef]
- Wang, R.; Lu, W.; Zhao, M.; Niu, Y.; Liu, Z.; Zhang, Y.; Chen, Z. A Sub-1 ppm/°C Current-Mode CMOS Bandgap Reference with Piecewise Curvature Compensation. IEEE Trans. Circuits Syst. Regul. Pap. 2018, 65, 904–913. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, Y.; Min, H. A High Accuracy and Configurable Voltage (1.2/1.8/2.5/3.3 V) Bandgap Reference with Base Current Compensation for DC–DC Converters. Electron. Lett. 2022, 58, 600–602. [Google Scholar] [CrossRef]
- Xie, J.; Wu, C.; Wu, J.; Li, J.; Luo, Z.; Sun, Q. A −184 dB PSRR and 2.47 μVrms Noise Self Biased Bandgap Reference Based on FVF Structure. Microelectron. J. 2024, 152, 106388. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y.; Yang, C.; Xiao, Y.; Hou, H.; Han, W. A 0.87-ppm/°C, 3.2–40 V VIN Reference Voltage Source with −121 dB PSRR at 100 Hz. Microelectron. J. 2025, 157, 106560. [Google Scholar] [CrossRef]
- Fu, X.; Colombo, D.M.; Yin, Y.; El-Sankary, K. Low Noise, High PSRR, High-Order Piecewise Curvature Compensated CMOS Bandgap Reference. IEEE Access 2022, 10, 110970–110982. [Google Scholar] [CrossRef]
- Wen, K.; Shen, Y.; Li, Y.; Liu, S. A 0.018%/V Line Sensitivity Voltage Reference with −82.46 dB PSRR at 100 Hz for Bio-Potential Signals Readout Systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 2031–2035. [Google Scholar] [CrossRef]
- Zawawi, R.B.A.; Choi, H.; Kim, J. High PSRR Wide Supply Range Dual-Voltage Reference Circuit for Bio-Implantable Applications. Electronics 2021, 10. [Google Scholar] [CrossRef]
- Liang, J.; Yi, S.; Bai, W.; Wang, L.; Zhan, C.; Liao, C.; Lam, H.-M.; Zhang, M.; Zhang, S.; Jiao, H. A −80 dB PSRR 4.99 ppm/°C TC Bandgap Reference with Nonlinear Compensation. Microelectron. J. 2020, 95, 104664. [Google Scholar] [CrossRef]
- Tsividis, Y.P. Accurate Analysis of Temperature Effects in IC-VBE Characteristics with Application to Bandgap Reference Sources. IEEE J. Solid-State Circuits 1980, 15, 1076–1084. [Google Scholar] [CrossRef]
- Brokaw, A.P. A Simple Three-Terminal IC Bandgap Reference. IEEE J. Solid-State Circuits 1974, 9, 388–393. [Google Scholar] [CrossRef]
- Carvajal, R.G.; Ramirez-Angulo, J.; Lopez-Martin, A.J.; Torralba, A.; Galan, J.A.G.; Carlosena, A.; Chavero, F.M. The Flipped Voltage Follower: A Useful Cell for Low-Voltage Low-Power Circuit Design. IEEE Trans. Circuits Syst. Regul. Pap. 2005, 52, 1276–1291. [Google Scholar] [CrossRef]
- Cai, G.; Lu, Y.; Zhan, C.; Martins, R.P. A Fully Integrated FVF LDO with Enhanced Full-Spectrum Power Supply Rejection. IEEE Trans. Power Electron. 2021, 36, 4326–4337. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, L.; Kong, F.; Cheung, C.; Najafizadeh, L. BiCMOS-Based Compensation: Toward Fully Curvature-Corrected Bandgap Reference Circuits. IEEE Trans. Circuits Syst. Regul. Pap. 2018, 65, 1210–1223. [Google Scholar] [CrossRef]
- Rashidian, H.; Shiri, N. A Sub-1 ppm/°C Dual-Reference Small-Area Bandgap Reference Comprising an Enhanceable Piecewise Curvature Compensation Circuit. AEU-Int. J. Electron. Commun. 2024, 175, 155064. [Google Scholar] [CrossRef]
- Yan, Z.; Zhang, B.; Yang, R.; Zheng, Y.; Li, J.; Luo, Z.; Sun, Q. A 1.2-V Compact Bandgap Reference with Curvature Compensation Technology. IEICE Electron. Express 2025, 22, 20250028. [Google Scholar] [CrossRef]













| Parameter | [4] | [22] | [30] | [31] | [32] | This Work |
|---|---|---|---|---|---|---|
| Year | 2024 | 2022 | 2018 | 2024 | 2025 | 2025 |
| Technology (nm) | 180 | 180 | 130 | 180 | 180 | 180 |
| Supply voltage (V) | 4.5–6 | 2.7–3.3 | 1.6 | 1.2–6 | 3.3 | 4.7–5.3 |
| Supply current (μA) | 4.2 | <46 | 180 | 18.7 | 46 | 23 |
| Reference voltage (V) | 3.0 | 1.2 | 1.112 | 1.262 | 1.218 | 3.0 |
| Temperature range (°C) | −40–120 | −10–110 | 0–150 | −50–130 | −40–125 | −40–125 |
| TC (ppm/°C) | 2.23 | 5–15 | 13.1 | 0.75 | 7.86 | 1.59 |
| Line regulation (mV/V) | 0.2 | 0.06 | 2.67 | 1.68 | 0.5846 | 0.00058 |
| PSRR (dB) | −78.7@10 Hz | −80@DC | −40@10 Hz | −78@DC | −65@1 Hz | −128.89@1 Hz |
| Area (mm2) | 0.104 | 0.448 | 0.1276 | 0.0079 | 0.01 | 0.0459 |
| Simulated/Measured | Meas. | Meas. | Meas. | Sim. | Sim. | Sim. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Yu, J.; Xiao, F.; Cai, C.; Wang, C.; Li, J.; Ma, C.; Mo, Y. A 3.0-V, High-Precision, High-PSRR BGR with High-Order Compensation and Improved FVF Pre-Regulation. Micromachines 2025, 16, 1405. https://doi.org/10.3390/mi16121405
Shen Y, Yu J, Xiao F, Cai C, Wang C, Li J, Ma C, Mo Y. A 3.0-V, High-Precision, High-PSRR BGR with High-Order Compensation and Improved FVF Pre-Regulation. Micromachines. 2025; 16(12):1405. https://doi.org/10.3390/mi16121405
Chicago/Turabian StyleShen, Yongkang, Jianhai Yu, Fading Xiao, Chang Cai, Chao Wang, Jinghu Li, Caiyan Ma, and Yonghao Mo. 2025. "A 3.0-V, High-Precision, High-PSRR BGR with High-Order Compensation and Improved FVF Pre-Regulation" Micromachines 16, no. 12: 1405. https://doi.org/10.3390/mi16121405
APA StyleShen, Y., Yu, J., Xiao, F., Cai, C., Wang, C., Li, J., Ma, C., & Mo, Y. (2025). A 3.0-V, High-Precision, High-PSRR BGR with High-Order Compensation and Improved FVF Pre-Regulation. Micromachines, 16(12), 1405. https://doi.org/10.3390/mi16121405






