The Influence and Compensation of Process on Measurement Accuracy in Digital Grating Focusing and Leveling Sensors
Abstract
1. Introduction
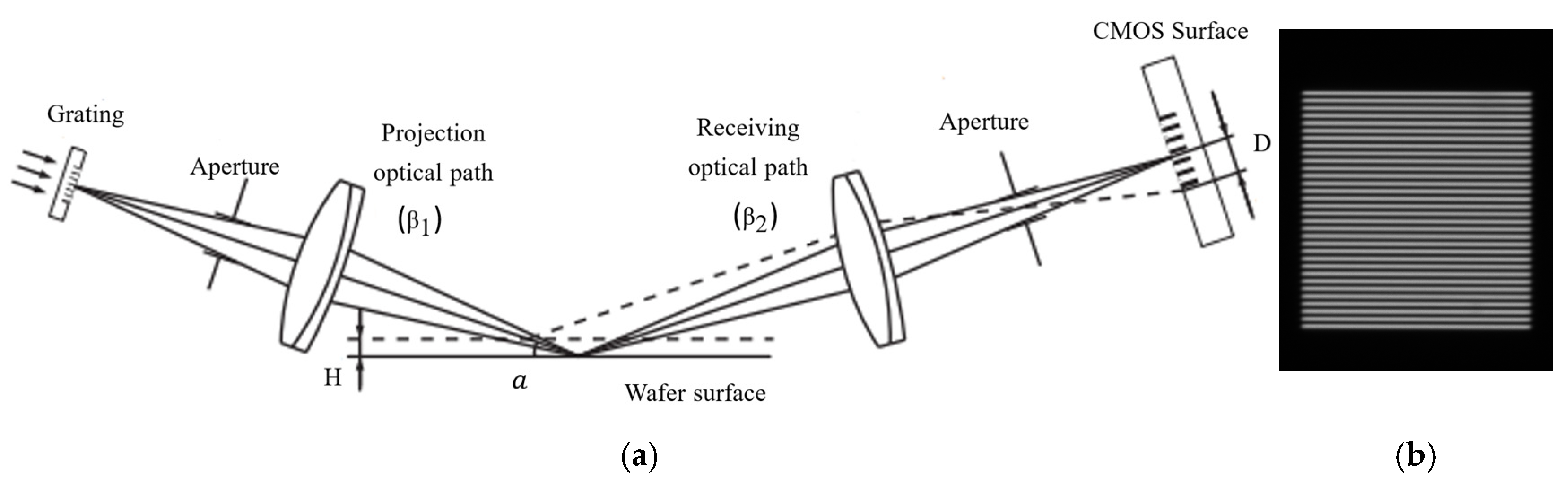
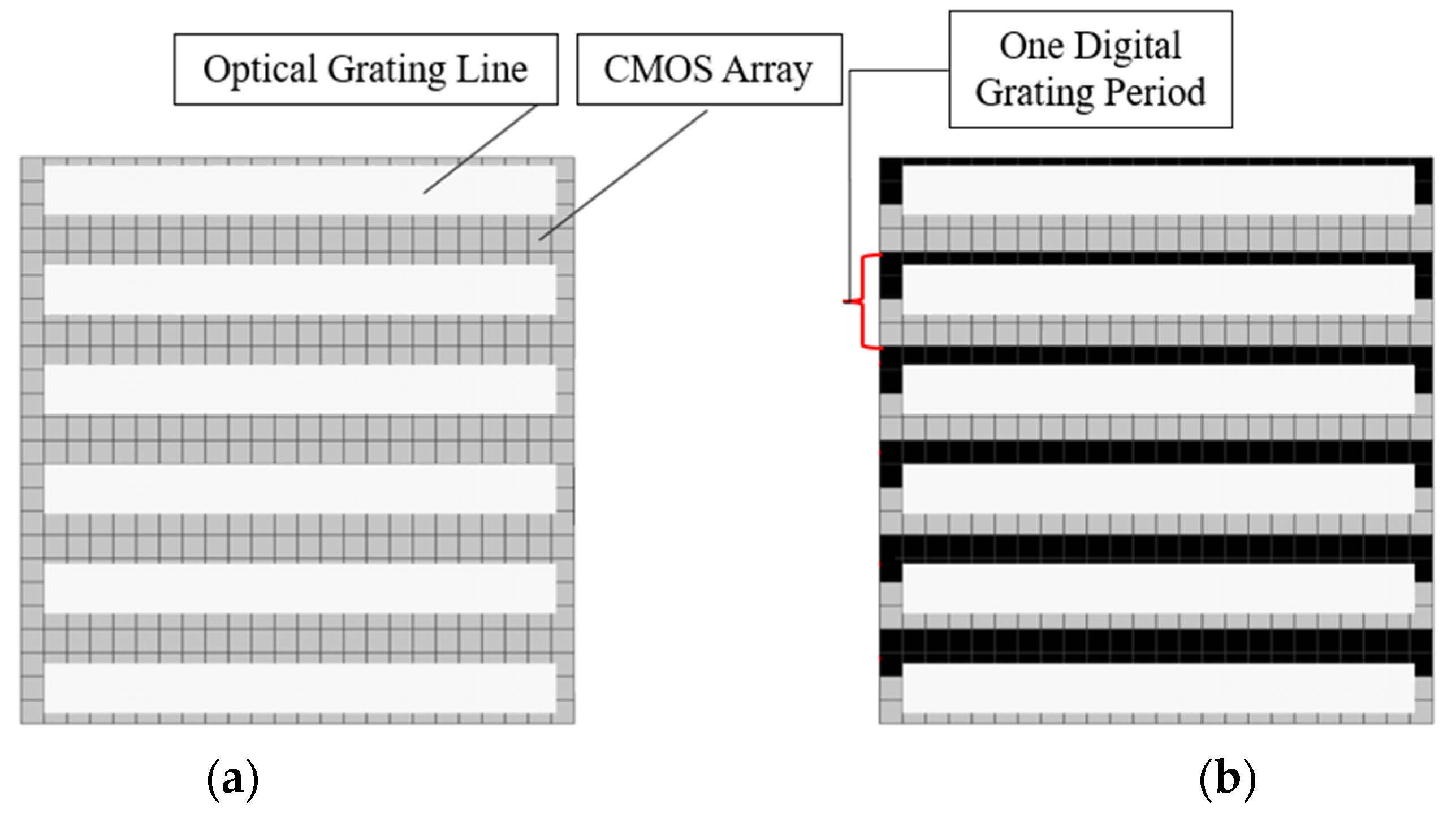
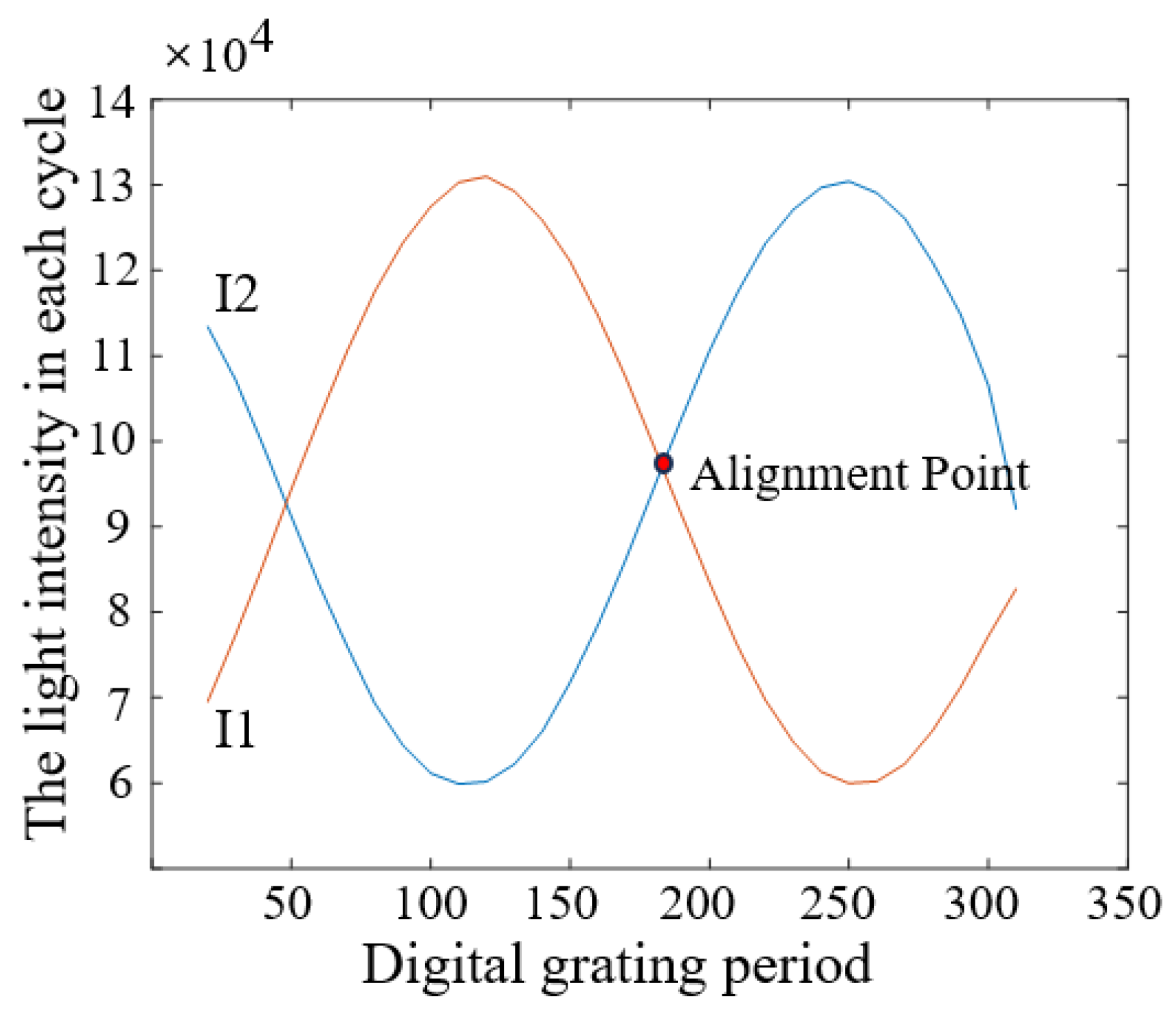
2. The Influence Mechanism of Process Pattern on Measurement Accuracy
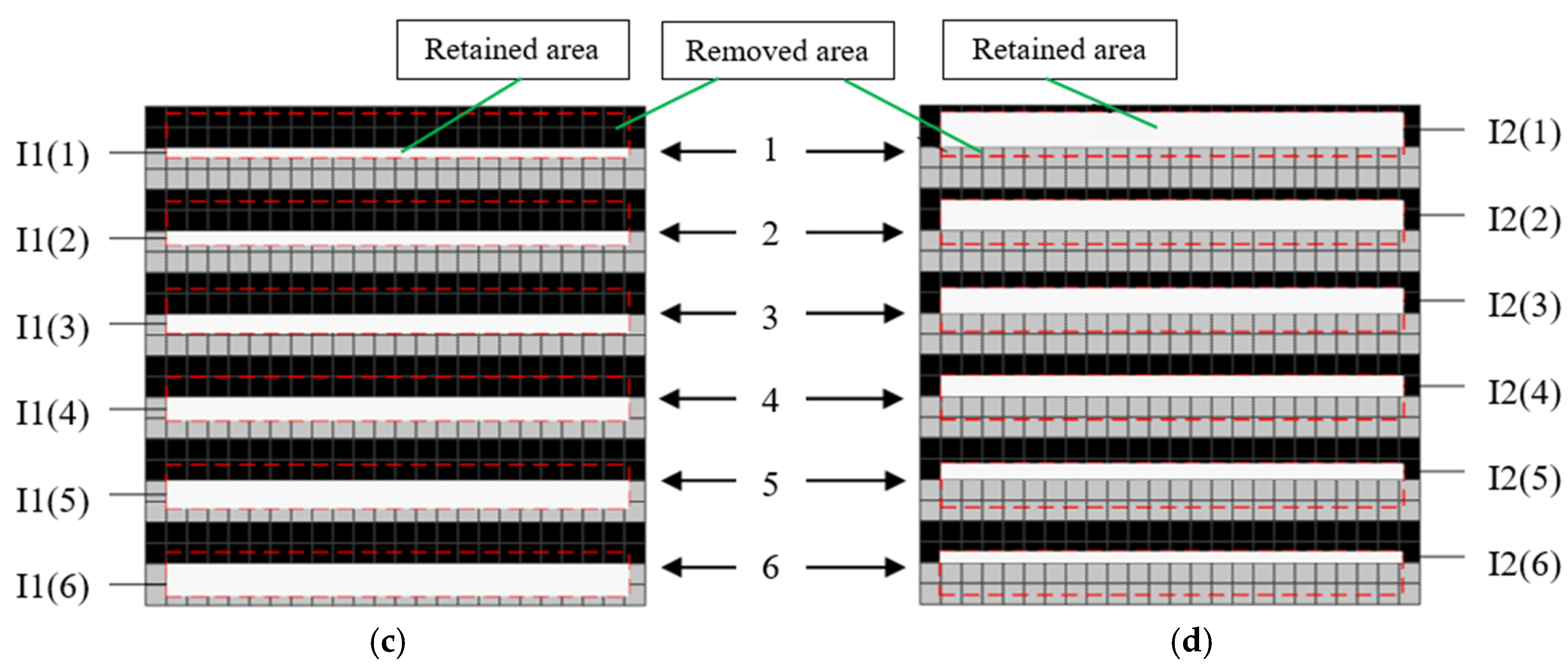
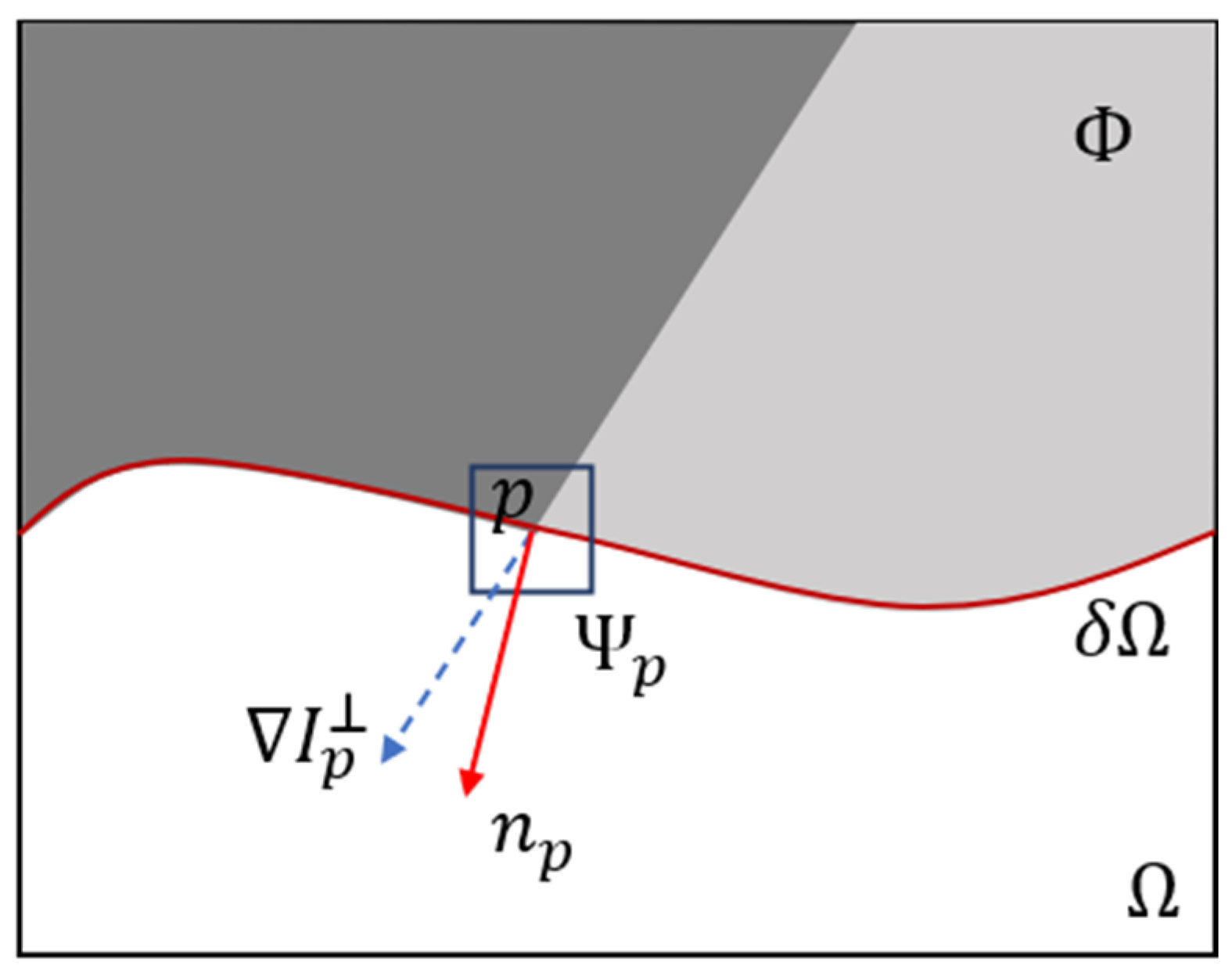
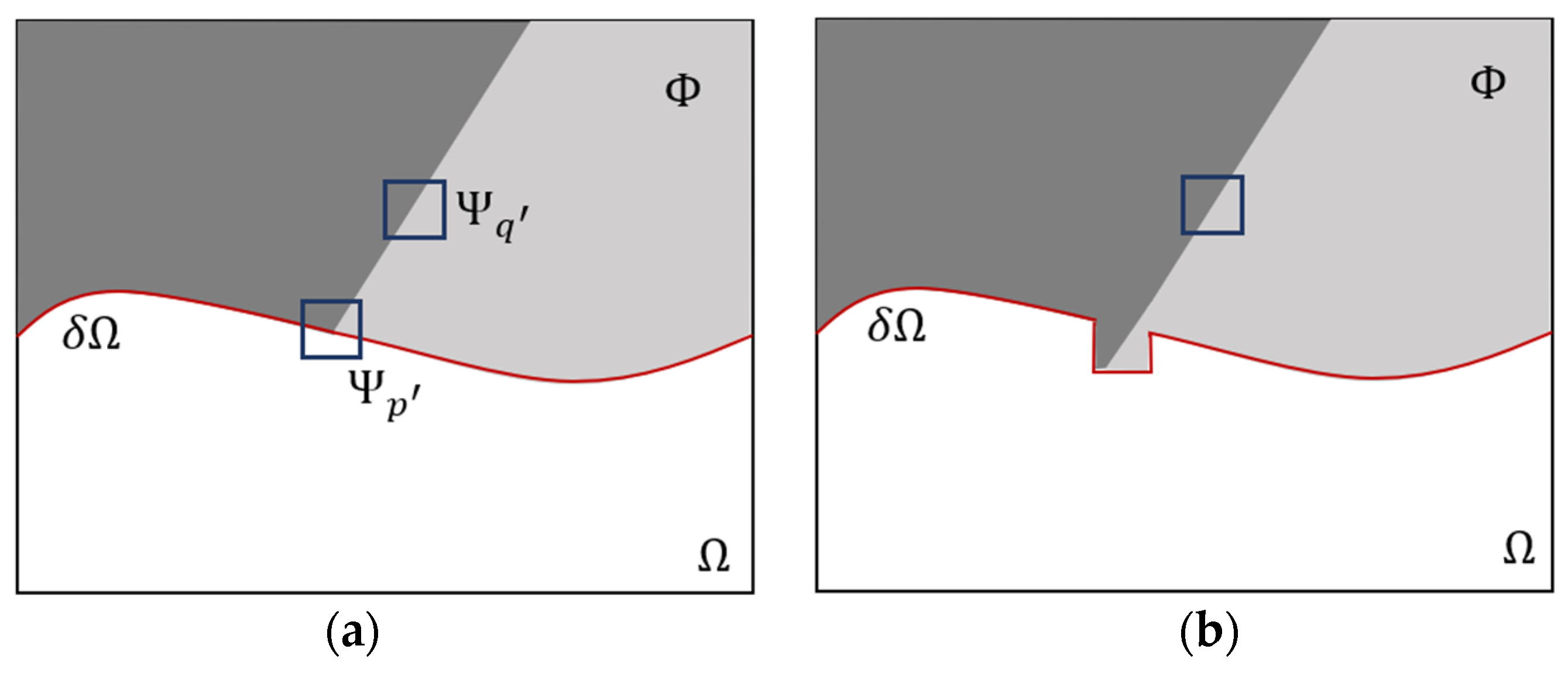
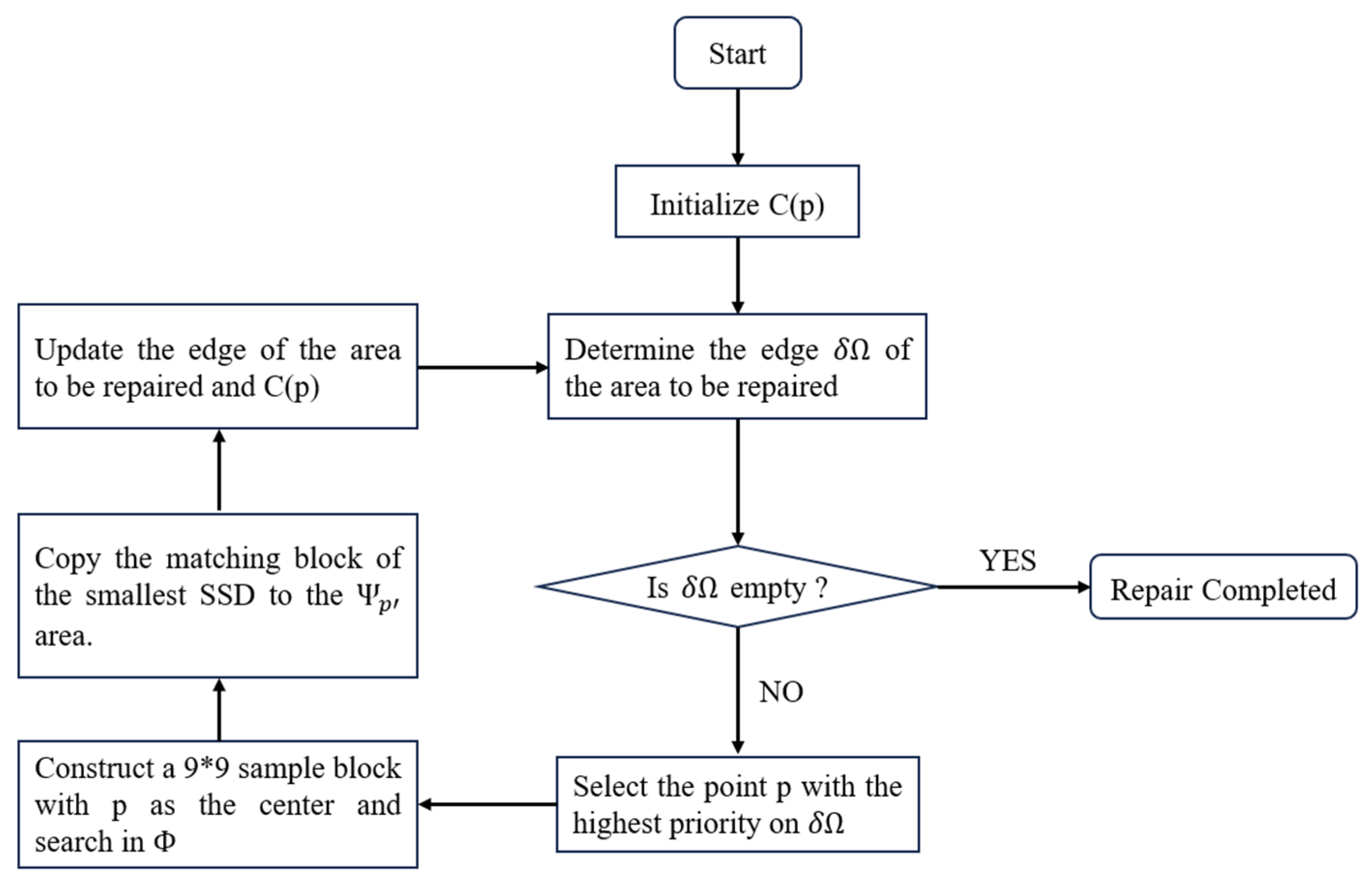
3. Compensation Algorithm Design and Implementation
- (1)
- Priority strategy
- (2)
- Searching and filling the best-matching block
- (3)
- Dynamic update of confidence term
4. Repair Effect and Performance Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ASML Netherlands BV. Level Sensor and Lithographic Apparatus. U.S. Patent 7265364B2, 10 June 2004. [Google Scholar]
- Nikon Corporation. Compensation for Goos-Hanchen Error in Autofocus Systems. U.S. Patent 5502311A, 24 March 2011.
- Guo, J.; Li S-g Zhao, Y.; Zong, M.-C. Nano-scale focus control technology in electron beam wafer pattern inspection system. Chin. Opt. 2019, 12, 242–255. [Google Scholar] [CrossRef]
- Guo, J. Wafer Height Measurement Technology in Electron Beam Inspection System; University of Chinese Academy of Sciences: Beijing, China, 2018. [Google Scholar]
- Ji, Y.-Y. A Novel Cross-Scale Three-Dimensional Displacement Measurement System; University of Chinese Academy of Sciences: Beijing, China, 2023. [Google Scholar]
- Sun, Y.W.; Li, S.G.; Ye, T.C.; Zong, M.C. Process Dependency of Focusing and Leveling Measurement System in Nanoscale Lithography. Acta Opt. Sin. 2016, 36, 0512002. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Y. Sample Height Measurement Using Digital Grating. U.S. Patent 20190320097 A1, 17 October 2019. [Google Scholar]
- Zeng, H.-F. Focus Control in Digital Lithography Machine; University of Chinese Academy of Sciences: Beijing, China, 2024. [Google Scholar]
- Zeng, H.-F.; Li, S.-G.; Li, X.-J. Process adaptability for digital grating-based focusing and leveling sensors. Chin. Opt. 2024, 17, 1150–1161. [Google Scholar] [CrossRef]
- Fan, G.-P.; He, H.-J.; Chen, F.; Zhai, D.-H. An image inpainting algorithm based on local properties. J. Optoelectron. Laser 2012, 23, 2410–2417. (In Chinese) [Google Scholar]
- Zhang, H.-Y.; Peng, Q.-C. A Survey on Digital Image Inpainting. J. Image Graph. 2007, 12, 1–10. [Google Scholar]
- Criminisi, A.; Perez, P.; Toyama, K. Object removal by exemplar-based inpainting. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 18–20 June 2003; pp. 721–728. [Google Scholar]
- Zhou, X.-C.; Chen, J.; Zhang, J.; Yin, X.-P.; Guo, L.-K. Image Inpainting Based on Improved Criminisi Algorithm by Threshold Demarcation and Region Division. Comput. Digit. Eng. 2023, 51, 1393–1397. (In Chinese) [Google Scholar]
- Huang, C. Research on Image Inpainting Algorithm Based on Criminisi and Software Implementation; Xidian University: Xi’an, China, 2022. [Google Scholar]


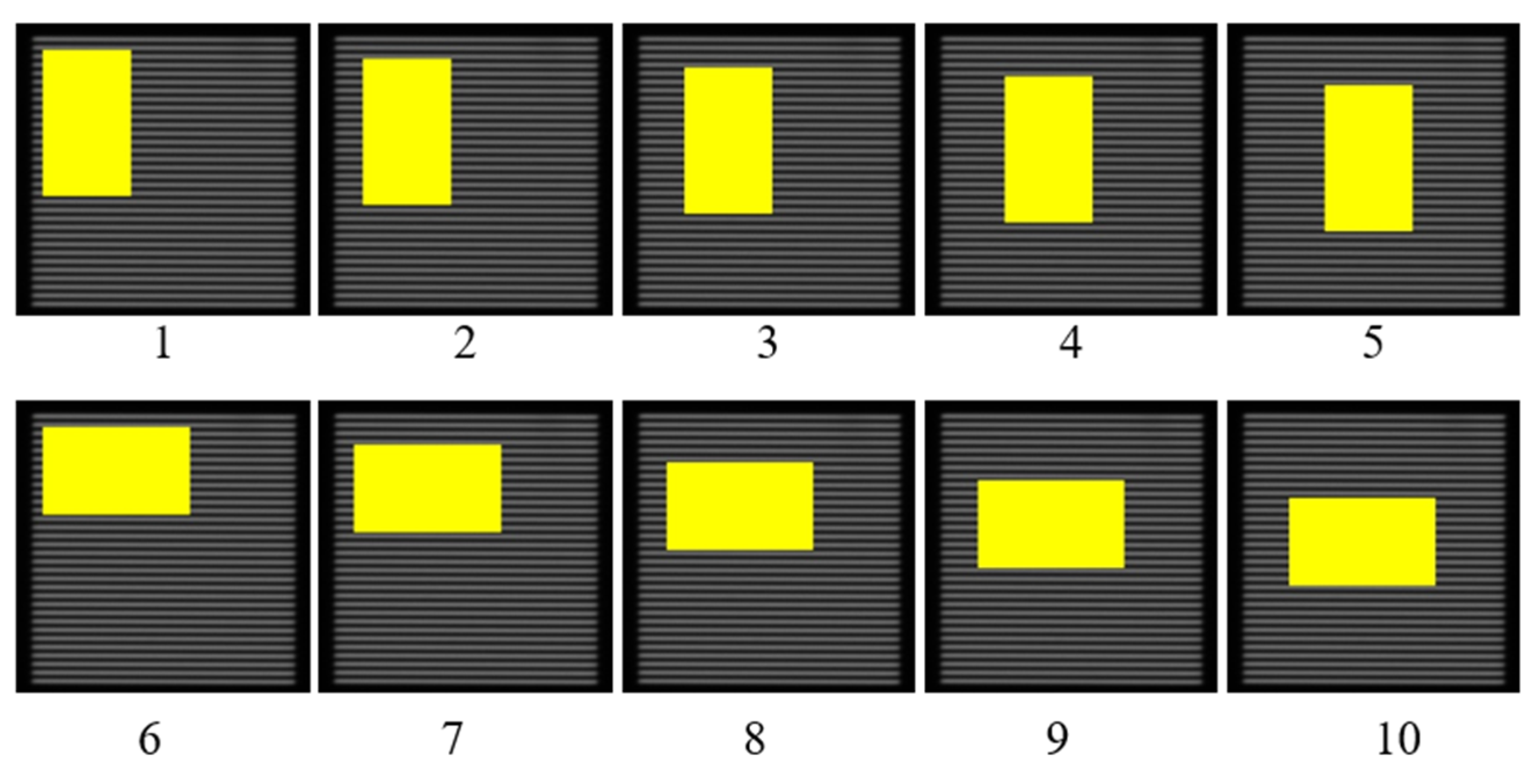

| Mask Area | Ref | 1% | 3% | 5% | 10% | 15% | |
|---|---|---|---|---|---|---|---|
| Items | |||||||
| Position 1 in Figure 7 | 184.1504 | 184.1525 | 184.1502 | 184.1524 | 184.1422 | 184.1594 | |
| 2 | 184.1502 | 184.1542 | 184.1515 | 184.1467 | 184.1912 | ||
| 3 | 184.1511 | 184.1260 | 184.1201 | 184.1073 | 184.0910 | ||
| 4 | 184.1499 | 184.1589 | 184.1766 | 184.0786 | 184.1491 | ||
| 5 | 184.1513 | 184.1405 | 184.0990 | 184.2744 | 184.9940 | ||
| 6 | 184.1504 | 184.1510 | 184.1447 | 184.1581 | 184.1725 | ||
| 7 | 184.1486 | 184.1511 | 184.1635 | 184.1403 | 184.1630 | ||
| 8 | 184.1501 | 184.1511 | 184.1595 | 184.1738 | 184.0880 | ||
| 9 | 184.1516 | 184.1539 | 184.1425 | 184.1716 | 183.3362 | ||
| 10 | 184.1537 | 184.1503 | 184.1497 | 184.0412 | 184.0578 | ||
| Mean alignment point (pix) | 184.1509 | 184.1487 | 184.1460 | 184.1434 | 184.1402 | ||
| Error in alignment Tx (pix) | 0.0005 | −0.0038 | −0.0043 | −0.0090 | −0.0020 | ||
| Error of D (nm) | 0.0860 | −0.6535 | −0.7395 | −1.5479 | −0.3440 | ||
| Mean error in Z direction H (nm) | 0.0400 | −0.3038 | −0.3438 | −0.7196 | −0.1599 | ||
| Max (pix) | 184.1537 | 184.1589 | 184.1766 | 184.2744 | 184.9940 | ||
| Min (pix) | 184.1486 | 184.1260 | 184.0990 | 184.0412 | 183.3362 | ||
| Error in alignment Tx (pix) | Ref-Max | −0.0033 | −0.0064 | −0.0264 | −0.1220 | −0.8518 | |
| Ref-Min | 0.0018 | 0.0265 | 0.0512 | 0.1112 | 0.8060 | ||
| Error of D (nm) | Ref-Max | −0.5675 | −1.1007 | −4.5404 | −20.9820 | −146.4960 | |
| Ref-Min | 0.3096 | 4.5576 | 8.8056 | 19.1246 | 138.6191 | ||
| Error in Z direction H (nm) | Ref-Max | −0.2638 | −0.5117 | −2.1108 | −9.7543 | −68.1039 | |
| Ref-Min | 0.1439 | 2.1188 | 4.0936 | 8.8908 | 64.4420 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Li, X.; He, G. The Influence and Compensation of Process on Measurement Accuracy in Digital Grating Focusing and Leveling Sensors. Micromachines 2025, 16, 1326. https://doi.org/10.3390/mi16121326
Li S, Li X, He G. The Influence and Compensation of Process on Measurement Accuracy in Digital Grating Focusing and Leveling Sensors. Micromachines. 2025; 16(12):1326. https://doi.org/10.3390/mi16121326
Chicago/Turabian StyleLi, Shiguang, Xianjie Li, and Guocai He. 2025. "The Influence and Compensation of Process on Measurement Accuracy in Digital Grating Focusing and Leveling Sensors" Micromachines 16, no. 12: 1326. https://doi.org/10.3390/mi16121326
APA StyleLi, S., Li, X., & He, G. (2025). The Influence and Compensation of Process on Measurement Accuracy in Digital Grating Focusing and Leveling Sensors. Micromachines, 16(12), 1326. https://doi.org/10.3390/mi16121326






