A Two-Stage Unet Framework for Sub-Resolution Assist Feature Prediction
Abstract
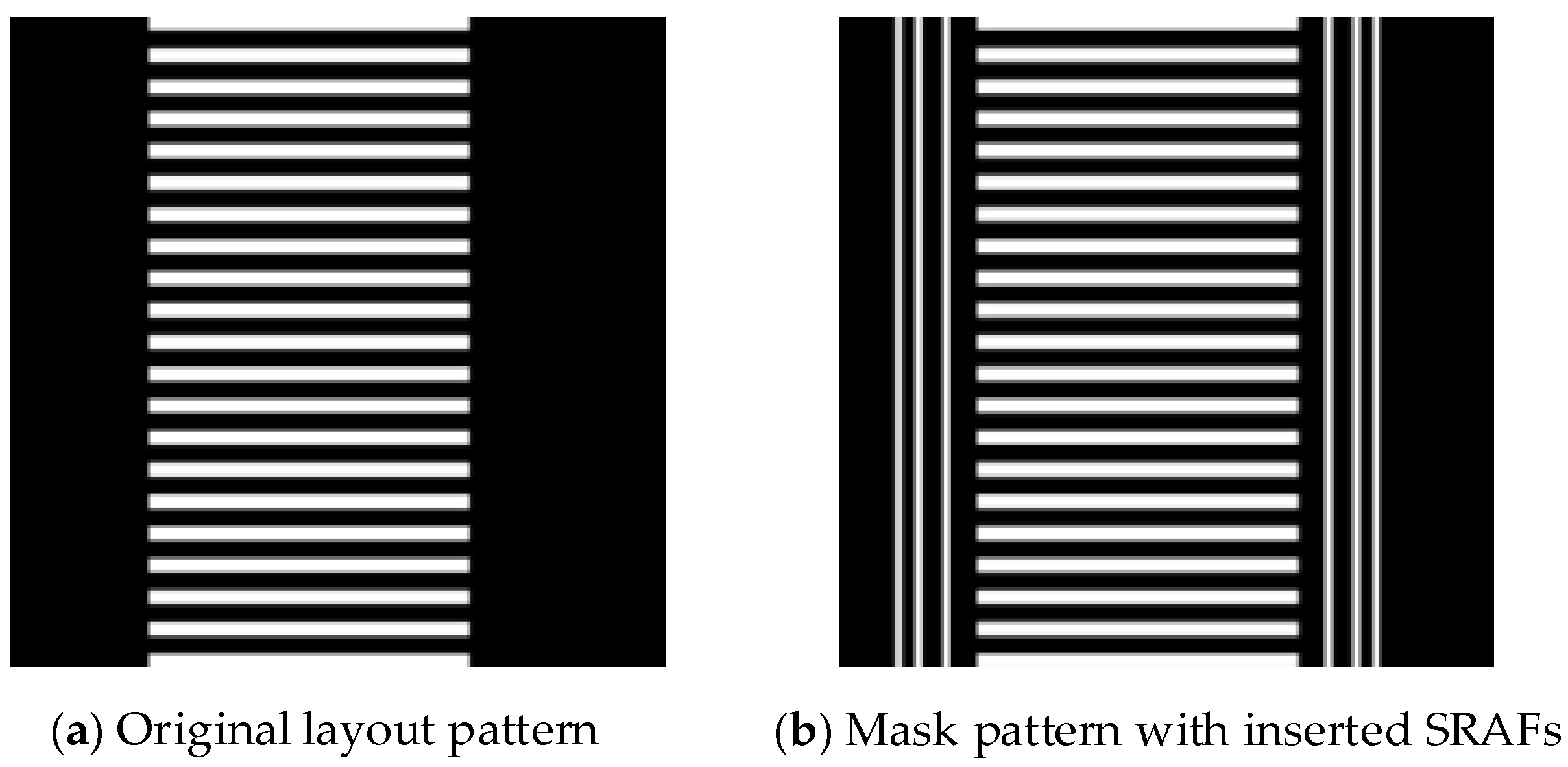
1. Introduction
2. Preliminaries
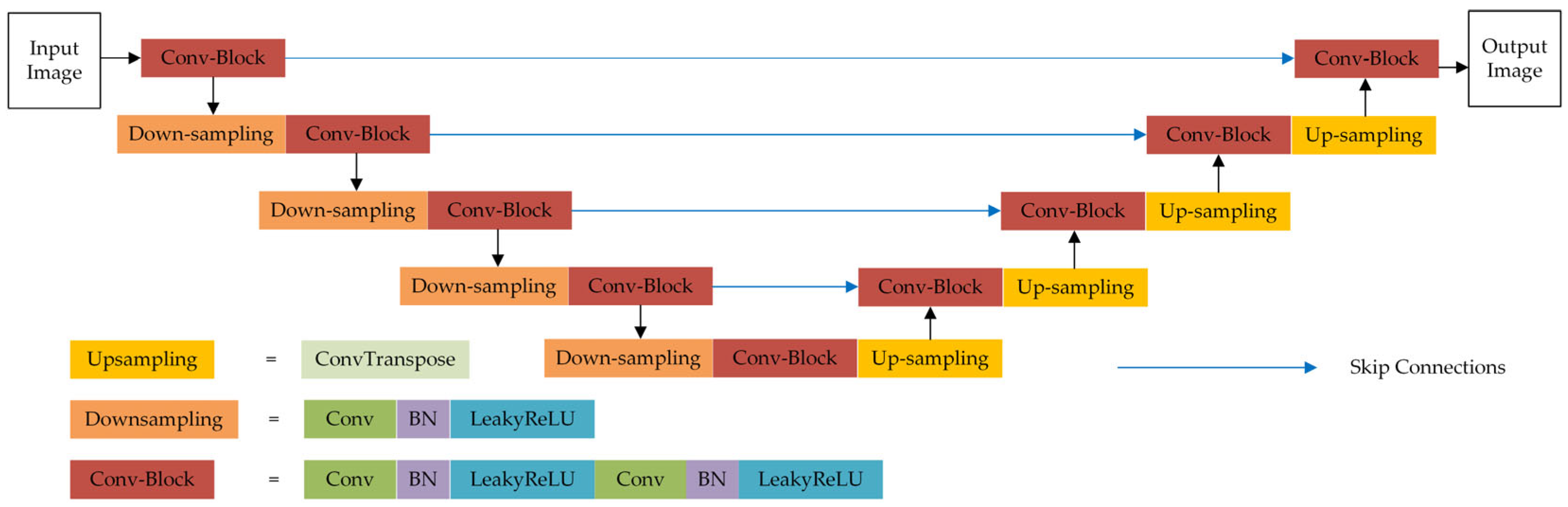
2.1. Unet
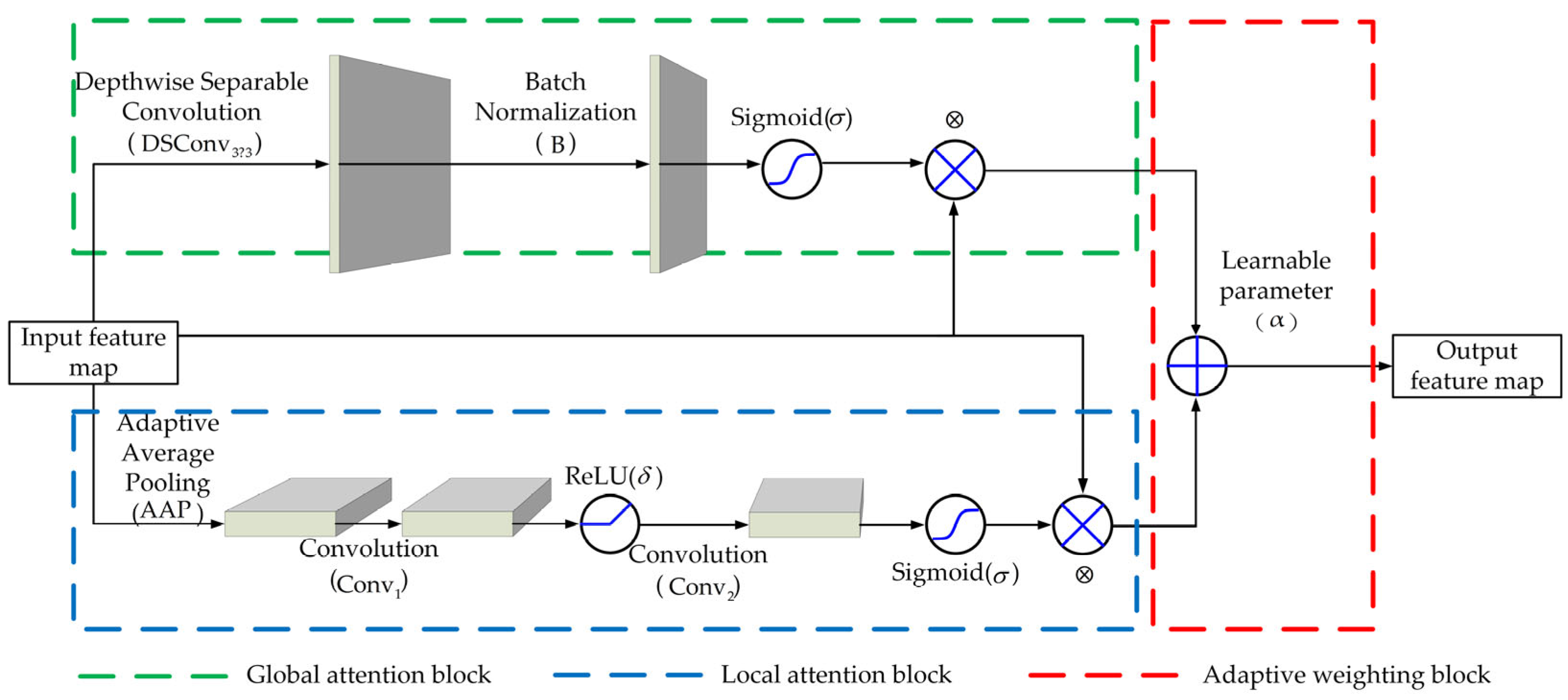
2.2. AHAM
2.3. WCA Algorithm
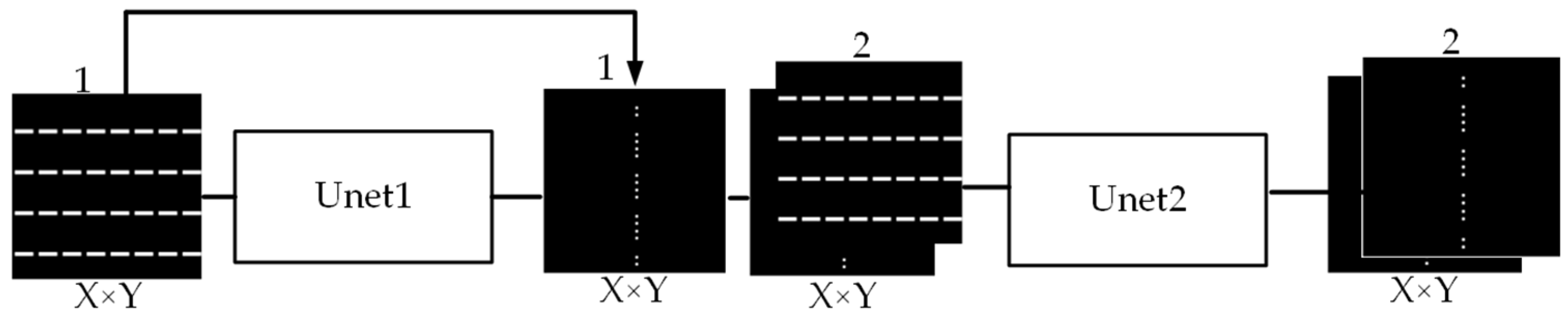
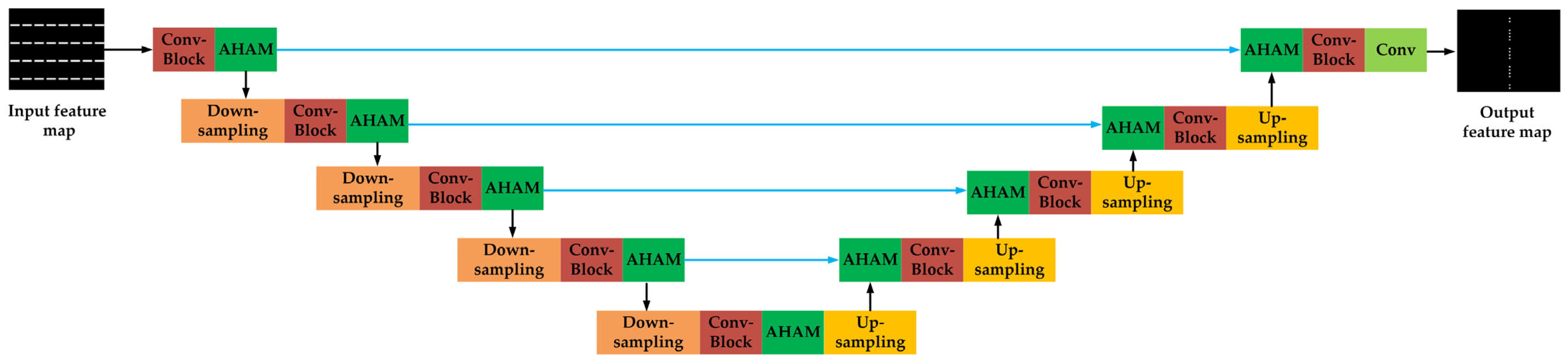
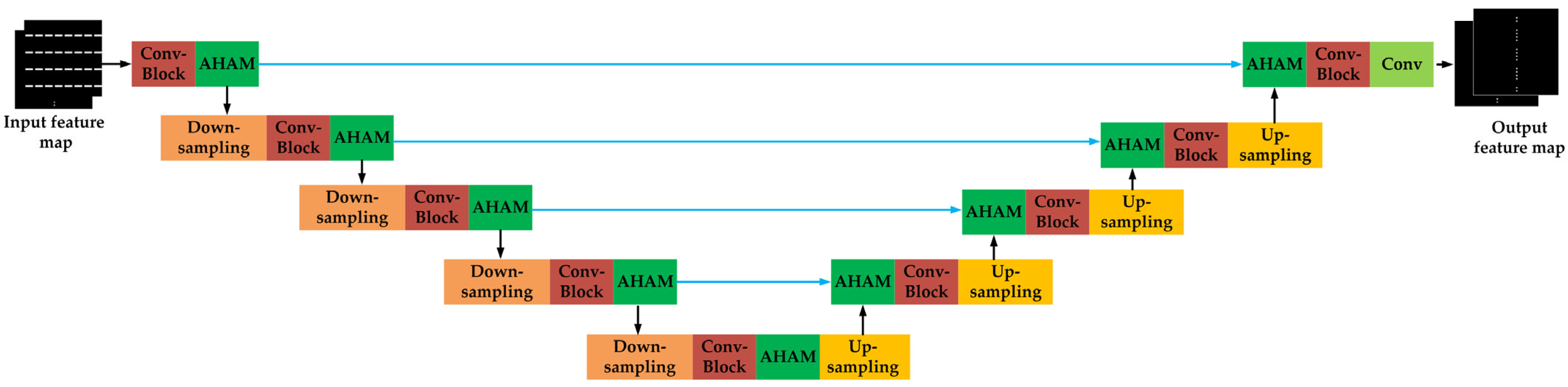
3. The Proposed Two-Stage Unet Framework
3.1. Unet1
3.2. Unet2
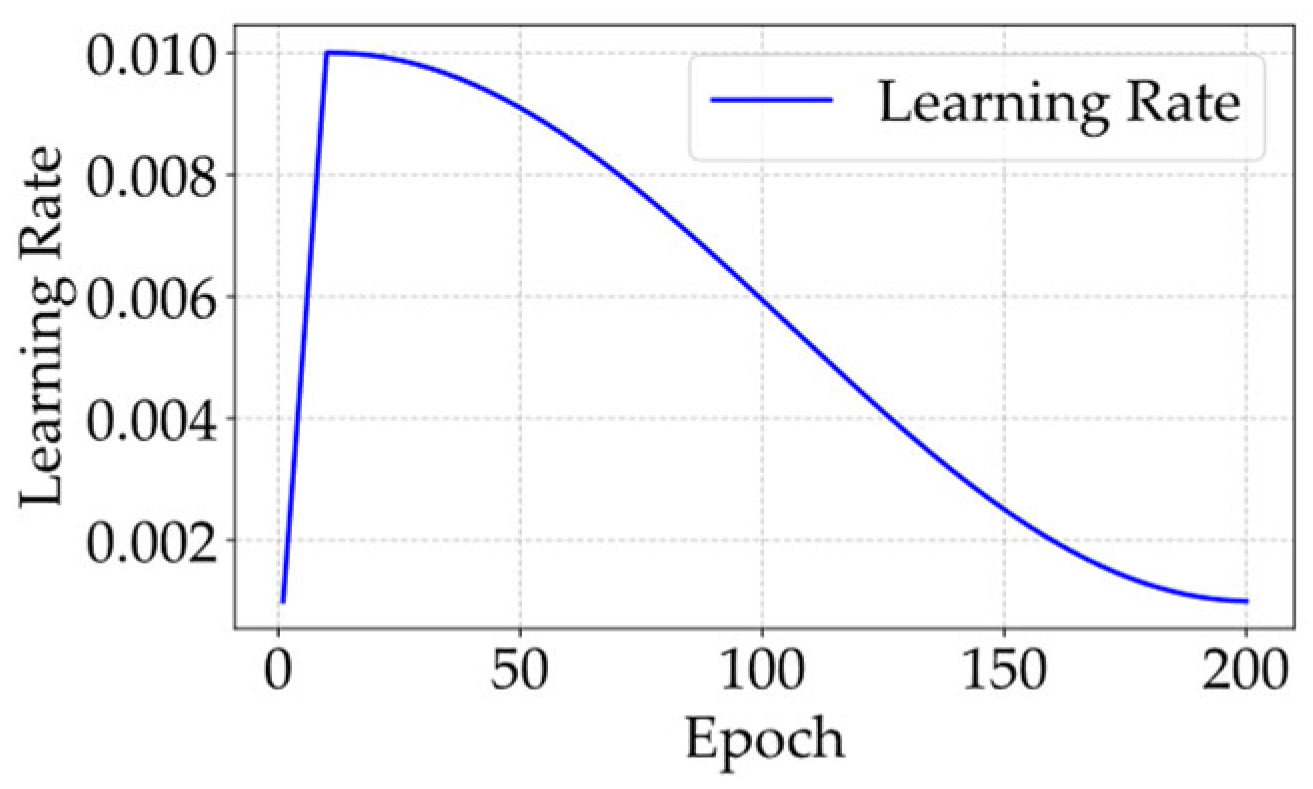
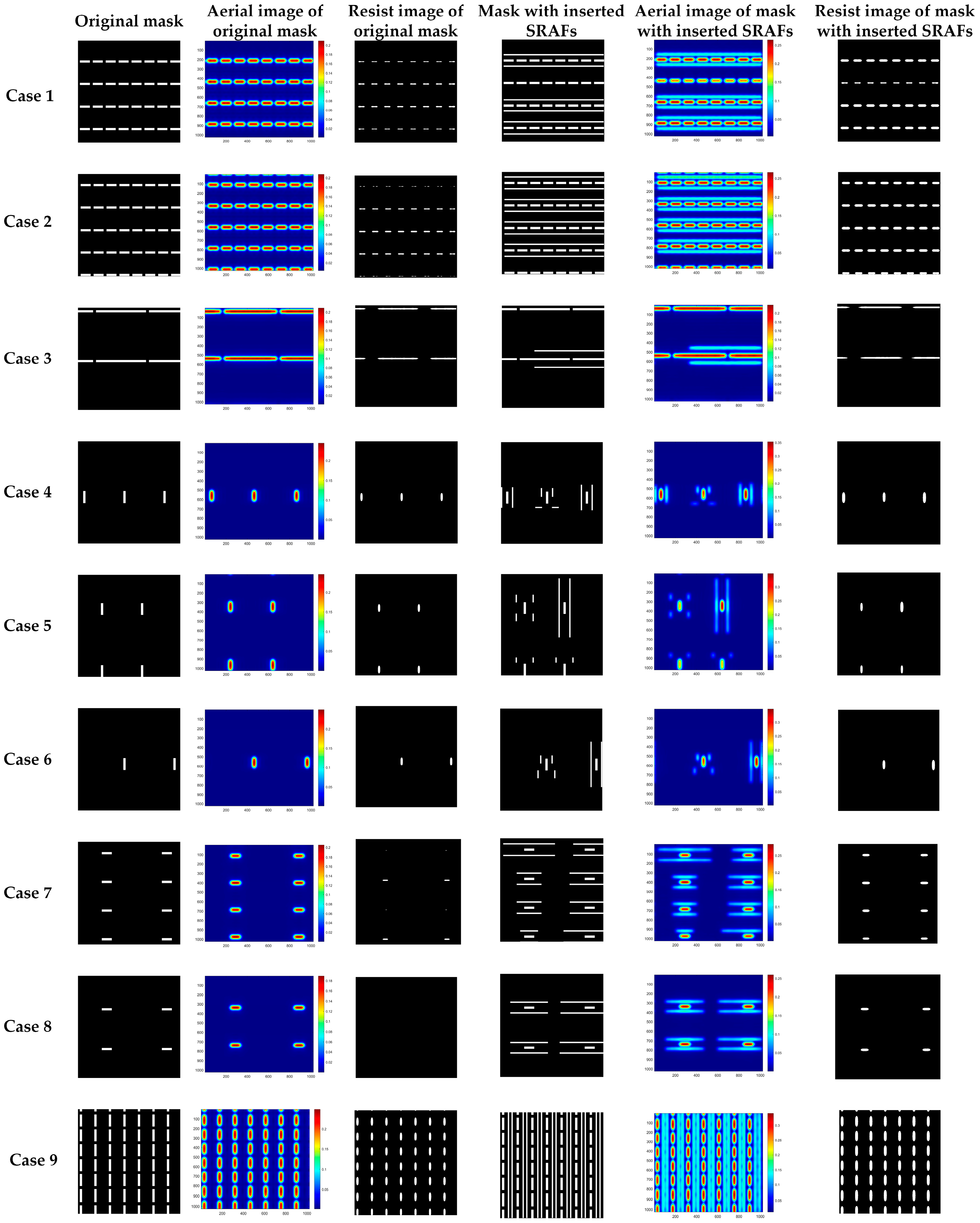
4. Simulation Results and Analysis
4.1. Results
4.2. Ablation Study
4.3. Comparison with Other Methods
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Module | Input Feature Map Size | Output Feature Map Size | Convolution Parameters (Kernel/Stride/Padding) | Padding Mode | |
|---|---|---|---|---|---|
| 1 | Conv_block | 1 × 1024 × 1024 | 32 × 1024 × 1024 | 3 × 3/1/1 | zeros |
| 2 | AHAM | 32 × 1024 × 1024 | 32 × 1024 × 1024 | ||
| 3 | Down-sampling | 32 × 1024 × 1024 | 32 × 512 × 512 | 3 × 3/2/1 | zeros |
| 4 | Conv_block | 32 × 512 × 512 | 64 × 512 × 512 | 3 × 3/1/1 | zeros |
| 5 | AHAM | 64 × 512 × 512 | 64 × 512 × 512 | ||
| 6 | Down-sampling | 64 × 512 × 512 | 64 × 256 × 256 | 3 × 3/2/1 | zeros |
| 7 | Conv_block | 64 × 256 × 256 | 128 × 256 × 256 | 3 × 3/1/1 | zeros |
| 8 | AHAM | 128 × 256 × 256 | 128 × 256 × 256 | ||
| 9 | Down-sampling | 128 × 256 × 256 | 128 × 128 × 128 | 3 × 3/2/1 | zeros |
| 10 | Conv_block | 128 × 128 × 128 | 256 × 128 × 128 | 3 × 3/1/1 | zeros |
| 11 | AHAM | 256 × 128 × 128 | 256 × 128 × 128 | ||
| 12 | Down-sampling | 256 × 128 × 128 | 256 × 64 × 64 | 3 × 3/2/1 | zeros |
| 13 | Conv_block | 256 × 64 × 64 | 512 × 64 × 64 | 3 × 3/1/1 | zeros |
| 14 | AHAM | 512 × 64 × 64 | 512 × 64 × 64 | ||
| 15 | Up-samling | 512 × 64 × 64 | 256 × 128 × 128 | 3 × 3/2/1 (ConvTranspose) | zeros |
| fused with layer 11 | 512 × 128 × 128 | ||||
| 16 | AHAM | 512 × 128 × 128 | 512 × 128 × 128 | ||
| 17 | Conv_block | 512 × 128 × 128 | 256 × 128 × 128 | 3 × 3/1/1 | zeros |
| 18 | Up-samling | 256 × 128 × 128 | 128 × 256 × 256 | 3 × 3/2/1 (ConvTranspose) | zeros |
| fused with layer 8 | 256 × 256 × 256 | ||||
| 19 | AHAM | 256 × 256 × 256 | 256 × 256 × 256 | ||
| 20 | Conv_block | 256 × 256 × 256 | 128 × 256 × 256 | 3 × 3/1/1 | zeros |
| 21 | Up-samling | 128 × 256 × 256 | 64 × 512 × 512 | 3 × 3/2/1 (ConvTranspose) | zeros |
| fused with layer 5 | 128 × 512 × 512 | ||||
| 22 | AHAM | 128 × 512 × 512 | 128 × 512 × 512 | ||
| 23 | Conv_block | 128 × 512 × 512 | 64 × 512 × 512 | 3 × 3/1/1 | zeros |
| 24 | Up-samling | 64 × 512 × 512 | 32 × 1024 × 1024 | 3 × 3/2/1 (ConvTranspose) | zeros |
| fused with layer 2 | 64 × 1024 × 1024 | ||||
| 25 | AHAM | 64 × 1024 × 1024 | 64 × 1024 × 1024 | ||
| 26 | Conv_block | 64 × 1024 × 1024 | 32 × 1024 × 1024 | 3 × 3/1/1 | zeros |
| 27 | Conv | 32 × 1024 × 1024 | 1 × 1024 × 1024 | 3 × 3/1/1 | zeros |
Appendix B
| Module | Input Feature Map Size | Output Feature Map Size | Convolution Parameters (Kernel/Stride/Padding) | Padding Mode | |
|---|---|---|---|---|---|
| 1 | Conv_block | 2 × 1024 × 1024 | 32 × 1024 × 1024 | 3 × 3/1/1 | zeros |
| 2 | AHAM | 32 × 1024 × 1024 | 32 × 1024 × 1024 | ||
| 3 | Down-sampling | 32 × 1024 × 1024 | 32 × 512 × 512 | 3 × 3/2/1 | zeros |
| 4 | Conv_block | 32 × 512 × 512 | 64 × 512 × 512 | 3 × 3/1/1 | zeros |
| 5 | AHAM | 64 × 512 × 512 | 64 × 512 × 512 | ||
| 6 | Down-sampling | 64 × 512 × 512 | 64 × 256 × 256 | 3 × 3/2/1 | zeros |
| 7 | Conv_block | 64 × 256 × 256 | 128 × 256 × 256 | 3 × 3/1/1 | zeros |
| 8 | AHAM | 128 × 256 × 256 | 128 × 256 × 256 | ||
| 9 | Down-sampling | 128 × 256 × 256 | 128 × 128 × 128 | 3 × 3/2/1 | zeros |
| 10 | Conv_block | 128 × 128 × 128 | 256 × 128 × 128 | 3 × 3/1/1 | zeros |
| 11 | AHAM | 256 × 128 × 128 | 256 × 128 × 128 | ||
| 12 | Down-sampling | 256 × 128 × 128 | 256 × 64 × 64 | 3 × 3/2/1 | zeros |
| 13 | Conv_block | 256 × 64 × 64 | 512 × 64 × 64 | 3 × 3/1/1 | zeros |
| 14 | AHAM | 512 × 64 × 64 | 512 × 64 × 64 | ||
| 15 | Up-samling | 512 × 64 × 64 | 256 × 128 × 128 | 3 × 3/2/1 (ConvTranspose) | zeros |
| fused with layer 11 | 512 × 128 × 128 | ||||
| 16 | AHAM | 512 × 128 × 128 | 512 × 128 × 128 | ||
| 17 | Conv_block | 512 × 128 × 128 | 256 × 128 × 128 | 3 × 3/1/1 | zeros |
| 18 | Up-samling | 256 × 128 × 128 | 128 × 256 × 256 | 3 × 3/2/1 (ConvTranspose) | zeros |
| fused with layer 8 | 256 × 256 × 256 | ||||
| 19 | AHAM | 256 × 256 × 256 | 256 × 256 × 256 | ||
| 20 | Conv_block | 256 × 256 × 256 | 128 × 256 × 256 | 3 × 3/1/1 | zeros |
| 21 | Up-samling | 128 × 256 × 256 | 64 × 512 × 512 | 3 × 3/2/1 (ConvTranspose) | zeros |
| fused with layer 5 | 128 × 512 × 512 | ||||
| 22 | AHAM | 128 × 512 × 512 | 128 × 512 × 512 | ||
| 23 | Conv_block | 128 × 512 × 512 | 64 × 512 × 512 | 3 × 3/1/1 | zeros |
| 24 | Up-samling | 64 × 512 × 512 | 32 × 1024 × 1024 | 3 × 3/2/1 (ConvTranspose) | zeros |
| fused with layer 2 | 64 × 1024 × 1024 | ||||
| 25 | AHAM | 64 × 1024 × 1024 | 64 × 1024 × 1024 | ||
| 26 | Conv_block | 64 × 1024 × 1024 | 32 × 1024 × 1024 | 3 × 3/1/1 | zeros |
| 27 | Conv | 32 × 1024 × 1024 | 2 × 1024 × 1024 | 3 × 3/1/1 | zeros |
References
- Chen, Q.; Mao, Z.; Yu, S.; Wu, W. Sub-resolution-assist-feature placement study to dense patterns in advanced lithography process. In Proceedings of the Semiconductor Technology International Conference, Shanghai, China, 13–14 March 2016; pp. 1–3. [Google Scholar]
- Beylier, C.; Martin, N.; Farys, V.; Foussadier, F.; Yesilada, E.; Robert, F.; Baron, S.; Dover, R.; Liu, H.-Y. Demonstration of an effective flexible mask optimization (FMO) flow. In Proceedings of the Optical Microlithography XXV, San Jose, CA, USA, 12–16 February 2012; Volume 8326, p. 832616. [Google Scholar]
- Su, X.; Gao, P.; Wei, Y.; Shi, W. SRAF rule extraction and insertion based on inverse lithography technology. In Proceedings of the Optical Microlithography XXXII, San Jose, CA, USA, 24–28 February 2012; Volume 10961, p. 109610P. [Google Scholar]
- Ping, Y.; McGowan, S.; Gong, Y.; Foong, Y.M.; Liu, J.; Qiu, J.; Shu, V.; Yan, B.; Ye, J.; Li, P.; et al. Process window enhancement using advanced RET techniques for 20nm contact layer. In Proceedings of the Optical Microlithography XXVII, San Jose, CA, USA, 23–27 February 2014; Volume 9052, p. 90521N. [Google Scholar]
- Viswanathan, R.; Azpiroz, J.T.; Selvam, P. Process optimization through model based SRAF printing prediction. In Proceedings of the Optical Microlithography XXV, San Jose, CA, USA, 12–16 February 2012; Volume 8326, p. 83261A. [Google Scholar]
- Chen, A.; Hansen, S.; Moers, M.; Shieh, J.; Engelen, A.; van Ingen Schenau, K.; Tseng, S. The contact hole solutions for future logic technology nodes. In Proceedings of the Quantum Optics, Optical Data Storage, and Advanced Microlithography, Beijing, China, 11–15 November 2007; Volume 6827, p. 68271O. [Google Scholar]
- Jun, J.; Park, M.; Park, C.; Yang, H.; Yim, D.; Do, M.; Lee, D.; Kim, T.; Choi, J.; Luk-Pat, G. Layout optimization with assist features placement by model based rule tables for 2x node random contact. In Proceedings of the Design-Process-Technology Co-optimization for Manufacturability IX, San Jose, CA, USA, 22–26 February 2015; Volume 9427, p. 94270D. [Google Scholar]
- Kodama, C.; Kotani, T.; Nojima, S.; Mimotogi, S. Sub-Resolution Assist Feature Arranging Method and Computer Program Product and Manufacturing Method of Semiconductor Device. U.S. Patent US20110294239A1, 19 August 2014. [Google Scholar]
- Yenikaya, B.; Wong, A.K.K.; Singh, V.K.; Sezginer, A. Model-based assist feature generation. In Proceedings of the Design for Manufacturability through Design-Process Integration, San Jose, CA, USA, 25 February–2 March 2007; Volume 6521, p. 73792Z. [Google Scholar]
- Capodieci, L.; Cain, J.P.; Song, J.; Choi, J.; Park, C.; Yang, H.; Kang, D.; Oh, M.; Park, M.; Moon, J. The new OPC method for obtaining the stability of MBAF OPC. In Proceedings of the Design-Process-Technology Co-optimization for Manufacturability XI, San Jose, CA, USA, 26 February–2 March 2017; Volume 10148, p. 1014813. [Google Scholar]
- Sakajiri, K.; Horiuchi, T.; Tritchkov, A.; Granik, Y. Model-based SRAF insertion through pixel-based mask optimization at 32nm and beyond. In Proceedings of the Photomask and Next-Generation Lithography Mask Technology XV, Yokohama, Japan, 16–18 April 2008; Volume 7028, p. 702811. [Google Scholar]
- Xu, X.; Matsunawa, T.; Nojima, S.; Kodama, C.; Kotani, T.; Pan, D.Z. A Machine Learning Based Framework for Sub-Resolution Assist Feature Generation. In Proceedings of the ACM, Santa Rosa, CA, USA, 3–6 April 2016; pp. 161–168. [Google Scholar]
- Geng, H.; Yang, H.; Ma, Y.; Mitra, J.; Yu, B. SRAF insertion via supervised dictionary learning. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 39, 2849–2859. [Google Scholar] [CrossRef]
- Liu, G.-T.; Tai, W.-C.; Lin, Y.-T.; Jiang, I.H.-R.; Shiely, J.P.; Cheng, P.-J. Sub-Resolution Assist Feature Generation with Reinforcement Learning and Transfer Learning. In Proceedings of the 2022 IEEE/ACM International Conference On Computer Aided Design (ICCAD), San Diego, CA, USA, 29 October–3 November 2022; pp. 1–9. [Google Scholar]
- Ciou, W.; Hu, T.; Tsai, Y.Y.; Hsuan, T.; Yang, E.; Yang, T.H.; Chen, K.C. SRAF placement with generative adversarial network. In Proceedings of the Optical Microlithography XXXIV, Online, 22–27 February 2021; Volume 11613, p. 1161305. [Google Scholar]
- Wang, S.; Su, J.; Zhang, Q.; Fong, W.; Sun, D.; Baron, S.; Zhang, C.; Lin, C.; Chen, B.D.; Howell, R.C. Machine learning assisted SRAF placement for full chip. In Proceedings of the Photomask Technology 2017, Monterey, CA, USA, 11–14 September 2017; Volume 10451, p. 104510D. [Google Scholar]
- Alawieh, M.B.; Lin, Y.; Zhang, Z.; Li, M.; Pan, D.Z. GAN-SRAF: Sub-Resolution Assist Feature Generation using Generative Adversarial Networks. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2021, 40, 373–385. [Google Scholar] [CrossRef]
- Wei, Y.; Brainard, R.L. Advanced Processes for 193-nm Immersion Lithography; SPIE Press: Bellingham, WA, USA, 2009. [Google Scholar]
- Wei, Y.Y. Advanced Lithography: Theory and Application of Very Large Scale Integrated Circuit; Science Press: Beijing, China, 2016. [Google Scholar]
- Li, F.; Mu, Y.; Fan, J.; Yu, C.; Liu, R.; Sun, S.; Wang, C.; Shi, J.; Cao, Q. Balancing mask manufacturability and image quality with inverse lithography: A study on variable fracture sizes. In Proceedings of the Optical and EUV Nanolithography XXXVII, Bellingham, WA, USA, 25 February–1 March 2024; Volume 12953, p. 1295310. [Google Scholar]
- Ai, F.; Su, X.; Dong, L.; Fan, T.; Wang, J.; Wei, Y. Rect-SRAF method in inverse lithography technology. Opt. Express 2025, 33, 30060–30072. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Volume 9351, pp. 234–241. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. arXiv 2023, arXiv:1706.03762. [Google Scholar] [PubMed]
- Huang, W.; Chen, J.; Cai, Y.; Hu, X. Hierarchical Hybrid Neural Networks with Multi-Head Attention for Document Classification. Int. J. Data Warehous. Min. 2022, 18, 268–283. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. arXiv 2021, arXiv:2103.14030. [Google Scholar] [CrossRef]
- Luong, M.T.; Pham, H.; Manning, C.D. Effective Approaches to Attention-based Neural Machine Translation. arXiv 2015, arXiv:1508.04025. [Google Scholar] [CrossRef]
- Yang, J.; Li, C.; Zhang, P.; Dai, X.; Xiao, B.; Yuan, L.; Gao, J. Focal Self-attention for Local-Global Interactions in Vision Transformers. arXiv 2021, arXiv:2107.00641. [Google Scholar]
- Smith, L.N. Cyclical learning rates for training neural networks. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 464–472. [Google Scholar]
- Ge, R.; Kakade, S.M.; Kidambi, R.; Netrapalli, P. The step decay schedule: A near optimal, geometrically decaying learning rate procedure for least squares. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Kalra, D.S.; Barkeshli, M. Why Warmup the Learning Rate? Underlying Mechanisms and Improvements. arXiv 2024, arXiv:2406.09405. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Warm Restarts. arXiv 2017, arXiv:1608.03983. [Google Scholar] [CrossRef]
- Niu, Z.; Li, H. Research and analysis of threshold segmentation algorithms in image processing. J. Phys. Conf. Ser. 2019, 1237, 022122. [Google Scholar] [CrossRef]
- He, L.; Ren, X.; Gao, Q.; Zhao, X.; Yao, B.; Chao, Y. The connected-component labeling problem: A review of state-of-the-art algorithms. Pattern Recognit. 2017, 70, 25–43. [Google Scholar] [CrossRef]
- Soille, P. Morphological Image Analysis: Principles and Applications. Sens. Rev. 1999, 28, 800–801. [Google Scholar]
- Ma, X.; Arce, G.R. Computational Lithography; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ma, X.; Li, Y.; Dong, L. Mask optimization approaches in optical lithography based on a vector imaging model. J. Opt. Soc. Am. A 2012, 29, 1300–1312. [Google Scholar] [CrossRef] [PubMed]
- Pistor, T.V. Electromagnetic Simulation and Modeling with Applications in Lithography. Ph.D. Thesis, Doctor of Philosophy, University of California, Berkeley, CA, USA, 2001. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2014; Volume 2, pp. 2672–2680. [Google Scholar]
- Mirza, M.; Osindero, S. Conditional Generative Adversarial Nets. arXiv 2014, arXiv:1411.1784. [Google Scholar] [CrossRef]
- Oktay, O.; Schlemper, J.; Le Folgoc, L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar] [CrossRef]


| Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 | Case 7 | Case 8 | Case 9 | Mean | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Original Mask | PE | 51,910 | 68,284 | 20,386 | 3545 | 4664 | 2296 | 15,401 | 8800 | 56,702 | 25,776.44 |
| EPE | 6.7591 | 7.1576 | 4.9673 | 4.1903 | 4.1348 | 4.0709 | 7.9880 | 9.1667 | 4.0952 | 5.8367 | |
| Mask with inserted SRAFs | PE | 26,994 | 29,690 | 17,237 | 3045 | 4416 | 1983 | 6699 | 3072 | 43,694 | 15,203.33 |
| EPE | 3.5148 | 3.1122 | 4.2000 | 3.5993 | 3.9149 | 3.5160 | 4.4746 | 3.2000 | 3.1557 | 3.5283 |
| Unet | Unet + WCA | Unet + AHAM | Unet + AHAM + WCA | |||||
|---|---|---|---|---|---|---|---|---|
| PE | EPE | PE | EPE | PE | EPE | PE | EPE | |
| Case 1 | 51,910 | 6.7591 | 45,235 | 5.8900 | 36,612 | 4.7672 | 26,994 | 3.5148 |
| Case 2 | 68,284 | 7.1577 | 68,284 | 7.1577 | 53,045 | 5.5603 | 29,690 | 3.1122 |
| Case 3 | 20,386 | 4.9673 | 15,974 | 3.8923 | 10,264 | 2.5010 | 17,237 | 4.2000 |
| Case 4 | 3227 | 3.8144 | 3027 | 3.5780 | 2872 | 3.3948 | 3045 | 3.5993 |
| Case 5 | 4222 | 3.7429 | 4584 | 4.0638 | 4327 | 3.8360 | 4416 | 3.9149 |
| Case 6 | 2135 | 3.7855 | 2146 | 3.8050 | 1989 | 3.5266 | 1983 | 3.5160 |
| Case 7 | 15,234 | 7.9015 | 11,361 | 5.8926 | 8379 | 4.3460 | 6699 | 3.4746 |
| Case 8 | 8800 | 9.1667 | 7303 | 7.6073 | 4415 | 4.5990 | 3072 | 3.2000 |
| Case 9 | 46,427 | 3.3531 | 43,830 | 3.1655 | 43,797 | 3.1632 | 43,694 | 3.1557 |
| Mean | 24,513.89 | 5.6276 | 22,416.00 | 5.0058 | 18,411.11 | 3.9660 | 15,203.33 | 3.5208 |
| Original Mask | FCN | GAN | CGAN | AUnet | Proposed Method | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PE | EPE | PE | EPE | PE | EPE | PE | EPE | PE | EPE | PE | EPE | |
| Case 1 | 51,910 | 6.7591 | 42,039 | 5.4738 | 51,910 | 6.7591 | 31,689 | 4.1262 | 29,176 | 3.7990 | 26,994 | 3.5148 |
| Case 2 | 68,284 | 7.1577 | 65,274 | 6.8421 | 68,284 | 7.1577 | 50,376 | 5.2805 | 36,578 | 3.8342 | 29,690 | 3.1122 |
| Case 3 | 20,386 | 4.9673 | 13,981 | 3.4067 | 20,386 | 4.9673 | 15,546 | 3.7880 | 20,386 | 4.9673 | 17,237 | 4.2000 |
| Case 4 | 3545 | 4.1903 | 3147 | 3.7199 | 3545 | 4.1903 | 2786 | 3.2931 | 3497 | 4.1336 | 3045 | 3.5993 |
| Case 5 | 4664 | 4.1348 | 4339 | 3.8466 | 4664 | 4.1348 | 4082 | 3.6188 | 4694 | 4.1613 | 4416 | 3.9149 |
| Case 6 | 2296 | 4.0709 | 2140 | 3.7943 | 2296 | 4.0709 | 1866 | 3.3085 | 2291 | 4.0621 | 1983 | 3.5160 |
| Case 7 | 15,401 | 7.9881 | 14,149 | 7.3387 | 15,121 | 7.8428 | 11,993 | 6.2204 | 14,628 | 7.5871 | 6699 | 3.4746 |
| Case 8 | 8800 | 9.1667 | 7455 | 7.7656 | 8800 | 9.1667 | 5200 | 5.4167 | 7433 | 7.7427 | 3072 | 3.2000 |
| Case 9 | 56,702 | 4.0952 | 52,311 | 3.7781 | 55,098 | 3.9793 | 49,385 | 3.5667 | 47,271 | 3.4141 | 43,694 | 3.1557 |
| Mean | 25,776.44 | 5.8367 | 22,759.44 | 5.1073 | 25,567.11 | 5.0877 | 19,213.67 | 4.2910 | 18,439.33 | 4.8557 | 15,203.33 | 3.5283 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, M.; Ma, L.; Dong, L.; Ma, X. A Two-Stage Unet Framework for Sub-Resolution Assist Feature Prediction. Micromachines 2025, 16, 1301. https://doi.org/10.3390/mi16111301
Lin M, Ma L, Dong L, Ma X. A Two-Stage Unet Framework for Sub-Resolution Assist Feature Prediction. Micromachines. 2025; 16(11):1301. https://doi.org/10.3390/mi16111301
Chicago/Turabian StyleLin, Mu, Le Ma, Lisong Dong, and Xu Ma. 2025. "A Two-Stage Unet Framework for Sub-Resolution Assist Feature Prediction" Micromachines 16, no. 11: 1301. https://doi.org/10.3390/mi16111301
APA StyleLin, M., Ma, L., Dong, L., & Ma, X. (2025). A Two-Stage Unet Framework for Sub-Resolution Assist Feature Prediction. Micromachines, 16(11), 1301. https://doi.org/10.3390/mi16111301





