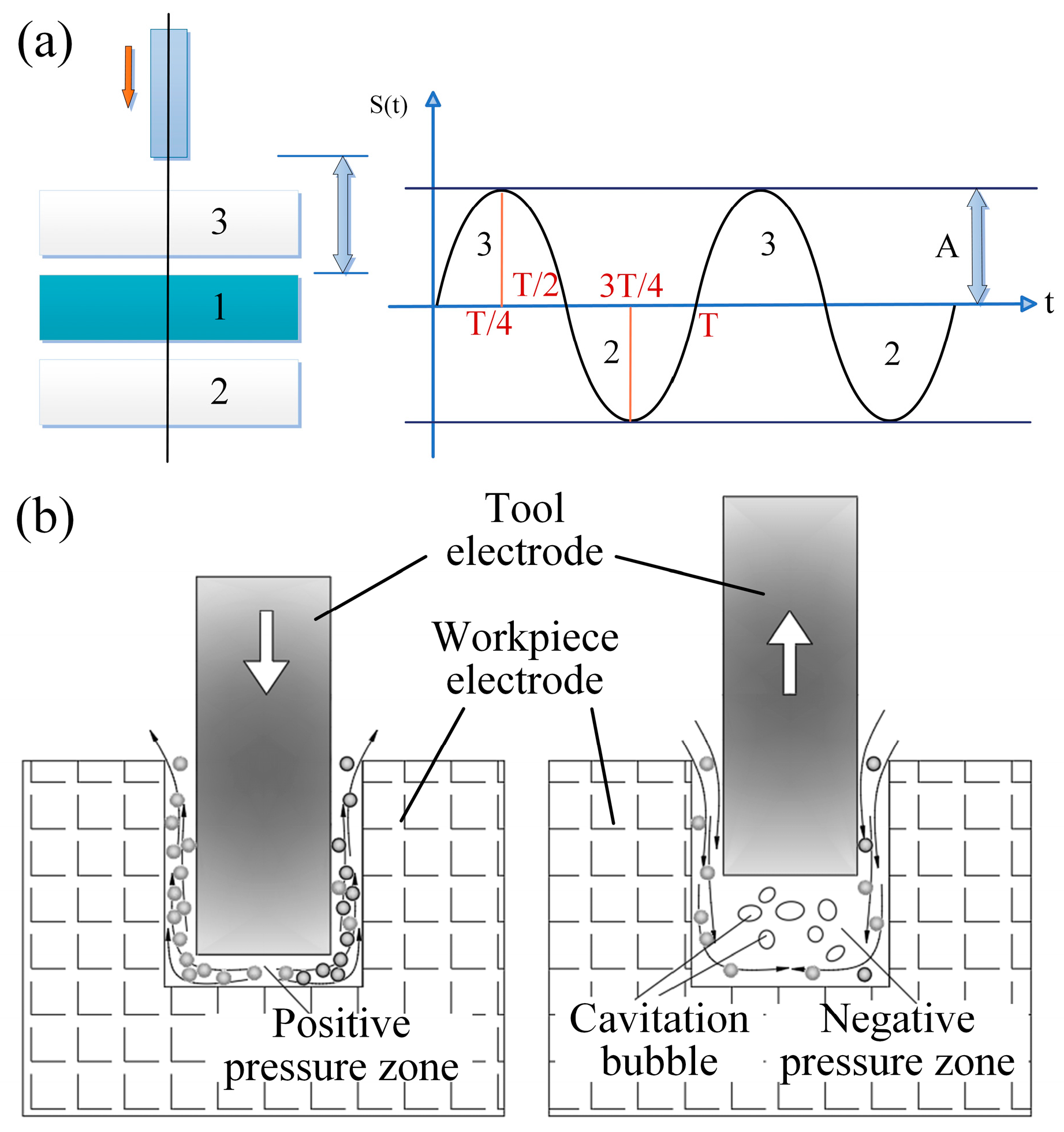
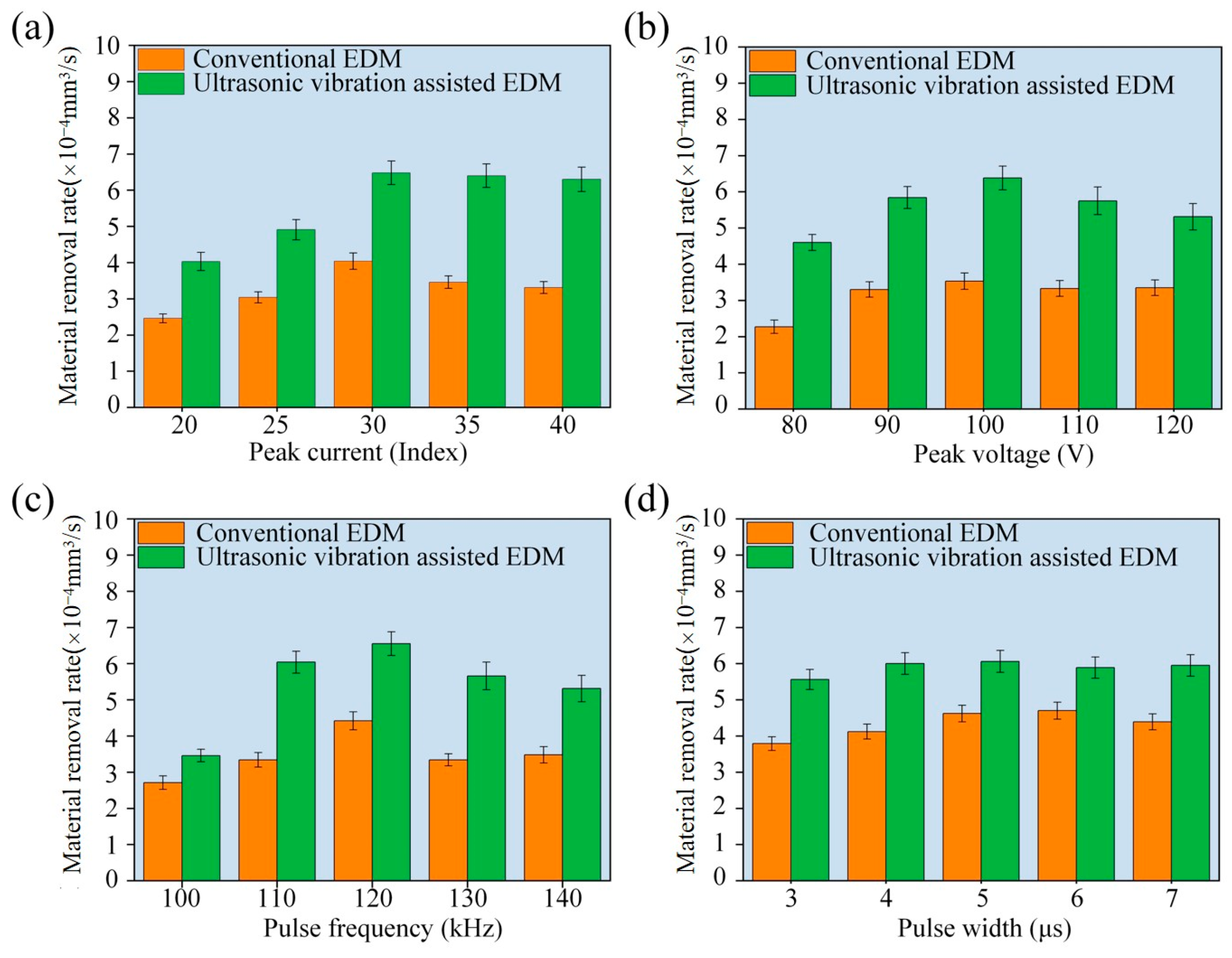
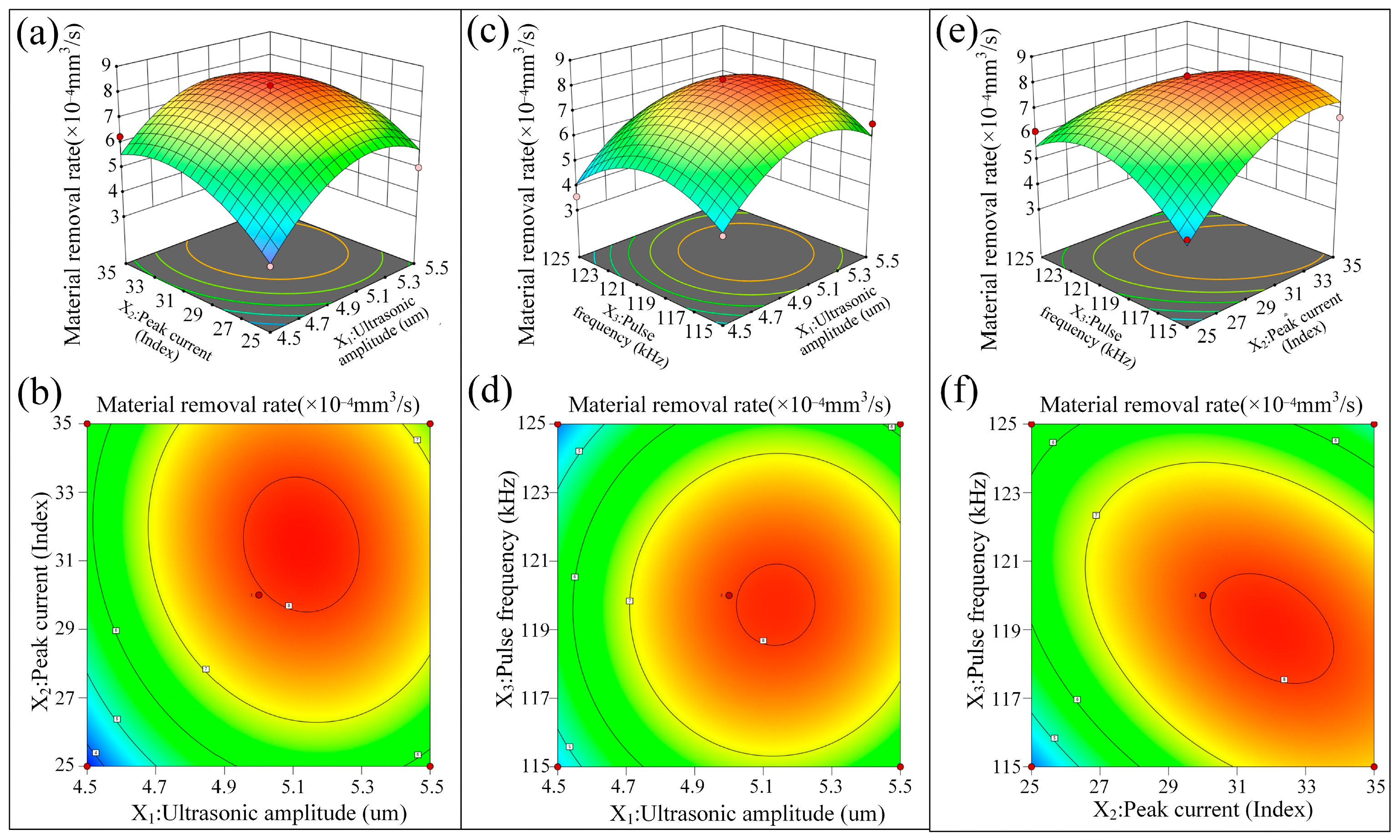
3.1. Effect of Ultrasonic Vibration on Machining
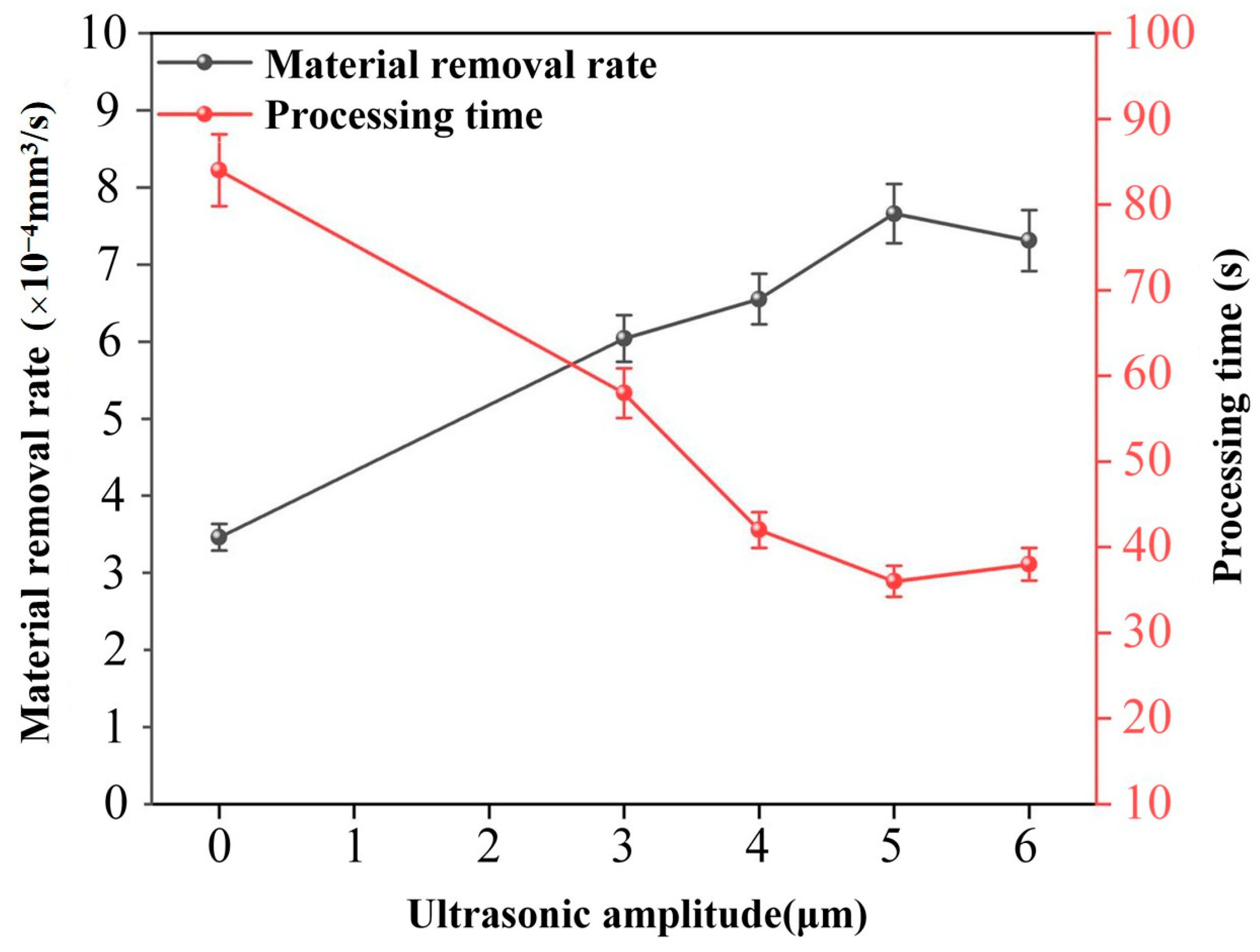
Figure 4 shows the effect of ultrasonic amplitude on the MRR and processing time under the conditions of a peak current of 30 Index, peak voltage of 100 V, pulse frequency of 120 kHz, and pulse width of 5 µs. As the ultrasonic amplitude increases, the MRR increases, while the processing time decreases. When the amplitude is 5um, the MRR reaches its maximum value, and the processing time reaches its minimum. Beyond this amplitude, the MRR starts to decrease, and the processing time correspondingly increases.
The ultrasonic vibration of the electrode causes the pressure of the machining zone to alternate. With increasing amplitude, the intensity of this alternating pressure becomes stronger. The resulting impact pressure makes it easier for erosion debris to detach from the surface of the workpiece. Simultaneously, the increased suction effect produced by the greater amplitude allows for speedy inflow of fresh working fluid into the discharge gap. This constant renewal of the fluid creates a cyclic process of efficient discharge, rapid debris removal, and re-discharge of the fluid, which improves the MRR and shortens the overall machining time.
When the ultrasonic amplitude is greater than 5 µm, the MRR starts to decrease. Although the cavitation effect still helps to remove the debris, an excessively large amplitude creates many oversized cavitation bubbles. Because these bubbles are non-conductive, they block the development of discharge channels. Consequently, stable discharges are not possible because the bubbles separate the electrode from the working fluid, and the number of effective discharges is reduced. Moreover, although an increased amplitude improves the alternating pressure in the discharge gap, beyond a critical value it causes rapid and irregular pressure fluctuations. These fluctuations cause disordered fluid flow, such as eddies and backflows, which make it difficult to remove the debris effectively. Instead of being expelled, debris-laden fluid may re-enter the machining zone and cause reaccumulation and degraded discharge stability. As a result, the MRR is reduced and the processing time is increased.
Figure 5 shows the CLSM and SEM images of the surface of the C/SiC composite after EDM.
Figure 5a presents the 3D morphology of the micro-hole created via EDM, where the blue region represents the machined area. The uneven color depth shows great height variations, and local pits and protrusions may be present.
Figure 5b shows the SEM morphology of the micro-hole, and the cross-sections of carbon fibers and SiC matrix between them can be clearly seen. These features are in agreement with the 3D morphology, both revealing pits and protrusions. The observed morphology proves that during EDM of C/SiC composites, the removal of the SiC matrix leaves protruding carbon fibers, indicating that the erosion rate and volume of the SiC matrix are higher than the carbon fibers.
Figure 5c presents the morphology of the micro-hole entrance after ultrasonic vibration excitation, in which the yellow areas are carbon fibers and SiC debris. The presence of these residues around the hole entrance clearly indicates that the EDM process of C/SiC composites is accompanied by the melting of the SiC matrix and cracking of the carbon fibers. Melting and fragmentation of the SiC matrix reveal the carbon fibers, which, under the impact of the explosive force of sparks, are prone to breaking and generating debris. Ultrasonic vibration helps the working fluid pump the fragments out of the hole quickly, which are concentrated around the entrance. From the carbon fiber fracture surface in
Figure 5d, it can be seen that the fiber removal also includes melting, because the fracture surface has traces of melting and not just mechanical fracturing. This result reveals that the melting and vaporization of the SiC matrix, as well as the combined fracture and melting of carbon fibers, are the primary material removal mechanisms in ultrasonic vibration-assisted micro-EDM of C/SiC composites.
Figure 6 shows a comparison of the recast layer and hole diameter of C/SiC composites processed using conventional EDM and ultrasonic vibration-assisted EDM. In locations 1 and 2 of
Figure 6a, the recast layer is relatively thick, unevenly shaped, rough, and unevenly distributed. When the hole depth is deep, the high temperature generated under discharge causes the rapid melting and partial vaporization of the workpiece surface. Because of the very short discharge time, a part of the molten material cannot be forced out of the discharge area in time and resolidifies on the surface, resulting in the recast layer seen in
Figure 6a. In contrast, the recast layer in
Figure 6b is much thinner and more homogeneous. This is due to the adoption of ultrasonic vibration, which generates a great number of microbubbles that collapse to generate intense shock waves due to cavitation. These shock waves break up and disperse molten material, which helps to remove erosion debris. At the same time, the pumping effect quickly removes the molten material from the discharge gap to avoid resolidification of the molten material on the machined surface. A large decrease in carbon fiber delamination is also observed in area 3 of
Figure 6b due to the improved fluid flow and debris removal caused by ultrasonic vibration. The enhanced heat dissipation reduces thermal accumulation in the machining area and thermal stress caused by the difference in thermal expansion coefficient between carbon fibers and SiC matrix, thus reducing delamination.
Figure 6c shows the morphology of the micro-hole entrance after conventional EDM; the hole diameter was 268.75 µm.
Figure 6d shows the hole entrance morphology obtained at an ultrasonic amplitude of 5 μm, with a smaller diameter of 256.47 µm. Residual fractured carbon fibers are shown in the red box regions of
Figure 6d. After ultrasonic vibration is introduced, the carbon fibers broken by cavitation are washed out by the working fluid and are gathered around the hole entrance, which verifies that carbon fiber fracture is one of the main erosion mechanisms in the ultrasonic vibration-assisted micro-EDM of C/SiC composites. The hole diameter decreased by about 12 μm after ultrasonic vibration was added. The improved removal of debris in the discharge gap caused by cavitation and pumping effects eliminates unstable discharge channels that can focus energy on the hole wall and produce excessive erosion and hole enlargement.