Optofluidic Lens Refractometer
Abstract
1. Introduction
2. Theoretical Analysis and Numerical Simulation
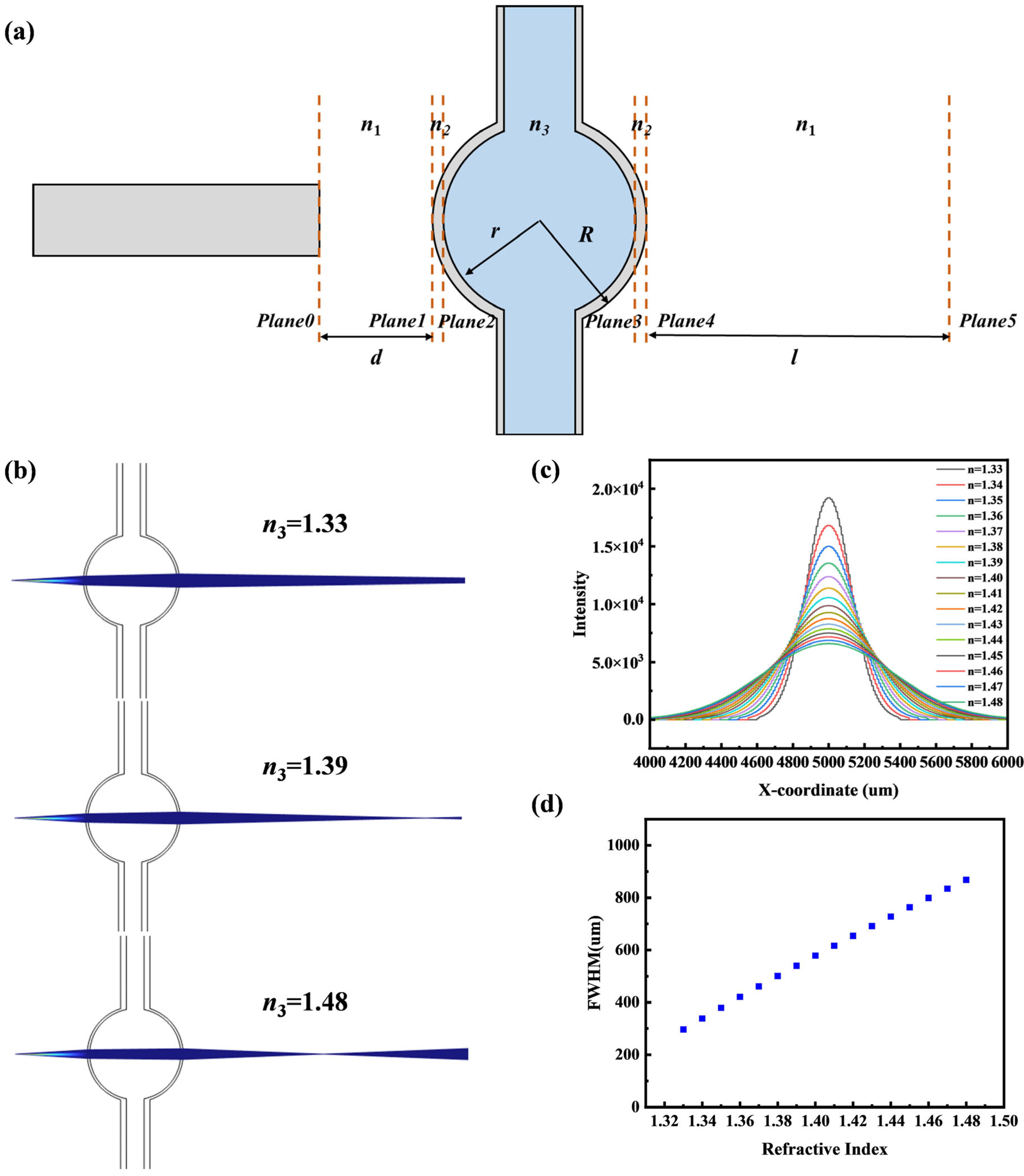
2.1. ABCD Matrix
2.2. Numerical Simulation
2.3. Robustness Testing
2.3.1. Microbubble Radius
2.3.2. Distance from Light Source
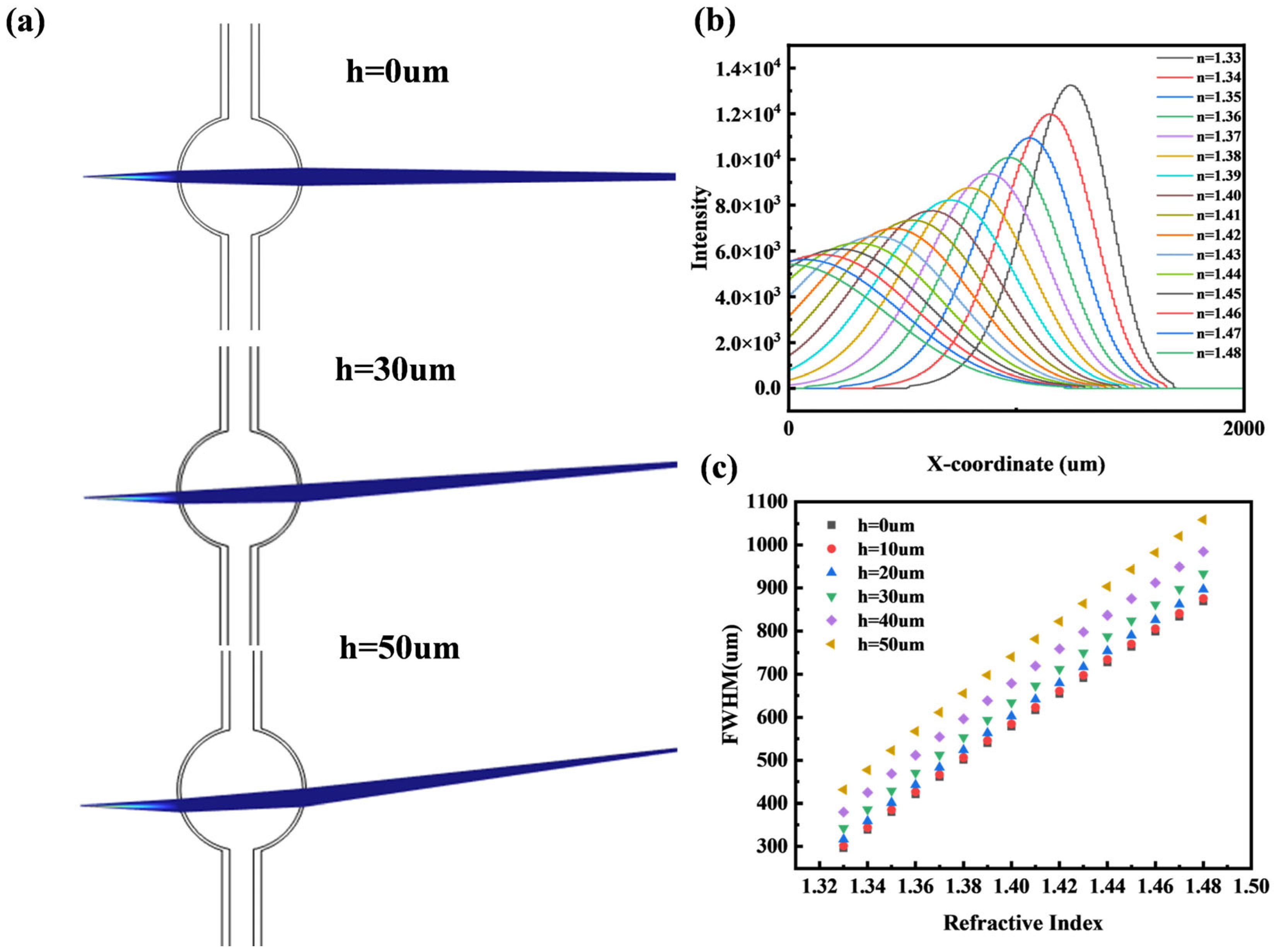
2.3.3. Microbubble Height Offset
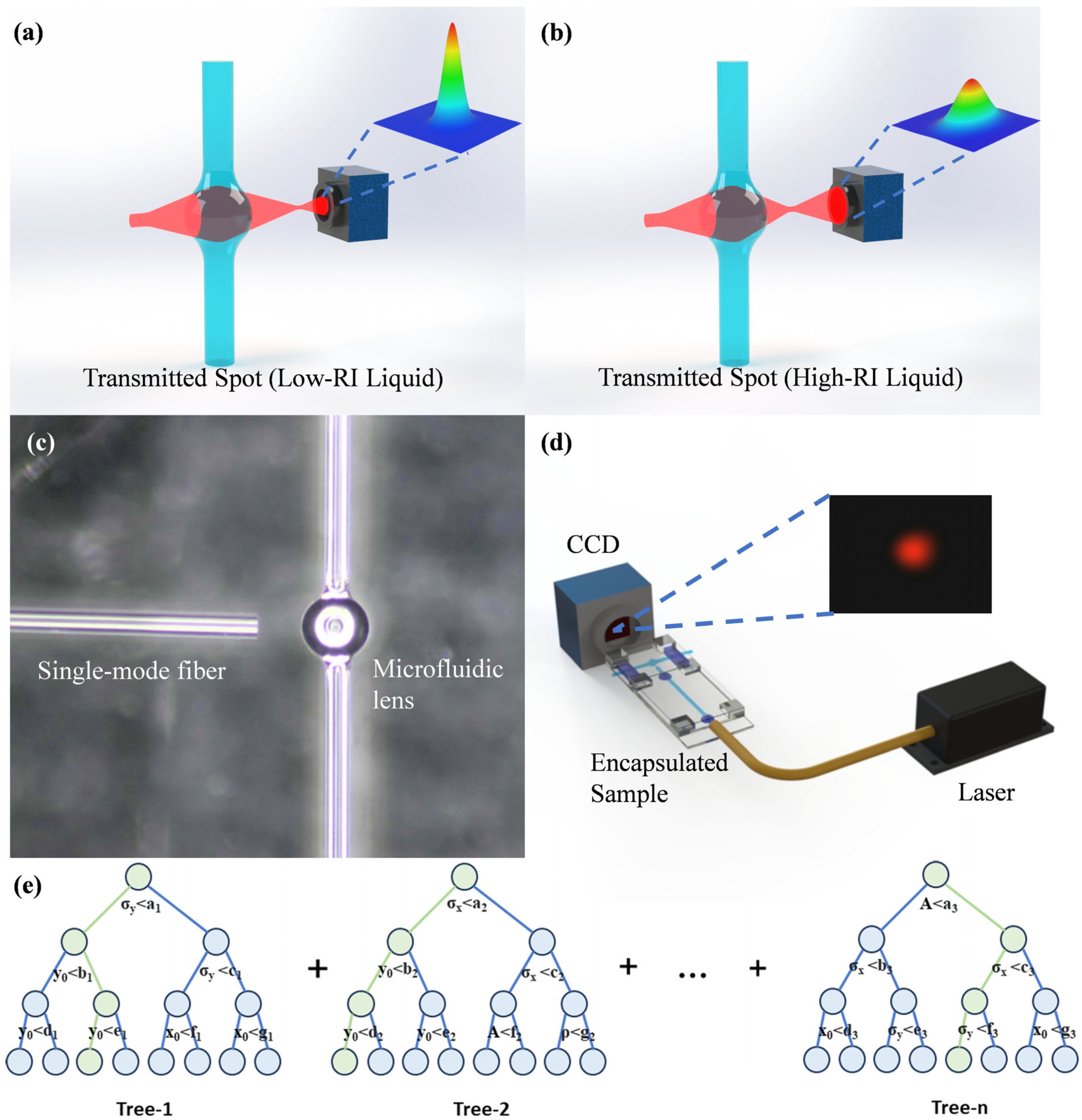
3. Materials and Methods
3.1. Materials
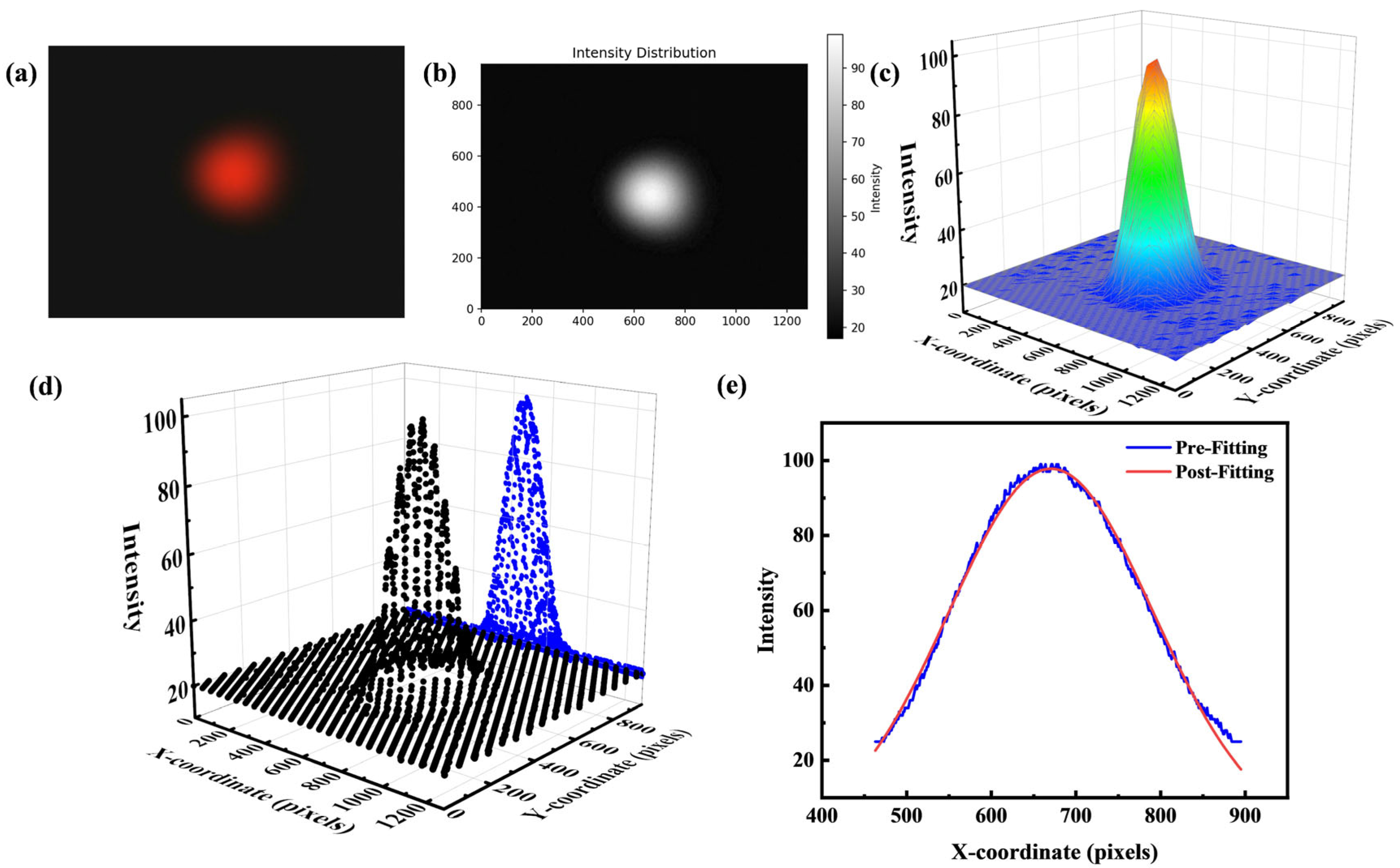
3.2. Method
4. Results and Discussion
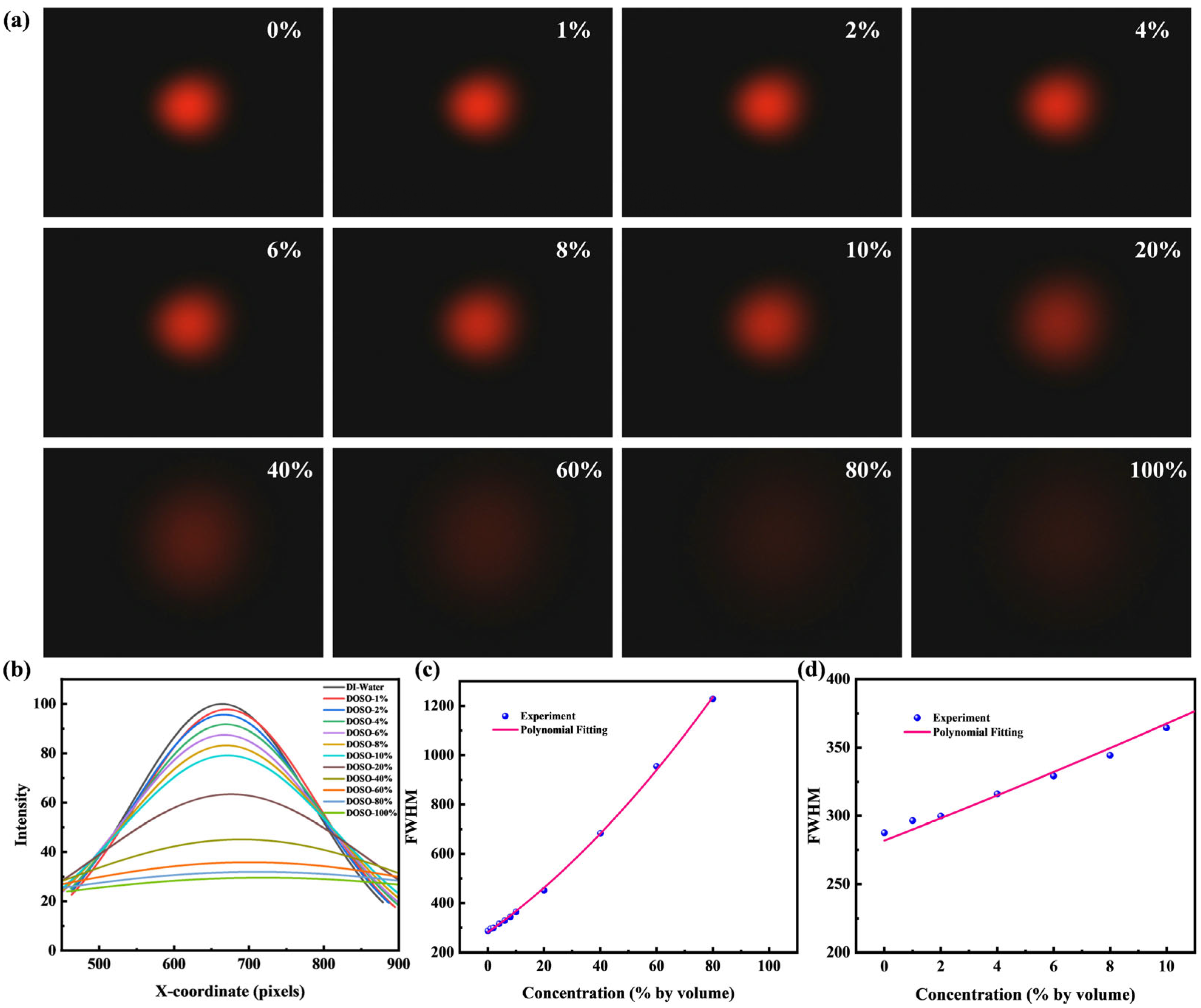
4.1. Fitted Half-Width
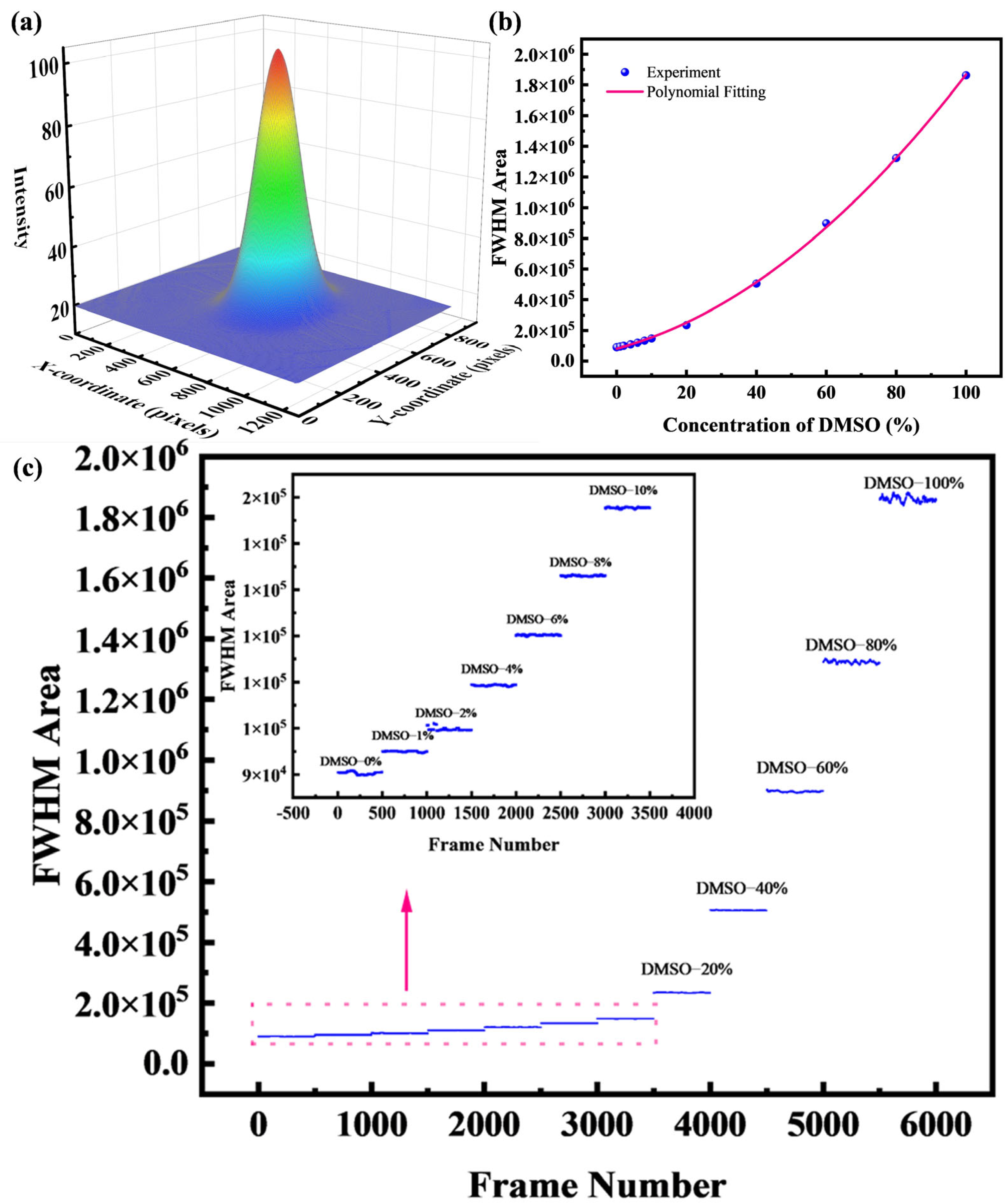
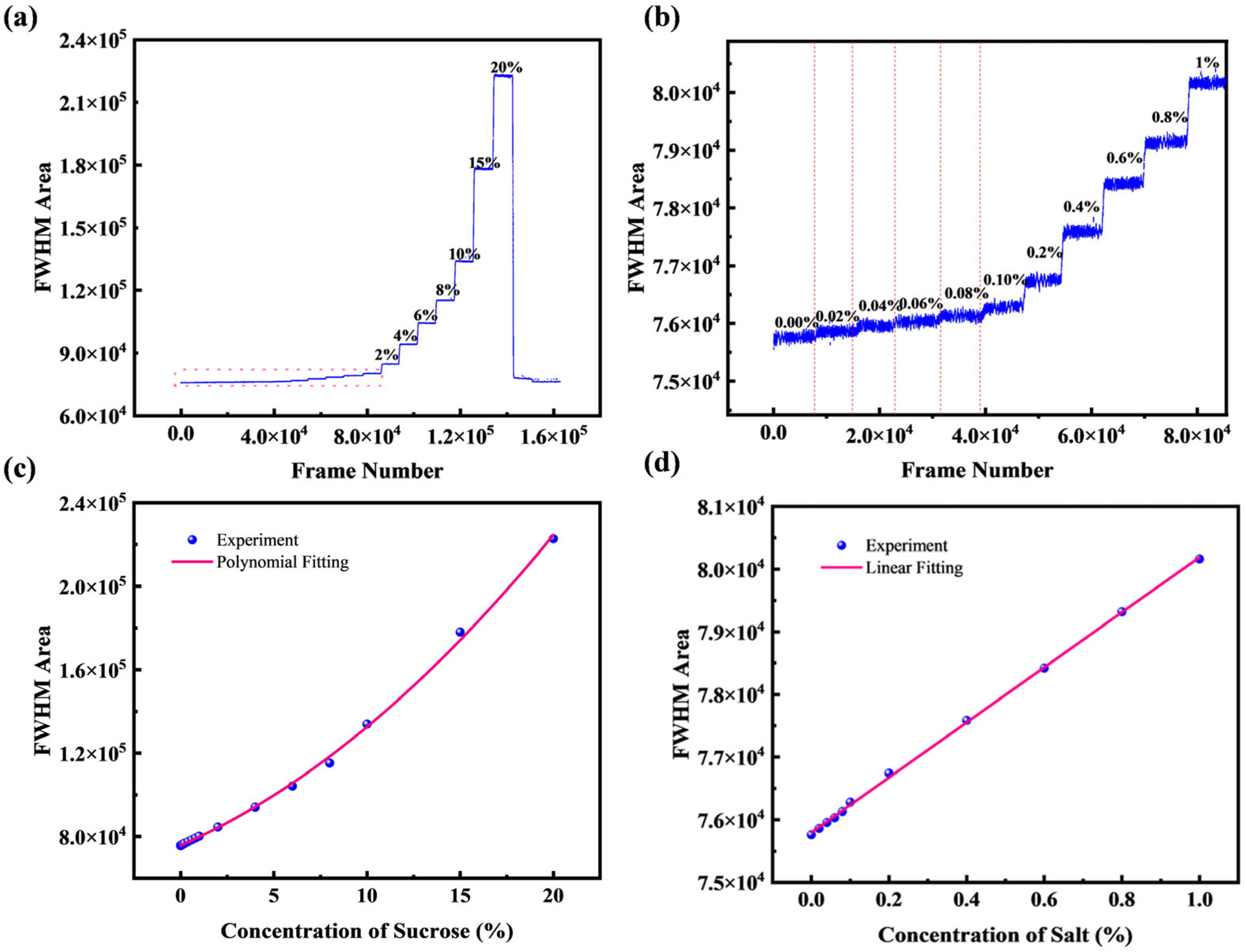
4.2. Fit the Half-Height Area
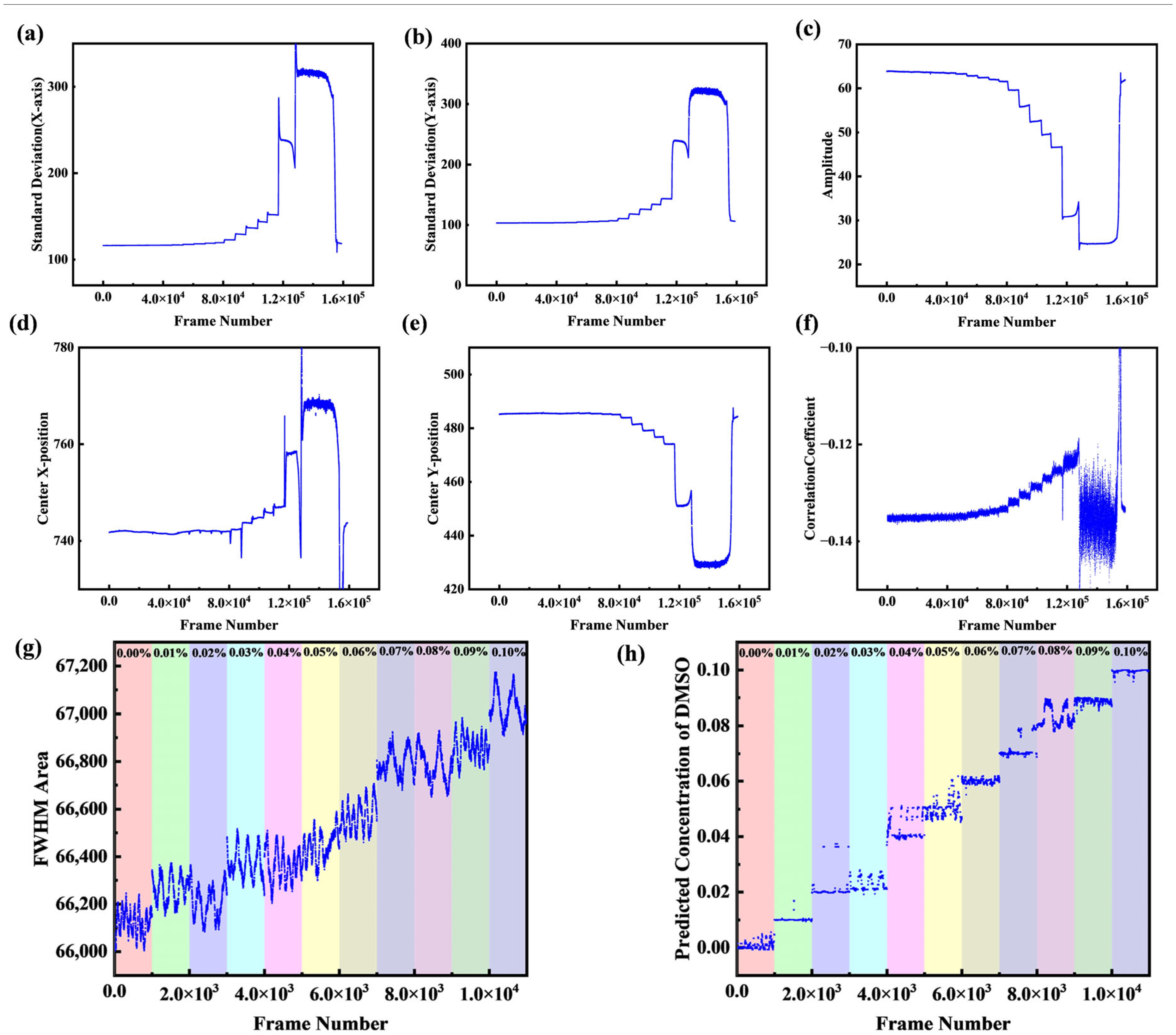
4.3. Gradient Boosting Decision Tree Algorithm
4.4. Resolution Affects Discussion
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, M.; Li, J.; Yuan, S.; Yang, X.; Lu, J.; Jiang, B. A centrifugal microfluidic system for automated detection of multiple heavy metal ions by aptamer-based colorimetric assay. Sens. Actuators B Chem. 2024, 403, 135210. [Google Scholar] [CrossRef]
- Steffen, W.; Richardson, K.; Rockström, J.; Cornell, S.E.; Fetzer, I.; Bennett, E.M.; Biggs, R.; Carpenter, S.R.; de Vries, W.; de Wit, C.A.; et al. Planetary boundaries: Guiding human development on a changing planet. Science 2015, 347, 1259855. [Google Scholar] [CrossRef]
- Lee, B. Review of the present status of optical fiber sensors. Opt. Fiber Technol. 2003, 9, 57–79. [Google Scholar] [CrossRef]
- Homola, J.; Yee, S.S.; Gauglitz, G. Surface plasmon resonance sensors: Review. Sens. Actuators B Chem. 1999, 54, 3–15. [Google Scholar] [CrossRef]
- Fan, X.; White, I.M.; Shopova, S.I.; Zhu, H.; Suter, J.D.; Sun, Y. Sensitive optical biosensors for unlabeled targets: A review. Anal. Chim. Acta 2008, 620, 8–26. [Google Scholar] [CrossRef] [PubMed]
- Bogaerts, W.; De Heyn, P.; Van Vaerenbergh, T.; De Vos, K.; Selvaraja, S.K.; Claes, T.; Dumon, P.; Bienstman, P.; Van Thourhout, D.; Baets, R. Silicon microring resonators. Laser Photonics Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Lyu, D.; Huang, Q.; Wu, X.; Nie, Y.; Yang, M. Optical fiber sensors for water and air quality monitoring: A review. Opt. Eng. 2024, 63, 031004. [Google Scholar] [CrossRef]
- Wang, X.; Tan, Q.; Yang, C.; Lu, N.; Jin, G. Photonic crystal refractive index sensing based on sandwich structure. Optik 2012, 123, 2113–2115. [Google Scholar] [CrossRef]
- Yang, Y.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. All-dielectric metasurface analogue of electromagnetically induced transparency. Nat. Commun. 2014, 5, 5753. [Google Scholar] [CrossRef]
- Jiang, X.; Qavi, A.J.; Huang, S.H.; Yang, L. Whispering-Gallery Sensors. Matter 2020, 3, 371–392. [Google Scholar] [CrossRef]
- Ran, Z.; Rao, Y.; Zhang, J.; Liu, Z.; Xu, B. A miniature fiber-optic refractive-index sensor based on laser-machined Fabry–Perot interferometer tip. J. Light. Technol. 2009, 27, 4426–4430. [Google Scholar]
- Yesudasu, V.; Pradhan, H.S.; Pandya, R.J. Recent progress in surface plasmon resonance based sensors: A comprehensive review. Heliyon 2021, 7, e06321. [Google Scholar] [CrossRef]
- Luchansky, M.S.; Bailey, R.C. High-Q Optical Sensors for Chemical and Biological Analysis. Anal. Chem. 2012, 84, 793–821. [Google Scholar] [CrossRef]
- Granizo, E.; Samokhvalov, P.; Nabiev, I. Functionalized Optical Microcavities for Sensing Applications. Nanomaterials 2025, 15, 206. [Google Scholar] [CrossRef]
- White, I.M.; Fan, X. On the performance quantification of resonant refractive index sensors. Opt. Express 2008, 16, 1020–1028. [Google Scholar] [CrossRef] [PubMed]
- Choosing a Refractometer. Available online: https://www.labcompare.com/10-Featured-Articles/19399-Choosing-a-Refractometer/ (accessed on 30 September 2025).
- Calixto, S.; Rosete-Aguilar, M.; Sanchez-Marin, F.J.; Calixto-Solano, M.; López-Mariscal, C. Refractive index measurement through image analysis with an optofluidic device. Opt. Express 2012, 20, 2073–2080. [Google Scholar] [CrossRef]
- Calixto, S.; Rosete-Aguilar, M.; Calixto-Solano, M. Nonspherical optofluidic lenses. In Microfluidics, BioMEMS, and Medical Microsystems X; Becker, H., Gray, B.L., Eds.; SPIE: Bellingham, WA, USA, 2012; Volume 8251, p. 82510V. [Google Scholar]
- Pandey, N.; Singh, M.P.; Pant, L.M.; Ghosh, A. A simple method to measure refractive index of optical glasses using focal displacement method. In Proceedings of the International Conference on Optics and Photonics 2015, Yokohama, Japan, 22–24 April 2015; Chakraborty, R., Bhattacharya, K., Eds.; SPIE: Bellingham, WA, USA, 2015; Volume 9654, p. 96540L. [Google Scholar]
- Li, S.-L.; Nie, Z.-Q.; Tian, Y.-T.; Liu, C. Liquid Refractive Index Measurement System Based on Electrowetting Lens. Micromachines 2019, 10, 515. [Google Scholar] [CrossRef] [PubMed]
- Calixto, S.; Rosete-Aguilar, M.; Monzón-Hernández, D.; Minkovich, V.P. Microfluidic configuration used to measure the refractive index of liquids. In Photonic Fiber and Crystal Devices: Advances in Materials and Innovations in Device Applications II; Yin, S., Guo, R., Eds.; SPIE: Bellingham, WA, USA, 2008; Volume 7056, p. 705622. [Google Scholar]
- Zhao, X.; Chen, Y.; Guo, Z.; Zhou, Y.; Guo, J.; Liu, Z.; Zhang, X.; Xiao, L.; Fei, Y.; Wu, X. Tunable optofluidic microbubble lens. Opt. Express 2022, 30, 7858–7869. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Z.; Zhou, Y.; Guo, J.; Liu, Z.; Luo, M.; Li, Y.; Wang, Q.; Zhang, M.; Yang, X.; et al. Highly sensitive, modification-free, and dynamic real-time stereo-optical immuno-sensor. Biosens. Bioelectron. 2023, 237, 115477. [Google Scholar] [CrossRef]
- Álvarez-Tamayo, R.I.; Prieto-Cortés, P. Refractive Index Fiber Laser Sensor by Using a Fiber Ball Lens Interferometer with Adjustable Free Spectral Range. Sensors 2023, 23, 3045. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Liu, C.-F. Low cost refractive index sensor based on optical lensed fiber. Microw. Opt. Technol. Lett. 2013, 55, 1744–1746. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Mienye, I.D.; Jere, N. A Survey of Decision Trees: Concepts, Algorithms, and Applications. IEEE Access 2024, 12, 86716–86730. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Kogelnik, H. Imaging of optical modes—Resonators with internal lenses. Bell Syst. Tech. J. 1965, 44, 455–494. [Google Scholar] [CrossRef]
- Bastiaans, M.J.; Alieva, T. Classification of lossless first-order optical systems and the linear canonical transformation. J. Opt. Soc. Am. A 2007, 24, 1053–1062. [Google Scholar] [CrossRef] [PubMed]
- Shao, J. Mathematical Statistics, 2nd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]



| Sensor Type | Sensing Principle | Key Advantages | Major Limitations |
|---|---|---|---|
| Resonance-Based | Resonant peak shift | Extremely high sensitivity | High cost |
| Complex fabrication | |||
| Traditional Refraction-Based | Critical angle | Simpler principle | No continuous real-time measurement |
| Refraction | High precision (lab models) | ||
| This Work | Algorithm-enhanced beam spot analysis | Low cost, high robustness | Depend on computation |
| Real-time measurement |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wang, Q.; Li, Y.; Liu, J.; Lin, Z.; Fan, M.; Zhang, Y.; Wu, X. Optofluidic Lens Refractometer. Micromachines 2025, 16, 1160. https://doi.org/10.3390/mi16101160
Zhang Y, Wang Q, Li Y, Liu J, Lin Z, Fan M, Zhang Y, Wu X. Optofluidic Lens Refractometer. Micromachines. 2025; 16(10):1160. https://doi.org/10.3390/mi16101160
Chicago/Turabian StyleZhang, Yifan, Qi Wang, Yuxiang Li, Junjie Liu, Ziyue Lin, Mingkai Fan, Yichi Zhang, and Xiang Wu. 2025. "Optofluidic Lens Refractometer" Micromachines 16, no. 10: 1160. https://doi.org/10.3390/mi16101160
APA StyleZhang, Y., Wang, Q., Li, Y., Liu, J., Lin, Z., Fan, M., Zhang, Y., & Wu, X. (2025). Optofluidic Lens Refractometer. Micromachines, 16(10), 1160. https://doi.org/10.3390/mi16101160







