Self-Calibratable Absolute Modular Rotary Encoder: Development and Experimental Research
Abstract
1. Introduction
2. Overview
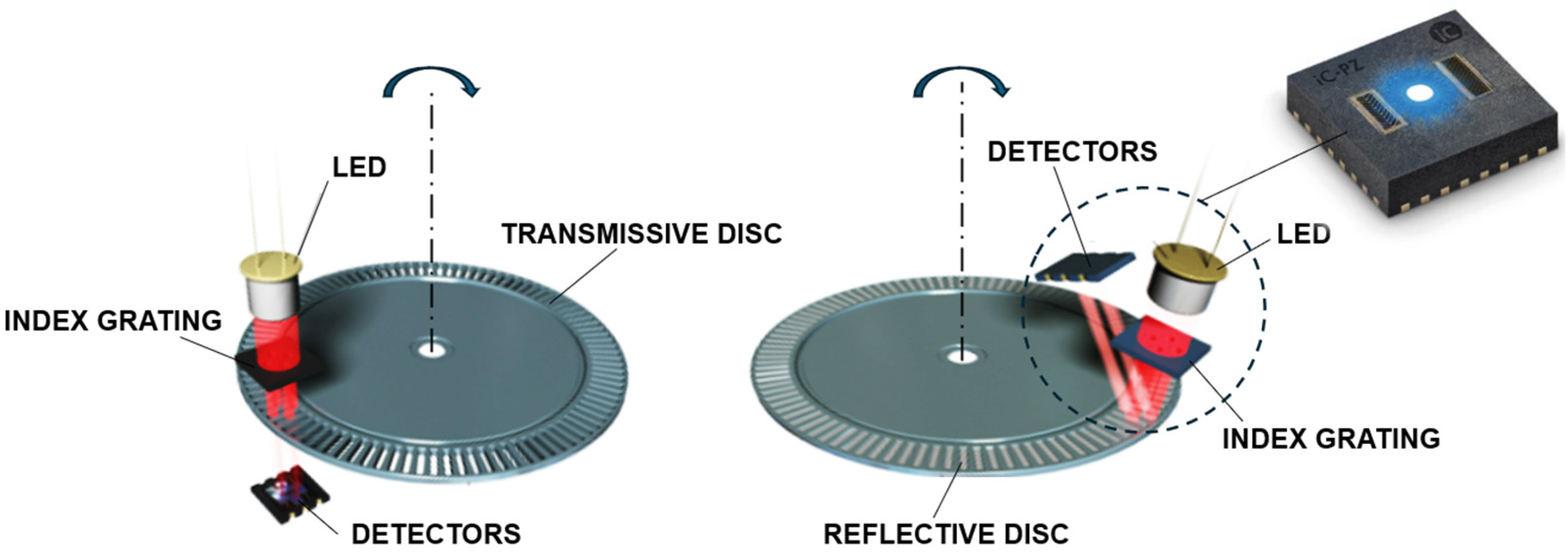
2.1. Working Principle of Optical Encoders
2.2. Errors in Modular Optical Rotary Encoders
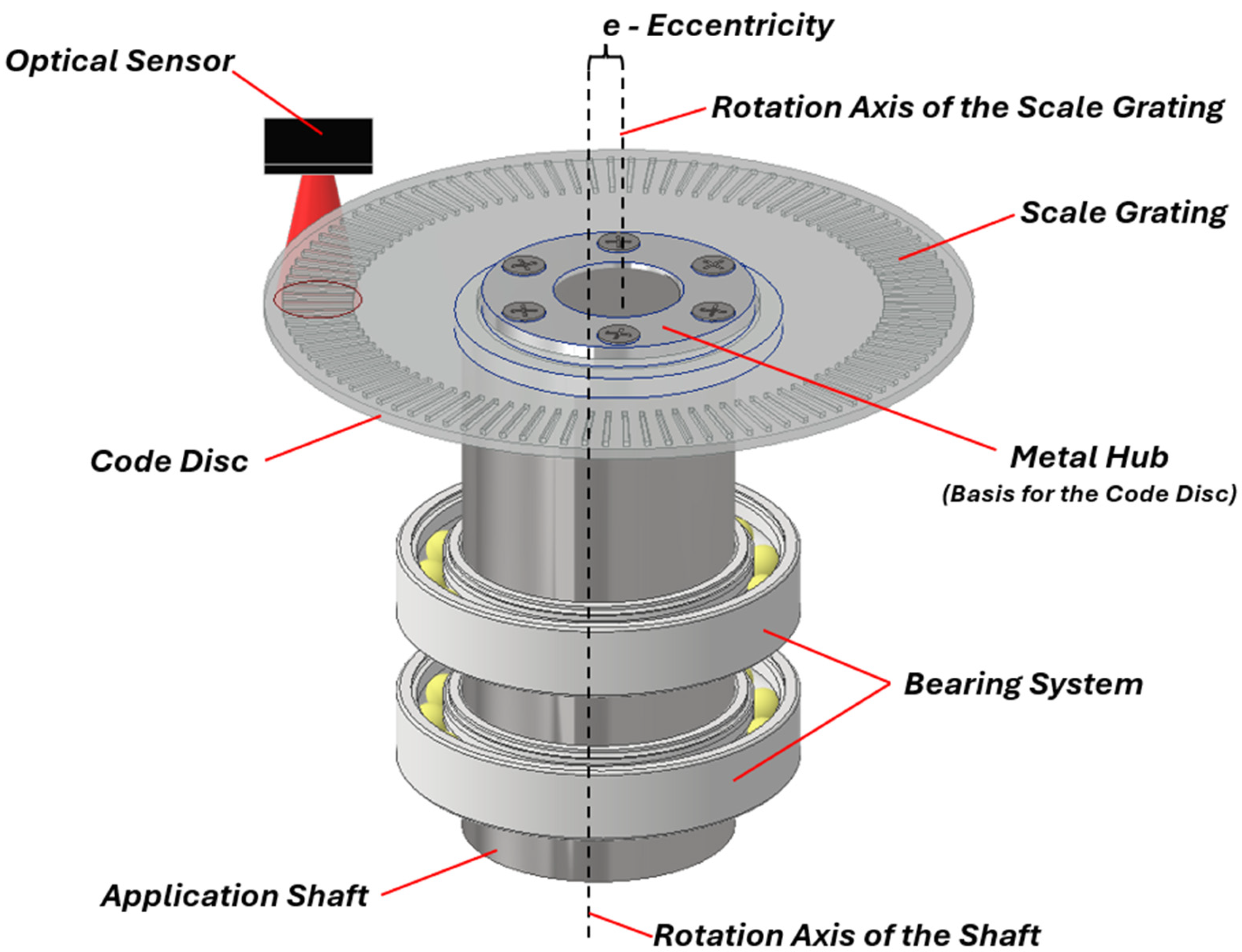
2.2.1. Low-Frequency Errors
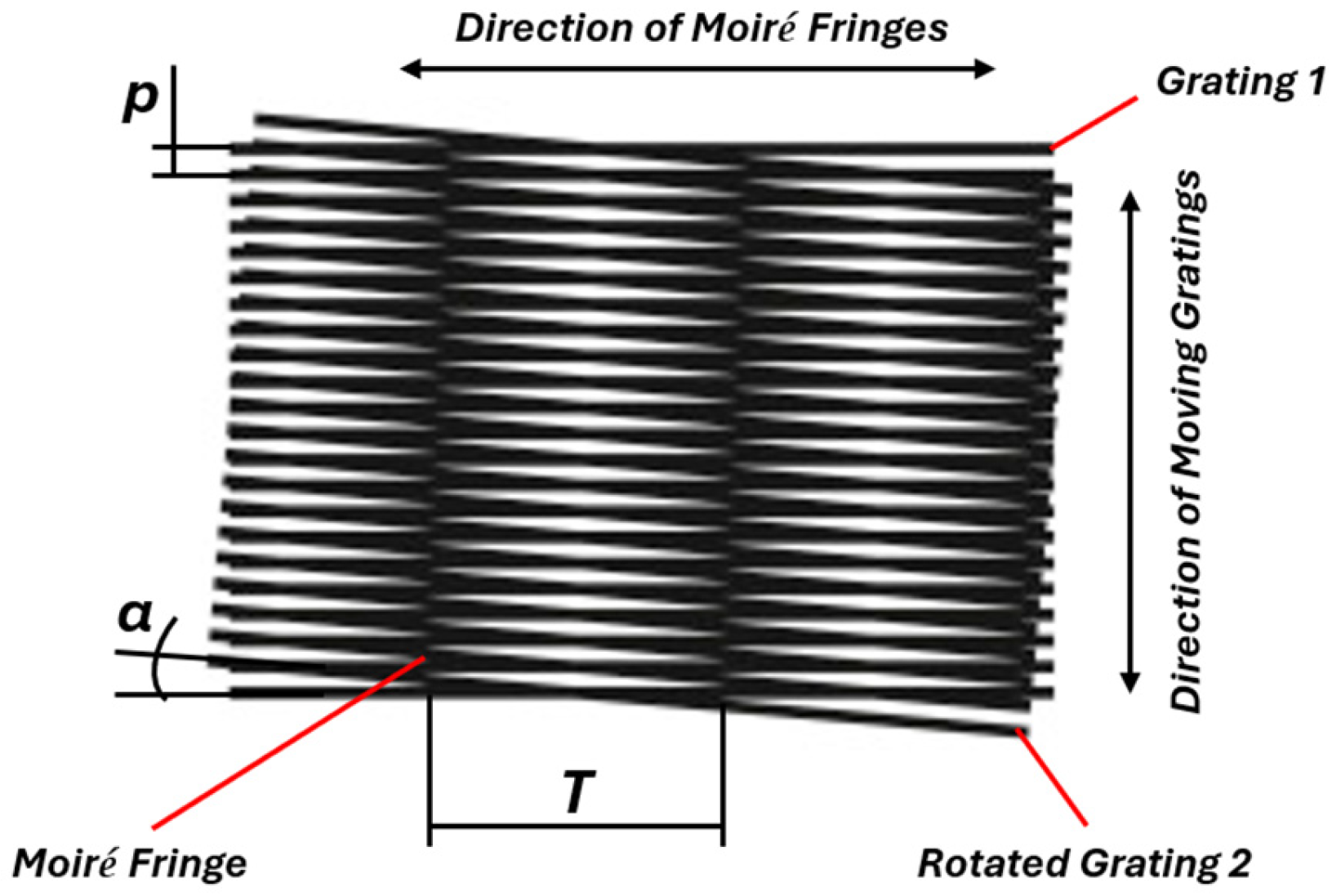
2.2.2. High-Frequency Errors
3. Materials and Methods
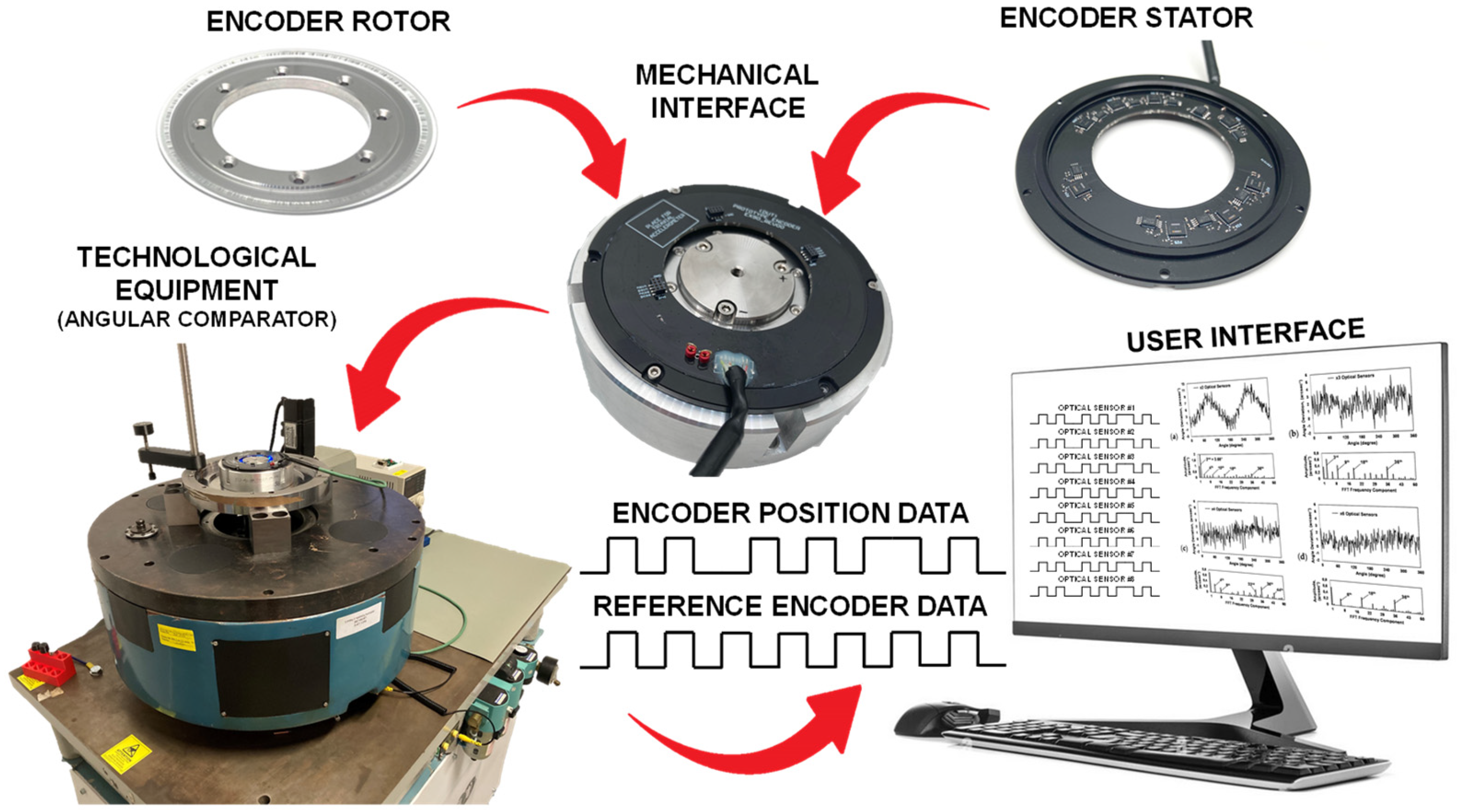
3.1. Development of the Sefl-Calibratable Optical Modular Encoder
3.1.1. Mechanical Design of the Encoder
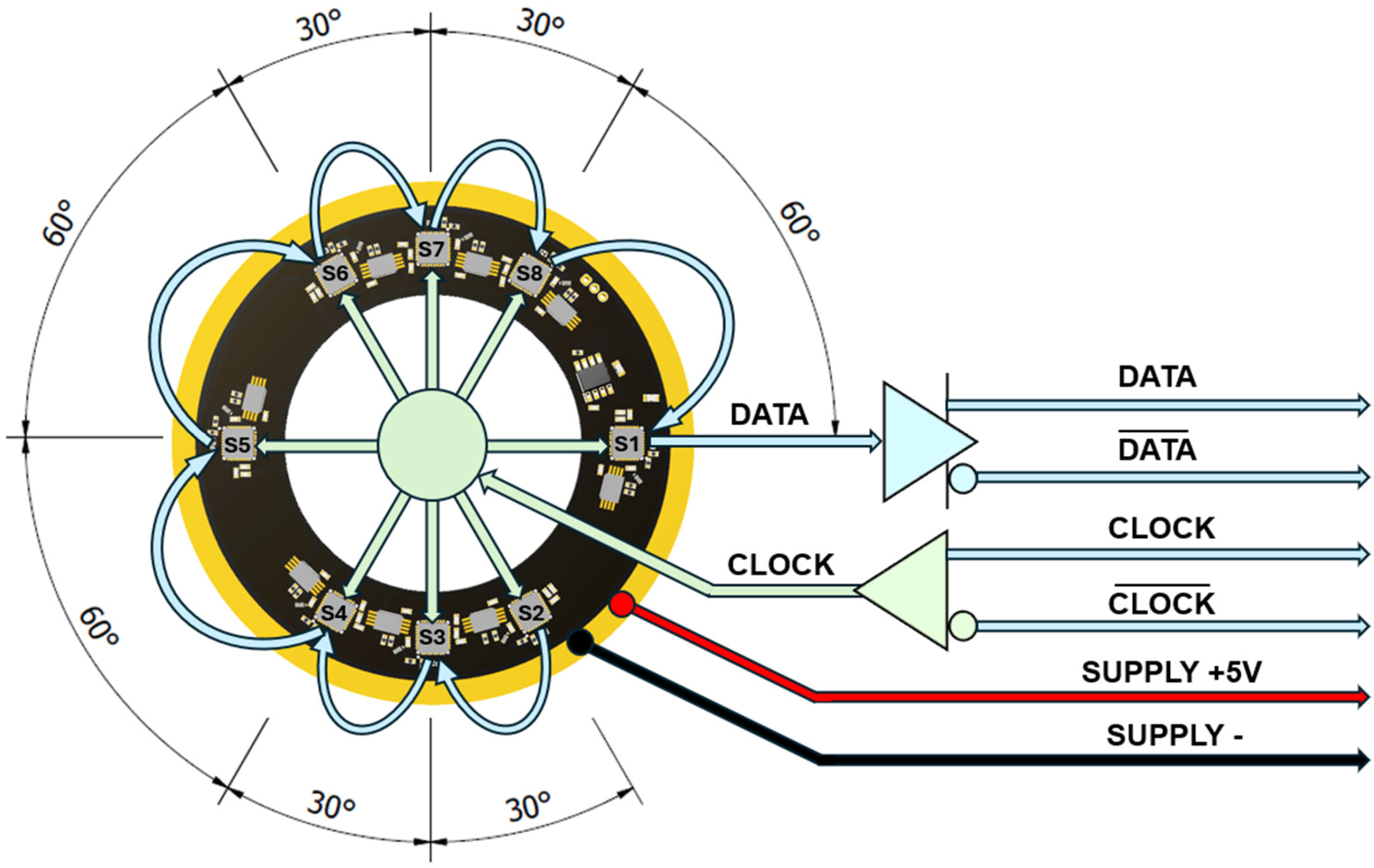
3.1.2. Electrical Design of the Encoder
3.2. Cross-Calibration of the Produced Optical Encoder
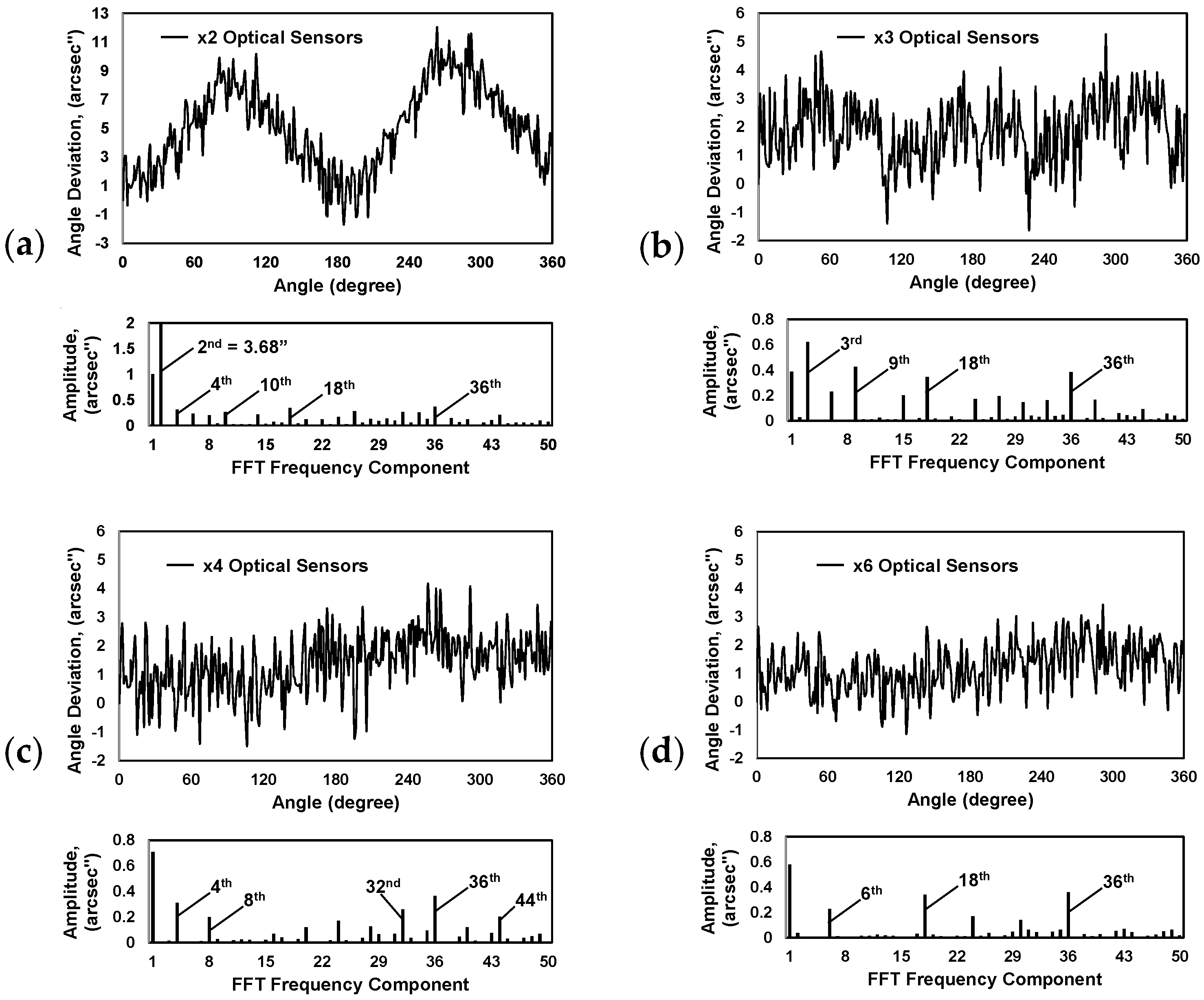
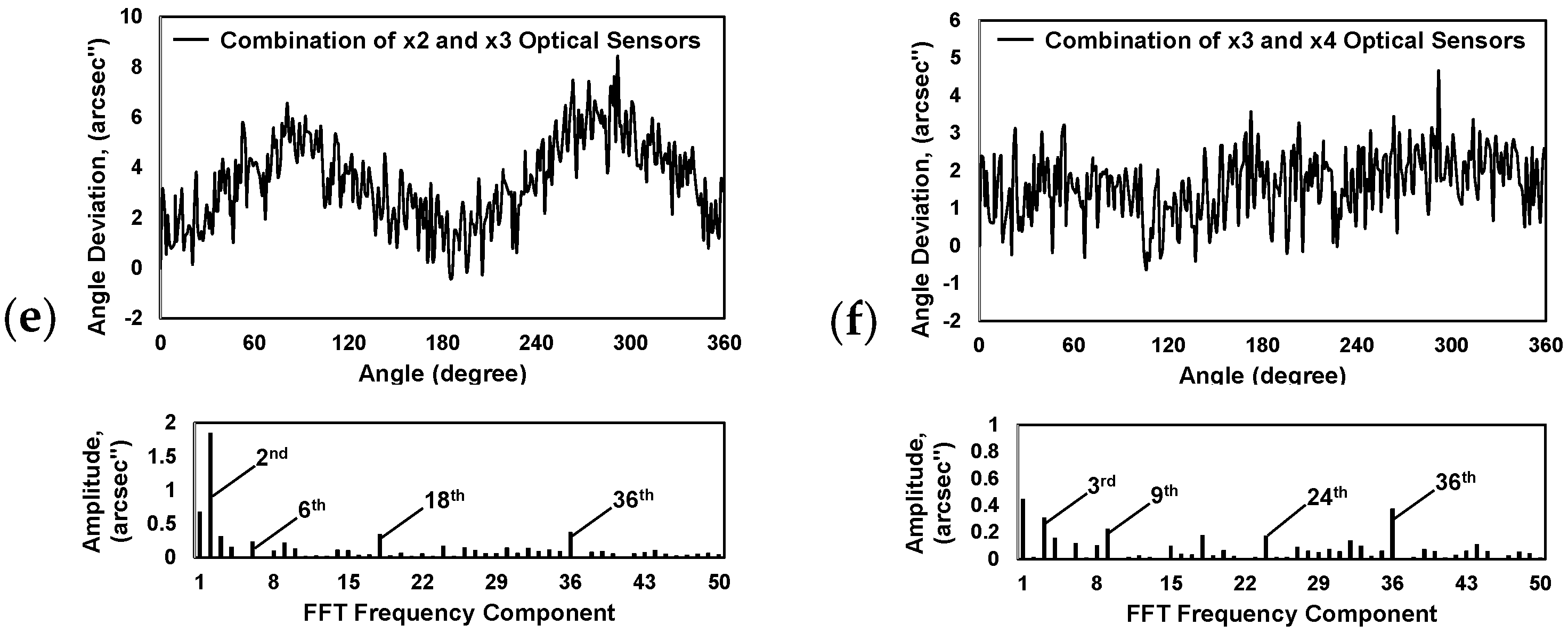
3.3. Self-Calibration of the Developed Optical Encoder
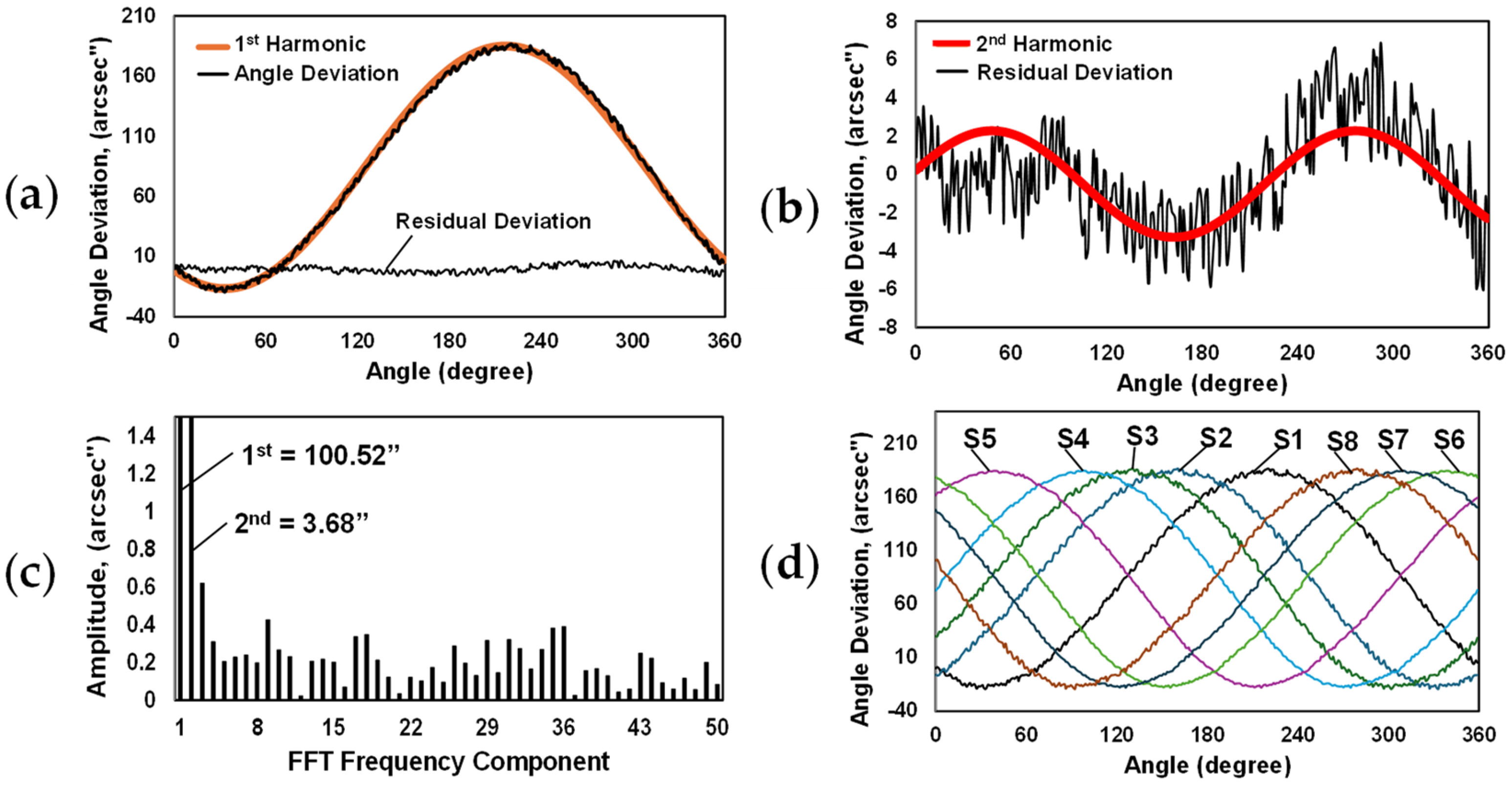
4. Experimental Results
5. Discussion and Conclusions
- Applying a self-calibration method by integrating additional optical sensors in a modular-type optical encoder is an effective approach to eliminate its mounting errors.
- In this way, a high accuracy of the encoder is ensured, while maintaining easy installation and all the advantages of the modular kit encoder.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vazques-Gutierrez, Y.; O’Sullivan, D.L.; Kavanagh, R.C. Study of the impact of the incremental optical encoder sensor on the dynamic performance of velocity servosystems. J. Eng. 2019, 17, 3807–3811. [Google Scholar] [CrossRef]
- Vazques-Gutierrez, Y.; O’Sullivan, D.L.; Kavanagh, R.C. Small-signal modelling of the incremental optical encoder for motor control. IEEE Trans. Ind. Electron. 2020, 67, 3452–3461. [Google Scholar] [CrossRef]
- Zhang, Z.; Olgac, N. Zero magnitude error tracking control for servo system with extremely low-resolution digital encoder. Int. J. Mechatron. Manuf. Syst. 2018, 10, 355–373. [Google Scholar] [CrossRef]
- Algburi, R.N.A.; Gao, H. Health assessment and fault detection system for an industrial robot using the rotary encoder signal. Energies 2019, 12, 2816. [Google Scholar] [CrossRef]
- Li, P.; Liu, X. Common sensors in industrial robots: A review. J. Phys. Conf. Ser. 2019, 1267, 012036. [Google Scholar] [CrossRef]
- Rodriguez-Donate, C.; Osornio-Rios, R.A.; Rivera-Guillen, J.R.; Romero-Troncoso, R.D.J. Fused smart sensor network for multi-axis forward kinematics estimation in industrial robots. Sensors 2011, 11, 4335–4357. [Google Scholar] [CrossRef]
- Burnashev, M.N.; Pavlov, P.A.; Filatov, Y.V. Development of precision laser goniometer system. Quantum Electron. 2013, 43, 130. [Google Scholar] [CrossRef]
- Kim, J.A.; Kim, J.W.; Kang, C.S.; Jin, J.; Eom, T.B. Calibration of angle artifacts and instruments using a high precision angle generator. Int. J. Precis. Eng. Manuf. 2013, 14, 367–371. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, Z.; Huang, M.; Qiao, D. The NIM continuous full circle angle standard. Meas. Sci. Technol. 2018, 29, 074013. [Google Scholar] [CrossRef]
- Pisani, M.; Astrua, M. The new INRIM rotating encoder angle comparator (REAC). Meas. Sci. Technol. 2017, 28, 045008. [Google Scholar] [CrossRef]
- Pavlov, P.A. Aspects of the cross-calibration method in laser goniometry. Meas. Tech. 2017, 58, 970–974. [Google Scholar] [CrossRef]
- Pavlov, P.A. A method for investigating the error of a laser dynamic goniometer. Meas. Tech. 2020, 63, 106–110. [Google Scholar] [CrossRef]
- Akgoz, S.A.; Yandayan, T. High precision calibration of polygons for emerging demands. J. Phys. Conf. Ser. 2018, 1065, 142005. [Google Scholar] [CrossRef]
- Lu, X.D.; Trumper, D.L. Self-calibration of on-axis rotary encoders. CRIP Ann. 2009, 56, 499–504. [Google Scholar] [CrossRef]
- Lu, X.D.; Graetz, R.; Ammin-Shahidi, D.; Smeds, K. On-axis self-calibration of angle encoders. CRIP Ann.-Manuf. Technol. 2007, 59, 529–534. [Google Scholar] [CrossRef]
- Gou, L.; Peng, D.; Chen, X.; Wu, L.; Tang, Q. A self-calibration method for angular displacement sensor working in harsh environments. IEEE Sens. J. 2019, 19, 3033–3040. [Google Scholar] [CrossRef]
- Ellin, A.; Dolsak, G. The design and application of rotary encoders. Sens. Rev. 2008, 28, 150–158. [Google Scholar] [CrossRef]
- Yu, H.; Wan, Q.; Sun, Y.; Lu, X.; Zhao, C. High precision angular measurement via dual imaging detectors. IEEE Sens. J. 2019, 19, 7308–7312. [Google Scholar] [CrossRef]
- Ren, S.; Liu, Q.; Zhao, H. Error analysis of circular gratings angle-measuring systems. In Proceedings of the 2016 International Conference on Electrical, Mechanical and Industrial Engineering, Phuket, Thailand, 24–25 April 2016. [Google Scholar] [CrossRef][Green Version]
- Watanabe, T.; Fujimoto, H.; Nakayama, K.; Masuda, T.; Kajitani, M. Automatic high-precision calibration system for angle encoder (II). SPIE Opt. + Photonics 2003, 5190, 400. [Google Scholar]
- Watanabe, T.; Fujimoto, H.; Masuda, T. Self-calibratable rotary encoder. J. Phys. Conf. Ser. 2005, 13, 240–245. [Google Scholar] [CrossRef]
- Watanabe, T.; Fujimoto, H. Application of a self-calibratable rotary encoder. Proc. ISMTII 2009, 3, 54–58. [Google Scholar]
- Watanabe, T. Compact self-calibratable rotary encoder. J. Jpn. Soc. Precis. Eng. 2012, 3, 2100–2102. [Google Scholar]
- Watanabe, T.; Kon, M.; Nabeshima, N.; Taniguchi, K. An angle encoder for super-high resolution and super-high accuracy using SelfA. Meas. Sci. Technol. 2014, 25, 065002. [Google Scholar] [CrossRef]
- Watanabe, T.; Fujimoto, H.; Nakayama, K.; Masuda, T.; Kajitani, M. Automatic high-precision calibration system for angle encoder. SPIE Opt. + Photonics 2001, 4401, 267. [Google Scholar]
- Ueyama, Y.; Furutani, R.; Watanabe, T. A super-high-accuracy angular index table. Meas. Sci. Technol. 2020, 31, 094006. [Google Scholar] [CrossRef]
- Kim, J.A.; Kim, J.W.; Kang, C.S.; Jin, J.; Eom, T.B. Precision angle comparator using self-calibration of scale errors based on the equal-division-averaged method. In Proceedings of the MacroScale 2011 “Recent Developments in Traceable Dimensional Measurements”, Wabern, Switzerland, 4–6 October 2011. [Google Scholar] [CrossRef]
- Kokuyama, W.; Watanabe, T.; Nozato, H.; Ota, A. Angular velocity calibration system with a self-calibratable rotary encoder. Measurement 2016, 82, 246–253. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, Z.; Lin, H.; Wang, Y. Development of portable and real-time self-calibration angle encoder. In Proceedings of the SPIE 9903, Seventh International Symposium on Precision Mechanical Measurements, Xia’men, China, 8–13 August 2015; SPIE: Bellingham, DC, USA, 2016; Volume 99030F. [Google Scholar] [CrossRef]
- Ishii, N.; Taniguchi, K.; Yamazaki, K.; Aoyama, H. Super-accurate angular encoder system with multi-detecting heads using VEDA method. J. Jpn. Soc. Precis. Eng. 2018, 84, 717–723. [Google Scholar] [CrossRef]
- Ishii, N.; Taniguchi, K.; Yamazaki, K.; Aoyama, H. Development of super-accurate angular encoder system with multi-detecting heads using VEDA method. J. Adv. Mech. Des. Syst. Manuf. 2018, 12, JAMDSM0106. [Google Scholar] [CrossRef]
- Masuda, T.; Kajitani, M. High accuracy calibration system for angular encoders. J. Robot. Mechatron. 1993, 5, 448–452. [Google Scholar] [CrossRef]
- Kiryanov, V.P.; Petukhov, A.D.; Kiryanov, A.V. Analysis of self-calibration algorithms in optical angular encoders. Optoelectron. Instument. Proc. 2022, 58, 223–233. [Google Scholar] [CrossRef]
- Ke, X.; Zhang, M.; Zhao, K. Moiré fringe method via scanning transmission electron microscopy. Small Methods 2021, 6, 2101040. [Google Scholar] [CrossRef] [PubMed]
- S’Ari, M.; Koniuch, N.; Brydson, R.; Hondow, N.; Brown, A. High-resolution imaging of organic pharmaceutical crystals by transmission electron microscopy and scanning moiré fringes. J. Microsc. 2020, 279, 197–206. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.T.; Tian, M.; Wang, Y.J.; Zhu, Y.L. Moiré fringe imaging of heterostructures by scanning transmission electron microscopy. Micron 2024, 185, 103679. [Google Scholar] [CrossRef]
- Prabhakara, V.; Jannis, D.; Béché, A.; Bender, H.; Verbeeck, J. Strain measurement in semiconductor FinFET devices using a novel moiré demodulation technique. Semicond. Sci. Technol. 2020, 35, 034002. [Google Scholar] [CrossRef]
- Wang, Q.; Ri, S.; Xia, P. Wide-view and accurate deformation measurement at microscales by phase extraction of scanning moiré pattern with a spatial phase-shifting technique. Appl. Opt. 2021, 60, 1637–1645. [Google Scholar] [CrossRef]
- Chen, R.; Zhang, Q.; He, W.; Xie, H.M. Orthogonal sampling moiré method and its application in microscale deformation field measurement. Opt. Lasers Eng. 2022, 149, 106811. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, Y.; Li, H.; An, H.; Wu, H. Spatial computer-generated Moiré profilometry. Sens. Actuators A Phys. 2024, 367, 115054. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Y.; Li, C.; Wan, Y.; Li, H.; Xu, C.; Zhang, H. Improved computer-generated moire profilometry with flat image calibration. Appl. Opt. 2021, 60, 1209–1216. [Google Scholar] [CrossRef]
- Wang, L.; Cao, Y.; Li, C.; Wan, Y.; Wang, Y.; Li, H.; Xu, C.; Zhang, H. Computer-generated moiré profilometry based on flat image demodulation. Opt. Rev. 2021, 28, 546–556. [Google Scholar] [CrossRef]
- Li, C.; Cao, Y.; Wang, L.; Wan, Y.; Li, H.; Xu, C.; Zhang, H. Computer-generated moiré profilometry based on fringe-superposition. Sci. Rep. 2020, 10, 17202. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, W.; Zhang, Y. Misalignment measurement with dual-frequency moiré fringe in nanoimprint lithography. Opt. Express 2020, 28, 6755–6765. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, H.; Xie, W.; Qu, Z. Lithography alignment technique based on moiré fringe. Photonics 2023, 10, 351. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, W.; Zhang, Y. Moiré-based sub-nano misalignment sensing via deep learning for lithography. Opt. Lasers Eng. 2021, 143, 106620. [Google Scholar] [CrossRef]
- Gurauskis, D.; Przystupa, K.; Kilikevičius, A.; Skowron, M.; Matijošius, J.; Caban, J.; Kilikevičienė, K. Development and Experimental Research of Different Mechanical Designs of an Optical Linear Encoder’s Reading Head. Sensors 2022, 22, 2977. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Lin, Y.; Huang, Y.; Xue, Z. Research on sinusoidal error compensation of Moiré signal using particle swarm optimization. IEEE Access. 2020, 8, 14820–14831. [Google Scholar] [CrossRef]
- Choi, I.; Yoon, S.J.; Park, Y.L. Linear electrostatic actuators with Moiré-effect optical proprioceptive sensing and electroadhesive braking. Int. J. Robot. Res. 2024, 43, 646–664. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, T.T.; Yuan, B.; Wang, L.Q. A digital Moiré fringe method for displacement sensors. Front. Inform. Technol. Electron. Eng. 2016, 17, 946–953. [Google Scholar] [CrossRef]
- Walcher, H. Position Sensing: Angle and Distance Measurement for Engineers; Elsevier: Amsterdam, The Netherlands, 2014; ISBN 978-1-4831-9378-6. [Google Scholar]
- Yang, Z.; Ma, X.; Yu, D.; Cao, B.; Niu, Q.; Li, M.; Xin, C. An ultracompact angular displacement sensor based on the Talbot effect of optical microgratings. Sensors 2023, 23, 1091. [Google Scholar] [CrossRef]
- Kao, C.F.; Huang, H.L.; Lu, H. Optical encoder based on the fractional Talbot effect using two-dimensional phase grating. Opt. Commun. 2010, 283, 1950–1955. [Google Scholar] [CrossRef]
- Kao, C.F.; Lu, H. Optical encoder based on the fractional Talbot effect. Opt. Commun. 2005, 250, 16–23. [Google Scholar] [CrossRef]
- Crespo, D.; Alonso, J.; Tomas, M.; Eusebio, B. Optical encoder based on the Lau effect. Opt. Eng. 2000, 39, 817–822. [Google Scholar] [CrossRef]
- Sudol, R.; Thompson, B.J. Lau effect: Theory and experiment. Appl. Opt. 1981, 20, 1107–1116. [Google Scholar] [CrossRef] [PubMed]
- Ye, G.; Liu, H.; Xie, H.; Asundi, A. Optimizing design of an optical encoder based on generalized grating imaging. Meas. Sci. Technol. 2016, 27, 115005. [Google Scholar] [CrossRef]
- Ye, G.; Liu, H.; Fan, S.; Li, X.; Yu, H.; Lei, B.; Shi, Y.; Yin, L.; Lu, B. A theoretical investigation of generalized grating imaging and its application to optical encoders. Opt. Commun. 2015, 354, 21–27. [Google Scholar] [CrossRef]
- Liu, H.; Ye, G.; Shi, Y.; Yin, L.; Chen, B.; Lu, B. Multiple harmonics suppression for optical encoders based on generalized grating imaging. J. Mod. Opt. 2016, 63, 1564–1572. [Google Scholar] [CrossRef]
- Ye, G.; Liu, H.; Lei, B.; Niu, D.; Xing, H.; Wei, P.; Lu, B.; Liu, H. Optimal design of a reflective diffraction grating scale with sine-trapezoidal groove for interferential optical encoders. Opt. Lasers Eng. 2020, 134, 106196. [Google Scholar] [CrossRef]
- Liu, C.H.; Cheng, C.H. Development of a multi-degree-of-freedom laser encoder using ±1 order and ±2 order diffraction rays. In Proceedings of the 10th International Symposium of Measurement Technology and Intelligent Instruments, Daejeon, Republic of Korea, 29 June–2 July 2011. [Google Scholar]
- Wiseman, K.B.; Kissinger, T.; Tatam, R.P. Three-dimensional interferometric stage encoder using a single access port. Opt. Lasers Eng. 2021, 137, 106342. [Google Scholar] [CrossRef]
- Qin, S.; Huang, Z.; Wang, X. Optical angular encoder installation error measurement and calibration by ring laser gyroscope. IEEE Trans. Instrum. Meas. 2010, 59, 506–511. [Google Scholar] [CrossRef]
- Li, X.; Ye, G.; Liu, H.; Ban, Y.; Shi, Y.; Yin, L.; Lu, B. A novel optical rotary encoder with eccentricity self-detection ability. Rev. Sci. Instrum. 2017, 88, 115005. [Google Scholar] [CrossRef]
- Jia, H.K.; Yu, L.D.; Zhao, H.N.; Jiang, Y.Z. A new method of angle measurement error analysis of rotary encoders. Appl. Sci. 2019, 9, 3415. [Google Scholar] [CrossRef]
- Yu, H.; Wan, Q.; Liang, L.; Zhao, C. Analysis and elimination of grating disk inclination error in photoelectric displacement measurement. IEEE Trans. Ind. Electron. 2024, 71, 6438–6445. [Google Scholar] [CrossRef]
- Sanchez-Brea, L.M.; Morlanes, T. Metrological errors in optical encoders. Meas. Sci. Technol. 2008, 19, 115104. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gurauskis, D.; Marinkovic, D.; Mažeika, D.; Kilikevičius, A. Self-Calibratable Absolute Modular Rotary Encoder: Development and Experimental Research. Micromachines 2024, 15, 1130. https://doi.org/10.3390/mi15091130
Gurauskis D, Marinkovic D, Mažeika D, Kilikevičius A. Self-Calibratable Absolute Modular Rotary Encoder: Development and Experimental Research. Micromachines. 2024; 15(9):1130. https://doi.org/10.3390/mi15091130
Chicago/Turabian StyleGurauskis, Donatas, Dragan Marinkovic, Dalius Mažeika, and Artūras Kilikevičius. 2024. "Self-Calibratable Absolute Modular Rotary Encoder: Development and Experimental Research" Micromachines 15, no. 9: 1130. https://doi.org/10.3390/mi15091130
APA StyleGurauskis, D., Marinkovic, D., Mažeika, D., & Kilikevičius, A. (2024). Self-Calibratable Absolute Modular Rotary Encoder: Development and Experimental Research. Micromachines, 15(9), 1130. https://doi.org/10.3390/mi15091130





