Static and Eigenvalue Analysis of Electrostatically Coupled and Tunable Shallow Micro-Arches for Sensing-Based Applications
Abstract
1. Introduction
2. Device Geometrical Properties and Operational Mechanism
2.1. Mathematical Modeling
2.2. Normalization Equations of Motions
2.3. Reduced-Order Model
3. Results and Discussions
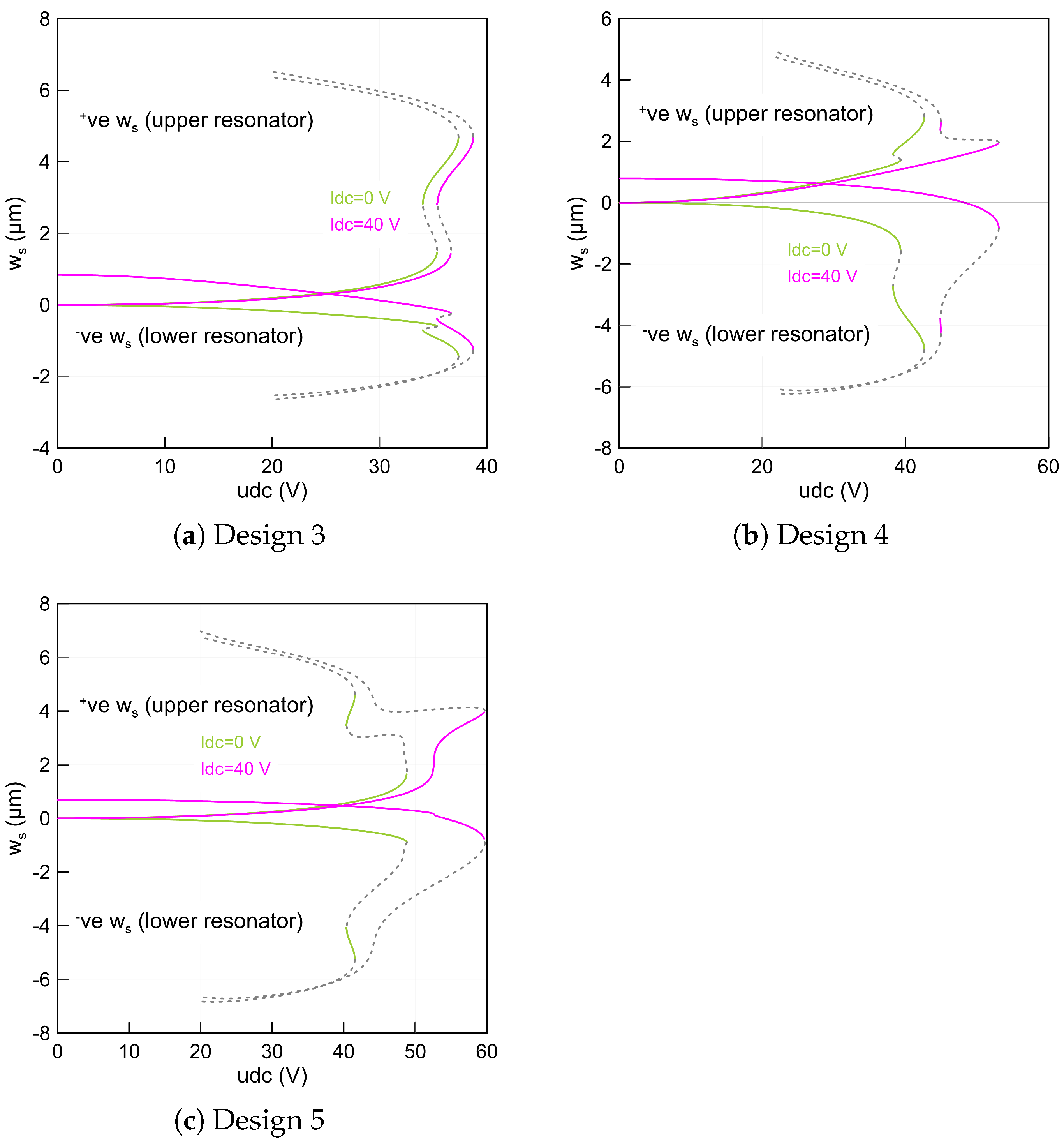
3.1. Static Analysis
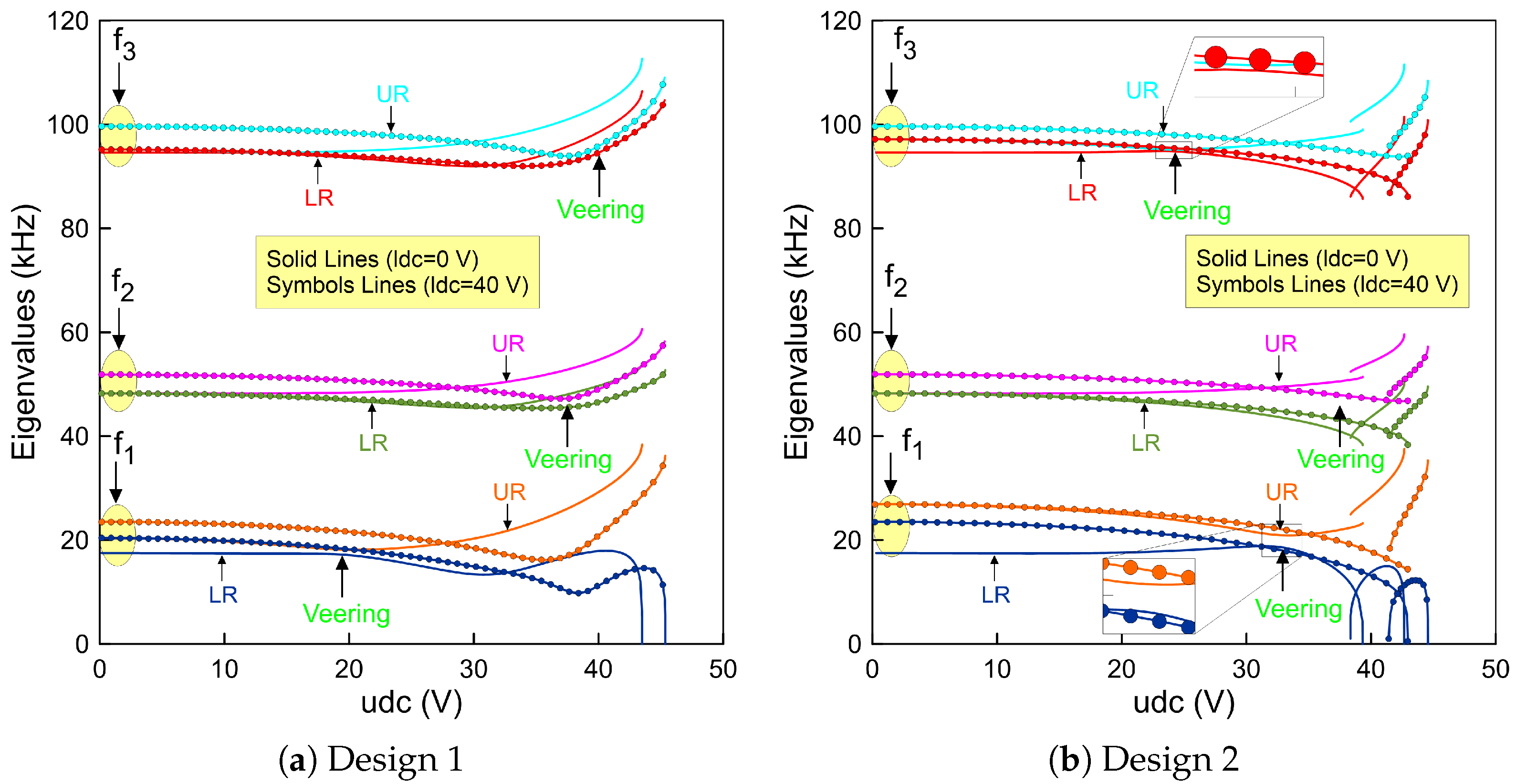
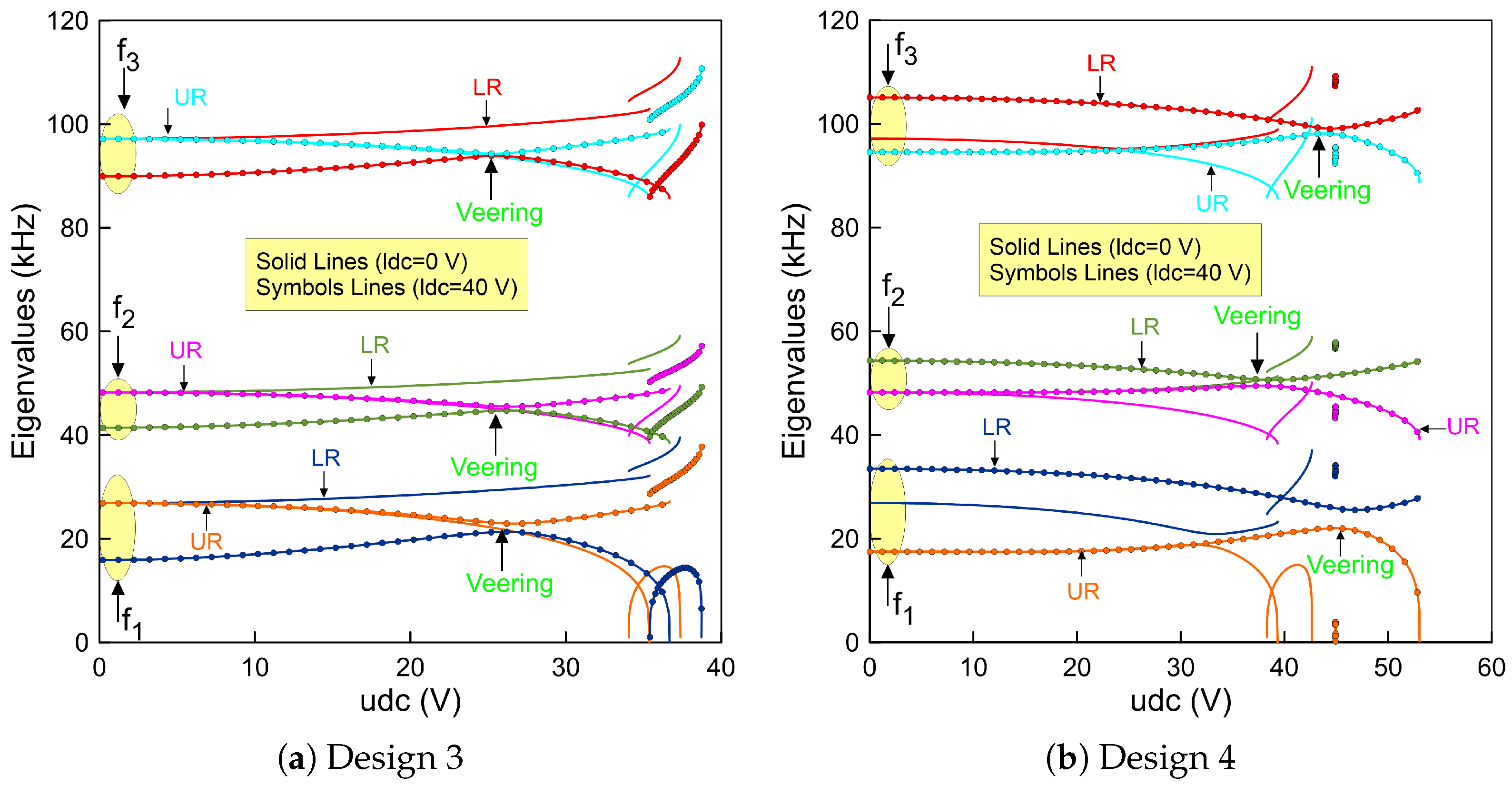
3.2. Fundamental Frequencies under Electrostatic Force
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nazir, S.; Kwon, O.S. Micro-electromechanical systems-based sensors and their applications. Appl. Sci. Converg. Technol. 2022, 31, 40–45. [Google Scholar] [CrossRef]
- Maluf, N.; Williams, K. An Introduction to Microelectromechanical Systems Engineering; Artech House: New York, NY, USA, 2004. [Google Scholar]
- Bogue, R. Recent developments in MEMS sensors: A review of applications, markets and technologies. Sens. Rev. 2013, 33, 300–304. [Google Scholar] [CrossRef]
- Pallay, M.; Daeichin, M.; Towfighian, S. Dynamic behavior of an electrostatic MEMS resonator with repulsive actuation. Nonlinear Dyn. 2017, 89, 1525–1538. [Google Scholar] [CrossRef]
- Lee, I.; Lee, J. Measurement uncertainties in resonant characteristics of MEMS resonators. J. Mech. Sci. Technol. 2013, 27, 491–500. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Younis, M.I. On using the dynamic snap-through motion of MEMS initially curved microbeams for filtering applications. J. Sound Vib. 2014, 333, 555–568. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Alici, G. Size-dependent electro-elasto-mechanics of MEMS with initially curved deformable electrodes. Int. J. Mech. Sci. 2015, 103, 247–264. [Google Scholar] [CrossRef]
- Ruzziconi, L.; Bataineh, A.M.; Younis, M.I.; Cui, W.; Lenci, S. Nonlinear dynamics of an electrically actuated imperfect microbeam resonator: Experimental investigation and reduced-order modeling. J. Micromech. Microeng. 2013, 23, 075012. [Google Scholar] [CrossRef]
- Buchaillot, L.; Millet, O.; Quévy, E.; Collard, D. Post-buckling dynamic behavior of self-assembled 3D microstructures. Microsyst. Technol. 2008, 14, 69–78. [Google Scholar] [CrossRef]
- Pane, I.Z.; Asano, T. Investigation on bistability and fabrication of bistable prestressed curved beam. Jpn. J. Appl. Phys. 2008, 47, 5291. [Google Scholar] [CrossRef]
- Alneamy, A.M.; Khater, M.E.; Abdel-Aziz, A.K.; Heppler, G.R.; Abdel-Rahman, E.M. Electrostatic arch micro-tweezers. Int. J. Non-Linear Mech. 2020, 118, 103298. [Google Scholar] [CrossRef]
- Krylov, S.; Ilic, B.R.; Schreiber, D.; Seretensky, S.; Craighead, H. The pull-in behavior of electrostatically actuated bistable microstructures. J. Micromech. Microeng. 2008, 18, 055026. [Google Scholar] [CrossRef]
- Tella, S.A.; Hajjaj, A.Z.; Younis, M.I. The effects of initial rise and axial loads on MEMS arches. J. Vib. Acoust. 2017, 139. [Google Scholar] [CrossRef]
- Alcheikh, N.; Ramini, A.; Hafiz, M.A.A.; Younis, M.I. Tunable clamped–guided arch resonators using electrostatically induced axial loads. Micromachines 2017, 8, 14. [Google Scholar] [CrossRef]
- Adam, C.; Ladurner, D.; Furtmüller, T. In-plane buckling of flexibly bonded three-layer pinned-fixed half-sine shallow arches. Int. J. Non-Linear Mech. 2023, 151, 104369. [Google Scholar] [CrossRef]
- Yang, Z.; Zhao, S.; Yang, J.; Liu, A.; Fu, J. Thermomechanical in-plane dynamic instability of asymmetric restrained functionally graded graphene reinforced composite arches via machine learning-based models. Compos. Struct. 2023, 308, 116709. [Google Scholar] [CrossRef]
- Li, C.; Zhu, C.; Lim, C.; Li, S. Nonlinear in-plane thermal buckling of rotationally restrained functionally graded carbon nanotube reinforced composite shallow arches under uniform radial loading. Appl. Math. Mech. 2022, 43, 1821–1840. [Google Scholar] [CrossRef]
- Ramini, A.; Bellaredj, M.L.F.; Hafiz, M.A.A.; Younis, M.I. Experimental investigation of snap-through motion of in-plane MEMS shallow arches under electrostatic excitation. J. MicroMech. Microeng. 2015, 26, 015012. [Google Scholar] [CrossRef]
- Krylov, S.; Dick, N. Dynamic stability of electrostatically actuated initially curved shallow micro beams. Contin. Mech. Thermodyn. 2010, 22, 445–468. [Google Scholar] [CrossRef]
- Alkharabsheh, S.A.; Younis, M.I. Dynamics of MEMS arches of flexible supports. J. Microelectromech. Syst. 2012, 22, 216–224. [Google Scholar] [CrossRef]
- Ouakad, H.M. Electrostatic fringing-fields effects on the structural behavior of MEMS shallow arches. Microsyst. Technol. 2018, 24, 1391–1399. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Sedighi, H.M. Static response and free vibration of MEMS arches assuming out-of-plane actuation pattern. Int. J. Non-Linear Mech. 2019, 110, 44–57. [Google Scholar] [CrossRef]
- Ramezany, A.; Qaradaghi, V.; Kumar, V.; Pourkamali, S. Frequency modulated electrostatically coupled resonators for sensing applications. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 30 October–3 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–3. [Google Scholar]
- Li, L.; Zhang, W.; Wang, J.; Hu, K.; Peng, B.; Shao, M. Bifurcation behavior for mass detection in nonlinear electrostatically coupled resonators. Int. J. Non-Linear Mech. 2020, 119, 103366. [Google Scholar] [CrossRef]
- Lyu, M.; Zhao, J.; Kacem, N.; Tang, B.; Liu, P.; Song, J.; Zhong, H.; Huang, Y. Computational investigation of high-order mode localization in electrostatically coupled microbeams with distributed electrodes for high sensitivity mass sensing. Mech. Syst. Signal Process. 2021, 158, 107781. [Google Scholar] [CrossRef]
- Song, J.; Lyu, M.; Kacem, N.; Liu, P.; Huang, Y.; Fan, K.; Zhao, J. Exploiting bifurcation behaviors in parametrically excited mode-localized resonators for mass sensing. J. Appl. Mech. 2022, 89, 111006. [Google Scholar] [CrossRef]
- Karabalin, R.; Cross, M.; Roukes, M. Nonlinear dynamics and chaos in two coupled nanomechanical resonators. Phys. Rev. B 2009, 79, 165309. [Google Scholar] [CrossRef]
- Baguet, S.; Nguyen, V.N.; Grenat, C.; Lamarque, C.H.; Dufour, R. Nonlinear dynamics of micromechanical resonator arrays for mass sensing. Nonlinear Dyn. 2019, 95, 1203–1220. [Google Scholar] [CrossRef]
- Rabenimanana, T.; Najar, F.; Ghommem, M.; Walter, V.; Kacem, N. On the equivalence between mass perturbation and DC voltage bias in coupled MEMS resonators: Theoretical and experimental investigation. J. Appl. Phys. 2022, 132, 024502. [Google Scholar] [CrossRef]
- Zhao, C.; Montaseri, M.H.; Wood, G.S.; Pu, S.H.; Seshia, A.A.; Kraft, M. A review on coupled MEMS resonators for sensing applications utilizing mode localization. Sens. Actuators A Phys. 2016, 249, 93–111. [Google Scholar] [CrossRef]
- Dick, A.J.; Balachandran, B.; Mote, C.D. Localization in microresonator arrays: Influence of natural frequency tuning. J. Comput. Nonlinear Dyn. 2010, 5, 011002. [Google Scholar] [CrossRef]
- Pierre, C. Mode localization and eigenvalue loci veering phenomena in disordered structures. J. Sound Vib. 1988, 126, 485–502. [Google Scholar] [CrossRef]
- Balachandran, B.; Perkins, E.; Fitzgerald, T. Response localization in micro-scale oscillator arrays: Influence of cubic coupling nonlinearities. Int. J. Dyn. Control 2015, 3, 183–188. [Google Scholar] [CrossRef]
- Spletzer, M.; Raman, A.; Wu, A.Q.; Xu, X.; Reifenberger, R. Ultrasensitive mass sensing using mode localization in coupled microcantilevers. Appl. Phys. Lett. 2006, 88, 254102. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, C.; Wang, C.; Cerica, D.; Baijot, M.; Xiao, Q.; Stoukatch, S.; Kraft, M. A mass sensor based on 3-DOF mode localized coupled resonator under atmospheric pressure. Sens. Actuators A Phys. 2018, 279, 254–262. [Google Scholar] [CrossRef]
- Zhao, C.; Wood, G.S.; Xie, J.; Chang, H.; Pu, S.H.; Kraft, M. A force sensor based on three weakly coupled resonators with ultrahigh sensitivity. Sens. Actuators A Phys. 2015, 232, 151–162. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, J.; Yuan, W.; Chang, H. A high-sensitivity micromechanical electrometer based on mode localization of two degree-of-freedom weakly coupled resonators. J. Microelectromech. Syst. 2016, 25, 937–946. [Google Scholar] [CrossRef]
- Zhang, H.; Li, B.; Yuan, W.; Kraft, M.; Chang, H. An acceleration sensing method based on the mode localization of weakly coupled resonators. J. Microelectromech. Syst. 2016, 25, 286–296. [Google Scholar] [CrossRef]
- Lacarbonara, W.; Arafat, H.N.; Nayfeh, A.H. Non-linear interactions in imperfect beams at veering. Int. J. Non-Linear Mech. 2005, 40, 987–1003. [Google Scholar] [CrossRef]
- Ouakad, H.M.; Alofi, A.M.; Nayfeh, A.H. Dynamic analysis of multilayers based MEMS resonators. Math. Probl. Eng. 2017, 2017, 1262650. [Google Scholar] [CrossRef]
- Alneamy, A.M.; Ouakad, H.M. Investigation into Mode Localization of Electrostatically Coupled Shallow Microbeams for Potential Sensing Applications. Micromachines 2022, 13, 989. [Google Scholar] [CrossRef]
- A reduced-order model for electrically actuated microbeam-based MEMS. J. Microelectromech. Syst. 2003, 12, 672–680. [CrossRef]


| Description | Value |
|---|---|
| Density () | 2330 kg/m3 |
| Young’s Modulus (E) | 129 GPa |
| Dielectric constant of the air () | 8.854 F/m |
| Resonators’ length () | 1000 µm |
| Resonators’ width (b) | 30 µm |
| Resonators’ thickness (h) | 2 µm |
| Capacitor gap ( and ) | 10 µm |
| Upper resonator mid-point rise () | −2:2 µm |
| Lower resonator mid-point rise () | −2.5:2 µm |
| Description | Expression |
|---|---|
| Viscous damping coefficient (c) | |
| Mid-plane stretching coefficient () | |
| Electrostatic force coefficient () |
| Design 1 | Design 2 | Design 3 | Design 4 | Design 5 | |
|---|---|---|---|---|---|
| 0 | 0 | 2 | −2 | −2.5 | |
| 1 | 2 | 2 | 0 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouakad, H.M.; Alneamy, A.M. Static and Eigenvalue Analysis of Electrostatically Coupled and Tunable Shallow Micro-Arches for Sensing-Based Applications. Micromachines 2023, 14, 903. https://doi.org/10.3390/mi14050903
Ouakad HM, Alneamy AM. Static and Eigenvalue Analysis of Electrostatically Coupled and Tunable Shallow Micro-Arches for Sensing-Based Applications. Micromachines. 2023; 14(5):903. https://doi.org/10.3390/mi14050903
Chicago/Turabian StyleOuakad, Hassen M., and Ayman M. Alneamy. 2023. "Static and Eigenvalue Analysis of Electrostatically Coupled and Tunable Shallow Micro-Arches for Sensing-Based Applications" Micromachines 14, no. 5: 903. https://doi.org/10.3390/mi14050903
APA StyleOuakad, H. M., & Alneamy, A. M. (2023). Static and Eigenvalue Analysis of Electrostatically Coupled and Tunable Shallow Micro-Arches for Sensing-Based Applications. Micromachines, 14(5), 903. https://doi.org/10.3390/mi14050903






