Multi-Objective Topology Optimization of a Broadband Piezoelectric Energy Harvester
Abstract
1. Introduction
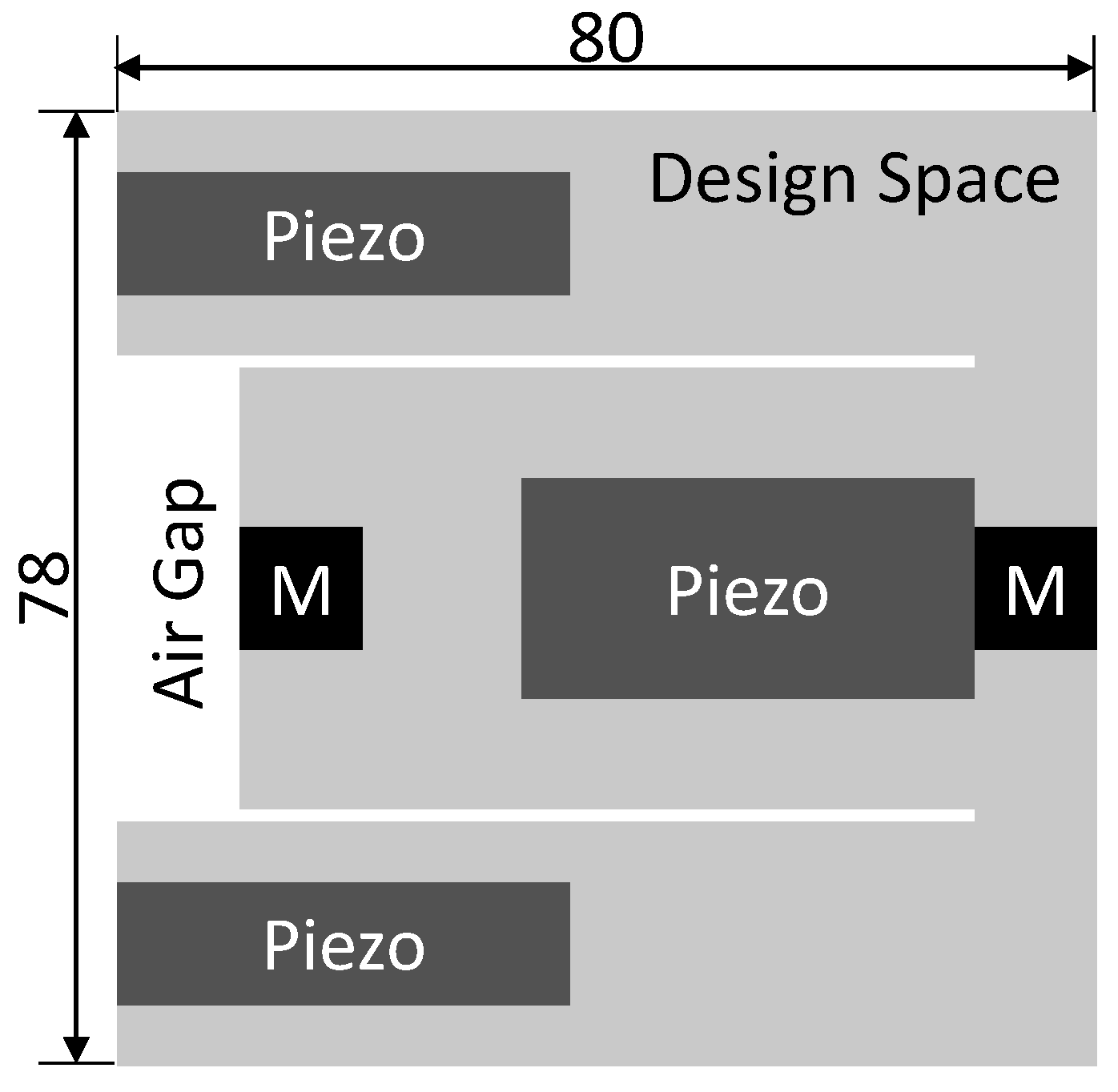
2. Definition and Modeling of Multi-Modal Piezoelectric Energy Harvester
2.1. Finite Element Modeling of Piezoelectric Energy Harvester
2.2. Folded-Beam Resonator
3. Topology Optimization Procedure
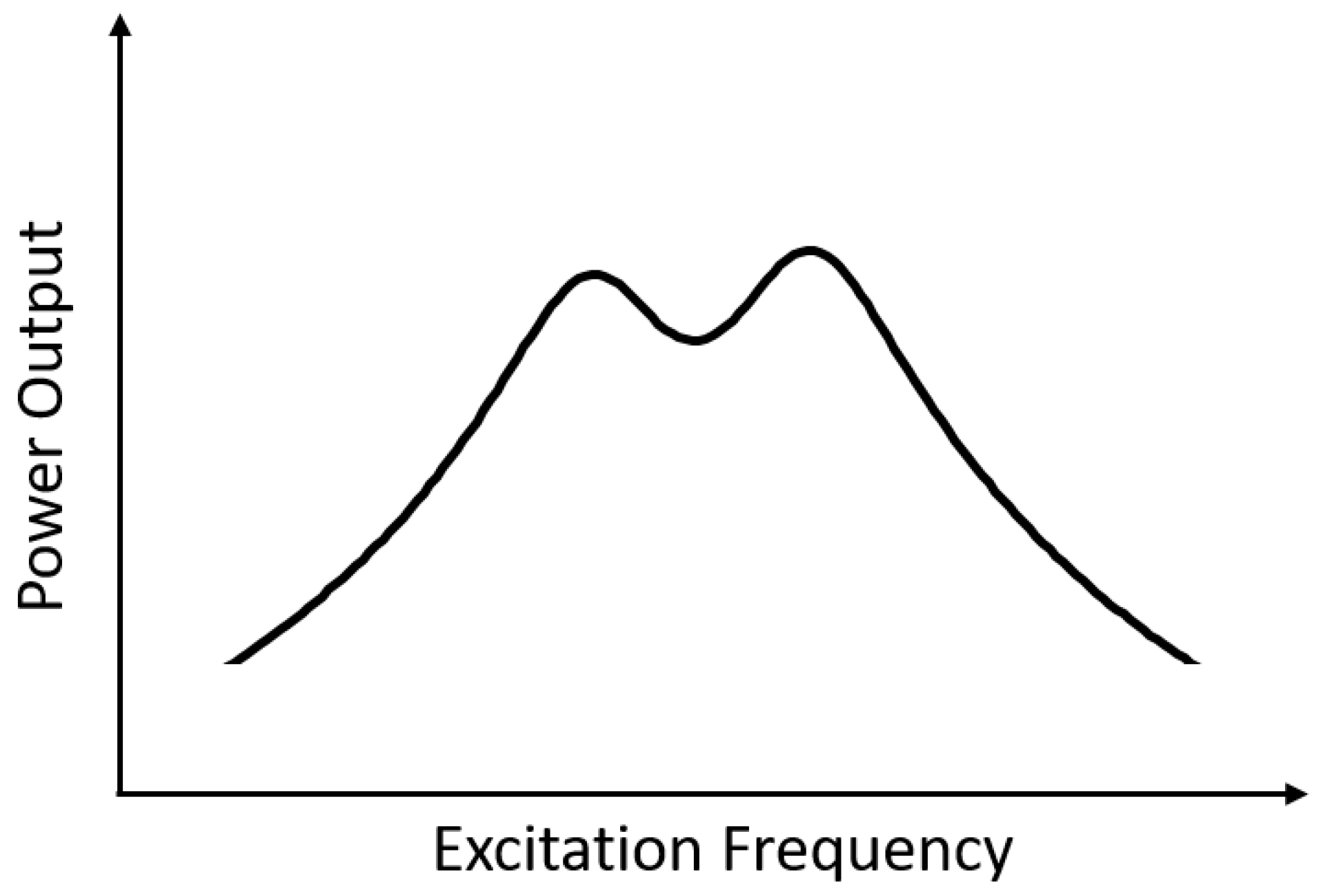
3.1. Objective Function and Sensitivity Analysis
3.2. Filters
3.2.1. Density Filter
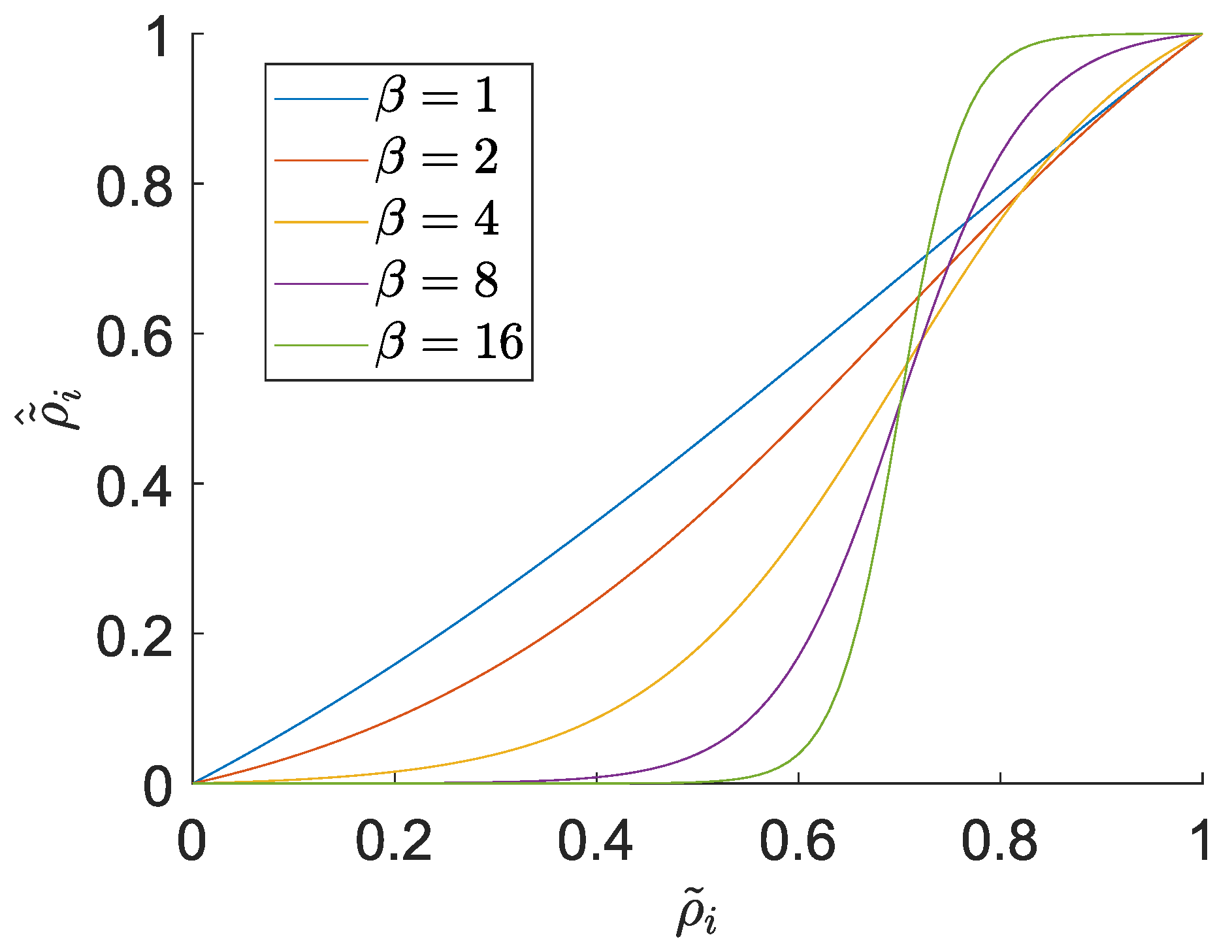
3.2.2. Threshold Projection
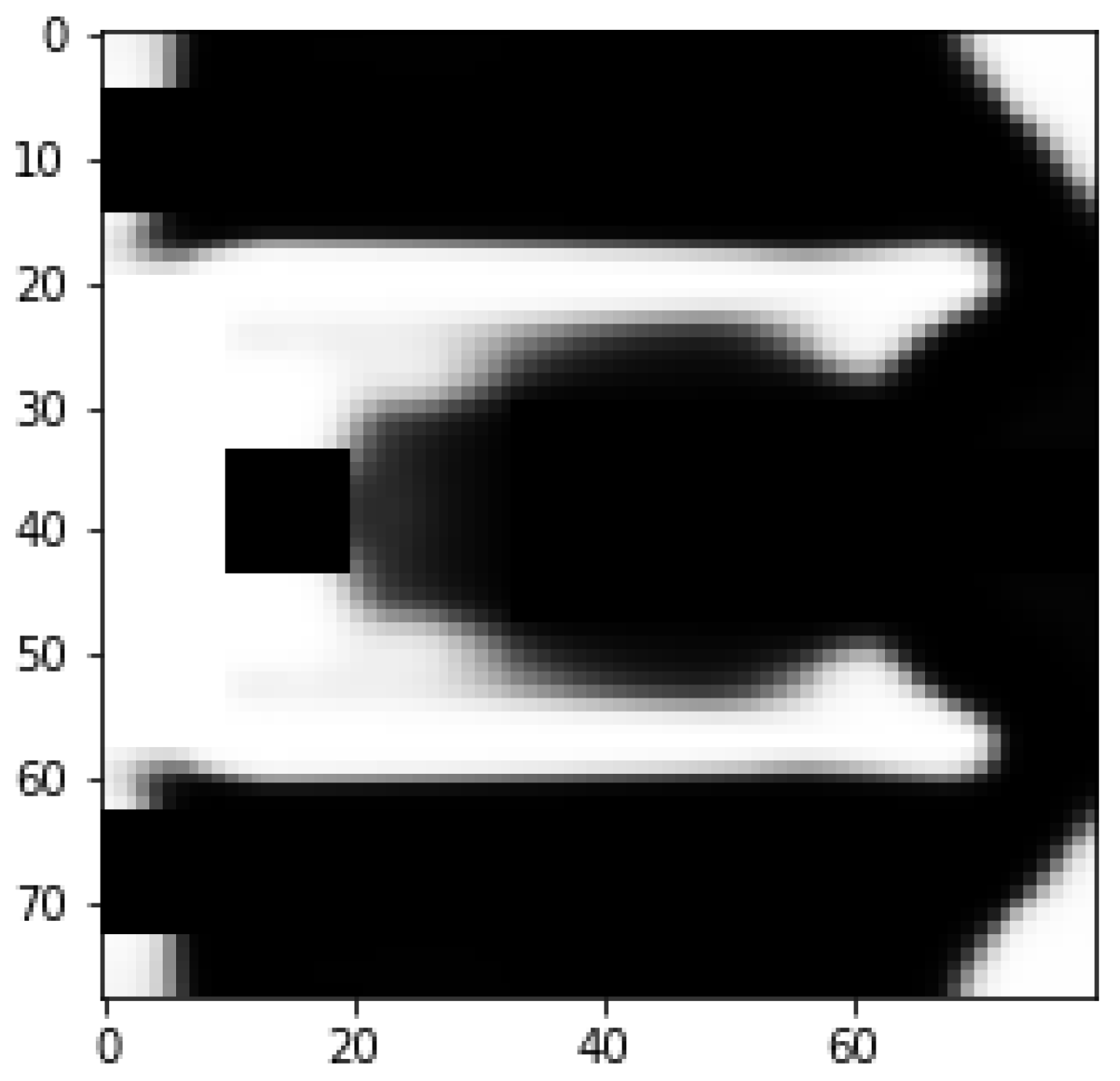
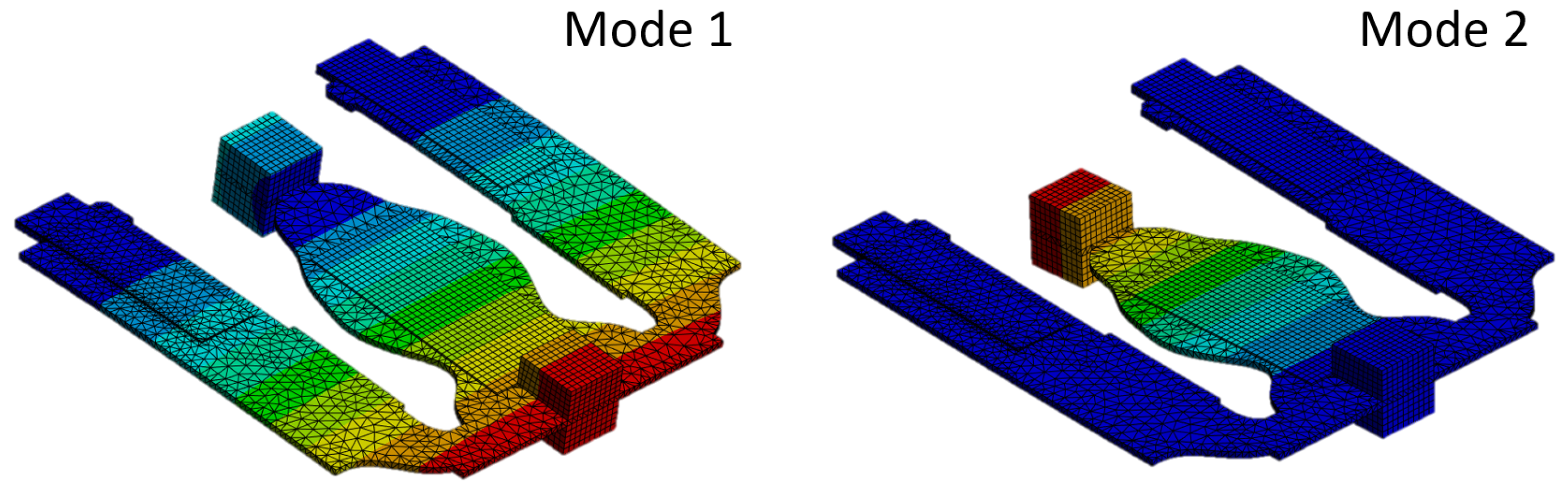
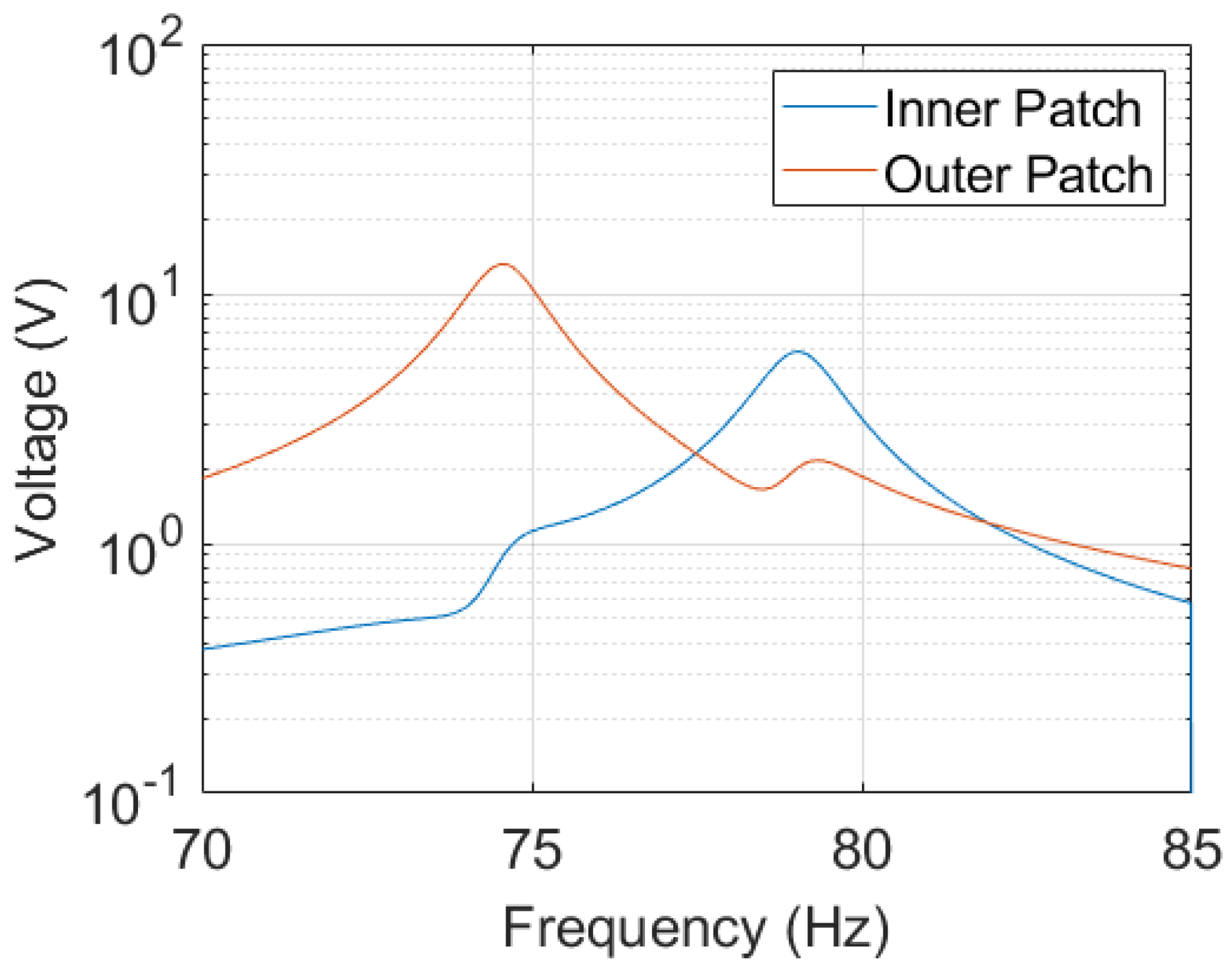
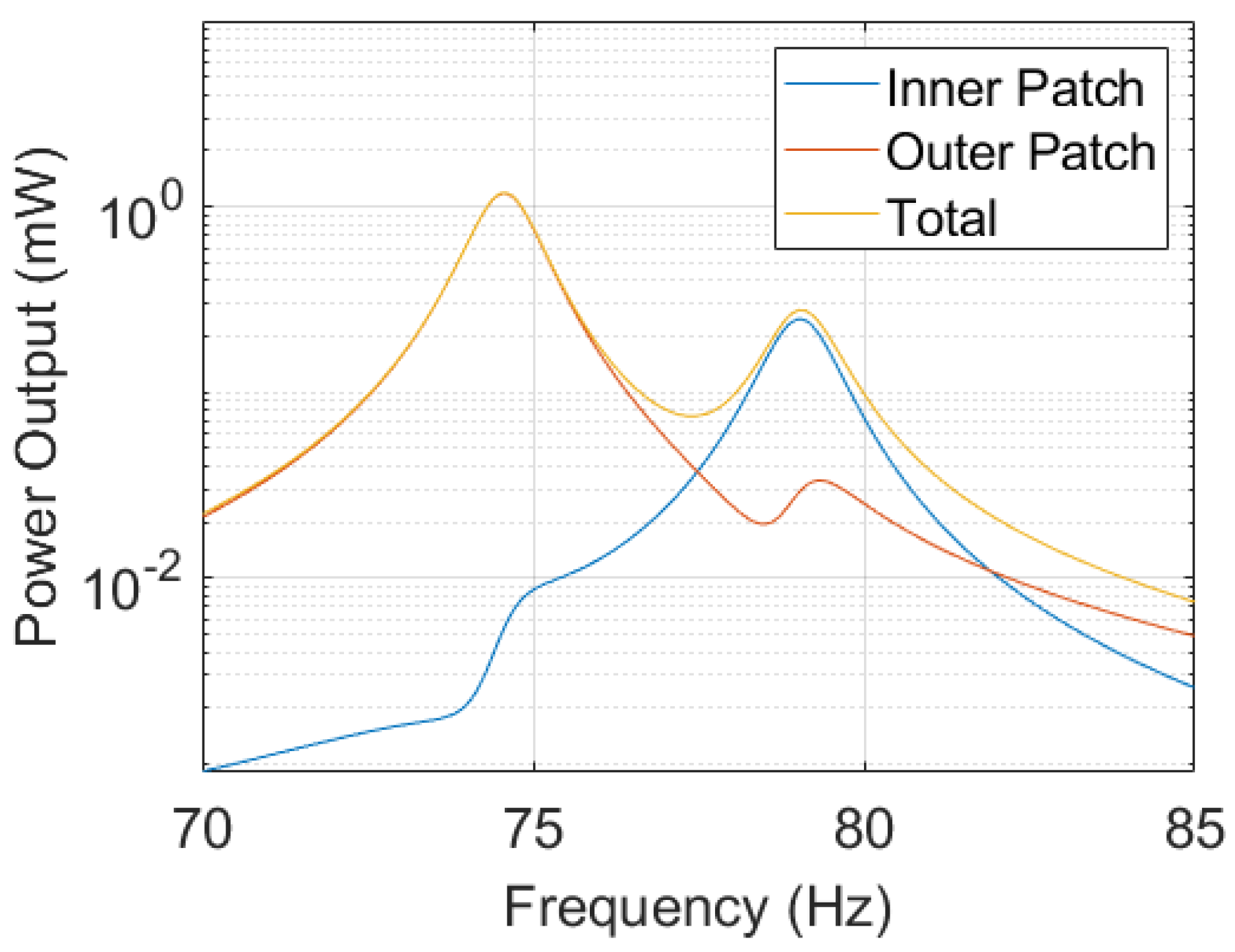
4. Optimization Results
5. Discussion
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PEH | Piezoelectric Energy Harvester |
| TO | Topology Optimization |
Appendix A
Appendix B
References
- Sah, D.K.; Amgoth, T. Renewable energy harvesting schemes in wireless sensor networks: A Survey. Inf. Fusion 2020, 63, 223–247. [Google Scholar] [CrossRef]
- Mohanty, A.; Parida, S.; Behera, R.K.; Roy, T. Vibration energy harvesting: A review. J. Adv. Dielectr. 2019, 9, 1930001. [Google Scholar] [CrossRef]
- Adendorff, K.; Naidoo, R.; Jimoh, A.A.; Okojie, D.E. A hybrid piezoelectric micro-power generator for use in low power applications. Renew. Sustain. Energy Rev. 2015, 49, 1136–1144. [Google Scholar]
- Bowen, C.; Kim, H.; Weaver, P.; Dunn, S. Piezoelectric and ferroelectric materials and structures for energy harvesting applications. Energy Environ. Sci. 2014, 7, 25–44. [Google Scholar] [CrossRef]
- Li, H.; Tian, C.; Deng, Z.D. Energy harvesting from low frequency applications using piezoelectric materials. Appl. Phys. Rev. 2014, 1, 041301. [Google Scholar] [CrossRef]
- Toprak, A.; Tigli, O. Piezoelectric energy harvesting: State-of-the-art and challenges. Appl. Phys. Rev. 2014, 1, 031104. [Google Scholar] [CrossRef]
- Liu, H.; Zhong, J.; Lee, C.; Lee, S.W.; Lin, L. A comprehensive review on piezoelectric energy harvesting technology: Materials, mechanisms, and applications. Appl. Phys. Rev. 2018, 5, 041306. [Google Scholar] [CrossRef]
- Tang, L.; Yang, Y.; Soh, C.K. Toward broadband vibration-based energy harvesting. J. Intell. Mater. Syst. Struct. 2010, 21, 1867–1897. [Google Scholar] [CrossRef]
- Qin, H.; Mo, S.; Jiang, X.; Shang, S.; Wang, P.; Liu, Y. Multimodal Multidirectional Piezoelectric Vibration Energy Harvester by U-Shaped Structure with Cross-Connected Beams. Micromachines 2022, 13, 396. [Google Scholar] [CrossRef] [PubMed]
- Caetano, V.J.; Savi, M.A. Multimodal pizza-shaped piezoelectric vibration-based energy harvesters. J. Intell. Mater. Syst. Struct. 2021, 32, 2505–2528. [Google Scholar] [CrossRef]
- Caetano, V.J.; Savi, M.A. Star-shaped piezoelectric mechanical energy harvesters for multidirectional sources. Int. J. Mech. Sci. 2022, 215, 106962. [Google Scholar] [CrossRef]
- Pertin, O.; Shrivas, P.; Guha, K.; Rao, K.S.; Iannacci, J. New and efficient design of multimode piezoelectric vibration energy harvester for MEMS application. Microsyst. Technol. 2021, 27, 3523–3531. [Google Scholar] [CrossRef]
- Bouhedma, S.; Zheng, Y.; Lange, F.; Hohlfeld, D. Magnetic frequency tuning of a multimodal vibration energy harvester. Sensors 2019, 19, 1149. [Google Scholar] [CrossRef]
- Bouhedma, S.; Hu, S.; Schütz, A.; Lange, F.; Bechtold, T.; Ouali, M.; Hohlfeld, D. Analysis and Characterization of Optimized Dual-Frequency Vibration Energy Harvesters for Low-Power Industrial Applications. Micromachines 2022, 13, 1078. [Google Scholar] [CrossRef]
- Wang, H.; Tang, L. Modeling and experiment of bistable two-degree-of-freedom energy harvester with magnetic coupling. Mech. Syst. Signal Process. 2017, 86, 29–39. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, X.; John, S. A dimensionless analysis of a 2DOF piezoelectric vibration energy harvester. Mech. Syst. Signal Process. 2015, 58, 355–375. [Google Scholar] [CrossRef]
- Sarker, M.R.; Julai, S.; Sabri, M.F.M.; Said, S.M.; Islam, M.M.; Tahir, M. Review of piezoelectric energy harvesting system and application of optimization techniques to enhance the performance of the harvesting system. Sens. Actuators A Phys. 2019, 300, 111634. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.; Kwak, B.M. Design optimization of piezoelectric energy harvester subject to tip excitation. J. Mech. Sci. Technol. 2012, 26, 137–143. [Google Scholar] [CrossRef]
- Rui, X.; Li, Y.; Liu, Y.; Zheng, X.; Zeng, Z. Experimental study and parameter optimization of a magnetic coupled piezoelectric energy harvester. Appl. Sci. 2018, 8, 2609. [Google Scholar] [CrossRef]
- Yang, H.; Wei, Y.; Zhang, W.; Ai, Y.; Ye, Z.; Wang, L. Development of piezoelectric energy harvester system through optimizing multiple structural parameters. Sensors 2021, 21, 2876. [Google Scholar] [CrossRef]
- Bouhedma, S.; Rao, Y.; Schütz, A.; Yuan, C.; Hu, S.; Lange, F.; Bechtold, T.; Hohlfeld, D. System-level model and simulation of a frequency-tunable vibration energy harvester. Micromachines 2020, 11, 91. [Google Scholar] [CrossRef]
- Hu, S.; Bouhedma, S.; Schütz, A.; Stindt, S.; Hohlfeld, D.; Bechtold, T. Design optimization of multi-resonant piezoelectric energy harvesters. Microelectron. Reliab. 2021, 120, 114114. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Chen, F.; Wang, J.; Yang, X. Topology optimization design and numerical analysis on cold plates for lithium-ion battery thermal management. Int. J. Heat Mass Transf. 2022, 183, 122087. [Google Scholar] [CrossRef]
- Sharma, A.K.; Kosta, M.; Shmuel, G.; Amir, O. Gradient-based topology optimization of soft dielectrics as tunable phononic crystals. Compos. Struct. 2022, 280, 114846. [Google Scholar] [CrossRef]
- Díaaz, A.R.; Kikuchi, N. Solutions to shape and topology eigenvalue optimization problems using a homogenization method. Int. J. Numer. Methods Eng. 1992, 35, 1487–1502. [Google Scholar] [CrossRef]
- Ma, Z.D.; Kikuchi, N.; Hagiwara, I. Structural topology and shape optimization for a frequency response problem. Comput. Mech. 1993, 13, 157–174. [Google Scholar] [CrossRef]
- Ma, Z.D.; Cheng, H.C.; Kikuchi, N. Structural design for obtaining desired eigenfrequencies by using the topology and shape optimization method. Comput. Syst. Eng. 1994, 5, 77–89. [Google Scholar] [CrossRef]
- Hu, S.; Liu, Z.; Bechtold, T. Fast Topology Optimization for Resonating Structures via Generalized Incremental Frequency Method and Modal Superposition-Based Model Order Reduction. In Advances in Structural and Multidisciplinary Optimization, Proceedings of the 13th World Congress of Structural and Multidisciplinary Optimization, Beijing, China, 20–24 May 2019; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Giannini, D.; Braghin, F.; Aage, N. Topology optimization of 2D in-plane single mass MEMS gyroscopes. Struct. Multidiscip. Optim. 2020, 62, 2069–2089. [Google Scholar] [CrossRef]
- Giannini, D.; Aage, N.; Braghin, F. Topology optimization of MEMS resonators with target eigenfrequencies and modes. Eur. J. Mech.-A/Solids 2022, 91, 104352. [Google Scholar] [CrossRef]
- He, M.; Zhang, X.; dos Santos Fernandez, L.; Molter, A.; Xia, L.; Shi, T. Multi-material topology optimization of piezoelectric composite structures for energy harvesting. Compos. Struct. 2021, 265, 113783. [Google Scholar] [CrossRef]
- He, M.; He, M.; Zhang, X.; Xia, L. Topology Optimization of Piezoelectric Energy Harvesters for Enhanced Open-Circuit Voltage Subjected to Harmonic Excitations. Materials 2022, 15, 4423. [Google Scholar] [CrossRef]
- Ikeda, T. Fundamentals of Piezoelectricity/by Takuro Ikeda; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Hu, S.; Fitzer, U.; Stindt, S.; Bechtold, T. Topology Optimization of a Folded Beam Piezoelectric Energy Harvester. IFAC-PapersOnLine 2022, 55, 379–384. [Google Scholar] [CrossRef]
- Lerch, R. Simulation of piezoelectric devices by two- and three-dimensional finite elements. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1990, 37, 233–247. [Google Scholar] [CrossRef]
- Zheng, B.; Chang, C.J.; Gea, H.C. Topology optimization of energy harvesting devices using piezoelectric materials. Struct. Multidiscip. Optim. 2009, 38, 17–23. [Google Scholar] [CrossRef]
- Diaz, A.; Sigmund, O. Checkerboard patterns in layout optimization. Struct. Optim. 1995, 10, 40–45. [Google Scholar] [CrossRef]
- Jog, C.S.; Haber, R.B. Stability of finite element models for distributed-parameter optimization and topology design. Comput. Methods Appl. Mech. Eng. 1996, 130, 203–226. [Google Scholar] [CrossRef]
- Sigmund, O.; Petersson, J. Numerical instabilities in topology optimization: A survey on procedures dealing with checkerboards, mesh-dependencies and local minima. Struct. Optim. 1998, 16, 68–75. [Google Scholar] [CrossRef]
- Wang, F.; Lazarov, B.S.; Sigmund, O. On projection methods, convergence and robust formulations in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 767–784. [Google Scholar] [CrossRef]
- dos Santos Guimarães, C.; de Silva Bussamra, F.L.; Pommier-Budinger, V.; Hernandes, J.A. Structural Shape Control Using Macro Fiber Composite Piezoelectric Sensors and Actuators. Mec. Comput. 2010, 29, 8263–8279. [Google Scholar]


| Density (kg/m) | Piezoelectric Constants (C/m) | ||
|---|---|---|---|
| 4700 | −2.227 | ||
| Young’s Modulus (GPa) | −0.671 | ||
| 45.21 | 16.665 | ||
| 12.39 | 0.0258 | ||
| 40.44 | 13.668 | ||
| Shear Modulus (GPa) | Dielectric Relative Constants | ||
| 6.03 | 1574.8 | ||
| 6.68 | 24.7 | ||
| 17.01 | 1528.7 | ||
| Poisson’s Ratio | |||
| 0.39 | |||
| 0.17 | |||
| 0.44 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Fitzer, U.; Nguyen, K.C.; Hohlfeld, D.; Korvink, J.G.; Bechtold, T. Multi-Objective Topology Optimization of a Broadband Piezoelectric Energy Harvester. Micromachines 2023, 14, 332. https://doi.org/10.3390/mi14020332
Hu S, Fitzer U, Nguyen KC, Hohlfeld D, Korvink JG, Bechtold T. Multi-Objective Topology Optimization of a Broadband Piezoelectric Energy Harvester. Micromachines. 2023; 14(2):332. https://doi.org/10.3390/mi14020332
Chicago/Turabian StyleHu, Siyang, Ulrike Fitzer, Khai Chau Nguyen, Dennis Hohlfeld, Jan G. Korvink, and Tamara Bechtold. 2023. "Multi-Objective Topology Optimization of a Broadband Piezoelectric Energy Harvester" Micromachines 14, no. 2: 332. https://doi.org/10.3390/mi14020332
APA StyleHu, S., Fitzer, U., Nguyen, K. C., Hohlfeld, D., Korvink, J. G., & Bechtold, T. (2023). Multi-Objective Topology Optimization of a Broadband Piezoelectric Energy Harvester. Micromachines, 14(2), 332. https://doi.org/10.3390/mi14020332








