A Pavement Piezoelectric Energy Harvester for Small Input Displacements
Abstract
:1. Introduction
2. Design Concept and Modeling
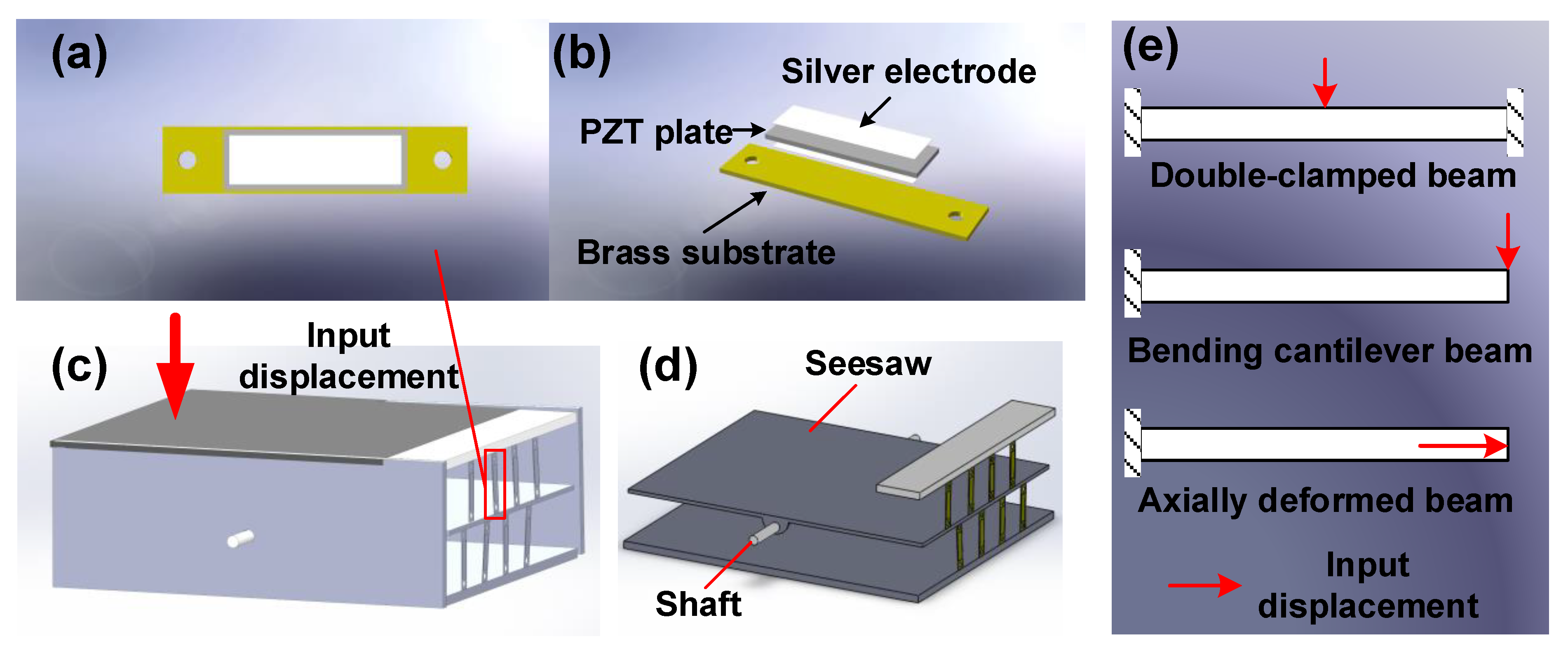
2.1. Design Concept
2.2. Modeling
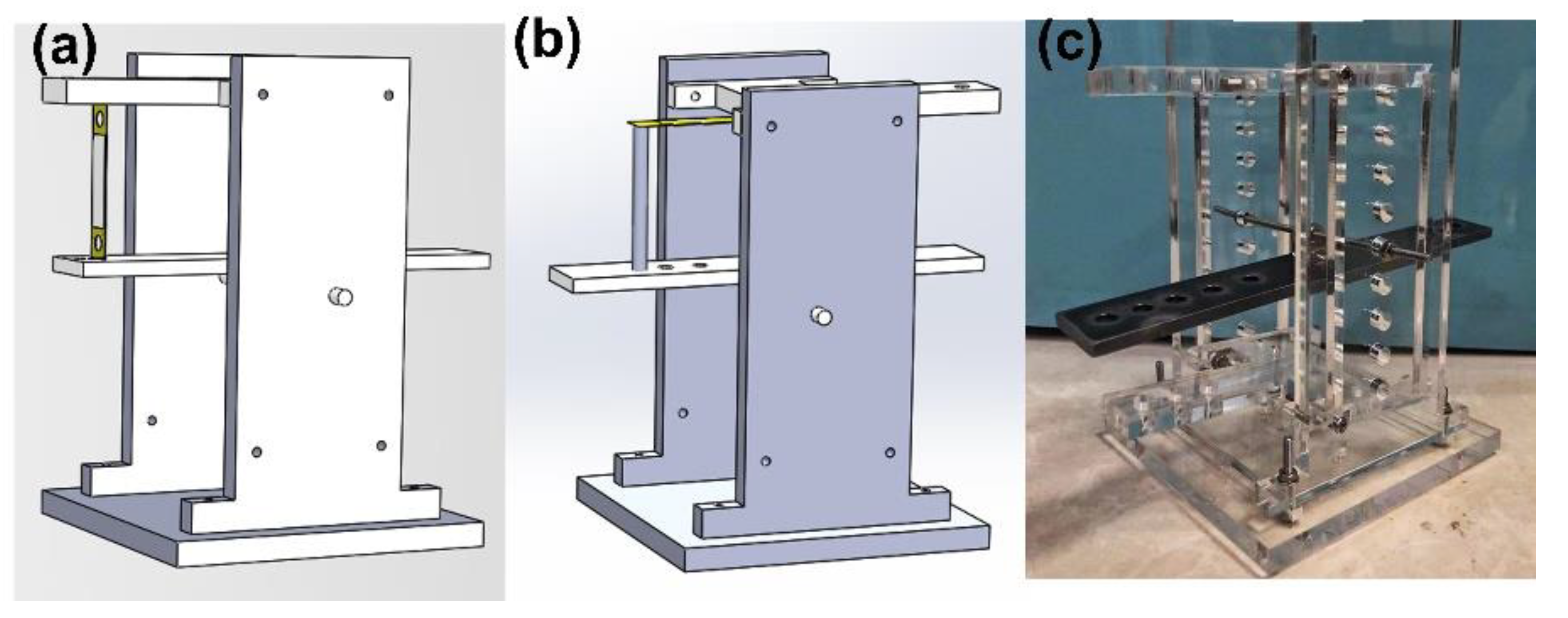
3. Prototype and Experiments
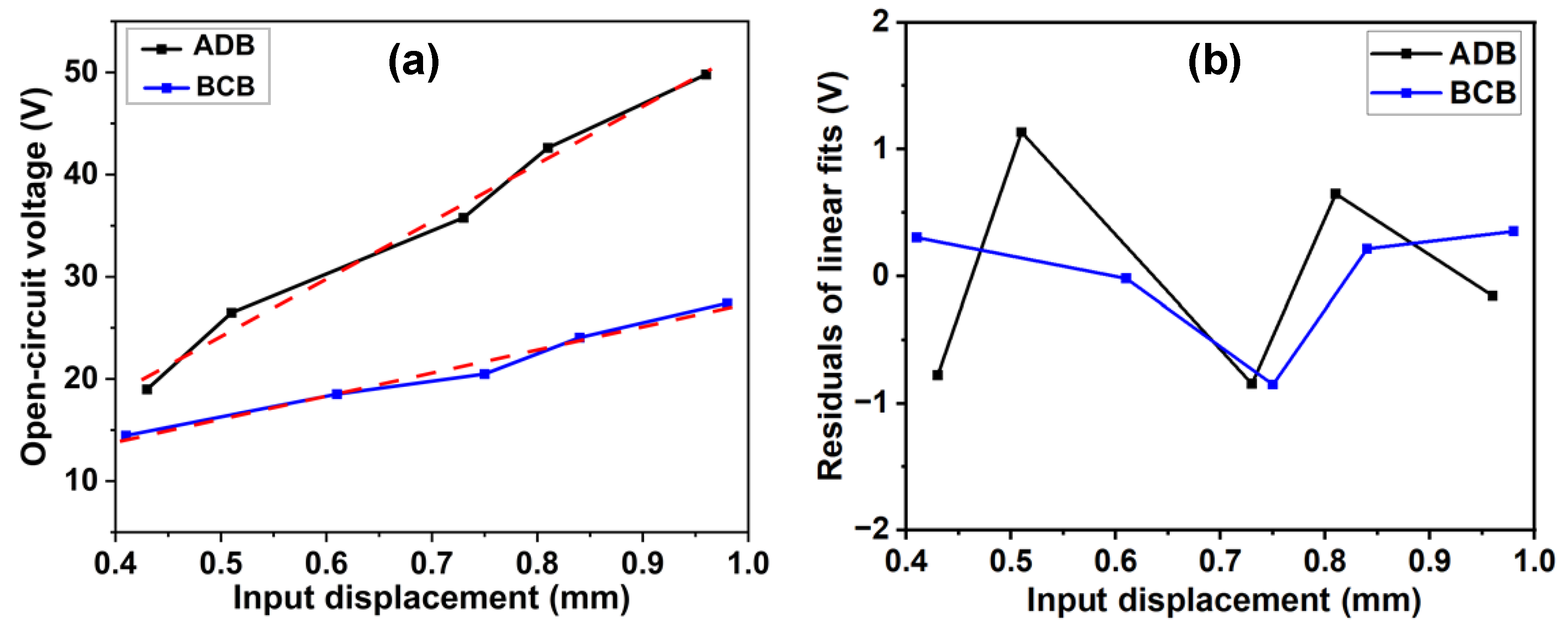
3.1. Comparison of Single ADB and BCB
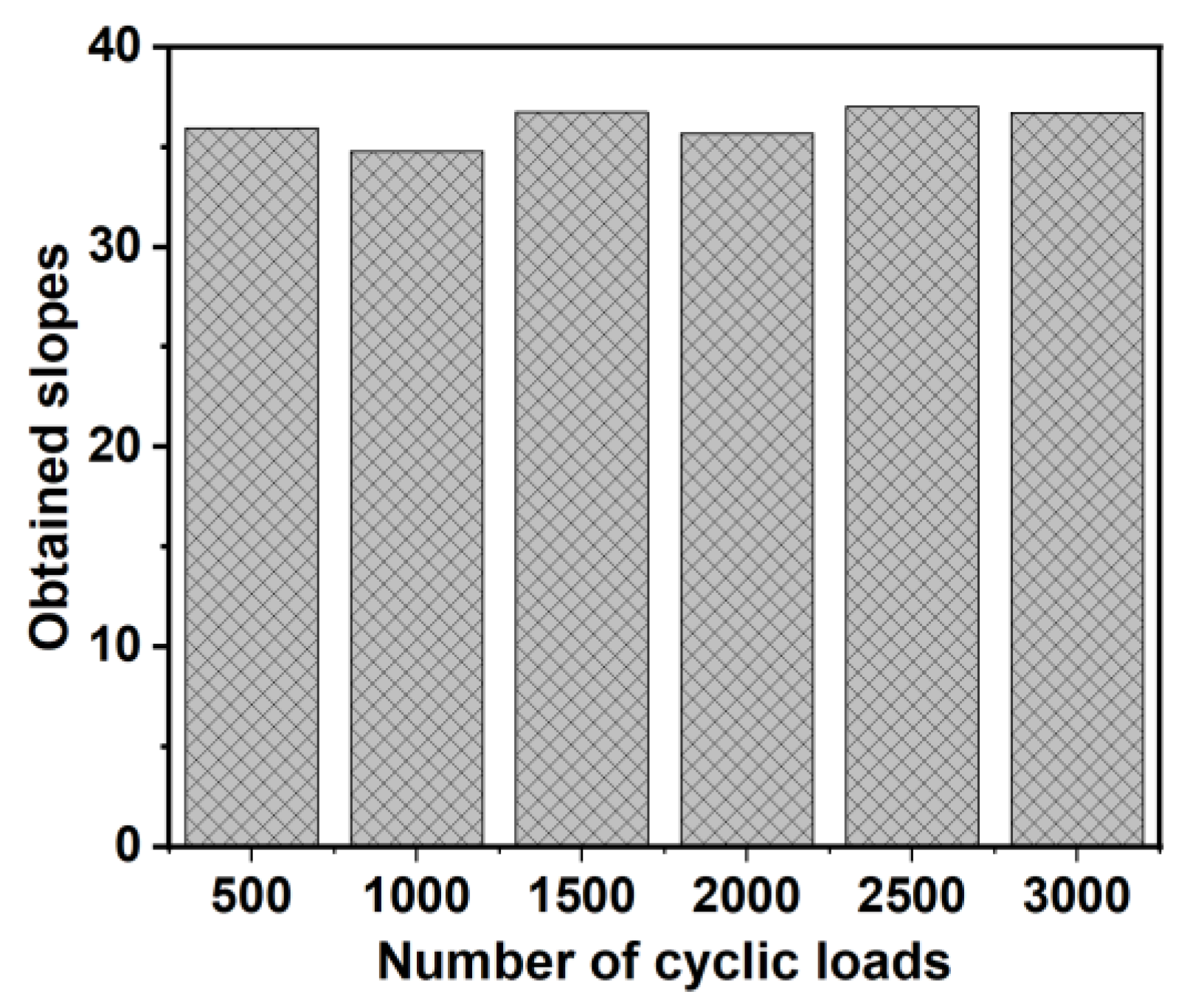
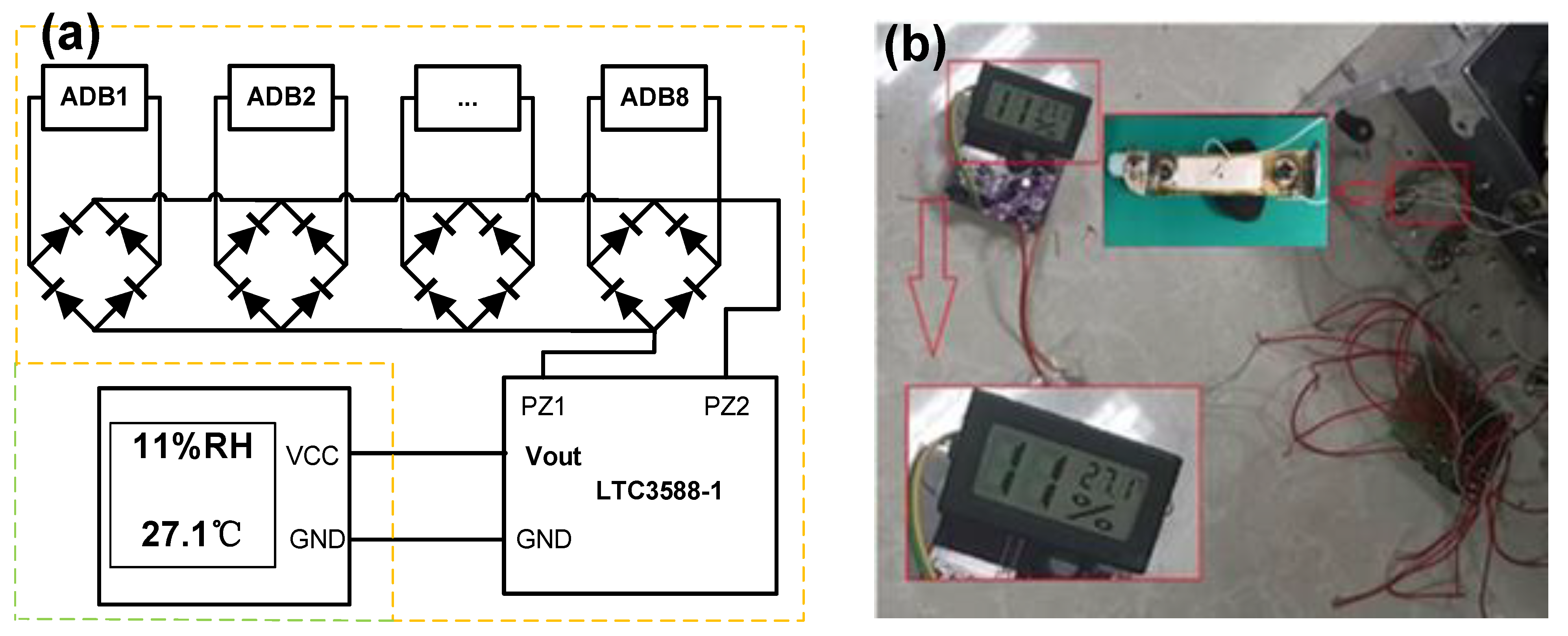
3.2. Characterizations and Applications of Proposed PPEH
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gammaitoni, L. There’s Plenty of Energy at the Bottom (Micro and Nano Scale Nonlinear Noise Harvesting). Contemp. Phys. 2012, 53, 119–135. [Google Scholar] [CrossRef]
- Moure, A.; Rodríguez, M.A.I.; Rueda, S.H.; Gonzalo, A.; Rubio-Marcos, F.; Cuadros, D.U.; Pérez-Lepe, A.; Fernández, J.F. Feasible Integration in Asphalt of Piezoelectric Cymbals for Vibration Energy Harvesting. Energy Convers. Manag. 2016, 112, 246–253. [Google Scholar] [CrossRef]
- Gholikhani, M.; Hossein, R.; Samer, D.; Papagiannakis, A.T. A Critical Review of Roadway Energy Harvesting Technologies. Appl. Energy 2020, 261, 114388. [Google Scholar] [CrossRef]
- Ting, C.-C.; Tsai, D.-Y.; Hsiao, C.-C. Developing a Mechanical Roadway System for Waste Energy Capture of Vehicles and Electric Generation. Appl. Energy 2012, 92, 1–8. [Google Scholar] [CrossRef]
- Pan, Y.; Lin, T.; Qian, F.; Liu, C.; Yu, J.; Zuo, J.; Zuo, L. Modeling and Field-Test of a Compact Electromagnetic Energy Harvester for Railroad Transportation. Appl. Energy 2019, 247, 309–321. [Google Scholar] [CrossRef]
- Jung, I.; Shin, Y.-H.; Kim, S.; Choi, J.-y.; Kang, C.-Y. Flexible Piezoelectric Polymer-Based Energy Harvesting System for Roadway Applications. Appl. Energy 2017, 197, 222–229. [Google Scholar] [CrossRef]
- Song, G.J.; Cho, J.Y.; Kim, K.-B.; Ahn, J.H.; Song, Y.; Hwang, W.; Hong, S.D.; Sung, T.H. Development of a Pavement Block Piezoelectric Energy Harvester for Self-Powered Walkway Applications. Appl. Energy 2019, 256, 113916. [Google Scholar] [CrossRef]
- Wang, C.; Yu, G.; Cao, H.; Wang, S.; Li, Y. Structure Simulation Optimization and Test Verification of Piezoelectric Energy Harvester Device for Road. Sens. Actuators A Phys. 2020, 315, 112322. [Google Scholar] [CrossRef]
- Pirisi, A.; Mussetta, M.; Grimaccia, F.; Zich, R.E. Novel Speed-Bump Design and Optimization for Energy Harvesting from Traffic. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1983–1991. [Google Scholar] [CrossRef]
- Gholikhani, M.; Nasouri, R.; Tahami, S.A.; Legette, S.; Dessouky, S.; Montoya, A. Harvesting Kinetic Energy from Roadway Pavement through an Electromagnetic Speed Bump. Appl. Energy 2019, 250, 503–511. [Google Scholar] [CrossRef]
- Wang, L.; Todaria, P.; Pandey, A.; O’Connor, J.; Chernow, B.; Zuo, L. An Electromagnetic Speed Bump Energy Harvester and Its Interactions with Vehicles. IEEE/ASME Trans. Mechatron. 2016, 21, 1985–1994. [Google Scholar] [CrossRef]
- Liu, M.; Lin, R.; Zhou, S.; Yu, Y.; Ishida, A.; McGrath, M.; Kennedy, B.; Hajj, M.; Zuo, L. Design, Simulation and Experiment of a Novel High Efficiency Energy Harvesting Paver. Appl. Energy 2018, 212, 966–975. [Google Scholar] [CrossRef]
- Ambrozkiewicz, B.; Czyz, Z.; Karpinski, P.; Staczek, P.; Litak, G.; Grabowski, L. Ceramic-Based Piezoelectric Material for Energy Harvesting Using Hybrid Excitation. Materials 2021, 14, 5816. [Google Scholar] [CrossRef] [PubMed]
- Qin, H.; Mo, S.; Jiang, X.; Shang, S.; Wang, P.; Liu, Y. Multimodal Multidirectional Piezoelectric Vibration Energy Harvester by U-Shaped Structure with Cross-Connected Beams. Micromachines 2022, 13, 396. [Google Scholar] [CrossRef]
- Duc, D.H.; Van Thom, D.; Cong, P.H.; Van Minh, P.; Nguyen, N.X. Vibration and Static Buckling Behavior of Variable Thickness Flexoelectric Nanoplates. Mech. Based Des. Struct. Mach. 2022, 2022, 1–29. [Google Scholar] [CrossRef]
- Thai, L.M.; Luat, D.T.; Phung, V.B.; Van Minh, P.; Van Thom, D. Finite Element Modeling of Mechanical Behaviors of Piezoelectric Nanoplates with Flexoelectric Effects. Arch. Appl. Mech. 2021, 92, 163–182. [Google Scholar] [CrossRef]
- Tho, N.C.; Thanh, N.T.; Tho, T.D.; Van Minh, P.; Hoa, L.K. Modelling of the Flexoelectric Effect on Rotating Nanobeams with Geometrical Imperfection. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 510. [Google Scholar] [CrossRef]
- Song, Y.; Yang, C.H.; Hong, S.K.; Hwang, S.J.; Kim, J.H.; Choi, J.Y.; Ryu, S.K.; Sung, T.H. Road Energy Harvester Designed as a Macro-Power Source Using the Piezoelectric Effect. Int. J. Hydrog. Hydrogen 2016, 41, 12563–12568. [Google Scholar] [CrossRef]
- Hong, S.D.; Ahn, J.H.; Kim, K.-B.; Kim, J.H.; Cho, J.Y.; Woo, M.S.; Song, Y.; Hwang, W.; Jeon, D.H.; Kim, J.; et al. Uniform Stress Distribution Road Piezoelectric Generator with Free-Fixed-End Type Central Strike Mechanism. Energy 2021, 239, 121812. [Google Scholar] [CrossRef]
- Yang, C.H.; Song, Y.; Woo, M.S.; Eom, J.H.; Song, G.J.; Kim, J.H.; Kim, J.; Lee, T.H.; Choi, J.Y.; Sung, T.H. Feasibility Study of Impact-Based Piezoelectric Road Energy Harvester for Wireless Sensor Networks in Smart Highways. Sens. Actuators A Phys. 2017, 261, 317–324. [Google Scholar] [CrossRef]
- Wen, S.; Xu, Q.; Zi, B. Design of a New Piezoelectric Energy Harvester Based on Compound Two-Stage Force Amplification Frame. IEEE Sens. J. 2018, 18, 3989–4000. [Google Scholar] [CrossRef]
- Yang, C.L.; Chen, K.-W.; Chen, C.-D. Model and Characterization of a Press-Button-Type Piezoelectric Energy Harvester. IEEE/ASME Trans. Mechatron. 2019, 24, 132–143. [Google Scholar] [CrossRef]
- Ahn, J.H.; Hwang, W.S.; Cho, J.Y.; Jeong, S.Y.; Song, G.J.; Hong, S.D.; Sung, T.H.; Jeong, S.; Yoo, H.H. A Bending-Type Piezoelectric Energy Harvester with a Displacement-Amplifying Mechanism for Smart Highways. J. Korean Phys. Soc. 2018, 73, 330–337. [Google Scholar] [CrossRef]
- Daqaq, M.F.; Masana, R.; Erturk, A.; Quinn, D.D. On the Role of Nonlinearities in Vibratory Energy Harvesting: A Critical Review and Discussion. Appl. Mech. Rev. 2014, 66, 040801. [Google Scholar] [CrossRef]
- Wu, Y.; Qiu, J.; Zhou, S.; Ji, H.; Chen, Y.; Li, S. A Piezoelectric Spring Pendulum Oscillator Used for Multi-Directional and Ultra-Low Frequency Vibration Energy Harvesting. Appl. Energy 2018, 231, 600–614. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, Y. A Wideband Vibration Energy Harvester Based on a Folded Asymmetric Gapped Cantilever. Appl. Phys. Lett. 2014, 104, 053902. [Google Scholar] [CrossRef]
- Papagiannakis, A.T.; Montoya, A.; Dessouky, S.; Helffrich, J. Development and Evaluation of Piezoelectric Prototypes for Roadway Energy Harvesting. J. Energy Eng. 2017, 143, 04017034. [Google Scholar] [CrossRef]






| Material Parameters | Beam Dimensions | ||||
|---|---|---|---|---|---|
| Young’s Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) | Length (mm) | Width (mm) | Thickness (mm) |
| 91 | 0.36 | 8600 | 50 | 11 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, B.; Wei, J.; Jiang, X.; Liu, Y. A Pavement Piezoelectric Energy Harvester for Small Input Displacements. Micromachines 2023, 14, 292. https://doi.org/10.3390/mi14020292
Yin B, Wei J, Jiang X, Liu Y. A Pavement Piezoelectric Energy Harvester for Small Input Displacements. Micromachines. 2023; 14(2):292. https://doi.org/10.3390/mi14020292
Chicago/Turabian StyleYin, Bin, Jiaming Wei, Xin Jiang, and Yan Liu. 2023. "A Pavement Piezoelectric Energy Harvester for Small Input Displacements" Micromachines 14, no. 2: 292. https://doi.org/10.3390/mi14020292
APA StyleYin, B., Wei, J., Jiang, X., & Liu, Y. (2023). A Pavement Piezoelectric Energy Harvester for Small Input Displacements. Micromachines, 14(2), 292. https://doi.org/10.3390/mi14020292







