Optimizing the Performance of the Sparse Matrix–Vector Multiplication Kernel in FPGA Guided by the Roofline Model
Abstract
1. Introduction
2. The SpMv and the Roofline Model
2.1. The SpMv Kernel
| Algorithm 1 Serially computed sparse matrix–vector multiplication (SpMv) with the sparse matrix A stored in CSR format. |
| Input:
Output: y
|
2.2. SpMv in FPGA
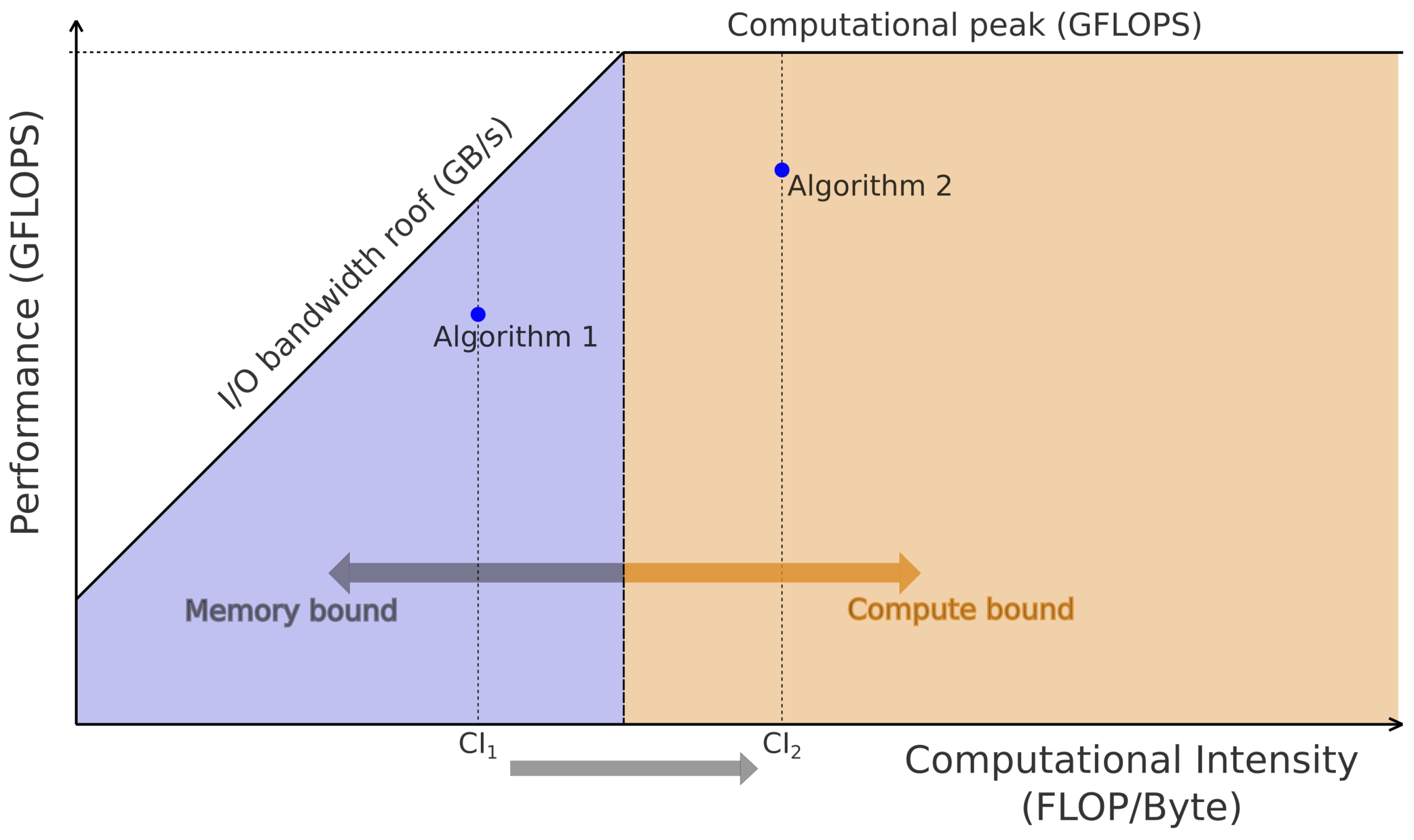
2.3. Roofline Model (RLM)
2.4. RLM in FPGAs
3. Implemented Kernel and RLM
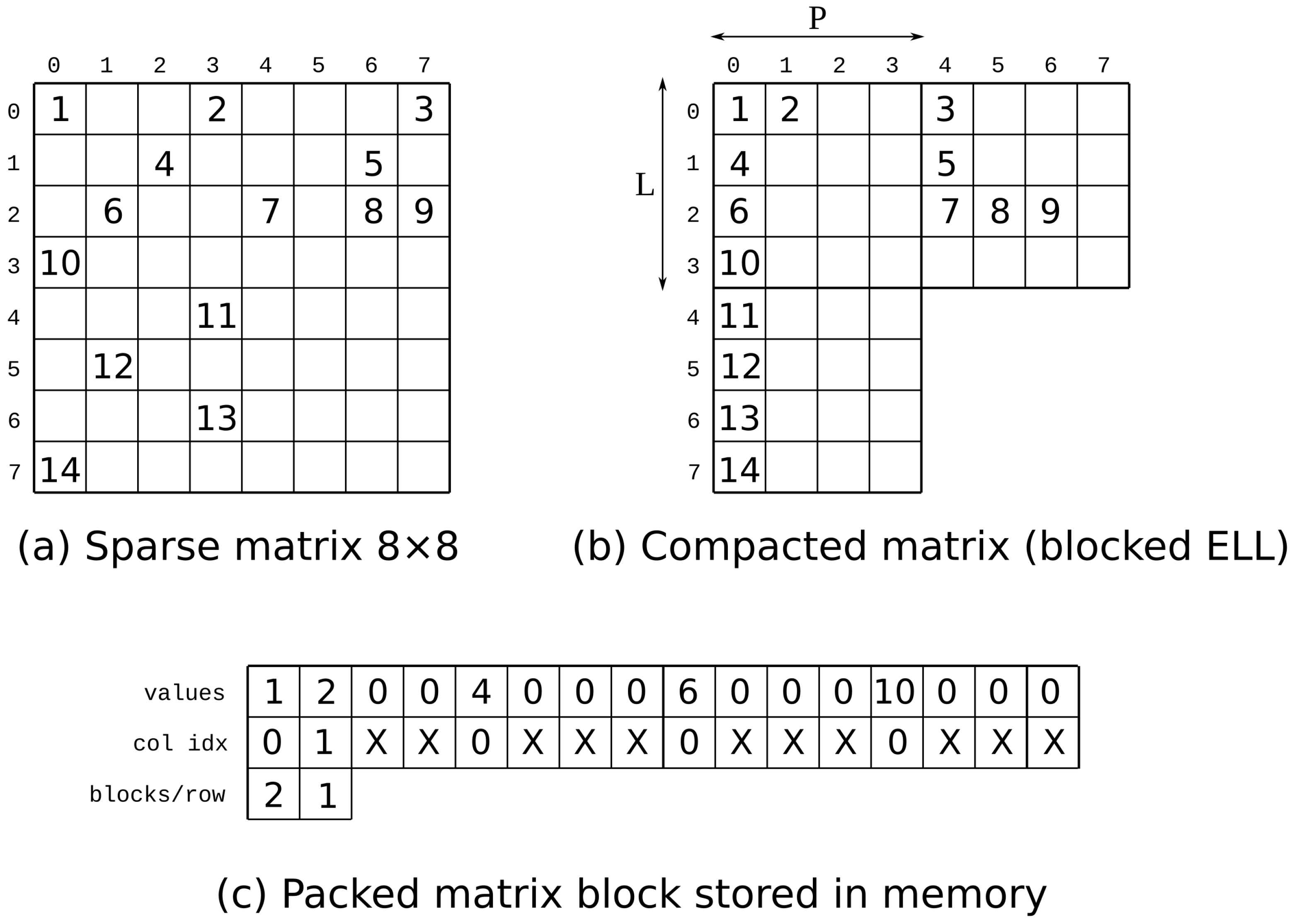
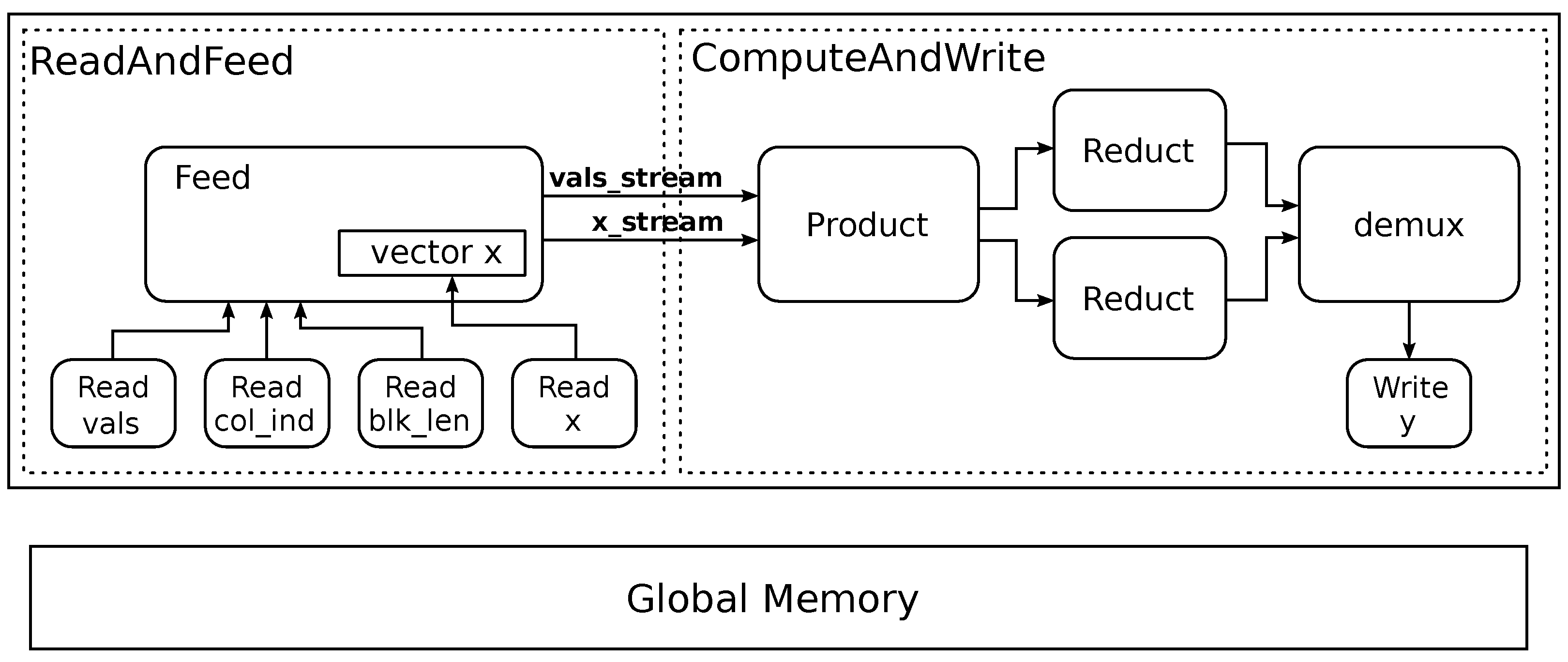
3.1. Implemented Kernel
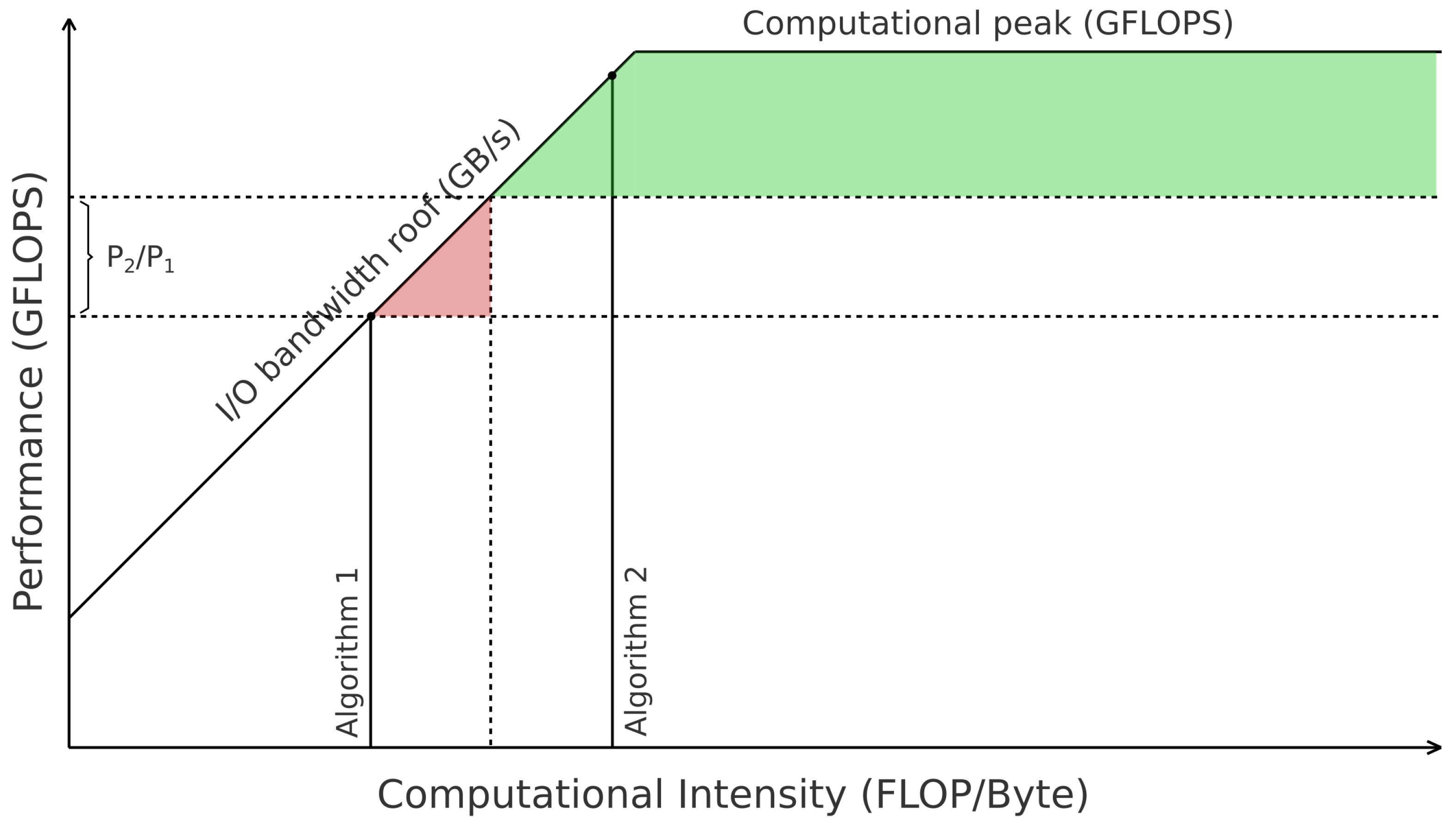
3.2. The RLM as a Guide to Optimizing the Performance of Blockwise SpMv
3.3. Extending the Proposal to Address Energy Consumption
4. Experimental Evaluation
4.1. Experimental Setup
- In the Alveo U50, we use the board’s internal sensors that provide current, voltage, and temperature readings while the kernel is running. The driver Xilinx Runtime (XRT) sends these values to the host.
- For the Intel processor, we measure CPU and memory consumption using RAPL (which estimates the dissipated power based on performance counters and a device power model).
4.2. Test Cases
4.3. Experimental Results
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kaxiras, S.; Martonosi, M. Computer Architecture Techniques for Power-Efficiency; Synthesis Lectures on Computer Architecture; Morgan & Claypool Publishers: Kentfield, CA, USA, 2008. [Google Scholar] [CrossRef]
- Ezzatti, P.; Quintana-Ortí, E.S.; Remón, A.; Saak, J. Power-aware computing. Concurr. Comput. Pract. Exp. 2019, 31, e5034. [Google Scholar] [CrossRef]
- Cong, J.; Lau, J.; Liu, G.; Neuendorffer, S.; Pan, P.; Vissers, K.; Zhang, Z. FPGA HLS Today: Successes, Challenges, and Opportunities. ACM Trans. Reconfig. Technol. Syst. 2022, 15, 1–42. [Google Scholar] [CrossRef]
- De Matteis, T.; de Fine Licht, J.; Hoefler, T. FBLAS: Streaming Linear Algebra on FPGA; IEEE Press: Piscateway, NJ, USA, 2020. [Google Scholar]
- Arora, A.; Anand, T.; Borda, A.; Sehgal, R.; Hanindhito, B.; Kulkarni, J.; John, L.K. CoMeFa: Compute-in-Memory Blocks for FPGAs. arXiv 2022, arXiv:arXiv.2203.12521. [Google Scholar]
- Que, Z.; Nakahara, H.; Nurvitadhi, E.; Boutros, A.; Fan, H.; Zeng, C.; Meng, J.; Tsoi, K.H.; Niu, X.; Luk, W. Recurrent Neural Networks With Column-Wise Matrix-Vector Multiplication on FPGAs. IEEE Trans. Very Large Scale Integr. Syst. 2022, 30, 227–237. [Google Scholar] [CrossRef]
- Kestur, S.; Davis, J.D.; Williams, O. BLAS Comparison on FPGA, CPU and GPU. In Proceedings of the 2010 IEEE Computer Society Annual Symposium on VLSI, Washington, DC, USA, 5–7 July 2010; pp. 288–293. [Google Scholar]
- Giefers, H.; Polig, R.; Hagleitner, C. Analyzing the energy-efficiency of dense linear algebra kernels by power-profiling a hybrid CPU/FPGA system. In Proceedings of the 2014 IEEE 25th International Conference on Application-Specific Systems, Architectures and Processors, Zurich, Switzerland, 18–20 June 2014; pp. 92–99. [Google Scholar]
- De Fine Licht, J.; Kwasniewski, G.; Hoefler, T. Flexible Communication Avoiding Matrix Multiplication on FPGA with High-Level Synthesis. In Proceedings of the 2020 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, New York, NY, USA, 23–25 February 2020; pp. 244–254. [Google Scholar] [CrossRef]
- Hill, K.; Craciun, S.; George, A.; Lam, H. Comparative analysis of OpenCL vs. HDL with image-processing kernels on Stratix-V FPGA. In Proceedings of the 2015 IEEE 26th International Conference on Application-specific Systems, Architectures and Processors (ASAP), Toronto, ON, Canada, 27–29 February 2015; pp. 189–193. [Google Scholar]
- Díaz, L.; Moreira, R.; Favaro, F.; Dufrechou, E.; Oliver, J.P. Energy Measurement Laboratory for Heterogeneous Hardware Evaluation. In Proceedings of the 2021 IEEE URUCON, Montevideo, Uruguay, 24–26 November 2021; pp. 268–272. [Google Scholar] [CrossRef]
- Mittal, S. A survey of FPGA-based accelerators for convolutional neural networks. Neural Comput. Appl. 2020, 32, 1109–1139. [Google Scholar] [CrossRef]
- Favaro, F.; Dufrechou, E.; Ezzatti, P.; Oliver, J.P. Exploring FPGA Optimizations to Compute Sparse Numerical Linear Algebra Kernels. In Proceedings of the ARC; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12083, pp. 258–268. [Google Scholar] [CrossRef]
- Favaro, F.; Oliver, J.P.; Ezzatti, P. Unleashing the computational power of FPGAs to efficiently perform SPMV operation. In Proceedings of the 40th International Conference of the Chilean Computer Science Society (SCCC 2021), La Serena, Chile, 15–19 November 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Wang, Z.; He, B.; Zhang, W.; Jiang, S. A performance analysis framework for optimizing OpenCL applications on FPGAs. In Proceedings of the 2016 IEEE International Symposium on High Performance Computer Architecture (HPCA), Barcelona, Spain, 12–16 March 2016; pp. 114–125. [Google Scholar] [CrossRef]
- Farahmand, F.; Ferozpuri, A.; Diehl, W.; Gaj, K. Minerva: Automated hardware optimization tool. In Proceedings of the 2017 International Conference on ReConFigurable Computing and FPGAs (ReConFig), Cancun, Mexico, 4–6 December 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Makrani, H.M.; Farahmand, F.; Sayadi, H.; Bondi, S.; Dinakarrao, S.P.; Homayoun, H.; Rafatirad, S. Pyramid: Machine Learning Framework to Estimate the Optimal Timing and Resource Usage of a High-Level Synthesis Design. In Proceedings of the 2019 29th International Conference on Field Programmable Logic and Applications (FPL), Los Alamitos, CA, USA, 15–19 September 2019; pp. 397–403. [Google Scholar] [CrossRef]
- Williams, S.; Waterman, A.; Patterson, D. Roofline: An Insightful Visual Performance Model for Multicore Architectures. Commun. ACM 2009, 52, 65–76. [Google Scholar] [CrossRef]
- Golub, G.H.; van Loan, C.F. Matrix Computations, 4th ed.; JHU Press: Baltimore, MA, USA, 2013. [Google Scholar]
- Fowers, J.; Ovtcharov, K.; Strauss, K.; Chung, E.S.; Stitt, G. A High Memory Bandwidth FPGA Accelerator for Sparse Matrix-Vector Multiplication. In Proceedings of the 2014 IEEE 22nd Annual International Symposium on Field-Programmable Custom Computing Machines, Boston, MA, USA, 11–13 March 2014; pp. 36–43. [Google Scholar] [CrossRef]
- Hosseinabady, M.; Nunez-Yanez, J.L. A Streaming Dataflow Engine for Sparse Matrix-Vector Multiplication using High-Level Synthesis. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2019, 39, 1272–1285. [Google Scholar] [CrossRef]
- Nguyen, T.; MacLean, C.; Siracusa, M.; Doerfler, D.; Wright, N.J.; Williams, S. FPGA-based HPC accelerators: An evaluation on performance and energy efficiency. Concurr. Comput. Pract. Exp. 2022, 34, e6570. [Google Scholar] [CrossRef]
- Du, Y.; Hu, Y.; Zhou, Z.; Zhang, Z. High-Performance Sparse Linear Algebra on HBM-Equipped FPGAs Using HLS: A Case Study on SpMV. In Proceedings of the 2022 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, Virtual Event, 27 February–1 March 2022. [Google Scholar]
- Xilinx Inc. Vitis SPARSE Library. 2020. Available online: https://xilinx.github.io/Vitis_Libraries/sparse/2020.2/index.html (accessed on 1 January 2023).
- da Silva, B.; Braeken, A.; D’Hollander, E.H.; Touhafi, A. Performance Modeling for FPGAs: Extending the Roofline Model with High-Level Synthesis Tools. Int. J. Reconfig. Comput. 2013, 2013, 428078. [Google Scholar] [CrossRef][Green Version]
- Yali, M.P. FPGA-Roofline: An Insightful Model for FPGA-based Hardware Accelerators in Modern Embedded Systems. Master’s Thesis, Faculty of the Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2014. [Google Scholar]
- Calore, E.; Schifano, S.F. Performance assessment of FPGAs as HPC accelerators using the FPGA Empirical Roofline. In Proceedings of the 2021 31st International Conference on Field-Programmable Logic and Applications (FPL), Dresden, Germany, 30 August–3 September 2021; pp. 83–90. [Google Scholar] [CrossRef]
- Panagou, I.; Gkeka, M.; Patras, A.; Lalis, S.; Antonopoulos, C.D.; Bellas, N. FPGA Roofline modeling and its Application to Visual SLAM. In Proceedings of the 2022 32nd International Conference on Field-Programmable Logic and Applications (FPL), Belfast, UK, 29 August–2 September 2022; pp. 130–135. [Google Scholar] [CrossRef]
- Diakite, D.; Gac, N.; Martelli, M. OpenCL FPGA Optimization guided by memory accesses and roofline model analysis applied to tomography acceleration. In Proceedings of the 2021 31st International Conference on Field-Programmable Logic and Applications (FPL), Dresden, Germany, 30 August–3 September 2021; pp. 109–114. [Google Scholar] [CrossRef]
- Nguyen, T.; Williams, S.; Siracusa, M.; MacLean, C.; Doerfler, D.; Wright, N.J. The Performance and Energy Efficiency Potential of FPGAs in Scientific Computing. In Proceedings of the 2020 IEEE/ACM Performance Modeling, Benchmarking and Simulation of High Performance Computer Systems (PMBS), Atlanta, GA, USA, 12 November 2020; pp. 8–19. [Google Scholar] [CrossRef]
- Siracusa, M.; Delsozzo, E.; Rabozzi, M.; Di Tucci, L.; Williams, S.; Sciuto, D.; Santambrogio, M.D. A Comprehensive Methodology to Optimize FPGA Designs via the Roofline Model. IEEE Trans. Comput. 2021, 71, 1903–1915. [Google Scholar] [CrossRef]
- Anzt, H.; Tomov, S.; Dongarra, J. Implementing a Sparse Matrix Vector Product for the SELL-C/SELL-C-o Formats on NVIDIA GPUs; Technical Report UT-EECS-14-727; University of Tennessee: Knoxville, TN, USA, 2014. [Google Scholar]
- Benner, P.; Ezzatti, P.; Quintana-Ortí, E.S.; Remón, A.; Silva, J.P. Tuning the Blocksize for Dense Linear Algebra Factorization Routines with the Roofline Model. In Proceedings of the Algorithms and Architectures for Parallel Processing—ICA3PP 2016 Collocated Workshops: SCDT, TAPEMS, BigTrust, UCER, DLMCS, Granada, Spain, 14–16 December 2016; pp. 18–29. [Google Scholar] [CrossRef]
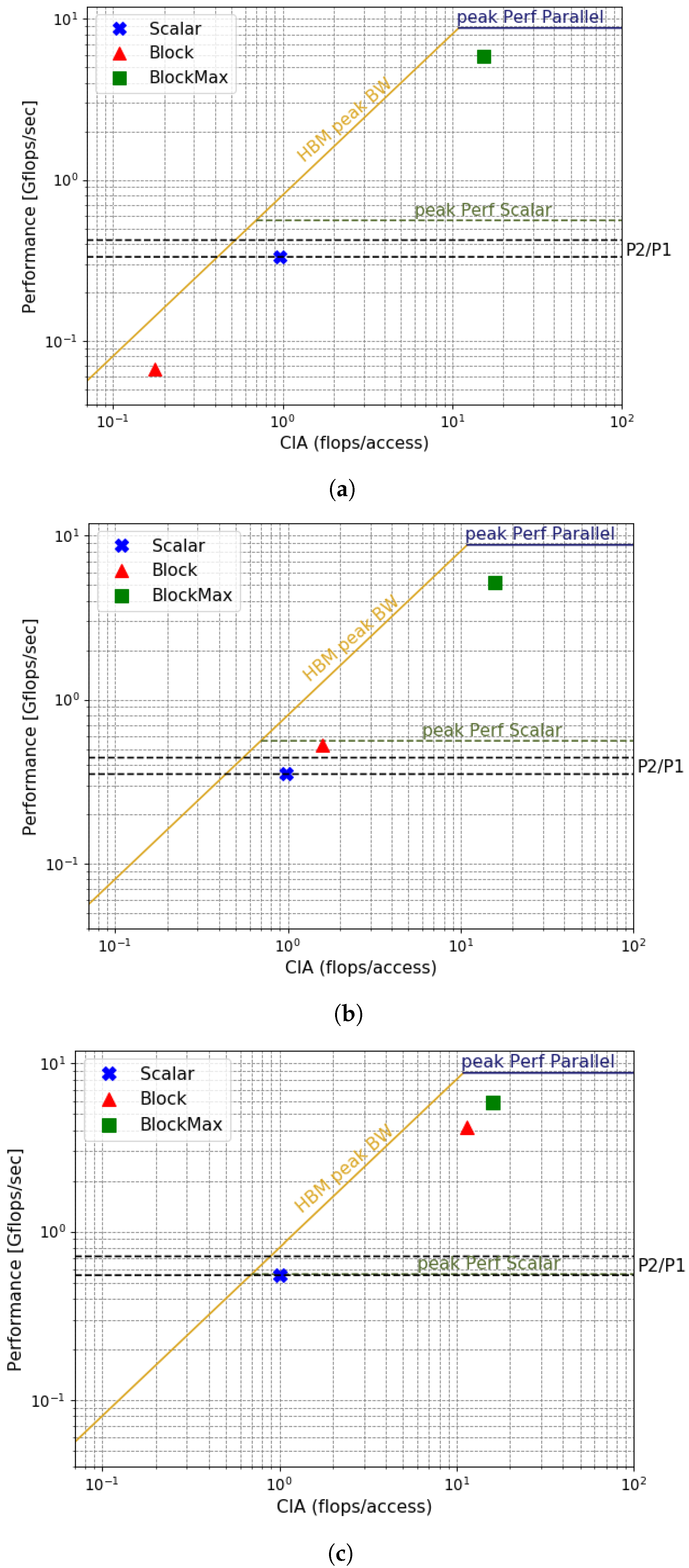
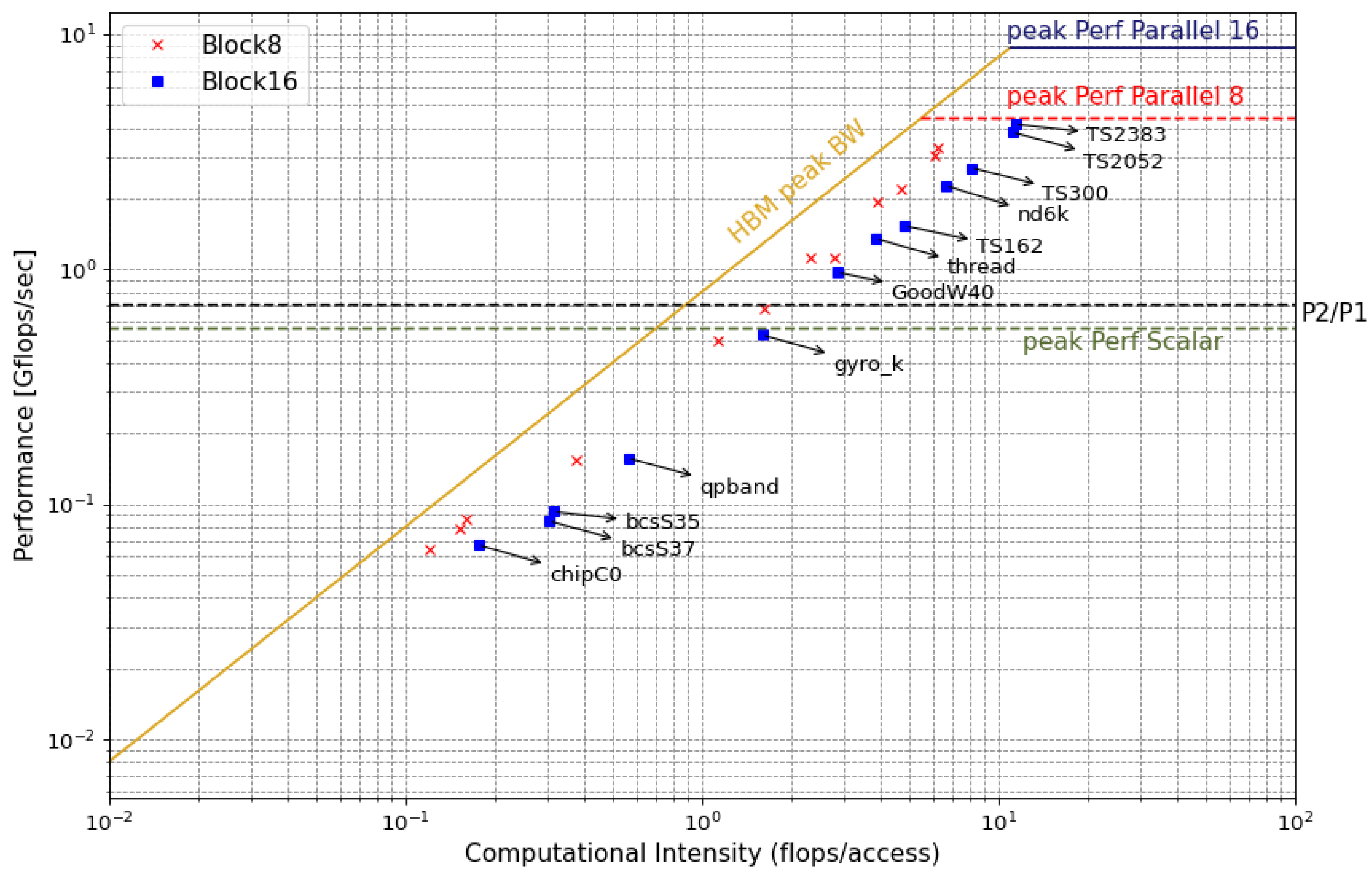
| Matrix | n | Avg. Density of Blocks (%) | |
|---|---|---|---|
| bcsS37 | 25,503 | 14,765 | 4 |
| bcsS35 | 30,237 | 18,211 | 4 |
| qpband | 20,000 | 30,000 | 5 |
| ex9 | 3363 | 51,417 | 21 |
| body4 | 17,546 | 69,742 | 6 |
| body6 | 19,366 | 77,057 | 6 |
| ted_B | 10,605 | 77,592 | 20 |
| ted_B_un | 10,605 | 77,592 | 20 |
| nasa2910 | 2910 | 88,603 | 24 |
| s3rmt3m3 | 5357 | 106,526 | 27 |
| s2rmq4m1 | 5489 | 143,300 | 34 |
| chipC0 | 20,082 | 281,150 | 1 |
| cbuckle | 13,681 | 345,098 | 31 |
| olafu | 16,146 | 515,651 | 33 |
| gyro_k | 17,361 | 519,260 | 10 |
| GoodW40 | 17,922 | 561,677 | 18 |
| bcsstk36 | 23,052 | 583,096 | 27 |
| msc23052 | 23,052 | 588,933 | 13 |
| msc10848 | 10,848 | 620,313 | 18 |
| raefsky4 | 19,779 | 674,195 | 27 |
| TS162 | 20,374 | 812,749 | 31 |
| nd3k | 9000 | 1,644,345 | 43 |
| thread | 29,736 | 2,249,892 | 24 |
| TS300 | 28,338 | 2,943,887 | 51 |
| nd6k | 18,000 | 3,457,658 | 42 |
| TS2052 | 25,626 | 6,761,100 | 70 |
| TS2383 | 38,120 | 16,171,169 | 71 |
| Matrix | MKL (ms) | Scalar (ms) | Block (ms) | MKL (mJ) | Scalar (mJ) | Block (mJ) |
|---|---|---|---|---|---|---|
| bcsS37 | 0.012 | 0.280 | 0.324 | 0.6 | 5.2 | 6.6 |
| bcsS35 | 0.012 | 0.331 | 0.366 | 0.6 | 6.2 | 7.5 |
| qpband | 0.017 | 0.258 | 0.356 | 0.8 | 4.8 | 7.3 |
| ex9 | 0.015 | 0.409 | 0.195 | 0.7 | 7.6 | 4.2 |
| body4 | 0.024 | 0.414 | 0.698 | 1.1 | 7.7 | 14.9 |
| body6 | 0.025 | 0.434 | 0.791 | 1.2 | 8.1 | 16.9 |
| ted_B | 0.031 | 0.625 | 0.285 | 1.5 | 11.7 | 6.1 |
| ted_B_un | 0.037 | 0.686 | 0.297 | 1.7 | 12.8 | 6.3 |
| nasa2910 | 0.022 | 0.890 | 0.243 | 1.0 | 16.6 | 5.2 |
| s3rmt3m3 | 0.026 | 0.595 | 0.259 | 1.2 | 11.1 | 5.5 |
| s2rmq4m1 | 0.028 | 0.686 | 0.273 | 1.2 | 12.8 | 5.8 |
| chipC0 | 0.067 | 1.576 | 7.772 | 3.1 | 29.4 | 167.1 |
| cbuckle | 0.073 | 1.775 | 0.738 | 3.2 | 33.1 | 15.7 |
| olafu | 0.117 | 2.527 | 1.008 | 5.3 | 47.1 | 21.5 |
| gyro_k | 0.097 | 2.754 | 1.837 | 4.7 | 51.4 | 39.2 |
| GoodW40 | 0.104 | 4.064 | 1.078 | 5.0 | 75.9 | 23.1 |
| bcsstk36 | 0.130 | 3.014 | 1.240 | 6.1 | 56.2 | 26.5 |
| msc23052 | 0.183 | 3.052 | 2.097 | 8.5 | 56.9 | 44.7 |
| msc10848 | 0.181 | 3.546 | 1.703 | 8.2 | 66.1 | 36.3 |
| raefsky4 | 0.125 | 3.097 | 1.369 | 6.3 | 57.7 | 29.2 |
| TS162 | 0.216 | 3.140 | 0.991 | 10.4 | 58.6 | 21.0 |
| nd3k | 0.322 | 6.755 | 1.841 | 15.9 | 126.0 | 39.3 |
| thread | 0.448 | 11.120 | 3.102 | 23.5 | 207.9 | 67.5 |
| TS300 | 0.986 | 10.290 | 2.024 | 49.3 | 192.3 | 43.7 |
| nd6k | 0.761 | 13.962 | 2.839 | 40.1 | 261.4 | 62.3 |
| TS2052 | 2.839 | 23.093 | 3.284 | 139.4 | 431.2 | 72.1 |
| TS2383 | 6.411 | 54.543 | 7.253 | 323.7 | 1019.5 | 159.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Favaro, F.; Dufrechou, E.; Oliver, J.P.; Ezzatti, P. Optimizing the Performance of the Sparse Matrix–Vector Multiplication Kernel in FPGA Guided by the Roofline Model. Micromachines 2023, 14, 2030. https://doi.org/10.3390/mi14112030
Favaro F, Dufrechou E, Oliver JP, Ezzatti P. Optimizing the Performance of the Sparse Matrix–Vector Multiplication Kernel in FPGA Guided by the Roofline Model. Micromachines. 2023; 14(11):2030. https://doi.org/10.3390/mi14112030
Chicago/Turabian StyleFavaro, Federico, Ernesto Dufrechou, Juan P. Oliver, and Pablo Ezzatti. 2023. "Optimizing the Performance of the Sparse Matrix–Vector Multiplication Kernel in FPGA Guided by the Roofline Model" Micromachines 14, no. 11: 2030. https://doi.org/10.3390/mi14112030
APA StyleFavaro, F., Dufrechou, E., Oliver, J. P., & Ezzatti, P. (2023). Optimizing the Performance of the Sparse Matrix–Vector Multiplication Kernel in FPGA Guided by the Roofline Model. Micromachines, 14(11), 2030. https://doi.org/10.3390/mi14112030






