MEMS Differential Pressure Sensor with Dynamic Pressure Canceler for Precision Altitude Estimation
Abstract
:1. Introduction
2. Materials and Methods
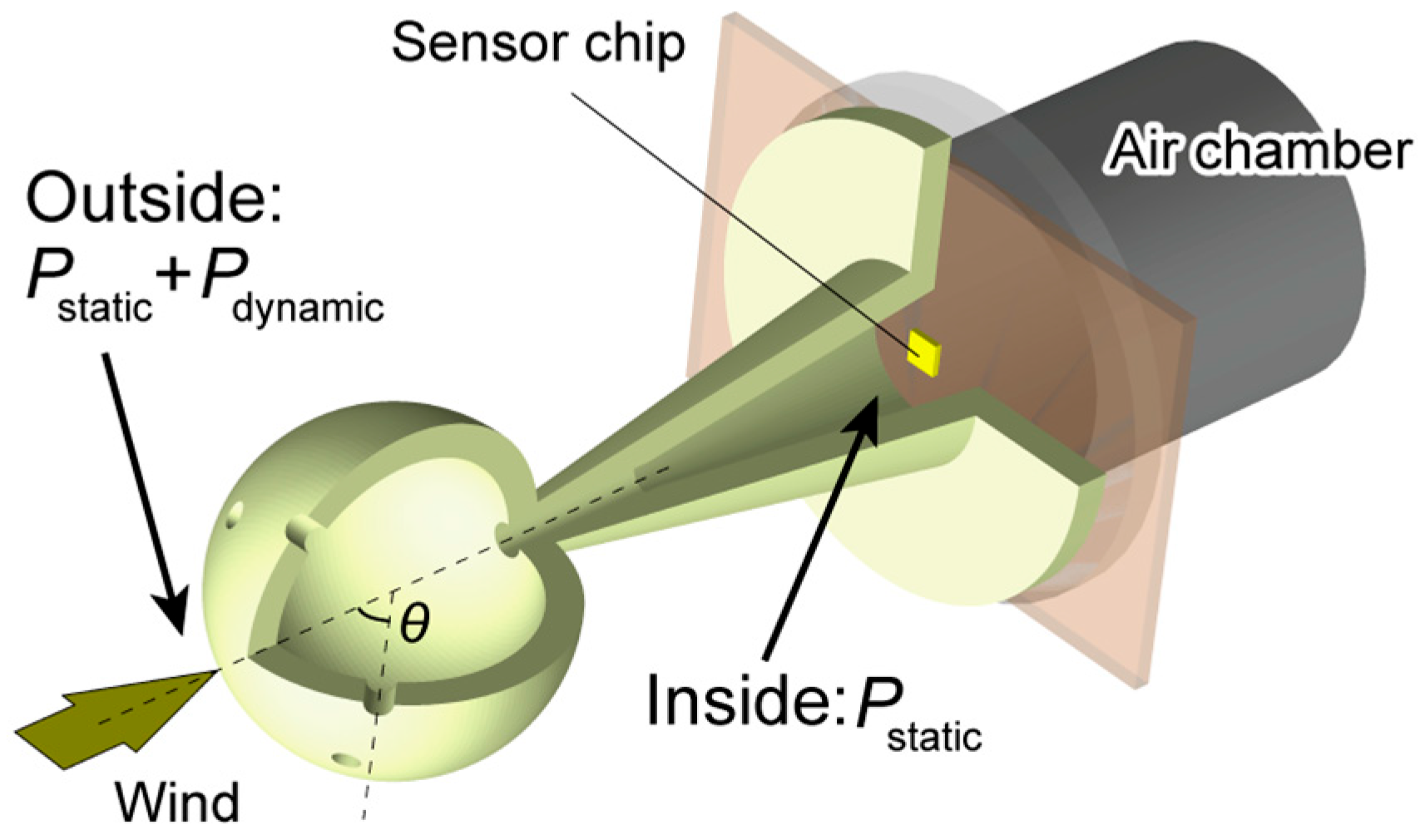
2.1. Theory and Requirements
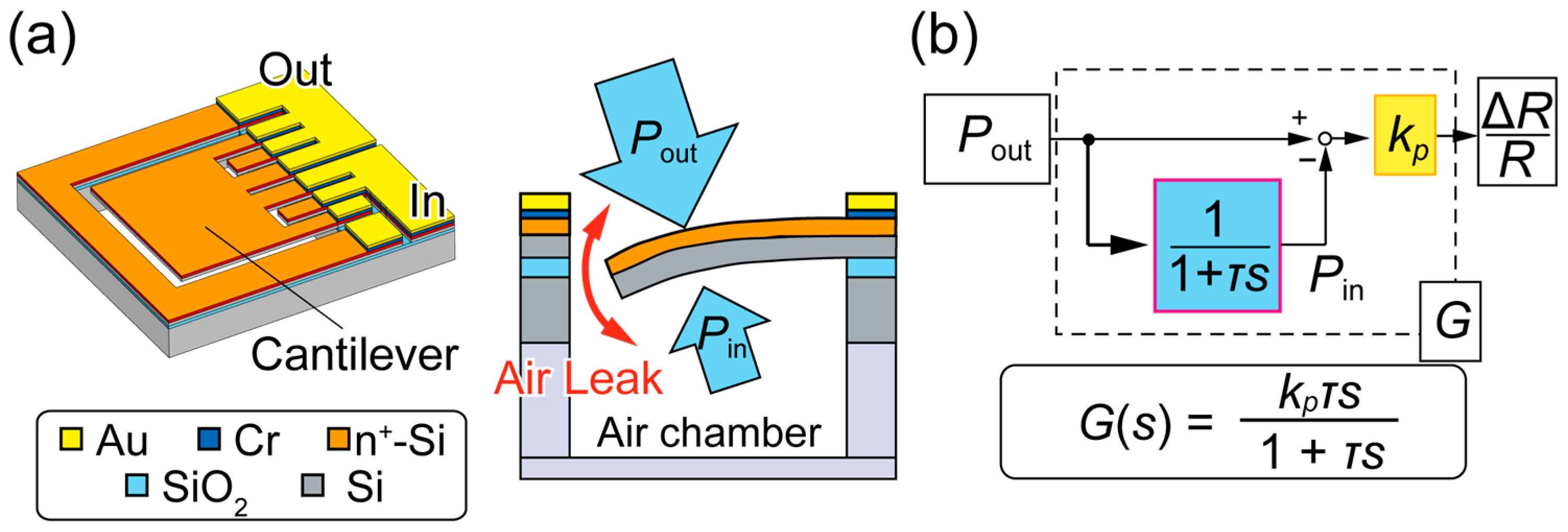
2.2. MEMS Pressure Sensor Element
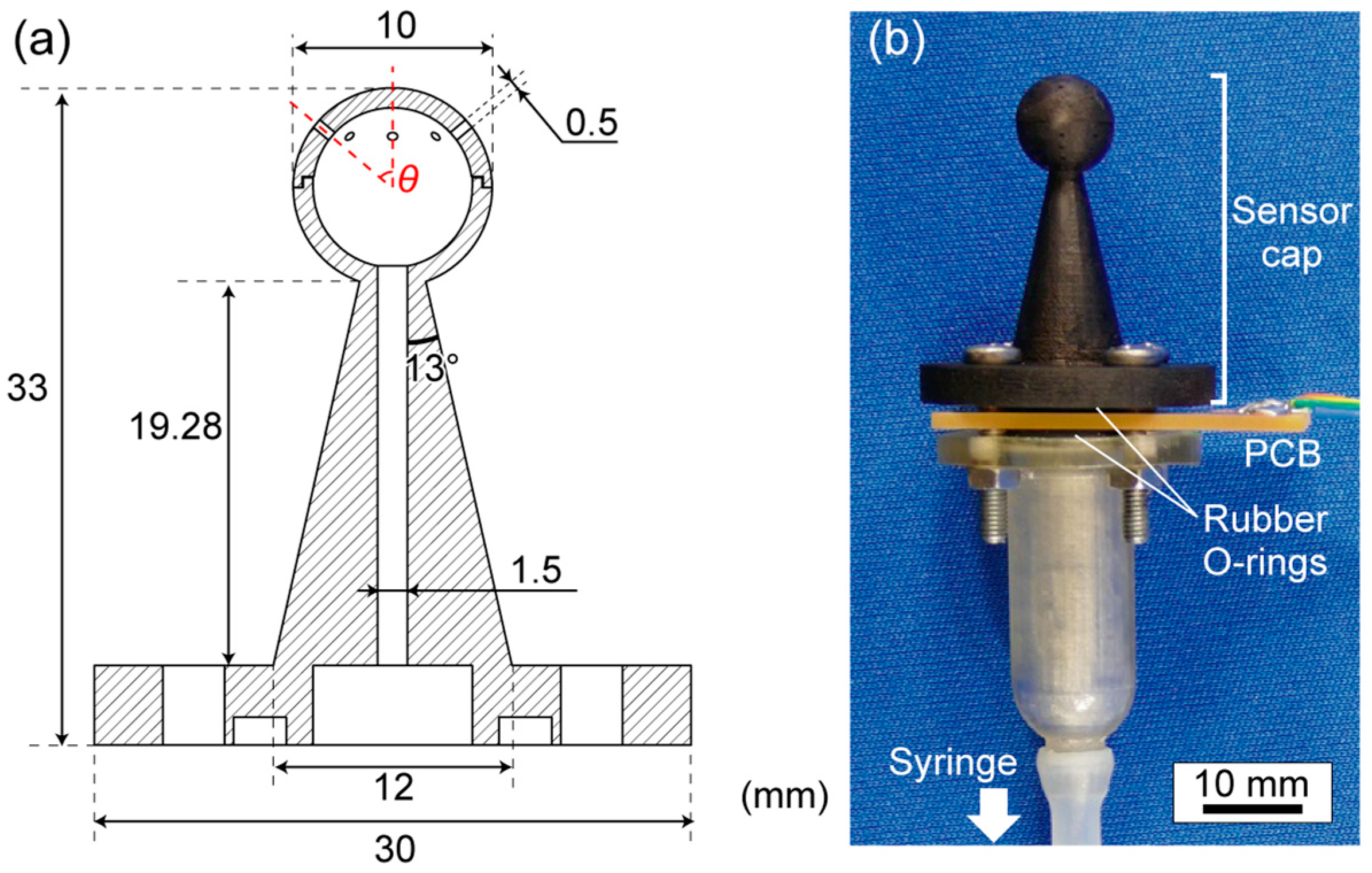
2.3. Sensor Cap
2.4. Discrete Transfer Function Model for Height Estimation
3. Results
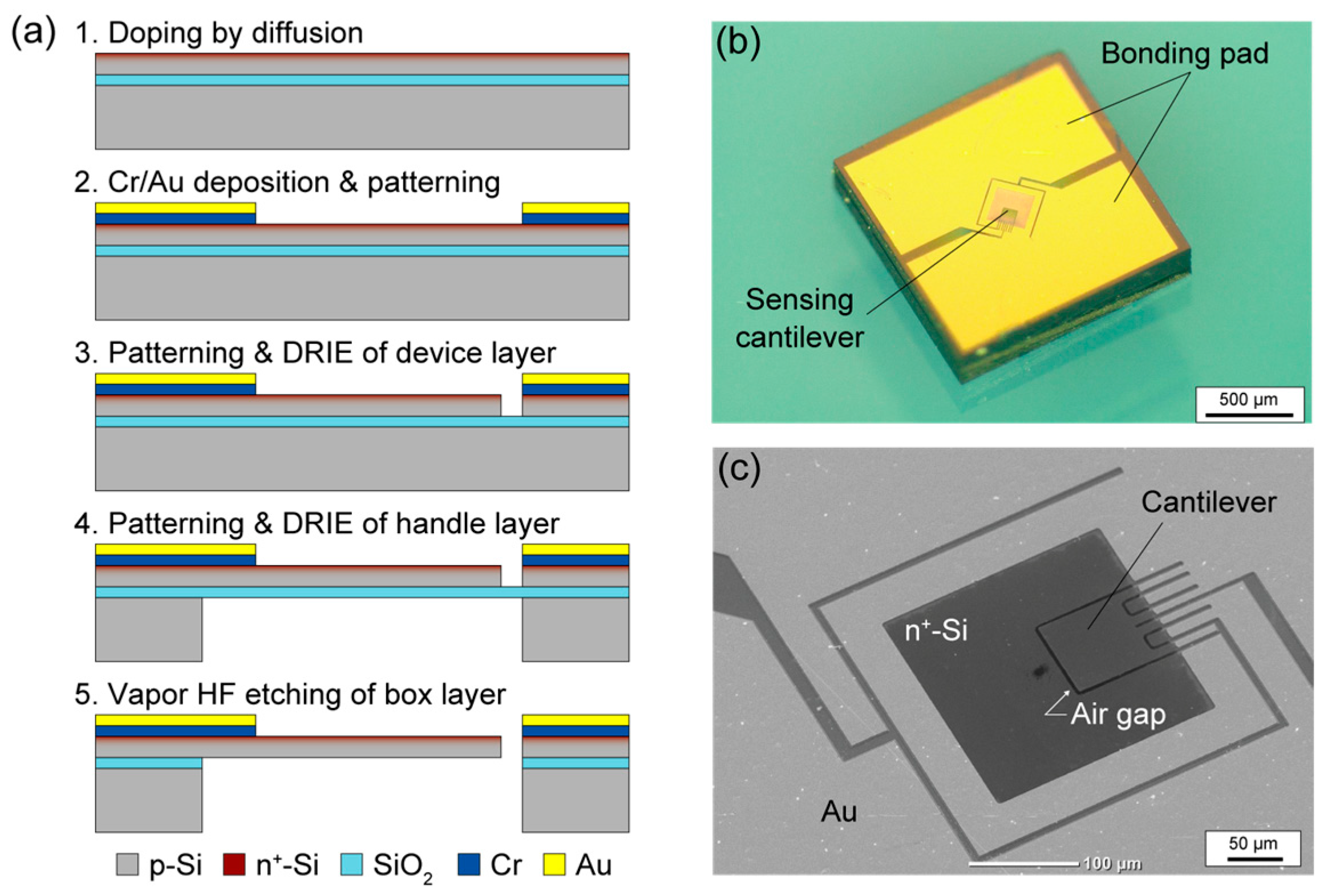
3.1. Fabrication of Sensing Elements
3.2. Sensor System Development
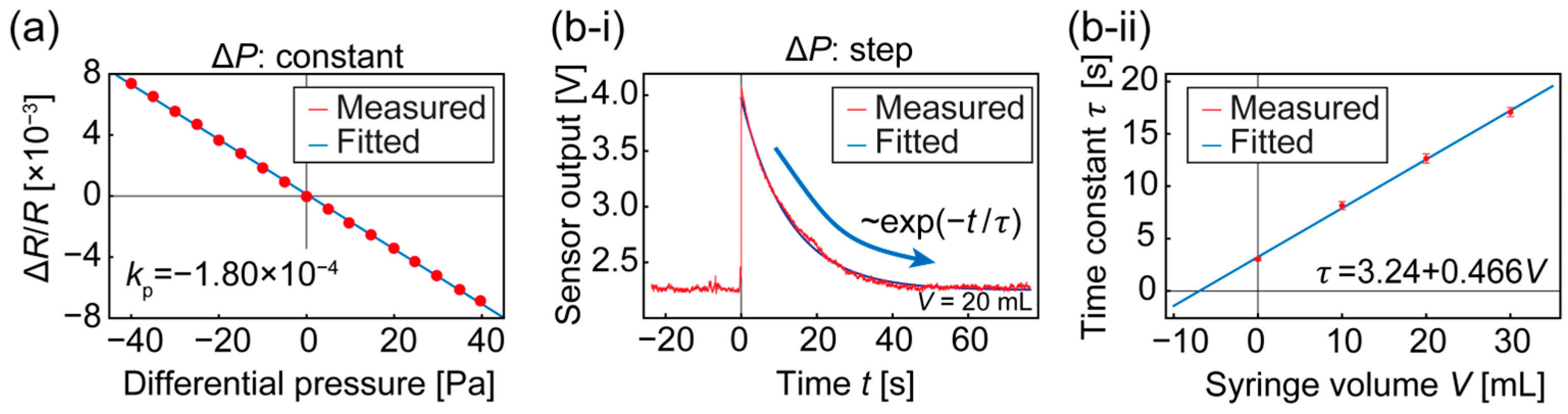
3.3. Sensor System Characterization
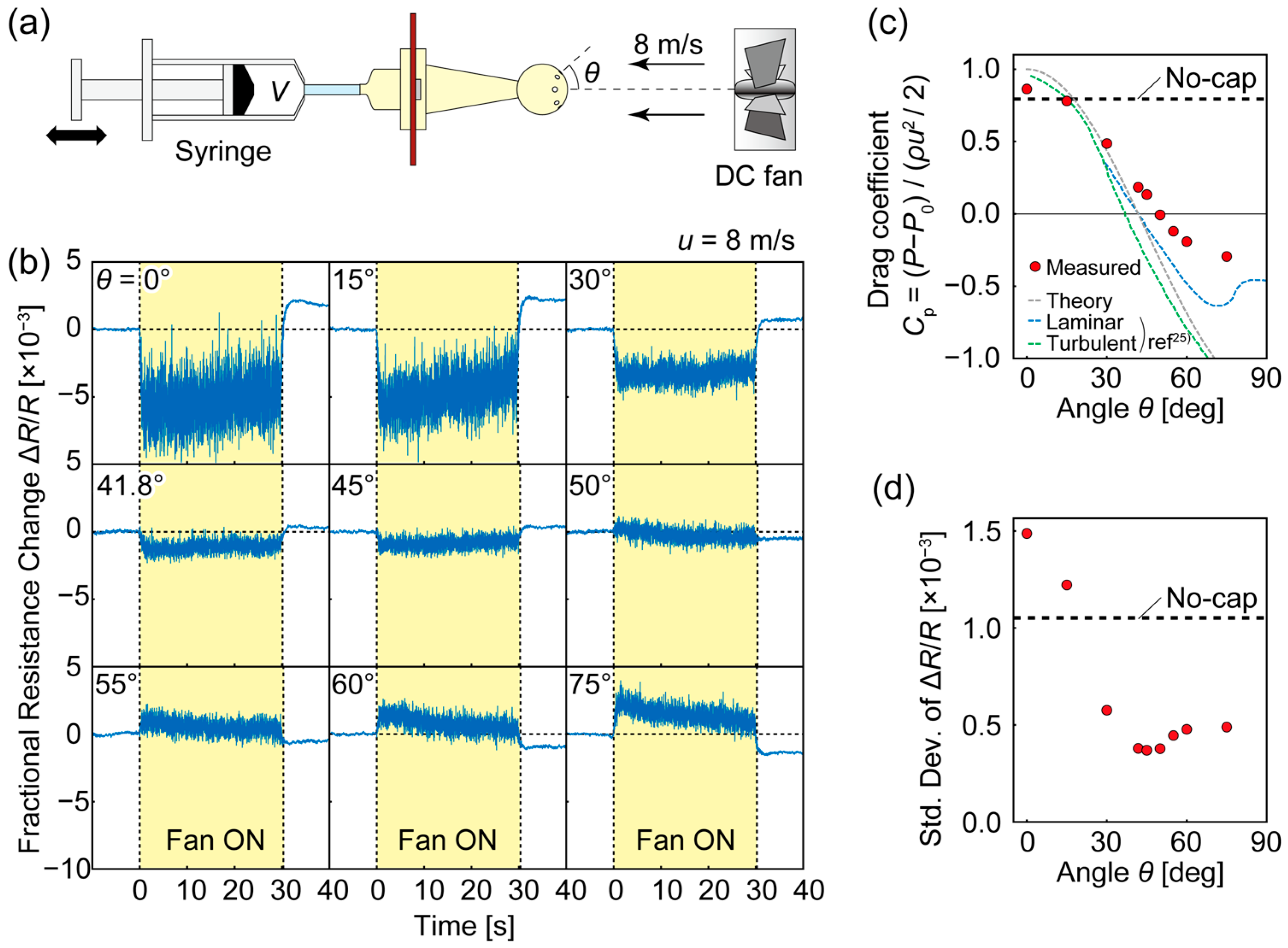
3.4. Evaluation of the Cap
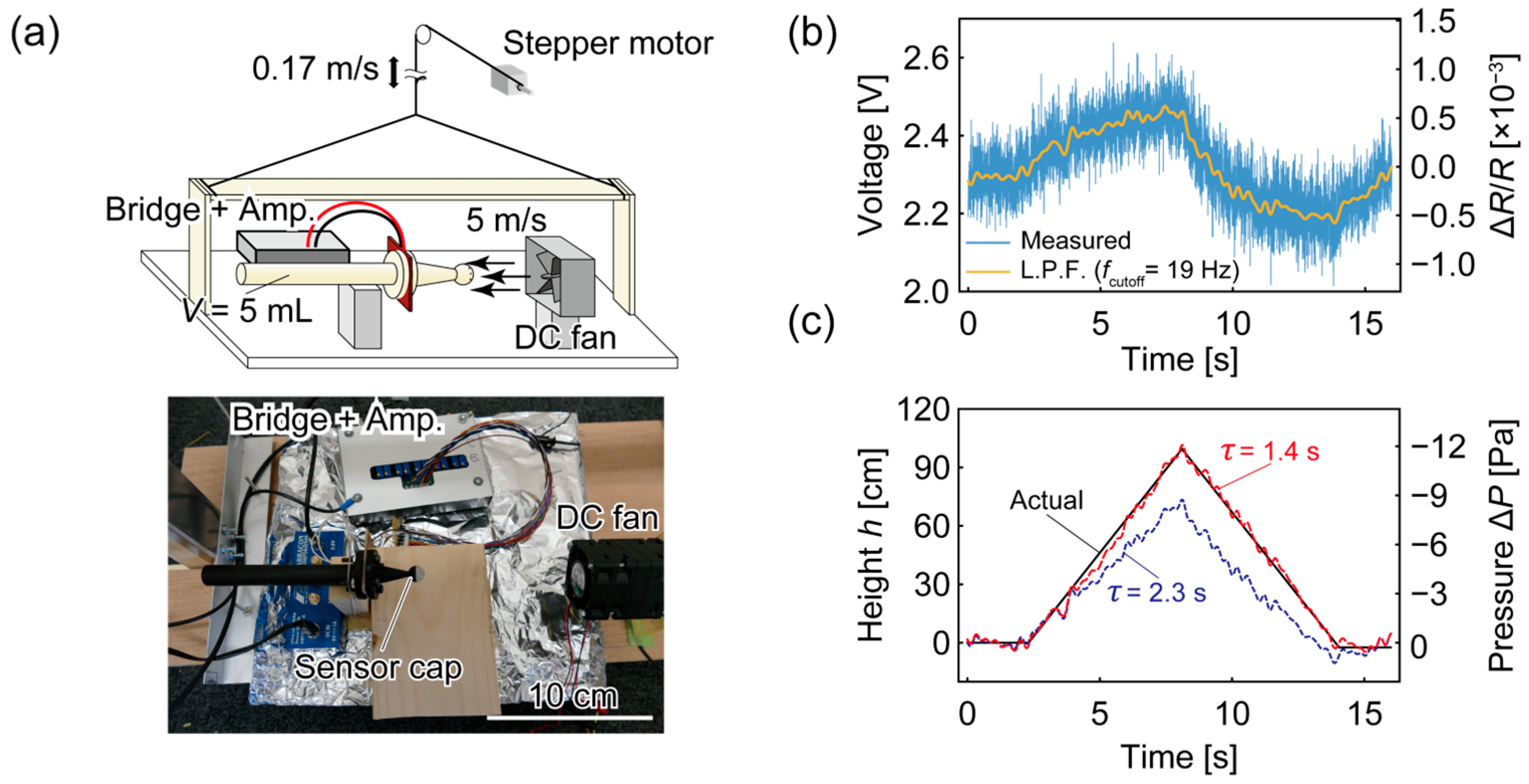
3.5. Height Estimation Method and Demonstration
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bandari, S.; Devi, L.N. An Optimal UAV Height Localization for Maximum Target Coverage Using Improved Deer Hunting Optimization Algorithm. Int. J. Intell. Robot Appl. 2022, 6, 773–790. [Google Scholar] [CrossRef]
- Tanigawa, M.; Luinge, H.; Schipper, L.; Slycke, P. Drift-Free Dynamic Height Sensor Using MEMS IMU Aided by MEMS Pressure Sensor. In Proceedings of the 2008 5th Workshop on Positioning, Navigation and Communication, Hannover, Germany, 27 March 2008; pp. 191–196. [Google Scholar]
- Son, Y.; Oh, S. A Barometer-IMU Fusion Method for Vertical Velocity and Height Estimation. In Proceedings of the 2015 IEEE Sensors, Busan, Republic of Korea, 1–4 November 2015; pp. 1–4. [Google Scholar]
- Dogru, S.; Marques, L. Pursuing Drones with Drones Using Millimeter Wave Radar. IEEE Robot Autom. Lett. 2020, 5, 4156–4163. [Google Scholar] [CrossRef]
- Rai, P.K.; Kumar, A.; Khan, M.Z.A.; Soumya, J.; Cenkeramaddi, L.R. Angle and Height Estimation Technique for Aerial Vehicles Using MmWave FMCW Radar. In Proceedings of the 2021 International Conference on COMmunication Systems and NETworkS, COMSNETS 2021, Bangalore, India, 5–9 January 2021; pp. 104–108. [Google Scholar]
- Wilson, A.N.; Kumar, A.; Jha, A.; Cenkeramaddi, L.R. Embedded Sensors, Communication Technologies, Computing Platforms and Machine Learning for UAVs: A Review. IEEE Sens. J. 2022, 22, 1807–1826. [Google Scholar] [CrossRef]
- Jung, I.-K.; Lacroix, S. High Resolution Terrain Mapping Using Low Attitude Aerial Stereo Imagery. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003; Volume 2, pp. 946–951. [Google Scholar]
- Meingast, M.; Geyer, C.; Sastry, S. Vision Based Terrain Recovery for Landing Unmanned Aerial Vehicles. In Proceedings of the Proceedings of the IEEE Conference on Decision and Control, Nassau, Bahamas, 14–17 December 2004; Volume 2, pp. 1670–1675. [Google Scholar]
- Qin, L.; Li, Y. Significant Wave Height Estimation Using Multi-Satellite Observations from GNSS-R. Remote Sens. 2021, 13, 4806. [Google Scholar] [CrossRef]
- Herbers, T.H.C.; Jessen, P.F.; Janssen, T.T.; Colbert, D.B.; MacMahan, J.H. Observing Ocean Surface Waves with GPS-Tracked Buoys. J. Atmos. Ocean Technol. 2012, 29, 944–959. [Google Scholar] [CrossRef]
- Doong, D.J.; Lee, B.C.; Kao, C.C. Wave Measurements Using GPS Velocity Signals. Sensors 2011, 11, 1043–1058. [Google Scholar] [CrossRef] [PubMed]
- del Rosario, M.B.; Redmond, S.J.; Lovell, N.H. Tracking the Evolution of Smartphone Sensing for Monitoring Human Movement. Sensors 2015, 15, 18901–18933. [Google Scholar] [CrossRef]
- Sabatini, A.M.; Genovese, V. A Sensor Fusion Method for Tracking Vertical Velocity and Height Based on Inertial and Barometric Altimeter Measurements. Sensors 2014, 14, 13324–13347. [Google Scholar] [CrossRef]
- Kumar, S.S.; Tanwar, A. Development of a MEMS-Based Barometric Pressure Sensor for Micro Air Vehicle (MAV) Altitude Measurement. Microsyst. Technol. 2020, 26, 901–912. [Google Scholar] [CrossRef]
- Li, Y.; Gao, Z.; He, Z.; Zhang, P.; Chen, R.; El-Sheimy, N. Multi-Sensor Multi-Floor 3D Localization With Robust Floor Detection. IEEE Access 2018, 6, 76689–76699. [Google Scholar] [CrossRef]
- Grevemeyer, I.; Herber, R.; Essen, H.-H. Microseismological Evidence for a Changing Wave Climate in the Northeast Atlantic Ocean. Nature 2000, 408, 349–352. [Google Scholar] [CrossRef] [PubMed]
- Minh-Dung, N.; Takahashi, H.; Uchiyama, T.; Matsumoto, K.; Shimoyama, I. A Barometric Pressure Sensor Based on the Air-Gap Scale Effect in a Cantilever. Appl. Phys. Lett. 2013, 103, 4824027. [Google Scholar] [CrossRef]
- Watanabe, R.; Minh-Dung, N.; Takahashi, H.; Takahata, T.; Matsumoto, K.; Shimoyama, I. Fusion of Cantilever and Diaphragm Pressure Sensors According to Frequency Characteristics. In Proceedings of the 2015 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Estoril, Portugal, 18–22 January 2015; pp. 212–214. [Google Scholar]
- Wada, R.; Takahashi, H. Time Response Characteristics of a Highly Sensitive Barometric Pressure Change Sensor Based on MEMS Piezoresistive Cantilevers. Jpn. J. Appl. Phys. 2020, 59, 070906. [Google Scholar] [CrossRef]
- Takahashi, H.; Dung, N.M.; Matsumoto, K.; Shimoyama, I. Differential Pressure Sensor Using a Piezoresistive Cantilever. J. Micromech. Microeng. 2012, 22, 055015. [Google Scholar] [CrossRef]
- World Meteorological Organization. Guide to Instruments and Methods of Observation (WMO-No. 8) 2021 Edition—Volume III: Observing Systems; World Meteorological Organization: Geneva, Switzerland, 2021. [Google Scholar]
- Lanzinger, E.; Schubotz, K. A Laboratory Intercomparison of Static Pressure Heads; World Meteorological Organization: Geneva, Switzerland, 2012; Volume 16. [Google Scholar]
- National Oceanic and Atmospheric Administration; National Aeronautics and Space Administration; United States Air Force. U.S. Standard Atmosphere, 1976; U.S. Goverment Publishing Office: Washington, DC, USA, 1976. [Google Scholar]
- Kundu, P.K.; Cohen, I.M.; Dowling, D.R. Fluid Mechanics, 5th ed.; Elsevier: Cambridge, MA, USA, 2012; ISBN 9780123821003. [Google Scholar]
- Fox, R.W.; Pritchard, P.J.; McDonald, A.T. Introduction to Fluid Mechanics, 7th ed.; Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Qorvo DWM1000—Qorvo. Available online: https://www.qorvo.com/products/p/DWM1000 (accessed on 1 August 2023).
- TDSR UWB Module—Products—TDSR. Available online: https://tdsr-uwb.com/uwb-module/ (accessed on 1 August 2023).
- Huang, Z.C.; Yeh, C.Y.; Tseng, K.H.; Hsu, W.Y. A UAV-RTK Lidar System for Wave and Tide Measurements in Coastal Zones. J. Atmos. Ocean Technol. 2018, 35, 1557–1570. [Google Scholar] [CrossRef]
- Romero-Andrade, R.; Trejo-Soto, M.E.; Vázquez-Ontiveros, J.R.; Hernández-Andrade, D.; Cabanillas-Zavala, J.L. Sampling Rate Impact on Precise Point Positioning with a Low-Cost Gnss Receiver. Appl. Sci. 2021, 11, 7669. [Google Scholar] [CrossRef]
- Marvelmind. Marvelmind Indoor Navigation System—Operating Manual. Available online: https://marvelmind.com/pics/marvelmind_navigation_system_manual.pdf (accessed on 14 October 2023).
- Nguyen, A. MmWave Radar Sensors: Object Versus Range. Available online: https://www.ti.com/jp/lit/pdf/swra593 (accessed on 14 October 2023).
- UV Verification Services Inc. RF Exposure Analysis for Millimeter Wave Radar Sensor Development Boards. Available online: https://dev.ti.com/tirex/explore/node?node=A__AIRQGZEx5ol-gjk4J66SuQ__radar_toolbox__1AslXXD__LATEST (accessed on 14 October 2023).
- OMRON. 2SMPB-02B Digital Barometric Pressure Sensor. Available online: https://components.omron.com/us-en/asset/54931 (accessed on 14 October 2023).
- Chapman, P.W.; Tufte, O.N.; Zook, J.D.; Long, D. Electrical Properties of Heavily Doped Silicon. J. Appl. Phys. 1963, 34, 3291–3295. [Google Scholar] [CrossRef]
- Hagiwara, T.; Takahashi, H.; Takahata, T.; Shimoyama, I. Ground Effect Measurement of Butterfly Take-Off. In Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018; pp. 832–835. [Google Scholar]
| Method | Range | Differential Accuracy |
|---|---|---|
| Ultrasound ToF [30] | 30 m | 2 cm |
| RF ToF [27] | 40 m | 2.1 cm |
| Radar [31,32] | ≈200 m | <5 cm |
| Absolute Pressure Sensor [33] | −730 m–9500 m 1 | 23 cm 2 |
| This Work | 200 m 3 | 2.8 cm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasunaga, S.; Takahashi, H.; Takahata, T.; Shimoyama, I. MEMS Differential Pressure Sensor with Dynamic Pressure Canceler for Precision Altitude Estimation. Micromachines 2023, 14, 1941. https://doi.org/10.3390/mi14101941
Yasunaga S, Takahashi H, Takahata T, Shimoyama I. MEMS Differential Pressure Sensor with Dynamic Pressure Canceler for Precision Altitude Estimation. Micromachines. 2023; 14(10):1941. https://doi.org/10.3390/mi14101941
Chicago/Turabian StyleYasunaga, Shun, Hidetoshi Takahashi, Tomoyuki Takahata, and Isao Shimoyama. 2023. "MEMS Differential Pressure Sensor with Dynamic Pressure Canceler for Precision Altitude Estimation" Micromachines 14, no. 10: 1941. https://doi.org/10.3390/mi14101941
APA StyleYasunaga, S., Takahashi, H., Takahata, T., & Shimoyama, I. (2023). MEMS Differential Pressure Sensor with Dynamic Pressure Canceler for Precision Altitude Estimation. Micromachines, 14(10), 1941. https://doi.org/10.3390/mi14101941








