A Design Methodology for Fault-Tolerant Neuromorphic Computing Using Bayesian Neural Network
Abstract
:1. Introduction
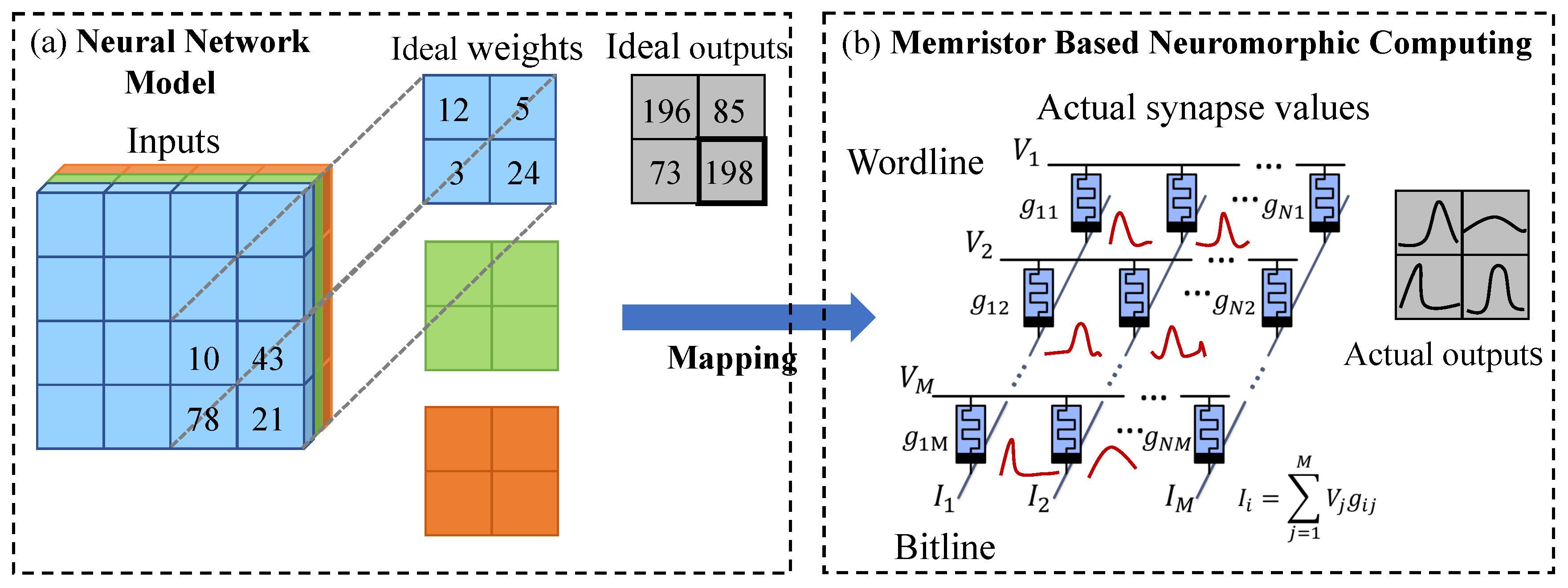
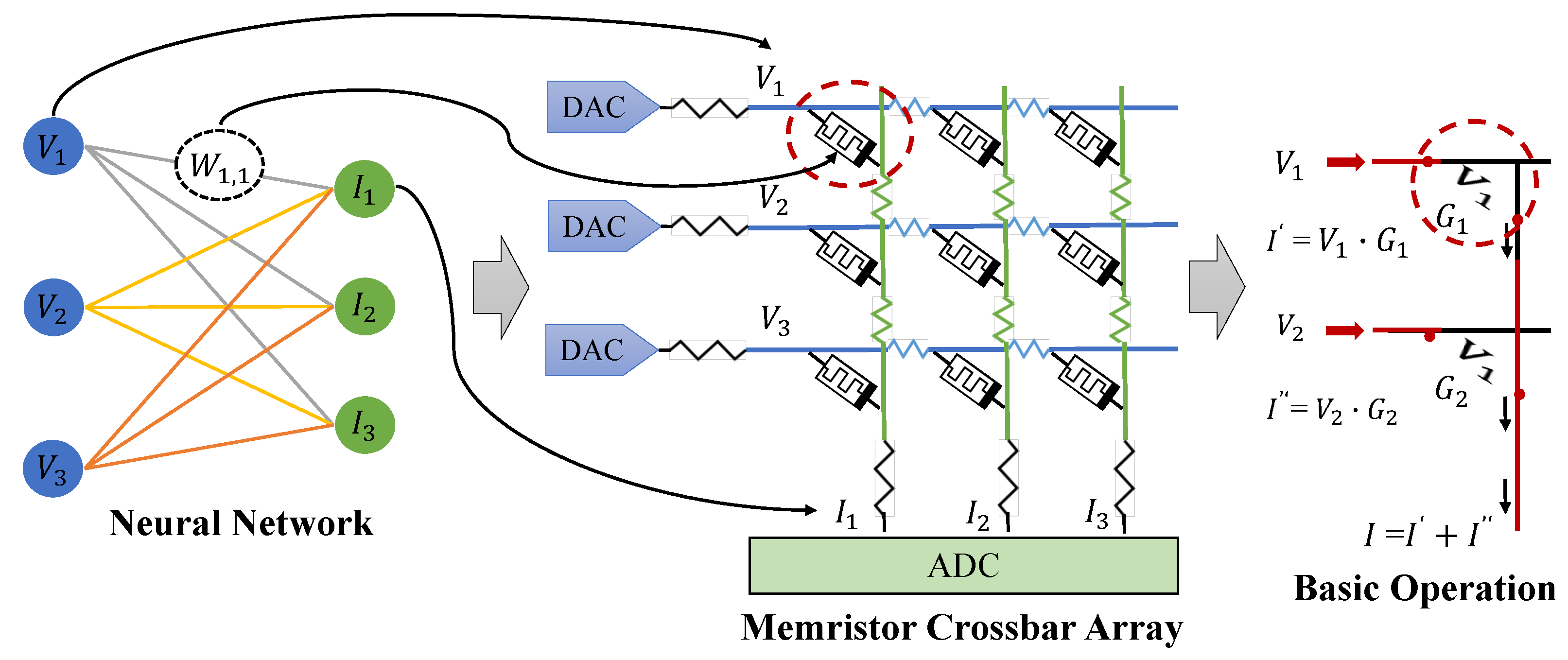
2. Background and Related Work
3. Preliminary Work on Bayesian Neural Networks
4. Proposed Methodology
4.1. Overview
- Log-normal variational posterior: We introduce a log-normal variational posterior to quantify and characterize the inevitable deviations in synapse weights represented by memristor crossbars, attempting to accommodate process variations and noise through algorithmic training.
- Variational Bayesian inference: We employ variational inference to find the network parameters of the log-normal variational posterior that minimize the KL divergence between the variational posterior and the true Bayesian posterior of weights.
4.2. Log-Normal Variational Posterior
4.3. Variational Bayesian Inference
- 1.
- Sample .
- 2.
- Let the network parameters be , where denotes the expected weight values that are error-free.
- 3.
- Let the variational parameters be .
- 4.
- Let the objective function be .
- 5.
- Calculate the gradient with respect to the parameter :
- 6.
- Calculate the gradient with the standard deviation parameter :
- 7.
- Update the variational parameters and .
5. Evaluation
5.1. Experimental Setup
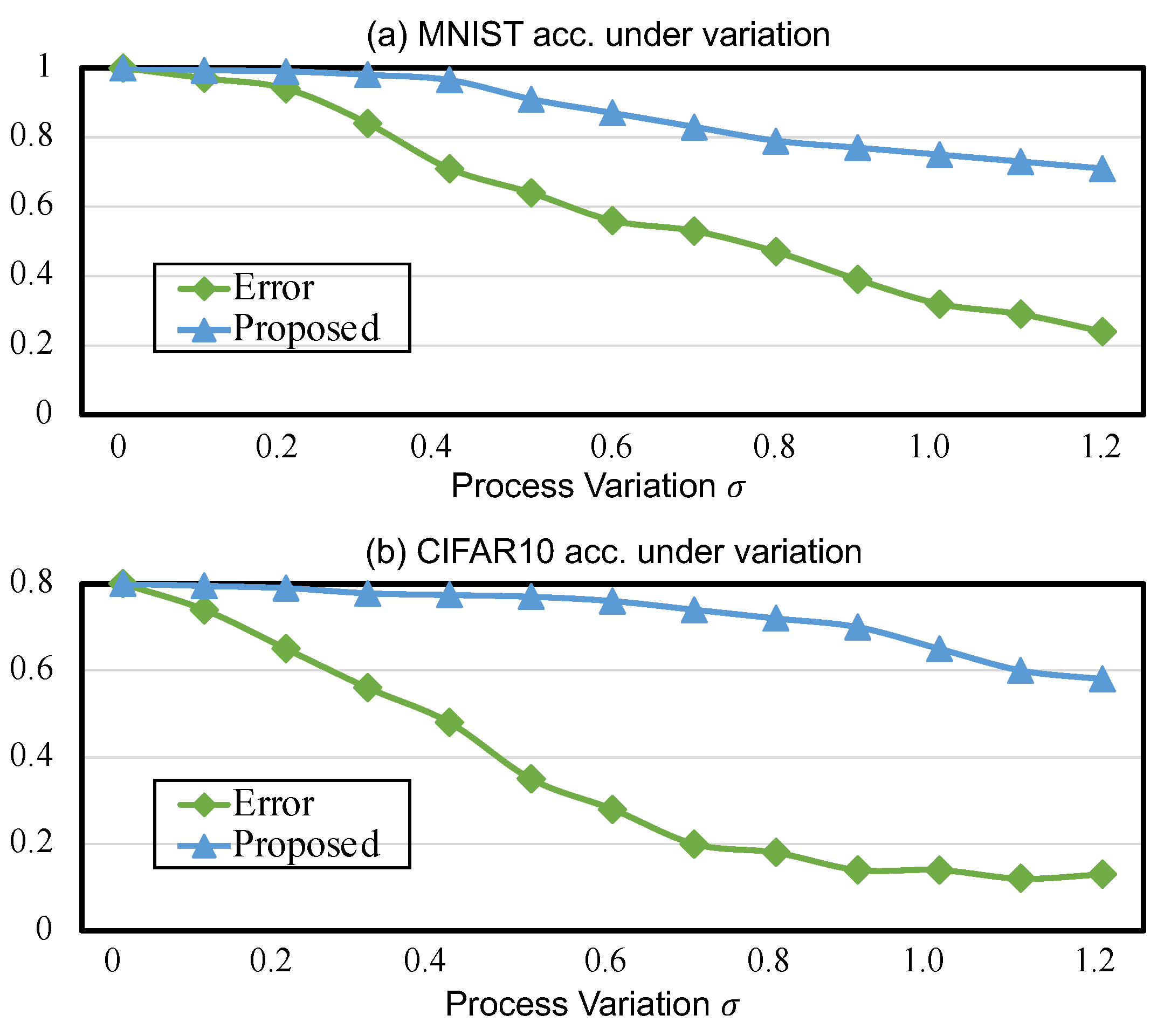
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, W.H.; Li, K.X.; Lin, W.Y.; Hsu, K.H.; Li, P.Y.; Yang, C.H.; Xue, C.X.; Yang, E.Y.; Chen, Y.K.; Chang, Y.S.; et al. A 65 nm 1 Mb nonvolatile computing-in-memory ReRAM macro with sub-16ns multiply-and-accumulate for binary DNN AI edge processors. In Proceedings of the 2018 IEEE International Solid-State Circuits Conference-(ISSCC), San Francisco, CA, USA, 11–15 February 2018; pp. 494–496. [Google Scholar]
- Song, L.; Qian, X.; Li, H.; Chen, Y. Pipelayer: A pipelined reram-based accelerator for deep learning. In Proceedings of the 2017 IEEE International Symposium on High Performance Computer Architecture (HPCA), Austin, TX, USA, 4–8 February 2017; pp. 541–552. [Google Scholar]
- Gokmen, T.; Onen, M.; Haensch, W. Training deep convolutional neural networks with resistive cross-point devices. Front. Neurosci. 2017, 11, 538. [Google Scholar] [CrossRef]
- Shafiee, A.; Nag, A.; Muralimanohar, N.; Balasubramonian, R.; Strachan, J.P.; Hu, M.; Williams, R.S.; Srikumar, V. ISAAC: A convolutional neural network accelerator with in situ analog arithmetic in crossbars. In Proceedings of the 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA), Seoul, Republic of Korea, 18–22 June 2016; Volume 44, pp. 14–26. [Google Scholar]
- Jain, S.; Sengupta, A.; Roy, K.; Raghunathan, A. RxNN: A framework for evaluating deep neural networks on resistive crossbars. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 40, 326–338. [Google Scholar] [CrossRef]
- Roy, S.; Sridharan, S.; Jain, S.; Raghunathan, A. TxSim: Modeling training of deep neural networks on resistive crossbar systems. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2021, 29, 730–738. [Google Scholar] [CrossRef]
- Visweswariah, C.; Ravindran, K.; Kalafala, K.; Walker, S.G.; Narayan, S.; Beece, D.K.; Piaget, J.; Venkateswaran, N.; Hemmett, J.G. First-order incremental block-based statistical timing analysis. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2006, 25, 2170–2180. [Google Scholar] [CrossRef]
- Xiong, J.; Zolotov, V.; He, L. Robust extraction of spatial correlation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2007, 26, 619–631. [Google Scholar] [CrossRef]
- Liu, M.; Xia, L.; Wang, Y.; Chakrabarty, K. Fault tolerance in neuromorphic computing systems. In Proceedings of the 24th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 21–24 January 2019; pp. 216–223. [Google Scholar]
- Li, B.; Yan, B.; Liu, C.; Li, H. Build reliable and efficient neuromorphic design with memristor technology. In Proceedings of the 24th Asia and South Pacific Design Automation Conference, Tokyo, Japan, 21–24 January 2019; pp. 224–229. [Google Scholar]
- Liu, T.; Wen, W.; Jiang, L.; Wang, Y.; Yang, C.; Quan, G. A fault-tolerant neural network architecture. In Proceedings of the 2019 56th ACM/IEEE Design Automation Conference (DAC), Las Vegas, NV, USA, 2–6 June 2019; pp. 1–6. [Google Scholar]
- Liu, B.; Li, H.; Chen, Y.; Li, X.; Wu, Q.; Huang, T. Vortex: Variation-aware training for memristor X-bar. In Proceedings of the 52nd Annual Design Automation Conference, San Francisco, CA, USA, 8–12 June 2015; pp. 1–6. [Google Scholar]
- Zhu, Y.; Zhang, G.L.; Wang, T.; Li, B.; Shi, Y.; Ho, T.Y.; Schlichtmann, U. Statistical training for neuromorphic computing using memristor-based crossbars considering process variations and noise. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 1590–1593. [Google Scholar]
- Chen, L.; Li, J.; Chen, Y.; Deng, Q.; Shen, J.; Liang, X.; Jiang, L. Accelerator-friendly neural-network training: Learning variations and defects in RRAM crossbar. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017; pp. 19–24. [Google Scholar]
- Pouyan, P.; Amat, E.; Rubio, A. Memristive crossbar memory lifetime evaluation and reconfiguration strategies. IEEE Trans. Emerg. Top. Comput. 2016, 6, 207–218. [Google Scholar] [CrossRef]
- Rehman, M.M.; Rehman, H.M.M.U.; Gul, J.Z.; Kim, W.Y.; Karimov, K.S.; Ahmed, N. Decade of 2D-materials-based RRAM devices: A review. Sci. Technol. Adv. Mater. 2020, 21, 147–186. [Google Scholar] [CrossRef] [PubMed]
- Rehman, M.M.; ur Rehman, H.M.M.; Kim, W.Y.; Sherazi, S.S.H.; Rao, M.W.; Khan, M.; Muhammad, Z. Biomaterial-based nonvolatile resistive memory devices toward ecofriendliness and biocompatibility. ACS Appl. Electron. Mater. 2021, 3, 2832–2861. [Google Scholar] [CrossRef]
- Lin, M.Y.; Cheng, H.Y.; Lin, W.T.; Yang, T.H.; Tseng, I.C.; Yang, C.L.; Hu, H.W.; Chang, H.S.; Li, H.P.; Chang, M.F. DL-RSIM: A simulation framework to enable reliable ReRAM-based accelerators for deep learning. In Proceedings of the 2018 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Diego, CA, USA, 5–8 November 2018; pp. 1–8. [Google Scholar]
- Hu, M.; Strachan, J.P.; Li, Z.; Grafals, E.M.; Davila, N.; Graves, C.; Lam, S.; Ge, N.; Yang, J.J.; Williams, R.S. Dot-product engine for neuromorphic computing: Programming 1T1M crossbar to accelerate matrix-vector multiplication. In Proceedings of the 2016 53nd ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 5–9 June 2016; pp. 1–6. [Google Scholar]
- Ye, N.; Mei, J.; Fang, Z.; Zhang, Y.; Zhang, Z.; Wu, H.; Liang, X. BayesFT: Bayesian Optimization for Fault Tolerant Neural Network Architecture. In Proceedings of the 2021 58th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 5–9 December 2021; pp. 487–492. [Google Scholar]
- Ye, N.; Cao, L.; Yang, L.; Zhang, Z.; Fang, Z.; Gu, Q.; Yang, G.Z. Improving the robustness of analog deep neural networks through a Bayes-optimized noise injection approach. Commun. Eng. 2023, 2, 25. [Google Scholar] [CrossRef]
- Graves, A. Practical variational inference for neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 12–15 December 2011; pp. 2348–2356. [Google Scholar]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight uncertainty in neural networks. arXiv 2015, arXiv:1505.05424. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Kingma, D.P.; Salimans, T.; Welling, M. Variational dropout and the local reparameterization trick. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 2575–2583. [Google Scholar]
- Atanov, A.; Ashukha, A.; Struminsky, K.; Vetrov, D.; Welling, M. The deep weight prior. arXiv 2018, arXiv:1810.06943. [Google Scholar]
- Chen, C.Y.; Shih, H.C.; Wu, C.W.; Lin, C.H.; Chiu, P.F.; Sheu, S.S.; Chen, F.T. RRAM defect modeling and failure analysis based on march test and a novel squeeze-search scheme. IEEE Trans. Comput. 2014, 64, 180–190. [Google Scholar] [CrossRef]
- Tomczak, J.; Welling, M. VAE with a VampPrior. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Playa Blanca, Spain, 9–11 April 2018; pp. 1214–1223. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Agarwal, S.; Plimpton, S.J.; Hughart, D.R.; Hsia, A.H.; Richter, I.; Cox, J.A.; James, C.D.; Marinella, M.J. Resistive memory device requirements for a neural algorithm accelerator. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 929–938. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, D.; Xie, X.; Wei, D. A Design Methodology for Fault-Tolerant Neuromorphic Computing Using Bayesian Neural Network. Micromachines 2023, 14, 1840. https://doi.org/10.3390/mi14101840
Gao D, Xie X, Wei D. A Design Methodology for Fault-Tolerant Neuromorphic Computing Using Bayesian Neural Network. Micromachines. 2023; 14(10):1840. https://doi.org/10.3390/mi14101840
Chicago/Turabian StyleGao, Di, Xiaoru Xie, and Dongxu Wei. 2023. "A Design Methodology for Fault-Tolerant Neuromorphic Computing Using Bayesian Neural Network" Micromachines 14, no. 10: 1840. https://doi.org/10.3390/mi14101840
APA StyleGao, D., Xie, X., & Wei, D. (2023). A Design Methodology for Fault-Tolerant Neuromorphic Computing Using Bayesian Neural Network. Micromachines, 14(10), 1840. https://doi.org/10.3390/mi14101840








