Investigation of Nonlinear Piezoelectric Energy Harvester for Low-Frequency and Wideband Applications
Abstract
:1. Introduction
2. Design and Modeling
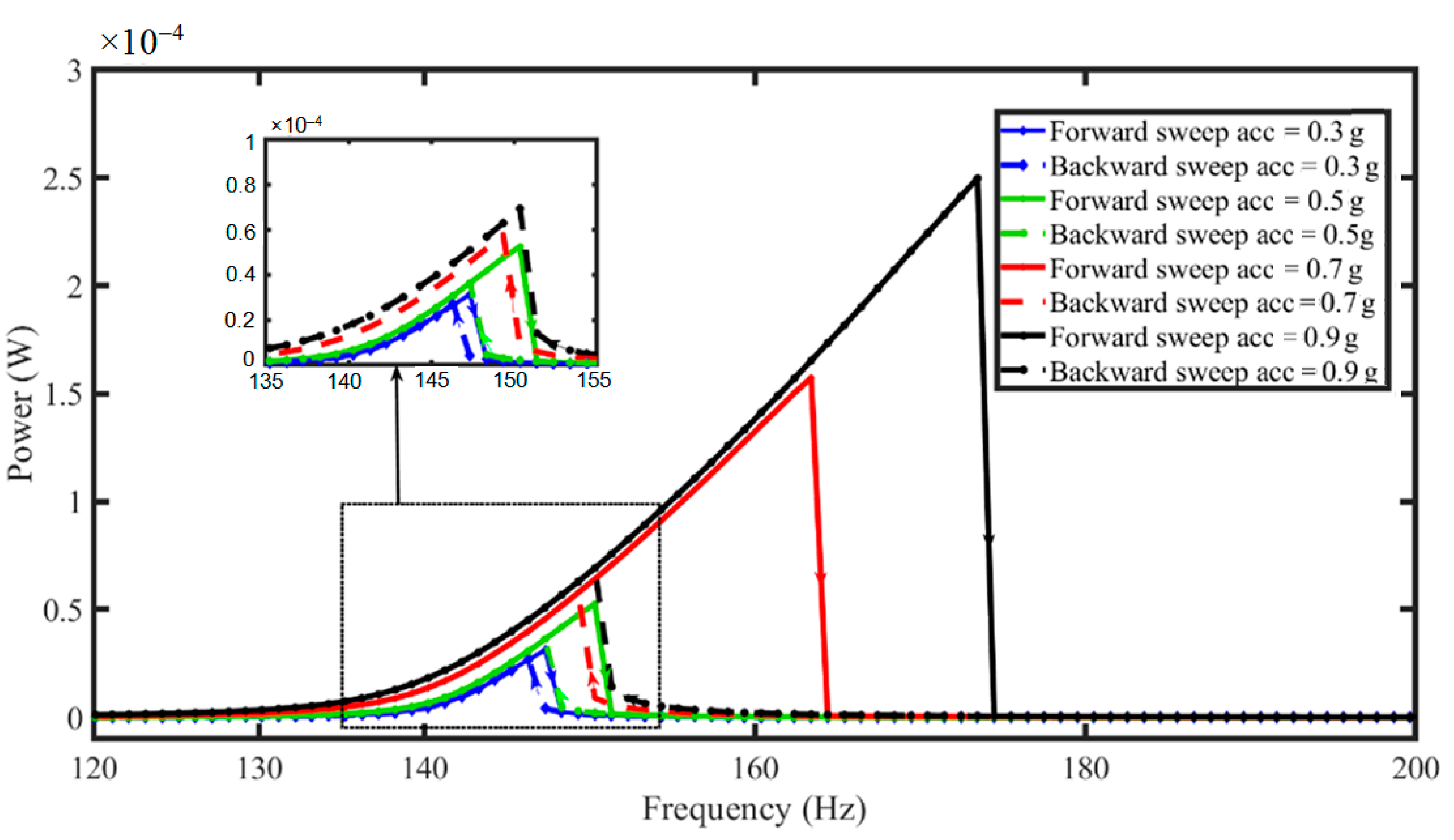
3. Result and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beeby, S.P.; Tudor, M.J.; White, N.M. Energy Harvesting Vibration Sources for Microsystems Applications. Meas. Sci. Technol. 2006, 17, R175. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, S.; Zu, J.; Inman, D. High-Performance Piezoelectric Energy Harvesters and Their Applications. Joule 2018, 2, 642–697. [Google Scholar] [CrossRef]
- Bowen, C.R.; Topolov, V.Y.; Kim, H.A. Springer Series in Materials Science- Modern Piezoelectric Energy- Harvesting Materials; Springer: Berlin/Heidelberg, Germany, 2016; Volume 238, ISBN 978-3-319-29141-3. [Google Scholar]
- Le Scornec, J.; Guiffard, B.; Seveno, R.; Le Cam, V.; Ginestar, S. Self-Powered Communicating Wireless Sensor with Flexible Aero-Piezoelectric Energy Harvester. Renew. Energy 2022, 184, 551–563. [Google Scholar] [CrossRef]
- Grossi, M. Energy Harvesting Strategies for Wireless Sensor Networks and Mobile Devices: A Review. Electronics 2021, 10, 661. [Google Scholar] [CrossRef]
- Liu, Y.; Khanbareh, H.; Halim, M.A.; Feeney, A.; Zhang, X.; Heidari, H.; Ghannam, R. Piezoelectric Energy Harvesting for Self-powered Wearable Upper Limb Applications. Nano Select 2021, 2, 1459–1479. [Google Scholar] [CrossRef]
- Yang, S.; Cui, X.; Guo, R.; Zhang, Z.; Sang, S.; Zhang, H. Piezoelectric Sensor Based on Graphene-Doped PVDF Nanofibers for Sign Language Translation. Beilstein J. Nanotechnol. 2020, 11, 1655–1662. [Google Scholar] [CrossRef]
- Cheng, X.; Xue, X.; Ma, Y.; Han, M.; Zhang, W.; Xu, Z.; Zhang, H.; Zhang, H. Implantable and Self-Powered Blood Pressure Monitoring Based on a Piezoelectric Thinfilm: Simulated, in Vitro and in Vivo Studies. Nano Energy 2016, 22, 453–460. [Google Scholar] [CrossRef]
- Ali, F.; Raza, W.; Li, X.; Gul, H.; Kim, K.H. Piezoelectric Energy Harvesters for Biomedical Applications. Nano Energy 2019, 57, 879–902. [Google Scholar] [CrossRef]
- Blokhina, E.; El Aroudi, A.; Alarcon, E.; Galayko, D. Nonlinearity in Energy Harvesting Systems-Micro- and Nanoscale Applications; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 978-3-319-20355-3. [Google Scholar]
- Hu, D.; Yao, M.; Fan, Y.; Ma, C.; Fan, M.; Liu, M. Strategies to Achieve High Performance Piezoelectric Nanogenerators. Nano Energy 2019, 55, 288–304. [Google Scholar] [CrossRef]
- Xu, Q.; Wen, J.; Qin, Y. Development and Outlook of High Output Piezoelectric Nanogenerators. Nano Energy 2021, 86, 106080. [Google Scholar] [CrossRef]
- Shi, Q.; Sun, Z.; Zhang, Z.; Lee, C. Triboelectric Nanogenerators and Hybridized Systems for Enabling Next-Generation IoT Applications. Research 2021, 2021, 1–30. [Google Scholar] [CrossRef]
- Fan, F.R.; Tian, Z.Q.; Wang, Z.L. Flexible Triboelectric Generator. Nano Energy 2012, 1, 328–334. [Google Scholar] [CrossRef]
- Kim, W.G.; Kim, D.W.; Tcho, I.W.; Kim, J.K.; Kim, M.S.; Choi, Y.K. Triboelectric Nanogenerator: Structure, Mechanism, and Applications. ACS Nano 2021, 15, 258–287. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.W.; Lee, J.H.; Kim, J.K.; Jeong, U. Material Aspects of Triboelectric Energy Generation and Sensors. NPG Asia Mater. 2020, 12, 6. [Google Scholar] [CrossRef]
- Singh, S.; Yadav, P.; Gupta, M.K.; Dzhardimalieva, G.I.; Yoon, J.; Maiti, C.; Yadav, B.C. Gigantic Stimulation in Response by Solar Irradiation in Self-Healable and Self-Powered LPG Sensor Based on Triboelectric Nanogenerator: Experimental and DFT Computational Study. Sens. Actuators B Chem. 2022, 359, 131573. [Google Scholar] [CrossRef]
- Chung, J.; Song, M.; Chung, S.-H.; Choi, W.; Lee, S.; Lin, Z.-H.; Hong, J.; Lee, S. Triangulated Cylinder Origami-Based Piezoelectric/Triboelectric Hybrid Generator to Harvest Coupled Axial and Rotational Motion. Research 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Elliott, A.D.T.; Miller, L.M.; Halvorsen, E.; Wright, P.K.; Mitcheson, P.D. Comparison between MEMS and Meso Scale Piezoelectric Energy Harvesters. In 7th Forum on New Materials-Part D. 7th Forum on New Materials (CIMTEC 2016); Trans Tech Publications Ltd.: Wollerau, Switzerland, 2016; Volume 100, pp. 109–114. [Google Scholar] [CrossRef]
- Toyabur, R.M.; Salauddin, M.; Park, J.Y. Design and Experiment of Piezoelectric Multimodal Energy Harvester for Low Frequency Vibration. Ceram. Int. 2017, 43, S675–S681. [Google Scholar] [CrossRef]
- Kim, I.H.; Jung, H.J.; Lee, B.M.; Jang, S.J. Broadband Energy-Harvesting Using a Two Degree-of-Freedom Vibrating Body. Appl. Phys. Lett. 2011, 98, 214102. [Google Scholar] [CrossRef]
- Nabavi, S.; Zhang, L. Nonlinear Multi-Mode Wideband Piezoelectric MEMS Vibration Energy Harvester. IEEE Sens. J. 2019, 19, 4837–4848. [Google Scholar] [CrossRef]
- Iannacci, J.; Sordo, G.; Serra, E.; Schmid, U. The MEMS Four-Leaf Clover Wideband Vibration Energy Harvesting Device: Design Concept and Experimental Verification. Microsyst. Technol. 2016, 22, 1865–1881. [Google Scholar] [CrossRef]
- Wu, H.; Tang, L.; Yang, Y.; Soh, C.K. A Novel Two-Degrees-of-Freedom Piezoelectric Energy Harvester. J. Intell. Mater. Syst. Struct. 2013, 24, 357–368. [Google Scholar] [CrossRef]
- Liu, H.; Lee, C.; Kobayashi, T.; Tay, C.J.; Quan, C. Piezoelectric MEMS-Based Wideband Energy Harvesting Systems Using a Frequency-up-Conversion Cantilever Stopper. Sens. Actuators A Phys. 2012, 186, 242–248. [Google Scholar] [CrossRef]
- Andò, B.; Baglio, S.; Bulsara, A.R.; Marletta, V.; Pistorio, A. Investigation of a Nonlinear Energy Harvester. IEEE Trans. Instrum. Meas. 2017, 66, 1067–1075. [Google Scholar] [CrossRef]
- Jung, S.M.; Yun, K.S. Energy-Harvesting Device with Mechanical Frequency-up Conversion Mechanism for Increased Power Efficiency and Wideband Operation. Appl. Phys. Lett. 2010, 96, 2012–2015. [Google Scholar] [CrossRef]
- Jia, Y. Review of Nonlinear Vibration Energy Harvesting: Duffing, Bistability, Parametric, Stochastic and Others. J. Intell. Mater. Syst. Struct. 2020, 31, 921–944. [Google Scholar] [CrossRef]
- Marzencki, M.; Defosseux, M.; Basrour, S. MEMS Vibration Energy Harvesting Devices with Passive Resonance Frequency Adaptation Capability. J. Microelectromech. Syst. 2009, 18, 1444–1453. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V.; Guizzetti, M.; Andò, B.; Baglio, S.; Trigona, C. Improved Energy Harvesting from Wideband Vibrations by Nonlinear Piezoelectric Converters. Procedia Chem. 2009, 1, 1203–1206. [Google Scholar] [CrossRef]
- Zou, H.X.; Li, M.; Zhao, L.C.; Gao, Q.H.; Wei, K.X.; Zuo, L.; Qian, F.; Zhang, W.M. A Magnetically Coupled Bistable Piezoelectric Harvester for Underwater Energy Harvesting. Energy 2021, 217, 119429. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, X.; Wang, L.; Chen, L. An Arch-Linear Composed Beam Piezoelectric Energy Harvester with Magnetic Coupling: Design, Modeling and Dynamic Analysis. J. Sound Vib. 2021, 513, 116394. [Google Scholar] [CrossRef]
- Vysotskyi, B.; Parrain, F.; Aubry, D.; Gaucher, P.; Le Roux, X.; Lefeuvre, E. Engineering the Structural Nonlinearity Using Multimodal-Shaped Springs in MEMS. J. Microelectromech. Syst. 2018, 27, 40–46. [Google Scholar] [CrossRef]
- Chen, K.; Gao, Q.; Fang, S.; Zou, D.; Yang, Z.; Liao, W.H. An Auxetic Nonlinear Piezoelectric Energy Harvester for Enhancing Efficiency and Bandwidth. Appl. Energy 2021, 298, 117274. [Google Scholar] [CrossRef]
- Wang, J.; Geng, L.; Zhou, S.; Zhang, Z.; Lai, Z.; Yurchenko, D. Design, Modeling and Experiments of Broadband Tristable Galloping Piezoelectric Energy Harvester. Acta Mech. Sin. Xuebao 2020, 36, 592–605. [Google Scholar] [CrossRef]
- Podder, P.; Amann, A.; Roy, S. Combined Effect of Bistability and Mechanical Impact on the Performance of a Nonlinear Electromagnetic Vibration Energy Harvester. IEEE/ASME Trans. Mechatron. 2016, 21, 727–739. [Google Scholar] [CrossRef]
- Fan, K.; Tan, Q.; Zhang, Y.; Liu, S.; Cai, M.; Zhu, Y. A Monostable Piezoelectric Energy Harvester for Broadband Low-Level Excitations. Appl. Phys. Lett. 2018, 112, 5–10. [Google Scholar] [CrossRef]
- Sreenivasulu, G.; Qu, P.; Petrov, V.; Qu, H.; Srinivasan, G. Sensitivity Enhancement in Magnetic Sensors Based on Ferroelectric-Bimorphs and Multiferroic Composites. Sensors 2016, 16, 262. [Google Scholar] [CrossRef]
- Zou, D.; Liu, G.; Rao, Z.; Tan, T.; Zhang, W.; Liao, W.H. Design of Vibration Energy Harvesters with Customized Nonlinear Forces. Mech. Syst. Signal Process. 2021, 153, 107526. [Google Scholar] [CrossRef]
- Paul, K.; Amann, A.; Roy, S. Tapered Nonlinear Vibration Energy Harvester for Powering Internet of Things. Appl. Energy 2021, 283, 116267. [Google Scholar] [CrossRef]
- Guyomar, D.; Badel, A.; Lefeuvre, E.; Richard, C. Materials and Conversion Improvement by Nonlinear Processing. Energy 2005, 52, 584–595. [Google Scholar]
- Liu, W.Q.; Badel, A.; Formosa, F.; Wu, Y.P. A New Figure of Merit for Wideband Vibration Energy Harvesters. Smart Mater. Struct. 2015, 24, 125012. [Google Scholar] [CrossRef]
- Nabavi, S.; Zhang, L. Design and Optimization of Wideband Multimode Piezoelectric MEMS Vibration Energy Harvesters. Proceedings 2017, 1, 586. [Google Scholar] [CrossRef] [Green Version]

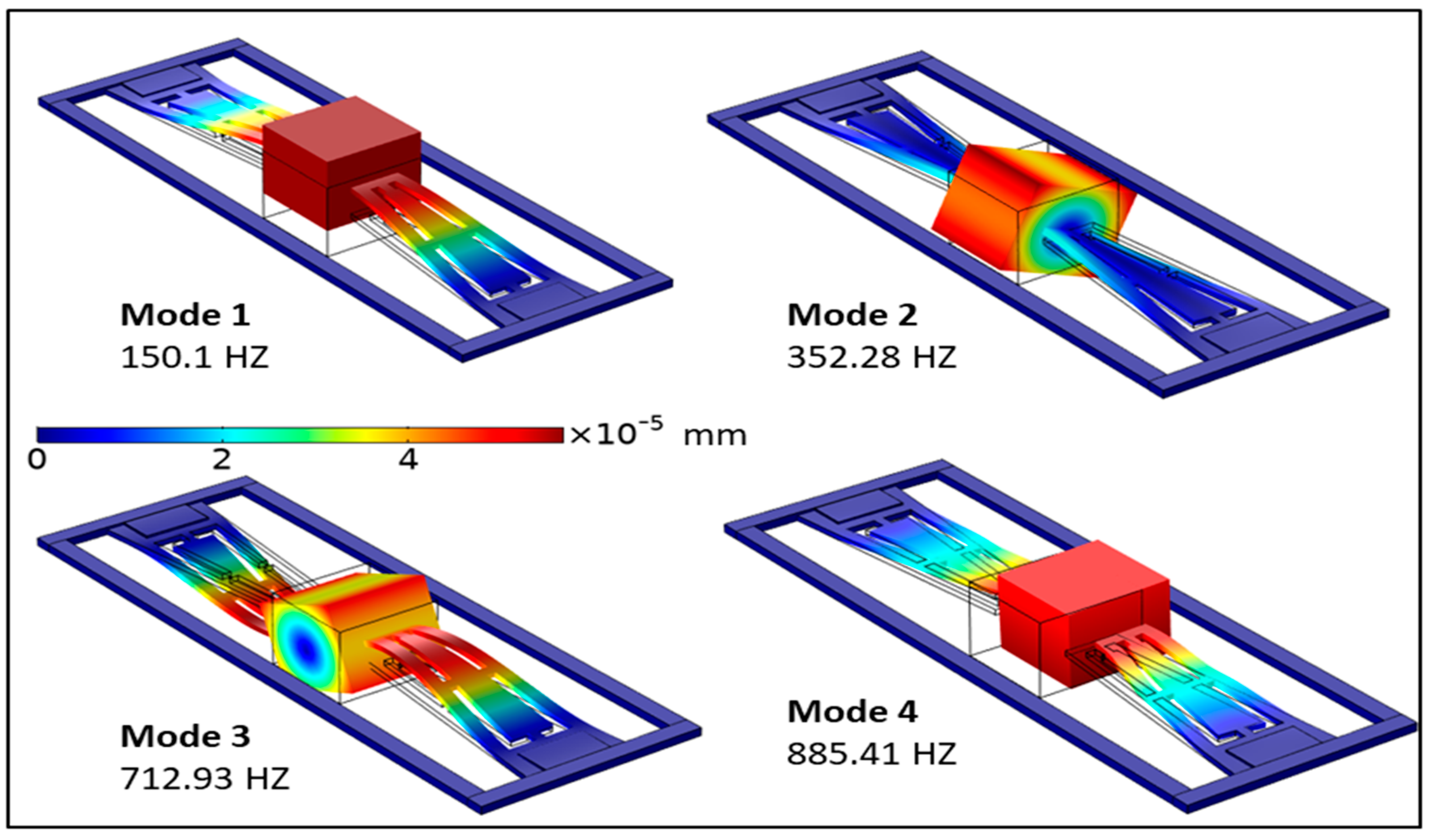
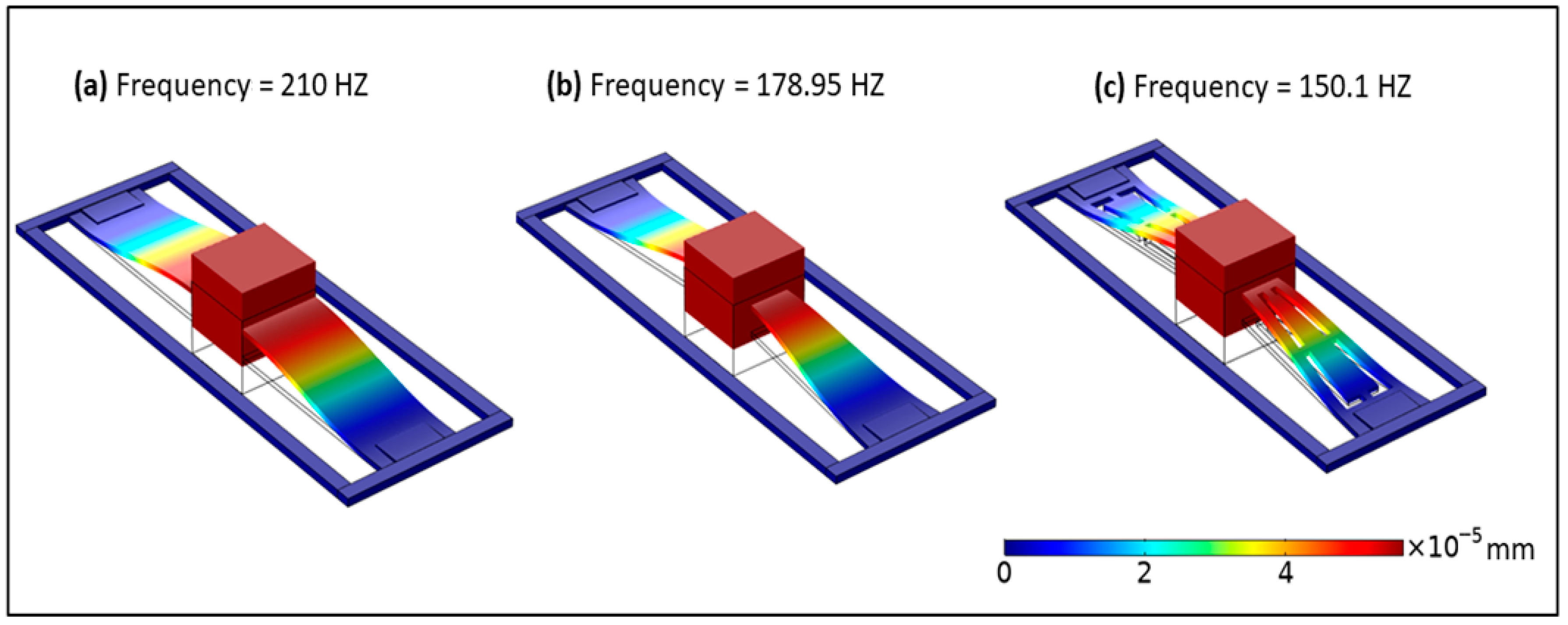
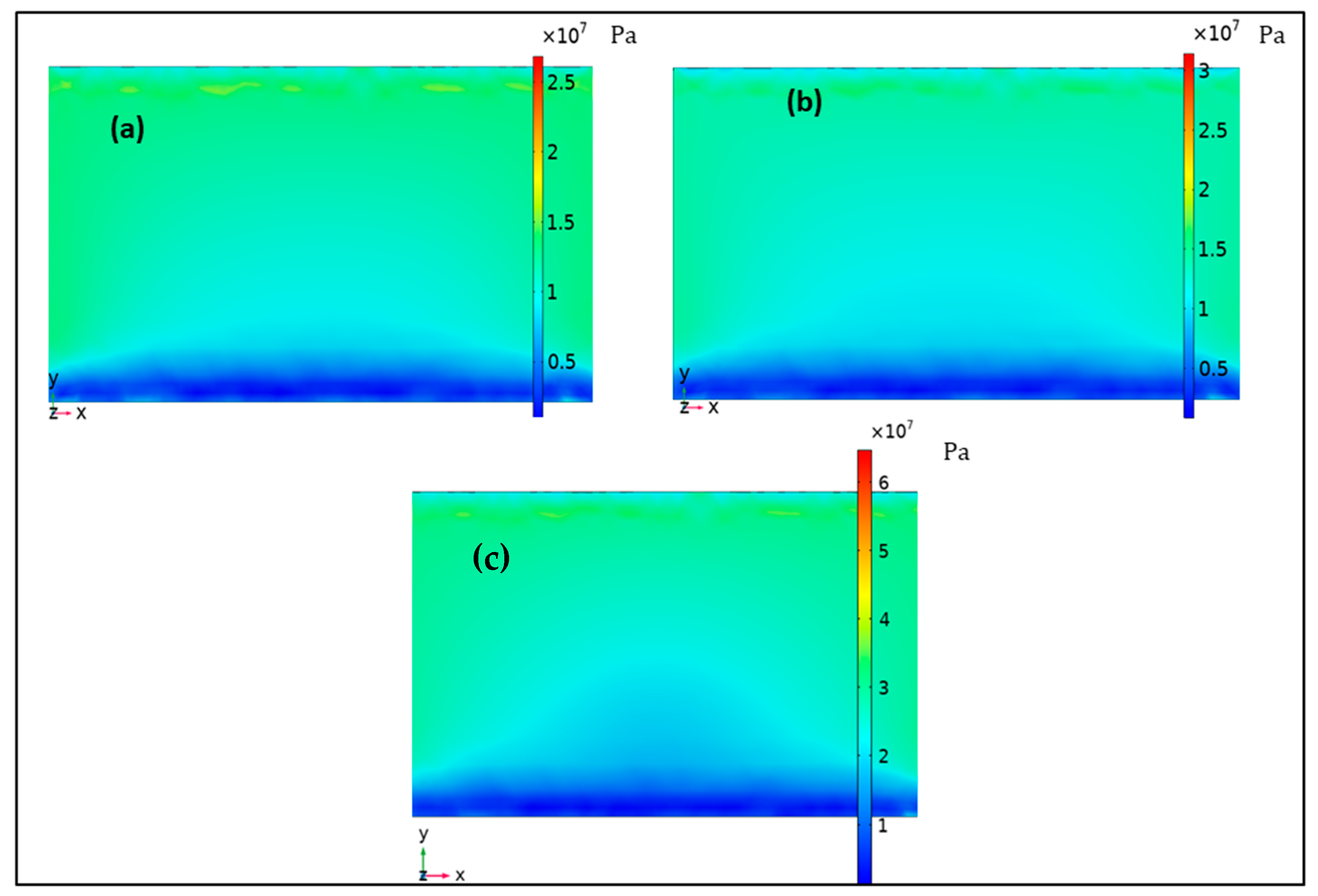
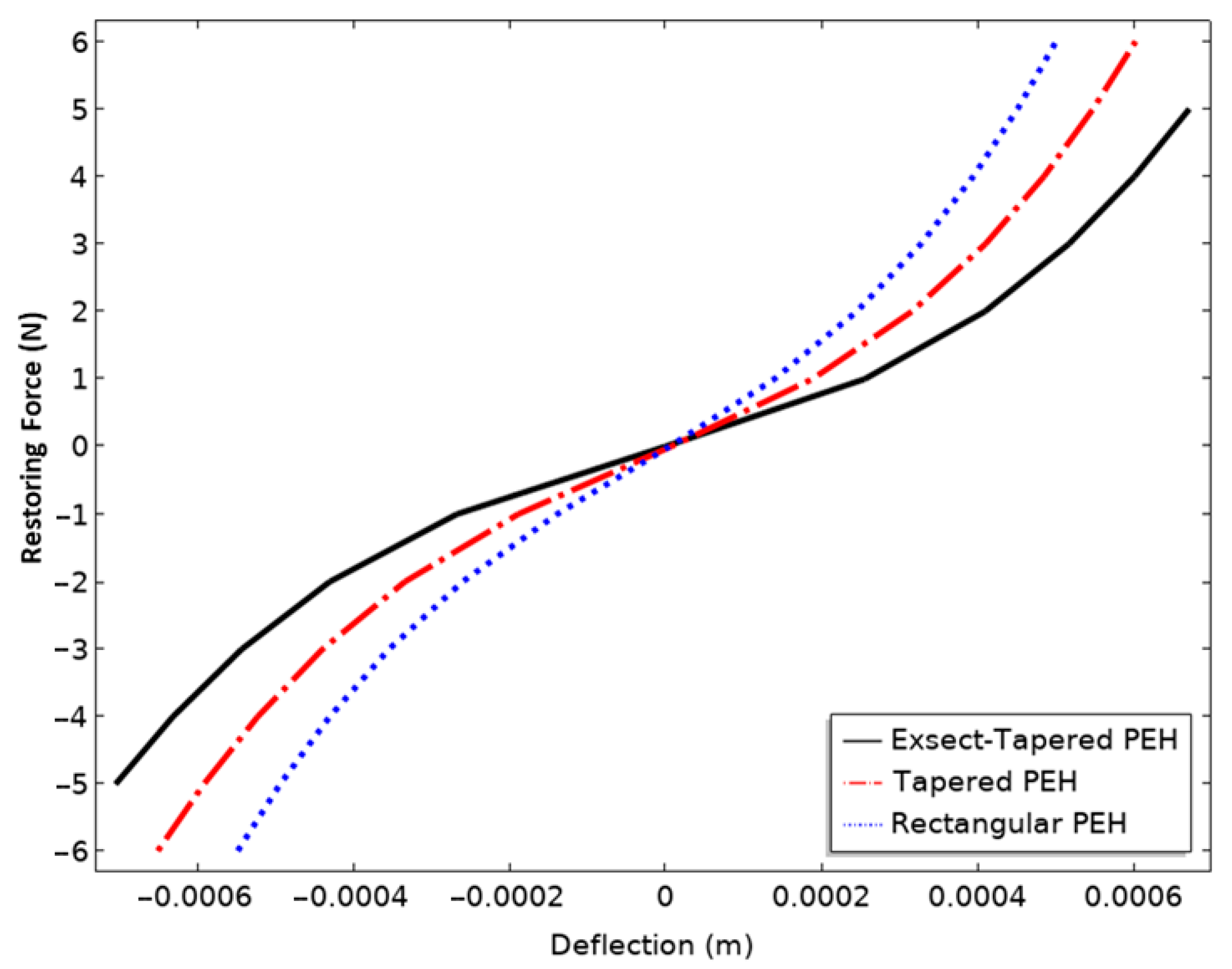
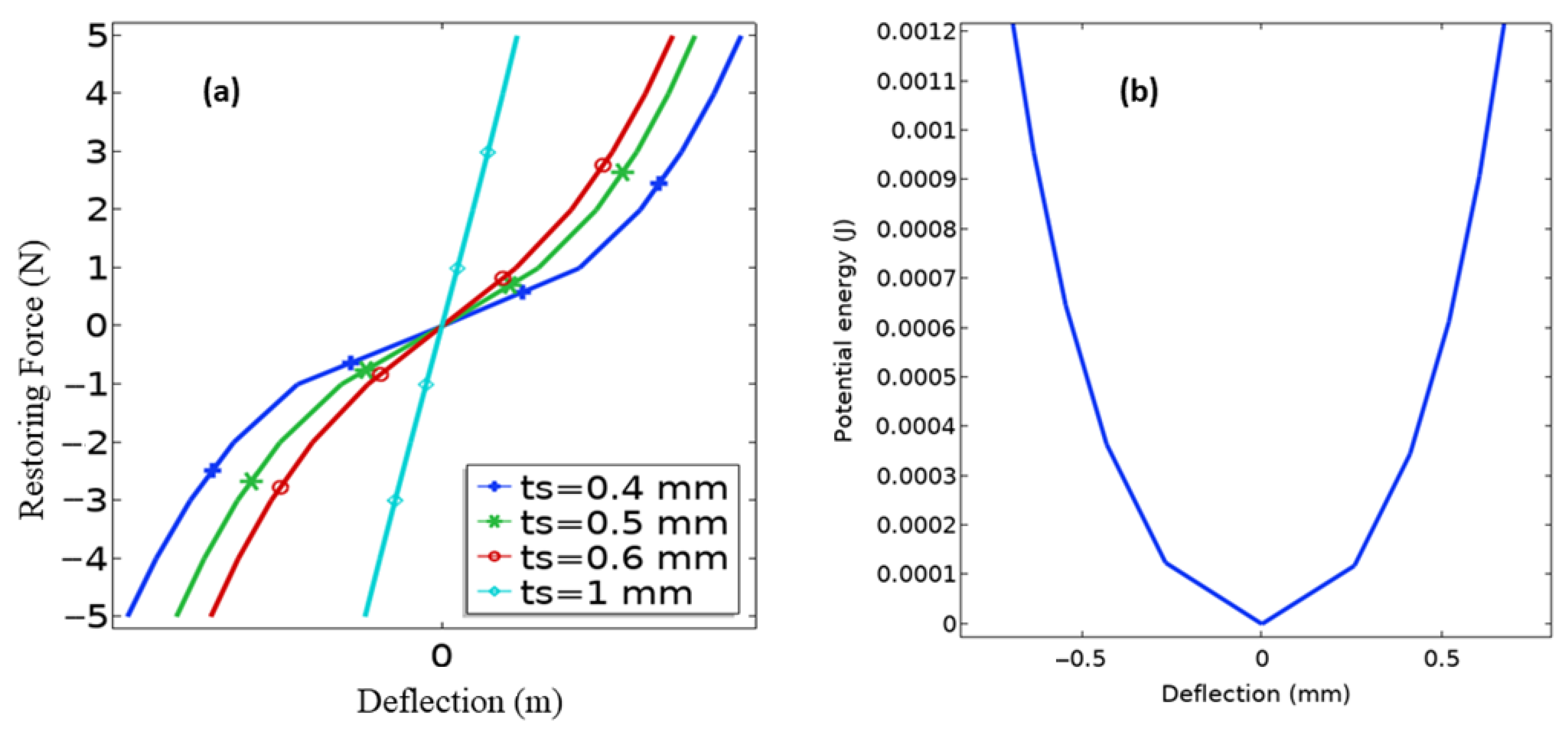
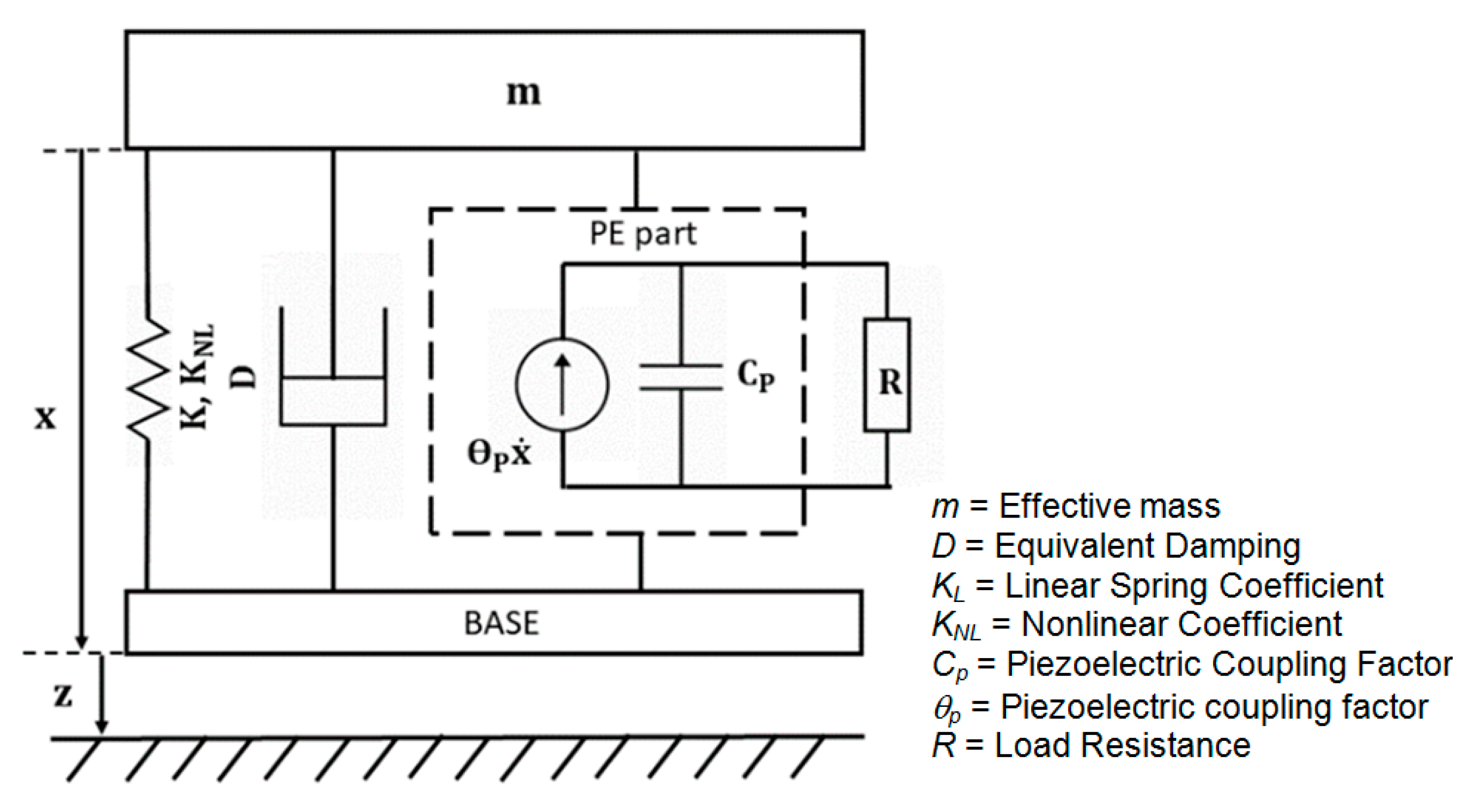

| Description | Value |
|---|---|
| 4.1 g, 4.7 g and 3.781 g | |
| Spring width at the fixed end | 8.6 mm |
| Spring width at the guided end | 4.3 mm |
| PZT-5H size | 5.6 mm × 3 mm × 0.2 mm |
| 0.5 mm | |
| ) | |
| 22 (GPa) | |
| 160 (GPa) | |
| ) | |
| ) | |
| 64 (GPa) | |
| 750 (pC/N) | |
| 39.84 (pF/m) | |
| Damping ratio, D | 0.003 |
| Coupling coefficient | 0.04156 |
| 5.65 (nF) | |
| Load Resistance, R | 0.27 MΩ |
| PEH | Stress (MPa) | kL (N/m) | kNL (N/m3) |
|---|---|---|---|
| Rectangular | 2.5 | 6847 | 1.73 × 1010 |
| Tapered | 3 | 4867 | 9.25 × 109 |
| Exsect-Tapered | 6 | 3227 | 8.92 × 109 |
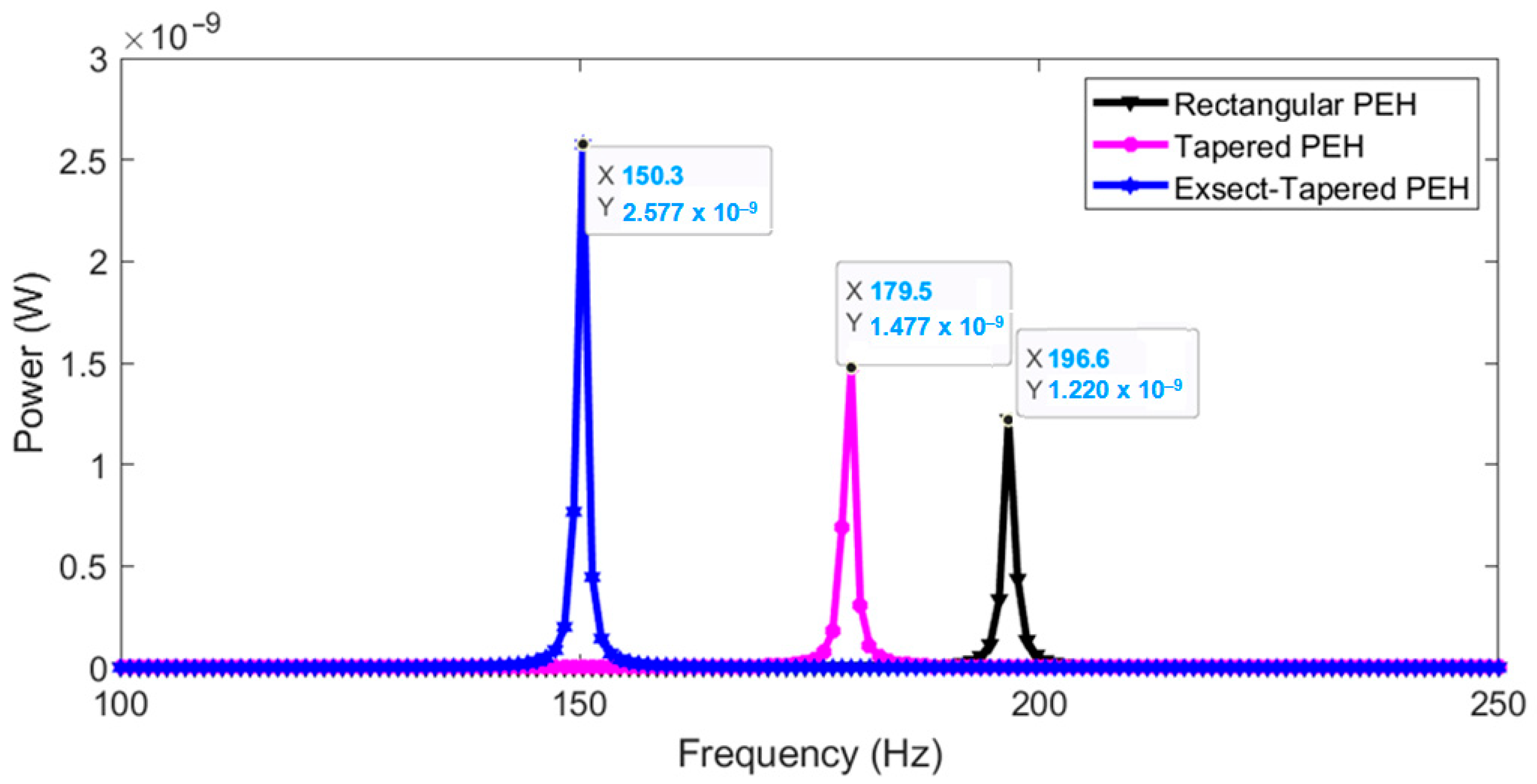
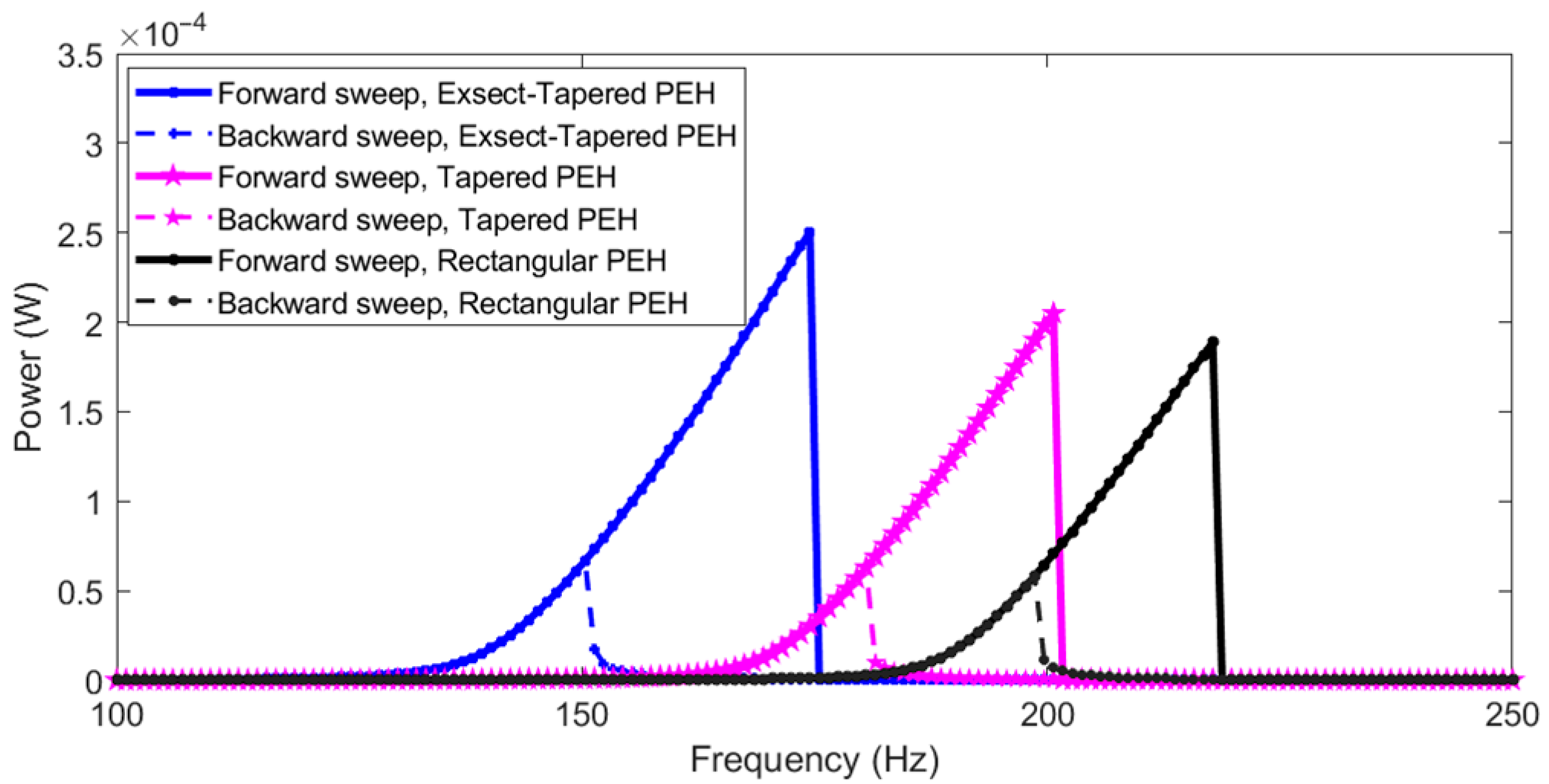
| Nonlinear PEH | Resonant Frequency (Hz) | Optimal Load (Ω) | Bandwidth (Hz) | |
|---|---|---|---|---|
| Rectangular | 196.6 | 1.0 × 105 | 7.8 | 1.8 |
| Tapered | 179.5 | 1.4 × 105 | 8.1 | 2.05 |
| Exsect-Tapered | 150.3 | 1.7 × 105 | 9 | 2.6 |
| S. No. | Wideband Harvester | Bandwidth (Hz) | Input Excitation (g) | Device Volume (cm3) | Generated Power Output (μW) | Normalized Power Density |
|---|---|---|---|---|---|---|
| 1. | Multimode [43] | 59 | 0.5 | 0.0041 | 0.61 | 595.12 |
| 2. | FUC [25] | 22 | 0.8 | 0.0161 | 0.19 | 18.43 |
| 3. | Clamped-Clamped [34] | 9.64 | 0.1 | 1.22 | 125 | 10245 |
| 4. | Rectangular nonlinear (Fixed-Guided) | 7.8 | 0.9 | 0.824 | 1800 | 2696.87 |
| Tapered nonlinear (Fixed-Guided) | 8.1 | 0.779 | 2050 | 3248.86 | ||
| Exsect-Tapered (This Work) | 9 | 0.753 | 2600 | 4262.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pertin, O.; Guha, K.; Jakšić, O.; Jakšić, Z.; Iannacci, J. Investigation of Nonlinear Piezoelectric Energy Harvester for Low-Frequency and Wideband Applications. Micromachines 2022, 13, 1399. https://doi.org/10.3390/mi13091399
Pertin O, Guha K, Jakšić O, Jakšić Z, Iannacci J. Investigation of Nonlinear Piezoelectric Energy Harvester for Low-Frequency and Wideband Applications. Micromachines. 2022; 13(9):1399. https://doi.org/10.3390/mi13091399
Chicago/Turabian StylePertin, Osor, Koushik Guha, Olga Jakšić, Zoran Jakšić, and Jacopo Iannacci. 2022. "Investigation of Nonlinear Piezoelectric Energy Harvester for Low-Frequency and Wideband Applications" Micromachines 13, no. 9: 1399. https://doi.org/10.3390/mi13091399
APA StylePertin, O., Guha, K., Jakšić, O., Jakšić, Z., & Iannacci, J. (2022). Investigation of Nonlinear Piezoelectric Energy Harvester for Low-Frequency and Wideband Applications. Micromachines, 13(9), 1399. https://doi.org/10.3390/mi13091399











