Comparison of Four Electrical Interfacing Circuits in Frequency Up-Conversion Piezoelectric Energy Harvesting
Abstract
1. Introduction
2. Theoretical Model
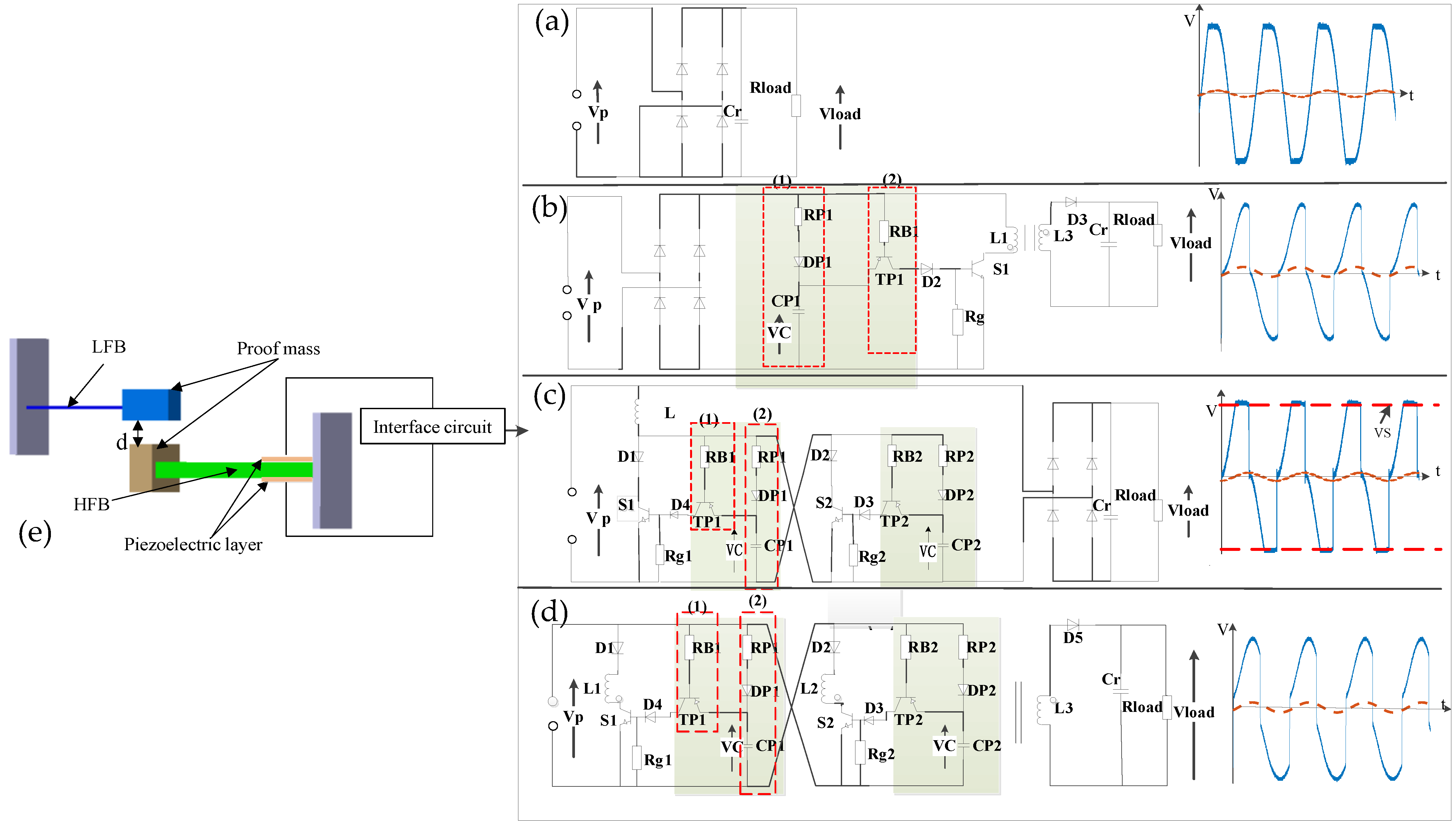
2.1. Device Configuration and Working Principle
2.2. Modeling of the FUC Energy Harvesting System
2.3. Voltage Model
2.4. Energy Extraction Circuit
3. Experimental Results
3.1. Experimental Setup
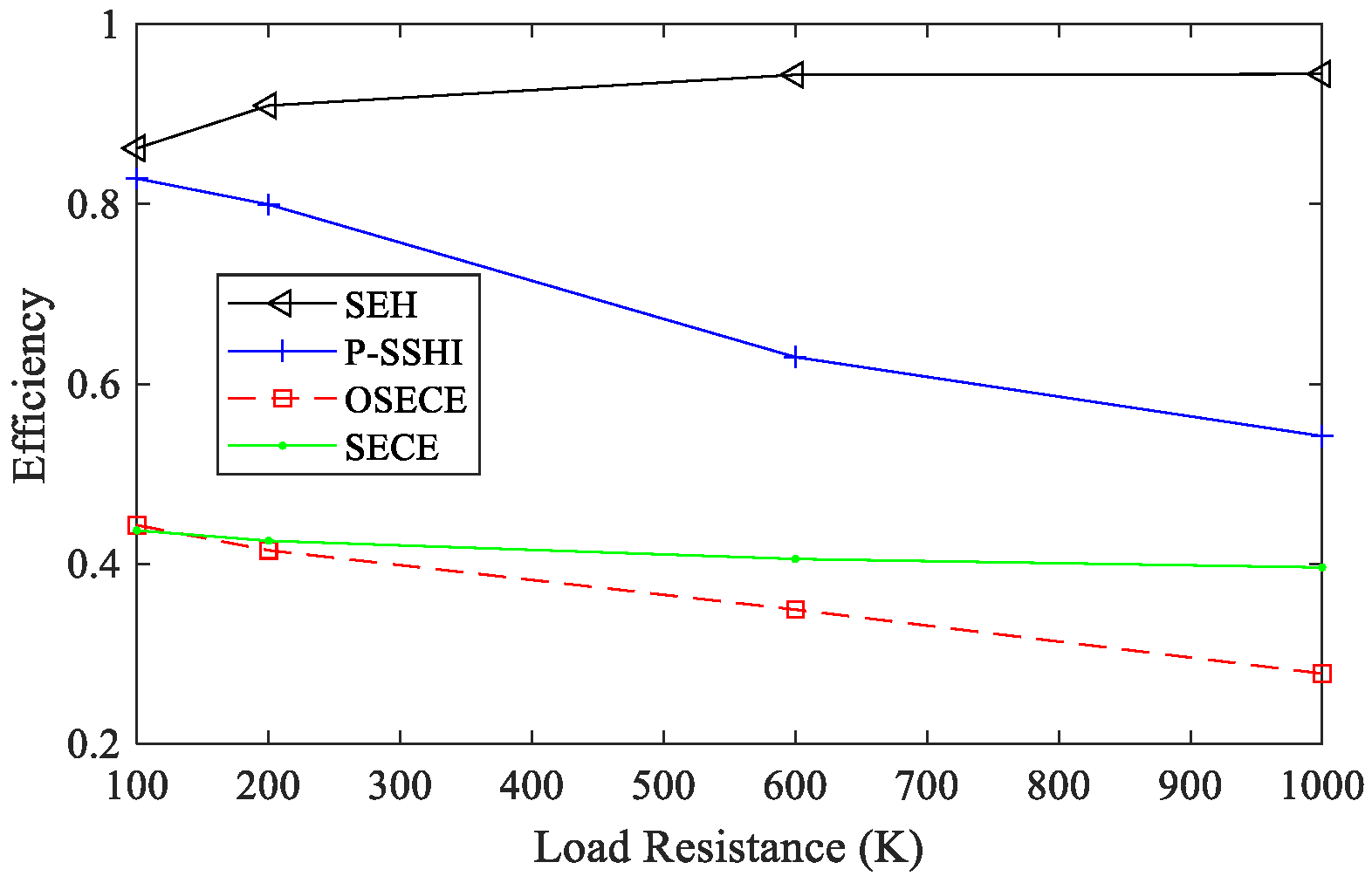
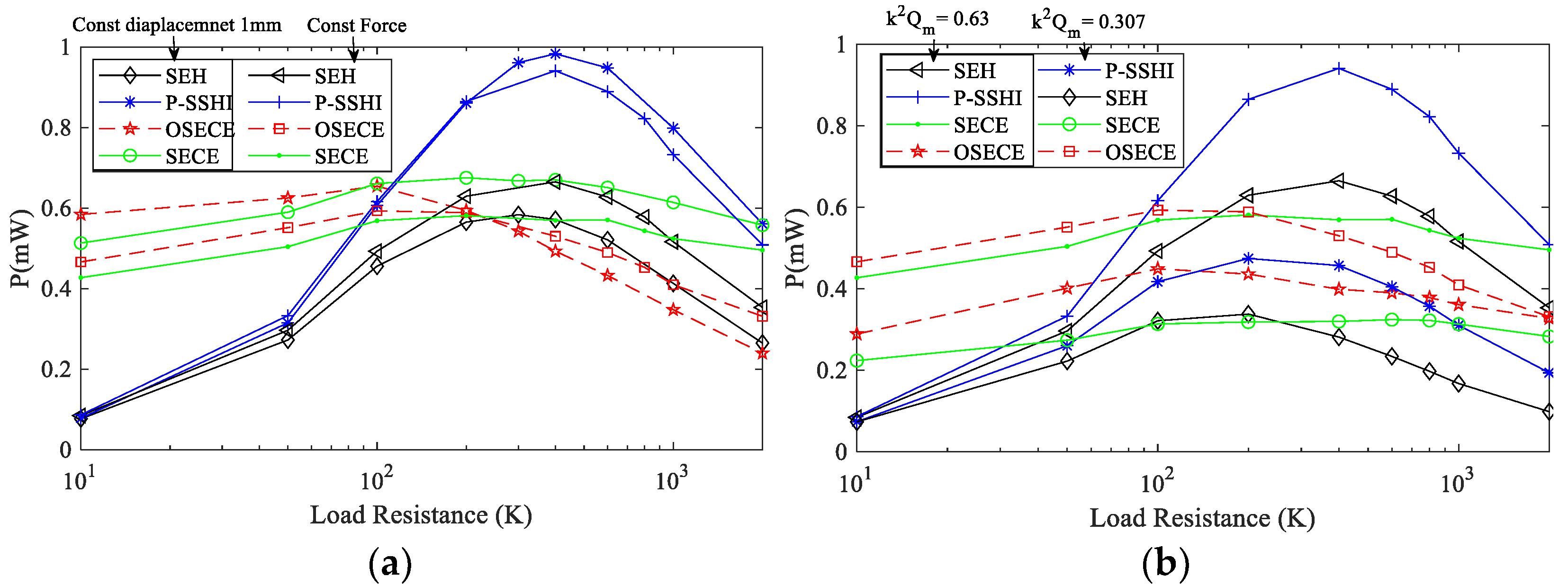
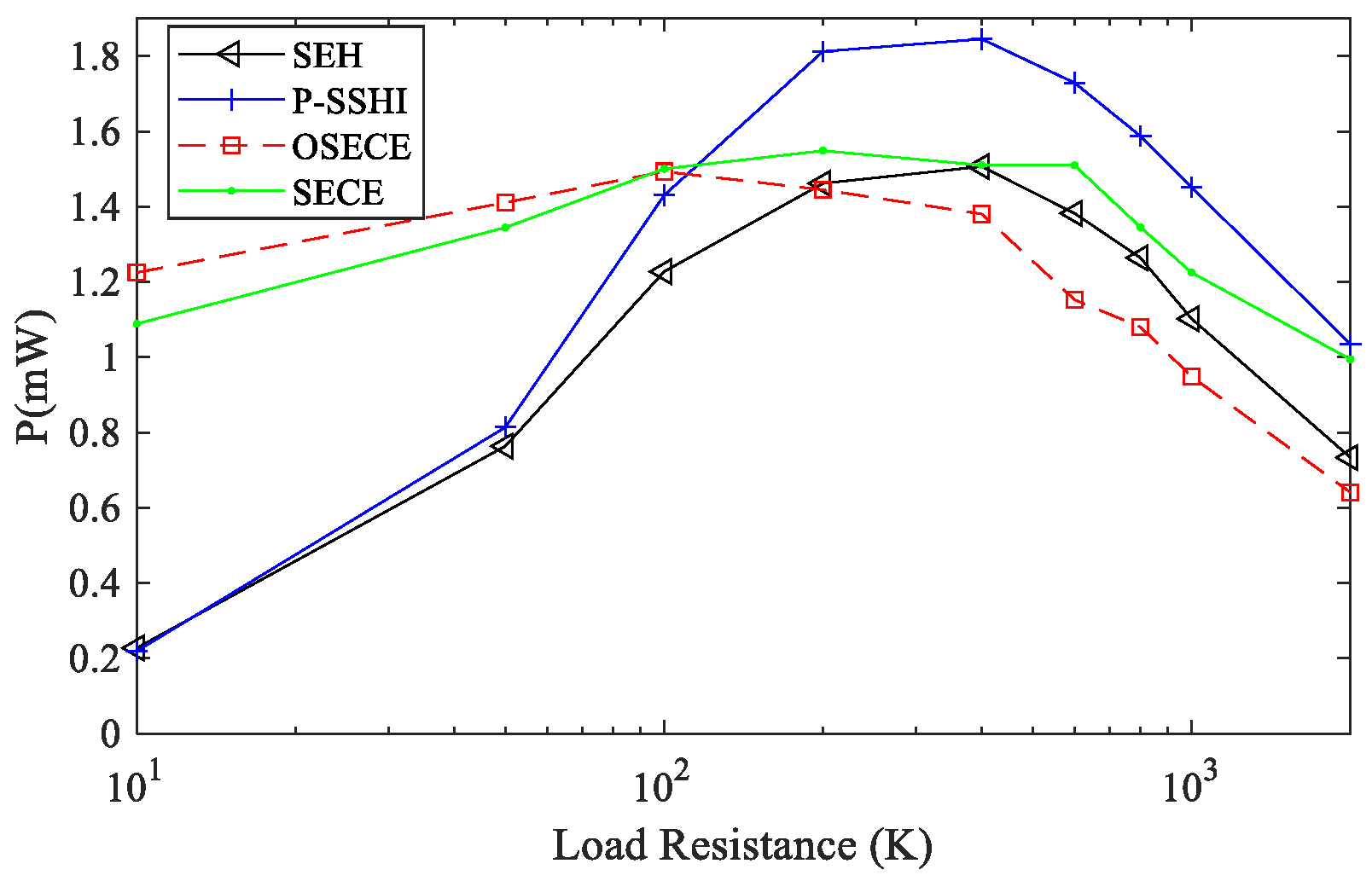
3.2. Experiments under Steady-State Conditions
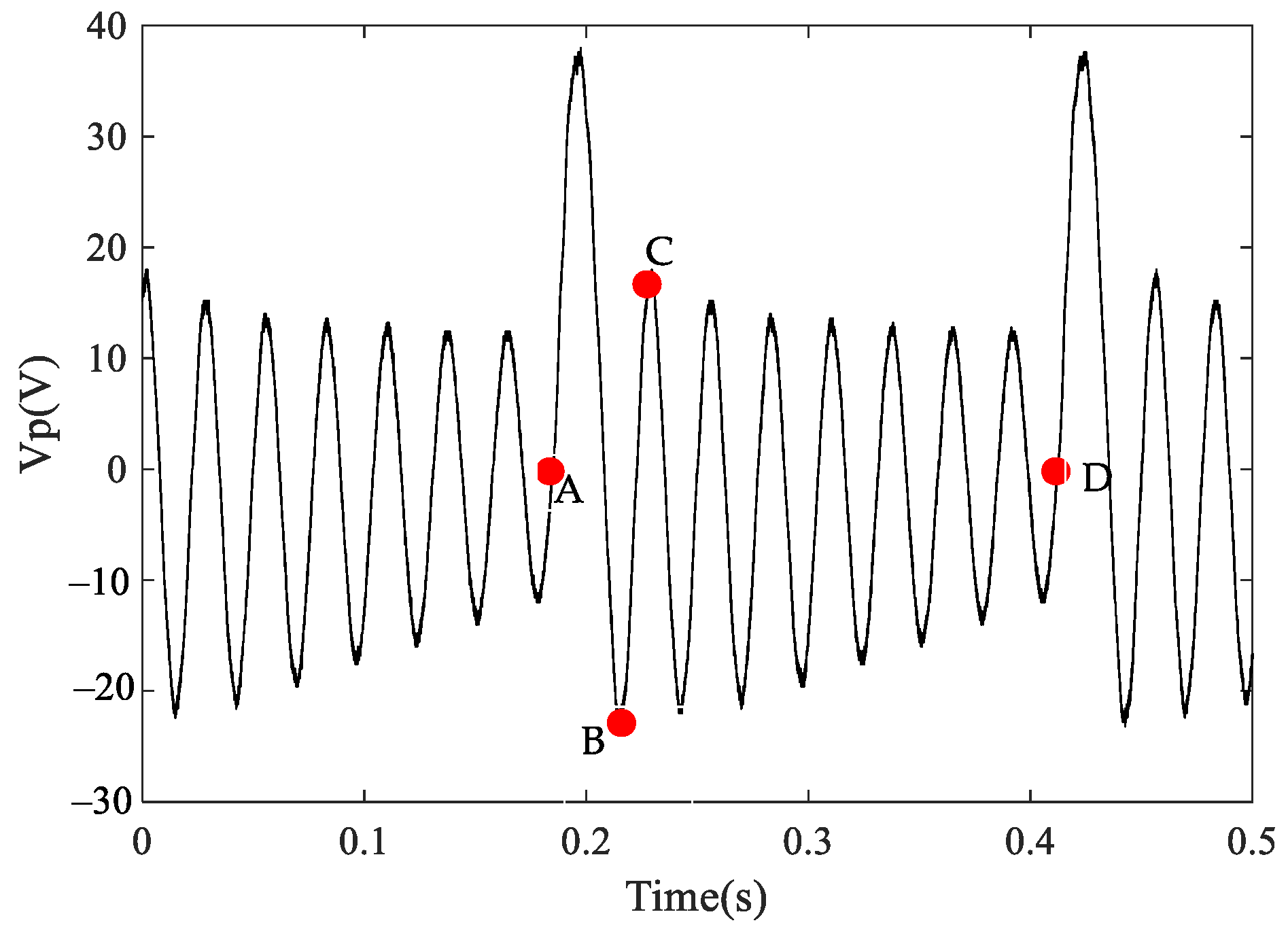
3.3. Experiments under Frequency Up-Conversion Conditions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hodge, V.; Okeefe, S.; Weeks, M.; Moulds, A. Wireless Sensor Networks for Condition Monitoring in the Railway Industry: A Survey. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1088–1106. [Google Scholar] [CrossRef]
- Guo, S.; Yang, L.; Yuan, Y.; Zhang, Z.; Cao, X. Elastic energy storage technology using spiral spring devices and its applications: A review. Energy Built Environ. 2022, 6, 5. [Google Scholar] [CrossRef]
- Sandhu, M.; Khalifa, S.; Jurdak, R.; Portmann, M. Task Scheduling for Energy-Harvesting-Based IoT: A Survey and Critical Analysis. IEEE Internet Things J. 2021, 8, 13825–13848. [Google Scholar] [CrossRef]
- Jo, S.; Byeng, D. A phononic crystal with differently configured double defects for broadband elastic wave energy localization and harvesting. Crystals 2021, 11, 643. [Google Scholar] [CrossRef]
- Gu, Y.; Liu, W.; Zhao, C.; Wang, P. A goblet-like non-linear electromagnetic generator for planar multidirectional vibration energy harvesting. Appl. Energy 2020, 266, 114846. [Google Scholar] [CrossRef]
- Shao, H.; Chen, G.; He, H. Elastic wave localization and energy harvesting defined by piezoelectric patches on phononic crystal waveguide. Phys. Lett. A 2021, 403, 127366. [Google Scholar] [CrossRef]
- Lee, G.; Lee, D. Piezoelectric energy harvesting using mechanical metamaterials and phononic crystals. Commun. Phys. 2022, 5, 94. [Google Scholar] [CrossRef]
- Fang, S.; Zhou, S.; Yurchenko, D.; Yang, T.; Liao, W. Multistability phenomenon in signal processing, energy harvesting, composite structures, and metamaterials: A review. Mech. Syst. Signal Process. 2022, 166, 108419. [Google Scholar] [CrossRef]
- Wen, Z.; Jin, Y.; Gao, P.; Zhuang, X.; Rabaczuk, T.; Djafari, B. Topological cavities in phononic plates for robust energy harvesting. Mech. Syst. Signal Process. 2022, 162, 108047. [Google Scholar] [CrossRef]
- Anton, S.; Sodano, H. A review of power harvesting using piezoelectric materials (2003–2006). Smart Mater. Struct. 2007, 16, R1–R21. [Google Scholar] [CrossRef]
- Shu, Y.; Lien, I. Efficiency of energy conversion for a piezoelectric power harvesting system. J. Micromech. Microeng. 2006, 16, 2429–2438. [Google Scholar] [CrossRef]
- Muralt, P.; Polcawich, R.; McKinstry, S. Piezoelectric thin films for sensors, actuators, and energy harvesting. MRS Bull. 2009, 34, 658–664. [Google Scholar] [CrossRef]
- Li, H.; Tian, C.; Deng, Z. Energy harvesting from low frequency applications using piezoelectric materials. Appl. Phys. Rev. 2014, 1, 041301. [Google Scholar] [CrossRef]
- Gu, L. Low-frequency piezoelectric energy harvesting prototype suitable for the MEMS implementation. Microelectron. J. 2011, 42, 277–282. [Google Scholar] [CrossRef]
- Halim, M.; Park, J. Piezoceramic based wideband energy harvester using impact-enhanced dynamic magnifier for low frequency vibration. Ceram. Int. 2015, 41, S702–S707. [Google Scholar] [CrossRef]
- Edwards, B.; Aw, K.; Hu, A. Mechanical frequency up-conversion for sub-resonance, low-frequency vibration harvesting. J. Intell. Mater. Syst. Struct. 2016, 27, 2145–2159. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Q.; Wang, W. Low-frequency wideband vibration energy harvesting by using frequency up-conversion and quin-stable nonlinearity. J. Sound Vib. 2017, 399, 169–181. [Google Scholar] [CrossRef]
- Liu, H.; Lee, C.; Kobayashi, T.; Tay, C.; Taya, C.; Quan, C. Piezoelectric MEMS-based wideband energy harvesting systems using a frequency-up-conversion cantilever stopper. Sens. Actuators A Phys. 2012, 186, 242–248. [Google Scholar] [CrossRef]
- Gu, L.; Livermore, C. Impact-driven, frequency up-converting coupled vibration energy harvesting device for low frequency operation. Smart Mater. Struct. 2011, 20, 045004. [Google Scholar] [CrossRef]
- Chen, S.; Ma, L.; Chen, T.; Liu, H. Modeling and verification of a piezoelectric frequency-up-conversion energy harvesting system. Microsyst. Technol. 2017, 23, 2459–2466. [Google Scholar] [CrossRef]
- Zhang, J.; Qin, L. A tunable frequency up-conversion wideband piezoelectric vibration energy harvester for low-frequency variable environment using a novel impact- and rope-driven hybrid mechanism. Appl. Energy 2019, 240, 26–34. [Google Scholar] [CrossRef]
- Halim, M.; Kabir, M.; Cho, H.; Park, J. A Frequency Up-Converted Hybrid Energy Harvester Using Transverse Impact-Driven Piezoelectric Bimorph for Human-Limb Motion. Micromachines 2019, 10, 701. [Google Scholar] [CrossRef]
- Abedini, A.; Wang, F. Energy harvesting of a frequency up-conversion piezoelectric harvester with controlled impact. Eur. Phys. J. Spec. Top. 2019, 228, 1459–1474. [Google Scholar] [CrossRef]
- Chen, S.; Ma, L.; Chen, T.; Liu, H.; Sun, L. A magnetic force induced frequency-up-conversion energy harvesting system. In Proceedings of the 2016 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland, New Zealand, 10 October 2016. [Google Scholar]
- Fang, S.; Chen, K.; Xing, J.; Zhou, S.; Liao, W. Tuned bistable nonlinear energy sink for simultaneously improved vibration suppression and energy harvesting. Int. J. Mech. Sci. 2021, 212, 106838. [Google Scholar] [CrossRef]
- Fang, S.; Chen, K.; Xing, J.; Zhou, S.; Liao, W. Analytical and experimental investigation of the centrifugal softening and stiffening effects in rotational energy harvesting. J. Sound Vib. 2020, 488, 115643. [Google Scholar] [CrossRef]
- Guyomar, D.; Badel, A.; Lefeuvre, E.; Richard, C. Toward Energy Harvesting Using Active Materials and Conversion Improvement by Nonlinear Processing. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 584–595. [Google Scholar] [CrossRef]
- Lefeuvre, E.; Badel, A.; Richard, C.; Guyomar, D. Piezoelectric Energy Harvesting Device Optimization by Synchronous Electric Charge Extraction. J. Intell. Mater. Syst. Struct. 2005, 16, 865–876. [Google Scholar] [CrossRef]
- Wu, Y.; Badel, A.; Formosa, F.; Liu, W. Piezoelectric vibration energy harvesting by optimized synchronous electric charge extraction. J. Intell. Mater. Syst. Struct. 2012, 24, 1445–1458. [Google Scholar] [CrossRef]
- Liu, W.; Qin, G.; Zhu, Q.; Hu, G. Synchronous extraction circuit with self-adaptive peak-detection mechanical switches design for piezoelectric energy harvesting. Appl. Energy 2018, 230, 1292–1303. [Google Scholar] [CrossRef]
- Liu, W.; Huang, Y.; Wang, J. Energy Current Analysis of an Improved Self-Adaptive Mechatronic Approach for P-SSHI. IEEE Trans. Ind. Electron. 2021, 68, 1434–1444. [Google Scholar] [CrossRef]
- Liu, W.; Qin, G.; Zhu, Q.; Hu, G. Self-adaptive memory foam switches for piezoelectric synchronous harvesting circuits. Smart Mater. Struct. 2018, 27, 117003. [Google Scholar] [CrossRef]
- Wu, Y.; Badel, A.; Formosa, F.; Liu, W. Nonlinear vibration energy harvesting device integrating mechanical stoppers used as synchronous mechanical switches. J. Intell. Mater. Syst. Struct. 2014, 25, 1658–1663. [Google Scholar] [CrossRef]
- Chen, Y.; Vasic, D.; Costa, F.; Wu, W.; Lee, C. A self-powered switching circuit for piezoelectric energy harvesting with velocity control. Eur. Phys. J. Appl. Phys. EDP Sci. 2012, 57, 30903. [Google Scholar] [CrossRef]
- Liang, J.; Liao, W. Improved Design and Analysis of Self-Powered Synchronized Switch Interface Circuit for Piezoelectric Energy Harvesting Systems. IEEE Trans. Ind. Electron. 2012, 59, 1950–1960. [Google Scholar] [CrossRef]
- Boisseau, S.; Gasnier, P.; Gallardo, M.; Despessem, G. Self-starting power management circuits for piezoelectric and electret-based electrostatic mechanical energy harvesters. J. Phys. Conf. Ser. 2013, 476, 2080. [Google Scholar] [CrossRef]
- Liu, W.; Badel, A.; Formosa, F.; Zhu, Q. Comparative Case Study on the Self-Powered Synchronous Switching Harvesting Circuits with BJT or MOSFET Switches. IEEE Trans. Power Electron. 2018, 33, 9506–9519. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, C.; Badel, A.; Formosa, F.; Zhu, Q.; Hu, G. Compact self-powered synchronous energy extraction circuit design with improved performance. Smart Mater. Struct. 2018, 27, 047001. [Google Scholar] [CrossRef]
- Chew, Z.; Zhu, M. Adaptive Self-configurable Rectifier for Extended Operating Range of Piezoelectric Energy Harvesting. IEEE Trans. Ind. Electron. 2019, 67, 3267–3276. [Google Scholar] [CrossRef]
- Lu, S.; Boussaid, F. A Highly Efficient P-SSHI Rectifier for Piezoelectric Energy Harvesting. IEEE Trans. Power Electron. 2015, 30, 5364–5369. [Google Scholar] [CrossRef]
- Liu, H.; Lee, C.; Kobayashi, T.; Tay, C.; Quan, C. Investigation of a MEMS piezoelectric energy harvester system with a frequency-widened-bandwidth mechanism introduced by mechanical stoppers. Smart Mater. Struct. 2012, 21, 035005. [Google Scholar] [CrossRef]
- Halim, M.; Park, J. Theoretical modeling and analysis of mechanical impact driven and frequency up-converted piezoelectric energy harvester for low-frequency and wide-bandwidth operation. Sens. Actuators A 2014, 208, 56–65. [Google Scholar] [CrossRef]
- Liu, H.; Tay, C.; Quan, C.; Kobayashi, T.; Lee, C. Piezoelectric MEMS Energy Harvester for Low-Frequency Vibrations With Wideband Operation Range and Steadily Increased Output Power. J. Microelectromech. Syst. 2011, 20, 1131–1142. [Google Scholar] [CrossRef]
- Chen, C.; Zhao, B.; Liang, J. Revisit of synchronized electric charge extraction (SECE) in piezoelectric energy harvesting by using impedance modeling. Smart Mater. Struct. 2019, 28, 105053. [Google Scholar] [CrossRef]
- Brenes, A.; Morel, A.; Gibus, D.; Yoo, C.; Gasnierb, P.; Lefeuvre, E.; Badel, A. Large-bandwidth piezoelectric energy harvesting with frequency-tuning synchronized electric charge extraction. Sens. Actuators A Phys. 2020, 302, 111759. [Google Scholar] [CrossRef]
- Wu, L.; Do, X.; Lee, S.; Ha, D. A self-powered and optimal SSHI circuit integrated with an active rectifier for piezoelectric energy harvesting. IEEE Trans. Circuits Syst. I Reg. Pap. 2017, 64, 537–549. [Google Scholar] [CrossRef]
- Hsieh, P.; Chen, C.; Chen, H. Improving the scavenged power of nonlinear piezoelectric energy harvesting interface at off-resonance by introducing switching delay. IEEE Trans. Power Electron. 2015, 30, 3142–3155. [Google Scholar] [CrossRef]
- Wu, Y.; Badel, A.; Formosa, F. Self-powered optimized synchronous electric charge extraction circuit for piezoelectric energy harvesting. J. Intell. Mater. Syst. Struct. 2014, 25, 2165–2176. [Google Scholar] [CrossRef]
- Chen, C.; Chen, Z.; Xiong, Y.; Shi, H.; Yang, Y. A high-efficiency, self-powered nonlinear interface circuit for bi-stable rotating piezoelectric vibration energy harvesting with nonlinear magnetic force. Int. J. Appl. Electromagn. Mech. 2016, 51, 235–248. [Google Scholar] [CrossRef]





| Interface | Harvested Power |
|---|---|
| SEH | |
| SP-SSHI | |
| SP-SECE | |
| SP-OSECE |
| Definition | Value | Definition | Value |
|---|---|---|---|
| Diode (Di, Dpi) | BAQ135 | Cr | 100 uF |
| Transformer | MSD1278T-105KL | Rbi | 3.3 kΩ |
| BJT (Si) | MMBTA05LT1G | Rgi | 1 MΩ |
| Rload | Pin-type resistance (external connection) | Rpi | 100 kΩ |
| Transistor (Tpi) | MMBTA56 | Cpi | 1 nf |
| Inductance L1, L2, L3 (H) | 1 × 10−3 |
| Parameter | Value |
|---|---|
| Clamped capacitance of the piezoelectric element C0 (F) | 20.68 × 10−9 |
| Piezoelectric coefficient α (N/V) | 5.557 × 10−4 |
| Open-circuit mechanical quality factor Qm | 63.8 |
| Squared electromechanical coupling coefficient k2 | 0.01 |
| Open-circuit resonance frequency of HFB f1 (Hz) | 36.25 |
| Stiffness of high-frequency beams (N/m) | 1450 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Chen, K.; Tang, H.; Liu, W. Comparison of Four Electrical Interfacing Circuits in Frequency Up-Conversion Piezoelectric Energy Harvesting. Micromachines 2022, 13, 1596. https://doi.org/10.3390/mi13101596
Lu H, Chen K, Tang H, Liu W. Comparison of Four Electrical Interfacing Circuits in Frequency Up-Conversion Piezoelectric Energy Harvesting. Micromachines. 2022; 13(10):1596. https://doi.org/10.3390/mi13101596
Chicago/Turabian StyleLu, Han, Kairui Chen, Hao Tang, and Weiqun Liu. 2022. "Comparison of Four Electrical Interfacing Circuits in Frequency Up-Conversion Piezoelectric Energy Harvesting" Micromachines 13, no. 10: 1596. https://doi.org/10.3390/mi13101596
APA StyleLu, H., Chen, K., Tang, H., & Liu, W. (2022). Comparison of Four Electrical Interfacing Circuits in Frequency Up-Conversion Piezoelectric Energy Harvesting. Micromachines, 13(10), 1596. https://doi.org/10.3390/mi13101596







