Development of a Flexible MEMS Sensor for Subsonic Flow
Abstract
:1. Introduction
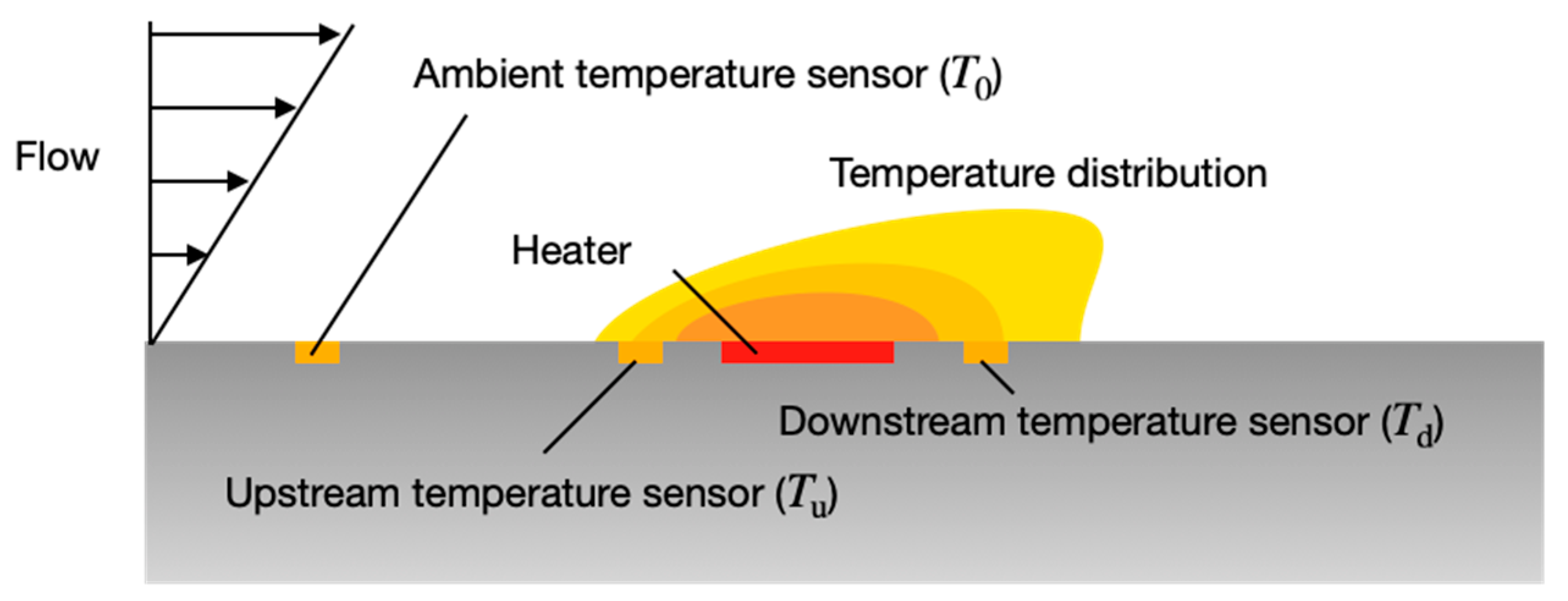
2. Measurement Principle
3. Design and Fabrication of the Sensor
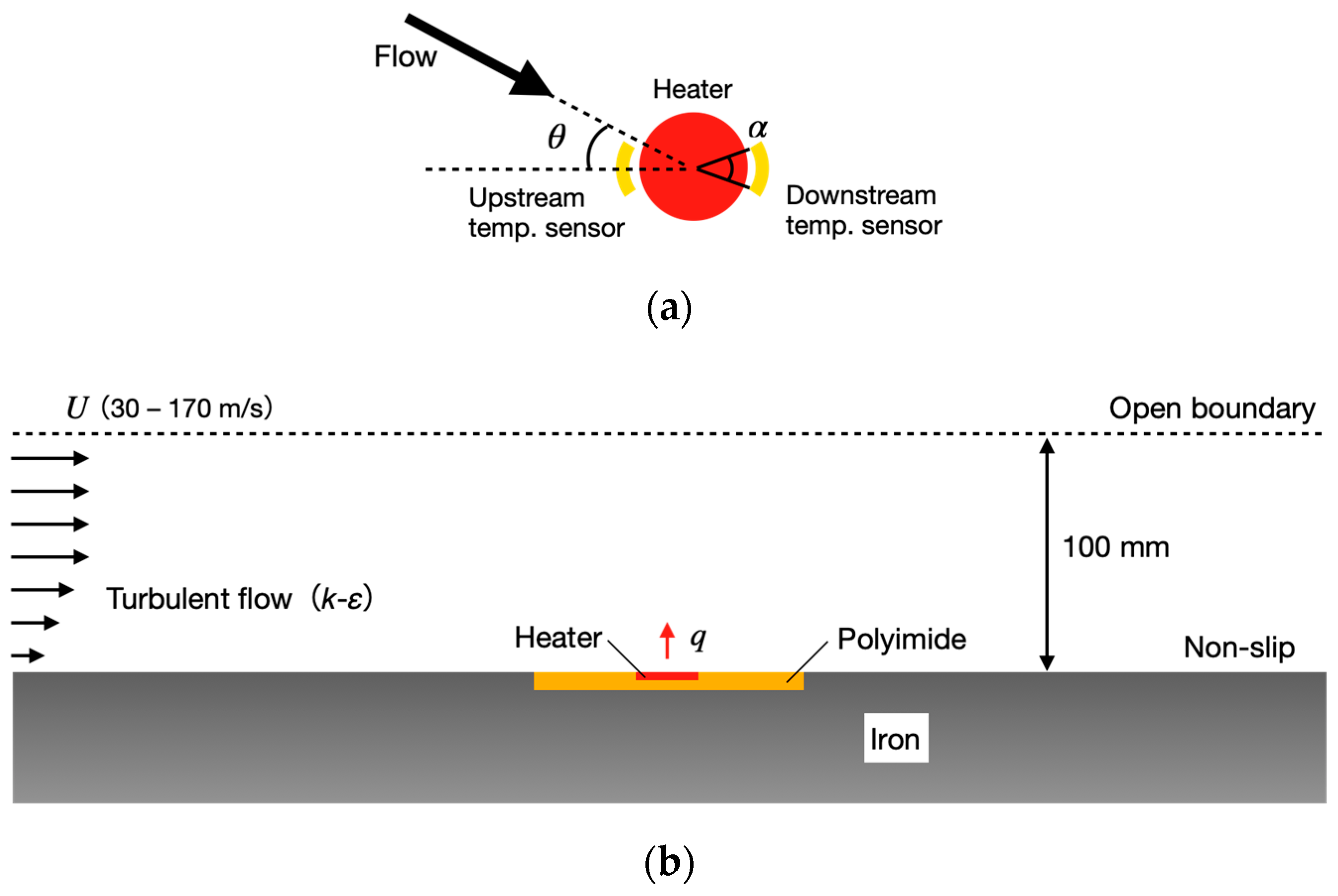
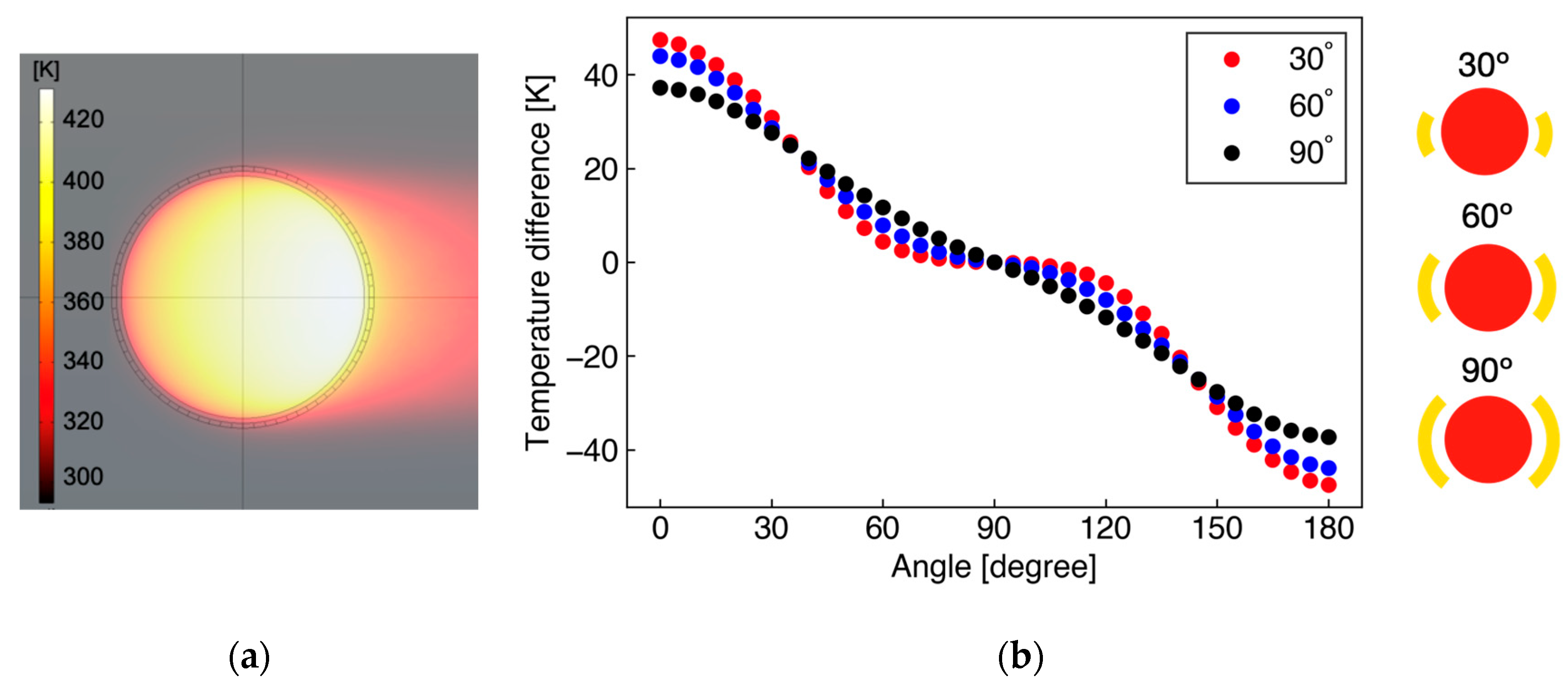
3.1. Numerical Simulation for Sensor Design
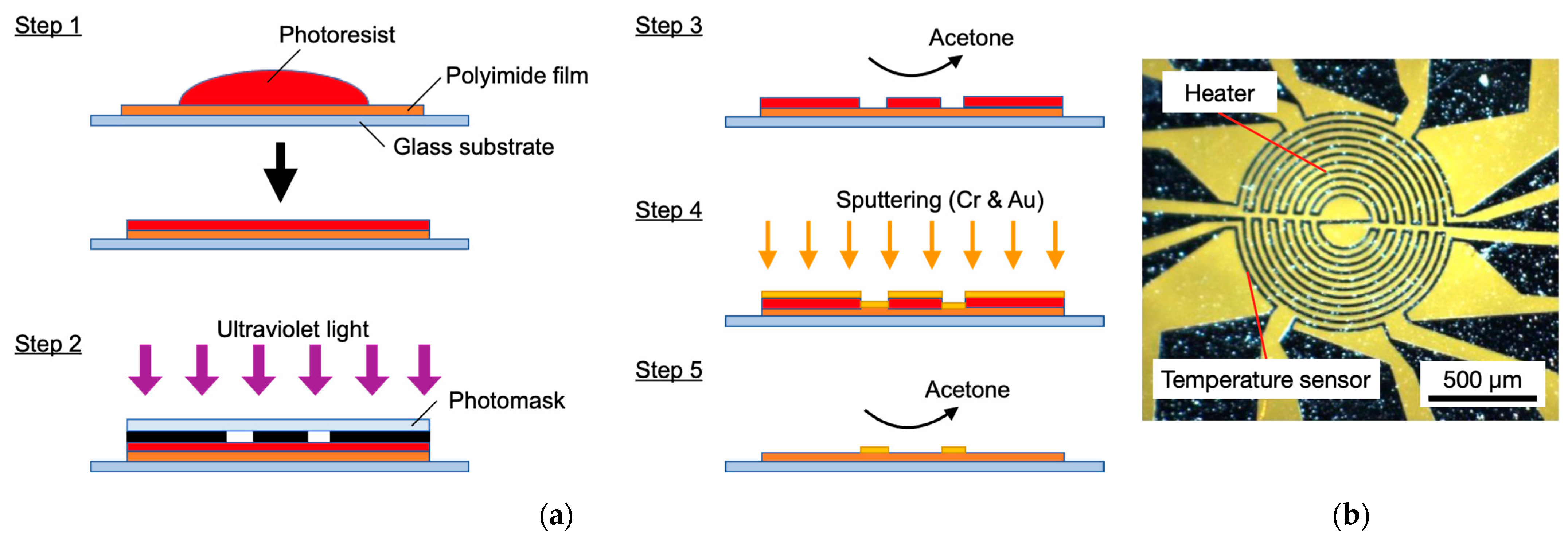
3.2. Sensor Fabrication
4. Experimental Results
4.1. Measurement System
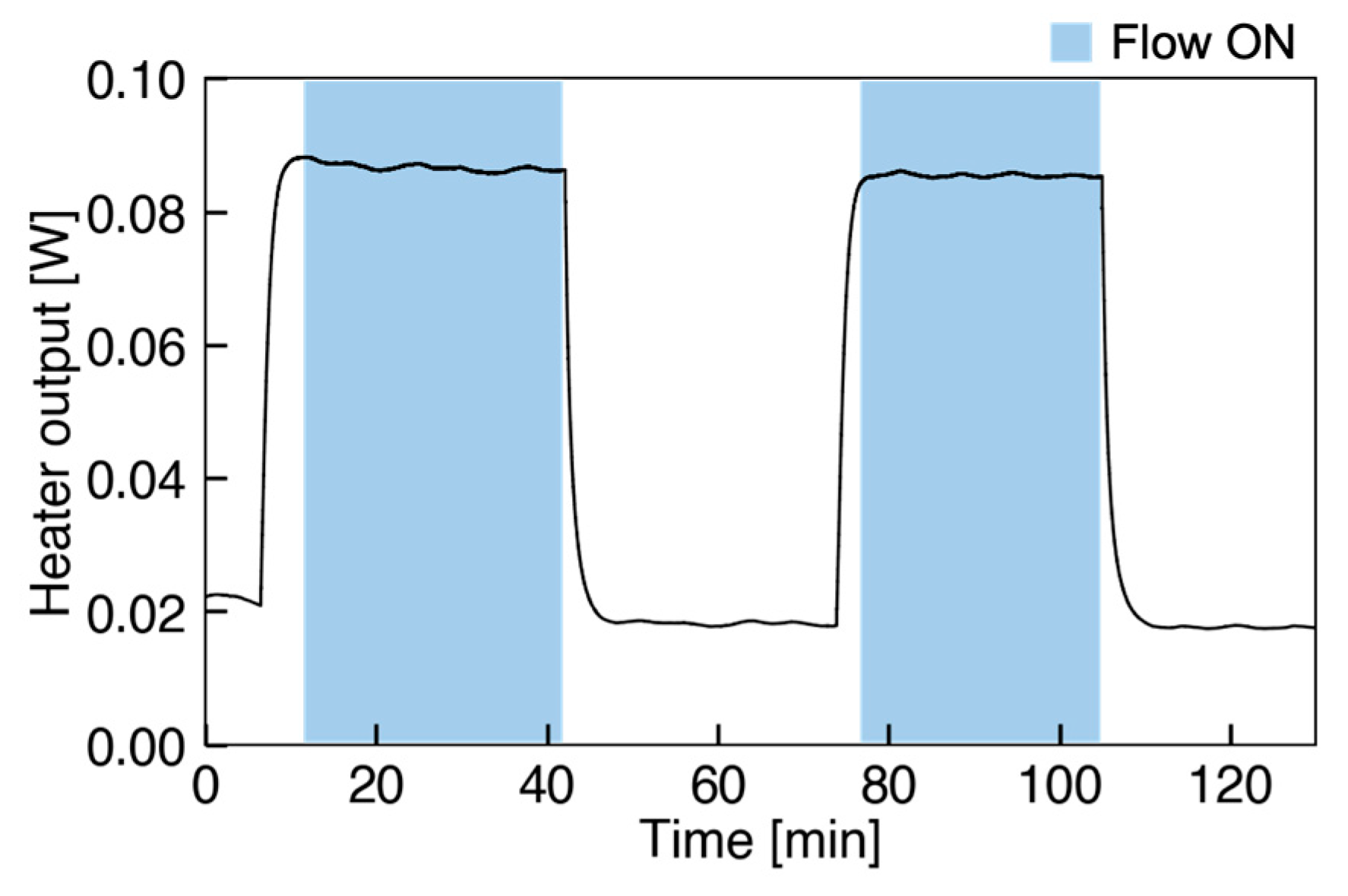
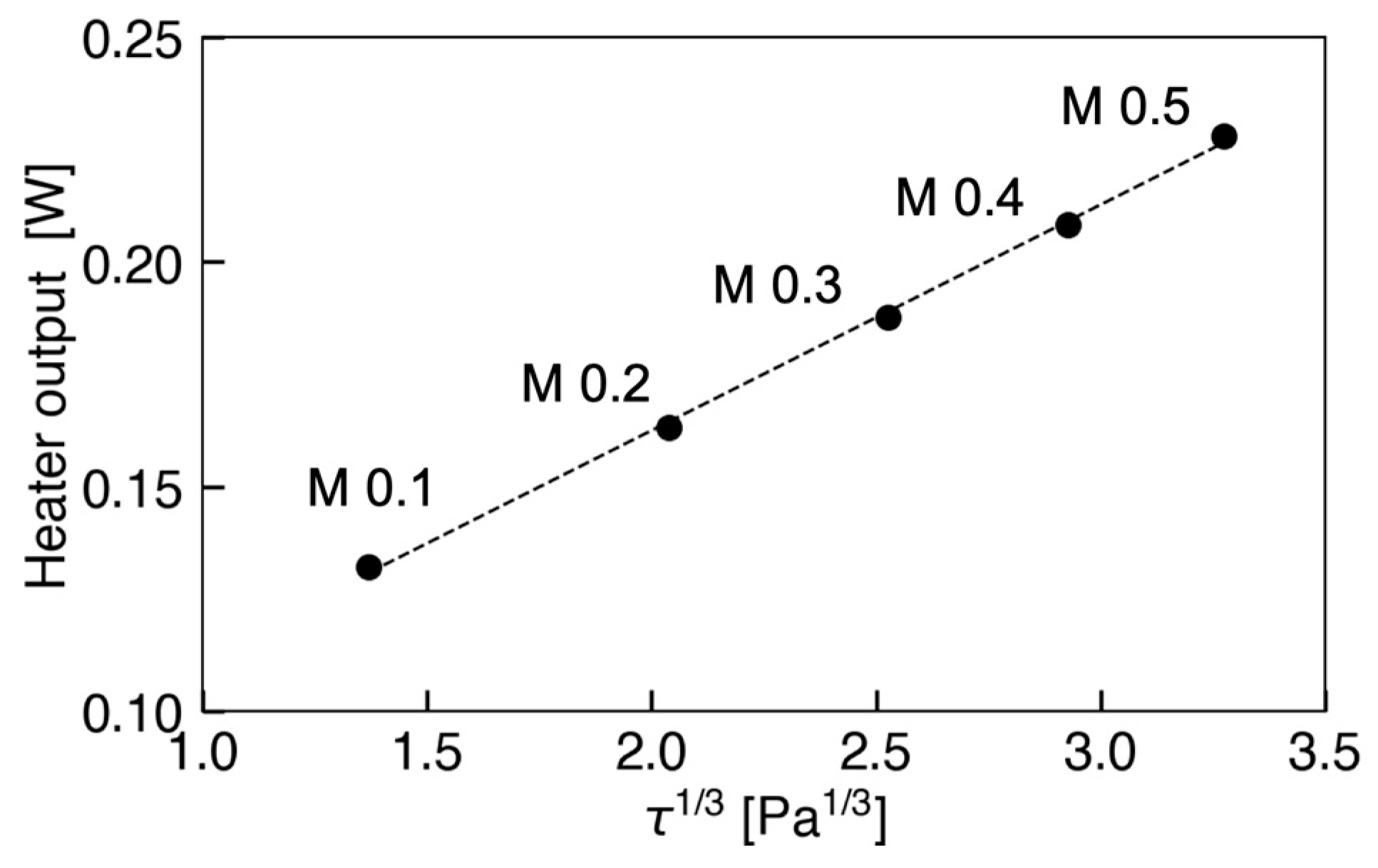
4.2. Wall Shear Stress Measurement
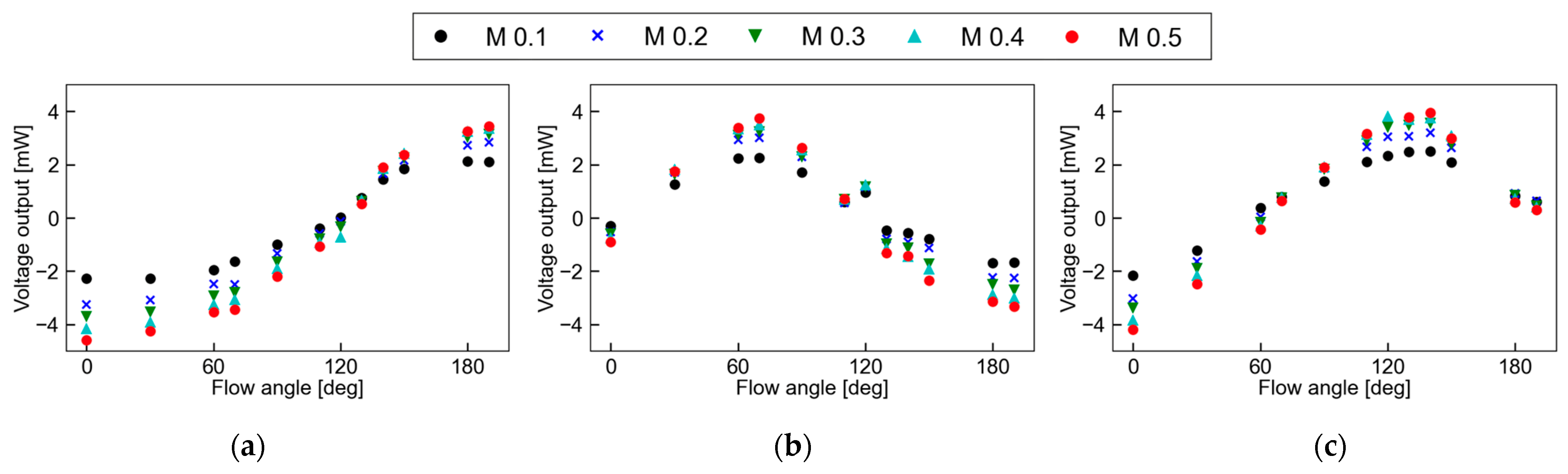
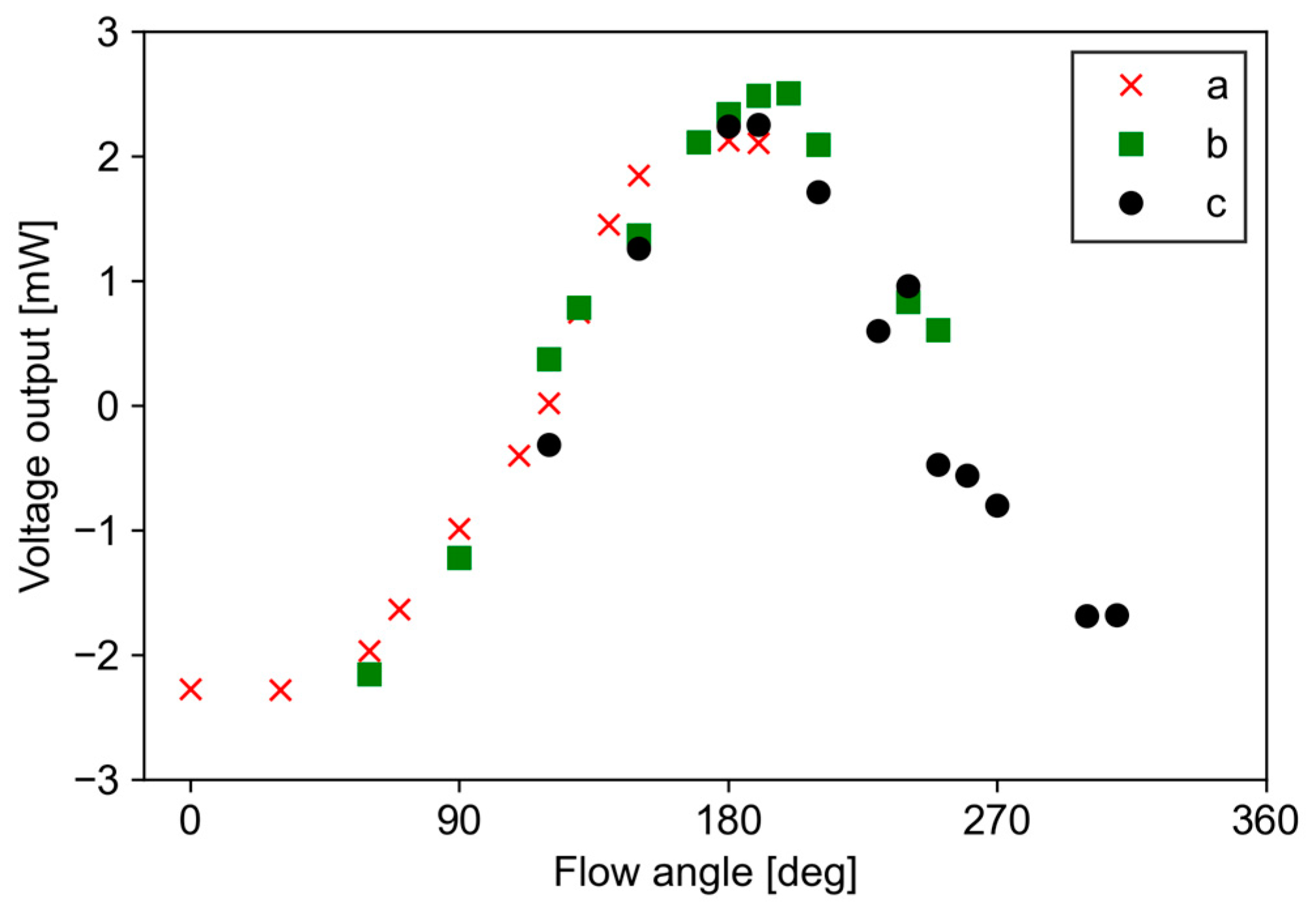
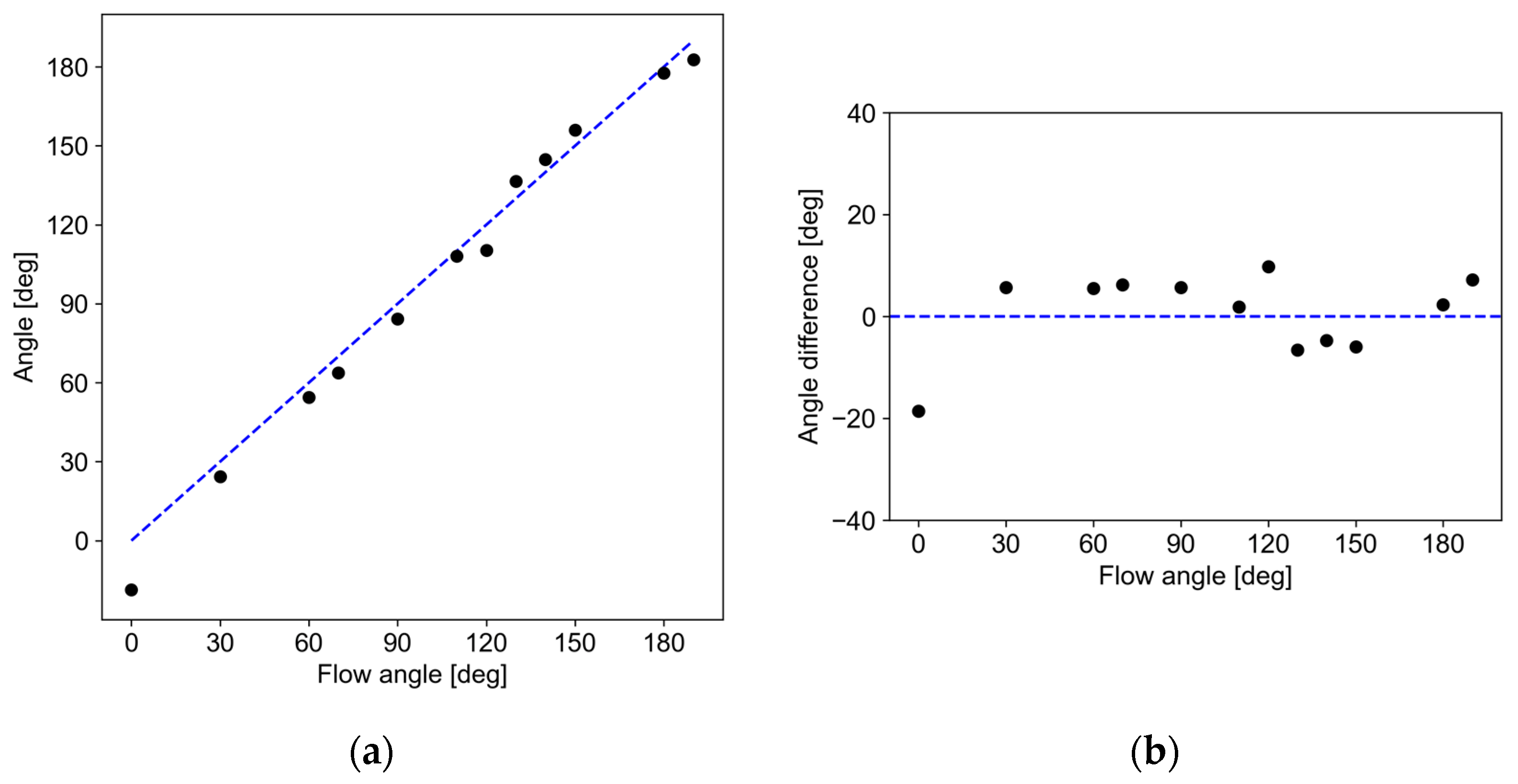
4.3. Flow Angle Measurement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- National Institute for Environmental Studies (NIES). National Greenhouse Gas Inventory Report of JAPAN; NIES: Tsukuba, Japan, 2022.
- Li, J.; Ji, L. Efficient design method for applying vortex generators in turbomachinery. J. Turbomach. 2019, 141, 081005. [Google Scholar] [CrossRef]
- Yi, W.; Ji, L. Control and entropy analysis of corner flow separation in a compressor cascade using streamwise grooves. Entropy 2019, 21, 928. [Google Scholar] [CrossRef]
- Gbadebo, S.A.; Cumpsty, N.A.; Hynes, T.P. Three-dimensional separations in axial compressors. J. Turbomach. 2005, 127, 331–339. [Google Scholar] [CrossRef]
- Yan, P.; Chu, N.; Wu, D.; Cao, L.; Yang, S.; Wu, P. Computational fluid dynamics-based pump redesign to improve efficiency and decrease unsteady radial forces. J. Fluids Eng. 2017, 139, 011101. [Google Scholar] [CrossRef]
- Park, D.; Shim, H.; Lee, Y. PIV measurement of separation bubble on an airfoil at low Reynolds numbers. J. Aerosp. Eng. 2020, 33, 04019105. [Google Scholar] [CrossRef]
- Segawa, T.; Suzuki, D.; Fujino, T.; Jukes, T.; Matsunuma, T. Feedback control of flow separation using plasma actuator and FBG sensor. Int. J. Aero. Eng. 2016, 16, 8648919. [Google Scholar] [CrossRef]
- Kuo, J.T.W.; Yu, L.; Meng, E. Micromachined thermal flow sensors—A review. Micromachines 2012, 3, 550–573. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Lee, C.-Y.; Chiang, C.-M. A MEMS-based air flow sensor with a free-standing micro-cantilever structure. Sensors 2007, 7, 2389–2401. [Google Scholar] [CrossRef]
- van Oudheusden, B.W.; van Herwaarden, A.W. High-sensitivity 2-D flow sensor with and etched thermal isolation structure. Sensor Actuator. A Phys. 1990, 22, 425–430. [Google Scholar] [CrossRef]
- Bailey, S.C.C.; Kunkel, C.J.; Hultmark, M.; Vallikivi, M.; Hill, J.P.; Meyer, K.A.; Tsay, C.; Arnold, C.B.; Smits, A.J. Turbulence measurements using a nanoscale thermal anemometry probe. J. Fluid. Mech. 2010, 663, 160–179. [Google Scholar] [CrossRef]
- Xu, W.; Lijin, B.; Duan, M.; Wang, X.; Wicaksana, J.; Min, A.; Ahmed, M.; Wang, R.; Fang, N.X.; Bermak, A.; et al. A wireless dual-mode micro thermal flow sensor system with extended flow range by using 0.18μm CMOS-MEMS process. In Proceedings of the IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018; pp. 824–827. [Google Scholar]
- Sabaté, N.; Santander, J.; Fonseca, L.; Gràcia, I.; Cané, C. Multi-range silicon micromachined flow sensor. Sensor Actuator. A Phys. 2004, 110, 282–288. [Google Scholar] [CrossRef]
- Djuzhev, N.A.; Ryabov, V.T.; Demin, G.D.; Makhiboroda, M.A.; Evsikov, I.D.; Pozdnyakov, M.M.; Bespalov, V.A. Measurement system for wide-range flow evaluation and thermal characterization of MEMS-based thermoresistive flow-rate sensors. Sensor Actuator. A-Phys. 2021, 330, 112832. [Google Scholar] [CrossRef]
- Luca, A.D.; Longobardi, G.; Udrea, F. SOI multidirectional thermoelectric flow sensor for harsh environment applications. In Proceedings of the International Semiconductor Conference (CAS), Sinaia, Romania, 12–14 October 2015; pp. 95–98. [Google Scholar]
- Barmpakos, D.; Famelis, I.T.; Moschos, A.; Marninatos, D.; Kaltsas, G. Design and evaluation of a multidirectional thermal flow sensor on flexible substrate. J. Sens. 2019, 8476489. [Google Scholar] [CrossRef]
- Miau, J.J.; Leu, T.S.; Yu, J.M.; Tu, J.K.; Wang, C.T.; Lebiga, V.; Mironov, D.; Pak, A.; Zinovyev, V.; Chung, K.M. Mems thermal film sensors for unsteady flow measurement. Sensor Actuator. A Phys. 2015, 235, 1–13. [Google Scholar] [CrossRef]
- Tan, Z.; Shikida, M.; Hirota, M.; Xing, Y.; Sato, K.; Iwasaki, T.; Iriye, Y. Characteristics of on-wall in-tube flexible thermal flow sensor under radially asymmetric flow condition. Sensor Actuator. A Phys. 2007, 138, 87–96. [Google Scholar] [CrossRef]
- Petropoulos, A.; Pagonis, D.N.; Kaltsas, G. Flexible PCB-MEMS flow sensor. Procedia Eng. 2012, 47, 236–239. [Google Scholar] [CrossRef]
- Buder, U.; Petz, R.; Kittel, M.; Nitsche, W.; Obermeier, E. AeroMEMS polyimider based wall double hot-wire sensors for flow separation. Sensor Actuator. A Phys. 2008, 142, 130–137. [Google Scholar] [CrossRef]
- Shikida, M.; Yoshikawa, K.; Iwai, S.; Sato, K. Flexible flow sensor for large-scale air-conditioning network systems. Sensor Actuator. A Phys. 2012, 188, 2–8. [Google Scholar] [CrossRef]
- Liu, P.; Zhu, R.; Que, R. A flexible flow sensor system and its characteristics for fluid mechanics measurements. Sensors 2009, 9, 9533–9543. [Google Scholar] [CrossRef]
- Buchner, R.; Froehner, K.; Sosna, C.; Benecke, W.; Lang, W. Toward flexible thermoelectric flow sensors: A new technological approach. J. Microelectromech. Syst. 2008, 17, 1114–1119. [Google Scholar] [CrossRef]
- Zhu, R.; Que, R.; Liu, P. Flexible micro flow sensor for micro aerial vehicles. Front. Mech. Eng. 2017, 12, 539–545. [Google Scholar] [CrossRef]
- Xu, K.; Lu, Y.; Yamaguchi, T.; Arie, T.; Akita, S.; Takei, K. Highly precise multifunctional thermal management-based flexible sensing sheets. ACS Nano 2019, 13, 14348–14356. [Google Scholar] [CrossRef]
- Que, R.; Zhu, R. A compact flexible thermal flow sensor for detecting two-dimensional flow vector. IEEE Sens. J. 2015, 15, 1931–1936. [Google Scholar] [CrossRef]
- Ejeian, F.; Azadi, S.; Razmjou, A.; Orooji, Y.; Kottapalli, A.; Warkiani, M.E.; Asadnia, M. Design and applications of MEMS flow sensors: A review. Sensor Actuator. A Phys. 2019, 295, 483–502. [Google Scholar] [CrossRef]
- Yoshida, K.; Kanaoka, Y.; Kimura, S.; Kiwata, T.; Komatsu, N. Three-dimensional simulation of heat transfer in a microscale flow vector sensor (Numerical study toward improving the sensitivity of the sensor in a high-speed airflow). Trans. Jpn. Soc. Mech. Eng. 2021, 87, 21–110. [Google Scholar] [CrossRef]
- Ou, Y.; Qu, F.; Wang, G.; Nie, M.; Li, Z.; Ou, W. A MEMS thermal shear stress sensor produced by a combination of substrate-free structures with anodic bonding technology. Appl. Phys. Lett. 2016, 109, 023512. [Google Scholar] [CrossRef]
- Goldstein, R.J. Fluid Mechanics Measurements, 2nd ed.; Taylor & Francis: Philadelphia, PA, USA, 1996; pp. 610–615. [Google Scholar]
- Wang, Y.-H.; Chen, C.-P.; Chang, C.-M.; Lin, C.-P.; Lin, C.-H.; Fu, L.-M.; Lee, C.-Y. MEMS-based gas flow sensors. Microfluid. Nanofluid. 2009, 6, 333–346. [Google Scholar] [CrossRef]
- Bradshaw, P.; Unsworth, K. Comment on “Evaluation of Preston tube calibration equations in supersonic flow”. AIAA. J. 1974, 12, 1293–1295. [Google Scholar] [CrossRef]
- Johnson, M.A.; Moradi, M.H. PID Control: New Identification and Design Methods; Springer: London, UK, 2005; pp. 1–106. [Google Scholar]


| Type | References | Flexibility | Direction | Angle | Max. Velocity [m/s] |
|---|---|---|---|---|---|
| Hard | 9 | N | N | N | 45 |
| 10 | N | N | N | 63 | |
| 11 | N | N | N | 45 | |
| 12 | N | Y | N | 73 | |
| 13 | N | Y | N | 19 | |
| 14 | N | Y | N | 5 | |
| 15 | N | Y | Y | 10 | |
| 16 | N | Y | Y | 1 | |
| Soft | 17 | Y | N | N | 7.5 |
| 18 | Y | N | N | 25 | |
| 19 | Y | N | N | 1.5 | |
| 20 | Y | Y | N | 15 | |
| 21 | Y | N | N | 25 | |
| 22 | Y | N | Y | 14 | |
| 23 | Y | Y | N | 33 | |
| 24 | Y | N | Y | 13 | |
| 25 | Y | Y | N | 1.5 | |
| 26 | Y | Y | Y | 30 | |
| This study | Y | Y | Y | 170 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murakami, K.; Shiraishi, D.; Mizumi, S.; Oya, Y.; Omura, N.; Shibata, T.; Ichikawa, Y.; Motosuke, M. Development of a Flexible MEMS Sensor for Subsonic Flow. Micromachines 2022, 13, 1299. https://doi.org/10.3390/mi13081299
Murakami K, Shiraishi D, Mizumi S, Oya Y, Omura N, Shibata T, Ichikawa Y, Motosuke M. Development of a Flexible MEMS Sensor for Subsonic Flow. Micromachines. 2022; 13(8):1299. https://doi.org/10.3390/mi13081299
Chicago/Turabian StyleMurakami, Koichi, Daiki Shiraishi, Shunsuke Mizumi, Yoshiko Oya, Naoto Omura, Takanori Shibata, Yoshiyasu Ichikawa, and Masahiro Motosuke. 2022. "Development of a Flexible MEMS Sensor for Subsonic Flow" Micromachines 13, no. 8: 1299. https://doi.org/10.3390/mi13081299
APA StyleMurakami, K., Shiraishi, D., Mizumi, S., Oya, Y., Omura, N., Shibata, T., Ichikawa, Y., & Motosuke, M. (2022). Development of a Flexible MEMS Sensor for Subsonic Flow. Micromachines, 13(8), 1299. https://doi.org/10.3390/mi13081299






