Auto-Regression Model-Based Off-Line PID Controller Tuning: An Adaptive Strategy for DC Motor Control
Abstract
:1. Introduction
- Finding angular speed vs. voltage ratio and a method to forecast it.
- A strategy to re-tune PID gains off-line by changing angular speed vs. voltage ratio.
- An option so that the controller can adapt its gains based on current parameters.
- Overshoot shall be less than 10%.
- Settling time less or equal to 0.25 s.
- No error at steady state (0%).
2. Methods
2.1. Theoretical Basis
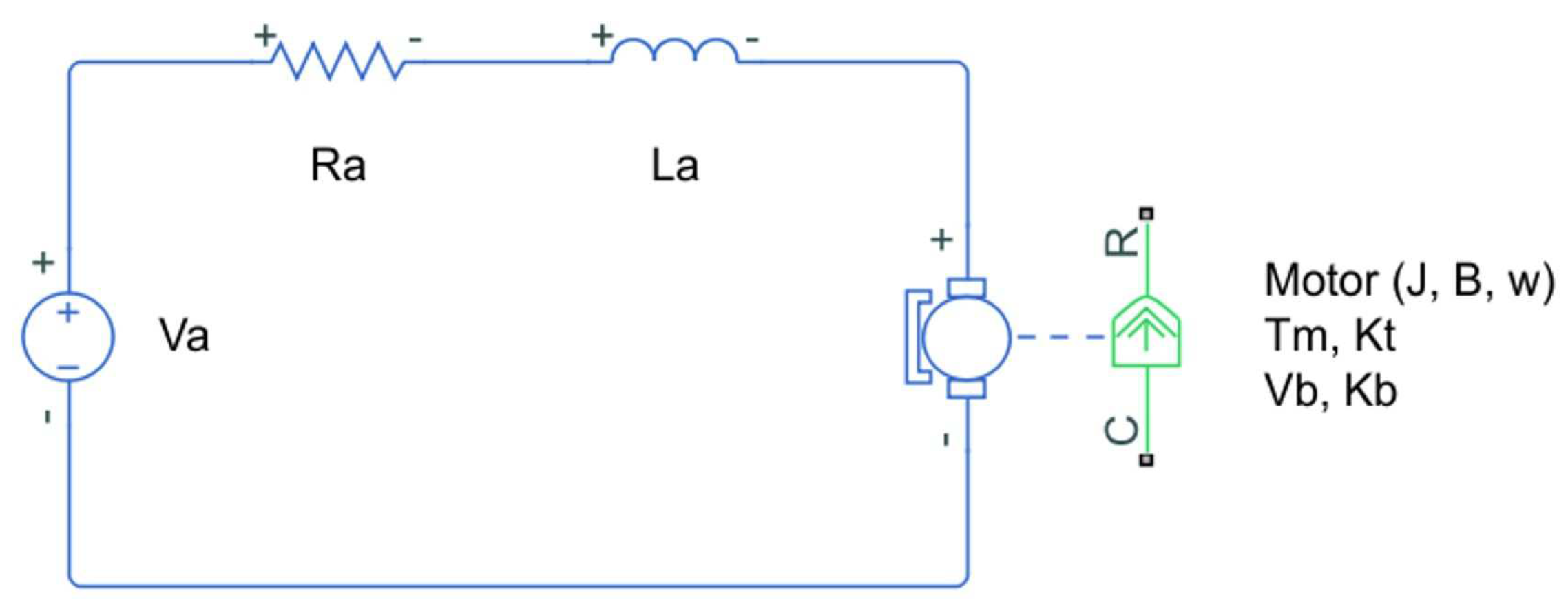
- The torque is proportional to the current. This relationship relies on the torque sensitivity constant ().
- The back electromotive force voltage is proportional to the angular velocity. This proportion depends on the voltage constant ().
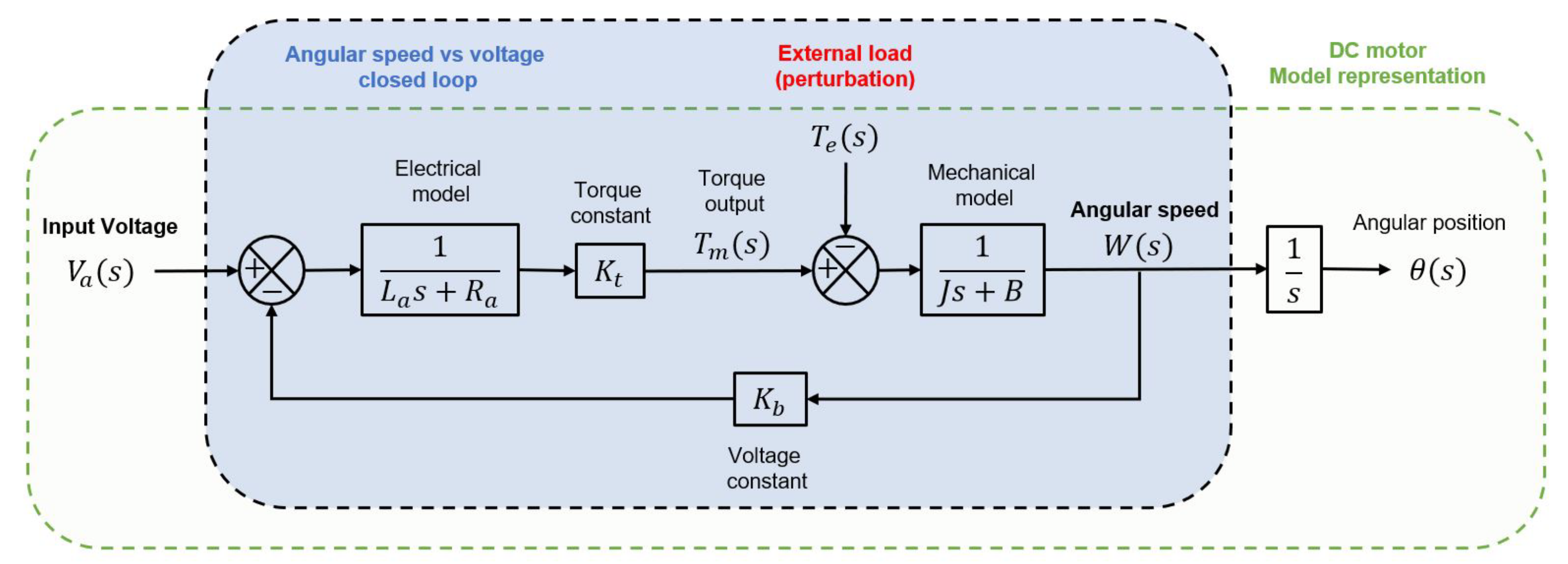
2.1.1. Transfer Function (TF) for a Direct Current (DC) Motor
2.1.2. DC Motor Identification
- Step and frequency response.
- State-space-based for modeling/identification.
2.1.3. Controller Approach
2.2. Modeling and Controlling the DC Motor through Its Transfer Function (TF)
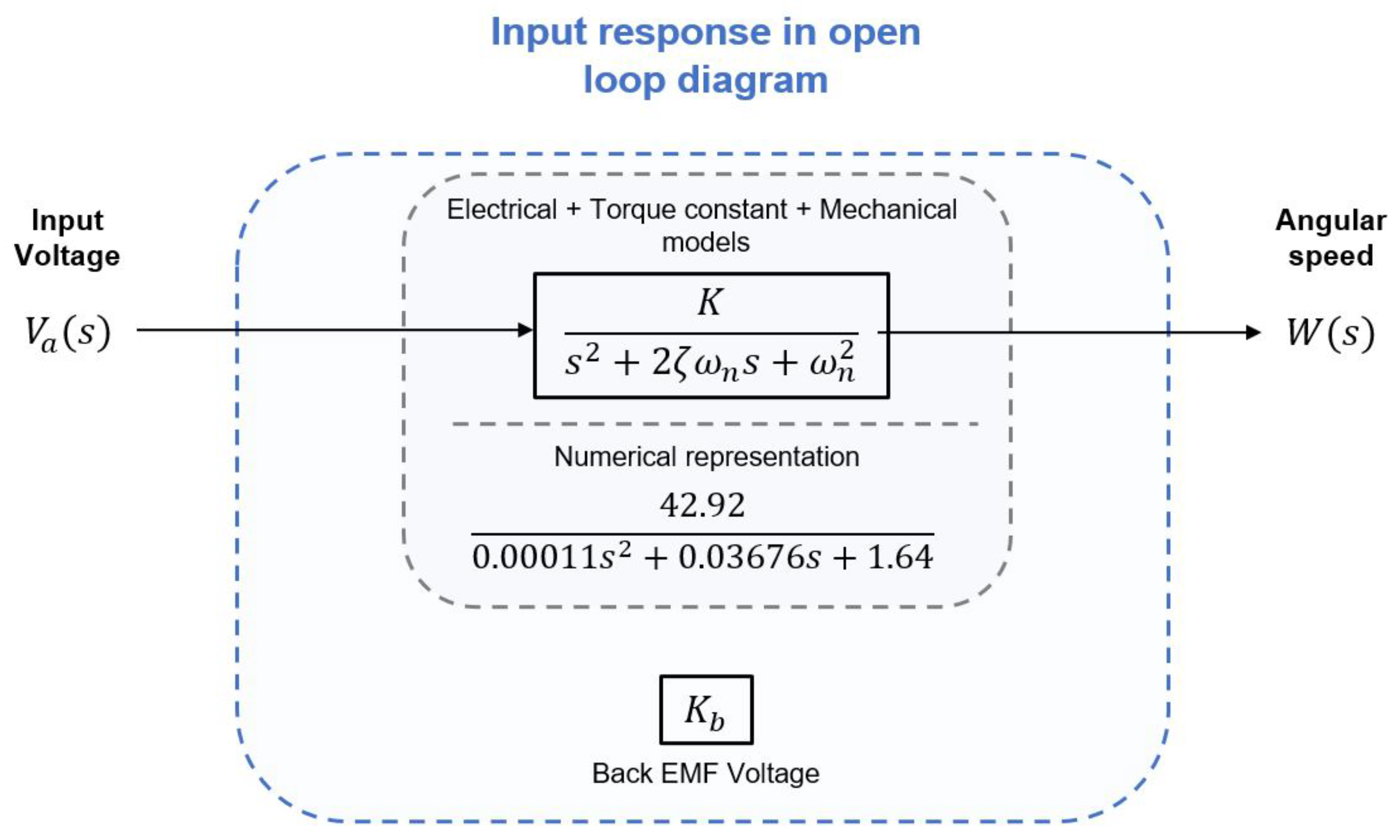
2.2.1. Open-Loop Simulation for Gathering Data
2.2.2. PID Controller Design for Closed-Loop Simulation
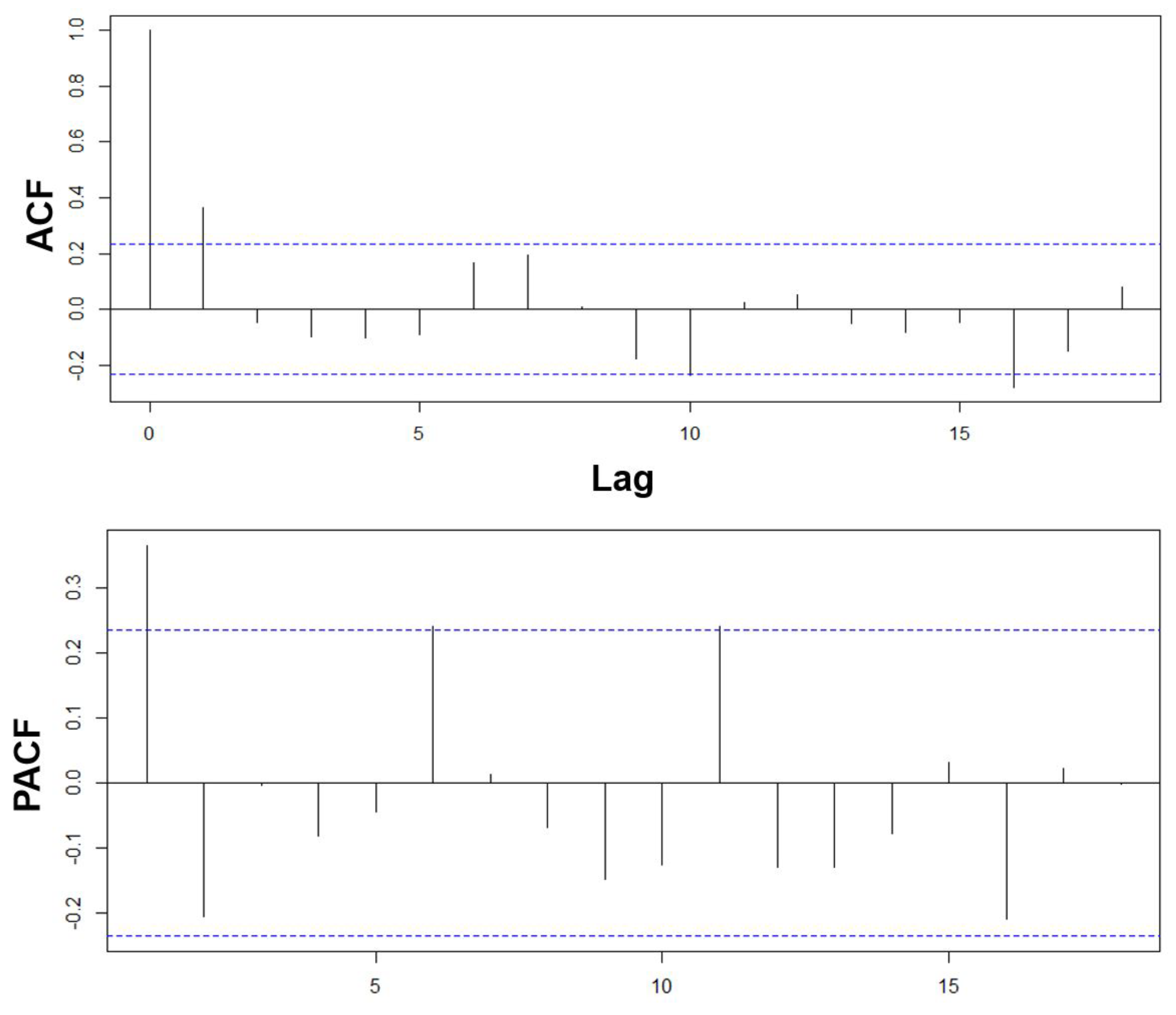
2.3. The Time Series (TS) Analysis and Stationary Check for the Proposed Model
- Forecasting a time series’s future values from current and past values.
- The determination of the transfer function of a system is subject to inertia.
- The design of simple control schemes utilizing potential deviations in the system output is compensated by adjusting the input variables.
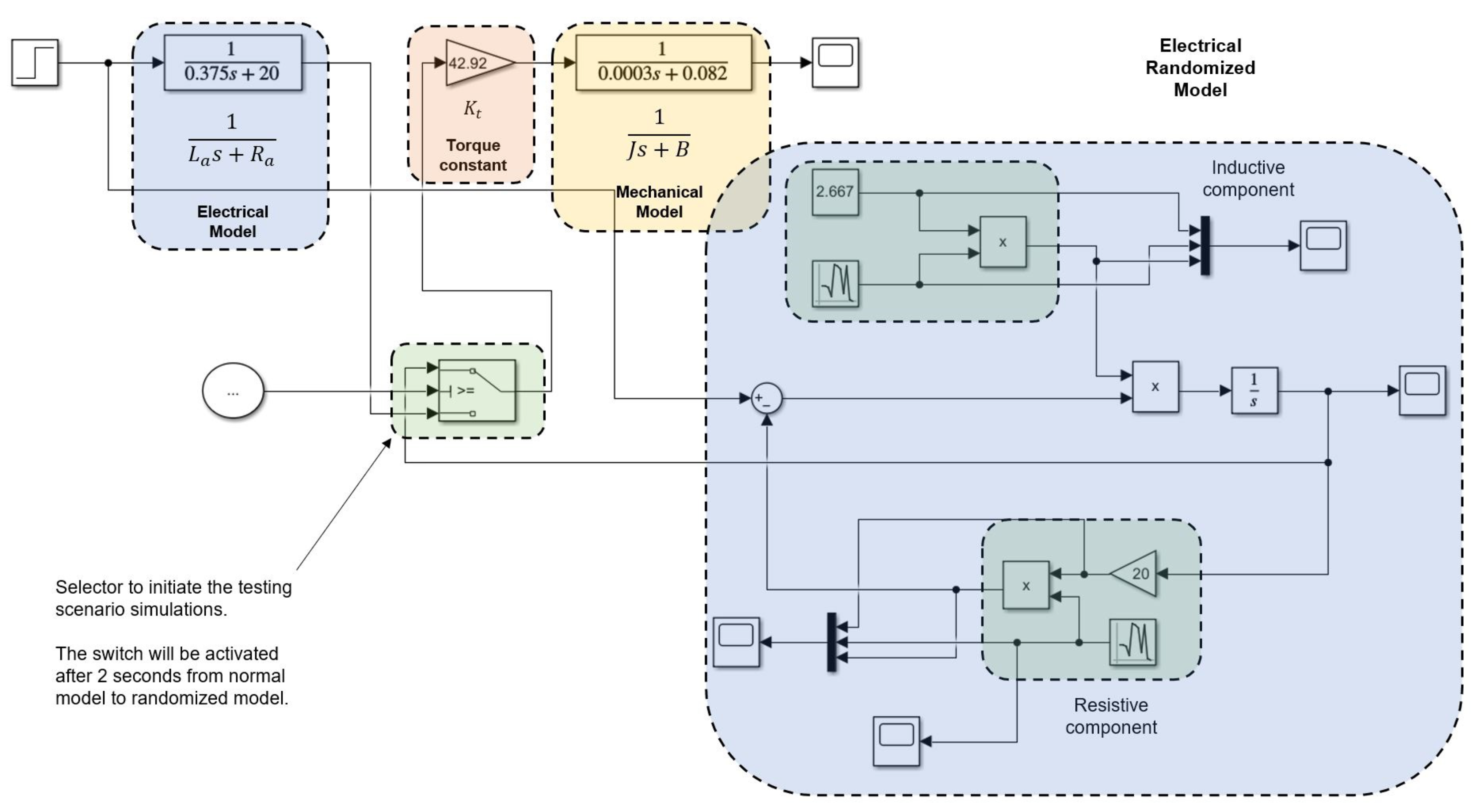
2.4. Proposed Testing for Simulation
3. Findings
3.1. In Terms of Control Performance
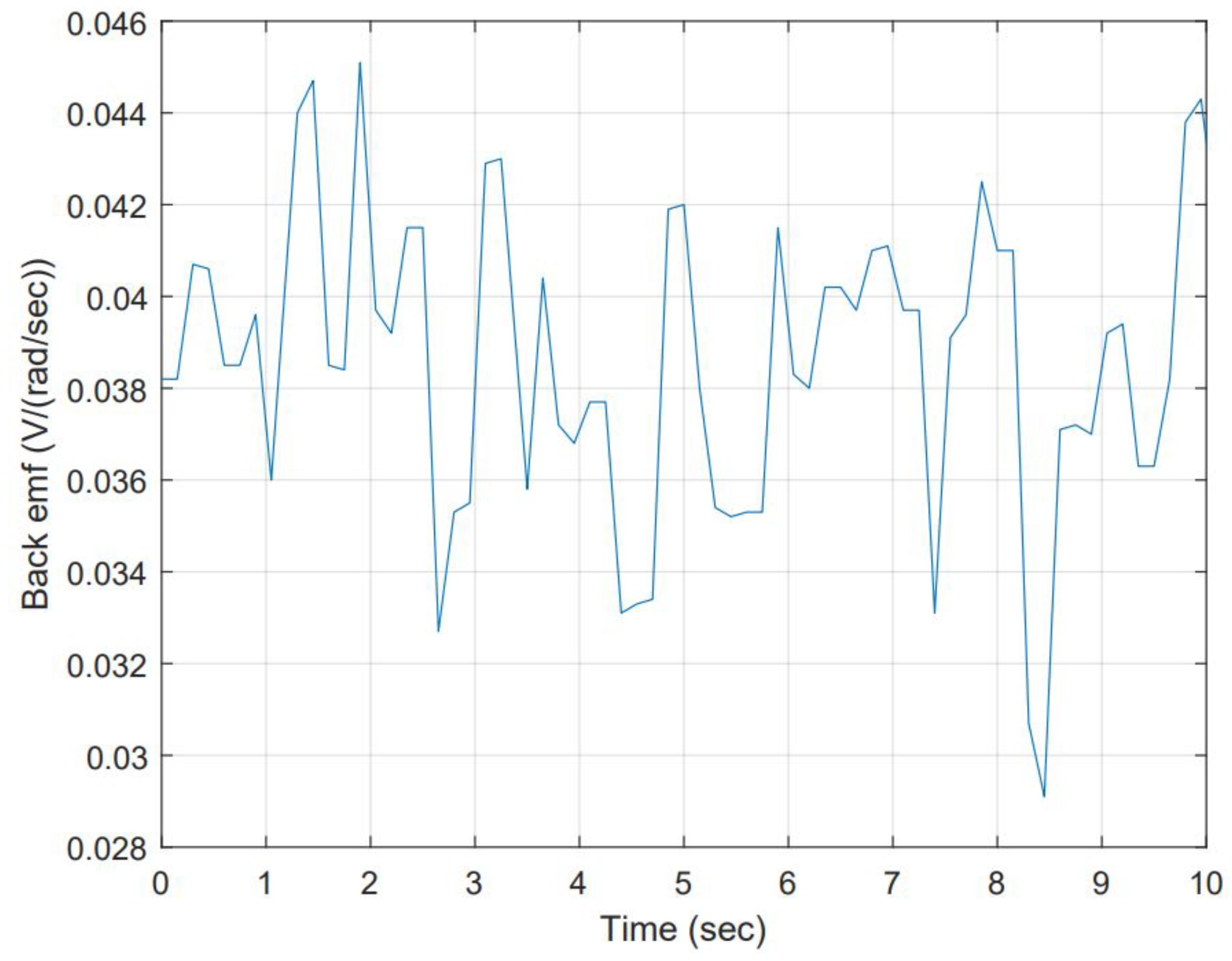
3.2. In Terms of Time Series, Assuming a Shortened Time Scenario to Collect Data
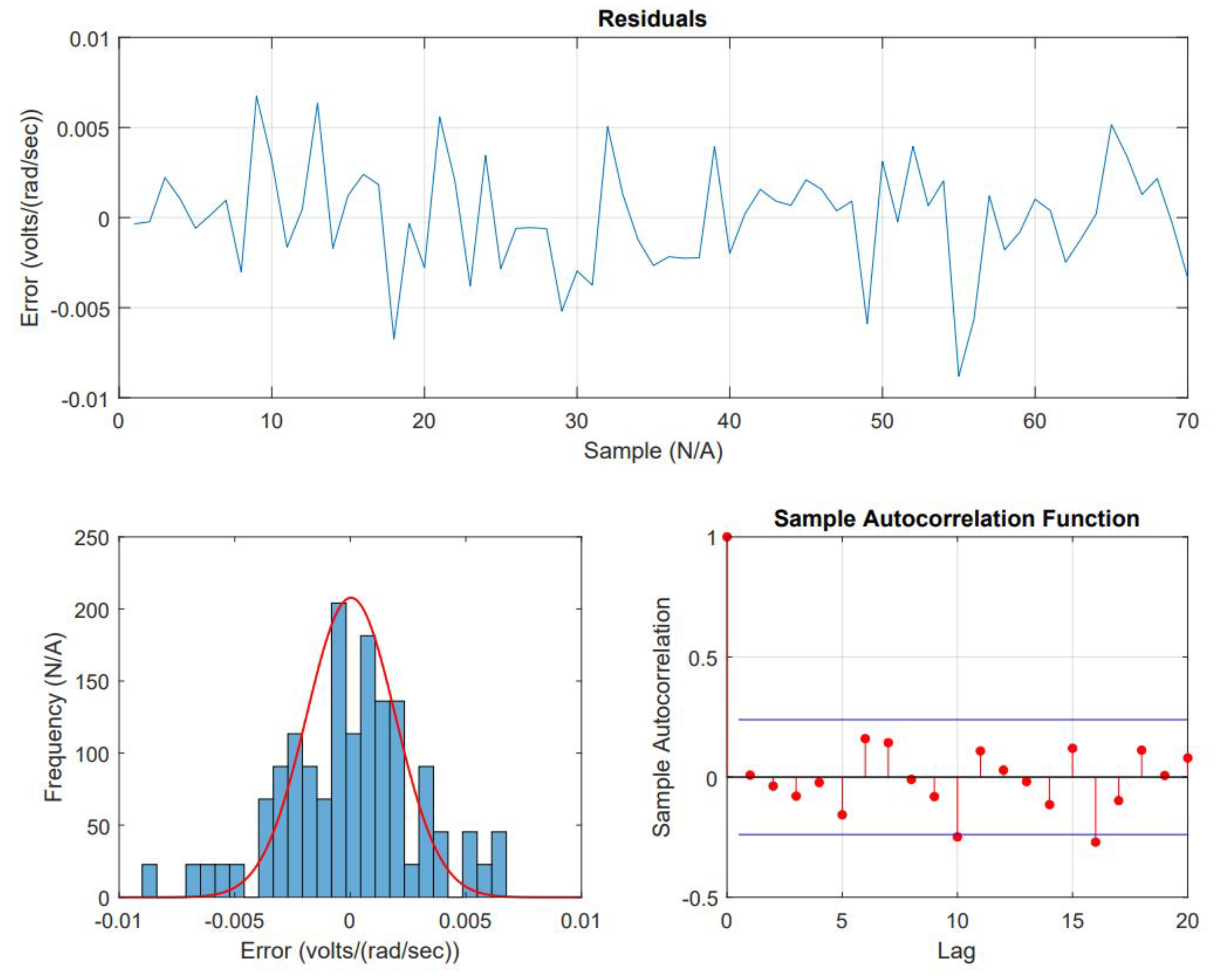
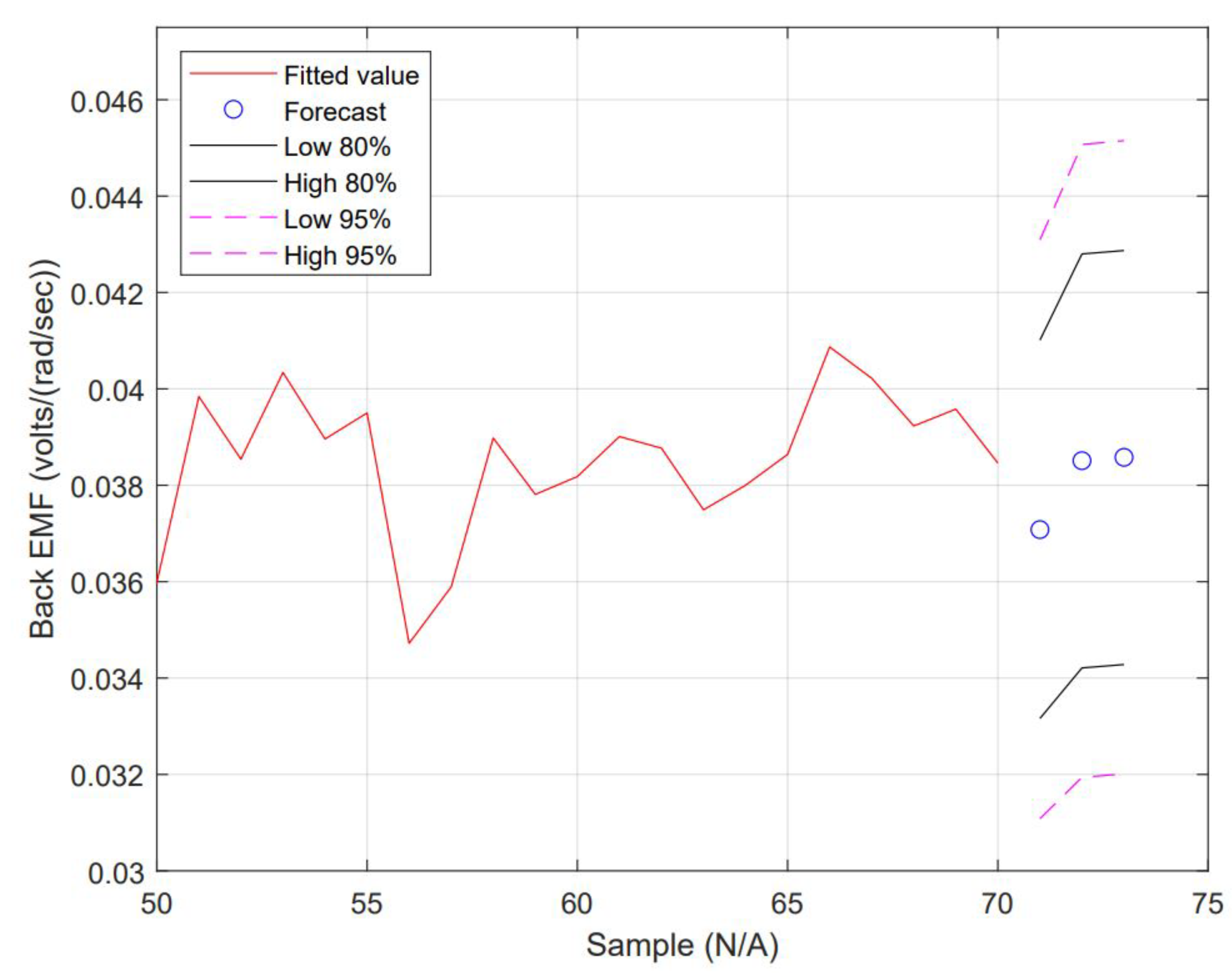
3.3. In Terms of an Auto-Regressive Moving Average Model
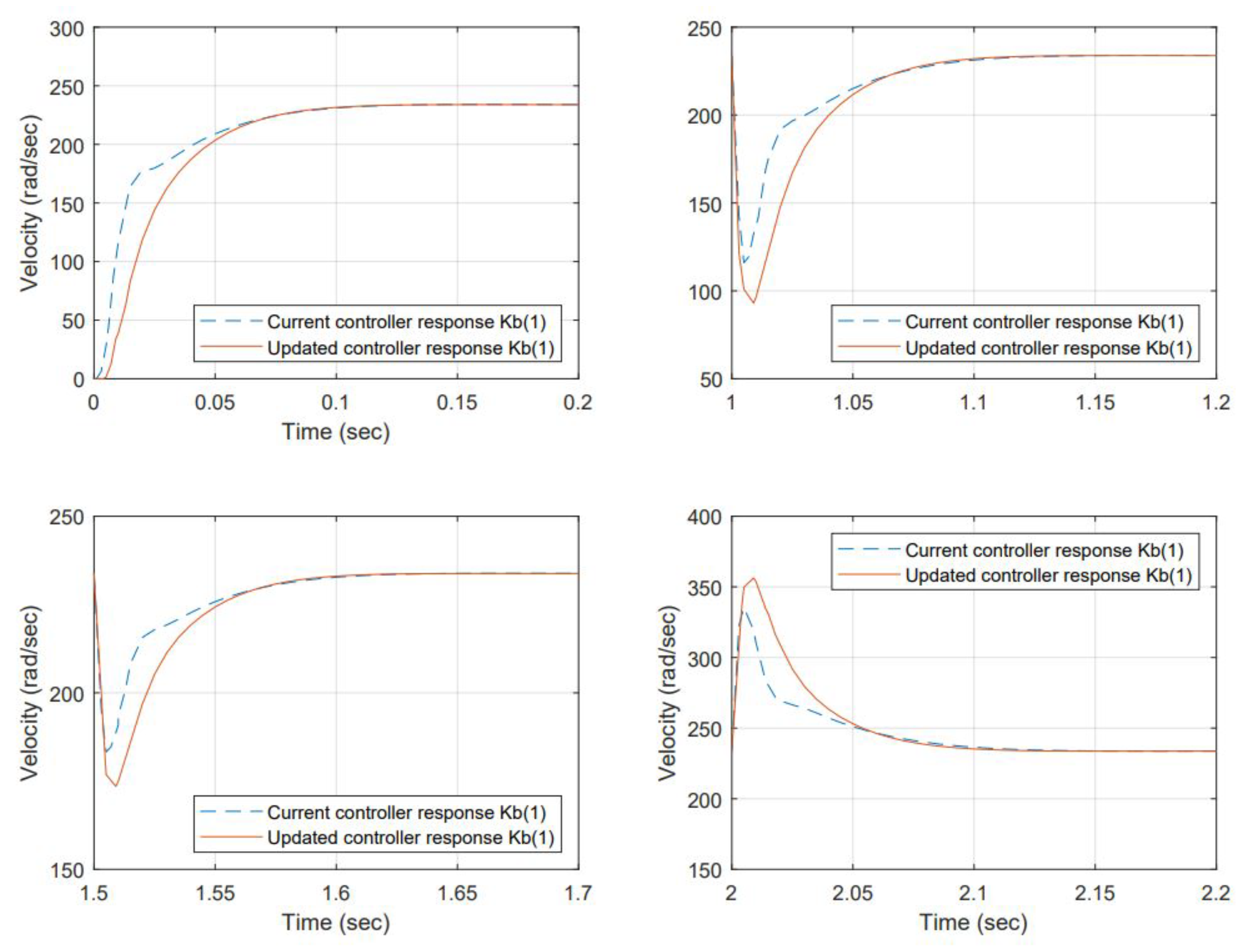
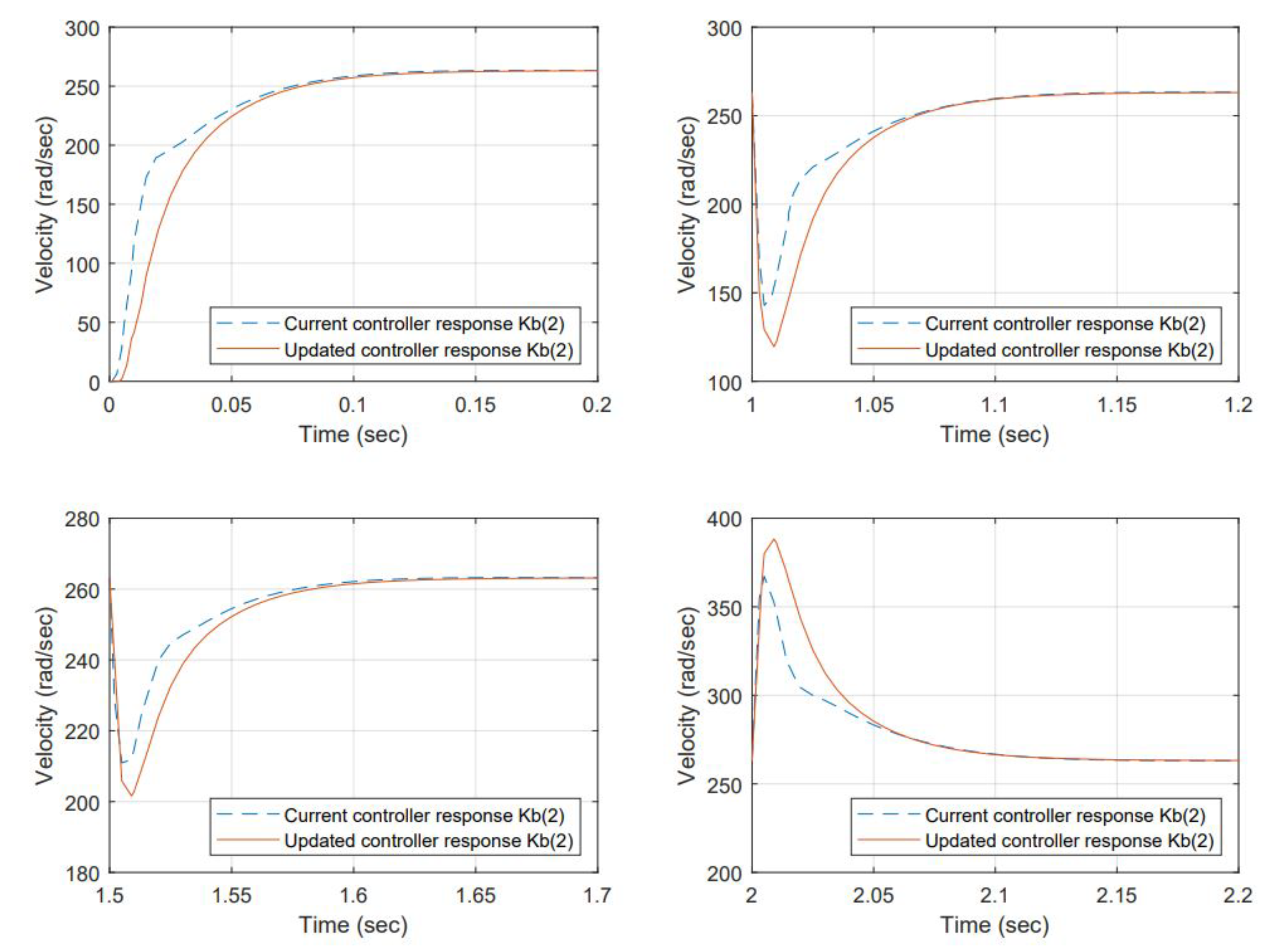
3.4. In Terms of Comparing Performance between the Controllers
4. Discussion
4.1. Conceptual Analysis
4.2. Using Physical Means for Testing and Developing Real Time Series
4.3. Opportunities for Coming Phases
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACF | Auto-Correlation Function |
| ADF | Augmented Dickey–Fuller’s |
| AI | Artificial Intelligence |
| AR | Auto-Regressive |
| ARIMA | Auto-Regressive Integrated Moving Range |
| ARMA | Auto-Regressive Moving Range |
| BDC | Brushed Direct Current |
| BLDC | Brushless Direct Current |
| CPU | Central Processing Unit |
| DC | Direct Current |
| FL | Fuzzy Logic |
| FLC | Fuzzy Logic Controllers |
| I | Integrated |
| MA | Moving Average |
| MCU | Microprocessor Unit |
| NN | Neural Networks |
| PACF | Partial Auto-Correlation Function |
| PI | Proportional-Integral |
| PID | Proportional-Integral-Derivative |
| TF | Transfer Function |
| TS | Time Series |
Appendix A. Code in R™ for Analyzing the Time Series Data
References
- Cho, Y.T. Characterizing Sources of Small DC Motor Noise and Vibration. Micromachines 2018, 9, 84. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodríguez-Molina, A.; Villarreal-Cervantes, M.G.; Aldape-Pérez, M. An adaptive control study for the DC motor using meta-heuristic algorithms. Soft Comput. 2019, 23, 889–906. [Google Scholar] [CrossRef]
- Chen, J.; Lu, Q.; Bai, J.; Xu, X.; Yao, Y.; Fang, W. A Temperature Control Method for Microaccelerometer Chips Based on Genetic Algorithm and Fuzzy PID Control. Micromachines 2021, 12, 1511. [Google Scholar] [CrossRef] [PubMed]
- Ding, F.; Luo, X.; Li, D.; Qiao, Z.; Wang, B. Optimal Controller Design for Ultra-Precision Fast-Actuation Cutting Systems. Micromachines 2022, 13, 33. [Google Scholar] [CrossRef] [PubMed]
- Arifin, B.; Nugroho, A.A.; Suprapto, B.; Prasetyowati, S.A.D.; Nawawi, Z. Review of Method for System Identification on Motors. In Proceedings of the 2021 8th International Conference on Electrical Engineering, Computer Science and Informatics (EECSI), Semarang, Indonesia, 20–21 October 2021; pp. 257–262. [Google Scholar]
- Gausemeier, J.; Schierbaum, T.; Dumitrescu, R.; Herbrechtsmeier, S.; Jungmann, A. Miniature robot BeBot: Mechatronic test platform for self-x properties. In Proceedings of the 2011 9th IEEE International Conference on Industrial Informatics, Lisbon, Portugal, 26–29 July 2011; pp. 451–456. [Google Scholar] [CrossRef]
- Qiao, H.; Peng, W.; Jin, P.; Su, J.; Lu, H. Performance Improvement of Single-Frequency CW Laser Using a Temperature Controller Based on Machine Learning. Micromachines 2022, 13, 1047. [Google Scholar] [CrossRef] [PubMed]
- Braem, S.; Bugg, J.M.; Schmidt, J.R.; Crump, M.J.; Weissman, D.H.; Notebaert, W.; Egner, T. Measuring Adaptive Control in Conflict Tasks. Trends Cogn. Sci. 2019, 23, 769–783. [Google Scholar] [CrossRef] [PubMed]
- Hughes, A.; Drury, B. Electric Motors and Drives: Fundamentals, Types and Applications; Newnes: Manchester, UK, 2019. [Google Scholar]
- Chapman, S.J. Electric Machinery Fundamentals, 5th ed.; McGraw Hill: New York, NY, USA, 2012. [Google Scholar]
- Amiri, M.S.; Ibrahim, M.F.; Ramli, R. Optimal parameter estimation for a DC motor using genetic algorithm. Int. J. Power Electron. Drive Syst. 2020, 11, 1047. [Google Scholar] [CrossRef]
- Wu, W. DC motor parameter identification using speed step responses. Model. Simul. Eng. 2012. [Google Scholar] [CrossRef] [Green Version]
- Pillai, B.M.; Suthakorn, J. Motion control applications: Observer based DC motor parameters estimation for novices. Int. J. Power Electron. Drive Syst. 2019, 10, 195–210. [Google Scholar] [CrossRef]
- Hover, F.; Chin, H. 2.017 J Design of Electromechanical Robotic Systems; Massachusetts Institute of Technology: Cambridge, MA, USA, 2009. [Google Scholar]
- Unbehauen, H.; Rao, G. A review of identification in continuous-time systems. Annu. Rev. Control 1998, 22, 145–171. [Google Scholar] [CrossRef]
- Basilio, J.C.; Moreira, M.V. State-space parameter identification in a second control laboratory. IEEE Trans. Educ. 2004, 47, 204–210. [Google Scholar] [CrossRef]
- Mamani, G.; Becedas, J.; Feliu-Batlle, V.; Sira-Ramirez, H. Open-loop algebraic identification method for a DC motor. In Proceedings of the 2007 European Control Conference (ECC), Kos, Greece, 2–6 July 2007; pp. 3430–3436. [Google Scholar]
- Mamani, G.; Becedas, J.; Feliu-Batlle, V. On-line fast algebraic parameter and state estimation for a DC motor applied to adaptive control. In Proceedings of the World Congress on Engineering, London, UK, 2–4 July 2008; Volume 2. [Google Scholar]
- Martínez, J.R.G.; Reséndiz, J.R.; Prado, M.Á.M.; Miguel, E.E.C. Assessment of jerk performance s-curve and trapezoidal velocity profiles. In Proceedings of the 2017 XIII International Engineering Congress (CONIIN), Santiago de Queretaro, Mexico, 15–19 May 2017; pp. 1–7. [Google Scholar]
- García-Martínez, J.R.; Cruz-Miguel, E.E.; Carrillo-Serrano, R.V.; Mendoza-Mondragón, F.; Toledano-Ayala, M.; Rodríguez-Reséndiz, J. A PID-type fuzzy logic controller-based approach for motion control applications. Sensors 2020, 20, 5323. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Huang, J.; Liang, X.; Yang, S.X.; Hu, W.; Tang, D. An intelligent multi-sensor variable spray system with chaotic optimization and adaptive fuzzy control. Sensors 2020, 20, 2954. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Miguel, E.E.; García-Martínez, J.R.; Rodríguez-Reséndiz, J.; Carrillo-Serrano, R.V. A new methodology for a retrofitted self-tuned controller with open-source fpga. Sensors 2020, 20, 6155. [Google Scholar] [CrossRef] [PubMed]
- Odry, Á.; Fullér, R.; Rudas, I.J.; Odry, P. Fuzzy control of self-balancing robots: A control laboratory project. Comput. Appl. Eng. Educ. 2020, 28, 512–535. [Google Scholar] [CrossRef]
- Kecskés, I.; Burkus, E.; Király, Z.; Odry, Á.; Odry, P. Competition of motor controllers using a simplified robot leg: Pid vs fuzzy logic. In Proceedings of the 2017 Fourth International Conference on Mathematics and Computers in Sciences and in Industry (MCSI), Corfu, Greece, 24–27 August 2017; pp. 37–43. [Google Scholar]
- Li, X.; Yuan, H.; Chen, W.; Yu, L.; Gu, X. Commutation Torque Ripple Reduction Strategy of Brushless DC Motor Drives Based on Boosting Voltage of DC-Link Small Capacitor. Micromachines 2022, 13, 226. [Google Scholar] [CrossRef] [PubMed]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Montgomery, D.C.; Jennings, C.L.; Kulahci, M. Introduction to Time Series Analysis and Forecasting; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Filliben, J.J.; Heckert, A. NIST/SEMATECH e-Handbook of Statistical Methods; U.S. Department of Commerce: Gaithersburg, MD, USA, 2002. [Google Scholar]






| Parameter | Value | Unit | |
|---|---|---|---|
| Armature resistance () * | 20.0 | ||
| Armature Inductance () * | 0.375 | H | |
| Electrical | Rated current () | 0.65 | A |
| Stall current () | 2.4 | A | |
| Output power (W) | 3.8 | W | |
| Rated voltage () | 12 | V | |
| Torque constant () ** | 42.92 | mN m/A | |
| Motor inertia (J) * | 0.0003 | ||
| Viscous Damping (B) * | 0.082 | mN m s/rad | |
| Mechanical | Back EMF () | 0.0382 | V/(rad/s) |
| Rated torque () | 15.0 | mN m | |
| Rated speed () | 261.8 | rad/s | |
| Stall torque () | 90.0 | mN m |
| Item | Forecast | Lo 80 | Hi 80 | Lo 95 | Hi 95 |
|---|---|---|---|---|---|
| 0 | 0.03708248 | 0.03315761 | 0.04100735 | 0.03107991 | 0.04308505 |
| 1 | 0.03850688 | 0.03421273 | 0.04280103 | 0.03193954 | 0.04507421 |
| 2 | 0.03857796 | 0.03428293 | 0.04287299 | 0.03200928 | 0.04514664 |
| –> | Sample 1 | Sample 2 | Sample 3 | Sample 4 | Sample 5 |
| Item | Load | Units | Timing |
|---|---|---|---|
| 1 | 0 | mN m | 0.5 s |
| 2 | 0 | mN m | 0.5 s |
| 3 | 15.75 | mN m | 0.5 s |
| 4 | 22.5 | mN m | 0.5 s |
| 5 | 8.75 | mN m | 0.5 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niembro-Ceceña, J.A.; Gómez-Loenzo, R.A.; Rodríguez-Reséndiz, J.; Rodríguez-Abreo, O.; Odry, Á. Auto-Regression Model-Based Off-Line PID Controller Tuning: An Adaptive Strategy for DC Motor Control. Micromachines 2022, 13, 1264. https://doi.org/10.3390/mi13081264
Niembro-Ceceña JA, Gómez-Loenzo RA, Rodríguez-Reséndiz J, Rodríguez-Abreo O, Odry Á. Auto-Regression Model-Based Off-Line PID Controller Tuning: An Adaptive Strategy for DC Motor Control. Micromachines. 2022; 13(8):1264. https://doi.org/10.3390/mi13081264
Chicago/Turabian StyleNiembro-Ceceña, José A., Roberto A. Gómez-Loenzo, Juvenal Rodríguez-Reséndiz, Omar Rodríguez-Abreo, and Ákos Odry. 2022. "Auto-Regression Model-Based Off-Line PID Controller Tuning: An Adaptive Strategy for DC Motor Control" Micromachines 13, no. 8: 1264. https://doi.org/10.3390/mi13081264
APA StyleNiembro-Ceceña, J. A., Gómez-Loenzo, R. A., Rodríguez-Reséndiz, J., Rodríguez-Abreo, O., & Odry, Á. (2022). Auto-Regression Model-Based Off-Line PID Controller Tuning: An Adaptive Strategy for DC Motor Control. Micromachines, 13(8), 1264. https://doi.org/10.3390/mi13081264







