Effect of Wind-Induced Vibration on Measurement Range of Microcantilever Anemometer
Abstract
:1. Introduction
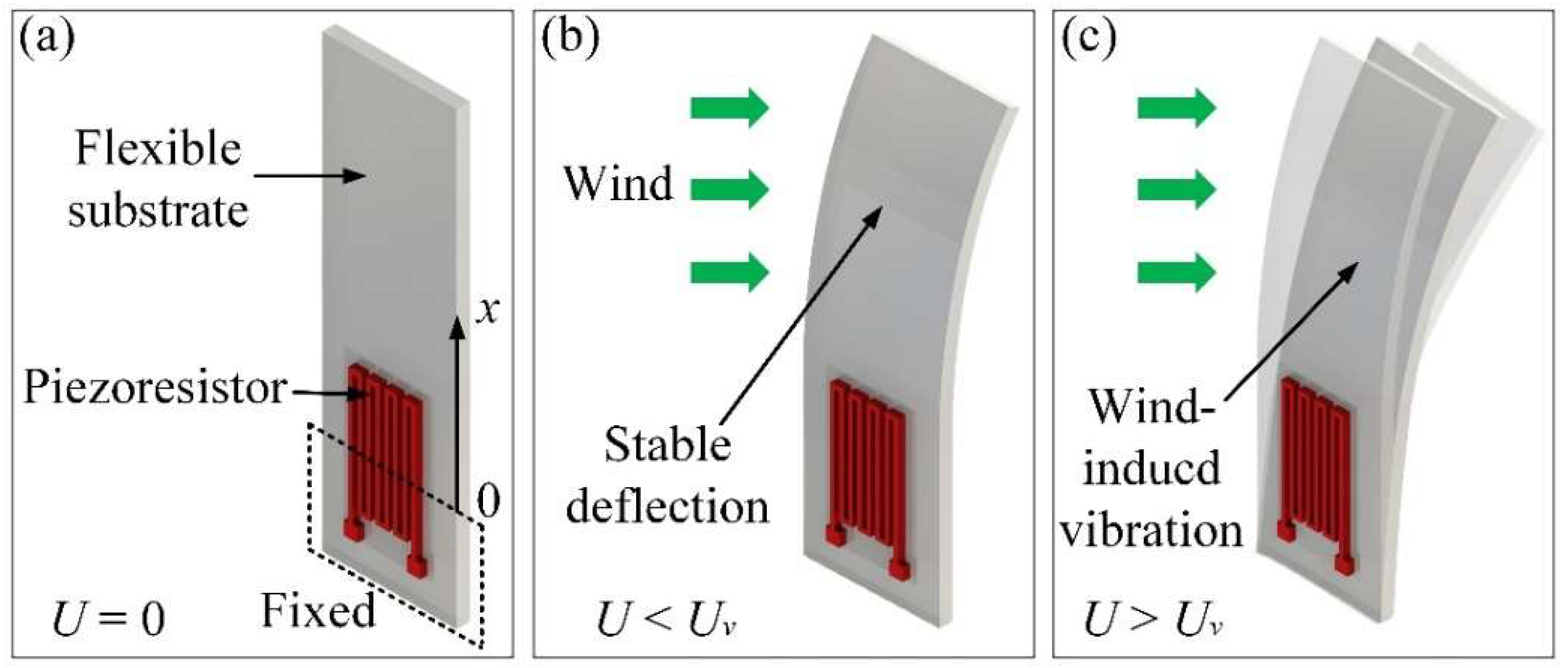
2. Principle and Design
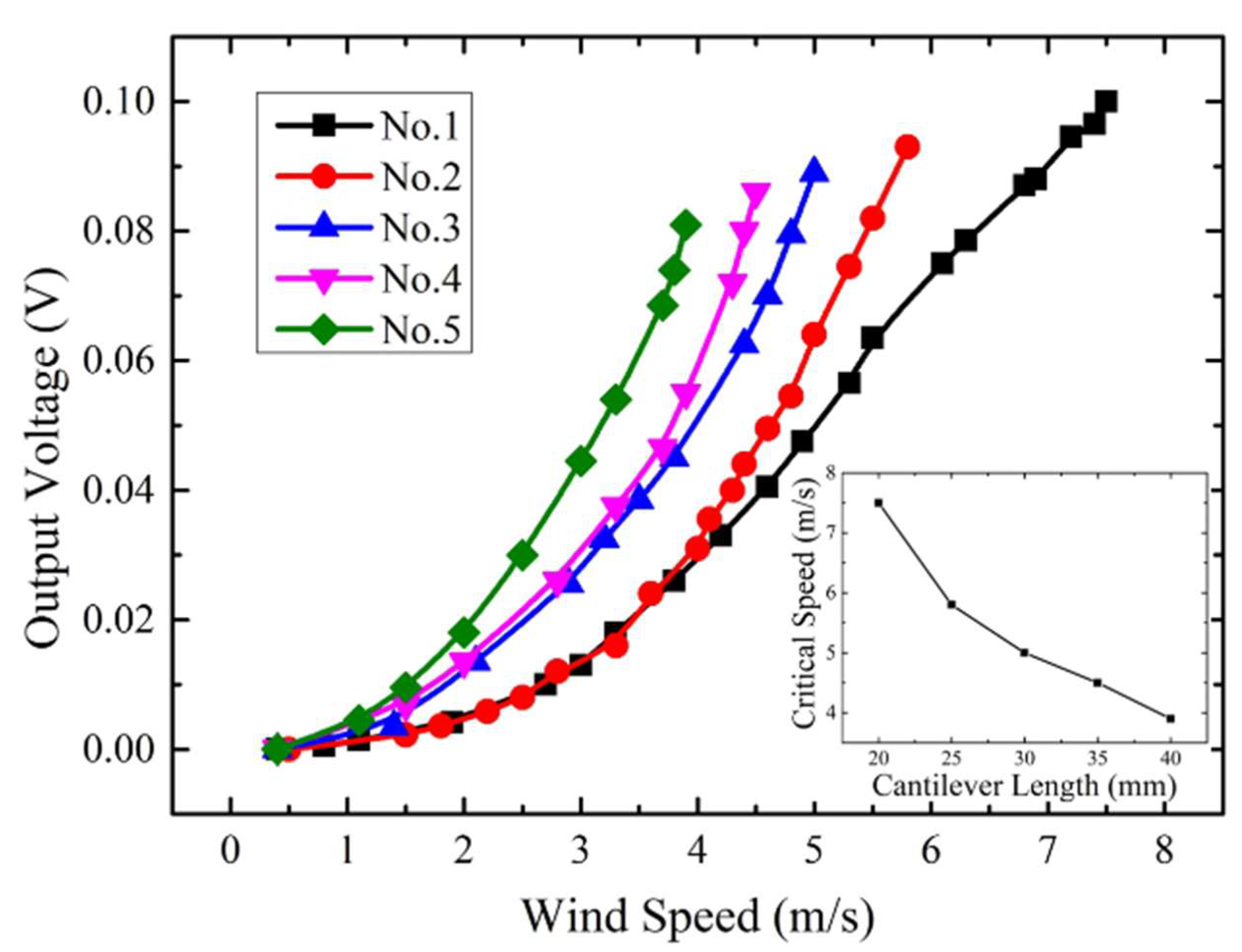
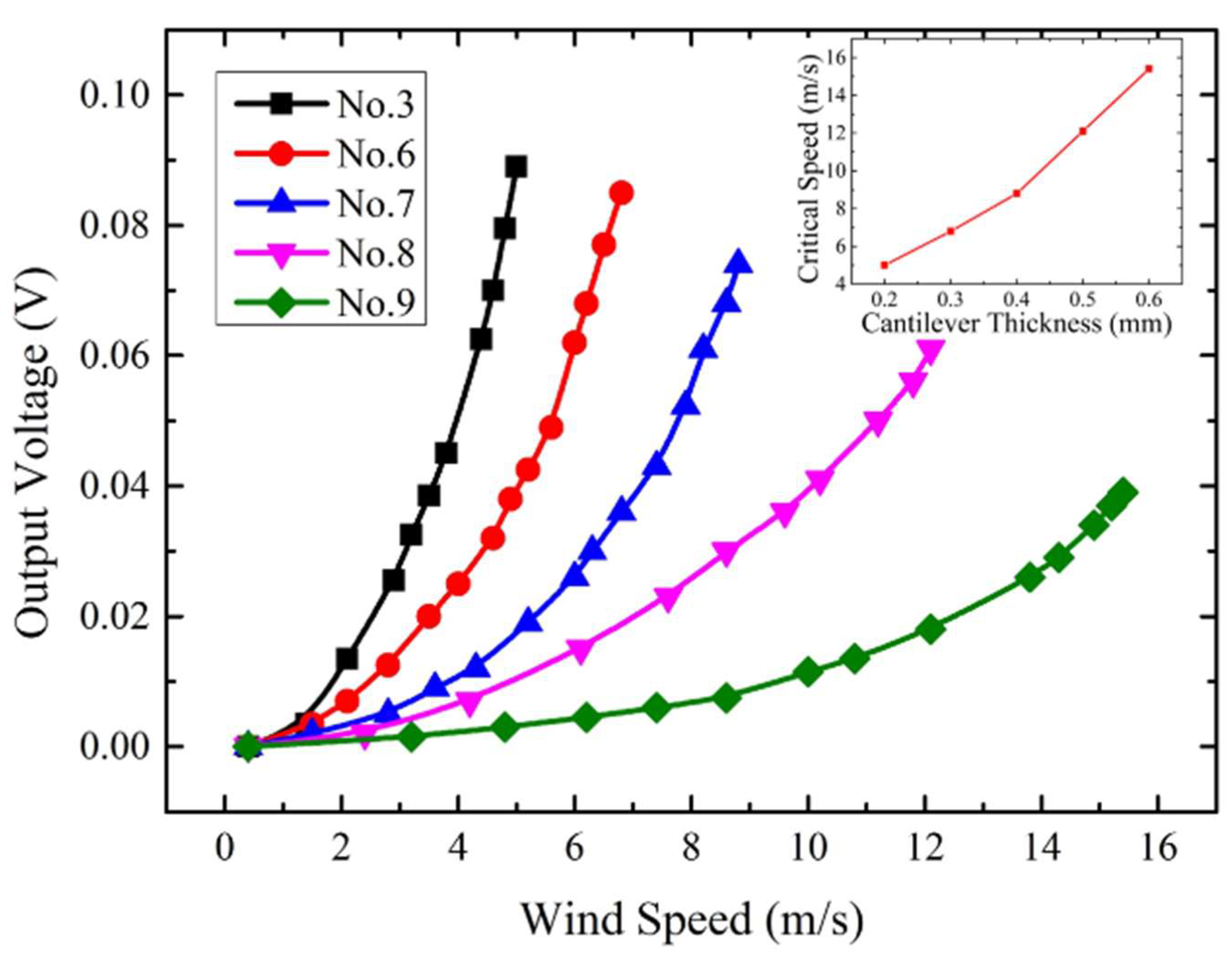
3. Experiment and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Veers, P.; Dykes, K.; Lantz, E.; Barth, S.; Bottasso, C.L.; Carlson, O.; Clifton, A.; Green, J.; Green, P.; Holttinen, H.; et al. Grand challenges in the science of wind energy. Science 2019, 366, 2027. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.L.; Geng, L.F.; Ding, L.; Zhu, H.J.; Yurchenko, D. The state-of-the-art review on energy harvesting from flow-induced vibrations. Appl. Energy 2020, 267, 114902. [Google Scholar] [CrossRef]
- He, X.; Yang, X.; Jiang, S. Enhancement of wind energy harvesting by interaction between vortex-induced vibration and galloping. Appl. Phys. Lett. 2018, 112, 033901. [Google Scholar] [CrossRef]
- Roundy, S.; Wright, P.K.; Rabaey, J. A study of low level vibrations as a power source for wireless sensor nodes. Comp. Commun. 2003, 26, 1131–1144. [Google Scholar] [CrossRef]
- Beeby, S.P.; Tudor, M.J.; White, N.M. Energy harvesting vibration sources for microsystems applications. Meas. Sci. Technol. 2006, 17, R175. [Google Scholar] [CrossRef]
- Chen, P.; An, J.; Shu, S.; Cheng, R.; Nie, J.; Jiang, T.; Wang, Z.L. Super-durable, low-wear, and high-performance fur-brush triboelectric nanogenerator for wind and water energy harvesting for smart agriculture. Adv. Energy Mater. 2021, 11, 2003066. [Google Scholar] [CrossRef]
- Yang, X.; He, X.; Li, J.; Jiang, S. Modeling and verification of piezoelectric wind energy harvesters enhanced by interaction between vortex-induced vibration and galloping. Smart Mater. Struct. 2019, 28, 115027. [Google Scholar] [CrossRef]
- Ge, Y.; Zhao, L.; Cao, J. Case study of vortex-induced vibration and mitigation mechanism for a long-span suspension bridge. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104866. [Google Scholar] [CrossRef]
- He, X.; Teh, K.S.; Li, S.; Dong, L.; Jiang, S. Modeling and experimental verification of an impact-based piezoelectric vibration energy harvester with a rolling proof mas. Sens. Actuators A Phys. 2017, 259, 171–179. [Google Scholar] [CrossRef]
- Dong, S.; Triantafyllou, G.S.; Karniadakis, G.E. Elimination of vortex streets in bluffbody flows. Phys. Rev. Lett. 2008, 100, 204501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nati, G.; Kotsonis, M.; Ghaemi, S.; Scarano, F. Control of vortex shedding from a blunt trailing edge using plasma actuators. Exp. Therm. Fluid Sci. 2013, 46, 199–210. [Google Scholar] [CrossRef]
- Feng, L.H.; Wang, J.J. Modification of a circular cylinder wake with synthetic jet: Vortex shedding modes and mechanism. Eur. J. Mech. 2014, 43, 14–32. [Google Scholar] [CrossRef]
- Carini, M.; Pralits, J.O.; Luchini, P. Feedback control of vortex shedding using a full-order optimal compensator. J. Fluids Struct. 2015, 53, 15–25. [Google Scholar] [CrossRef]
- Chen, W.; Liu, Y.; Hu, H.; Xu, F.; Li, H. Suppression of vortex shedding from a circular cylinder by using a traveling wave wall. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; p. 0399. [Google Scholar]
- Leissa, A.; Qatu, M. Vibrations of Continuous Systems; McGraw-Hill: New York, NY, USA, 2011; pp. 103–175. [Google Scholar]
- Gerhart, P.; Gross, R.; Hochstein, J. Fundamentals of Fluid Mechanics; Addison-Wesley, Reading: Boston, MA, USA, 1992. [Google Scholar]
- Seo, Y.; Kim, B. A self-resonant micro flow velocity sensor based on a resonant frequency shift by flow-induced vibration. J. Micromech. Microeng. 2010, 20, 075024. [Google Scholar] [CrossRef]
- Dowell, E. A Modern Course in Aeroelasticity; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Wang, G.; Feng, X. Effects of surface elasticity and residual surface tension on the natural frequency of microbeams. Appl. Phys. Lett. 2007, 90, 231904. [Google Scholar] [CrossRef]
- Meng, E.; Li, P.-Y.; Tai, Y.-C. A biocompatible Parylene thermal flow sensing array. Sens. Actuators A Phys. 2008, 144, 18–28. [Google Scholar] [CrossRef]




| No. | Length (L) (mm) | Width (W) (mm) | Thickness (T) (mm) | Young’s Modulus (GPa) |
|---|---|---|---|---|
| 1 | 20 | 15 | 0.2 | 2.0 |
| 2 | 25 | 15 | 0.2 | 2.0 |
| 3 | 30 | 15 | 0.2 | 2.0 |
| 4 | 35 | 15 | 0.2 | 2.0 |
| 5 | 40 | 15 | 0.2 | 2.0 |
| 6 | 30 | 15 | 0.3 | 2.0 |
| 7 | 30 | 15 | 0.4 | 2.0 |
| 8 | 30 | 15 | 0.5 | 2.0 |
| 9 | 30 | 15 | 0.6 | 2.0 |
| 10 | 30 | 15 | 0.2 | 2.3 |
| 11 | 30 | 15 | 0.2 | 3.3 |
| 12 | 30 | 15 | 0.2 | 3.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Y.; Wan, S.; He, X. Effect of Wind-Induced Vibration on Measurement Range of Microcantilever Anemometer. Micromachines 2022, 13, 720. https://doi.org/10.3390/mi13050720
Ye Y, Wan S, He X. Effect of Wind-Induced Vibration on Measurement Range of Microcantilever Anemometer. Micromachines. 2022; 13(5):720. https://doi.org/10.3390/mi13050720
Chicago/Turabian StyleYe, Yizhou, Shu Wan, and Xuefeng He. 2022. "Effect of Wind-Induced Vibration on Measurement Range of Microcantilever Anemometer" Micromachines 13, no. 5: 720. https://doi.org/10.3390/mi13050720
APA StyleYe, Y., Wan, S., & He, X. (2022). Effect of Wind-Induced Vibration on Measurement Range of Microcantilever Anemometer. Micromachines, 13(5), 720. https://doi.org/10.3390/mi13050720







