Influence of Surface Tension on Dynamic Characteristics of Single Bubble in Free-Field Exposed to Ultrasound
Abstract
:1. Introduction
2. Materials and Methods
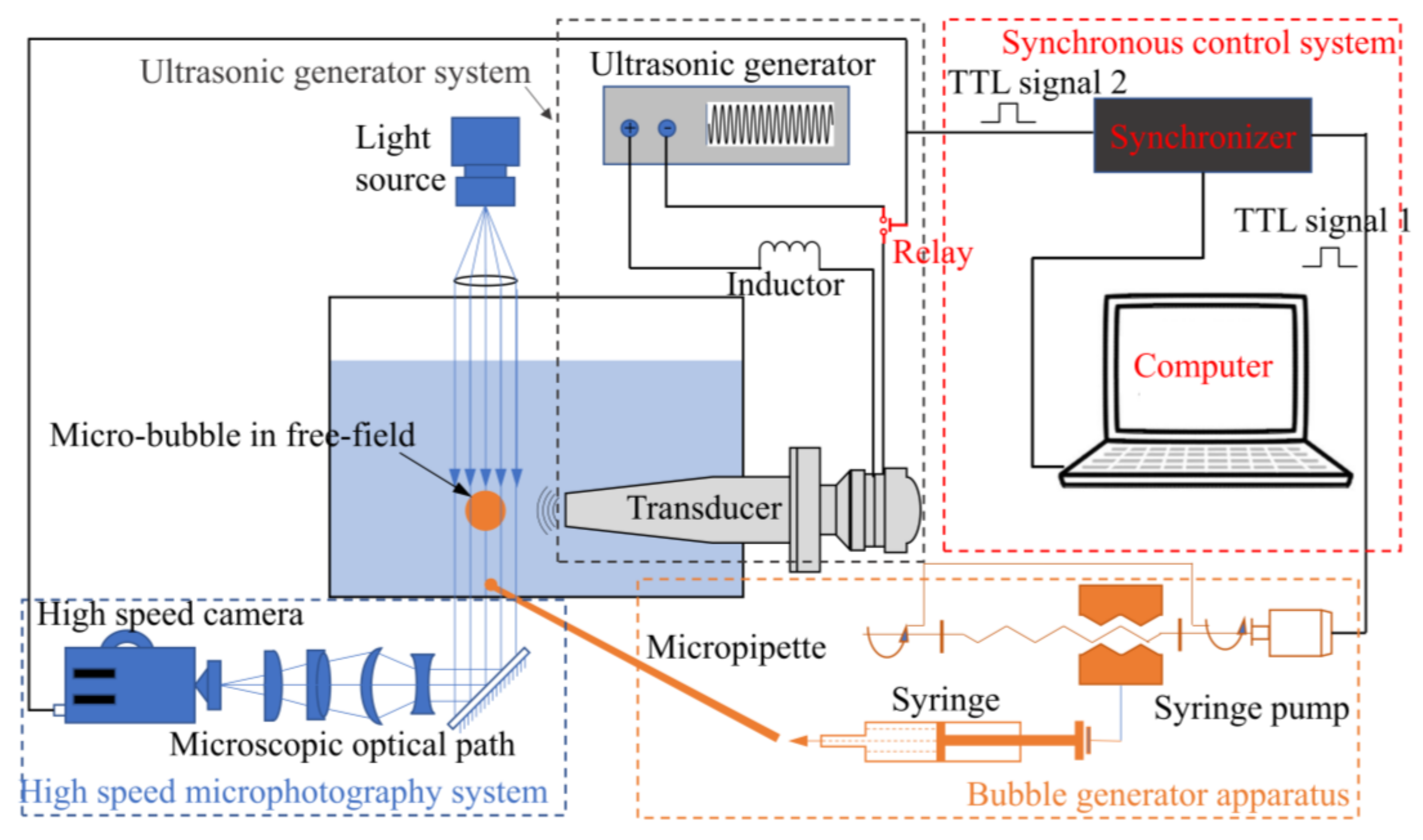
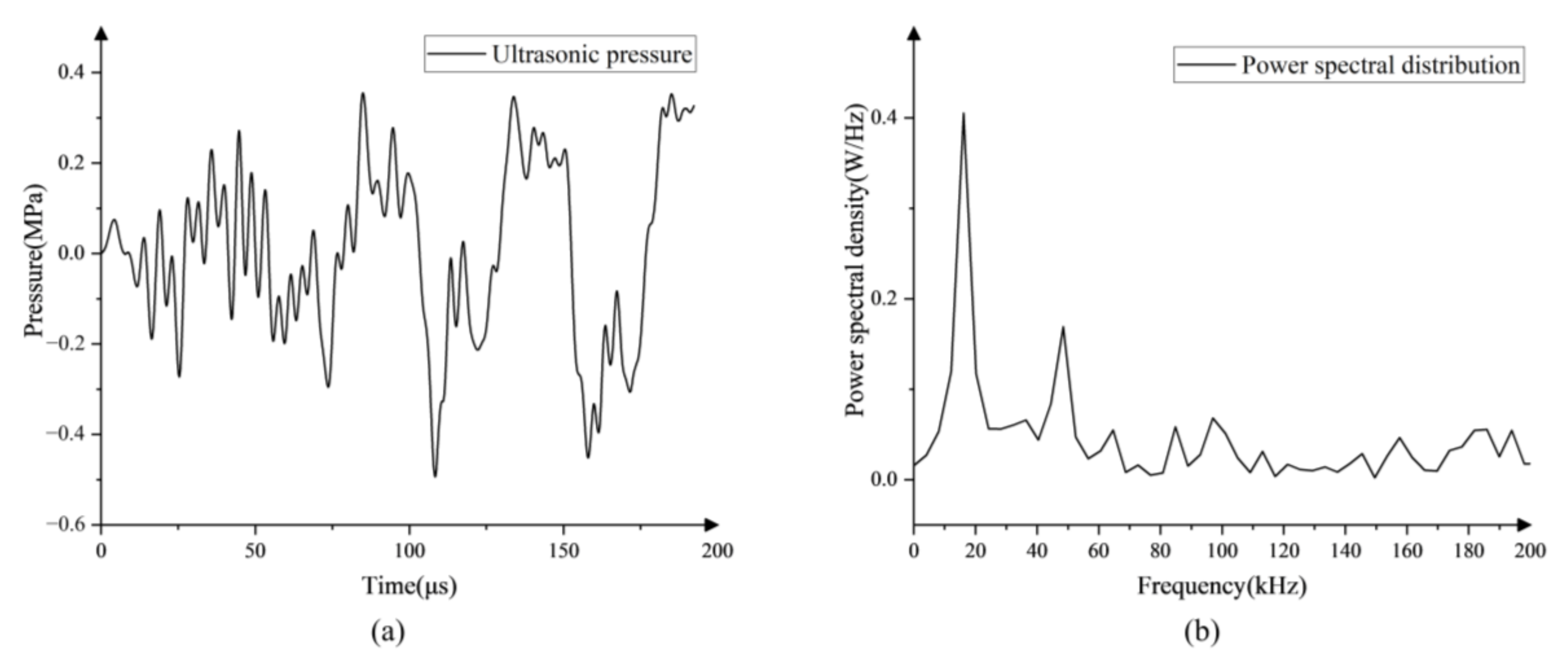
2.1. Experimental Setup
2.2. Materials
2.3. Image Analysis
2.4. Analysis of Bubbles’ Typical Characteristics
3. Results
3.1. Time Evolution of Bubble Shape in the Free-Field
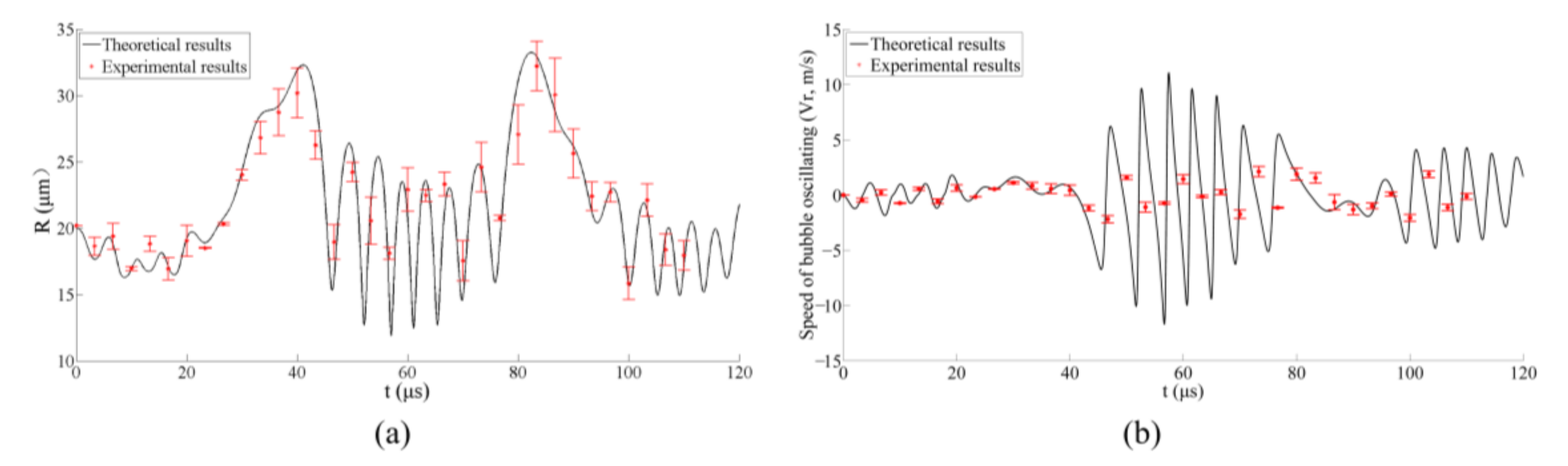
3.2. The Characteristics of Bubble Oscillate versus Time in Free-Field
3.3. The Displacement of the Bubble versus Time in Free-Field
4. Discussion
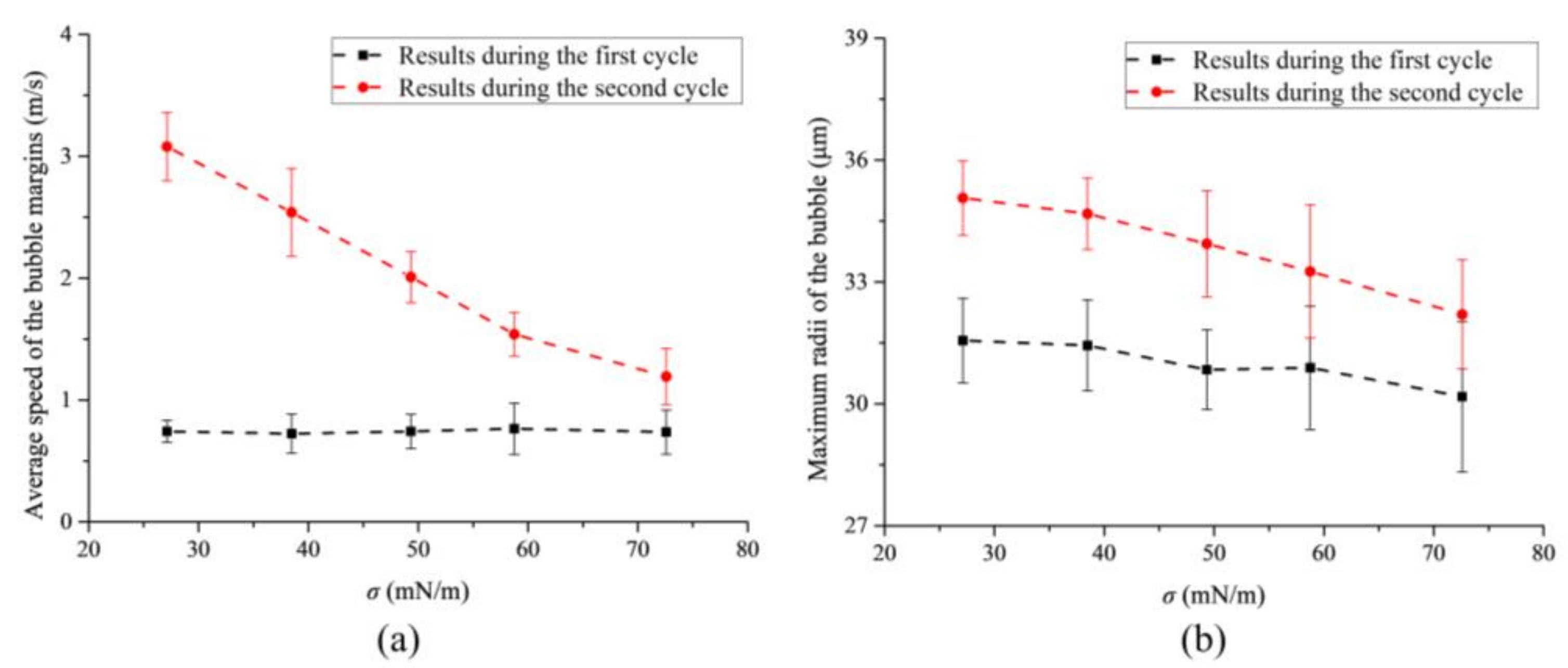
- As the surface tension of the liquid decreases, the maximum radius, oscillating speed, and the destabilization of the bubble increase when it oscillates in each cycle.
- As time goes on, the maximum radius, oscillating speed, and the destabilization of the bubble increase during the later oscillating cycle, then the bubble dynamics are found to be more sensitive to the surface tension of the liquid.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Johansson, O.; Pamidi, T.; Shankar, V. Extraction of tungsten from scheelite using hydrodynamic and acoustic cavitation. Ultrason. Sonochem. 2021, 71, 105408. [Google Scholar] [CrossRef]
- Priyadarshi, A.; Khavari, M.; Subroto, T.; Conte, M.; Prentice, P.; Pericleous, K.; Eskin, D.; Durodola, J.; Tzanakis, I. On the governing fragmentation mechanism of primary intermetallics by induced cavitation. Ultrason. Sonochem. 2021, 70, 105260. [Google Scholar] [CrossRef]
- Vyas, N.; Wang, Q.X.; Walmsley, A.D. Improved biofilm removal using cavitation from a dental ultrasonic scaler vibrating in carbonated water. Ultrason. Sonochem. 2021, 70, 105338. [Google Scholar] [CrossRef]
- Yusof, N.S.M.; Babgi, B.; Alghamdi, Y.; Aksu, M.; Madhavan, J.; Ashokkumar, M. Physical and chemical effects of acoustic cavitation in selected ultrasonic cleaning applications. Ultrason. Sonochem. 2016, 29, 568–576. [Google Scholar] [CrossRef]
- Sagar, H.J.; Hanke, S.; Underberg, M.; Feng, C.; el Moctar, O.; Kaiser, S.A. Experimental and Numerical Investigation of Damage on an Aluminum Surface by Single-Bubble Cavitation. Mater. Perform. Charact. 2018, 7, 985–1003. [Google Scholar] [CrossRef]
- Ye, L.Z.; Zhu, X.J.; He, Y.; Wei, X.M. Ultrasonic cavitation damage characteristics of materials and a prediction model of cavitation impact load based on size effect. Ultrason. Sonochem. 2020, 66, 105115. [Google Scholar] [CrossRef]
- Inui, A.; Honda, A.; Yamanaka, S.; Ikeno, T.; Yamamoto, K. Effect of ultrasonic frequency and surfactant addition on microcapsule destruction. Ultrason. Sonochem. 2021, 70, 105308. [Google Scholar] [CrossRef]
- Vyas, N.; Dehghani, H.; Sammons, R.L.; Wang, Q.X.; Leppinen, D.M.; Walmsley, A.D. Imaging and analysis of individual cavitation microbubbles around dental ultrasonic scalers. Ultrasonics 2017, 81, 66–72. [Google Scholar] [CrossRef]
- Versluis, M.; Goertz, D.E.; Palanchon, P.; Heitman, I.L.; van der Meer, S.M.; Dollet, B.; de Jong, N.; Lohse, D. Microbubble shape oscillations excited through ultrasonic parametric driving. Phys. Rev. E 2010, 82, 026321. [Google Scholar] [CrossRef] [Green Version]
- Tronson, R.; Tchea, M.F.; Ashokkumar, M.; Grieser, F. The Behavior of Acoustic Bubbles in Aqueous Solutions Containing Soluble Polymers. J. Phys. Chem. B 2012, 116, 13806–13811. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, C.; Yu, H.X.; Li, D.C. Dynamics Characterization of the Acoustically Driven Single Microbubble near the Rigid and Elastic Wall. Instrum. Exp. Tech. 2020, 63, 583–590. [Google Scholar] [CrossRef]
- Patil, P.B.; Raut-Jadhav, S.; Pandit, A.B. Effect of intensifying additives on the degradation of thiamethoxam using ultrasound cavitation. Ultrason. Sonochem. 2021, 70, 105310. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Zhang, Z.; Zhu, Z.W.; Sun, D.W. Effects of nano-bubbles and constant/variable-frequency ultrasound-assisted freezing on freezing behaviour of viscous food model systems. J. Food Eng. 2021, 292, 9. [Google Scholar] [CrossRef]
- Grieser, F.; Ashokkumar, M. The effect of surface active solutes on bubbles exposed to ultrasound. Adv. Colloid Interface Sci. 2001, 89, 423–438. [Google Scholar] [CrossRef]
- Lee, J.; Kentish, S.E.; Ashokkurnar, M. The effect of surface-active solutes on bubble coalescence in the presence of ultrasound. J. Phys. Chem. B 2005, 109, 5095–5099. [Google Scholar] [CrossRef]
- Wang, S.P.; Zhang, A.M.; Liu, Y.L.; Zhang, S.; Cui, P. Bubble dynamics and its applications. J. Hydrodyn. 2018, 30, 975–991. [Google Scholar] [CrossRef]
- Camerotto, E.; Brems, S.; Hauptmann, M.; Pacco, A.; Struyf, H.; Mertens, P.W.; De Gendt, S. Influence of surface tension on cavitation noise spectra and particle removal efficiency in high frequency ultrasound fields. J. Appl. Phys. 2012, 112, 9. [Google Scholar] [CrossRef] [Green Version]
- Curtiss, G.A.; Leppinen, D.M.; Wang, Q.X.; Blake, J.R. Ultrasonic cavitation near a tissue layer. J. Fluid Mech. 2013, 730, 245–272. [Google Scholar] [CrossRef]
- Luo, J.; Xu, W.L.; Luo, M.; Zhai, Y.W.; Zhang, Q. Study on the mesoscale causes of the influence of surface tension on material erosion in a cavitation field. J. Hydraul. Res. 2021, 60, 82–93. [Google Scholar] [CrossRef]
- Sabzeghabae, A.N.; Devia-Cruz, L.F.; Gutierrez-Herrera, E.; Camacho-Lopez, S.; Aguilar, G. Bubble dynamics of laser-induced cavitation in plasmonic gold nanorod solutions and the relative effect of surface tension and viscosity. Opt. Laser Technol. 2021, 134, 106621. [Google Scholar] [CrossRef]
- Lee, J.; Tuziuti, T.; Yasui, K.; Kentish, S.; Grieser, F.; Ashokkumar, M.; Iida, Y. Influence of surface-active solutes on the coalescence, clustering, and fragmentation of acoustic bubbles confined in a microspace. J. Phys. Chem. C 2007, 111, 19015–19023. [Google Scholar] [CrossRef]
- Liu, X.M.; He, J.; Lu, J.; Ni, X.W. The effect of surface tension on bubble oscillation near a rigid boundary. Acta Phys. Sin. 2009, 58, 4020–4025. [Google Scholar]
- Liu, X.M.; Liu, X.H.; Hou, Y.F.; He, J.; Lu, J.; Ni, X.W. Effect of Temperature on the Behaviour of a Laser-Induced Cavitation Bubble Near a Rigid Boundary. Lasers Eng. 2011, 21, 181–193. [Google Scholar]
- Wu, H.; Zheng, H.; Li, Y.Y.; Ohl, C.D.; Yu, H.X.; Li, D.C. Effects of surface tension on the dynamics of a single micro bubble near a rigid wall in an ultrasonic field. Ultrason. Sonochem. 2021, 78, 105735. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Zhang, H.S. Surface tension effects on the behavior of a cavity growing, collapsing, and rebounding near a rigid wall. Phys. Rev. E 2004, 70, 056310. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Huang, B.; Gao, D. Numerical investigation on the influence of surface tension and viscous force on the bubble dynamics with a CLSVOF method. J. Mech. Sci. Technol. 2016, 30, 2547–2556. [Google Scholar] [CrossRef]
- Wu, X.Y.; Liang, J.F. Translation and nonspherical oscillation of single bubble in ultrasound field. Acta Phys. Sin. 2021, 70, 184301. [Google Scholar] [CrossRef]
- Ohl, S.W.; Klaseboer, E.; Khoo, B.C. Bubbles with shock waves and ultrasound: A review. Interface Focus 2015, 5, 20150019. [Google Scholar] [CrossRef]
- Palanchon, P.; Klein, J.; de Jong, N. Production of standardized air bubbles: Application to embolism studies. Rev. Sci. Instrum. 2003, 74, 2558–2563. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, C.; Pu, Z.H.; Yu, H.X.; Li, D.C. Effect of low-frequency ultrasonic field at different power on the dynamics of a single bubble near a rigid wall. Ultrason. Sonochem. 2019, 58, 104704. [Google Scholar] [CrossRef]
- Ashokkumar, M.; Grieser, F. The effect of surface active solutes on bubbles in an acoustic field. Phys. Chem. Chem. Phys. 2007, 9, 5631–5643. [Google Scholar] [CrossRef]
- Ashokkumar, M.; Guan, J.; Tronson, R.; Matula, T.J.; Nuske, J.W.; Grieser, F. Effect of surfactants, polymers, and alcohol on single bubble dynamics and sonoluminescence. Phys. Rev. E Stat. Nonlin. Soft Matter. Phys. 2002, 65, 046310. [Google Scholar] [CrossRef]




| Name | Content | Concentration (c, mol/L) | Density 1 (σ, g/cm3) | Surface Tension 1 (σ, mN/m) | Viscosity 1 (μl, cP) |
|---|---|---|---|---|---|
| Liquid A | Deionized water | — | 0.99 | 72.59 | 1.00 |
| Liquid B | SDS aqueous solution | 1.0 × 10−5 | 0.99 | 58.75 | 1.00 |
| Liquid C | SDS aqueous solution | 1.0 × 10−4 | 0.99 | 49.34 | 1.00 |
| Liquid D | SDS aqueous solution | 1.0 × 10−3 | 0.99 | 38.47 | 1.00 |
| Liquid E | SDS aqueous solution | 1.0 × 10−2 | 0.99 | 27.13 | 1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Zhang, T.; Lai, X.; Yu, H.; Li, D.; Zheng, H.; Chen, H.; Ohl, C.-D.; Li, Y. Influence of Surface Tension on Dynamic Characteristics of Single Bubble in Free-Field Exposed to Ultrasound. Micromachines 2022, 13, 782. https://doi.org/10.3390/mi13050782
Wu H, Zhang T, Lai X, Yu H, Li D, Zheng H, Chen H, Ohl C-D, Li Y. Influence of Surface Tension on Dynamic Characteristics of Single Bubble in Free-Field Exposed to Ultrasound. Micromachines. 2022; 13(5):782. https://doi.org/10.3390/mi13050782
Chicago/Turabian StyleWu, Hao, Tianshu Zhang, Xiaochen Lai, Haixia Yu, Dachao Li, Hao Zheng, Hui Chen, Claus-Dieter Ohl, and Yuanyuan Li. 2022. "Influence of Surface Tension on Dynamic Characteristics of Single Bubble in Free-Field Exposed to Ultrasound" Micromachines 13, no. 5: 782. https://doi.org/10.3390/mi13050782
APA StyleWu, H., Zhang, T., Lai, X., Yu, H., Li, D., Zheng, H., Chen, H., Ohl, C.-D., & Li, Y. (2022). Influence of Surface Tension on Dynamic Characteristics of Single Bubble in Free-Field Exposed to Ultrasound. Micromachines, 13(5), 782. https://doi.org/10.3390/mi13050782





