High-Performance SAW Low Temperature Sensors with Double Electrode Transducers Based on 128° YX LiNbO3
Abstract
1. Introduction
2. Materials and Methods
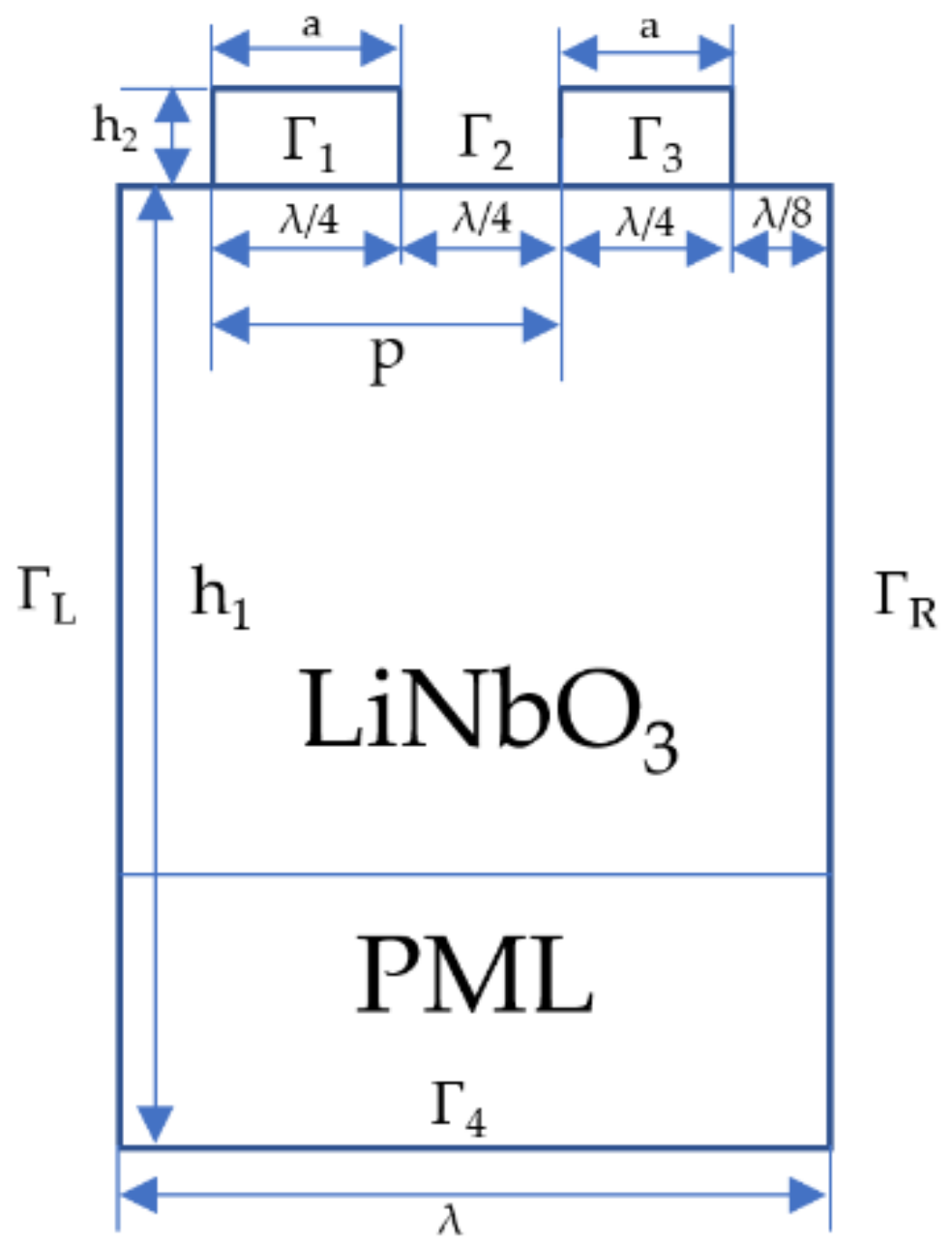
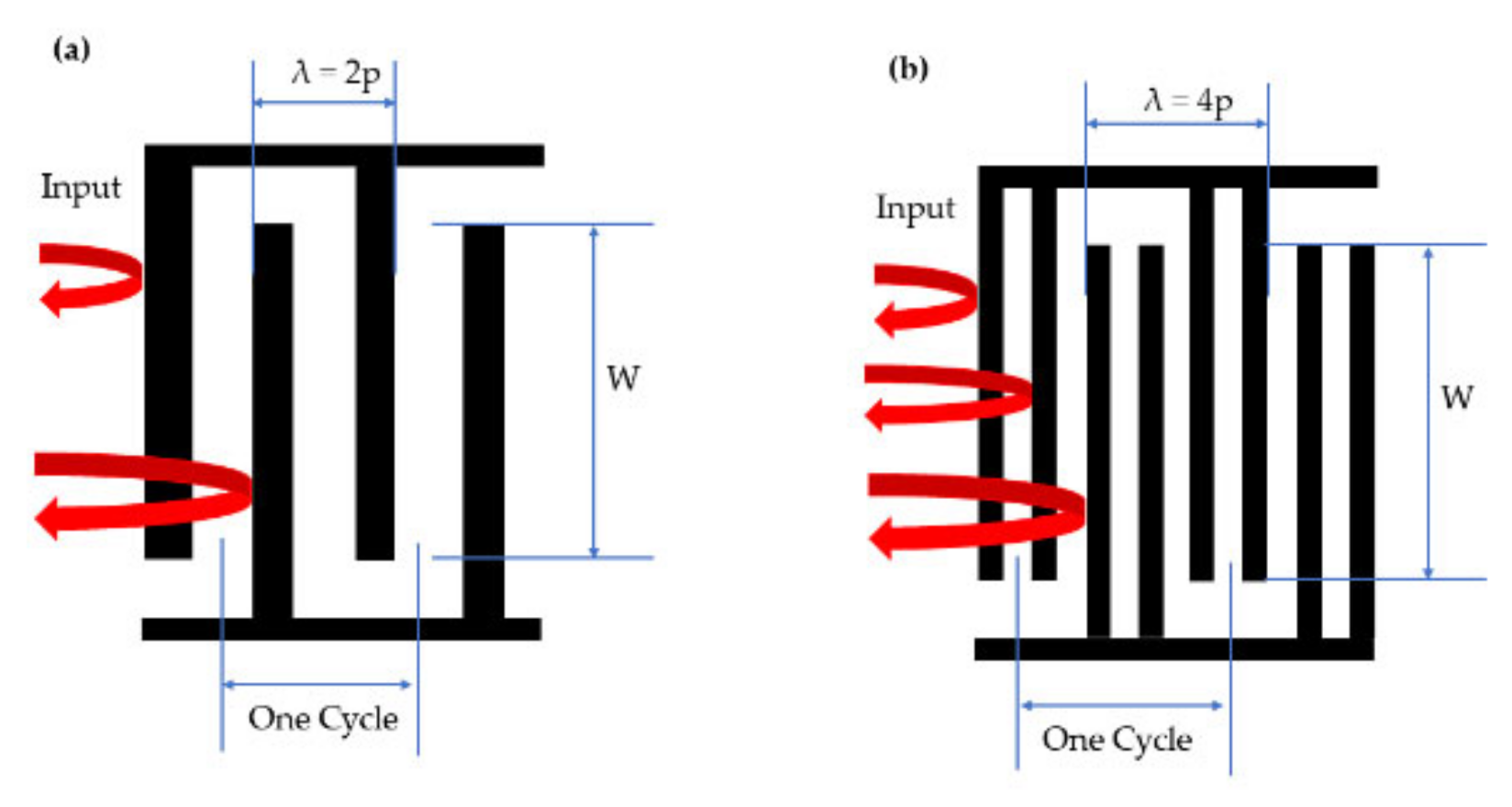
2.1. Calculation Principle
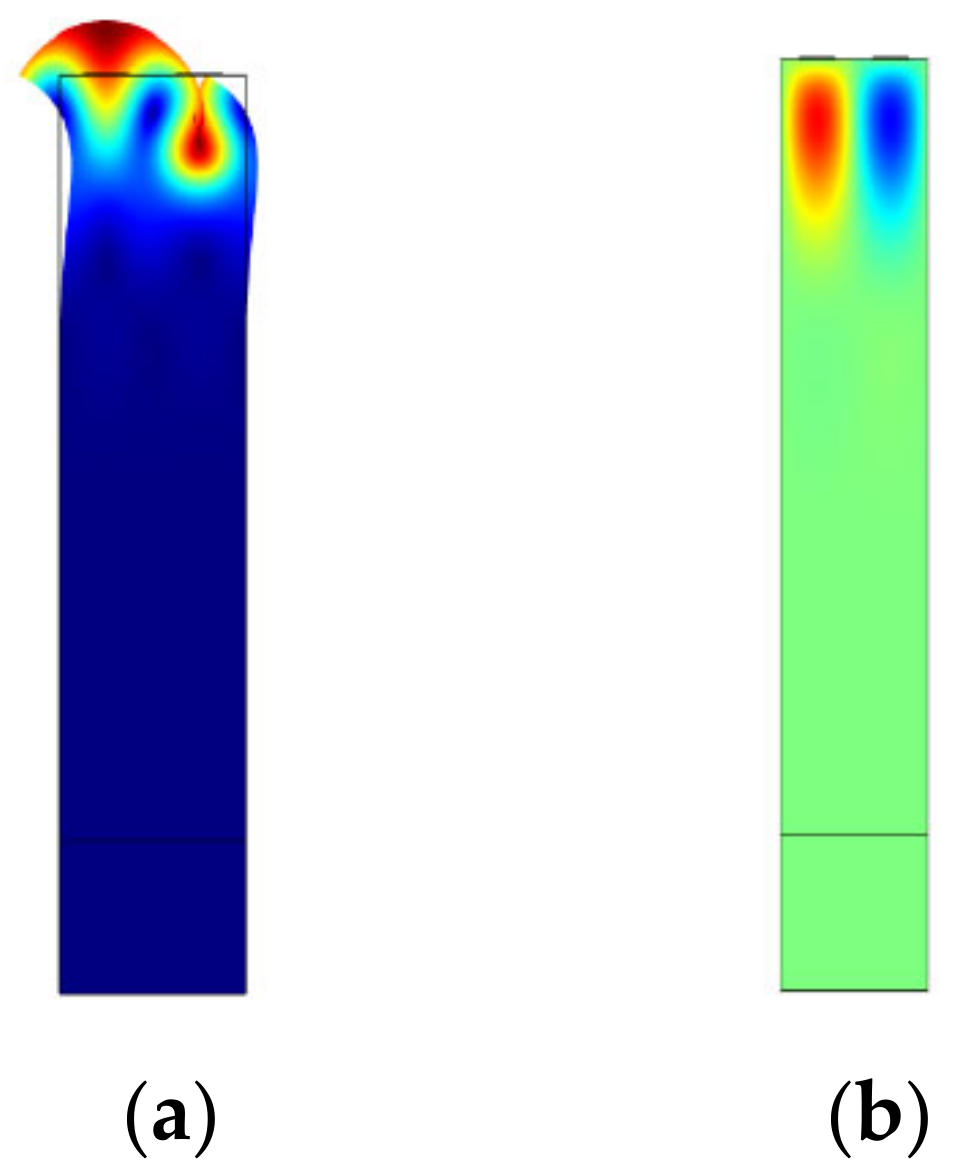
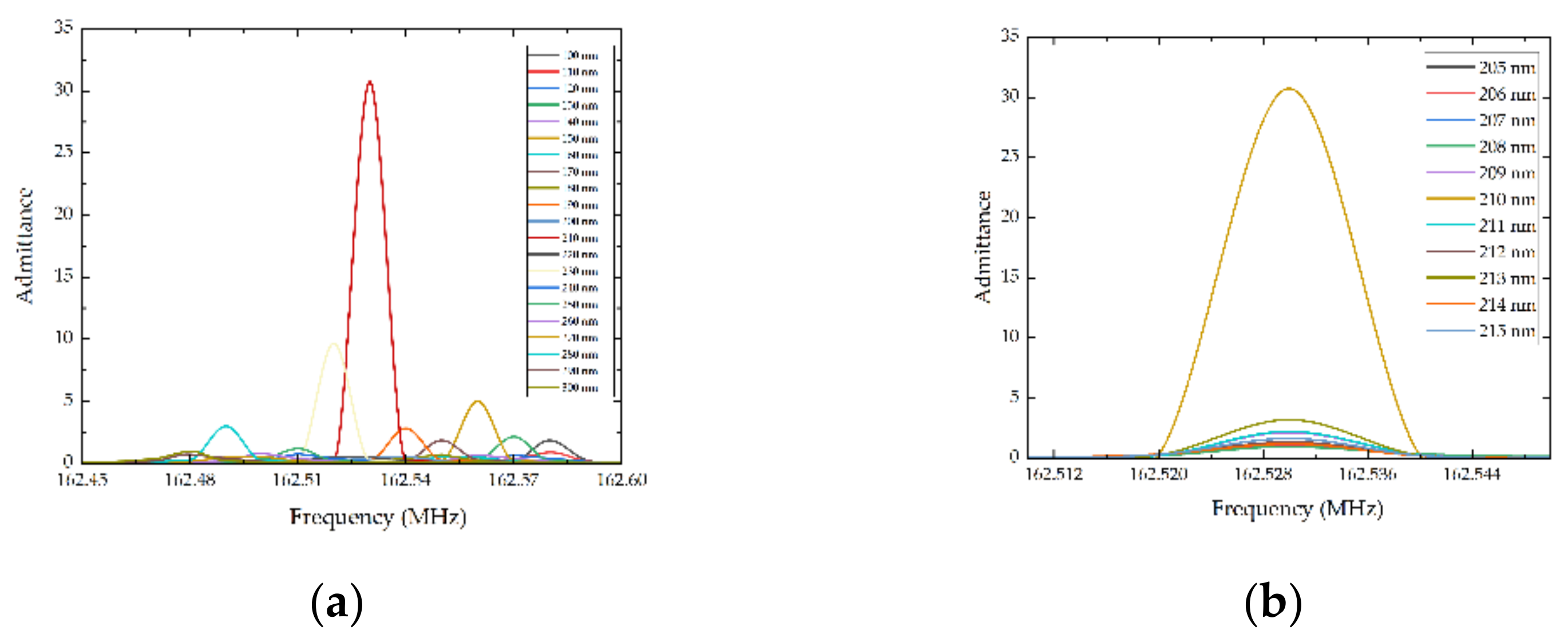
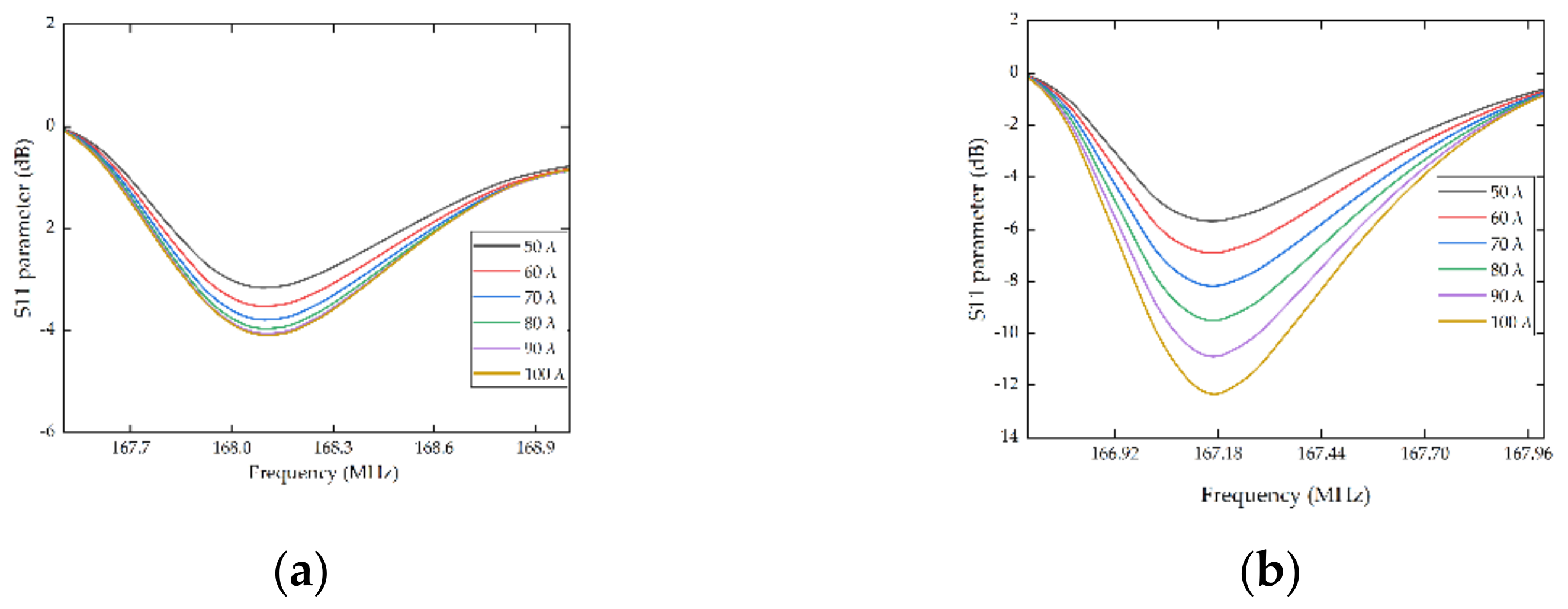
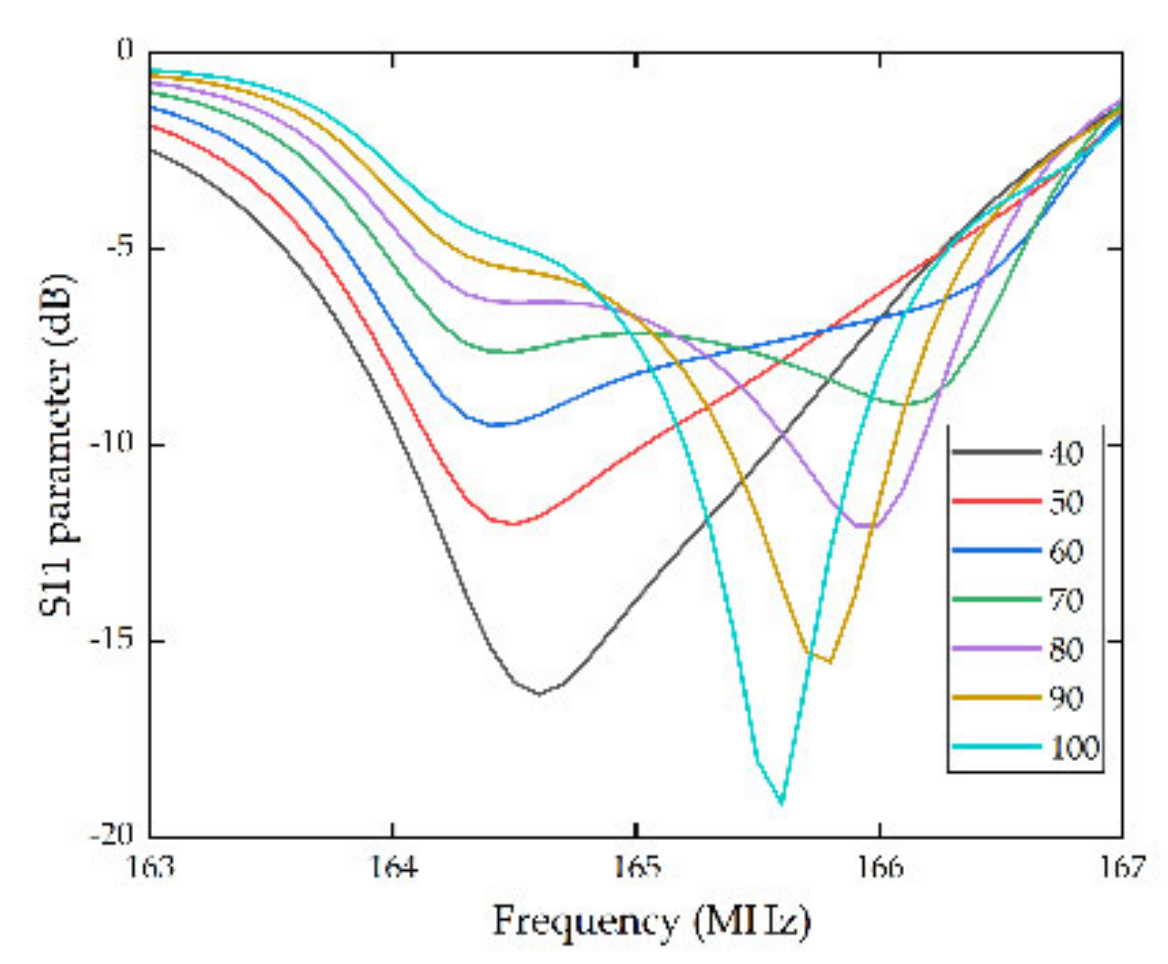
2.2. Temperature Sensor Simulation
2.3. Sensor Fabrication
2.4. Cryogenic Temperature Measurement
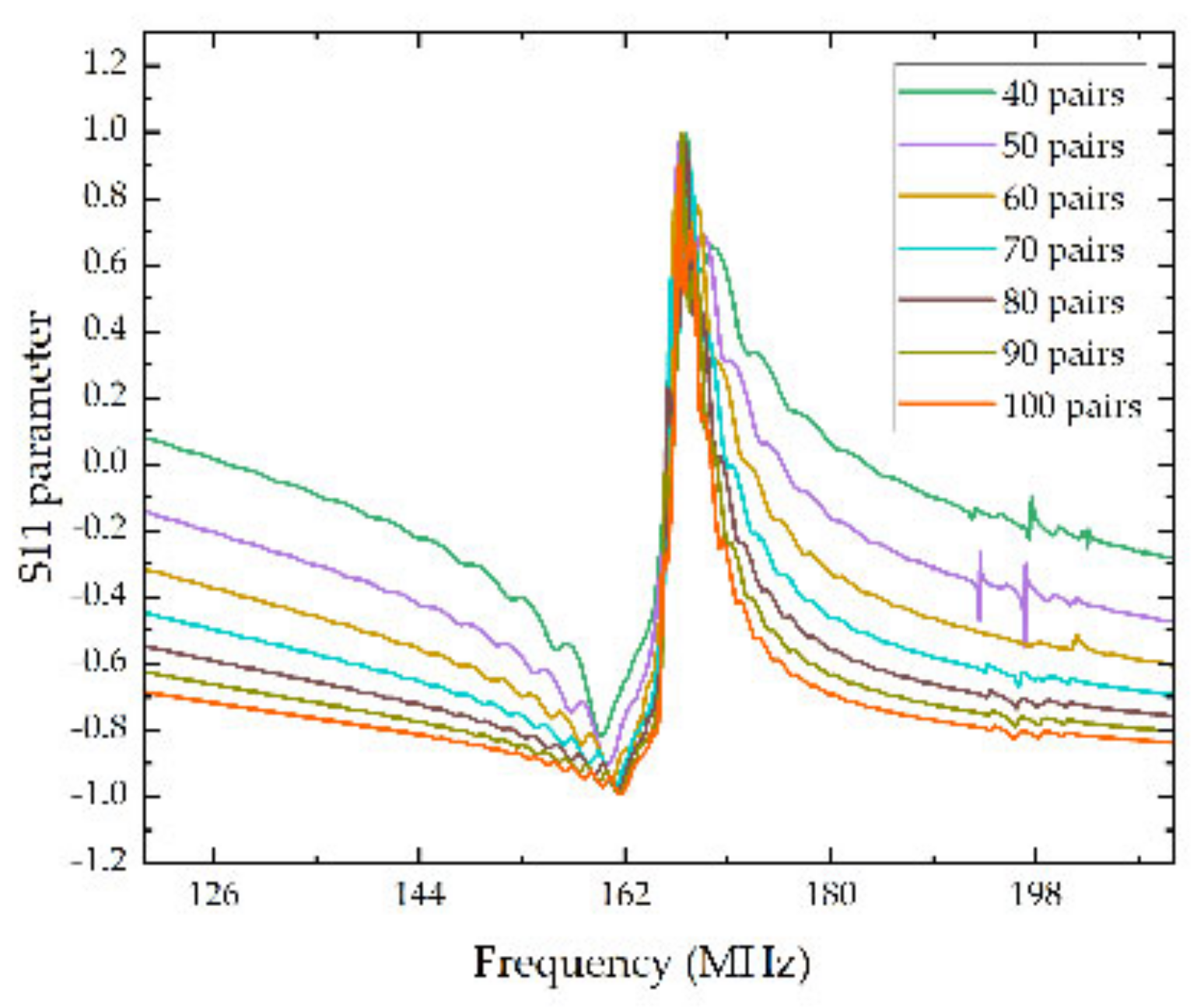
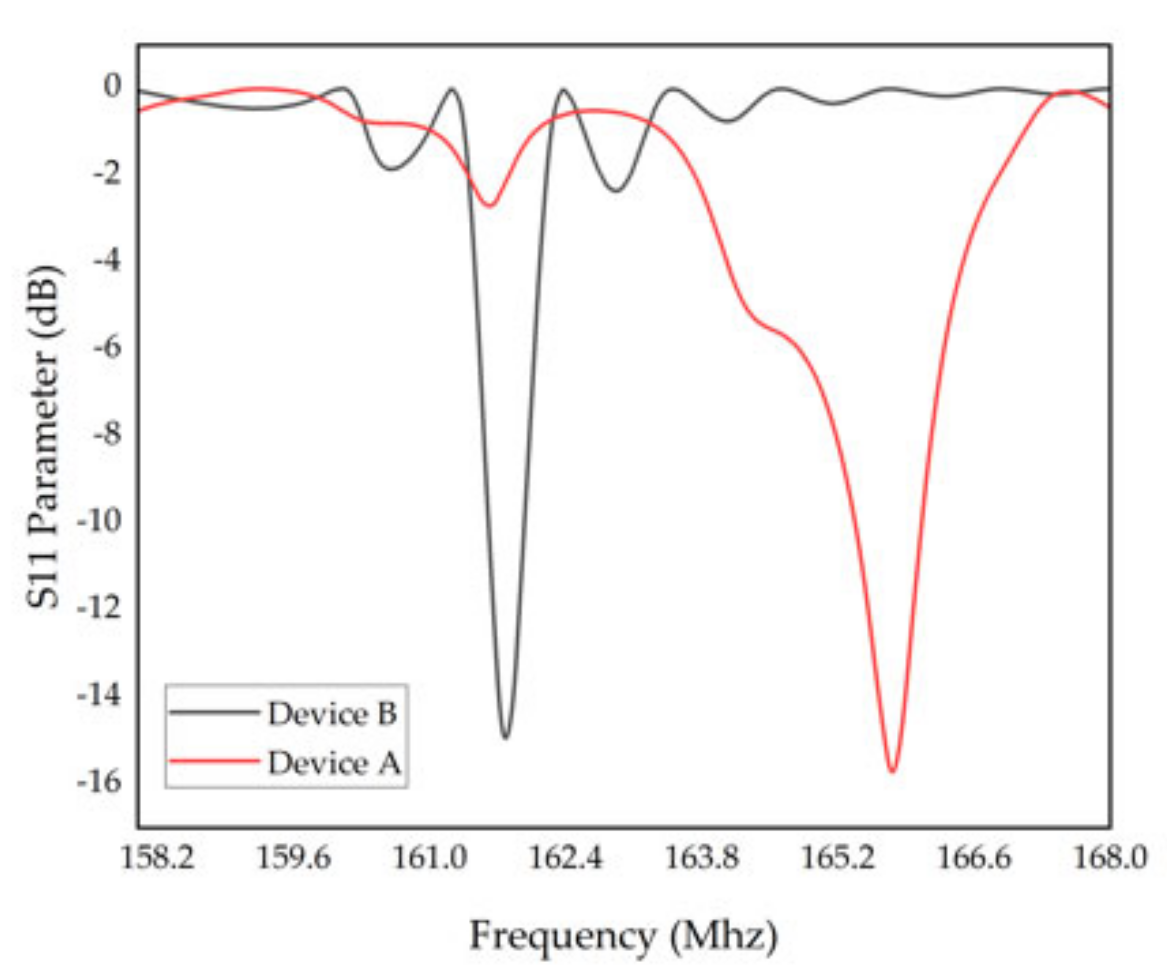
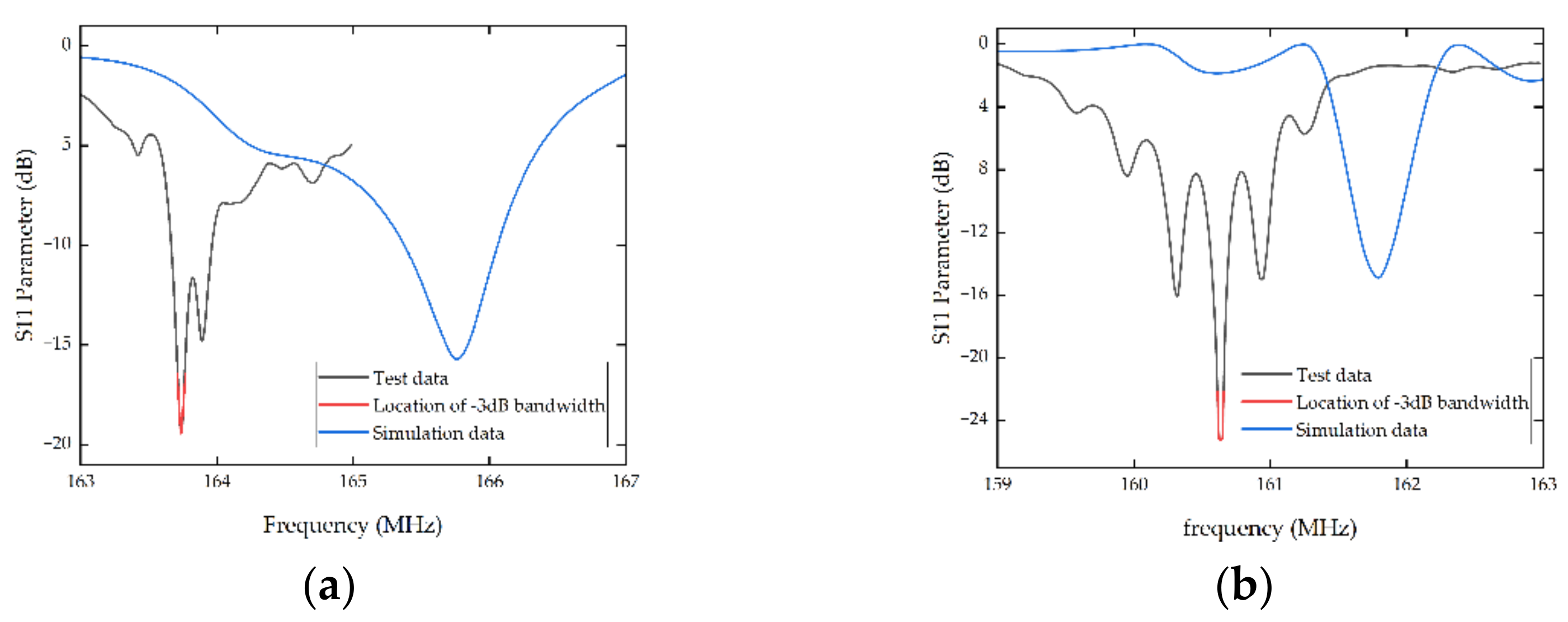
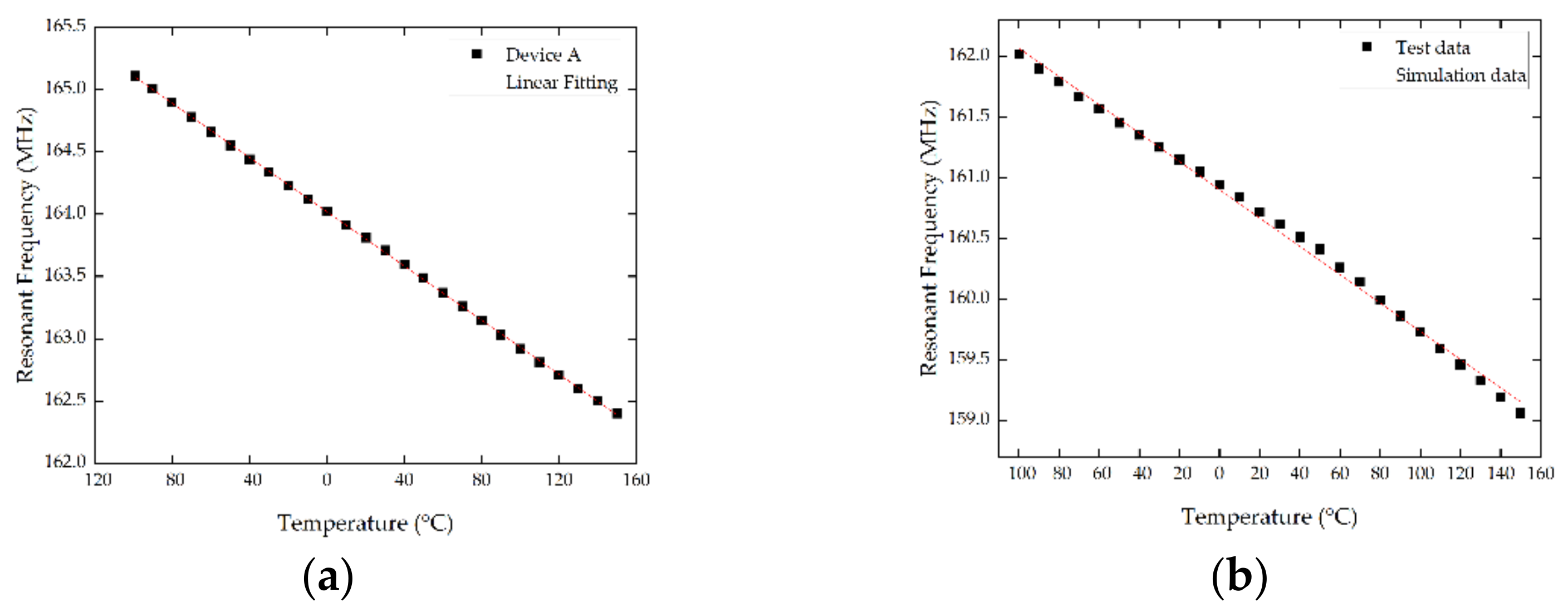
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sampath, U.; Kim, D.-G.; Kim, H.; Song, M. Cryogenic Temperature Sensor Based on Fresnel Reflection From a Polymer-Coated Facet of Optical Fiber. IEEE Sens. J. 2018, 18, 3640–3644. [Google Scholar] [CrossRef]
- Zaynetdinov, M.; See, E.M.; Geist, B.; Ciovati, G.; Robinson, H.D.; Kochergin, V. A Fiber Bragg Grating Temperature Sensor for 2–400 K. IEEE Sens. J. 2015, 15, 1908–1912. [Google Scholar] [CrossRef]
- Gupta, S.; Mizunami, T.; Yamao, T.; Shimomura, T. Fiber Bragg Grating Cryogenic Temperature Sensors. Appl. Opt. 1996, 35, 5202–5205. [Google Scholar] [CrossRef] [PubMed]
- Riza, N.A.; Arain, M.A. Cryogenic Temperature Measurement Using Silicon Carbide-Based Wireless Optical Sensor. IEEE Photonics Technol. Lett. 2006, 18, 2599–2601. [Google Scholar] [CrossRef]
- Rayleigh, Lord On Waves Propagated along the Plane Surface of an Elastic Solid. Proc. Lond. Math. Soc. 1885, s1–17, 4–11. [CrossRef]
- Gugliandolo, G.; Capra, P.P.; Campobello, G.; Donato, N. Cryogenic Characterization of SAW Resonators. In Proceedings of the 2019 14th International Conference on Advanced Technologies, Systems and Services in Telecommunications (TELSIKS), Nis, Serbia, 23–25 October 2019; pp. 311–314. [Google Scholar]
- Aubert, T.; Elmazria, O.; Assouar, B.; Blampain, E.; Hamdan, A.; Genève, D.; Weber, S. Investigations on AlN/Sapphire Piezoelectric Bilayer Structure for High-Temperature SAW Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 999–1005. [Google Scholar] [CrossRef]
- Aubert, T.; Bardong, J.; Elmazria, O.; Bruckner, G.; Assouar, B. Iridium Interdigital Transducers for High-Temperature Surface Acoustic Wave Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 194–197. [Google Scholar] [CrossRef]
- Mueller, A.; Giangu, I.; Stavrinidis, A.; Stefanescu, A.; Stavrinidis, G.; Dinescu, A.; Konstantinidis, G. Sezawa Propagation Mode in GaN on Si Surface Acoustic Wave Type Temperature Sensor Structures Operating at GHz Frequencies. IEEE Electron. Device Lett. 2015, 36, 1299–1302. [Google Scholar] [CrossRef]
- Nicoloiu, A.; Stan, G.E.; Nastase, C.; Boldeiu, G.; Besleaga, C.; Dinescu, A.; Mueller, A. The Behavior of Gold Metallized AlN/Si- and AlN/Glass-Based SAW Structures as Temperature Sensors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 1938–1948. [Google Scholar] [CrossRef]
- Campobello, G.; Crupi, G.; Donato, N. Cryogenic Electrical Characterization and Equivalent-Circuit Modeling of SAW Resonators. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020; pp. 1–5. [Google Scholar]
- Xu, H.; Jin, H.; Dong, S.; Chen, J.; Song, X.; Xuan, W.; Shi, L.; Huang, S.; Zhang, P.; Luo, J. A Langasite Surface Acoustic Wave Wide-Range Temperature Sensor with Excellent Linearity and High Sensitivity. AIP Adv. 2021, 11, 015143. [Google Scholar] [CrossRef]
- Nakamura, H.; Nakanishi, H.; Goto, R.; Hashimoto, K. Suppression of Transverse-Mode Spurious Responses for Saw Resonators on SiO2/Al/LiNbO3 Structure by Selective Removal of SiO2. IEEE Transac. Ultrason. Ferroelectr. Freq. Control 2011, 58, 2188–2193. [Google Scholar] [CrossRef]
- Islam, M.S.; Beamish, J. Piezoelectric Creep in LiNbO3, PMN-PT and PZT-5A at Low Temperatures. J. Appl. Phys. 2019, 126, 204101. [Google Scholar] [CrossRef]
- Bigler, E.; Hauden, D.; Theobald, G. Stress-Sensitivity Mapping for Surface Acoustic Waves on Quartz. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1989, 36, 57–62. [Google Scholar] [CrossRef]
- Hietala, S.L.; Hietala, V.M.; Brinker, C.J. Dual SAW Sensor Technique for Determining Mass and Modulus Changes. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2001, 48, 262–267. [Google Scholar] [CrossRef]
- Lee, P.C.Y.; Liu, N.H. Plane Harmonic Waves in an Infinite Piezoelectric Plate with Dissipation. In Proceedings of the 2002 IEEE International Frequency Control Symposium and PDA Exhibition (Cat. No.02CH37234), New Orleans, LA, USA, 31 May 2002; pp. 162–169. [Google Scholar]
- Chung, G.-S.; Phan, D.-T. Finite Element Modeling of Surface Acoustic Waves in Piezoelectric Thin Films. J. Korean Phys. Soc. 2010, 57, 446–4550. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H. Investigation of Surface Acoustic Wave Propagation Characteristics in New Multilayer Structure: SiO2/IDT/LiNbO3/Diamond/Si. Micromachines 2021, 12, 1286. [Google Scholar] [CrossRef]
- Sakharov, S.; Kondratiev, S.; Zabelin, A.; Naumenko, N.; Azarov, A.; Zhgoon, S.; Shvetsov, A. Theoretical and Experimental Investigation of Langasite as Material for Wireless High Temperature SAW Sensors. In Proceedings of the 2010 IEEE International Ultrasonics Symposium, San Diego, CA, USA, 11–14 October 2010; pp. 535–538. [Google Scholar]
- Yan, Y.; Wang, Y.; Carka, D.; Li, F. Surface Acoustic Wave Sensors for Temperature and Strain Measurements. In Proceedings of the 2020 IEEE International Ultrasonics Symposium (IUS), Las Vegas, NV, USA, 7 September 2020; pp. 1–5. [Google Scholar]
- Smith, R.T.; Welsh, F.S. Temperature Dependence of the Elastic, Piezoelectric, and Dielectric Constants of Lithium Tantalate and Lithium Niobate. J. Appl. Phys. 1971, 42, 2219–2230. [Google Scholar] [CrossRef]
- Kim, Y.S.; Smith, R.T. Thermal Expansion of Lithium Tantalate and Lithium Niobate Single Crystals. J. Appl. Phys. 1969, 40, 4637–4641. [Google Scholar] [CrossRef]
- Geng, W.; Zhao, C.; Xue, F.; Qiao, X.; He, J.; Xue, G.; Liu, Y.; Wei, H.; Bi, K.; Mei, L.; et al. Influence of Structural Parameters on Performance of SAW Resonators Based on 128° YX LiNbO3 Single Crystal. Nanomaterials 2022, 12, 2109. [Google Scholar] [CrossRef]
- Sha, G.; Harlow, C.; Chernatynskiy, A.; Daw, J.; Khafizov, M. In-Situ Measurement of Irradiation Behavior in LiNbO3. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2020, 472, 46–52. [Google Scholar] [CrossRef]
- Darinskii, A.N.; Weihnacht, M.; Schmidt, H. Anisotropy Effects in the Reflection of Surface Acoustic Waves from Obstacles. IEEE Trans. Ultrason. Ferroelect. Freq. Control 2013, 60, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Stefanescu, A.; Neculoiu, D.; Mueller, A.; Dinescu, A.; Konstantinidis, G.; Stavrinidis, A. Analysis of GaN Based SAW Resonators Including FEM Modeling. Rom. J. Inf. Sci. Technol. 2011, 14, 334–345. [Google Scholar]
- Ralib, A.A.M.; Nordin, A.N.; Alam, A.H.M.Z.; Hashim, U.; Othman, R. Piezoelectric Thin Films for Double Electrode CMOS MEMS Surface Acoustic Wave (SAW) Resonator. Microsyst. Technol. 2015, 21, 1931–1940. [Google Scholar] [CrossRef]
- Song, Y.-H.; Lu, R.; Gong, S. Analysis and Removal of Spurious Response in SH0 Lithium Niobate MEMS Resonators. IEEE Trans. Electron Devices 2016, 63, 2066–2073. [Google Scholar] [CrossRef]
- Li, Q.; Qian, L.; Fu, S.; Song, C.; Zeng, F.; Pan, F. Characteristics of One-Port Surface Acoustic Wave Resonator Fabricated on ZnO/6H-SiC Layered Structure. J. Phys. D Appl. Phys. 2018, 51, 145305. [Google Scholar] [CrossRef]
- Ai, Y.; Yang, S.; Cheng, Z.; Zhang, L.; Jia, L.; Dong, B.; Wang, J.; Zhang, Y. Enhanced Performance of AlN SAW Devices with Wave Propagation along The [11–20] direction on c-Plane Sapphire Substrate. J. Phys. D Appl. Phys. 2019, 52, 215103. [Google Scholar] [CrossRef]
- Ding, A.; Kirste, L.; Lu, Y.; Driad, R.; Kurz, N.; Lebedev, V.; Christoph, T.; Feil, N.M.; Lozar, R.; Metzger, T.; et al. Enhanced Electromechanical Coupling in SAW Resonators Based on Sputtered Non-Polar Al0.77Sc0.23N 11 2 ¯ 0 Thin Films. Appl. Phys. Lett. 2020, 116, 101903. [Google Scholar] [CrossRef]



| Parameters | Initial Values |
|---|---|
| Resonant frequency (f, MHz) | 162 |
| SAW wavelength (λ, um) | 24 |
| Width of IDT (a, um) | 6 |
| Al Electrode thickness (h2, nm) | 140 |
| Pitch (p, um) | 12 |
| Metal ratio | 0.5 |
| Aperture | 50λ |
| The thickness of LiNbO3 (h1, um) | 5λ |
| Parameters | Ultimate Values of Device A |
|---|---|
| Resonant frequency (f, MHz) | 162 |
| SAW wavelength (λ, um) | 24 |
| Width of IDT (a, um) | 6 |
| Al Electrode thickness (h2, nm) | 210 |
| Pitch (p, um) | 12 |
| Metal ratio | 0.5 |
| Aperture | 80λ |
| Reflecting grid logarithm (Ng) | 100 |
| Pairs of electrodes (Np) | 80 |
| Parameters | Values of Device B |
|---|---|
| Resonant frequency (f, MHz) | 160 |
| SAW wavelength (λ, um) | 24 |
| Width of IDT (a, um) | 3 |
| Al Electrode thickness (h2, nm) | 210 |
| Pitch (p, um) | 12 |
| Metal ratio | 0.5 |
| Aperture | 80λ |
| Pairs of electrodes | 80 |
| Reflecting grid logarithm (Ng) | 100 |
| The thickness of LiNbO3 (h1, um) | 5λ |
| Piezoelectric Substrate | Frequency (MHz) | Q value |
|---|---|---|
| LiNbO3 [29] | 150 | 1150 |
| 128° YX LiNbO3 [24] | 224.85 | 1364.5 |
| ZnO/6H-SiC [30] | 688 | 1080 |
| AlN/Al2O3 [31] | 688.75 | 1082 |
| Sc0.23Al0.77N/Al2O3 [32] | 1910 | 659 |
| Device A of this work | 163.74 | 2955.60 |
| Device B of this work | 160.625 | 5757.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Wang, H.; Zhang, F.; Ding, Q. High-Performance SAW Low Temperature Sensors with Double Electrode Transducers Based on 128° YX LiNbO3. Micromachines 2022, 13, 1912. https://doi.org/10.3390/mi13111912
Zhu J, Wang H, Zhang F, Ding Q. High-Performance SAW Low Temperature Sensors with Double Electrode Transducers Based on 128° YX LiNbO3. Micromachines. 2022; 13(11):1912. https://doi.org/10.3390/mi13111912
Chicago/Turabian StyleZhu, Jiajun, Hongliang Wang, Feng Zhang, and Qi Ding. 2022. "High-Performance SAW Low Temperature Sensors with Double Electrode Transducers Based on 128° YX LiNbO3" Micromachines 13, no. 11: 1912. https://doi.org/10.3390/mi13111912
APA StyleZhu, J., Wang, H., Zhang, F., & Ding, Q. (2022). High-Performance SAW Low Temperature Sensors with Double Electrode Transducers Based on 128° YX LiNbO3. Micromachines, 13(11), 1912. https://doi.org/10.3390/mi13111912





