Micromanufactured Tactile Samples for Characterization of Rough and Dry Tactile Perception
Abstract
1. Introduction
2. Tactile Samples and Methods
2.1. Ranking Method
2.2. Roughness Perception Experiments
2.2.1. Tactile Samples for Roughness Perception Experiments
2.2.2. Roughness Perception Experiments with Tactile Samples
2.3. Dry/Wet Perception Experiments
2.3.1. Tactile Samples for Dry/Wet Perception Experiments
2.3.2. Dry/Wet Perception Experiments Using Tactile Samples with Random Patterns
2.3.3. Dry/Wet Perception Experiments Using Tactile Samples with Square Patterns
| Tactile Perception | Texture of Tactile Samples | Parameters | Objectives: To Investigate | Number of Participants | Results |
|---|---|---|---|---|---|
| Roughness | Stripe (Figure 1) | Ridge and groove widths | The effects of the ridge and groove widths | 11 (10 males and 1 female, aged 20 to 29 years) | Section 3.1 |
| Which of the ridge and the groove widths was more dominant | 5 (5 males, aged 20 to 29 years) | Section 3.1 | |||
| Dryness | Random (Figure 2) | Etching time/roughness | The effects of the surface roughness | 9 (8 males and 1 female, aged 20 to 29 years) | Section 3.2.1 |
| Square (Figure 3) | Square width and gap between the squares () | The effects of the feature size | 14 (12 males and 2 females, aged 20 to 29 years) | Section 3.2.2 | |
| Square width and gap between the squares | How the dryness perception varied with the feature size below and above 30 µm | 7 (7 males, aged 20 to 29 years) | Section 3.2.2 | ||
| The effects of the gap | 10 (9 males and 1 female, aged 20 to 29 years) | Section 3.2.2 |
3. Results and Discussion
3.1. Roughness Perception Experiments
3.2. Dry/Wet Perception Experiments
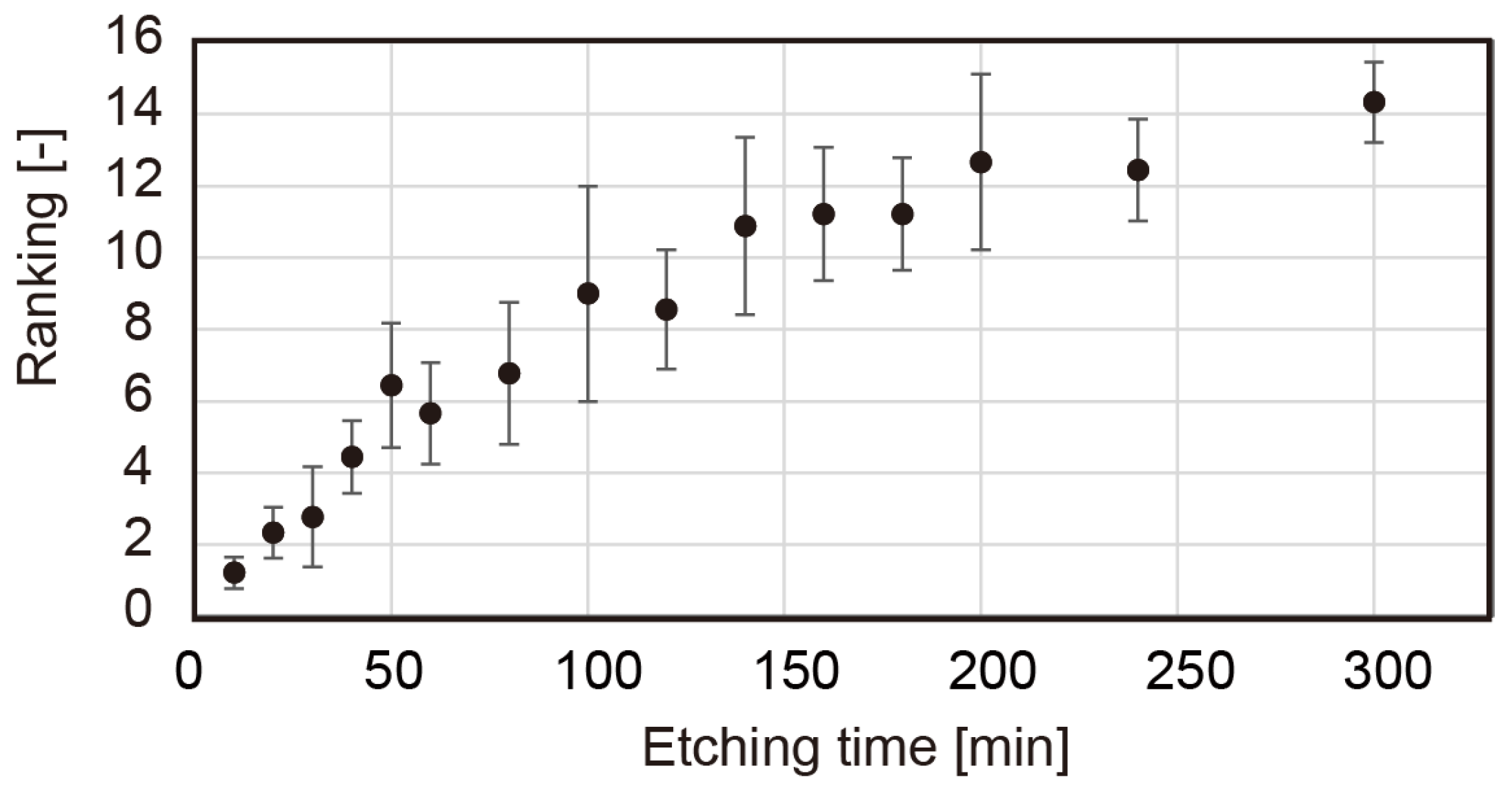
3.2.1. Experiments with Tactile Samples with Random Patterns
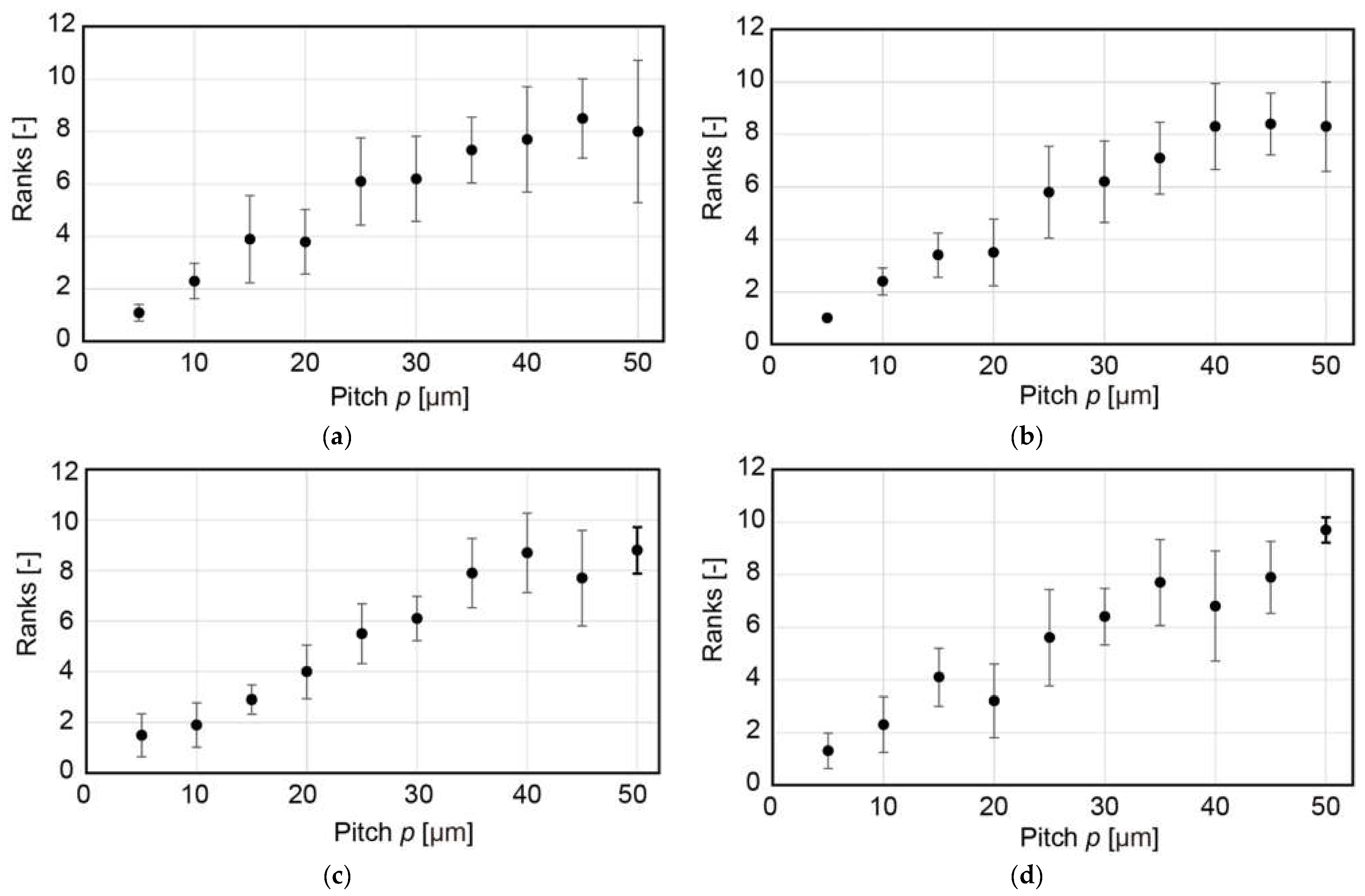
3.2.2. Experiments with Tactile Samples with Square Patterns
3.3. Discussion
3.3.1. Roughness Feeling
3.3.2. Dry/Wet Feeling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Okamoto, S.; Nagano, H.; Yamada, Y. Psychophysical dimensions of tactile perception of textures. IEEE Trans. Hapt. 2013, 6, 81–93. [Google Scholar] [CrossRef] [PubMed]
- Tachi, S. Telexistence: Enabling humans to be virtually ubiquitous. IEEE Comput. Graph. Appl. 2016, 36, 8–14. [Google Scholar] [CrossRef]
- Tanaka, M.; Numazawa, Y. Rating and valuation of human haptic sensation. Int. J. Appl. Electromagn. Mech. 2004, 19, 573–579. [Google Scholar] [CrossRef]
- Tang, W.; Chen, N.; Zhang, J.; Chen, S.; Ge, S.; Zhu, H.; Zhang, S.; Yang, H. Characterization of tactile perception and optimal exploration movement. Tribol. Lett. 2015, 58, 28. [Google Scholar] [CrossRef]
- Kosemura, Y.; Ishikawa, H.; Watanabe, J.; Miki, N. Characterization of surfaces virtually created using MEMS tactile display. Jpn. J. Appl. Phys. 2014, 53, 6–11. [Google Scholar] [CrossRef]
- Kosemura, Y.; Hasegawa, S.; Miki, N. Surface properties that can be displayed by a MEMS-based mechanical tactile display. Micro Nano Lett. 2016, 11, 240. [Google Scholar] [CrossRef]
- Tymms, C.; Zorin, D.; Gardner, E.P. Tactile perception of the roughness of 3D-printd textures. J. Neurophsiol. 2017, 119, 862. [Google Scholar] [CrossRef] [PubMed]
- van Kuilenburg, J.; Masen, M.A.; Groenendijk, M.N.W.; Bana, V.; van der Heide, E. An experimental study on the relation between surface textures and tactile friction. Tribol. Int. 2012, 48, 15. [Google Scholar] [CrossRef]
- Xu, J.; Nonomura, Y.; Mineta, T. Evaluation of tactile sensation using periodic Si micro-bump arrayed surface with various bump sizes. IEEJ Trans. Sens. Micromach. 2019, 139, 393–399. [Google Scholar] [CrossRef]
- Kawazoe, M.; Kosemura, Y.; Miki, N. Encoding and presentation of surface textures using a mechanotactile display. Sens. Actuators A Phys. 2017, 261, 30–39. [Google Scholar] [CrossRef]
- Kawazoe, N.; Miki, N. Tactile samples with variable surface textures to investigate tactile perception characteristic. J. Micromech. Microeng. 2020, 30, 105011. [Google Scholar] [CrossRef]
- Nakamae, M. Study of the Reliability of Visual Evaluation by the Ranking Method: Analysis of ordinal scale and psychological scaling using the normalized-rank approach. Jpn. J. Radiol. Technol. 2000, 56, 725–730. [Google Scholar] [CrossRef]
- Okamoto, S.; Nagano, H.; Ho, H.N. Pervasive Haptics: Science, Design, and Application; Springer: Tokyo, Japan, 2016; pp. 3–20. [Google Scholar]
- Yoshioka, T.; Gibb, B.; Dorsch, A.K.; Hsiao, S.S.; Johnson, K.O. Neural coding mechanisms underlying perceived roughness of finely textured surfaces. J. Neurosci. 2001, 21, 6905–6916. [Google Scholar] [CrossRef]
- Connor, C.E.; Hsiao, S.S.; Phillips, J.R.; Johnson, K.O. Tactile roughness: Neural codes that account for psychophysical magnitude estimates. J. Neurosci. 1990, 10, 3823–3836. [Google Scholar] [CrossRef]
- Blake, D.T.; Hsiao, S.S.; Johnson, K.O. Neural coding mechanisms in tactile pattern recognition: The relative contributions of slowly and rapidly adapting mechanoreceptors to perceived roughness. J. Neurosci. 1997, 17, 7480–7489. [Google Scholar] [CrossRef]
- Bensmaia, S.J.; Hollins, M. The vibrations of texture. Somatosens. Motor Res. 2003, 20, 33–43. [Google Scholar] [CrossRef]
- Lederman, S.J. Tactile roughness of grooved surfaces: The touching process and effects of macro- and microsurface structure. Percept. Psychophys. 1974, 16, 385–395. [Google Scholar] [CrossRef]
- Cascio, C.J.; Sathian, K. Temporal cues contribute to tactile perception of roughness. J. Neurosci. 2001, 21, 5289–5296. [Google Scholar] [CrossRef]
- Hwang, S.J.; Oh, D.J.; Jung, P.G.; Lee, S.M.; Go, J.S.; Kim, J.-H.; Hwang, K.-Y.; Ko, J.S. Dry etching of polydimethylsiloxane using microwave plasma. J. Micromech. Microeng. 2009, 19, 095010. [Google Scholar] [CrossRef]
- Hill, S.; Qian, W.; Chen, W.; Fu, J. Surface micromachining of polydimethylsiloxane for microfluidics applications. Biomicrofluidics 2016, 10, 54114. [Google Scholar] [CrossRef] [PubMed]
- Akhtar, T.; Chen, J.; Ettelaie, R.; Holmes, M.; Henson, B. Human roughness perception and possible factors effecting roughness sensation. J. Text. Stud. 2016, 48, 181–192. [Google Scholar] [CrossRef] [PubMed]
- Miki, N.; Spearing, S.M. Effect of nanoscale surface roughness on the bonding energy of direct-bonded silicon wafers. J. Appl. Phys. 2003, 94, 6800. [Google Scholar] [CrossRef]
- Shibahara, M.; Sato, K. Illusion of wetness by dynamic touch. IEEE Trans. Hapt. 2019, 12, 533–541. [Google Scholar] [CrossRef] [PubMed]
- Drewing, K.; Weyel, C.; Celebi, H.; Kaya, D. Feeling and feelings: Affective and perceptual dimensions of touched materials and their connection. In Proceedings of the IEEE World Haptics Conference (WHC), Munich, Germany, 5 June 2017. [Google Scholar] [CrossRef]
- Kawasegi, N.; Fujii, M.; Shimizu, T.; Sekiguchi, N.; Sumioka, J.; Doi, Y. Physical properties and tactile sensory perception of microtexturedmolded plastics. Precis. Eng. 2014, 38, 292–299. [Google Scholar] [CrossRef]


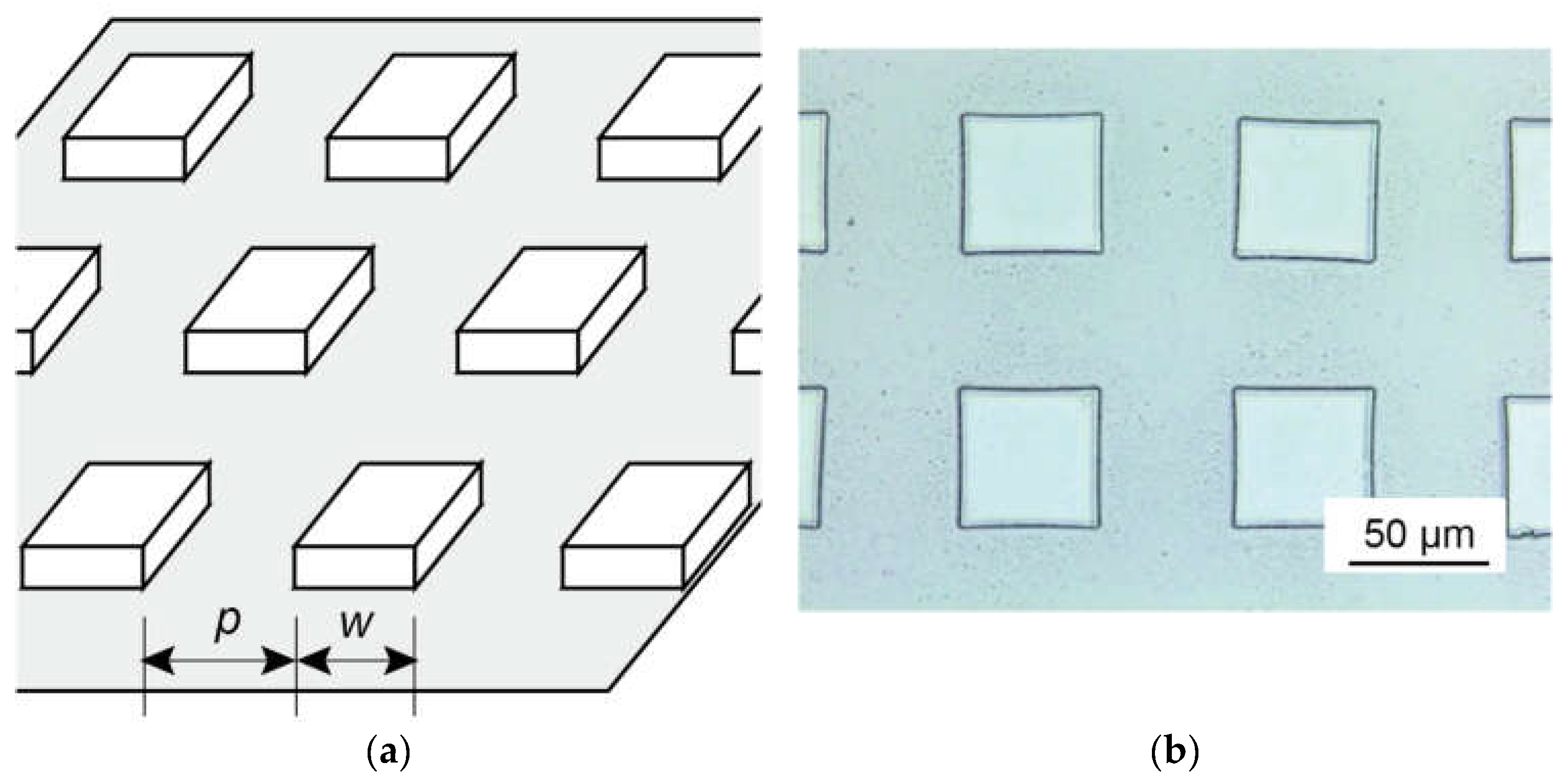



| (, ) (µm) | (25, 10) | (25, 20) | (25, 30) | (25, 40) | (25, 50) |
| (15, 10) | N.S. | + | + | + | + |
| (15, 20) | − | N.S. | + | + | + |
| (15, 30) | − | − | N.S. | + | + |
| (15, 40) | − | − | N.S. | N.S. | N.S. |
| (15, 50) | − | − | − | N.S. | N.S. |
| (,) (µm) | (50, 10) | (50, 20) | (50, 30) | (50, 40) | (50, 50) |
| (40, 10) | N.S. | + | + | + | + |
| (40, 20) | − | N.S. | N.S. | + | + |
| (40, 30) | − | − | − | N.S. | + |
| (40, 40) | − | − | − | − | N.S. |
| (40, 50) | − | − | − | − | − |
| (µm) | : 15 –25 (µm) | : 40 –50 (µm) |
| 10 | 7 | 7 |
| 20 | 8 | 6 |
| 30 | 9 | 0 * |
| 40 | 10 | 2 * |
| 50 | 9 | 3 * |
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
| 0.1 | * | * | * | * | * | * | * | * | * | |
| 0.2 | * | * | * | * | * | * | * | * | ||
| 0.3 | * | * | * | * | * | * | * | |||
| 0.4 | * | * | * | * | * | * | ||||
| 0.5 | * | * | * | * | * | |||||
| 0.6 | * | * | * | * | ||||||
| 0.7 | * | * | * | |||||||
| 0.8 | * | * | ||||||||
| 0.9 | N.S. | |||||||||
| 1.0 |
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | |
| 0.1 | * | * | * | * | * | * | * | * | * | |
| 0.2 | * | * | * | * | * | * | * | * | ||
| 0.3 | * | * | * | * | * | * | * | |||
| 0.4 | * | * | * | * | * | * | ||||
| 0.5 | N.S. | * | * | * | * | |||||
| 0.6 | N.S. | * | * | * | ||||||
| 0.7 | N.S. | * | * | |||||||
| 0.8 | N.S. | N.S. | ||||||||
| 0.9 | N.S. | |||||||||
| 1.0 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
| 5 | * | * | * | * | * | * | * | * | * | |
| 10 | * | * | * | * | * | * | * | * | ||
| 15 | N.S. | * | * | * | * | * | * | |||
| 20 | N.S. | * | * | * | * | * | ||||
| 25 | N.S. | * | * | * | * | |||||
| 30 | N.S. | * | * | * | ||||||
| 35 | N.S. | N.S. | * | |||||||
| 40 | N.S. | N.S. | ||||||||
| 45 | N.S. | |||||||||
| 50 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
| 5 | * | * | * | * | * | * | * | * | * | |
| 10 | * | * | * | * | * | * | * | * | ||
| 15 | N.S. | * | * | * | * | * | * | |||
| 20 | N.S. | * | * | * | * | * | ||||
| 25 | N.S. | * | * | * | * | |||||
| 30 | N.S. | * | * | * | ||||||
| 35 | N.S. | N.S. | * | |||||||
| 40 | N.S. | N.S. | ||||||||
| 45 | N.S. | |||||||||
| 50 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
| 5 | * | * | * | * | * | * | * | * | * | |
| 10 | * | * | * | * | * | * | * | * | ||
| 15 | * | * | * | * | * | * | * | |||
| 20 | N.S. | * | * | * | * | * | ||||
| 25 | N.S. | * | * | * | * | |||||
| 30 | N.S. | * | * | * | ||||||
| 35 | N.S. | * | * | |||||||
| 40 | N.S. | * | ||||||||
| 45 | N.S. | |||||||||
| 50 |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | |
| 5 | N.S. | * | * | * | * | * | * | * | * | |
| 10 | * | * | * | * | * | * | * | * | ||
| 15 | N.S. | * | * | * | * | * | * | |||
| 20 | N.S. | * | * | * | * | * | ||||
| 25 | N.S. | * | * | * | * | |||||
| 30 | N.S. | * | * | * | ||||||
| 35 | N.S. | * | * | |||||||
| 40 | N.S. | * | ||||||||
| 45 | N.S. | |||||||||
| 50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yanagibashi, K.; Miki, N. Micromanufactured Tactile Samples for Characterization of Rough and Dry Tactile Perception. Micromachines 2022, 13, 1685. https://doi.org/10.3390/mi13101685
Yanagibashi K, Miki N. Micromanufactured Tactile Samples for Characterization of Rough and Dry Tactile Perception. Micromachines. 2022; 13(10):1685. https://doi.org/10.3390/mi13101685
Chicago/Turabian StyleYanagibashi, Keiichiro, and Norihisa Miki. 2022. "Micromanufactured Tactile Samples for Characterization of Rough and Dry Tactile Perception" Micromachines 13, no. 10: 1685. https://doi.org/10.3390/mi13101685
APA StyleYanagibashi, K., & Miki, N. (2022). Micromanufactured Tactile Samples for Characterization of Rough and Dry Tactile Perception. Micromachines, 13(10), 1685. https://doi.org/10.3390/mi13101685







