Thermally Enhanced Darcy-Forchheimer Casson-Water/Glycerine Rotating Nanofluid Flow with Uniform Magnetic Field
Abstract
1. Introduction
2. Problem Formulation
3. Solution Methodology
4. Results and Discussion
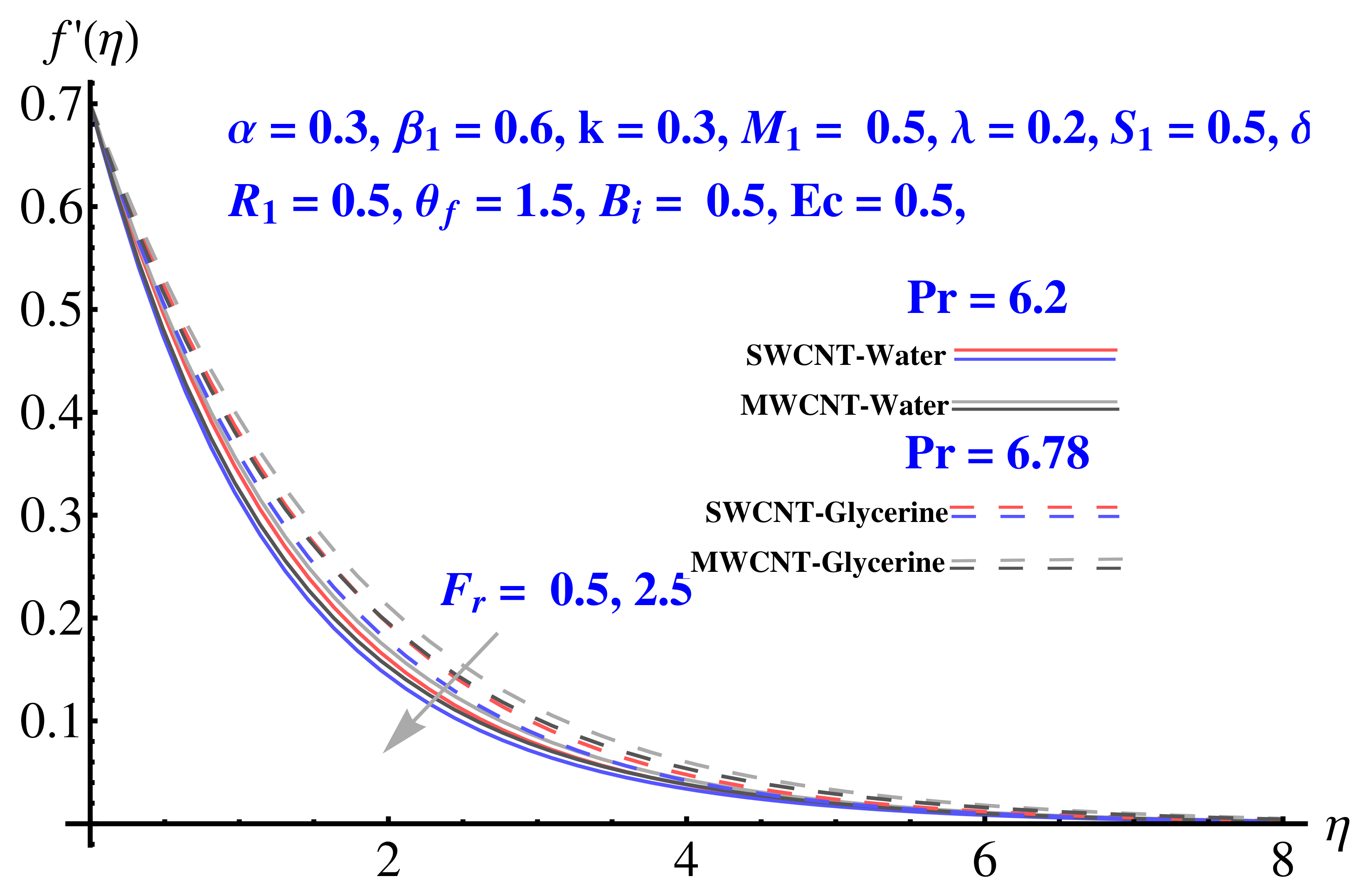
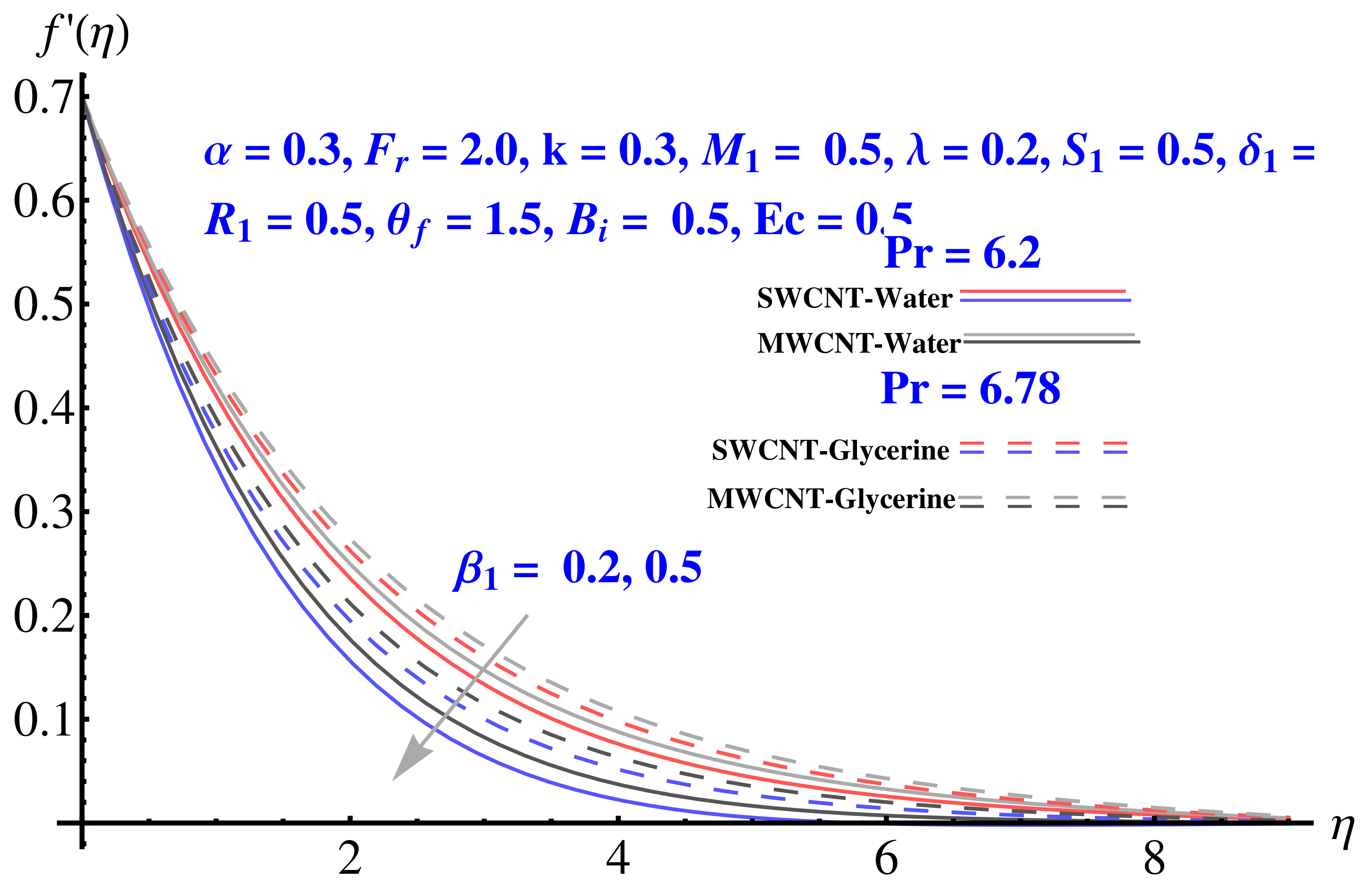
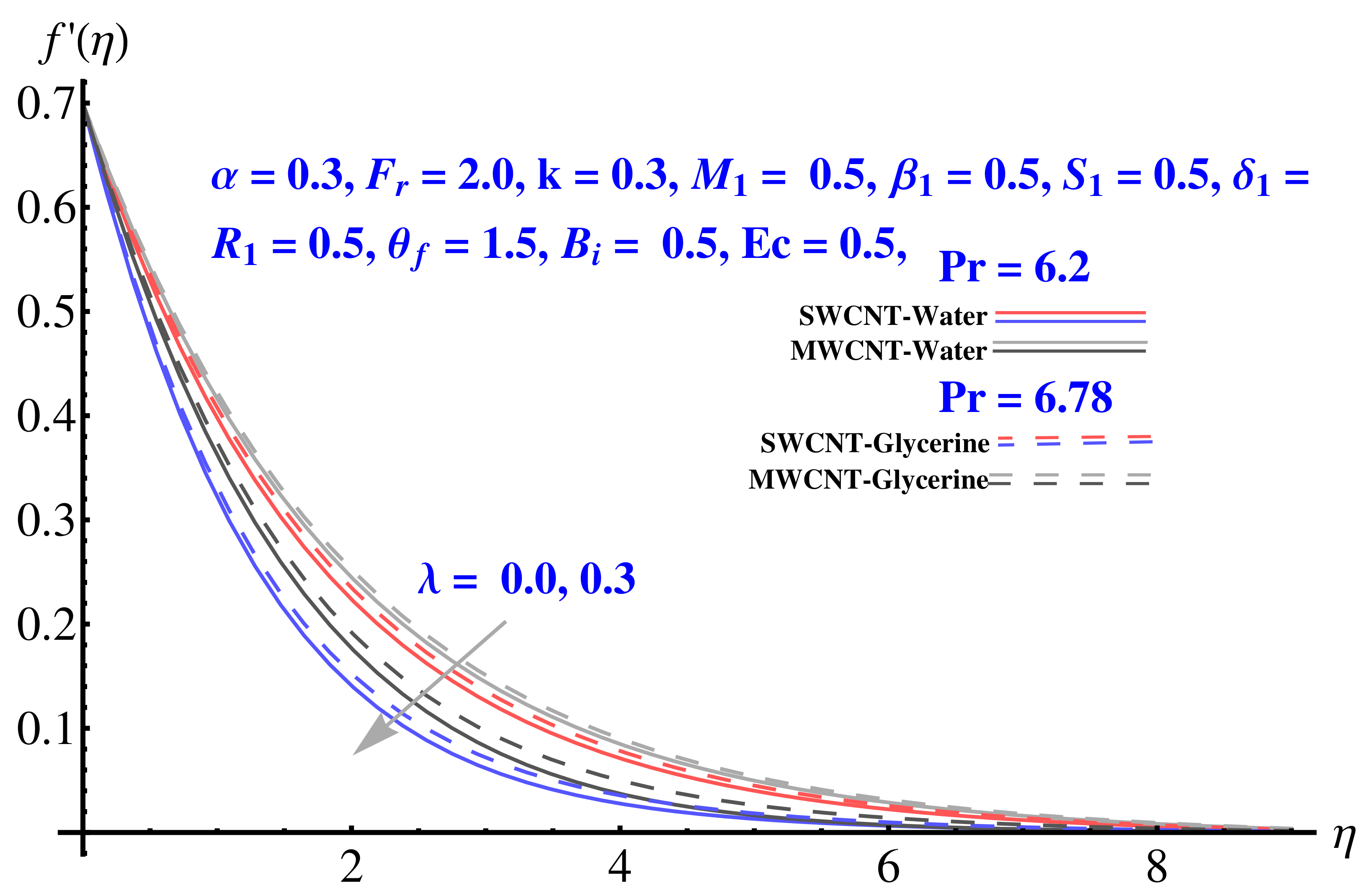
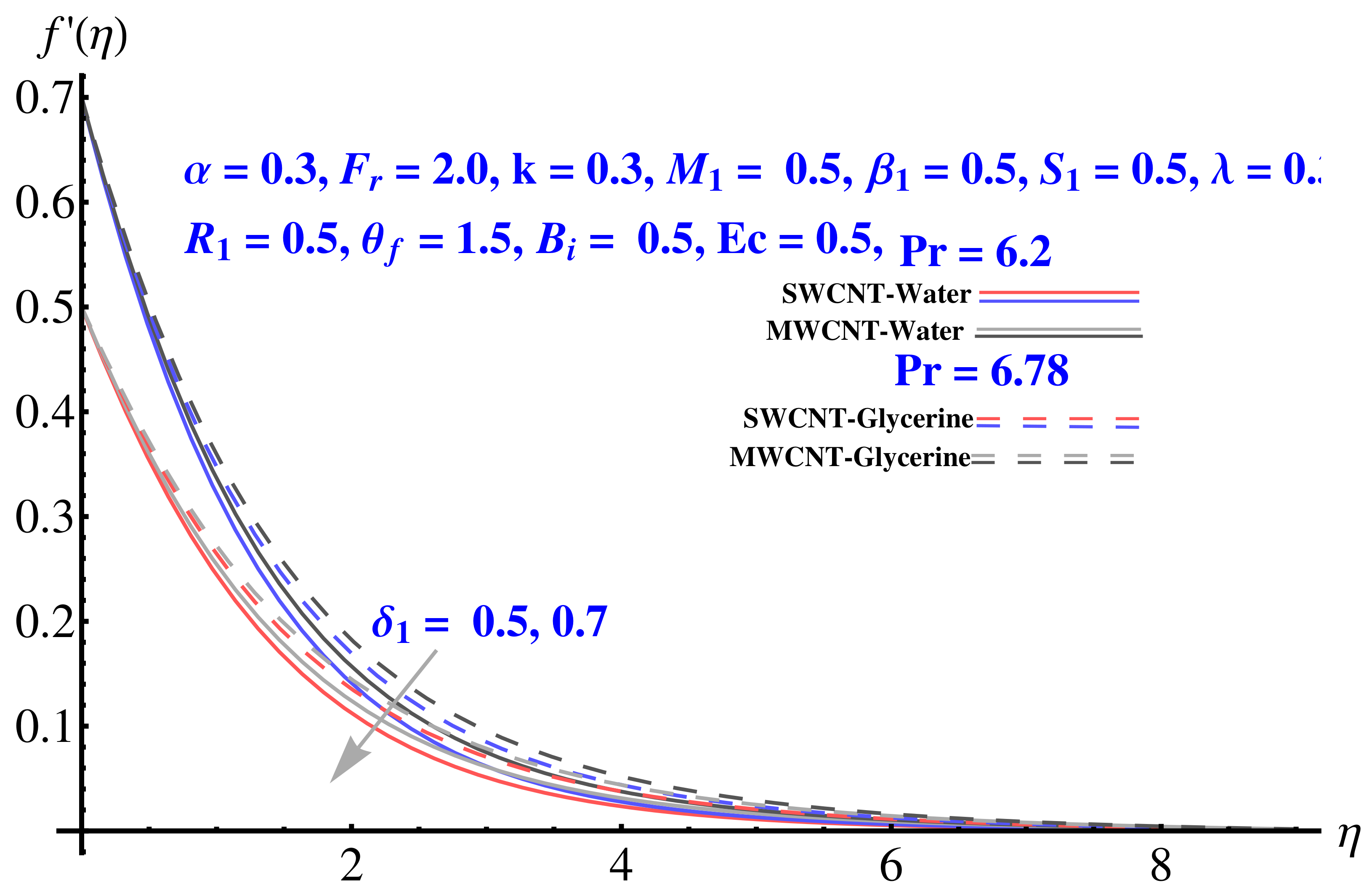
4.1. Radial Velocity
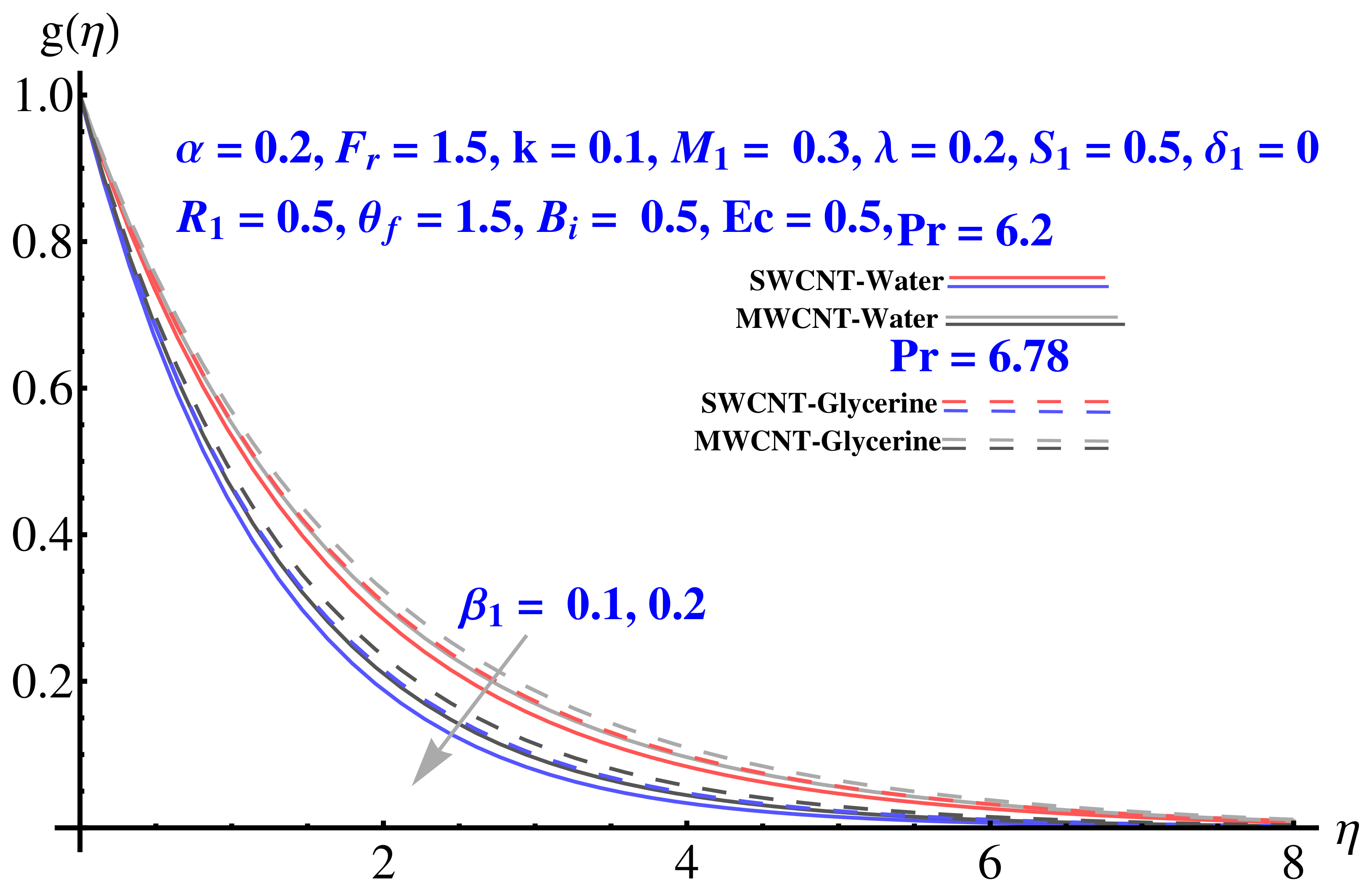
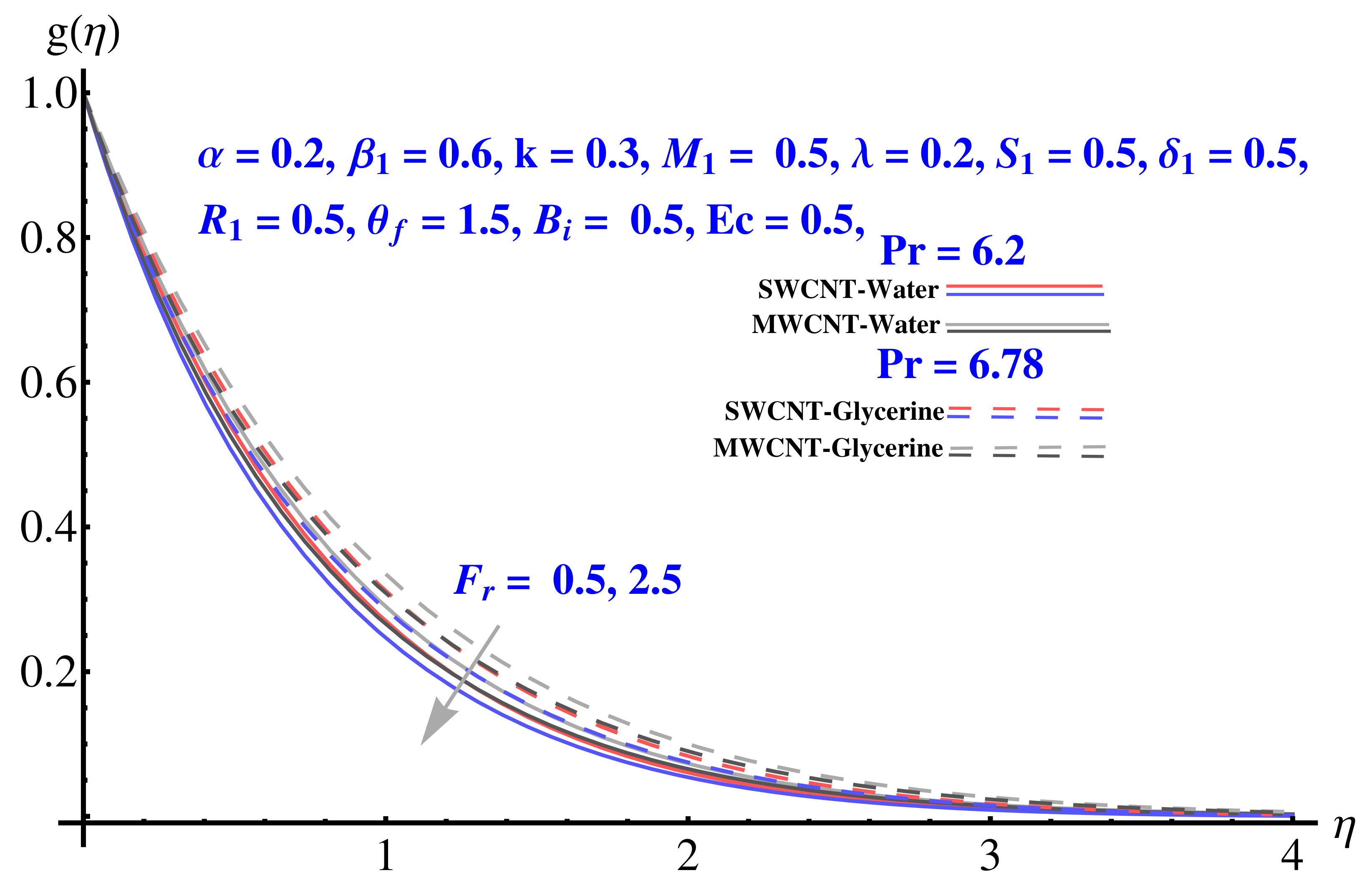
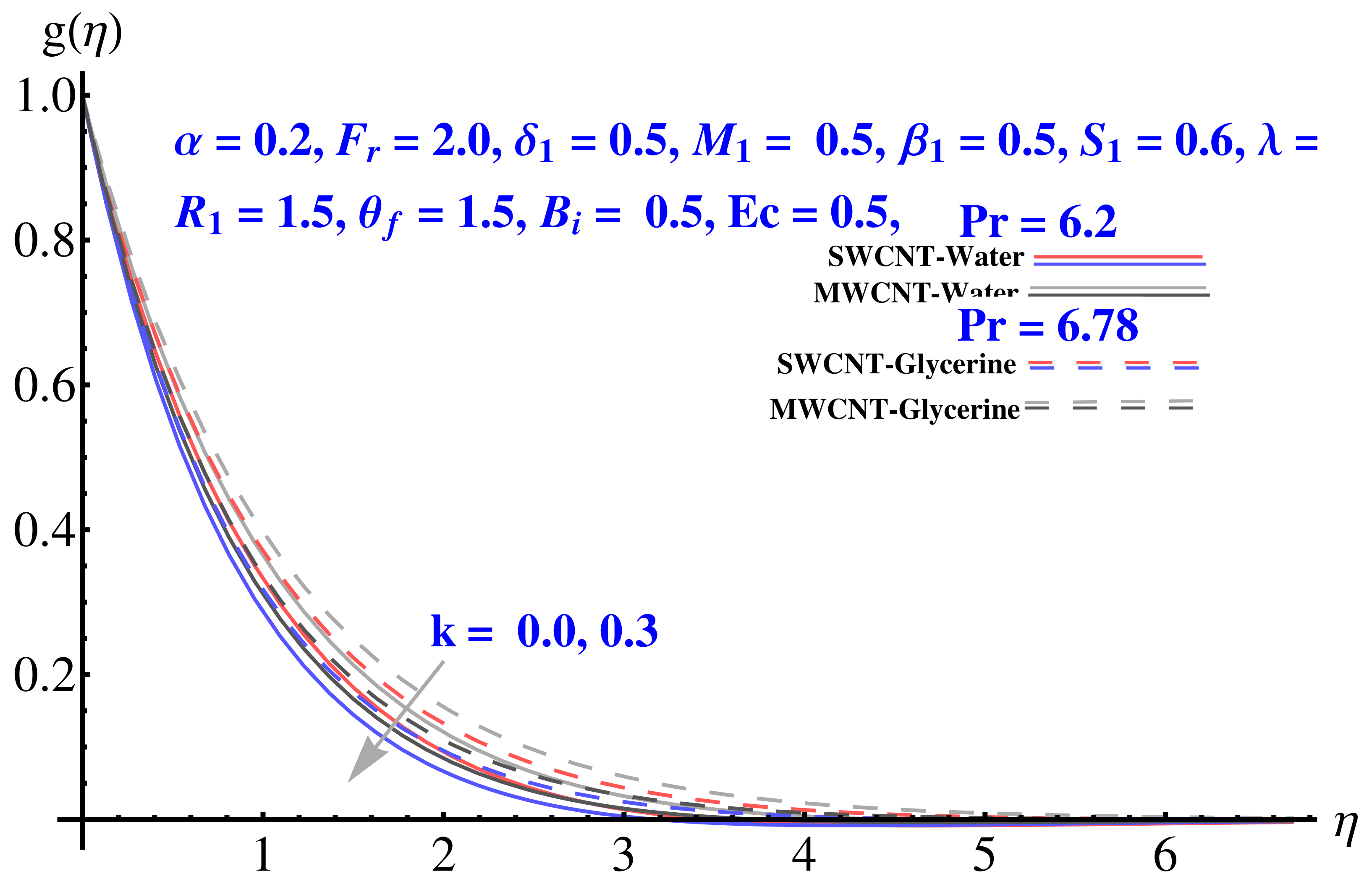
4.2. Tangential Velocity
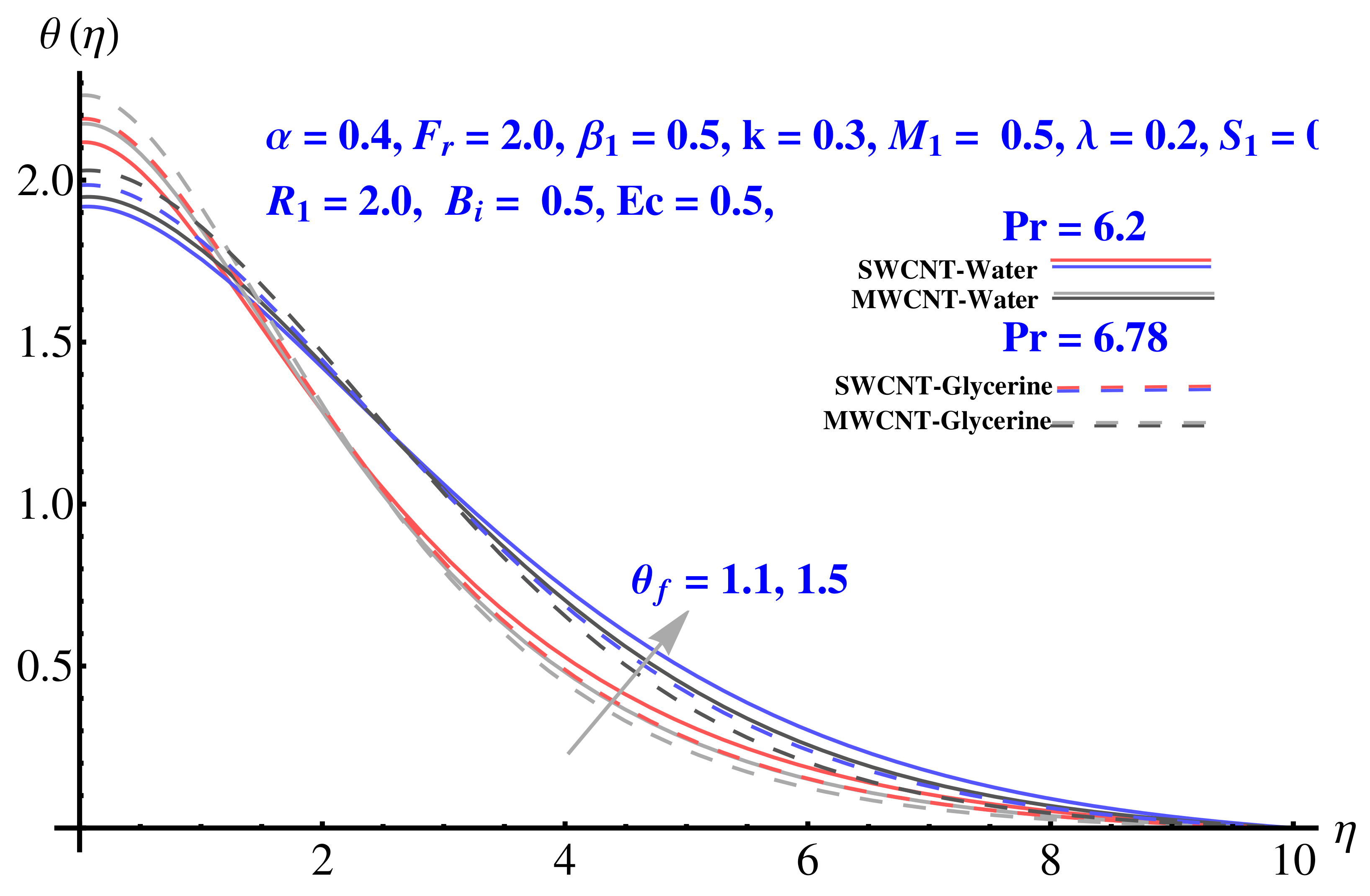
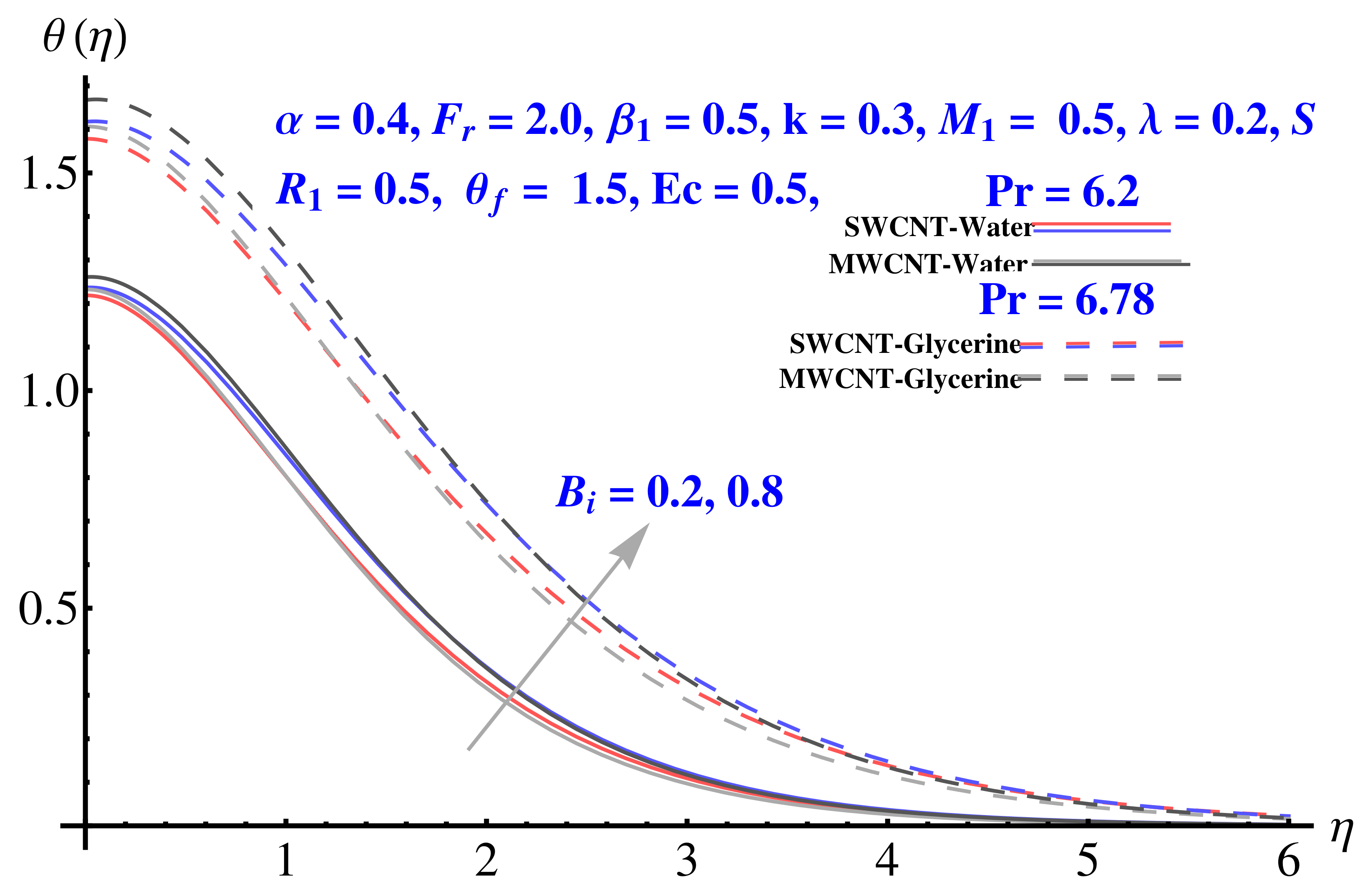
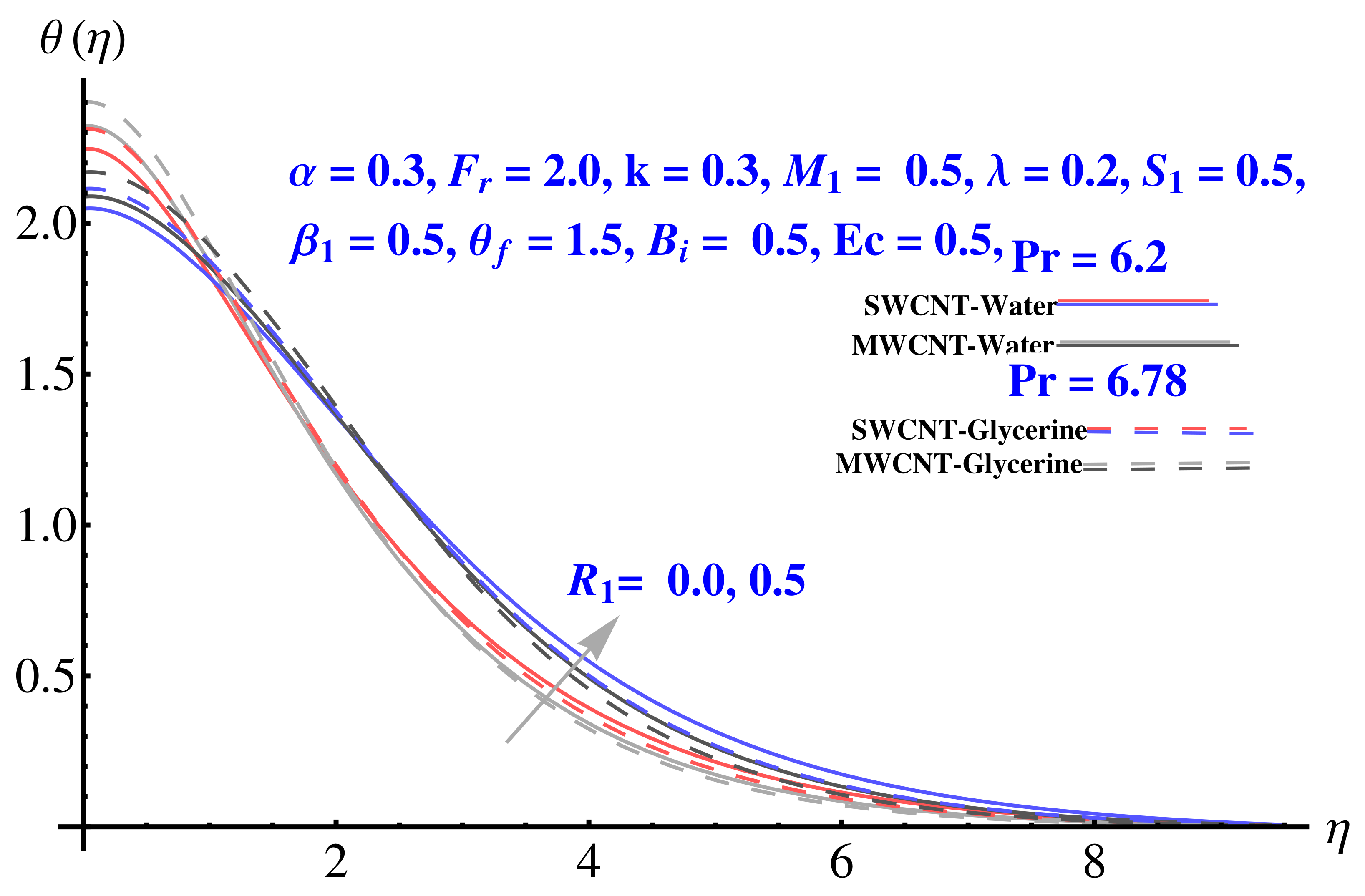
4.3. Temperature Field
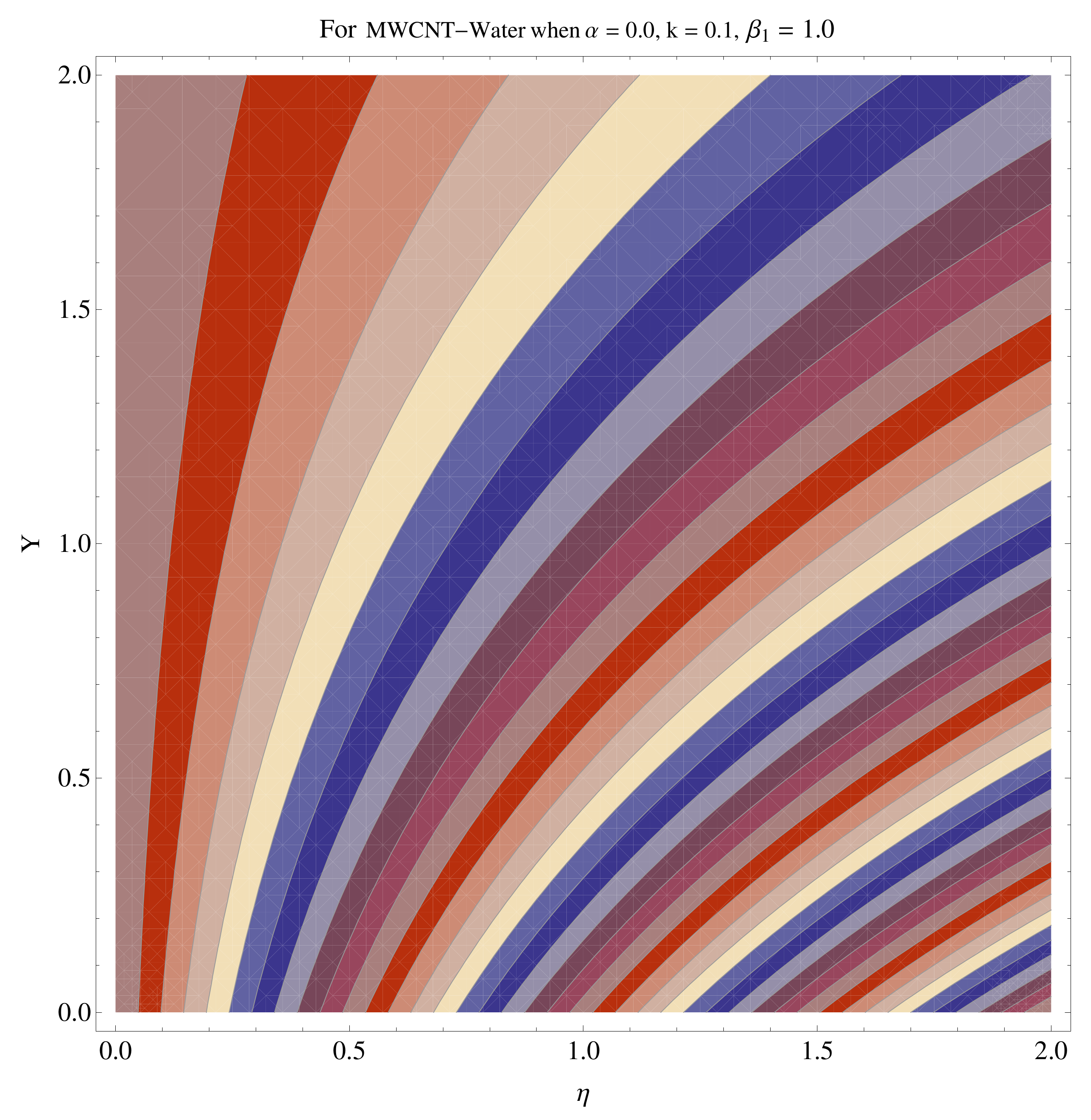
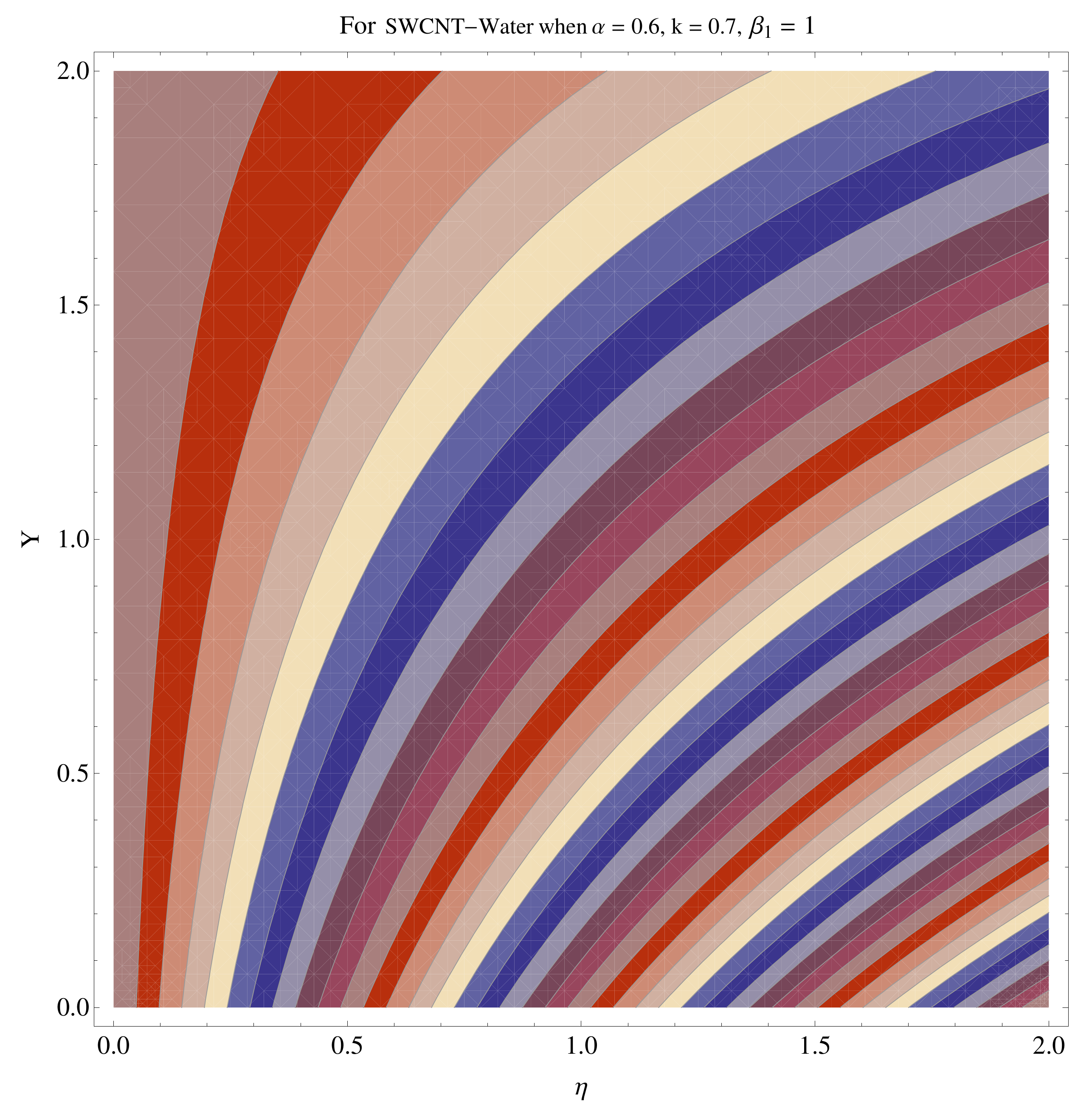
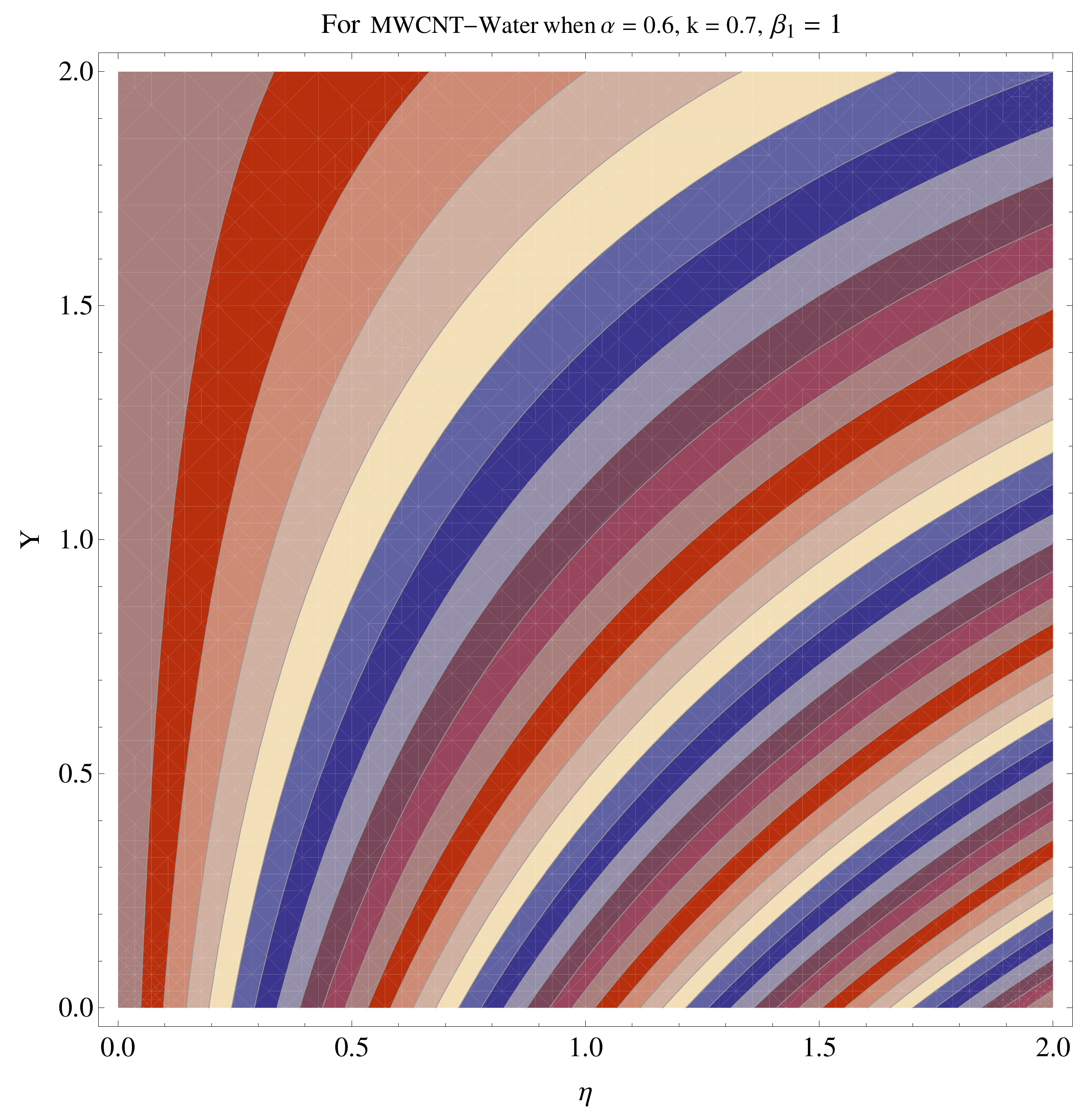
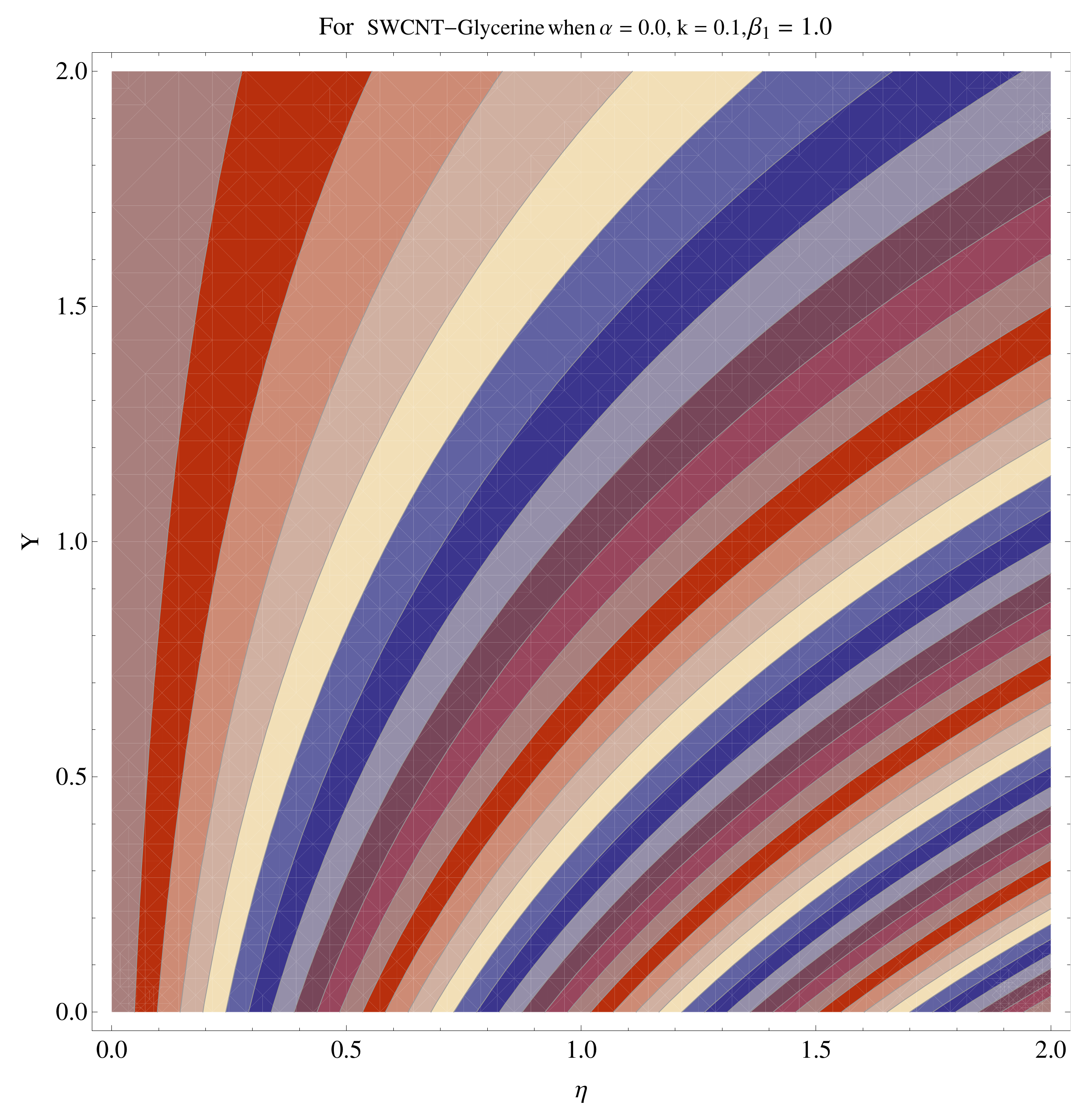
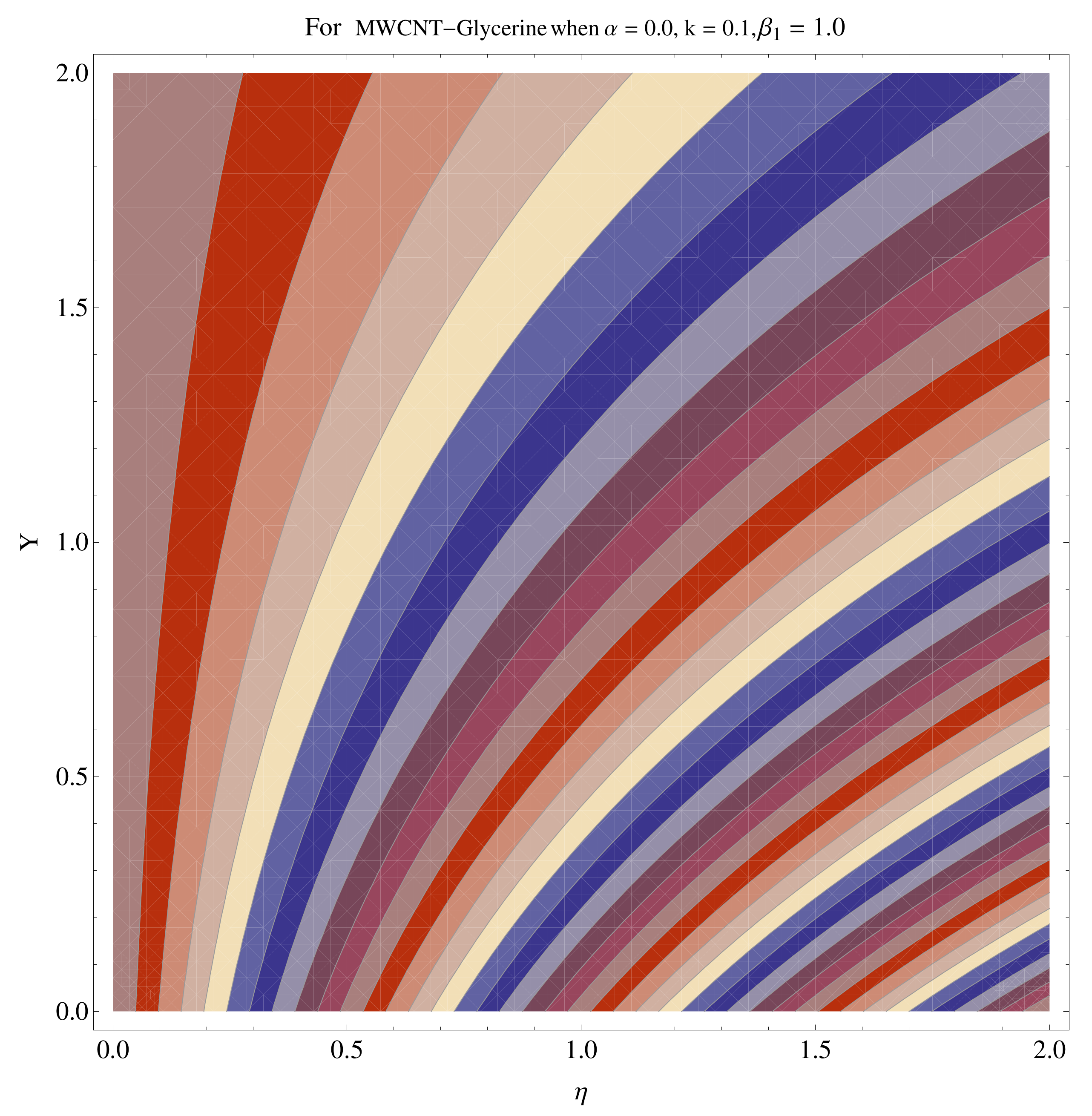
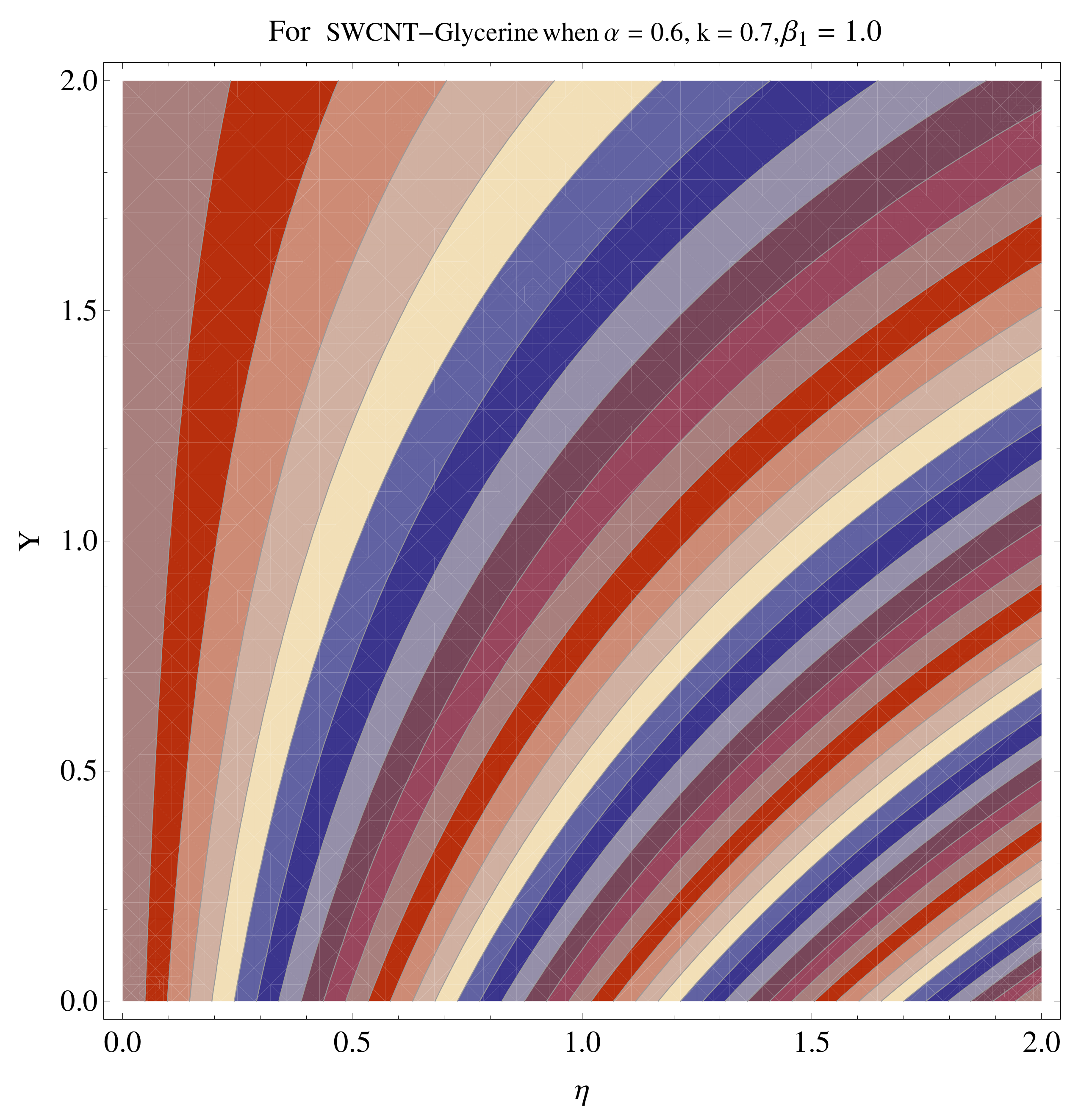
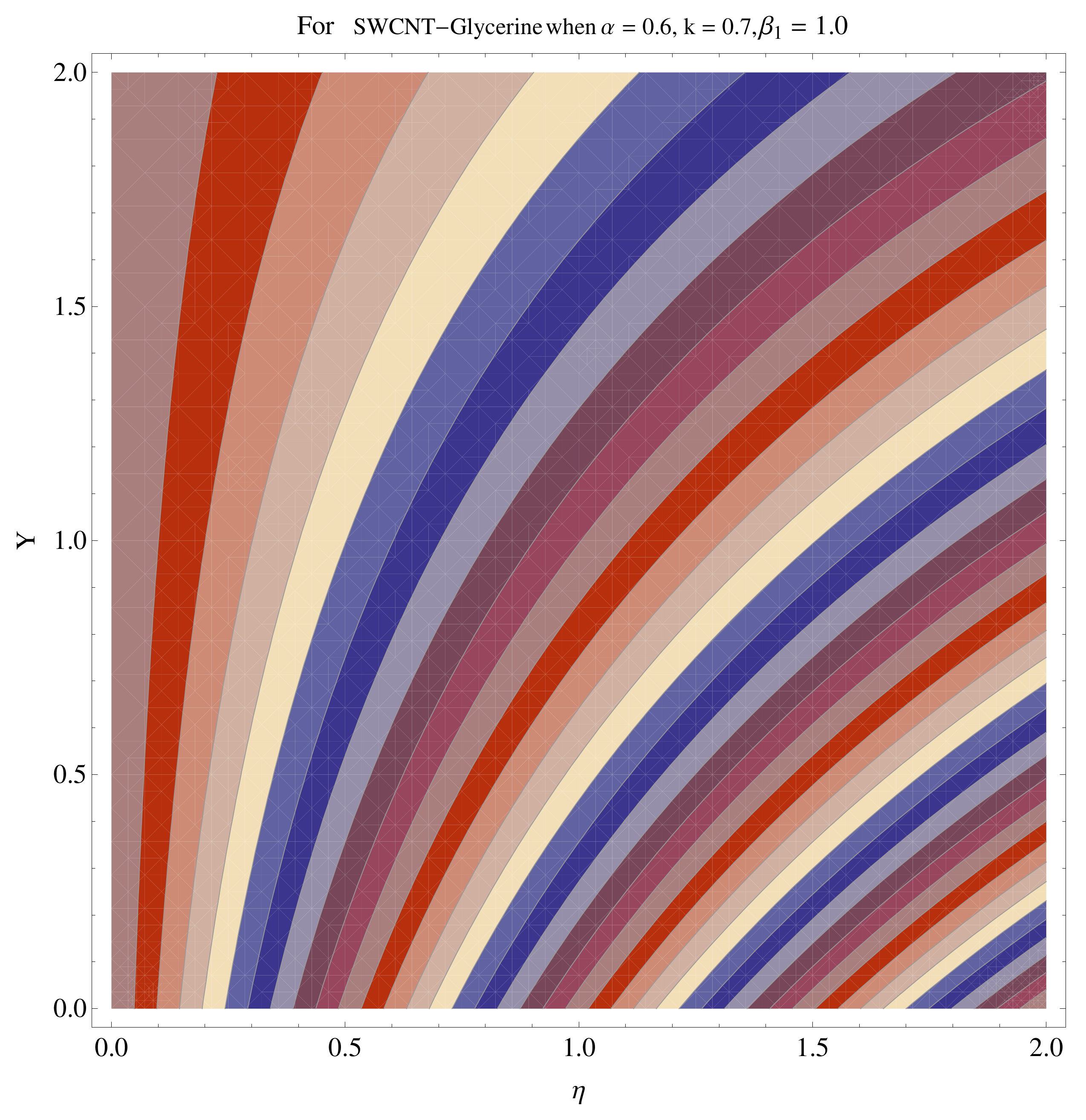
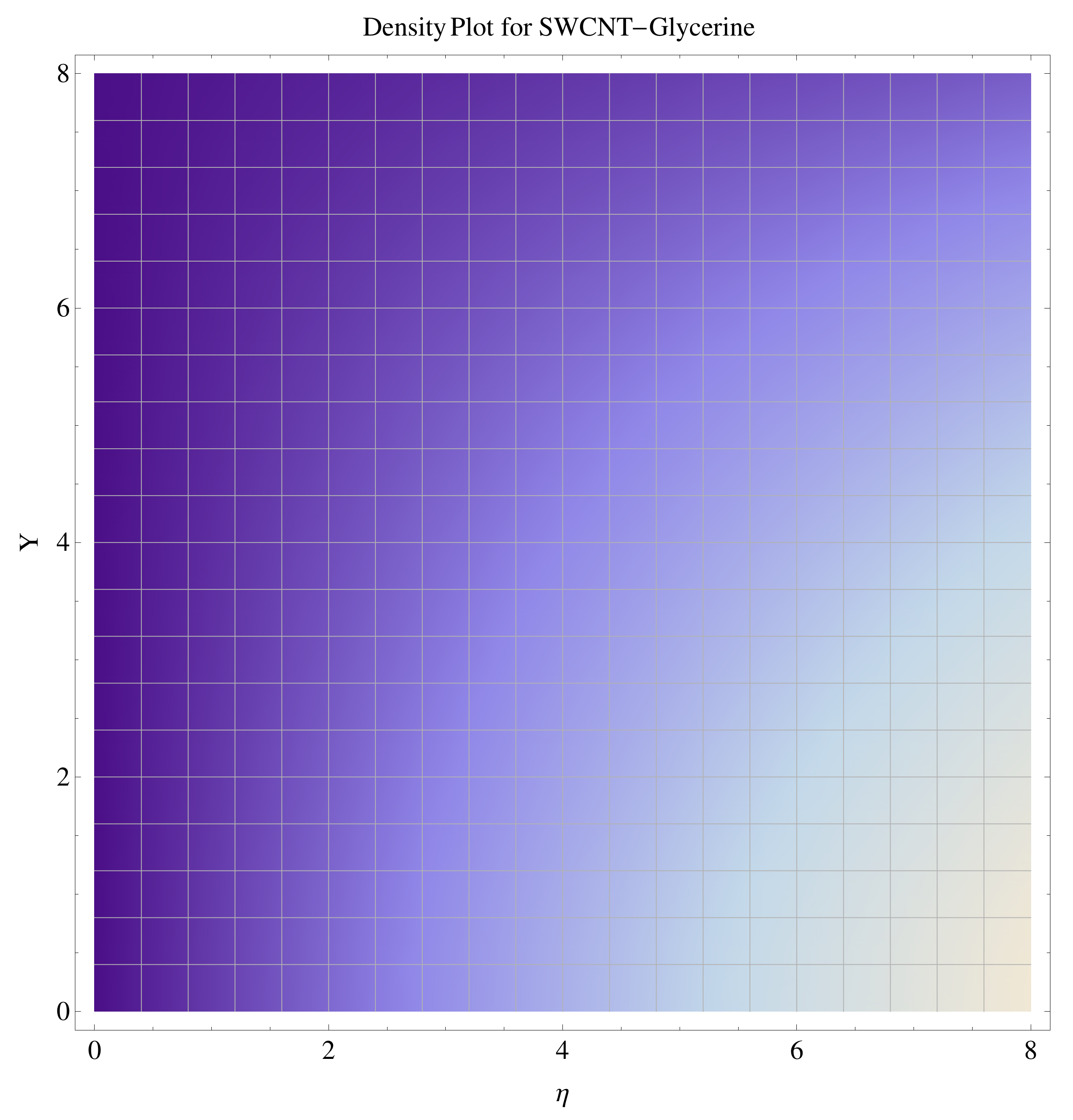
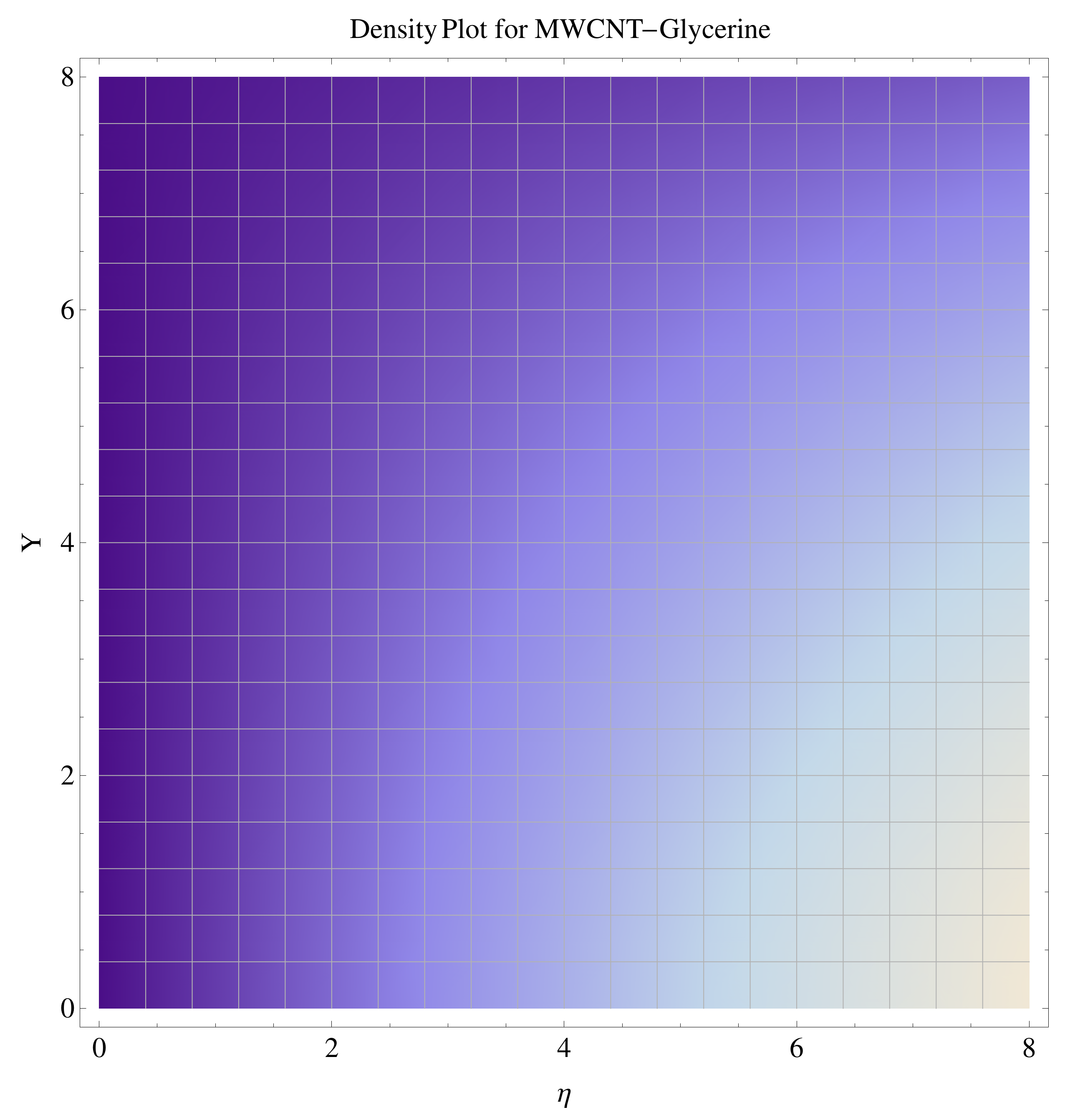
4.4. Contour and Density Graphs
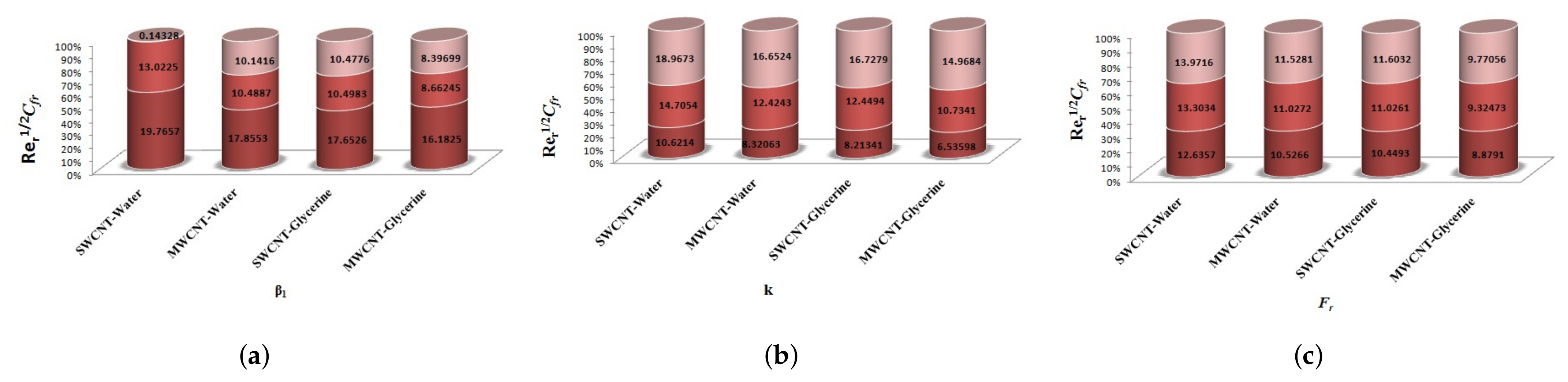
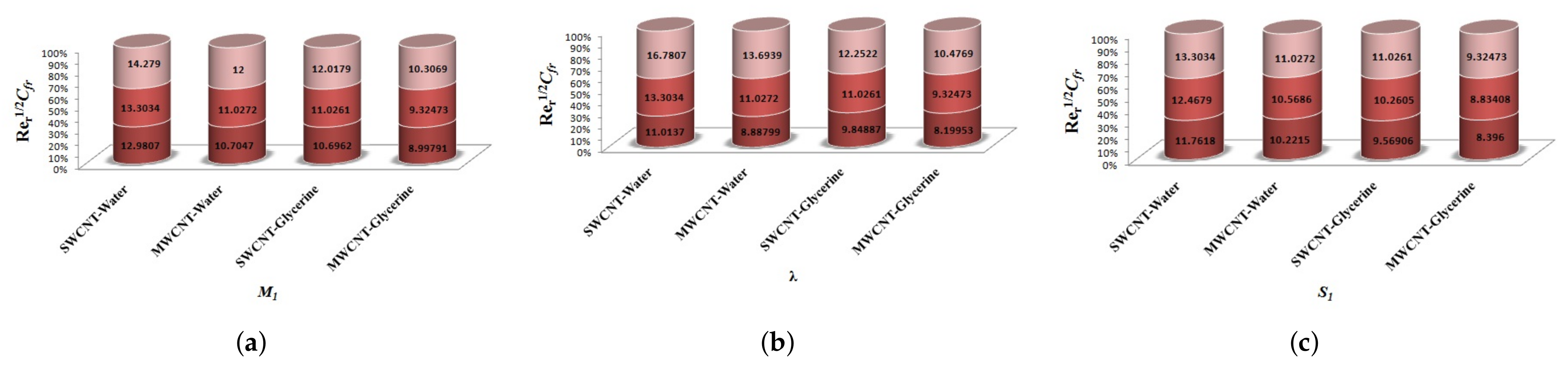
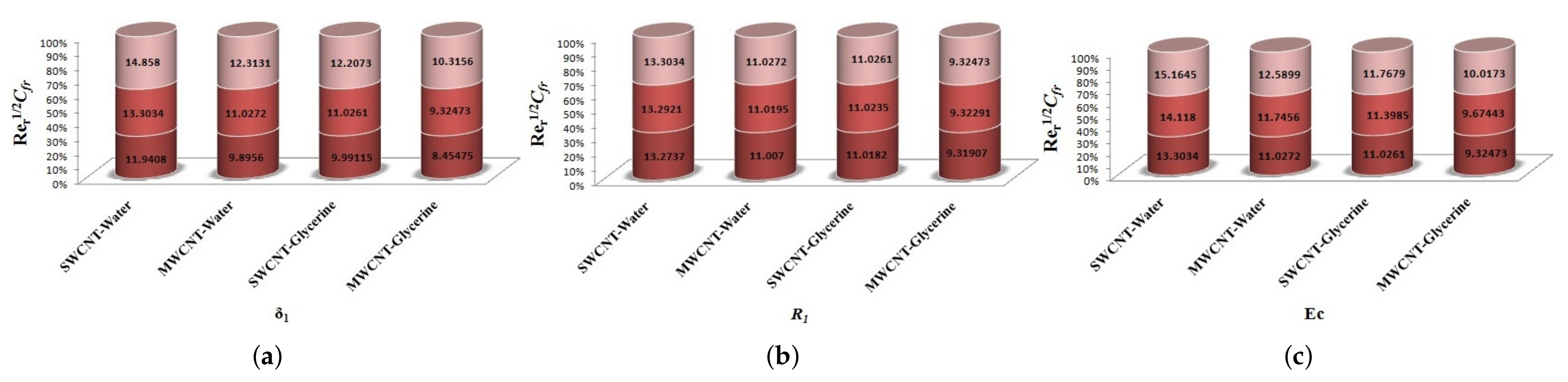
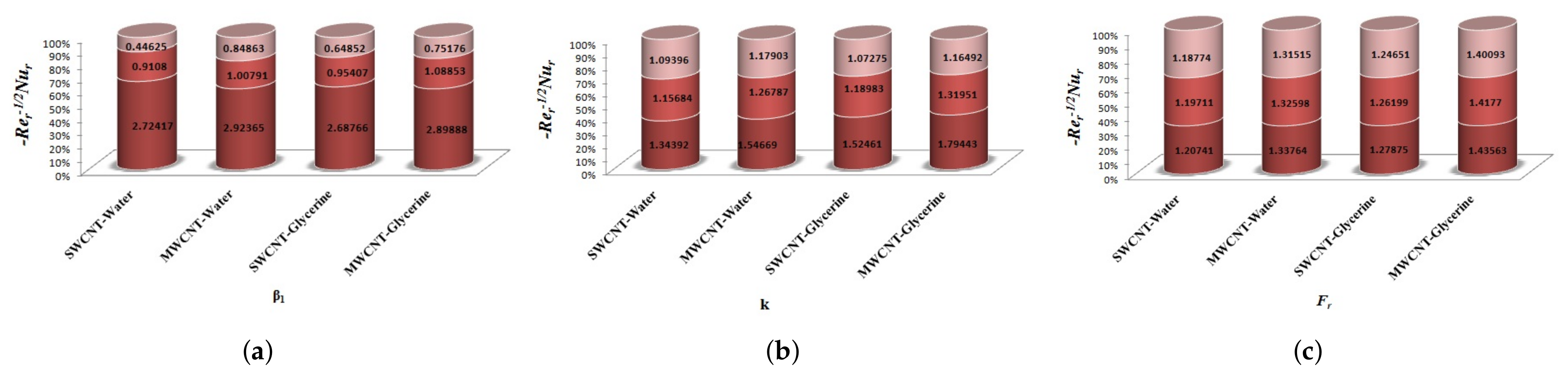
4.5. Skin Friction and Nusselt number
5. Conclusions
- The enhanced Forcheimer number results in a decline in radial velocity;
- Casson parameter restricts the fluid velocity at larger values;
- The larger the porosity parameter, the larger the resistance offered by the medium to the fluid flow and the consequent result is the decline in velocity;
- The larger permeability parameter (K) results a drastic declination in both cases (SWCNT and MWCNT) when the values of K are increased;
- A larger Casson factor results in the shrinkage in the corresponding boundary layer of thermal field;
- Forchheimer number, permeability parameter and porosity parameter on tangential decrease the velocity field;
- The convective boundary results in enhancement of temperature facing the disk surface as compared to the ambient fluid;
- The contour graphs have been sketched for various values of Casson parameter and permeability parameter against the single- and multi-walled Carbon nanotubes—Water/Glycerine nanofluid.
- Skin-friction for larger values of Forchheimer number.
- The non-linear radiation parameter significantly increases the heat flux rate.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| MHD | Magnetohydrodynamic |
| ODEs | Ordinary Differential Equations |
| PDEs | Partial Differential Equation |
| CNTs | Carbon Nanotubes |
| density of given nanofluid | |
| density of carbon nanotubes | |
| Velocity components/m·s | |
| P | Pressure /Pa |
| dynamic viscosity of considered base fluid /kgm s | |
| dynamic viscosity of the given nanofluid /kgm s | |
| T | Local temperature/K |
| Ambient temperature/K | |
| Nondimensional velocity components | |
| Gravitational force | |
| Grashof number | |
| K | Permeability parameter |
| Forchheimer number (inertia) | |
| Casson parameter | |
| Volume fraction (solid) | |
| Angular Velocity (angular) | |
| Skin-friction (wall drag force) | |
| Local Nusselt number | |
| Local Reynolds number | |
| magnetic number | |
| Prandtl number | |
| Eckert parameter | |
| Ratio of Grashof and Reynolds square | |
| Suction parameter |
References
- Choi, S.U.S. Enhancing Thermal Conductivity of Fluids with Nanoparticles. In Developments and Applications of Non-Newtonian Flows; Siginer, D.A., Wang, H.P., Eds.; FED-Vol. 231/MD-Vol. 66; ASME: New York, NY, USA, 1995; pp. 99–105. [Google Scholar]
- Lin, Y.; Zheng, L.; Zhang, X.; Ma, L.; Chen, G. MHD pseudoplastic nanofluid unsteady flow and heat transfer in a finite thin film over stretching surface with internal heat generation. Int. J. Heat Mass Transf. 2015, 84, 903–911. [Google Scholar] [CrossRef]
- Bai, Y.; Liu, X.; Zhang, Y.; Zhang, M. Stagnation-point heat and mass transfer of MHD Maxwell nanofluids over a stretching surface in the presence of thermophoresis. J. Mol. Liq. 2016, 224, 1172–1180. [Google Scholar] [CrossRef]
- Madhu, M.; Kishan, N.; Chamkha, A.J. Unsteady flow of a Maxwell nanofluid over a stretching surface in the presence of magnetohydrodynamic and thermal radiation effects. Propuls. Power Res. 2017, 6, 31–40. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Sajjadi, H.; Amri Delouei, A.; Atashafrooz, M.; Li, Z. Magnetic force and radiation influences on nanofluid transportation through a permeable media considering Al2O3 nanoparticles, mixed convection of a nanofluid in a threedimensional channel. J. Therm. Anal. Calorim. 2019, 136, 2477–2485. [Google Scholar] [CrossRef]
- Hayat, T.; Kiyani, M.Z.; Alsaedi, A.; Khan, M.I.; Ahmad, I. Mixed convective three dimensional flow of Williamson nanofluid subject to chemical reaction. Int. J. Heat Mass Transf. 2018, 127, 422–429. [Google Scholar] [CrossRef]
- Zadi, M.; Hashemi Pour, S.M.R.; Karimdoost Yasuri, A.; Chamkha, A.J. Mixed convection of a nanofluid in a three-dimensional channel. J. Therm. Anal. Calorim. 2019, 136, 2461–2475. [Google Scholar]
- Turkyilmazoglu, M.; Senel, P. Heat and mass transfer of the flow due to a rotating rough and porous disk. Int. J. Therm. Sci. 2013, 63, 146–158. [Google Scholar] [CrossRef]
- Bödewadt, U.T. Die Drehströmungüberfestem Grund. Z. Angew. Math. Mech. 1940, 20, 241–252. [Google Scholar] [CrossRef]
- Mustafa, M.; Khan, J.A.; Hayat, T.; Alsaedi, A. On Bödewadt flow and heat transfer of nanofluids over a stretching stationary disk. J. Mol. Liq. 2015, 211, 119–125. [Google Scholar] [CrossRef]
- Mustafa, M. MHD nanofluid flow over a rotating disk with partial slip effects: Buongiorno model. Int. J. Heat Mass Transf. 2017, 108, 1910–1916. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Armaghani, T.; Chamkha, A.J.; Ganji, D.D. Natural convection analysis in a cavity with an inclined elliptical heater subject to shape factor of nanoparticles and magnetic field. Arab. J. Sci. Eng. 2019. [Google Scholar] [CrossRef]
- Forchheimer, P. Wasserbewegungdurchboden. Z. Ver. Dtsch. Ing. 1901, 45, 1782–1788. [Google Scholar]
- Shehzad, S.A.; Abbasi, F.M.; Hayat, T.; Alsaedi, A. Cattaneo—Christov heat flux model for Darcy–Forchheimer flow of an Oldroyd-B fluid with variable conductivity and non-linear convection. J. Mol. Liq. 2016, 224, 274–278. [Google Scholar] [CrossRef]
- Bakar, S.A.; Arifin, N.M.; Nazar, R.; Ali, F.M.; Pop, I. Forced convection boundary layer stagnation-point flow in Darcy-Forchheimer porous medium past a shrinking sheet. Front. Heat Mass Transf. 2016, 7, 38. [Google Scholar]
- Hayat, T.; Muhammad, T.; Al-Mezal, S.; Liao, S.J. Darcy-Forchheimer flow with variable thermal conductivity and Cattaneo-Christov heat flux. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 2355–2369. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Abbasbandy, S.; Rashad, A.M.; Vajravelu, K. Radiation effects on mixed convection over a wedge embedded in a porous medium filled with a nanofluid. Transp. Porous Media 2012, 91, 261–279. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Abbasbandy, S.; Rashad, A.M.; Vajravelu, K. Radiation effects on mixed convection about a cone embedded in a porous medium filled with a nanofluid. Meccanica 2013, 48, 275–285. [Google Scholar] [CrossRef]
- Donaldson, K.; Aitken, R.; Tran, L.; Stone, V.; Duffin, R.; Forrest, G.; Alexander, A. Carbon nanotubes: A review of their properties in relation to pulmonary toxicology and workplace safety. Toxicol. Sci. 2006, 92, 5–22. [Google Scholar] [CrossRef] [PubMed]
- Coleman, J.N.; Khan, U.; Blau, W.J.; Gunko, Y.K. Small but strong: A review of the mechanical properties of carbon nanotube–polymer composites. Carbon 2006, 44, 1624–1652. [Google Scholar] [CrossRef]
- Kim, G.M.; Nam, I.W.; Yang, B.; Yoon, H.N.; Lee, H.K.; Park, S. Carbon nanotube (CNT) incorporated cementitious composites for functional construction materials: The state of the art. Compos. Struct. 2019, 227, 111244. [Google Scholar] [CrossRef]
- Janas, D.; Koziol, K.K. A review of production methods of carbon nanotube and graphene thin films for electrothermal applications. Nanoscale 2014, 6, 3037–3045. [Google Scholar] [CrossRef] [PubMed]
- Keidar, M.; Waas, A.M. On the conditions of carbon nanotube growth in the arc discharge. Nanotechnology 2004, 15, 1571–1575. [Google Scholar] [CrossRef][Green Version]
- Mukul, K.; Yoshinori, A. Chemical vapor deposition of carbon nanotubes: A review on growth mechanism and mass production. J. Nanosci. Nanotechnol. 2010, 10, 3739–3758. [Google Scholar]
- Dai, H.J. Carbon nanotubes: Synthesis, integration, and properties. Acc. Chem. Res. 2002, 35, 1035–1044. [Google Scholar] [CrossRef] [PubMed]
- Ahmadian, A.; Bilal, M.; Khan, M.A.; Asjad, M.I. The non-Newtonian maxwell nanofluid flow between two parallel rotating disks under the effects of magnetic field. Sci. Rep. 2020, 10, 17088. [Google Scholar] [CrossRef] [PubMed]
- Karen, C.; Fredy, O.; Camilo, Z.; Bernardo, H.; Elizabeth, P.; Robison, B.S. Surfactant concentration and pH effects on the zeta potential values of alumina nanofluids to inspect stability. Colloids Surf. A Physicochem. Eng. Asp. 2019, 583, 123960. [Google Scholar]
- Choudhary, R.; Khurana, D.; Kumar, A.; Subudhi, S. Stability analysis of Al2O3/water nanofluids. J. Exp. Nanosci. 2017, 12, 140–151. [Google Scholar] [CrossRef]
- Lim, C.Y.; Lim, A.E.; Lam, Y.C. pH change in electroosmotic flow hysteresis. Anal. Chem. 2017, 89, 9394–9399. [Google Scholar] [CrossRef]
- Lim, A.E.; Lim, C.Y.; Lam, Y.C. Electroosmotic flow hysteresis for dissimilar anionic solutions. Anal. Chem. 2016, 88, 8064–8073. [Google Scholar] [CrossRef]
- Alotaibi, H.; Althubiti, S.; Eid, M.R.; Mahny, K.L. Numerical treatment of mhd flow of casson nanofluid via convectively heated non-linear extending surface with viscous dissipation and suction/injection effects. Comput. Mater. Contin. 2020, 66, 229–245. [Google Scholar] [CrossRef]
- Rafique, K.; Alotaibi, H.; Nofal, T.A.; Anwar, M.I.; Misiran, M.; Khan, I. Numerical Solutions of Micropolar Nanofluid over an Inclined Surface Using Keller Box Analysis. J. Math. 2020, 6617652. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Alqarni, M.S.; Wakif, A.; Khan, I.; Bhutta, M.S. Numerical Scrutinization of Darcy-Forchheimer Relation in Convective Magnetohydrodynamic Nanofluid Flow Bounded by Nonlinear Stretching Surface in the Perspective of Heat and Mass Transfer. Micromachines 2021, 12, 374. [Google Scholar] [CrossRef]
- Rasool, G.; Khan, W.A.; Bilal, S.M.; Khan, I. MHD Squeezed Darcy Forchheimer Nanofluid flow between two h-distance apart horizontal plates. Open Phys. 2020, 18, 1–8. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A. Numerical Exploration of the Features of Thermally Enhanced Chemically Reactive Radiative Powell-Eyring Nanofluid Flow via Darcy Medium over Non-linearly Stretching Surface Affected by a Transverse Magnetic Field and Convective Boundary Conditions. Appl. Nanosci. 2020. [Google Scholar] [CrossRef]
- Shaw, S.; Dogonchi, A.S.; Nayak, M.K.; Makinde, O.D. Impact of Entropy Generation and Nonlinear Thermal Radiation on Darcy–Forchheimer Flow of MnFe2O4-Casson/Water Nanofluid due to a Rotating Disk: Application to Brain Dynamics. Arab. J. Sci. Eng. 2020, 45, 5471–5490. [Google Scholar] [CrossRef]









| Base Fluid | Nanoparticles | ||||||
|---|---|---|---|---|---|---|---|
| Properties | Water | Kerosene | Glycerin | Ethylene Glycol | EngineOil | SWCNT | MWCNT |
| (J/kg K) | 4179 | 2090 | 2427 | 2430 | 1910 | 427 | 796 |
| (KG/m) | 997 | 783 | 1115 | 884 | 2600 | 1600 | |
| k (W/mK) | 6600 | 3000 | |||||
| 21 | 48 | 65 | 70 | 27 | 44 | ||
| Pr | 21 | 6450 | − | − | |||
| k | Water | Glycerine | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SWCNT | MWCNT | SWCNT | MWCNT | ||||||||||
| k | Water | Glycerine | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SWCNT | MWCNT | SWCNT | MWCNT | ||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shafiq, A.; Rasool, G.; Alotaibi, H.; Aljohani, H.M.; Wakif, A.; Khan, I.; Akram, S. Thermally Enhanced Darcy-Forchheimer Casson-Water/Glycerine Rotating Nanofluid Flow with Uniform Magnetic Field. Micromachines 2021, 12, 605. https://doi.org/10.3390/mi12060605
Shafiq A, Rasool G, Alotaibi H, Aljohani HM, Wakif A, Khan I, Akram S. Thermally Enhanced Darcy-Forchheimer Casson-Water/Glycerine Rotating Nanofluid Flow with Uniform Magnetic Field. Micromachines. 2021; 12(6):605. https://doi.org/10.3390/mi12060605
Chicago/Turabian StyleShafiq, Anum, Ghulam Rasool, Hammad Alotaibi, Hassan M. Aljohani, Abderrahim Wakif, Ilyas Khan, and Shakeel Akram. 2021. "Thermally Enhanced Darcy-Forchheimer Casson-Water/Glycerine Rotating Nanofluid Flow with Uniform Magnetic Field" Micromachines 12, no. 6: 605. https://doi.org/10.3390/mi12060605
APA StyleShafiq, A., Rasool, G., Alotaibi, H., Aljohani, H. M., Wakif, A., Khan, I., & Akram, S. (2021). Thermally Enhanced Darcy-Forchheimer Casson-Water/Glycerine Rotating Nanofluid Flow with Uniform Magnetic Field. Micromachines, 12(6), 605. https://doi.org/10.3390/mi12060605










