Printing a Pacinian Corpuscle: Modeling and Performance
Abstract
1. Introduction
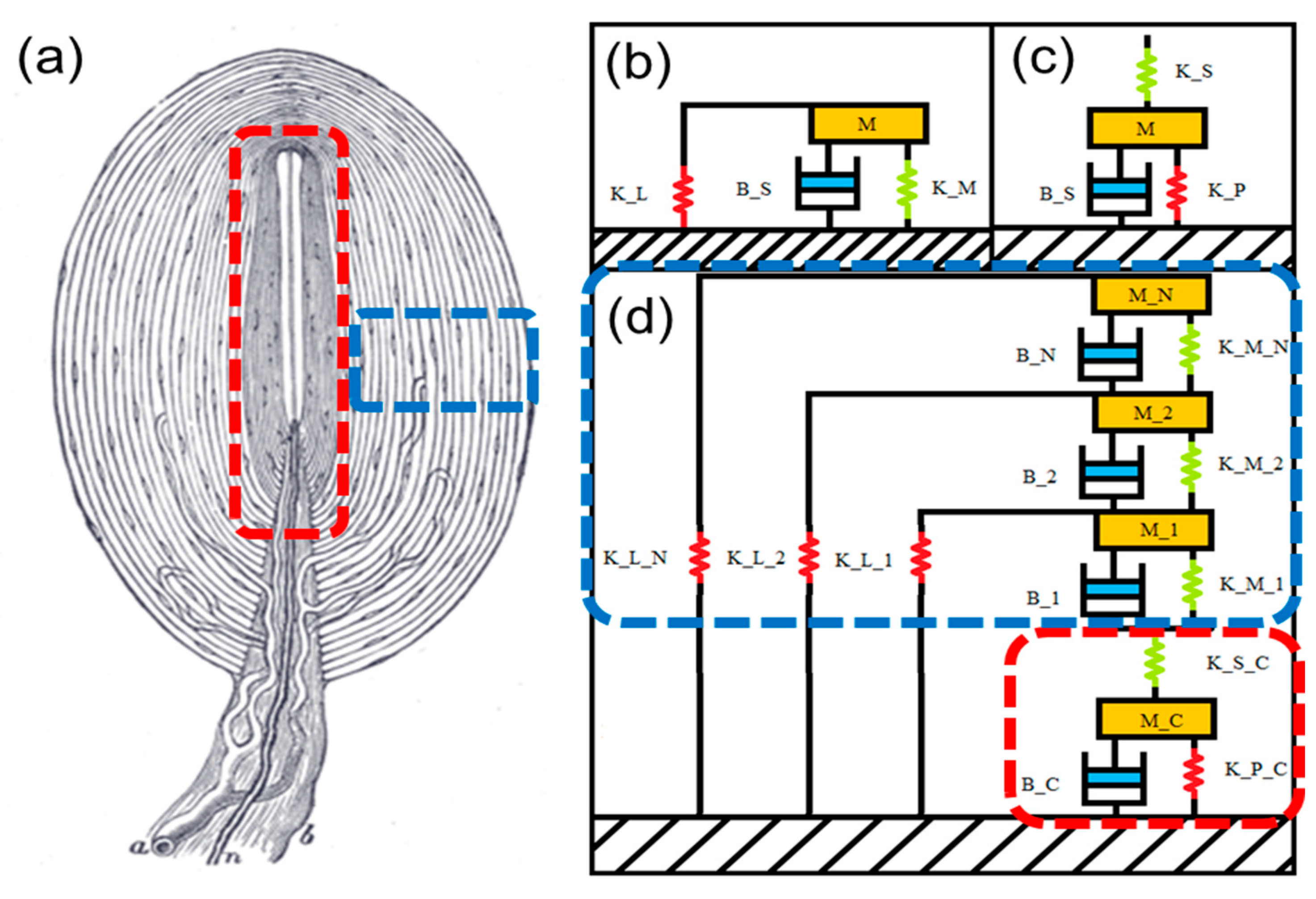
2. Theory
3. Design and Simulation
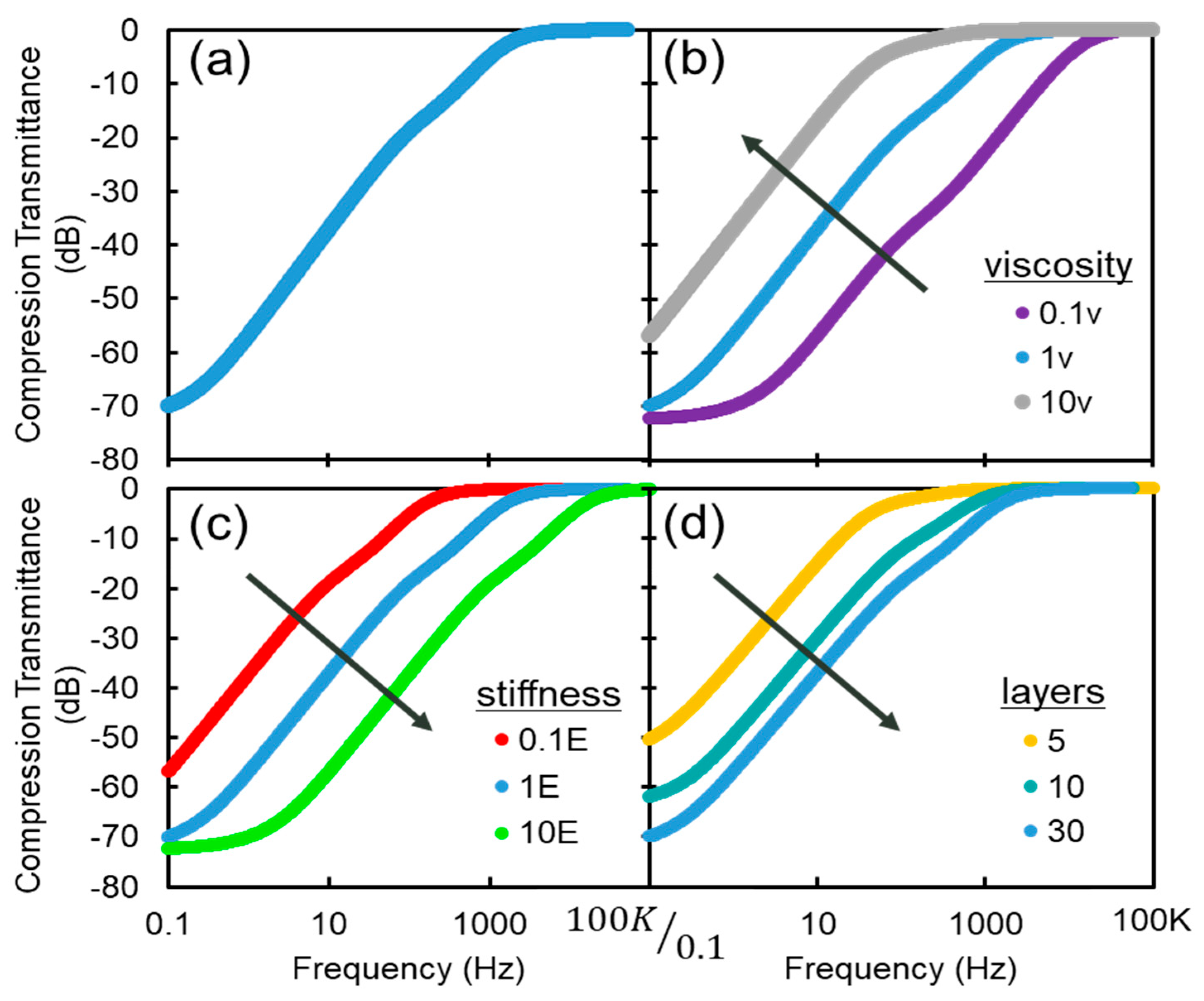
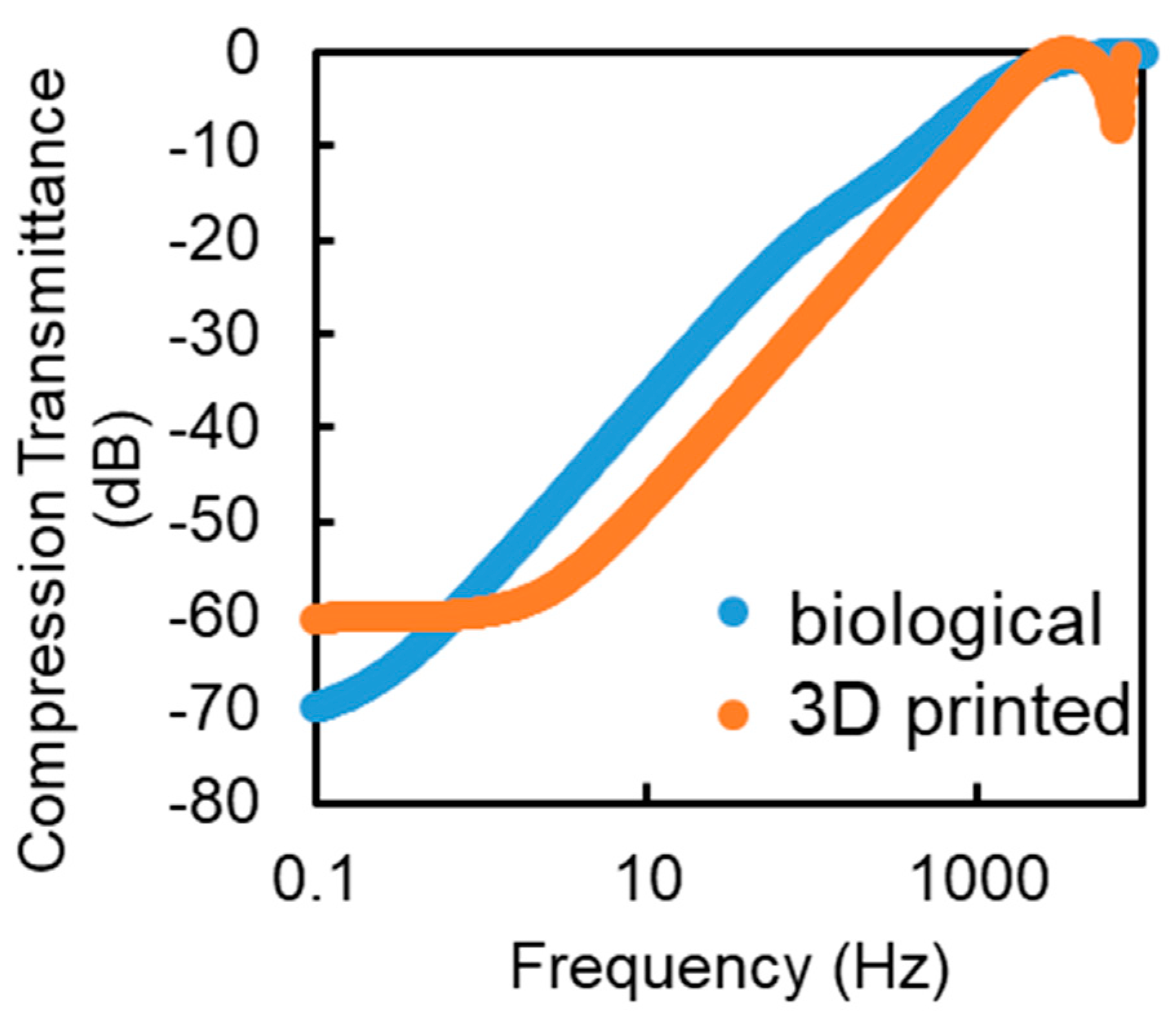
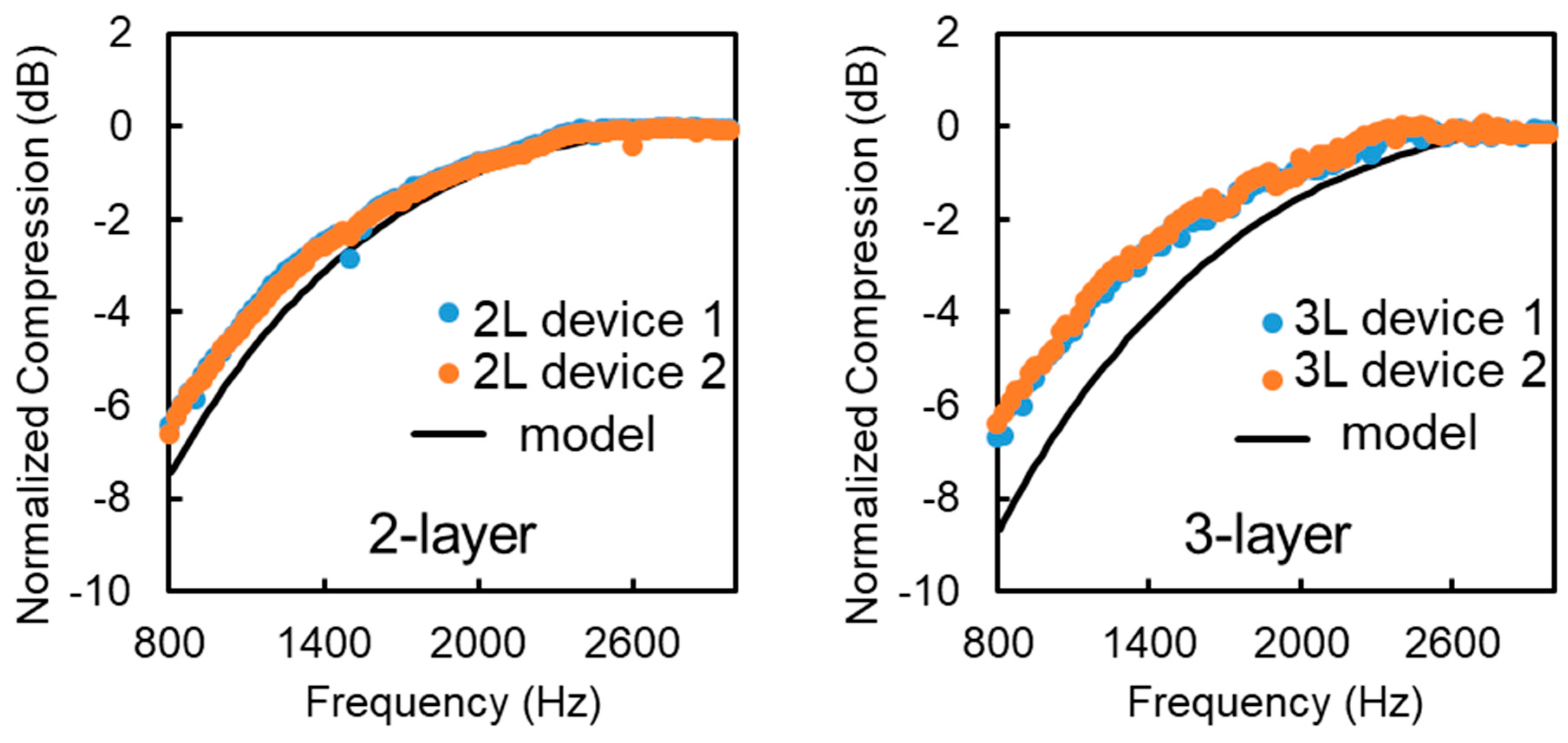
4. Results and Discussion
4.1. Fabrication
4.2. Experiments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Surface area of a layer |
| EL | Elastic modulus of lamella |
| EM | Elastic modulus of interlamellar matrix |
| H | Width of interlamellar spacing |
| L | Length of Pacinian corpuscle |
| µ | Viscosity of interlamellar fluid |
| R | Radius of lamella |
| T | Thickness of lamella |
| X | Lamella displacement |
| K | Stiffness |
| B | Viscous Resistance |
| M | Mass of the lamella |
References
- Scheibert, J.; Leurent, S.; Prevost, A.; Debregeas, G. The Role of Fingerprints in the Coding of Tactile Information Probed with a Biomimetic Sensor. Science 2009, 323, 1503–1506. [Google Scholar] [CrossRef] [PubMed]
- Merzenich, M.M.; Harrington, T. The sense of flutter-vibration evoked by stimulation of the hairy skin of primates: Comparison of human sensory capacity with the responses of mechanoreceptive afferents innervating the hairy skin of monkeys. Exp. Brain Res. 1969, 9, 236–260. [Google Scholar] [CrossRef] [PubMed]
- Muniak, M.A.; Ray, S.; Hsiao, S.S.; Dammann, J.F.; Bensmaia, S.J. The Neural Coding of Stimulus Intensity: Linking the Population Response of Mechanoreceptive Afferents with Psychophysical Behavior. J. Neurosci. 2007, 27, 11687–11699. [Google Scholar] [CrossRef] [PubMed]
- Lamoré, P.J.J.; Muijser, H.; Keemink, C.J. Envelope detection of amplitude-modulated high-frequency sinusoidal signals by skin mechanoreceptors. J. Acoust. Soc. Am. 1986, 79, 1082–1085. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.; Bolanowski, S.; Holmes, M.H. The structure and function of pacinian corpuscles: A review. Prog. Neurobiol. 1994, 42, 79–128. [Google Scholar] [CrossRef]
- Bolanowski, S., Jr.; Zwislocki, J. Intensity and frequency characteristics of pacinian corpuscles. II. Receptor potentials. J. Neurophysiol. 1984, 51, 812–830. [Google Scholar] [CrossRef] [PubMed]
- Brisben, A.J.; Hsiao, S.S.; Johnson, K.O. Detection of Vibration Transmitted Through an Object Grasped in the Hand. J. Neurophysiol. 1999, 81, 1548–1558. [Google Scholar] [CrossRef]
- Johansson, R.S.; Landstro, U.; Lundström, R. Responses of mechanoreceptive afferent units in the glabrous skin of the human hand to sinusoidal skin displacements. Brain Res. 1982, 244, 17–25. [Google Scholar] [CrossRef]
- Gardner, E.P. Touch. e LS. 2010. Available online: https://doi.org/10.1002/9780470015902.a0000219.pub2 (accessed on 19 April 2021).
- Loewenstein, W.R.; Skalak, R. Mechanical transmission in a Pacinian corpuscle. An analysis and a theory. J. Physiol. 1966, 182, 346–378. [Google Scholar] [CrossRef]
- Hubbard, S.J. A study of rapid mechanical events in a mechanoreceptor. J. Physiol. 1958, 141, 198–218. [Google Scholar] [CrossRef]
- Loewenstein, W.R.; Mendelson, M. Components of receptor adaptation in a Pacinian corpuscle. J. Physiol. 1965, 177, 377–397. [Google Scholar] [CrossRef]
- Bouley, D.M.; Alarcón, C.N.; Hildebrandt, T.; O’Connell-Rodwell, C.E. The distribution, density and three-dimensional histomorphology of Pacinian corpuscles in the foot of the Asian elephant (Elephas maximus) and their potential role in seismic communication. J. Anat. 2007, 211, 428–435. [Google Scholar] [CrossRef]
- O’Connell-Rodwell, C.E. Keeping an “ear” to the ground: Seismic communication in elephants. Physiology 2007, 22, 287–294. [Google Scholar] [CrossRef]
- Ellis, R.; Ismaeil, O.; Lipsett, M. Design and evaluation of a high-performance haptic interface. Robotica 1996, 14, 321–327. [Google Scholar] [CrossRef]
- Brooks, R.; Torres-Jara, E.; Vasilescu, I.; Coral, R.; Robotics, H. A Soft Touch: Compliant Tactile Sensors for Sensitive Manipulation; Technical Report MIT-CSAIL-TR-2006-014; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Cramphorn, L.; Ward-Cherrier, B.; Lepora, N.F. Tactile manipulation with biomimetic active touch. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 123–129. [Google Scholar]
- Berger, T.W.; Dibazar, A.; Yousefi, A.; Park, H.O. Systems and Methods for Security Breach Detection. US Patent 8,077,036, 13 December 2011. [Google Scholar]
- Cauna, N.; Mannan, G. The structure of human digital Pacinian corpuscles (corpuscula lamellosa) and its functional significance. J. Anat. 1958, 92, 1–20.4. [Google Scholar]
- Grandori, F.; Pedotti, A. Theoretical Analysis of Mechano-to-Neural Transduction in Pacinian Corpuscle. IEEE Trans. Biomed. Eng. 1980, 27, 559–565. [Google Scholar] [CrossRef]
- Freeman, A.W.; Johnson, K.O. Cutaneous mechanoreceptors in macaque monkey: Temporal discharge patterns evoked by vibration, and a receptor model. J. Physiol. 1982, 323, 21–41. [Google Scholar] [CrossRef]
- Güçlü, B.; Schepis, E.A.; Yelke, S.; Yucesoy, C.A.; Bolanowski, S.J. Ovoid geometry of the Pacinian corpuscle is not the determining factor for mechanical excitation. Somatosens. Mot. Res. 2006, 23, 119–126. [Google Scholar] [CrossRef]
- Dong, Y.; Mihalas, S.; Kim, S.S.; Yoshioka, T.; Bensmaia, S.; Niebur, E. A simple model of mechanotransduction in primate glabrous skin. J. Neurophysiol. 2013, 109, 1350–1359. [Google Scholar] [CrossRef]
- Biswas, A.; Manivannan, M.; Srinivasan, M.A. Multiscale Layered Biomechanical Model of the Pacinian Corpuscle. IEEE Trans. Haptics 2014, 8, 31–42. [Google Scholar] [CrossRef]
- Quindlen, J.C.; Stolarski, H.K.; Johnson, M.D.; Barocas, V.H. A multiphysics model of the Pacinian corpuscle. Integr. Biol. 2016, 8, 1111–1125. [Google Scholar] [CrossRef] [PubMed]
- Dubový, P.; Bednárová, J. The extracellular matrix of rat Pacinian corpuscles: An analysis of its fine structure. Brain Struct. Funct. 1999, 200, 615–623. [Google Scholar] [CrossRef] [PubMed]
- Quindlen, J.C.; Bloom, E.T.; Ortega, L.E.; Moeller, A.T.; Barocas, V.H. Micropipette aspiration of the Pacinian corpuscle. J. Biomech. 2017, 63, 104–109. [Google Scholar] [CrossRef]
- Newman, S.; Cloître, M.; Allain, C.; Forgacs, G.; Beysens, D. Viscosity and elasticity during collagen assembly in vitro: Relevance to matrix-driven translocation. Biopolymers 1997, 41, 337–347. [Google Scholar] [CrossRef]
- Biswas, A. Characterization and Modeling of Vibrotactile Sensitivity Threshold of Human Finger Pad and the Pacinian Corpuscle. Ph.D. Thesis, Indian Institute of Technology Madras, Tamil Nadu, India, 2015. [Google Scholar]
- Lane, S.; Barrett-Snyder, K.; Lazarus, N.; Alberts, W.C.K.; Hanrahan, B. Vibration sensing the mammalian way: An artificial Pacinian corpuscle. Bioinspir. Biomim. 2020, 15, 046001. [Google Scholar] [CrossRef]
- Wallin, T.J.; Pikul, J.H.; Bodkhe, S.; Peele, B.N.; Mac Murray, B.C.; Therriault, D.; McEnerney, B.W.; Dillon, R.P.; Giannelis, E.P.; Shepherd, R.F. Click chemistry stereolithography for soft robots that self-heal. J. Mater. Chem. B 2017, 5, 6249–6255. [Google Scholar] [CrossRef]
- Gray, J.A.B.; Sato, M. The movement of sodium and other ions in Pacinian corpuscles. J. Physiol. 1955, 129, 594–607. [Google Scholar] [CrossRef]
- Pease, D.C.; Quilliam, T.A. Electron microscopy of the pacinian corpuscle. J. Cell Biol. 1957, 3, 331–342. [Google Scholar] [CrossRef] [PubMed]
- Fraitag, S.; Gherardi, R.; Wechsler, J. Hyperplastic pacinian corpuscles: An uncommonly encountered lesion of the hand. J. Cutan. Pathol. 1994, 21, 457–460. [Google Scholar] [CrossRef]
- Pawson, L.; Bolanowski, S.J. Voltage-gated sodium channels are present on both the neural and capsular structures of Pacinian corpuscles. Somatosens. Mot. Res. 2002, 19, 231–237. [Google Scholar] [CrossRef] [PubMed]
- Mikroskopische Anatomie des vegetativen Nervensystems. J. Am. Med. Assoc. 1929, 92, 924. [CrossRef]
- Zelená, J. The development of Pacinian corpuscles. J. Neurocytol. 1978, 7, 71–91. [Google Scholar] [CrossRef] [PubMed]
- Yang, L. Mechanical Properties of Collagen Fibrils and Elastic Fibers Explored by AFM; University of Twente: Enschede, The Netherlands, 2008. [Google Scholar]
- Rydqvist, B.; Purali, N.; Lännergren, J. Visco-elastic properties of the rapidly adapting stretch receptor muscle of the crayfish. Acta Physiol. Scand. 1994, 150, 151–159. [Google Scholar] [CrossRef]
- Gray, H. Anatomy of the Human Body. Am. J. Med. Sci. 1919, 157, 704. [Google Scholar] [CrossRef]
- Quindlen, J.C.; Güçlü, B.; Schepis, E.A.; Barocas, V.H. Computational Parametric Analysis of the Mechanical Response of Structurally Varying Pacinian Corpuscles. J. Biomech. Eng. 2017, 139, 071012. [Google Scholar] [CrossRef]


| Parameter | Pacinian Corpuscle [24] | 3D-Printed Design |
|---|---|---|
| Elastic Modulus of Lamella | 1 kPa | 5.5 MPa |
| Fluid Viscosity | 3 mPa∙s | 4.5 Pa∙s |
| Lamellar Thickness | 0.1–0.4 µm | 1 mm |
| Interlamellar Spacing | 1–8 µm | 2 mm |
| Core Radius | 15 µm | 4 mm |
| Length | 1 mm | 2 cm |
| Number of Layers | 20–60 | 1–5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrett-Snyder, K.; Lane, S.; Lazarus, N.; Alberts, W.C.K.; Hanrahan, B. Printing a Pacinian Corpuscle: Modeling and Performance. Micromachines 2021, 12, 574. https://doi.org/10.3390/mi12050574
Barrett-Snyder K, Lane S, Lazarus N, Alberts WCK, Hanrahan B. Printing a Pacinian Corpuscle: Modeling and Performance. Micromachines. 2021; 12(5):574. https://doi.org/10.3390/mi12050574
Chicago/Turabian StyleBarrett-Snyder, Kieran, Susan Lane, Nathan Lazarus, W. C. Kirkpatrick Alberts, and Brendan Hanrahan. 2021. "Printing a Pacinian Corpuscle: Modeling and Performance" Micromachines 12, no. 5: 574. https://doi.org/10.3390/mi12050574
APA StyleBarrett-Snyder, K., Lane, S., Lazarus, N., Alberts, W. C. K., & Hanrahan, B. (2021). Printing a Pacinian Corpuscle: Modeling and Performance. Micromachines, 12(5), 574. https://doi.org/10.3390/mi12050574






