Numerical Analysis of Thermal Radiative Maxwell Nanofluid Flow Over-Stretching Porous Rotating Disk
Abstract
1. Introduction
2. Literature Review
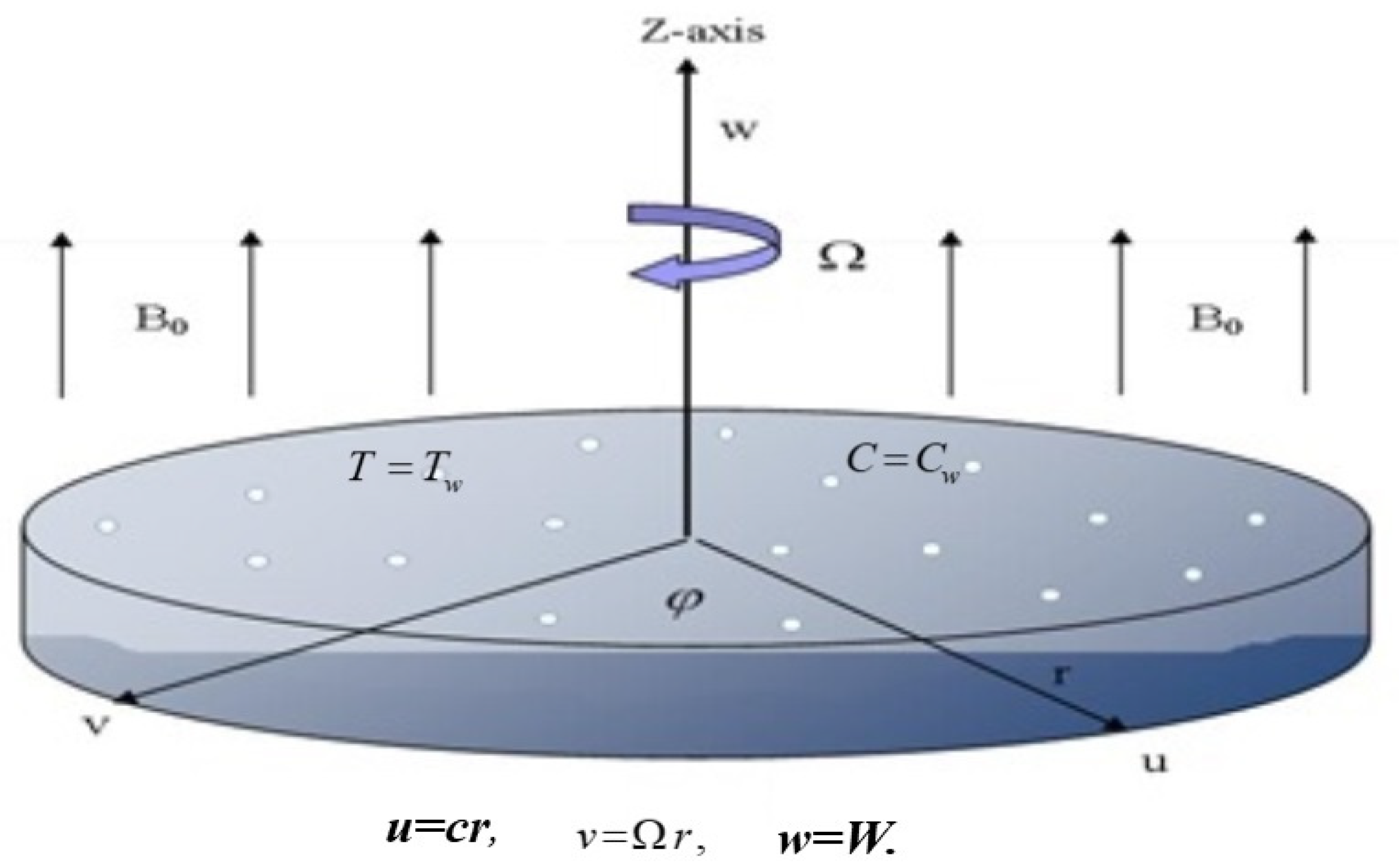
3. Formulation of the Problem
3.1. Governing Equations
3.2. Similarity Transformation
4. Solution Procedures
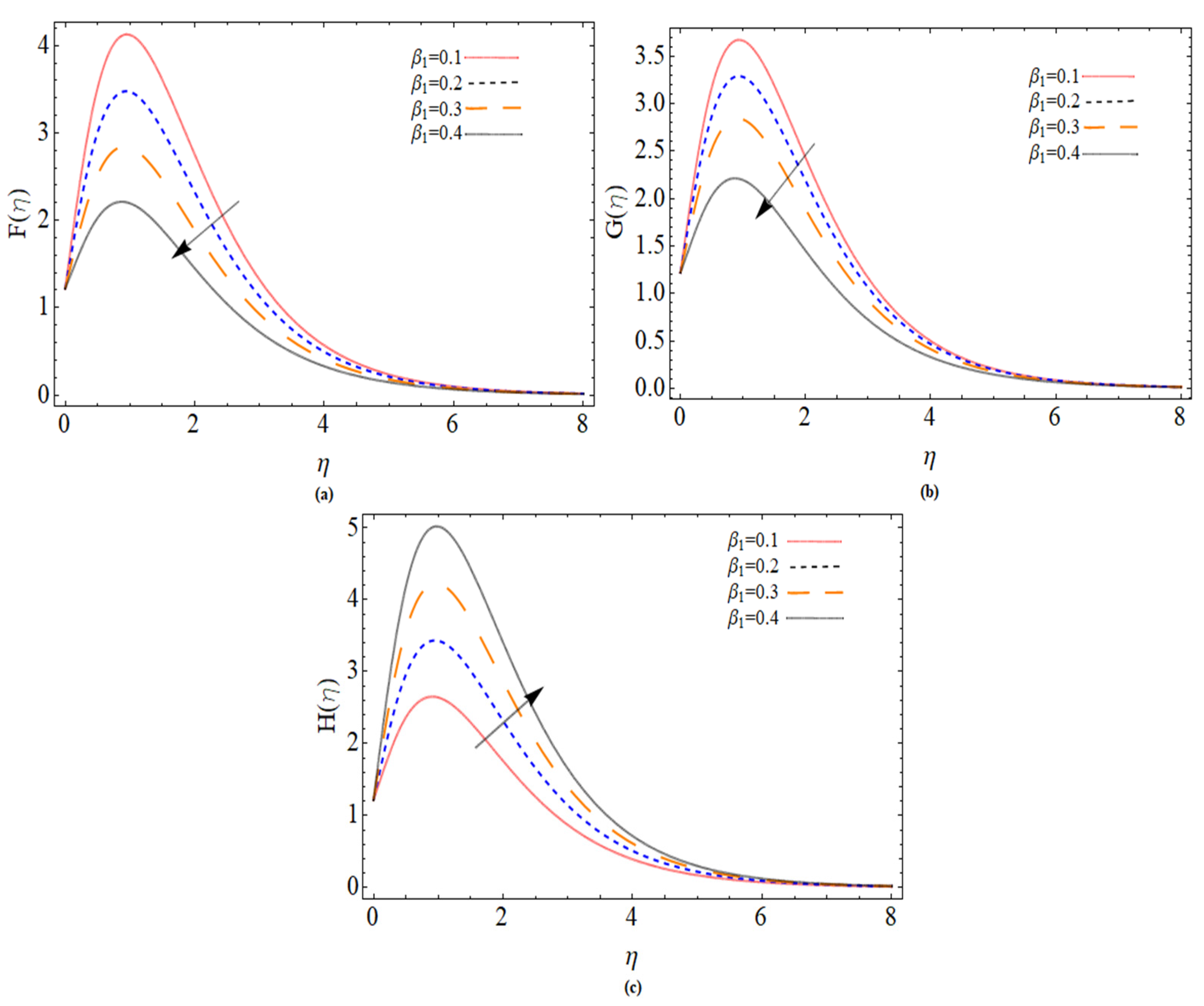
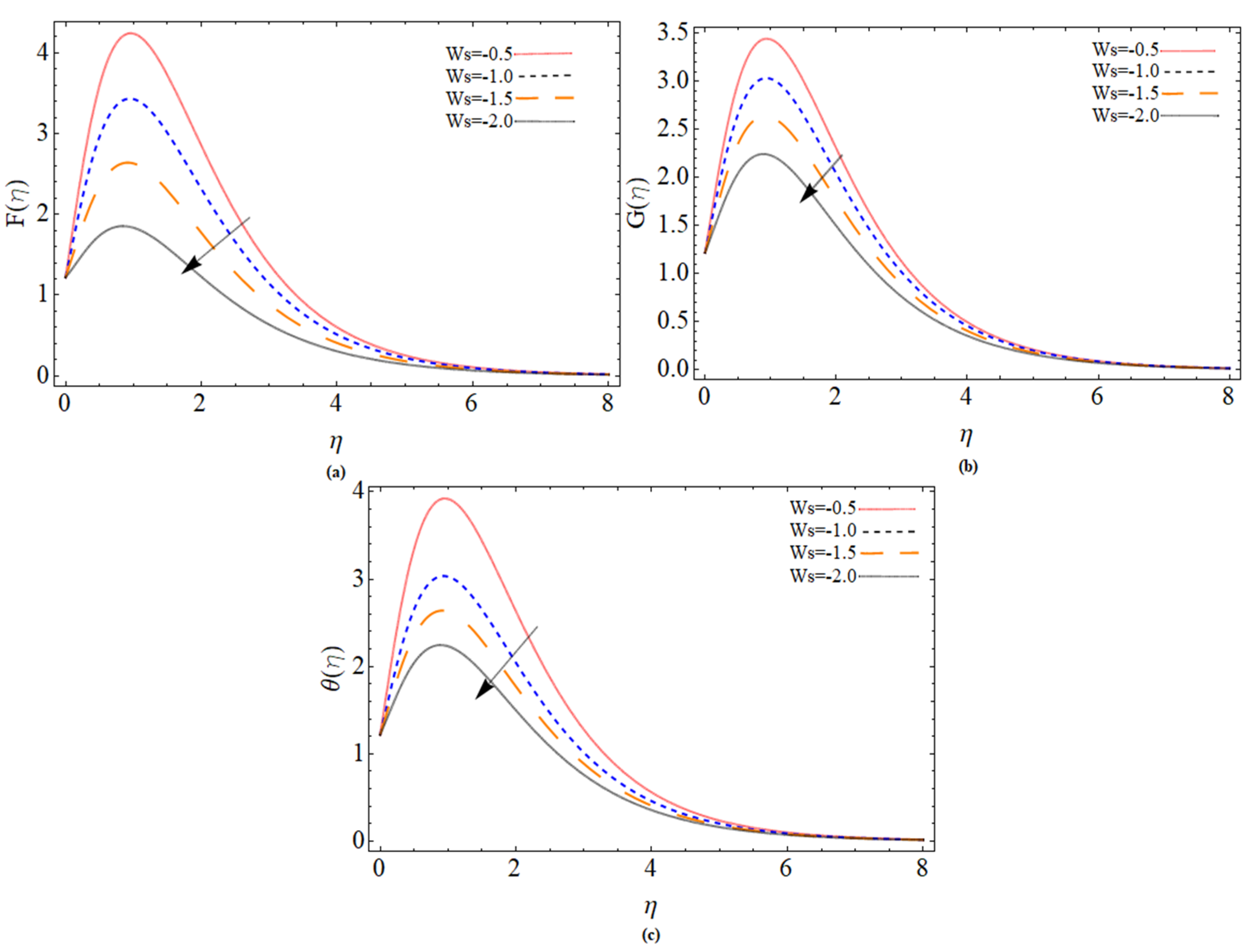
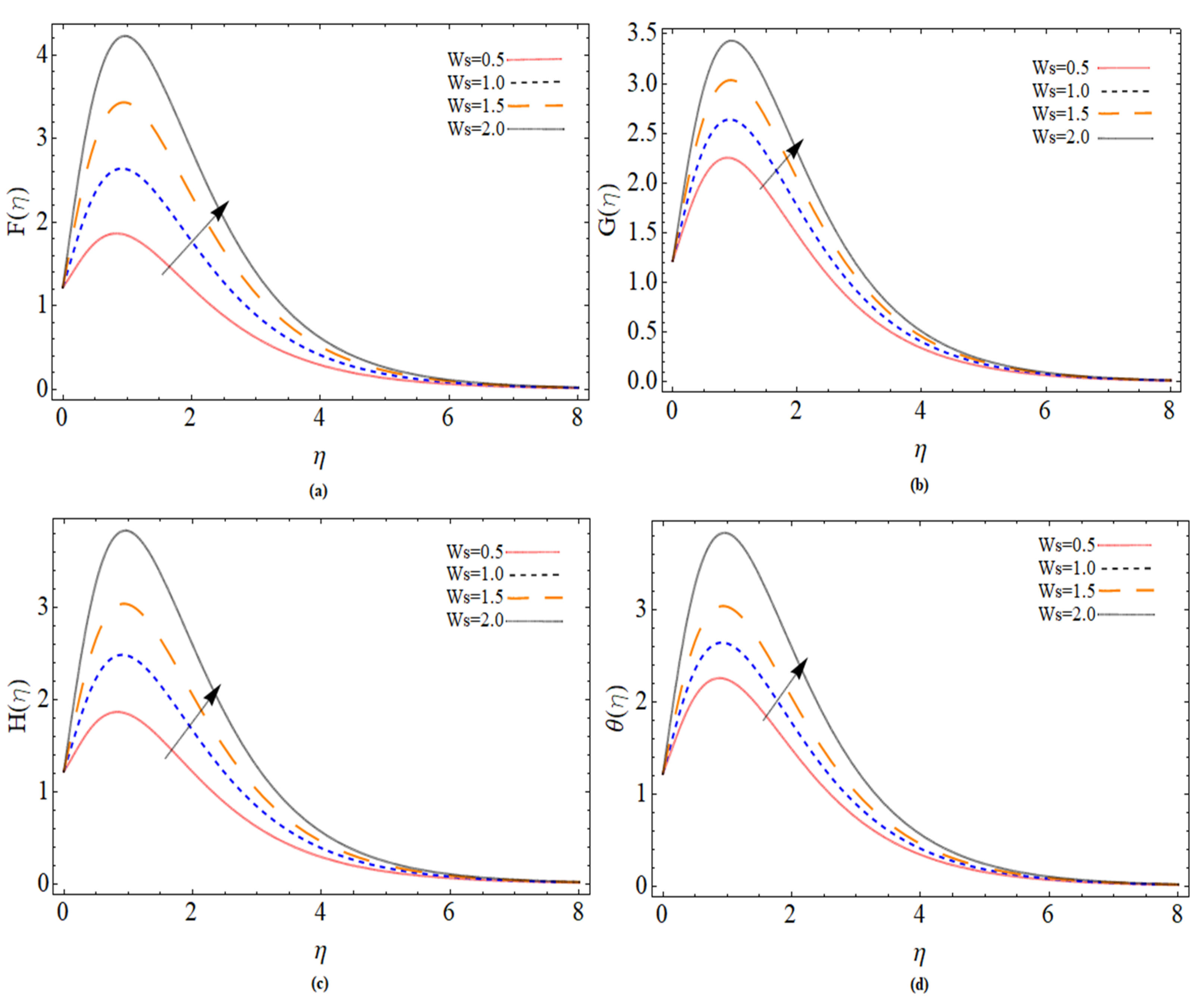
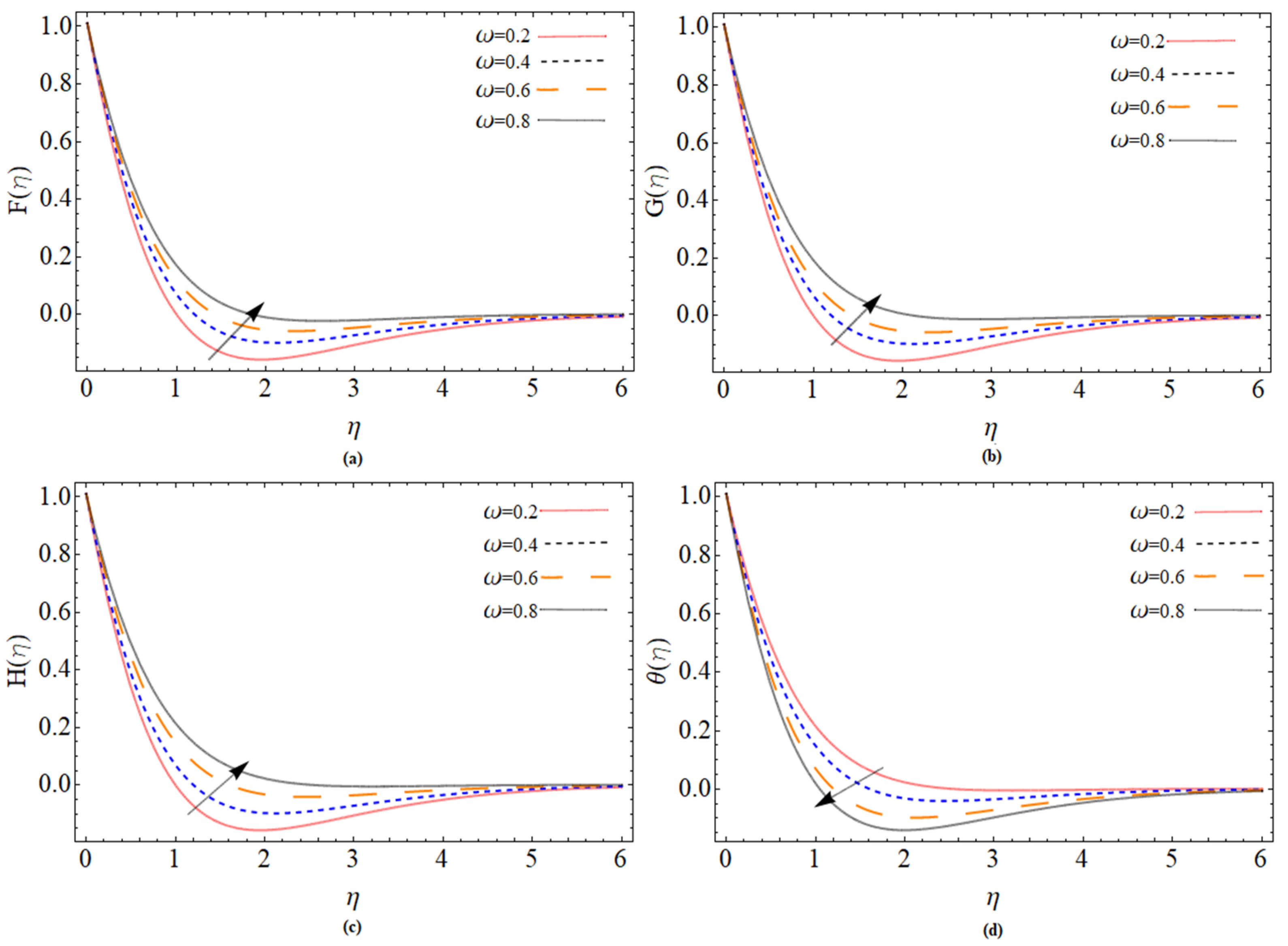
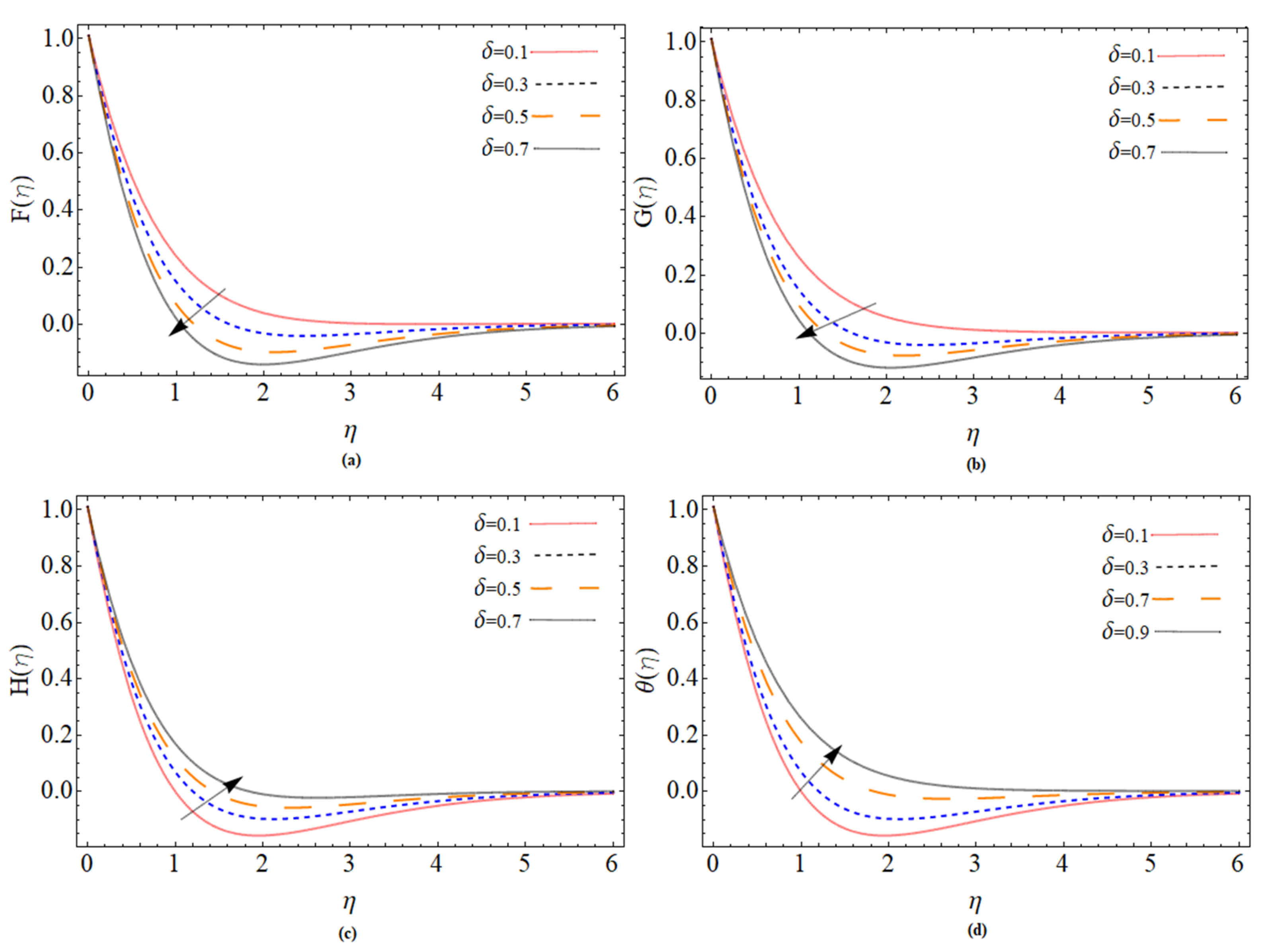
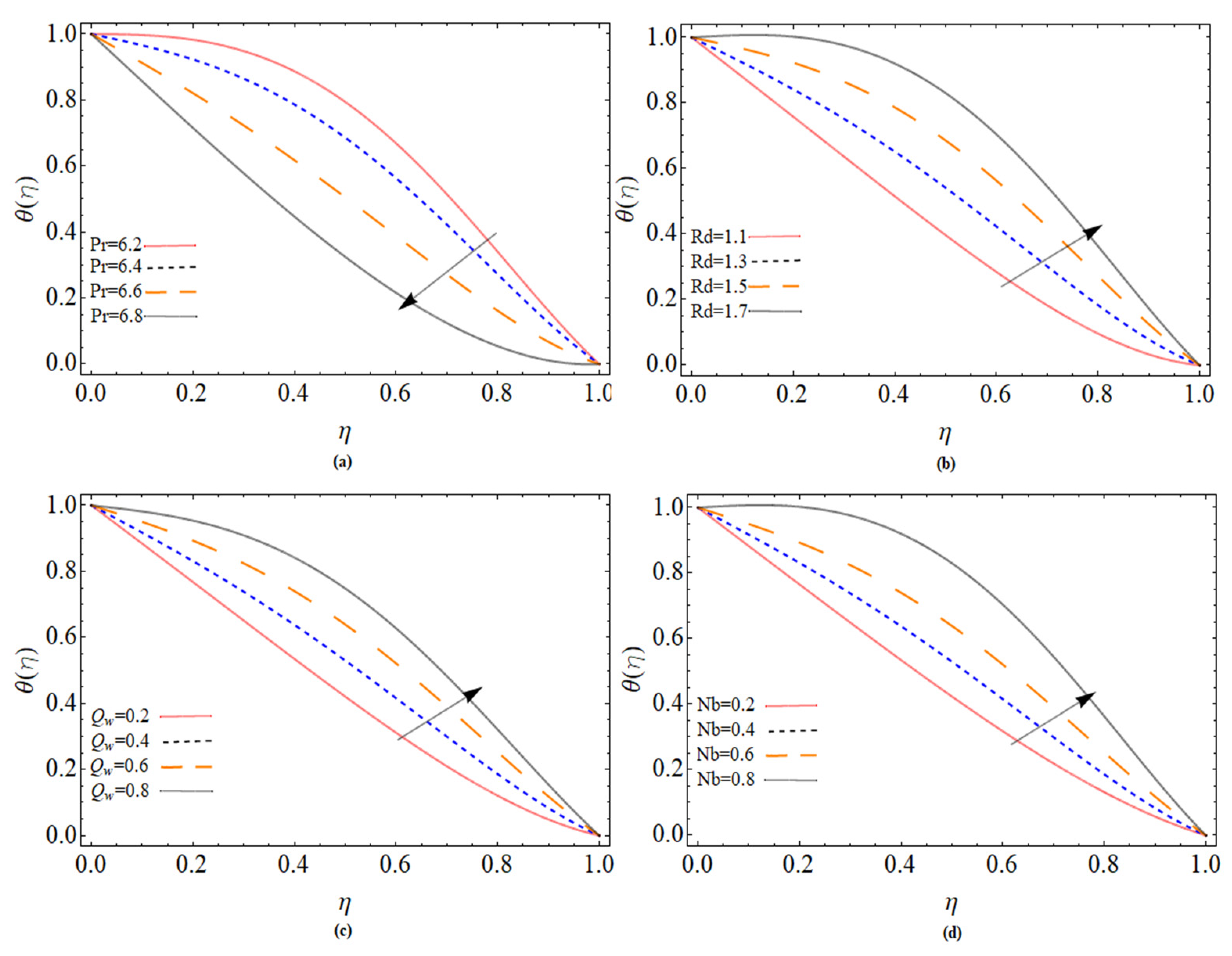
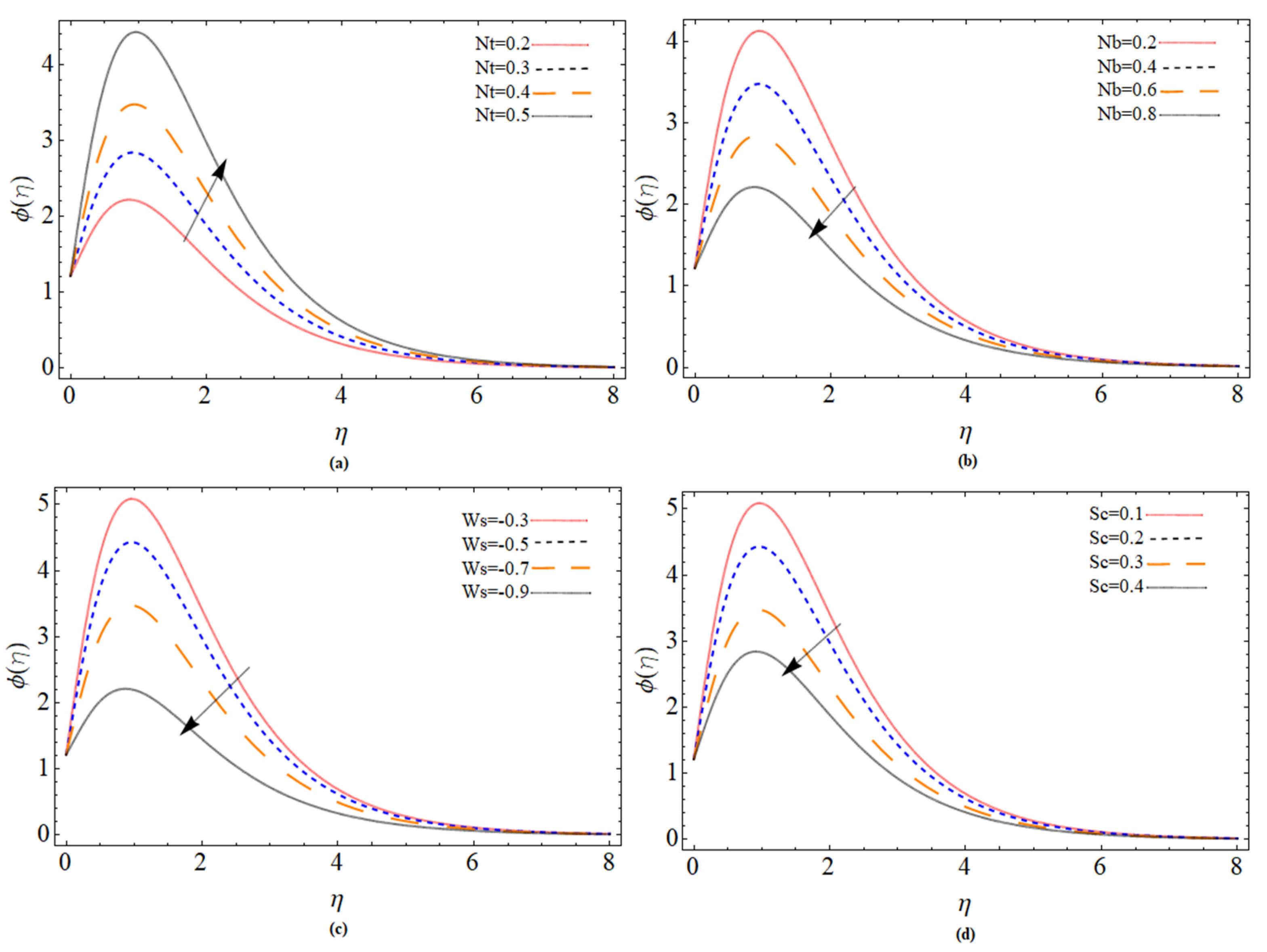
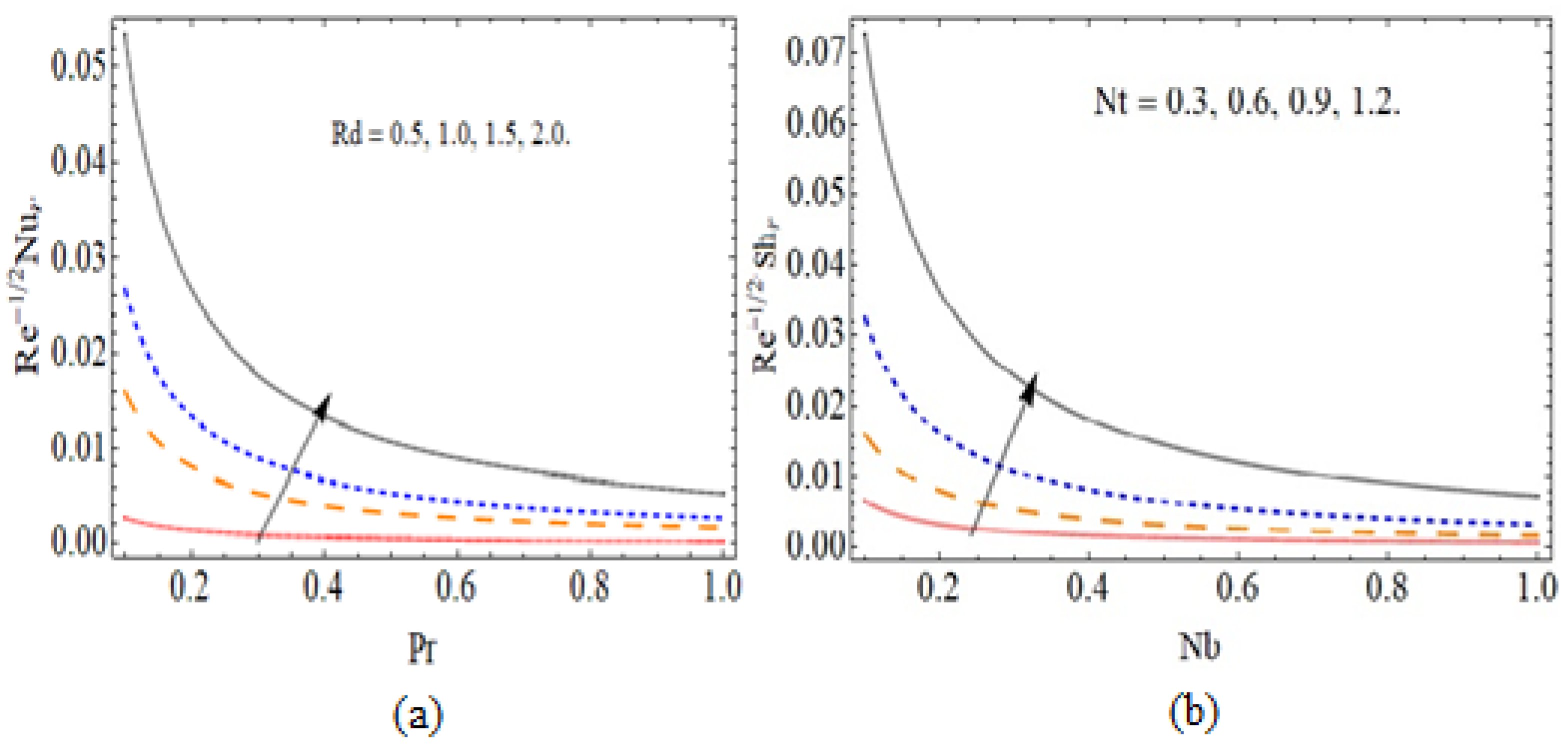
5. Results and Discussion
6. Conclusions
- The centrifugal force is more effective and dominant near the disk surface, so causes the maximum velocity in the neighborhood of the surface of the disk.
- The fluid velocity reduces by the action of suction effects. Because the suction effect gripping the fluid particles towards the pores of the disk, which causes the momentum boundary layer reduction.
- The axial, radial and tangential velocities are boosts with the increases of injection parameter.
- The enhancement in rotation parameter also boosts the azimuthal and radial flows.
- The thermal energy profile enhances by the consequence of Brownian motion parameter Nb. The Brownian motion produces random movement between fluid particles, which generate more heat, as a result, the fluid temperature increases.
- The fluid temperature decline with Prandtl number , while incline with thermal radiation parameter, .
- The nanofluid concentration field enhances with , while causes the reduction of concentration profile.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kármán, T.V. Über laminare und turbulente Reibung. ZAMM J. Appl. Math. Mech. Z. Für Angew. Math. Mech. 1921, 1, 233–252. [Google Scholar] [CrossRef]
- Cochran, W. The flow due to a rotating disc. Math. Proc. Camb. Philos. Soc. 1934, 30, 365–375. [Google Scholar] [CrossRef]
- Wagner, C. Heat transfer from a rotating disk to ambient air. J. Appl. Phys. 1948, 19, 837–839. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. MHD fluid flow and heat transfer due to a stretching rotating disk. Int. J. Therm. Sci. 2012, 51, 195–201. [Google Scholar] [CrossRef]
- Liang, M.; Fu, C.; Xiao, B.; Luo, L.; Wang, Z. A fractal study for the effective electrolyte diffusion through charged porous media. Int. J. Heat Mass Transf. 2019, 137, 365–371. [Google Scholar] [CrossRef]
- Millsaps, K.; Pohlhausen, K. Heat transfer by laminar flow from a rotating plate. J. Aeronaut. Sci. 1952, 19, 120–126. [Google Scholar] [CrossRef]
- Mustafa, I.; Javed, T.; Ghaffari, A. Heat transfer in MHD stagnation point flow of a ferrofluid over a stretchable rotating disk. J. Mol. Liq. 2016, 219, 526–532. [Google Scholar] [CrossRef]
- Mustafa, M. MHD nanofluid flow over a rotating disk with partial slip effects: Buongiorno model. Int. J. Heat Mass Transf. 2017, 108, 1910–1916. [Google Scholar] [CrossRef]
- Rashidi, M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab.: Lemont, IL, USA, 1995. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Analytical solutions of single and multi-phase models for the condensation of nanofluid film flow and heat transfer. Eur. J. Mech. B Fluids 2015, 53, 272–277. [Google Scholar] [CrossRef]
- Pourmehran, O.; Rahimi-Gorji, M.; Hatami, M.; Sahebi, S.; Domairry, G. Numerical optimization of microchannel heat sink (MCHS) performance cooled by KKL based nanofluids in saturated porous medium. J. Taiwan Inst. Chem. Eng. 2015, 55, 49–68. [Google Scholar] [CrossRef]
- Hatami, M.; Song, D.; Jing, D. Optimization of a circular-wavy cavity filled by nanofluid under the natural convection heat transfer condition. Int. J. Heat Mass Transf. 2016, 98, 758–767. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Akbar, N.S.; Lee, C.; Khan, Z.H. Numerical study of boundary layer flow and heat transfer of Oldroyd-B nanofluid towards a stretching sheet. PLoS ONE 2013, 8, e69811. [Google Scholar] [CrossRef]
- Afify, A.A.; Abd El-Aziz, M. Lie group analysis of flow and heat transfer of non-Newtonian nanofluid over a stretching surface with convective boundary condition. Pramana 2017, 88, 31. [Google Scholar] [CrossRef]
- Yang, C.; Li, W.; Nakayama, A. Convective heat transfer of nanofluids in a concentric annulus. Int. J. Therm. Sci. 2013, 71, 249–257. [Google Scholar] [CrossRef]
- Hayat, T.; Qayyum, S.; Alsaedi, A.; Asghar, S. Radiation effects on the mixed convection flow induced by an inclined stretching cylinder with non-uniform heat source/sink. PLoS ONE 2017, 12, e0175584. [Google Scholar] [CrossRef] [PubMed]
- Xiao, B.; Huang, Q.; Chen, H.; Chen, X.; Long, G. A fractal model for capillary flow through a single tortuous capillary with roughened surfaces in fibrous porous media. Fractals 2021, 29, 2150017. [Google Scholar]
- Attia, H.A. Numerical study of flow and heat transfer of a non-Newtonian fluid on a rotating porous disk. Appl. Math. Comput. 2005, 163, 327–342. [Google Scholar] [CrossRef]
- Griffiths, P.T. Flow of a generalised Newtonian fluid due to a rotating disk. J. Non-Newton. Fluid Mech. 2015, 221, 9–17. [Google Scholar] [CrossRef]
- Tabassum, M.; Mustafa, M. A numerical treatment for partial slip flow and heat transfer of non-Newtonian Reiner-Rivlin fluid due to rotating disk. Int. J. Heat Mass Transf. 2018, 123, 979–987. [Google Scholar] [CrossRef]
- Doh, D.; Muthtamilselvan, M. Thermophoretic particle deposition on magnetohydrodynamic flow of micropolar fluid due to a rotating disk. Int. J. Mech. Sci. 2017, 130, 350–359. [Google Scholar] [CrossRef]
- Whitaker, S. Flow in porous media I: A theoretical derivation of Darcy’s law. Transp. Porous Media 1986, 1, 3–25. [Google Scholar] [CrossRef]
- Muskat, M. The flow of homogeneous fluids through porous media. Soil Sci. 1938, 46, 169. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Alqarni, M.S.; Wakif, A.; Khan, I.; Bhutta, M.S. Numerical Scrutinization of Darcy-Forchheimer Relation in Convective Magnetohydrodynamic Nanofluid Flow Bounded by Nonlinear Stretching Surface in the Perspective of Heat and Mass Transfer. Micromachines 2021, 12, 374. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A. Numerical exploration of the features of thermally enhanced chemically reactive radiative Powell–Eyring nanofluid flow via Darcy medium over non-linearly stretching surface affected by a transverse magnetic field and convective boundary conditions. Appl. Nanosci. 2020, 1–18. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T. Darcy-Forchheimer nanofluidic flow manifested with Cattaneo-Christov theory of heat and mass flux over non-linearly stretching surface. PLoS ONE 2019, 14, e0221302. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Baleanu, D. Consequences of Soret–Dufour effects, thermal radiation, and binary chemical reaction on Darcy Forchheimer flow of nanofluids. Symmetry 2020, 12, 1421. [Google Scholar] [CrossRef]
- Shafiq, A.; Rasool, G.; Khalique, C.M. Significance of thermal slip and convective boundary conditions in three-dimensional rotating Darcy-Forchheimer nanofluid flow. Symmetry 2020, 12, 741. [Google Scholar] [CrossRef]
- Ahmed, J.; Khan, M.; Ahmad, L. Stagnation point flow of Maxwell nanofluid over a permeable rotating disk with heat source/sink. J. Mol. Liq. 2019, 287, 110853. [Google Scholar] [CrossRef]
- Ferdows, M.; Shamshuddin, M.; Zaimi, K. Dissipative-Radiative Micropolar Fluid Transport in a NonDarcy Porous Medium with Cross-Diffusion Effects. CFD Lett. 2020, 12, 70–89. [Google Scholar] [CrossRef]
- Devi, S.S.U.; Mabood, F. Entropy anatomization on Marangoni Maxwell fluid over a rotating disk with nonlinear radiative flux and Arrhenius activation energy. Int. Commun. Heat Mass Transf. 2020, 118, 104857. [Google Scholar] [CrossRef]

| Mustafa et al. [7] | Ahmed et al. [31] | Present Paper | |
|---|---|---|---|
| 0 | −1.1737 | −1.1379 | −1.1380 |
| 1 | −0.9483 | −0.9485 | −0.9487 |
| 2 | −0.3262 | −0.3264 | −0.3266 |
| 5 | 3.1937 | 3.11937 | 3.11939 |
| 10 | 12.7209 | 12.7209 | 12.7811 |
| 20 | 40.9057 | 40.9057 | 40.9058 |
| RK4 | bvp4c | Absolute Error | |
|---|---|---|---|
| 1.0 | 1.000000 | 1.000000 | 8.146310 |
| 1.2 | 1.199831 | 1.199831 | 3.387821 |
| 1.4 | 0.988459 | 0.988459 | 2.845561 |
| 1.6 | 0.879189 | 0.879189 | 2.813281 |
| 1.8 | 0.539393 | 0.539393 | 3.287961 |
| Bvp4c | Bvp4c | ||||
| 3.0 | 0.7718284 | 0.7718285 | 1.0 | 1.457986 | 1.457995 |
| 4.0 | 0.6999885 | 0.6999885 | 1.5 | 1.531211 | 1.531220 |
| 5.0 | 0.6290089 | 0.6290088 | 2.0 | 1.596949 | 1.596949 |
| 6.0 | 0.5632372 | 0.5632370 | 2.5 | 1.685639 | 1.685639 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.-S.; Bilal, M.; Khan, M.A.; Muhammad, T. Numerical Analysis of Thermal Radiative Maxwell Nanofluid Flow Over-Stretching Porous Rotating Disk. Micromachines 2021, 12, 540. https://doi.org/10.3390/mi12050540
Zhou S-S, Bilal M, Khan MA, Muhammad T. Numerical Analysis of Thermal Radiative Maxwell Nanofluid Flow Over-Stretching Porous Rotating Disk. Micromachines. 2021; 12(5):540. https://doi.org/10.3390/mi12050540
Chicago/Turabian StyleZhou, Shuang-Shuang, Muhammad Bilal, Muhammad Altaf Khan, and Taseer Muhammad. 2021. "Numerical Analysis of Thermal Radiative Maxwell Nanofluid Flow Over-Stretching Porous Rotating Disk" Micromachines 12, no. 5: 540. https://doi.org/10.3390/mi12050540
APA StyleZhou, S.-S., Bilal, M., Khan, M. A., & Muhammad, T. (2021). Numerical Analysis of Thermal Radiative Maxwell Nanofluid Flow Over-Stretching Porous Rotating Disk. Micromachines, 12(5), 540. https://doi.org/10.3390/mi12050540







