A Magnetically Actuated Superhydrophobic Ratchet Surface for Droplet Manipulation
Abstract
1. Introduction
2. Materials and Methods
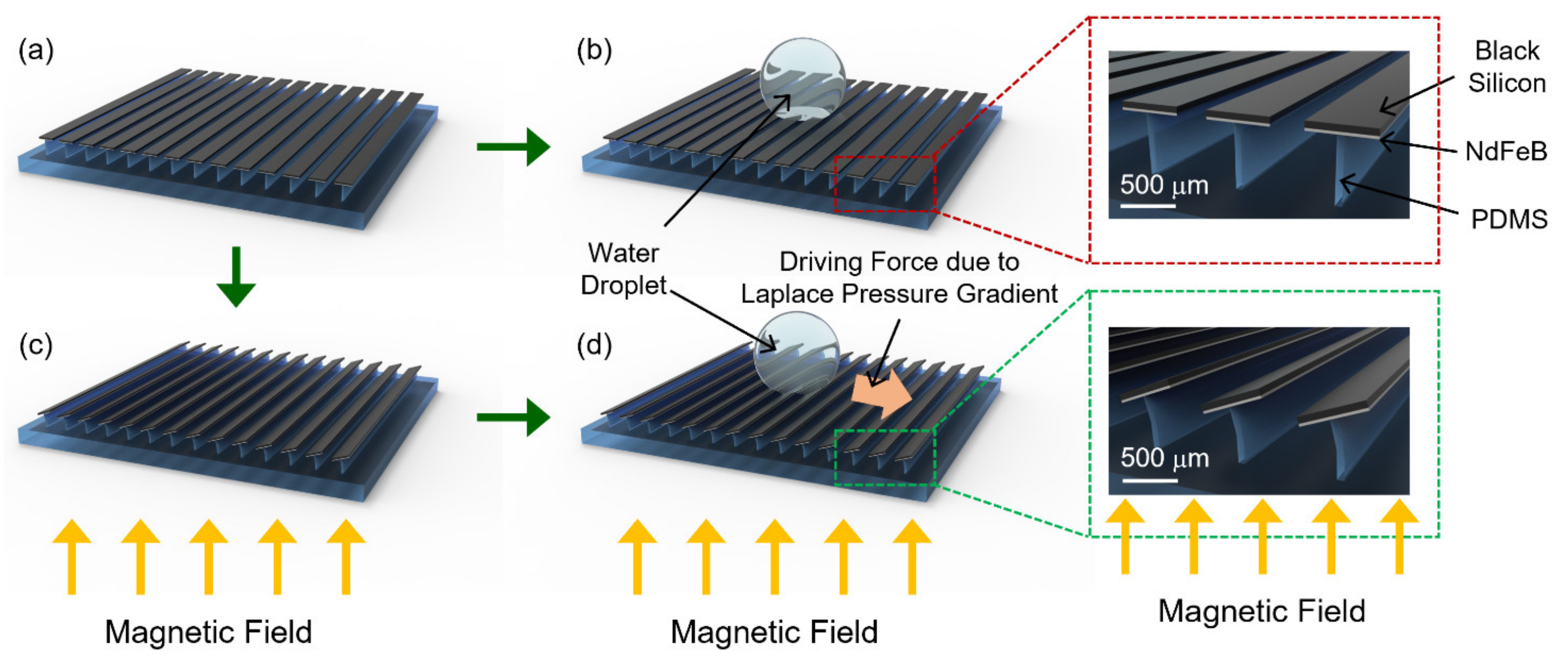
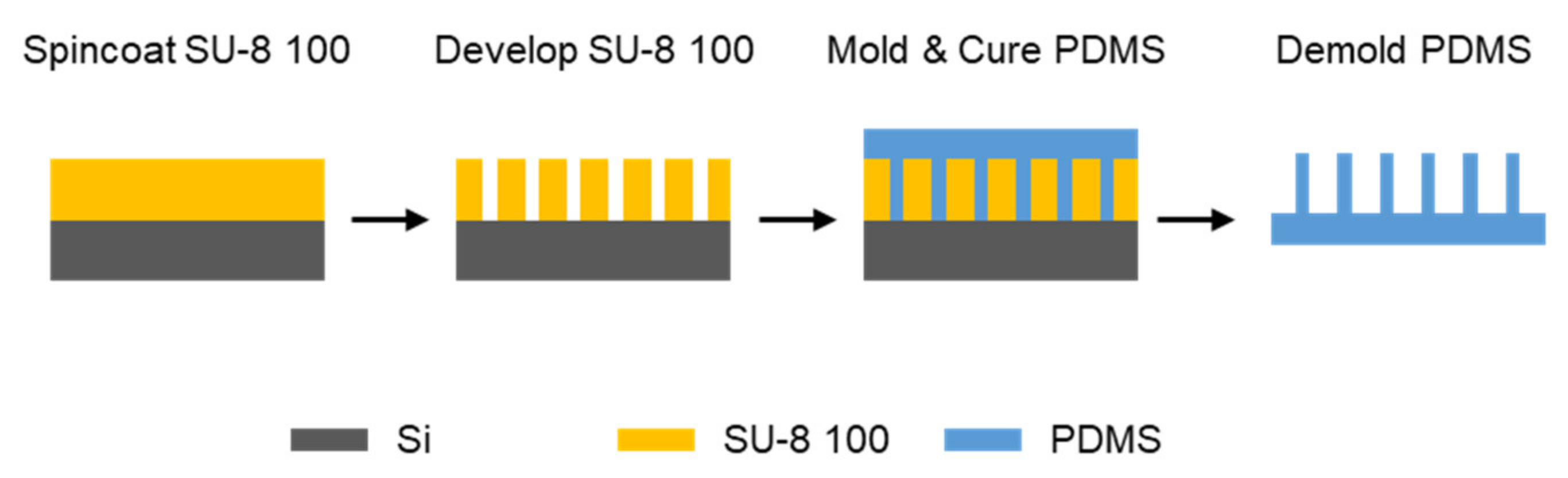
2.1. Fabrication of an Elastomer Ridge Array
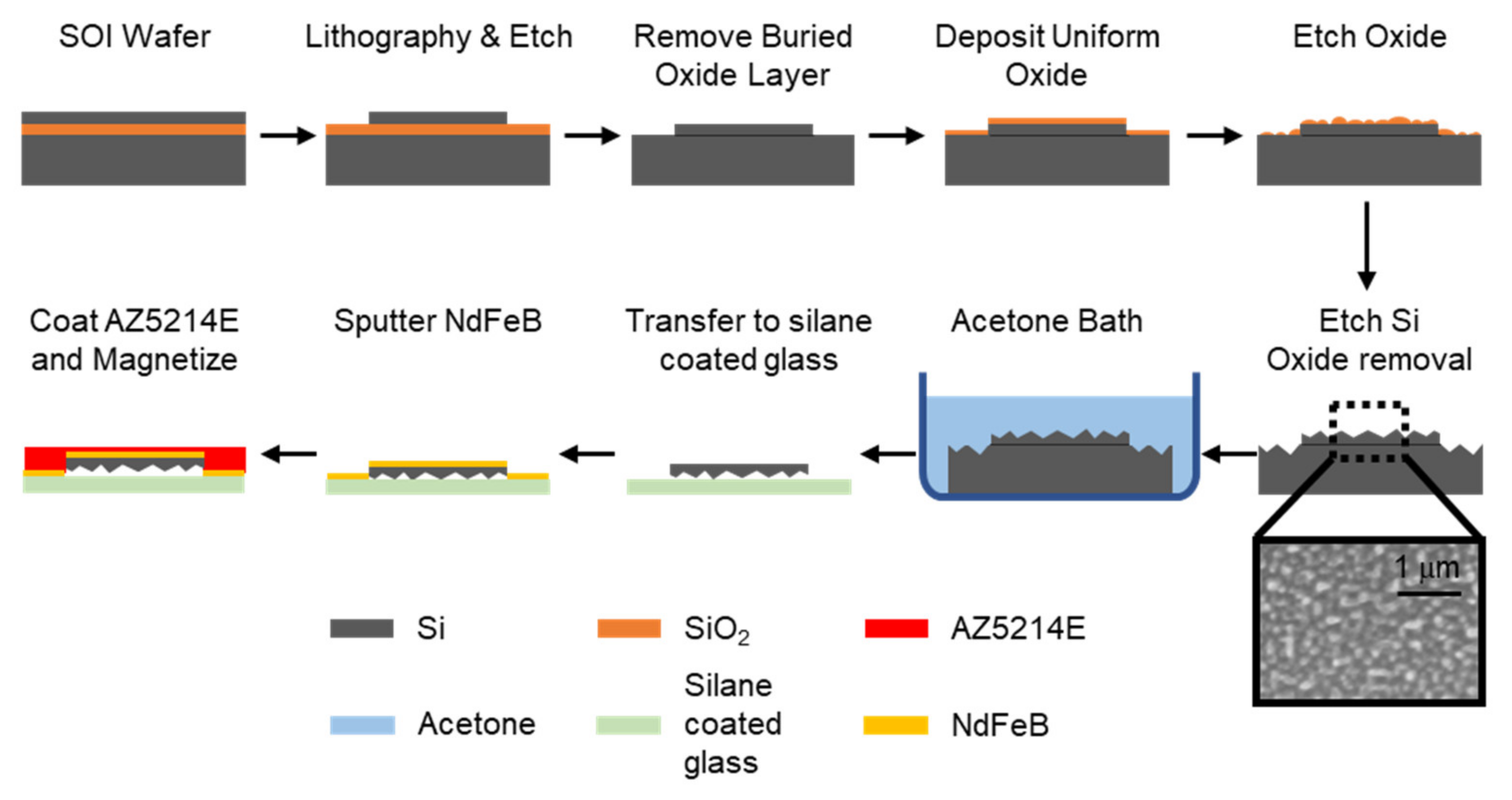
2.2. Fabrication of Nanostructured Black Silicon Strips
2.3. Transferring Black Silicon Strips and Sputtering a Magnetic Material
2.4. Transfer Printing of Black Silicon Magnetic Strips on Elastomer Ridges
2.5. High-Speed Camera Capturing
3. Results and Discussion
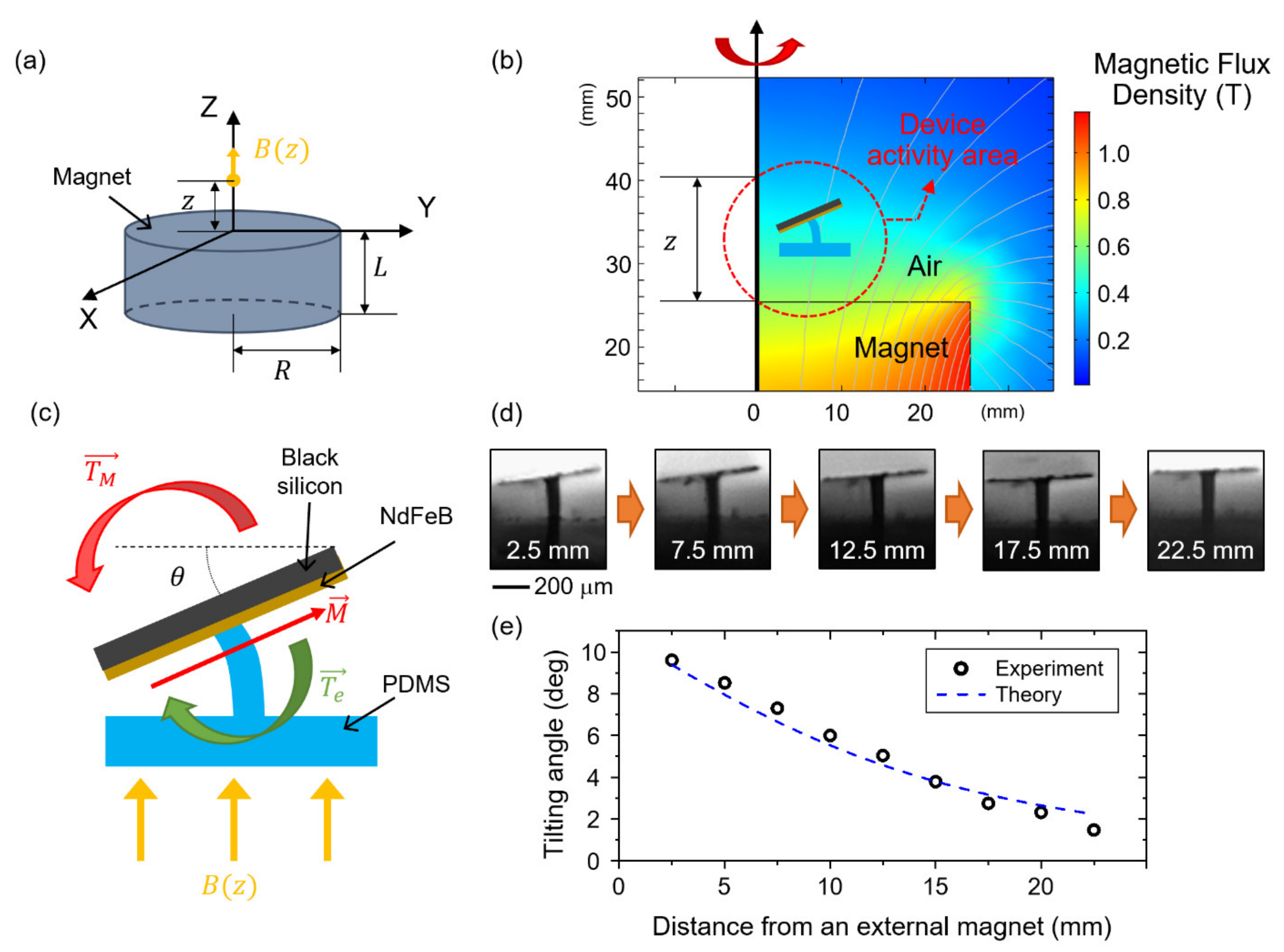
3.1. Characterization of Magnetomechanical Properties
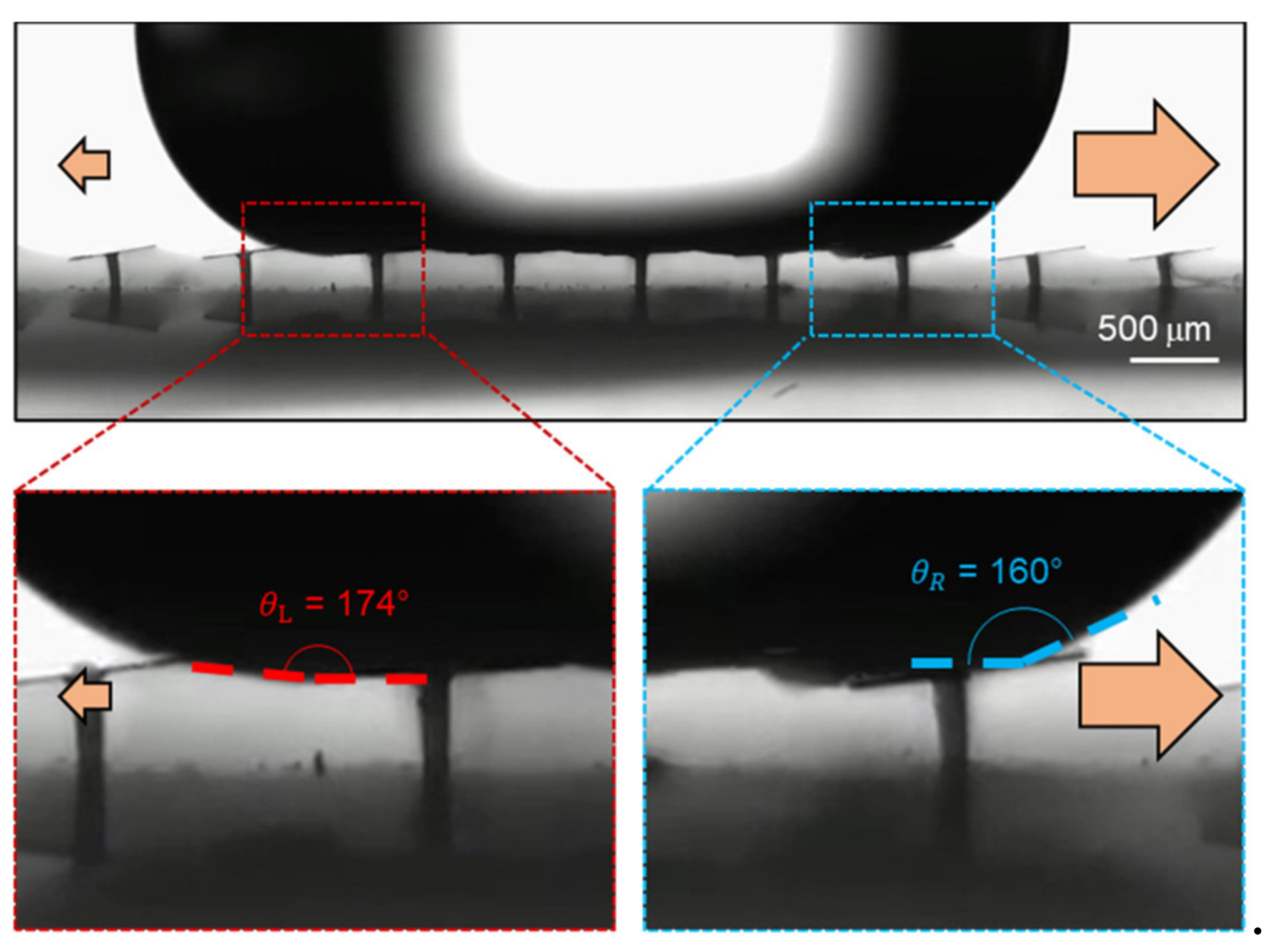
3.2. Droplet Spreading Behavior
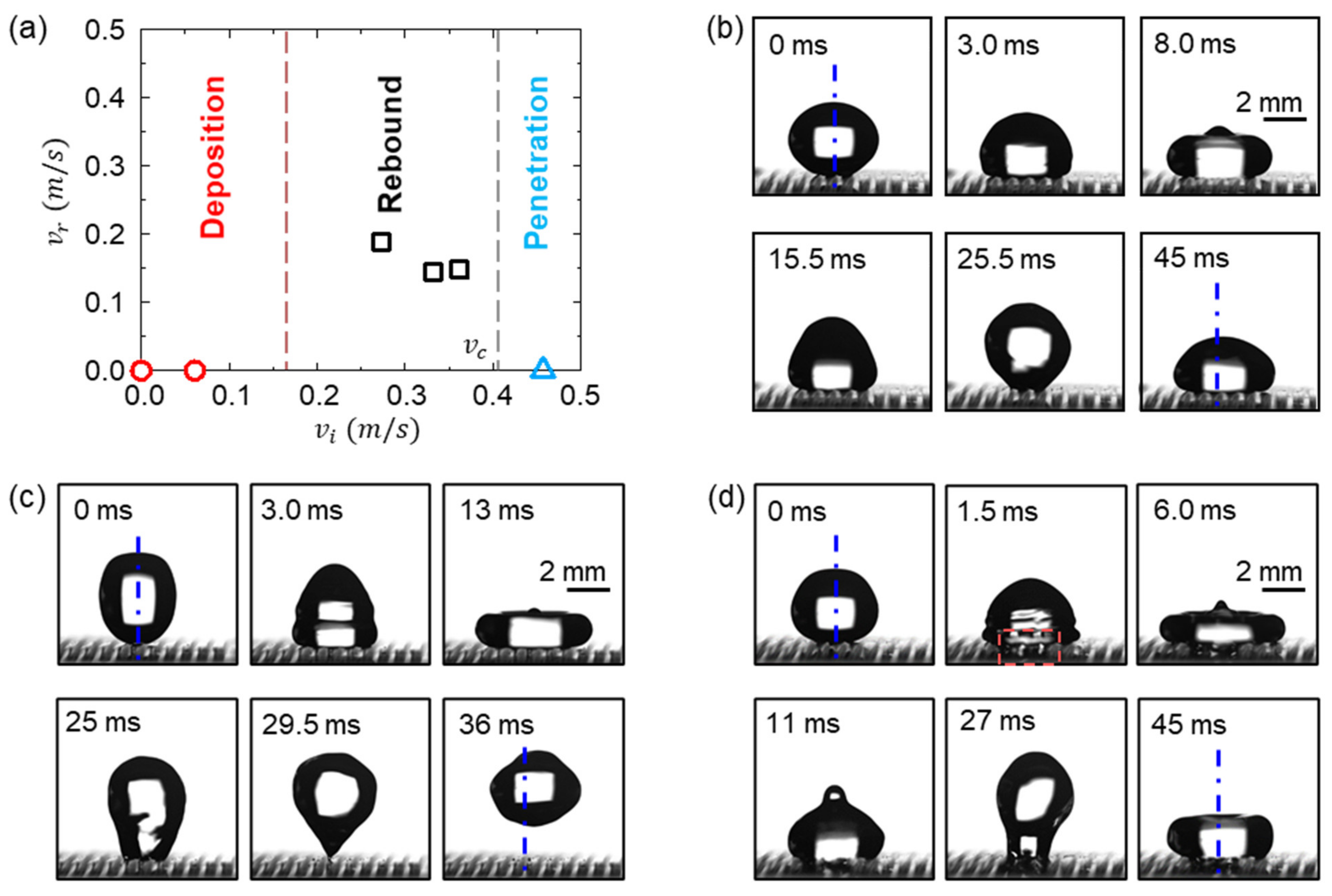
3.3. Droplet Impact Behavior
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sun, D.; Böhringer, K.F. An Active Self-Cleaning Surface System for Photovoltaic Modules Using Anisotropic Ratchet Conveyors and Mechanical Vibration. Microsyst. Nanoeng. 2020, 6. [Google Scholar] [CrossRef]
- Sun, D.; Böhringer, K.F. Self-Cleaning: From Bio-Inspired Surface Modification to MEMS/Microfluidics System Integration. Micromachines 2019, 10, 101. [Google Scholar] [CrossRef]
- Tan, C.L.C.; Sapiha, K.; Leong, Y.F.H.; Choi, S.; Anariba, F.; Thio, B.J.R. Lotus-like Effect for Metal Filings Recovery and Particle Removal on Heated Metal Surfaces Using Leidenfrost Water Droplets. Soft Matter 2015, 11, 5400–5407. [Google Scholar] [CrossRef] [PubMed]
- Nightingale, A.M.; Phillips, T.W.; Bannock, J.H.; De Mello, J.C. Controlled Multistep Synthesis in a Three-Phase Droplet Reactor. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef]
- Bawazer, L.A.; McNally, C.S.; Empson, C.J.; Marchant, W.J.; Comyn, T.P.; Niu, X.; Cho, S.; Mcpherson, M.J.; Binks, B.P.; Demello, A.; et al. Combinatorial Microfluidic Droplet Engineering for Biomimetic Material Synthesis. Sci. Adv. 2016, 2, e1600567. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, T.H. Full-Range Magnetic Manipulation of Droplets via Surface Energy Traps Enables Complex Bioassays. Adv. Mater. 2013, 25, 2903–2908. [Google Scholar] [CrossRef] [PubMed]
- Su, F.; Ozev, S.; Chakrabarty, K. Ensuring the Operational Health of Droplet-Based Microelectrofluidic Biosensor Systems. IEEE Sens. J. 2005, 5, 763–772. [Google Scholar] [CrossRef]
- Regan, D.P.; Howell, C. Droplet Manipulation with Bioinspired Liquid-Infused Surfaces: A Review of Recent Progress and Potential for Integrated Detection. Curr. Opin. Colloid Interface Sci. 2019, 39, 137–147. [Google Scholar] [CrossRef]
- Cho, S.K.; Moon, H.; Kim, C.J. Creating, Transporting, Cutting, and Merging Liquid Droplets by Electrowetting-Based Actuation for Digital Microfluidic Circuits. J. Microelectromech. Syst. 2003, 12, 70–80. [Google Scholar] [CrossRef]
- Li, A.; Li, H.; Li, Z.; Zhao, Z.; Li, K.; Li, M.; Song, Y. Programmable Droplet Manipulation by a Magnetic-Actuated Robot. Sci. Adv. 2020, 6, eaay5808. [Google Scholar] [CrossRef]
- Linke, H.; Alemán, B.J.; Melling, L.D.; Taormina, M.J.; Francis, M.J.; Dow-Hygelund, C.C.; Narayanan, V.; Taylor, R.P.; Stout, A. Self-Propelled Leidenfrost Droplets. Phys. Rev. Lett. 2006, 96, 154502. [Google Scholar] [CrossRef]
- Ok, J.T.; Lopez-Oña, E.; Nikitopoulos, D.E.; Wong, H.; Park, S. Propulsion of Droplets on Micro- and Sub-Micron Ratchet Surfaces in the Leidenfrost Temperature Regime. Microfluid. Nanofluid. 2011, 10, 1045–1054. [Google Scholar] [CrossRef]
- Agapov, R.L.; Boreyko, J.B.; Briggs, D.P.; Srijanto, B.R.; Retterer, S.T.; Collier, C.P.; Lavrik, N.V. Length Scale of Leidenfrost Ratchet Switches Droplet Directionality. Nanoscale 2014, 6, 9293–9299. [Google Scholar] [CrossRef] [PubMed]
- Jia, Z.; Chen, M.; Zhu, H. Reversible Self-Propelled Leidenfrost Droplets on Ratchet Surfaces. Appl. Phys. Lett. 2017, 110, 091603. [Google Scholar] [CrossRef]
- Li, J.; Zhou, X.; Zhang, Y.; Hao, C.; Zhao, F.; Li, M.; Tang, H.; Ye, W.; Wang, Z. Rectification of Mobile Leidenfrost Droplets by Planar Ratchets. Small 2020, 16, 1901751. [Google Scholar] [CrossRef] [PubMed]
- Duncombe, T.A.; Erdem, E.Y.; Shastry, A.; Baskaran, R.; Böhringer, K.F. Controlling Liquid Drops with Texture Ratchets. Adv. Mater. 2012, 24, 1545–1550. [Google Scholar] [CrossRef] [PubMed]
- Sekeroglu, K.; Gurkan, U.A.; Demirci, U.; Demirel, M.C. Transport of a Soft Cargo on a Nanoscale Ratchet. Appl. Phys. Lett. 2011, 99, 063703. [Google Scholar] [CrossRef]
- Sun, D.; Gomez, G.; Bohringer, K.F. Droplet Manipulation Using AC Ewod-Actuated Anisotropic Ratchet Conveyor. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems and Eurosensors XXXIII, TRANSDUCERS 2019 and EUROSENSORS XXXIII, Berlin, Germany, 23–27 June 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 2270–2273. [Google Scholar]
- Yang, Z.; Park, J.K.; Kim, S. Magnetically Responsive Elastomer-Silicon Hybrid Surfaces for Fluid and Light Manipulation. Small 2018, 14, 1702839. [Google Scholar] [CrossRef] [PubMed]
- Park, J.K.; Kim, S. Droplet Manipulation on a Structured Shape Memory Polymer Surface. Lab Chip 2017, 17, 1793–1801. [Google Scholar] [CrossRef]
- Camacho, J.M.; Sosa, V. Alternative Method to Calculate the Magnetic Field of Permanent Magnets with Azimuthal Symmetry. Educ. Rev. Mex. Física E 2013, 59, 8–17. [Google Scholar]
- Bai, H.; Tian, X.; Zheng, Y.; Ju, J.; Zhao, Y.; Jiang, L. Direction Controlled Driving of Tiny Water Drops on Bioinspired Artificial Spider Silks. Adv. Mater. 2010, 22, 5521–5525. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.T.; Chen, J.C.; Huang, K.J.; Yeh, J.A. Droplet Manipulation on a Hydrophobic Textured Surface with Roughened Patterns. J. Microelectromech. Syst. 2006, 15, 697–707. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, Z.; Zhang, C.; Yang, C. Reduced Contact Time of a Droplet Impacting on a Moving Superhydrophobic Surface. Appl. Phys. Lett. 2020, 117, 151602. [Google Scholar] [CrossRef]
- Antonini, C.; Amirfazli, A.; Marengo, M. Drop Impact and Wettability: From Hydrophilic to Superhydrophobic Surfaces. Phys. Fluids 2012, 24, 102104. [Google Scholar] [CrossRef]
- Tsai, P.; Pacheco, S.; Pirat, C.; Lefferts, L.; Lohse, D. Drop Impact upon Micro- and Nanostructured Superhydrophobic Surfaces. Langmuir 2009, 25, 12293–12298. [Google Scholar] [CrossRef]
- Qu, J.; Yang, Y.; Yang, S.; Hu, D.; Qiu, H. Droplet Impingement on Nano-Textured Superhydrophobic Surface: Experimental and Numerical Study. Appl. Surf. Sci. 2019, 491, 160–170. [Google Scholar] [CrossRef]
- Yuan, Z.; Wen, J.; Matsumoto, M.; Kurose, R. Anti-Wetting Ability of the Hydrophobic Surface Decorated by Submillimeter Grooves. Int. J. Multiph. Flow 2020, 131, 103404. [Google Scholar] [CrossRef]
- Kumar, M.; Bhardwaj, R.; Sahu, K.C. Motion of a Droplet on an Anisotropic Microgrooved Surface. Langmuir 2019, 35, 2957–2965. [Google Scholar] [CrossRef]
- Hee Kwon, D.; Joon Lee, S. Impact and Wetting Behaviors of Impinging Microdroplets on Superhydrophobic Textured Surfaces. Appl. Phys. Lett. 2012, 100, 171601. [Google Scholar] [CrossRef]
- Yuan, Z.; Matsumoto, M.; Kurose, R. Directional Migration of an Impinging Droplet on a Surface with Wettability Difference. Phys. Rev. Fluids 2020, 5, 113605. [Google Scholar] [CrossRef]
- Deng, T.; Varanasi, K.K.; Hsu, M.; Bhate, N.; Keimel, C.; Stein, J.; Blohm, M. Nonwetting of Impinging Droplets on Textured Surfaces. Appl. Phys. Lett. 2009, 94, 133109. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, C.; Ji, B.; Park, J.; Feng, J.; Kim, S. A Magnetically Actuated Superhydrophobic Ratchet Surface for Droplet Manipulation. Micromachines 2021, 12, 325. https://doi.org/10.3390/mi12030325
Son C, Ji B, Park J, Feng J, Kim S. A Magnetically Actuated Superhydrophobic Ratchet Surface for Droplet Manipulation. Micromachines. 2021; 12(3):325. https://doi.org/10.3390/mi12030325
Chicago/Turabian StyleSon, ChangHee, BingQiang Ji, JunKyu Park, Jie Feng, and Seok Kim. 2021. "A Magnetically Actuated Superhydrophobic Ratchet Surface for Droplet Manipulation" Micromachines 12, no. 3: 325. https://doi.org/10.3390/mi12030325
APA StyleSon, C., Ji, B., Park, J., Feng, J., & Kim, S. (2021). A Magnetically Actuated Superhydrophobic Ratchet Surface for Droplet Manipulation. Micromachines, 12(3), 325. https://doi.org/10.3390/mi12030325







