Performance Analysis of Surface Reconstruction Algorithms in Vertical Scanning Interferometry Based on Coherence Envelope Detection
Abstract
1. Introduction
2. Principle and Method
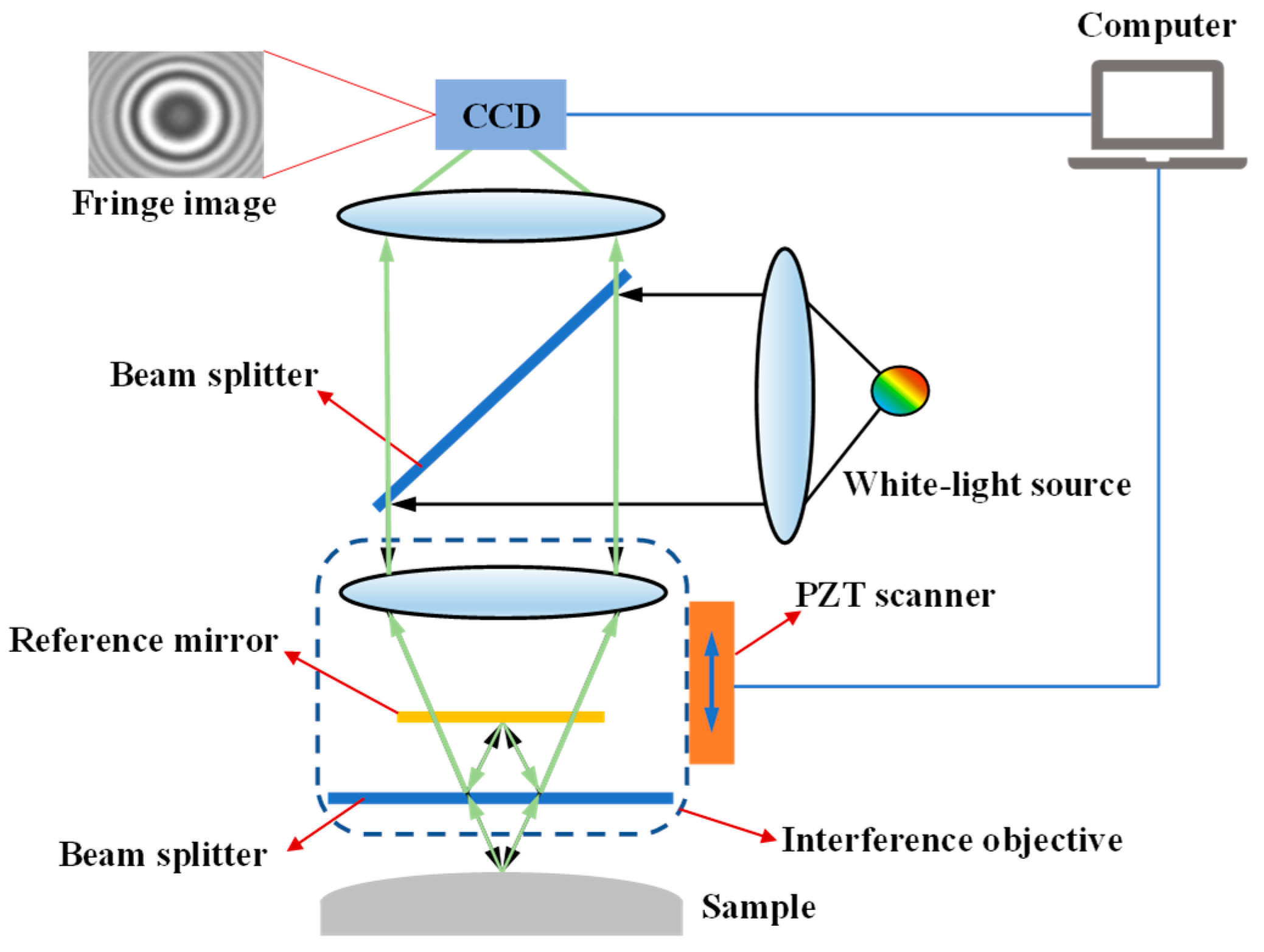
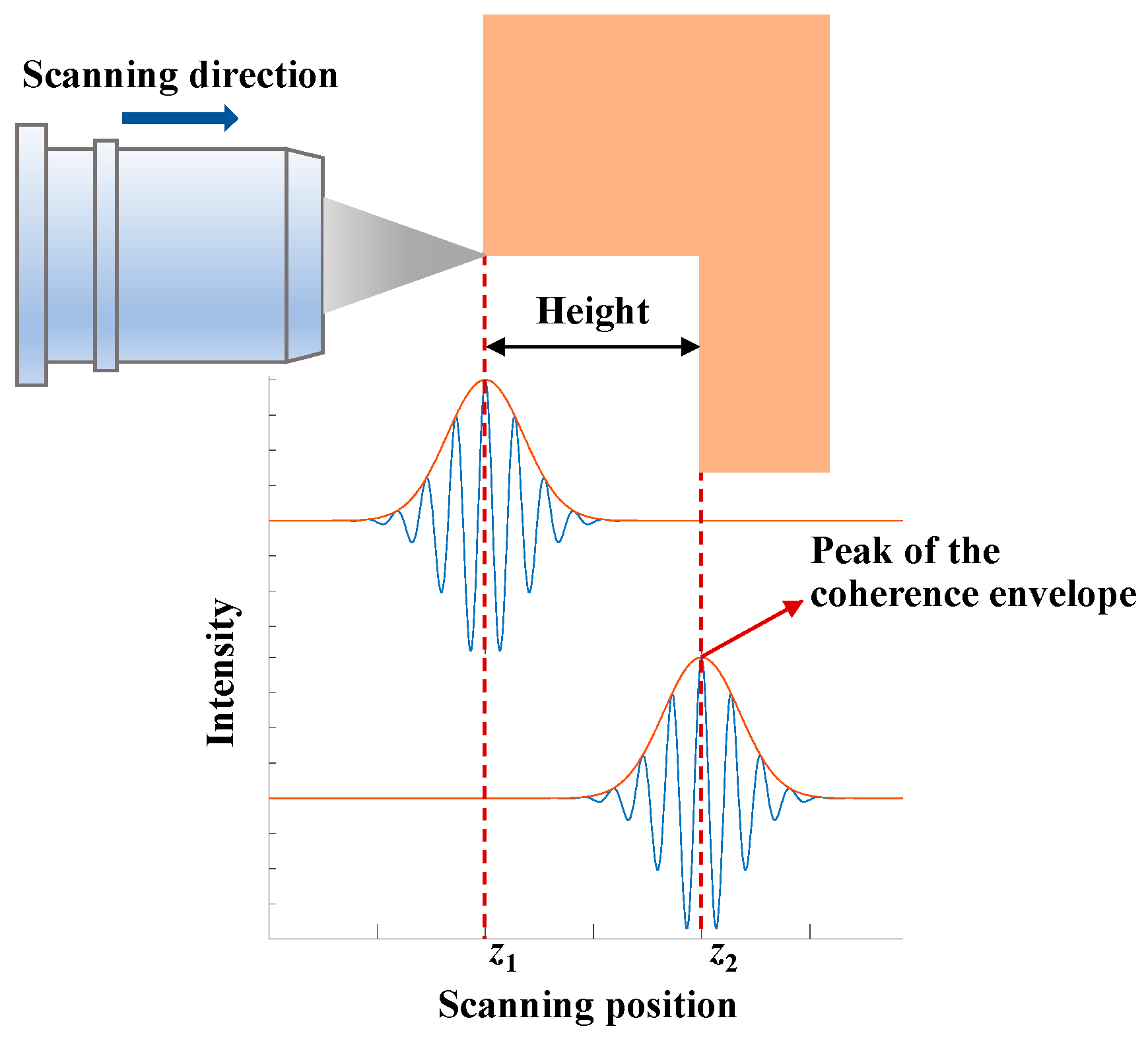
2.1. Vertical Scanning Interferometry
2.2. Fringe Analysis Algorithm
2.2.1. Centroid Method
2.2.2. Fourier Transform Method
2.2.3. Hilbert Transform Method
3. Simulation Results and Discussion
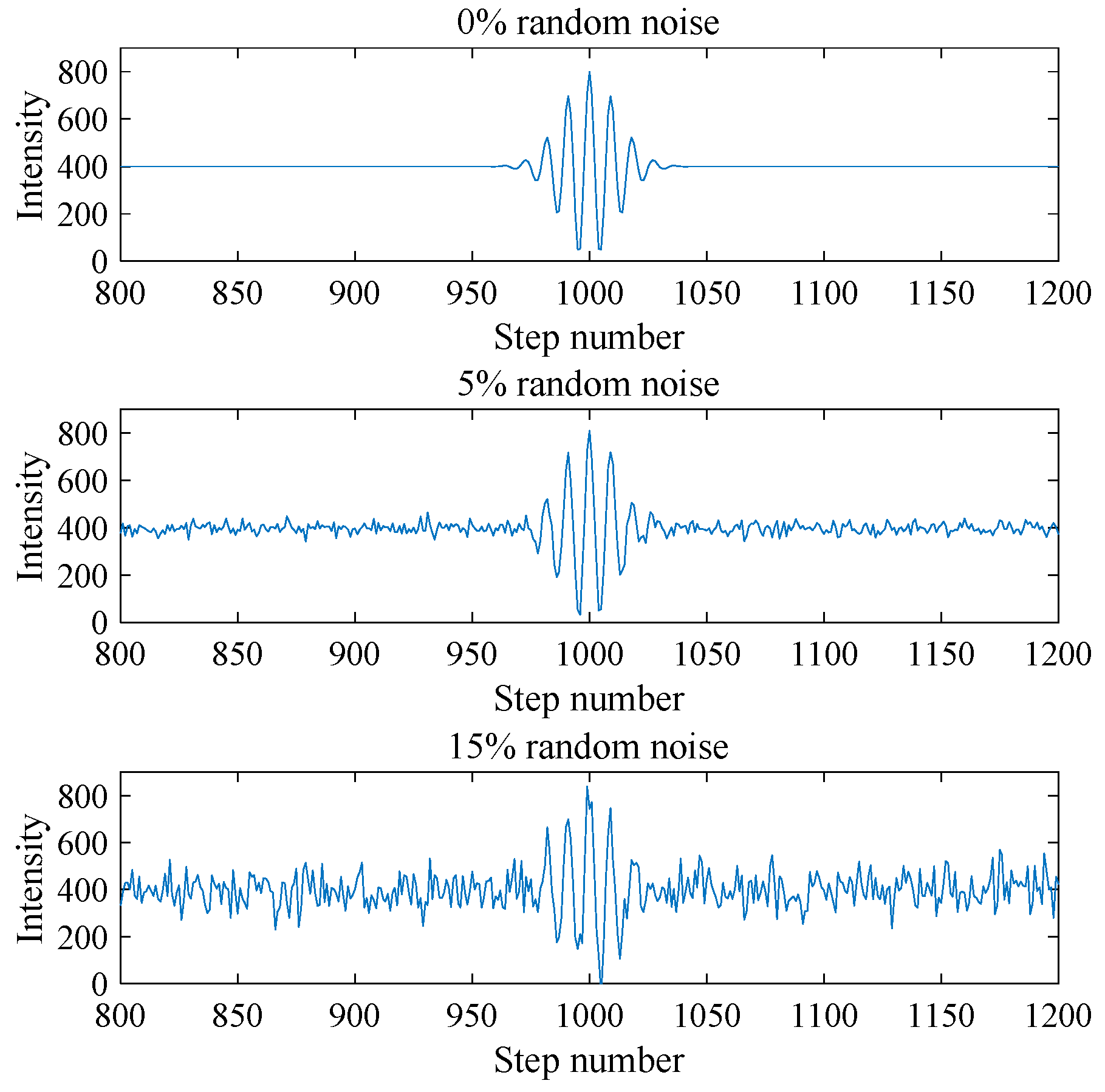
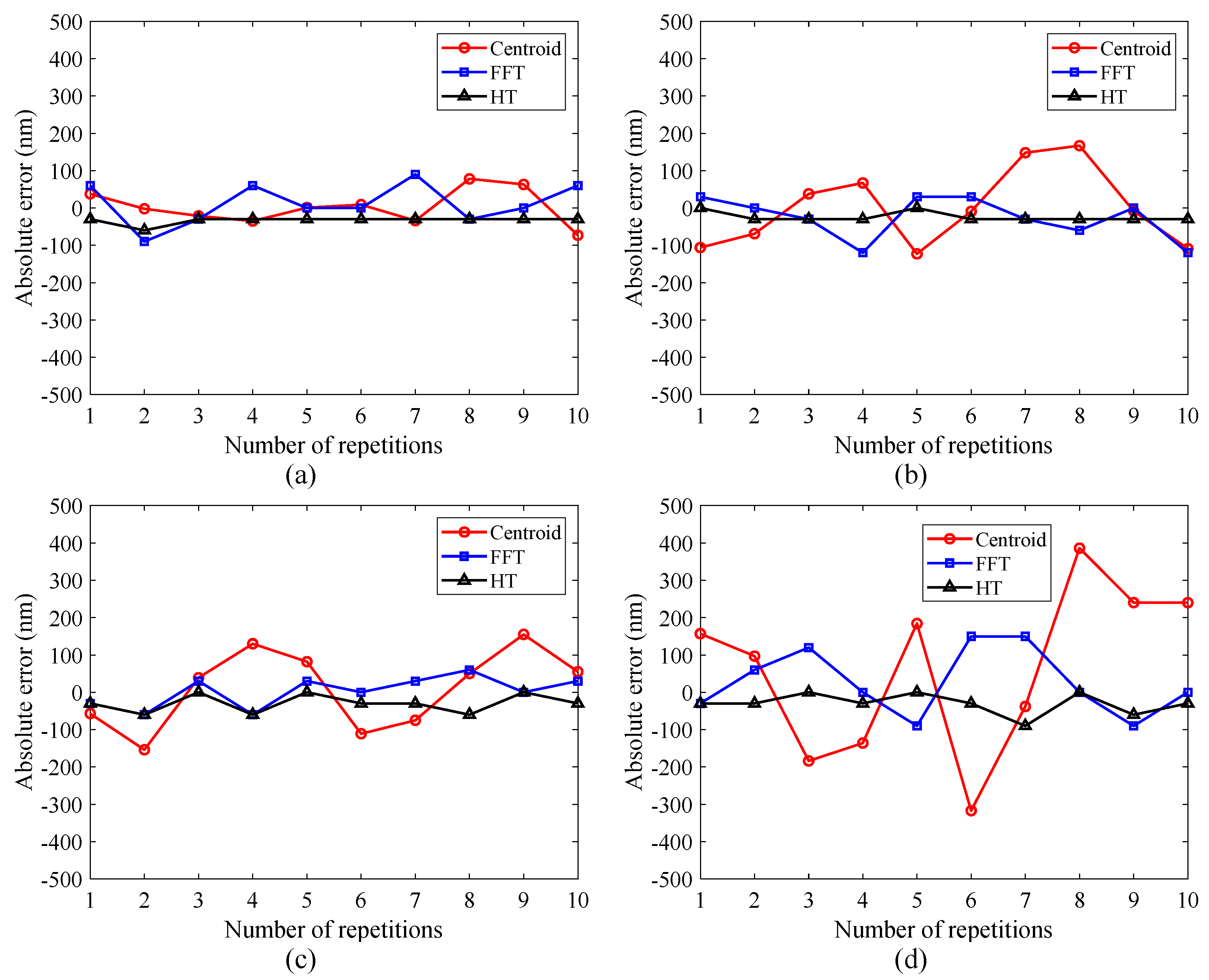
3.1. Effect of Random Noise
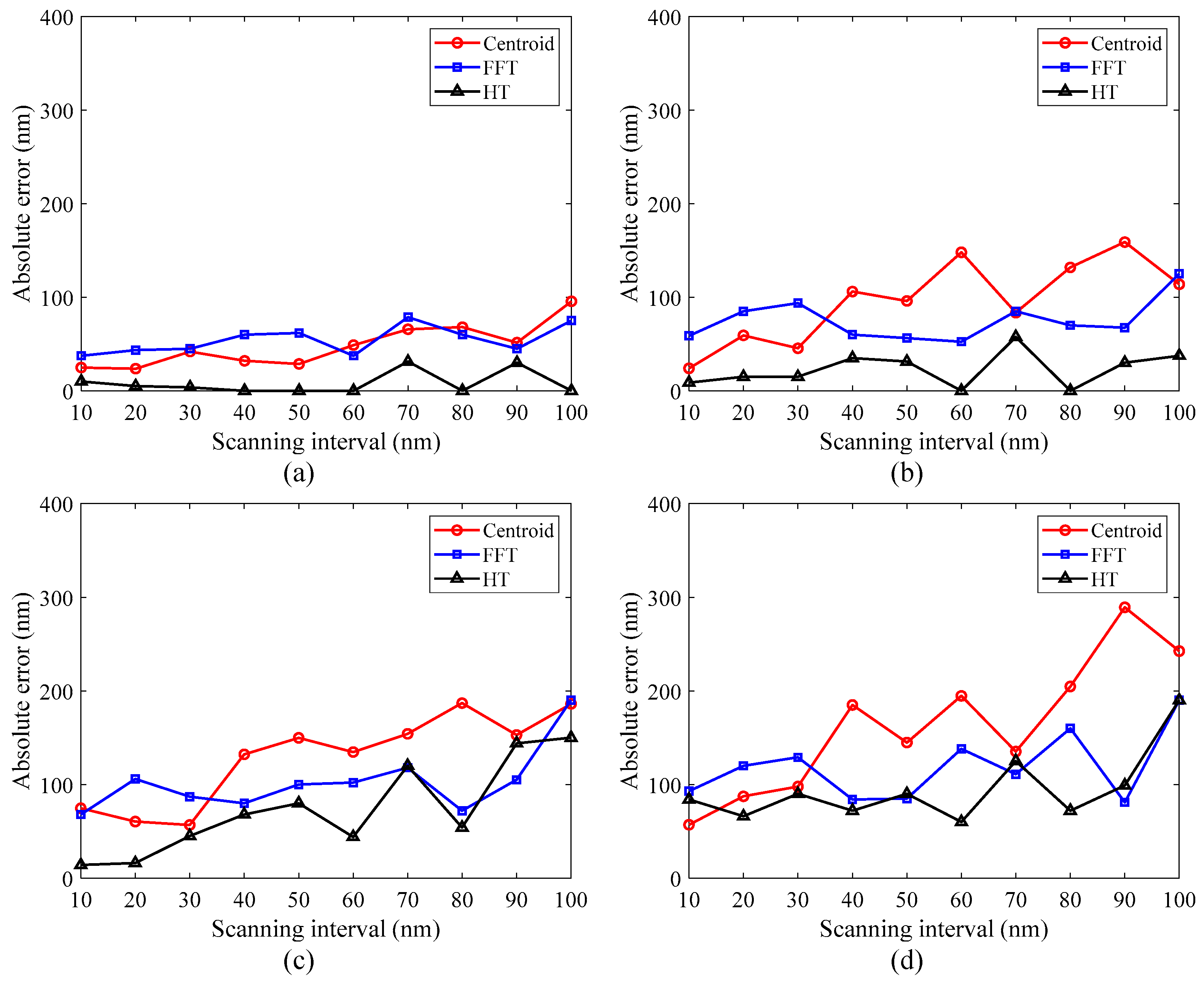
3.2. Effect of Scanning Interval
4. Experimental Verification and Discussion
4.1. Experimental Setup
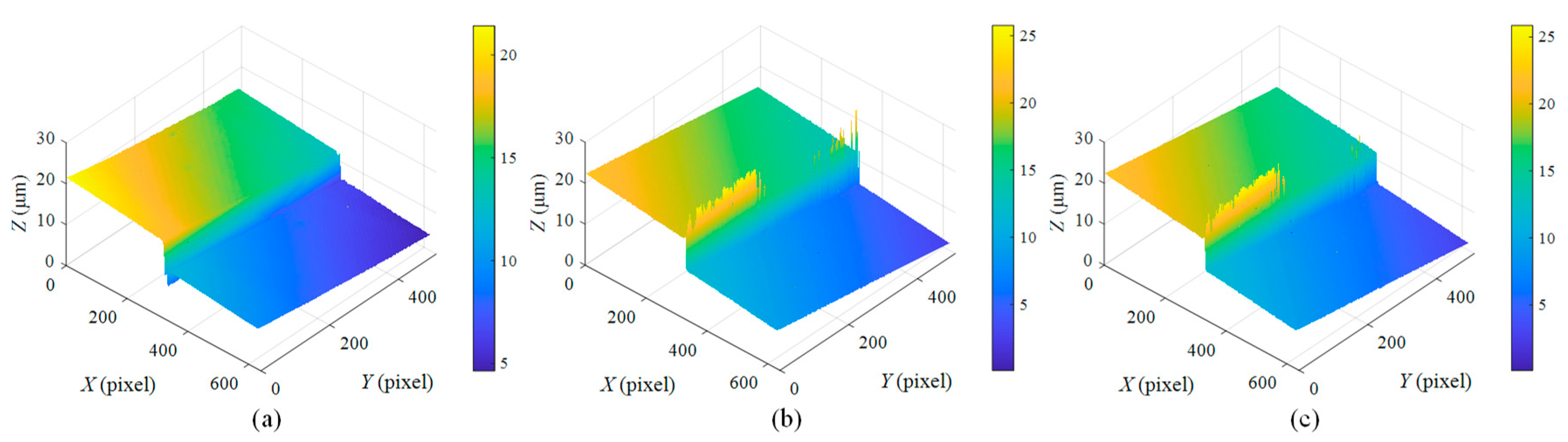
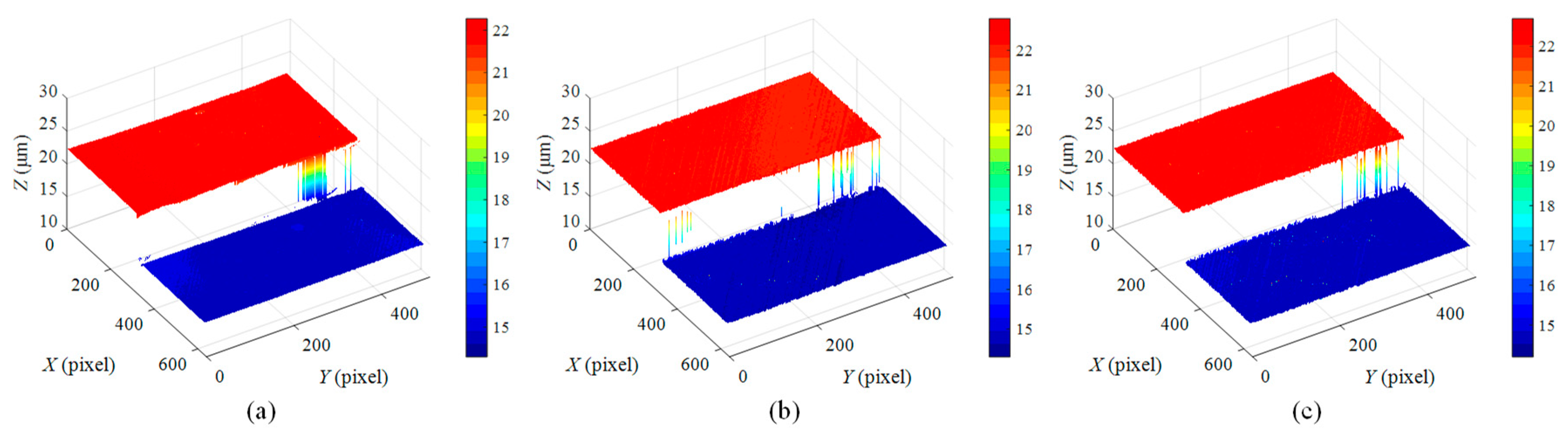
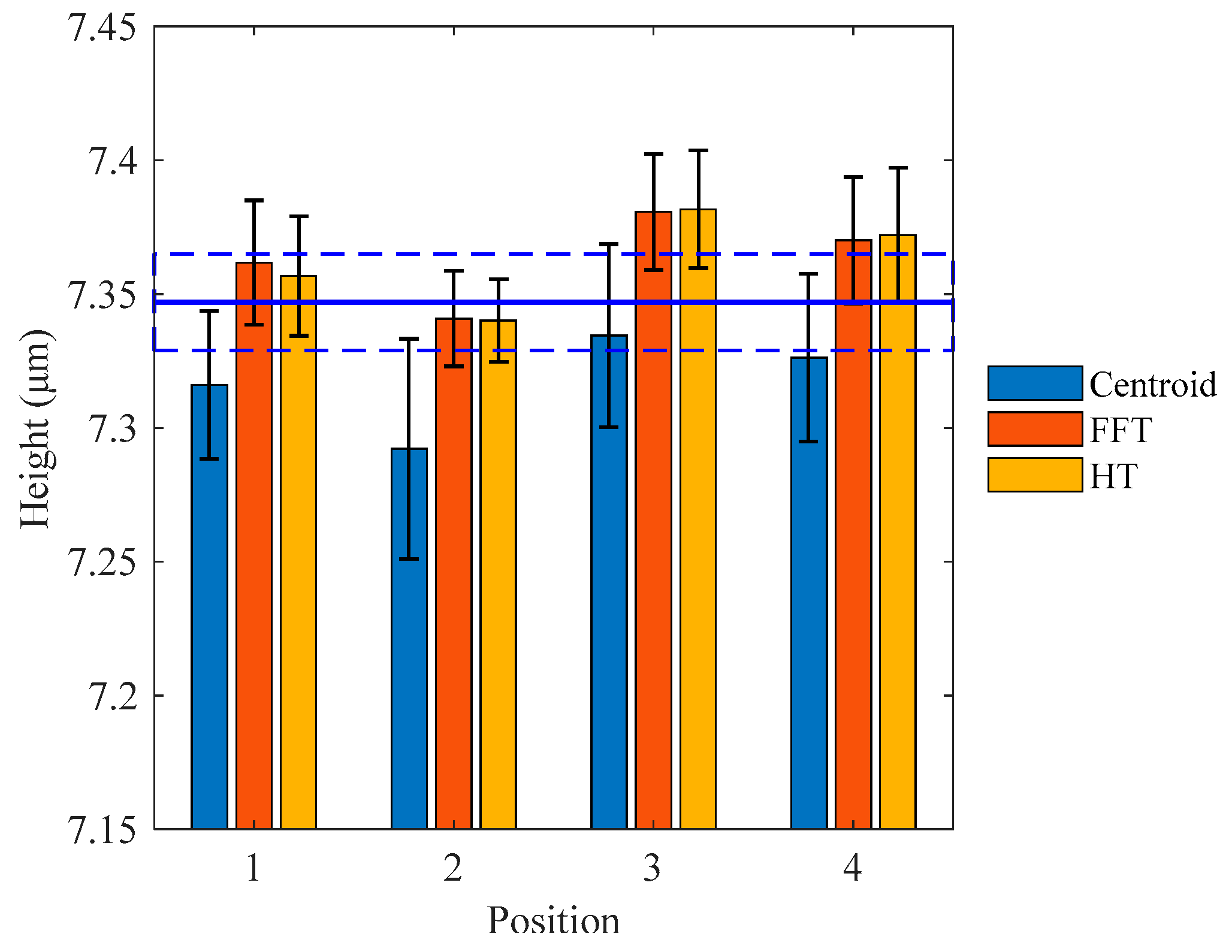
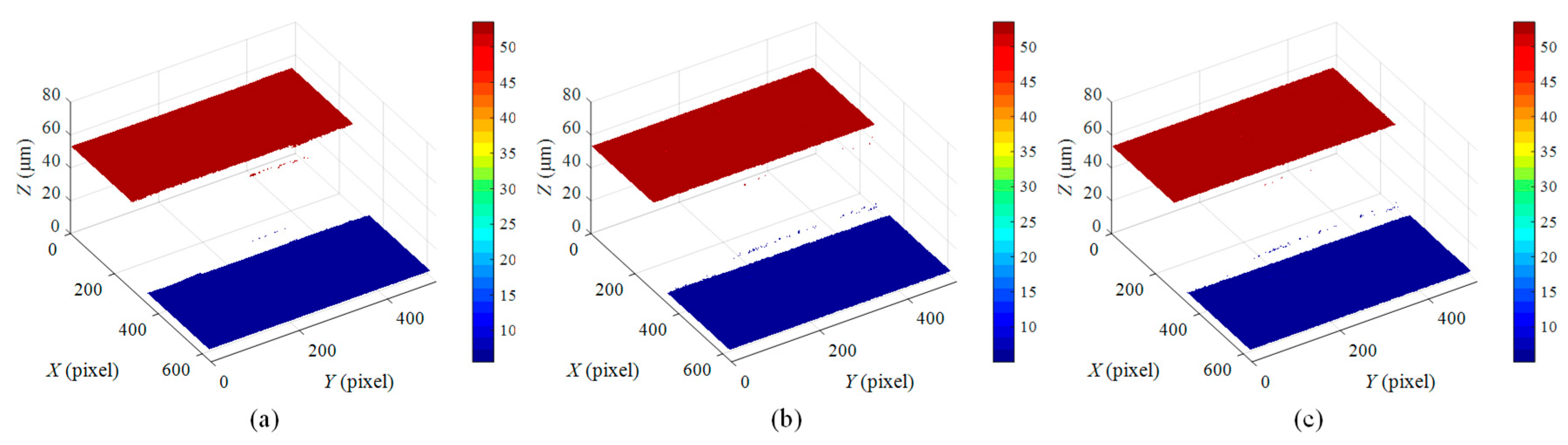
4.2. Experimental Results
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Xie, F.; Ma, S.; Dong, L. Review of surface profile measurement techniques based on optical interferometry. Opt. Lasers Eng. 2017, 93, 164–170. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, G. A review of interferometry for geometric measurement. Meas. Sci. Technol. 2018, 29, 102001. [Google Scholar] [CrossRef]
- Wu, D.X.; Fang, F.Z. Development of surface reconstruction algorithms for optical interferometric measurement. Front. Mech. Eng. 2020, 1–31. [Google Scholar]
- Fang, F.Z.; Zhang, X.D.; Weckenmann, A.; Zhang, G.X.; Evans, C. Manufacturing and measurement of freeform optics. CIRP Ann. Manuf. Technol. 2013, 62, 823–846. [Google Scholar] [CrossRef]
- Fang, F.Z.; Cheng, Y.; Zhang, X.D. Design of freeform optics. Adv. Opt. Techn. 2013, 2, 445–453. [Google Scholar] [CrossRef]
- Ghim, Y.-S.; Rhee, H.-G.; Davies, A.; Yang, H.-S.; Lee, Y.-W. 3D surface mapping of freeform optics using wavelength scanning lateral shearing interferometry. Opt. Express 2014, 22, 5098–5105. [Google Scholar] [CrossRef]
- Fuerschbach, K.; Thompson, K.P.; Rolland, J.P. Interferometric measurement of a concave, φ-polynomial, Zernike mirror. Opt. Lett. 2014, 39, 18–21. [Google Scholar] [CrossRef]
- Albero, J.; Bargiel, S.; Passilly, N.; Dannberg, P.; Stumpf, M.; Zeitner, U.; Rousselot, C.; Gastinger, K.; Gorecki, C. Micromachined array-type Mirau interferometer for parallel inspection of MEMS. J. Micromech. Microeng. 2011, 21, 065005. [Google Scholar] [CrossRef]
- Fang, F.Z.; Zeng, Z.; Zhang, X.D.; Jiang, L.L. Measurement of micro-V-groove dihedral using white light interferometry. Opt. Commun. 2016, 359, 297–303. [Google Scholar] [CrossRef]
- Zhang, T.; Gao, F.; Jiang, X. Surface topography acquisition method for double-sided near-right-angle structured surfaces based on dual-probe wavelength scanning interferometry. Opt. Express 2017, 25, 24148–24156. [Google Scholar] [CrossRef]
- Gao, F.; Muhamedsalih, H.; Jiang, X. Surface and thickness measurement of a transparent film using wavelength scanning interferometry. Opt. Express 2012, 20, 21450–21456. [Google Scholar] [CrossRef]
- Harasaki, A.; Schmit, J.; Wyant, J.C. Improved vertical-scanning interferometry. Appl. Opt. 2000, 39, 2107–2115. [Google Scholar] [CrossRef] [PubMed]
- The International Organization for Standardization. Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 604: Nominal Characteristics of Non-Contact (Coherence Scanning Interferometry) Instruments; ISO 25178-604; The International Organization for Standardization: Geneva, Switzerland, 2013. [Google Scholar]
- Park, M.-C.; Kim, S.-W. Direct quadratic polynomial fitting for fringe peak detection of white light scanning interferograms. Opt. Eng. 2000, 39, 952–959. [Google Scholar] [CrossRef]
- De Groot, P. Coherence scanning interferometry. In Optical Measurement of Surface Topography; Springer: Middlefield, OH, USA, 2011; pp. 187–208. [Google Scholar]
- Chen, S.; Palmer, A.; Grattan, K.; Meggitt, B. Fringe order identification in optical fibre white-light interferometry using centroid algorithm method. Electron. Lett. 1992, 28, 553–555. [Google Scholar] [CrossRef]
- Ai, C.; Novak, E.L. Centroid Approach for Estimating Modulation Peak in Broad-Bandwidth Interferometry. U.S. Patent 5,633,715, 27 May 1997. [Google Scholar]
- Harasaki, A.; Wyant, J.C. Fringe modulation skewing effect in white-light vertical scanning interferometry. Appl. Opt. 2000, 39, 2101–2106. [Google Scholar] [CrossRef]
- Chim, S.S.; Kino, G.S. Phase measurements using the Mirau correlation microscope. Appl. Opt. 1991, 30, 2197–2201. [Google Scholar] [CrossRef]
- Su, X.; Chen, W. Fourier transform profilometry: A review. Opt. Lasers Eng. 2001, 35, 263–284. [Google Scholar] [CrossRef]
- Dong, Z.; Chen, Z. Advanced Fourier transform analysis method for phase retrieval from a single-shot spatial carrier fringe pattern. Opt. Lasers Eng. 2018, 107, 149–160. [Google Scholar] [CrossRef]
- Wei, D.; Xiao, M.; Yang, P. Do we need all the frequency components of a fringe signal to obtain position information in a vertical scanning wideband interferometer? Opt. Commun. 2019, 430, 234–237. [Google Scholar] [CrossRef]
- Gomez, C.; Su, R.; De Groot, P.; Leach, R. Noise reduction in coherence scanning interferometry for surface topography measurement. Nanomanuf. Metrol. 2020, 3, 68–76. [Google Scholar] [CrossRef]
- Chim, S.S.; Kino, G.S. Three-dimensional image realization in interference microscopy. Appl. Opt. 1992, 31, 2550–2553. [Google Scholar] [CrossRef] [PubMed]
- Lei, Z.; Liu, X.; Chen, L.; Lu, W.; Chang, S. A novel surface recovery algorithm in white light interferometry. Measurement 2016, 80, 1–11. [Google Scholar] [CrossRef]
- Lei, Z.; Liu, X.; Zhao, L.; Yang, W.; Chen, C.; Guo, X. A rapid measurement method for structured surface in white light interferometry. J. Microsc. 2019, 276, 118–127. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Chen, Z.; Ding, Z.; Ren, H.; Nelson, J.S. Real-time phase-resolved functional optical coherence tomography by use of optical Hilbert transformation. Opt. Lett. 2002, 27, 98–100. [Google Scholar] [CrossRef] [PubMed]
- Pavliček, P.; Michalek, V. White-light interferometry—Envelope detection by Hilbert transform and influence of noise. Opt. Lasers Eng. 2012, 50, 1063–1068. [Google Scholar] [CrossRef]
- Trusiak, M.; Styk, A.; Patorski, K. Hilbert–Huang transform based advanced Bessel fringe generation and demodulation for full-field vibration studies of specular reflection micro-objects. Opt. Lasers Eng. 2018, 110, 100–112. [Google Scholar] [CrossRef]
- Gianto, G.; Salzenstein, F.; Montgomery, P. Comparison of envelope detection techniques in coherence scanning interferometry. Appl. Opt. 2016, 55, 6763–6774. [Google Scholar] [CrossRef]
- Feng, S.; Chen, Q.; Gu, G.; Tao, T.; Zhang, L.; Hu, Y.; Yin, W.; Zuo, C. Fringe pattern analysis using deep learning. Adv. Photonics 2019, 1, 025001–025007. [Google Scholar] [CrossRef]
- Larkin, K.G. Efficient nonlinear algorithm for envelope detection in white light interferometry. J. Opt. Soc. Am. A 1996, 13, 832–843. [Google Scholar] [CrossRef]
- Vo, Q.; Fang, F.Z.; Zhang, X.D.; Gao, H.M. Surface recovery algorithm in white light interferometry based on combined white light phase shifting and fast Fourier transform algorithms. Appl. Opt. 2017, 56, 8174–8185. [Google Scholar] [CrossRef]
- Kiselev, I.; Kiselev, E.I.; Drexel, M.; Hauptmannl, M. Precision of evaluation methods in white light interferometry. Correlogram correlation method. Measurement 2018, 123, 125–128. [Google Scholar] [CrossRef]
- Jiang, X. In situ real-time measurement for micro-structured surfaces. CIRP Ann. Manuf. Technol. 2011, 60, 563–566. [Google Scholar] [CrossRef]
- Li, D.; Tong, Z.; Jiang, X.; Blunt, L.; Gao, F. Calibration of an interferometric on-machine probing system on an ultra-precision turning machine. Measurement 2018, 118, 96–104. [Google Scholar] [CrossRef]
- Gao, W.; Haitjema, H.; Fang, F.Z.; Leach, R.; Cheung, C.; Savio, E.; Linares, J. On-machine and in-process surface metrology for precision manufacturing. CIRP Ann. Manuf. Technol. 2019, 68, 843–866. [Google Scholar] [CrossRef]
- Li, M.; Quan, C.; Tay, C. Continuous wavelet transform for micro-component profile measurement using vertical scanning interferometry. Opt. Laser Technol. 2008, 40, 920–929. [Google Scholar] [CrossRef]
- De Groot, P. Principles of interference microscopy for the measurement of surface topography. Adv. Opt. Photonics 2015, 7, 1–65. [Google Scholar] [CrossRef]
- Chen, S.; Palmer, A.; Grattan, K.; Meggitt, B. Digital signal-processing techniques for electronically scanned optical-fiber white-light interferometry. Appl. Opt. 1992, 31, 6003–6010. [Google Scholar] [CrossRef]
- Montgomery, P.C.; Salzenstein, F.; Montaner, D.; Serio, B.; Pfeiffer, P. Implementation of a fringe visibility based algorithm in coherence scanning interferometry for surface roughness measurement. In Proceedings of the Optical Measurement Systems for Industrial Inspection VIII, Munich, Germany, 13–16 May 2013; p. 87883G. [Google Scholar]
- Yang, S.M.; Yang, L.L.; Zhang, G.F.; Wang, T.; Yang, X.K. Modeling and calibration of the galvanometric laser scanning three-dimensional measurement system. Nanomanuf. Metrol. 2018, 1, 180–192. [Google Scholar] [CrossRef]
- Zhang, T.; Gao, F.; Muhamedsalih, H.; Lou, S.; Martin, H.; Jiang, X. Improvement of the fringe analysis algorithm for wavelength scanning interferometry based on filter parameter optimization. Appl. Opt. 2018, 57, 2227–2234. [Google Scholar] [CrossRef]
- Bruker Corporation. User Guide: Step Height Standards; Bruker Corporation: Tucson, AZ, USA, 2015. [Google Scholar]
- Petzing, J.; Coupland, J.; Leach, R. The Measurement of Rough Surface Topography using Coherence Scanning Interferometry; Good Practice Guide No.116; National Physical Laboratory: Teddington, UK, 2010; pp. 28–30. [Google Scholar]




| Method | Theoretical Height (μm) | Mean Height (μm) | Standard Deviation (μm) | Computation Time (μs) |
|---|---|---|---|---|
| Centroid | 30 | 30.063 | 0.223 | 20.8 |
| Fast Fourier transform (FFT) | 30 | 30.027 | 0.090 | 1281.8 |
| Hilbert transform (HT) | 30 | 29.970 | 0.028 | 215.5 |
| Method | Mean Height (μm) | Standard Deviation (μm) | Measurement Error (μm) | Computation Time (s) |
|---|---|---|---|---|
| Centroid | 7.317 | 0.036 | 0.030 | 8.728 |
| FFT | 7.364 | 0.026 | 0.017 | 69.515 |
| HT | 7.362 | 0.027 | 0.015 | 35.256 |
| NPFLEX | 7.339 | 0.005 | 0.008 | - |
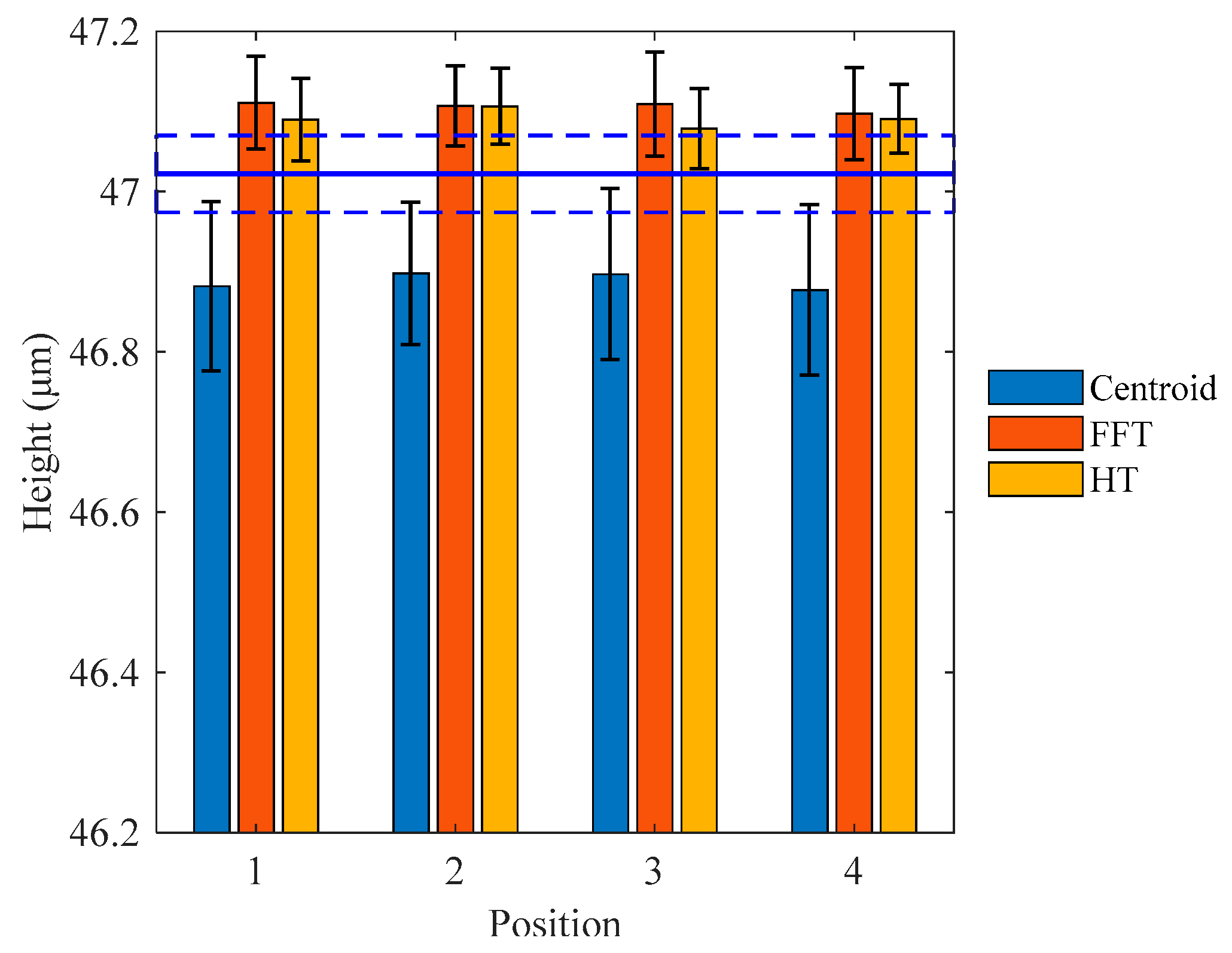
| Method | Mean Height (μm) | Standard Deviation (μm) | Measurement Error (μm) | Computation Time (s) |
|---|---|---|---|---|
| Centroid | 46.889 | 0.097 | 0.133 | 31.268 |
| FFT | 47.106 | 0.055 | 0.084 | 261.094 |
| HT | 47.092 | 0.047 | 0.070 | 126.866 |
| NPFLEX | 47.052 | 0.023 | 0.030 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Liang, F.; Kang, C.; Fang, F. Performance Analysis of Surface Reconstruction Algorithms in Vertical Scanning Interferometry Based on Coherence Envelope Detection. Micromachines 2021, 12, 164. https://doi.org/10.3390/mi12020164
Wu D, Liang F, Kang C, Fang F. Performance Analysis of Surface Reconstruction Algorithms in Vertical Scanning Interferometry Based on Coherence Envelope Detection. Micromachines. 2021; 12(2):164. https://doi.org/10.3390/mi12020164
Chicago/Turabian StyleWu, Dongxu, Fusheng Liang, Chengwei Kang, and Fengzhou Fang. 2021. "Performance Analysis of Surface Reconstruction Algorithms in Vertical Scanning Interferometry Based on Coherence Envelope Detection" Micromachines 12, no. 2: 164. https://doi.org/10.3390/mi12020164
APA StyleWu, D., Liang, F., Kang, C., & Fang, F. (2021). Performance Analysis of Surface Reconstruction Algorithms in Vertical Scanning Interferometry Based on Coherence Envelope Detection. Micromachines, 12(2), 164. https://doi.org/10.3390/mi12020164







